Theoretical Economics Letters
Vol.05 No.04(2015), Article ID:58996,9 pages
10.4236/tel.2015.54066
Coordination Always Occurs in a Two-Strategy Pure-Coordination Logit Game on Scale-Free Networks*
Tomohiko Konno
Institute of Advanced Study, Waseda University, Tokyo, Japan
Email: tomo.konno@aoni.waseda.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 July 2015; accepted 21 August 2015; published 24 August 2015
ABSTRACT
We show that coordination always occurs in scale-free networks by social local interactions regardless of the values of parameters, while it occurs in regular networks if and only if the number of links times a payoff parameter exceeds the threshold. Scale-free networks are ubiquitous in the reality. We study a two-strategy pure coordination game on networks that indicate who plays with whom. A player chooses a strategy by Logit choice and the strategies are dynamically updated. Stable steady states are investigated.
Keywords:
Games on Networks, Scale-Free Networks, Coordination Games, Local Social Interaction, Strategy Diffusion, Network Heterogeneity

1. Introduction
We study a two-strategy pure coordination game on networks that indicate who plays with whom. A player follows logit choice in the games. We show that one strategy always prevails by social local interactions regardless of the values of parameters in scale-free networks, while it prevails if and only if the condition is satisfied with regular networks, which is the number of links times payoff parameter exceeds the threshold. There are a lot of situations in which people derive benefits from choosing the same action as neighbors’ ones. We do not interact nor derive benefits directly from all the other people but our neighbors, which is a social network. We study how social networks affect coordination phenomenon. For this purpose, we study a pure coordination game in networks. We show how the heterogeneity in degree distribution affects the cooperation phenomena because real networks are typically heterogeneous. We compare the outcomes of regular networks with those of scale-free networks since regular networks are representative of homogenous networks and scale-free networks are representative of heterogeneous networks. Studying a model in scale-free networks reveals how network heterogeneity affects the outcome. A model in a scale-free network is realistic and significant because many real social networks are scale-free at least in tail distribution. A scale-freeness in tail distribution determines the outcome of a model on a network.
A regular network is a network where all the vertices have the same degree that is the number of links . A scale-free network is a network where degree distribution follows
. A scale-free network is a network where degree distribution follows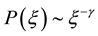 . They are illustrated in Figure 1 and Figure 2. Figure 3 illustrates a degree distribution in a logarithmic plot. We consider scale-free networks with
. They are illustrated in Figure 1 and Figure 2. Figure 3 illustrates a degree distribution in a logarithmic plot. We consider scale-free networks with  since most real scale-free networks are this type. Also the network size is infinity and there is no degree correlation in the present paper.
since most real scale-free networks are this type. Also the network size is infinity and there is no degree correlation in the present paper.
It is recently found that many social networks such as inter-firm transactions are not alike regular networks rather they are scale-free networks. For example, [1] studies the network of inter-firm transactions in Japan, which is a scale-free and hierarchical network. It is known that an underlying network structure changes an out- come of a model. The network heterogeneity affects an outcome and, in particular, scale-free networks lead to drastic changes because scale-free networks have great network heterogeneity.
Figure 1. Regular network.
Figure 2. Scale-free network.
Figure 3. Degree distribution in log-log plot.
2. The Model
There are two strategies, A and B in a coordination game. The payoff matrix is given by
 (1)
(1)
If one derives payoff from choosing the same strategy as neighbors’, it is called neighborhood effect. No extra payoff is derived by taking either strategy. We consider such a game in order to investigate how the neighbor- hood effect is strengthened by the network. No strategy is risk dominant and the payoff is symmetric in the game, because the purpose of the present paper is to investigate “pure” neighborhood effect. The case with risk dominance will be studied by our other paper.
A game with this payoff matrix has applications in reality; some examples are provided as follows. Does a player choose which of Social Network Service? PC or Macintosh? Which programming language? In these examples, payoffs arise if one chooses the same strategy as others’. Evidently, there are many kinds of goods with such neighborhood effect. This model can describes the phenomena regarding fashion by focusing on the argument that people tend to follow other people.
Let 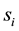 denote the strategy of player i and
denote the strategy of player i and 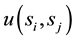 denote the payoff of player i from the game with player j. Because this is a two-strategy coordination game, we assume that
denote the payoff of player i from the game with player j. Because this is a two-strategy coordination game, we assume that  takes either
takes either 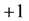 or
or  without loss of generality, each corresponds to strategy A and
without loss of generality, each corresponds to strategy A and 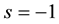 to B respectively. The payoff function
to B respectively. The payoff function  is given by
is given by
 . (2)
. (2)
A player plays the games with multiple players. The network indicates who plays the games with whom. A player is set on a vertex. Players play games only with players on adjacent vertices and extract payoff from each game. An example is illustrated in Figure 4. This is a standard for games on networks. We derive an average payoff over social interactions in some cases. On the other hand, we derive payoff from each social interaction in some cases. We are going to study such games where the payoff increases as social interactions increases.
Let the notation  denote all the players adjacent to player i. The payoff of the player i is given by
denote all the players adjacent to player i. The payoff of the player i is given by

Let 

strategy in each time step. The chosen player knows the strategies of adjacent players. We assume that player i chooses the strategy with the following Logit probability:

Figure 4. If the strategy of player i is A, then the payoff of player i is 6a. If the strategy is B, the payoff is 4a.
where 
3. The Model in a Regular Network
The analysis of the model in a regular network is discussed in detail in Appendix. If both of the probabilities of choosing strategies A and B are the same, we say that neither strategy prevails. On the other hand, if a probability of either strategy is larger than the other, we define one strategy prevails. To conclude, in regular networks with degree
• If
• If
A strategy with larger initial probability prevails in the steady state if the condition 
4. The Model in a Scale-Free Network
We will show that unlike regular networks, one strategy always prevails regardless of the values of parameters in scale-free networks. In a scale-free network, people tend to choose the same strategy by the neighborhood effect. It also holds true for a heterogeneous network.
4.1. Mean Field Approximation
We use the mean-field approximation for heterogeneous networks to solve the model in scale-free networks. The mean-field approximation is developed in our previous paper [14] to the best of our knowledge.
4.2. 
Let 










where



We solve Equation (6) to obtain the mean strategy of players with degree


We explained the neighborhood effect problem of players with degree

4.3. A Strategy of Player with Degree x
Because in mean-field approximation, a vertex with arbitrary degree 




We replace all of the 


The mean strategy of players with 

Because we already obtained

one strategy always prevails and people tend to choose the same strategy regardless of the values of parameters. The strategy with larger initial probability prevails in the steady state. This is the first main result of our paper.
Proposition 1. In the scale-free networks, one strategy always prevails regardless of the values of parameters a, 


We confirm the proposition by numerical simulations in Section 4.5.
4.4. Network Heterogeneity
The network heterogeneity and the mean degree of nearest neighbors are proportional. Therefor, the more heterogeneous a network is, the more likely one strategy prevails.
4.5. Numerical Simulations
We will confirm Proposition 1 by numerical simulations. The coordination games are done on regular network and on scale-free network. The mean degree



The results are illustrated in Figure 5. In regular network, 


4.6. Intuition: Why Does One Strategy Always Prevail Regardless of the Values of Parameters in Scale-Free Networks?
Because players on hub vertices are linked to numerous players, the difference between choosing the best strategy and otherwise is huge. One strategy always prevails in hub players es. Most vertices linked to normal vertices, which does not have big degree, are hubs. Because hub players choose the same strategy yet, players on normal vertices choose the same strategy as well. Therefore, one strategy always prevails in scale-free networks.

Figure 5. The x axis indicates the payoff parameter 

5. Concluding Remarks
We studied a coordination game in networks. We studied scale-free networks since many real networks were scale-free ones or heterogeneous ones. In regular networks, one strategy prevailed if and only if the condition was satisfied, whereas one strategy always prevailed regardless of the values of parameters in scale-free networks. This suggested that people tended to choose the same strategy in scale-free networks.
Cite this paper
TomohikoKonno, (2015) Coordination Always Occurs in a Two-Strategy Pure-Coordination Logit Game on Scale-Free Networks. Theoretical Economics Letters,05,561-570. doi: 10.4236/tel.2015.54066
References
- 1. Konno, T. (2009) Network Structure of Japanese rms. Scale-Free, Hierarchy, and Degree Correlation: Analysis from 800,000 rms. Economics.
- 2. Vega-Redondo, F. (2007) Complex Social Networks. Cambridge Univerity Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511804052
- 3. Goyal, S. (2007) Connections: An Introduction to the Economics of Networks. Princeton University Press, Princeton.
- 4. Jackson, M. (2008) Social and Economic Networks. Princeton University Press, Princeton.
- 5. Ellison, G. (1993) Learning, Local Interaction, and Coordination. Econometrica, 61, 1047-1071.
- 6. Morris, S. (2000) Contagion. The Review of Economic Studies, 67, 57-78. http://dx.doi.org/10.1111/1467-937X.00121
- 7. Alos-Ferrer, C. and Weidenholzer, S. (2008) Contagion and Efficiency. Journal of Economic Theory, 143, 251-274.
- 8. Lopez-Pintado, D. (2006) Contagion and Coordination in Random Networks. International Journal of Game Theory, 34, 371-381.
- 9. Galeotti, A., Goyal, S., Jackson, M., Vega-Redondo, F. and Yariv, L. (2010) Network Games. Review of Economic Studies, 77, 218-244.
- 10. Blume, L. (1993) The Statistical Mechanics of Strategic Interaction. Games and Economic Behavior, 5, 387-424.
- 11. Arthur, W., Durlauf, S. and Lane, D. (1997) The Economy as an Evolving Complex System II. Addison-Wesley, Reading.
- 12. Young, H. (2001) Individual Strategy and Social Structure: An Evolutionary Theory of Institutions. Princeton University, Princeton.
- 13. Brock, W. and Durlauf, S. (2001) Discrete Choice with Social Interactions. The Review of Economic Studies, 68, 235-260.
- 14. Konno, T. (2011) A Condition for Cooperation in a Game on Complex Networks. Journal of Theoretical Biology, 269 224-233. http://dx.doi.org/10.1016/j.jtbi.2010.10.033
- 15. Barabasi, A. and Albert, R. (1999) Emergence of Scaling in Random Networks. Science, 286, 509-512. http://dx.doi.org/10.1126/science.286.5439.509
- 16. Dorogovtsev, S., Mendes, J. and Samukhin, A. (2000) Structure of Growing Networks with Preferential Linking. Physical Review Letters, 85, 4633-4636.
- 17. Baxter, R. (1982) Exactly Solved Models in Statistical Mechanics. Academic Press, London.
- 18. Kubo, R. (1965) Statistical Mechanics: An Advanced Course with Problems and Solutions. North-Holland Publishing Company, Haarlem.
- 19. Greiner, W., Neise, L. and Stocker, H. (1995) Thermodynamics and Statistical Mechanics. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0827-3
- 20. Ising, E. (1925) Beitrag zur theorie des ferromagnetismus. Zeitschrift fur Physik A Hadrons and Nuclei, 31, 253-258.
Appendix A. Analysis of the Model in Regular Network
We present the result in a regular network that a strategy prevails by the neighborhood effect if and only if the condition 
We let 




The mean of strategy 

We solve the model by mean-field approximation in which the strategies taken by adjacent vertices are replaced by the average value of strategy

where


Thus, the mean of strategy, 


Because

there are only two cases that are illustrated in Figure 6 and Figure 7, in which the lines are Equation (A.5) and the curves are Equation (A.6).
We will study two cases one by one.
Figure 6. Case A.
Figure 7. Case B.
Appendix A.1. Case A:
This case is illustrated in Figure 6. The only fixed point is the origin and it is stable, because the slope of tangent hyperbolic function at the origin is less than 1. The average of the strategy over all the players in the network is

Then, 

If both strategies are equally likely,




neighborhood effect, players tend to choose one strategy, and this strategy prevails in the entire network. We show that if and only if
Appendix A.2. Case B:
This case is illustrated in Figure 7. There are three fixed points; however, the origin is an unstable fixed point because



the stable fixed points are distinguished from the unstable ones. The two stable fixed points exhibit symmetry to the origin; thus, we only need to study the positive fixed points. This case occurs if and only if

and the initial value of


To conclude, in a regular network with degree
• If
• If
NOTES
*This research was partly supported by a grant-in-aid from the Seimeikai Foundation.










