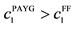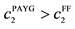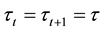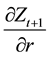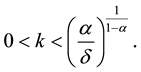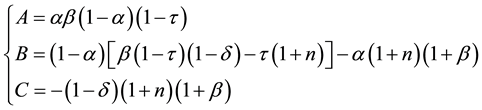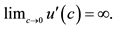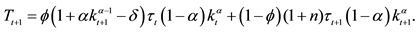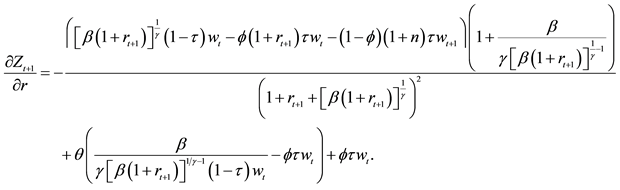Theoretical Economics Letters
Vol.04 No.09(2014), Article ID:52186,11 pages
10.4236/tel.2014.49107
Partially Funded Social Security and Inter-Generational Distribution
Hyeon Park
Department of Economics and Finance, Manhattan College, New York, USA
Email: hyeon.park@manhattan.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 October 2014; revised 23 November 2014; accepted 5 December 2014
ABSTRACT
This paper introduces a parametric model of partially funded social security system and analyzes inter-generational distribution of consumption and welfare in an OLG general equilibrium. This paper specifically aims to examine the effects of transition toward more funded system on saving and capital accumulation. It is shown that an increase in intensity of fundedness increases capital accumulation unless the income effect from interest rate change outweighs other effects and negatively affects the total saving severely. By deriving closed form solutions for the variables, this paper finds that an increase in the intensity of fundedness increases saving but decreases consumption, when population growth rate is greater than the net return to capital. This paper also finds that for a partially funded system, an increase in tax rate increases public saving but reduces private saving unambiguously, while the effects on consumption and capital accumulation are not conclusive.
Keywords:
Partially Funded Social Security, Inter-Generational Distribution, Welfare

1. Introduction
This paper introduces a parametric model of a comprehensive social security system, by which different social security plans are represented via certain degrees of fundedness. As pointed out by many researchers including Feldstein, Kunze, and Kaganovich and Zilcha [1] -[3] , the transition from an unfunded pension system to a fully funded or more funded one may be necessary due to the demographic change toward aging society1 in many developed countries. Based on this notion, this paper develops a model of a unified pension system that can directly show the transition effect of the system on many variables related with welfare and growth2. This paper particularly assumes a generic social security system financed by a payroll tax but parameterized by the intensity of fundedness. Thus given any payroll tax rate, the funded portion is to be invested for the pension income of current young for their retirement years, while the remaining portion to be transferred to current old as their pension benefits. Zero fundedness specifies PAYG system, in which all taxed amount should be used to finance pensions for the current old. If it is the case of full intensity, then the scheme specifies fully-funded social security system. Between these two extremes, there are many partially funded systems. By this model, it is possible to evaluate many types of national pension plans in which different combinations of funded and non-funded are allowed.
With the unified social security system, this paper analyzes inter-generational distribution regarding con- sumption and welfare in general equilibrium. This paper specifically compares the saving, consumption, and capital accumulation under the three different social security systems, PAYG, Fully Funded, and Partially Funded and examines the effects of alternative system on these variables. One contribution of this paper is to derive closed form solutions for these variables so that direct comparison among different systems is made possible. The solution is based on the maximization problem of two-period intertemporal choice model in an environment of OLG production economy populated by young generations who work, consume and save and the old who consume out of their personal savings and/or public pensions. It is well known that a social security system gives the old generation opportunities to smooth out consumption stream over time. However there is crowding-out effect between private saving and public saving and the effect largely depends on the size of fundedness. When the interest rate increases, given fundedness intensity, it increases public saving/transfer. But this in turn tends to decrease the incentive for private saving, while the private saving itself is subject to income and substitution effects in an inter-temporal choice when there is a change in interest rate. The result shows that increase in intensity of fundedness increases capital accumulation under the condition that the total saving would not decrease a lot from income effect which outweighs substitution effect and others with higher interest rate. Likewise the increase in intensity increases private saving but decreases consumption, when population growth rate is greater than the net return to capital. This paper also finds that, for a partially funded system, an increase in tax rate increases public saving but reduces private saving unambiguously, while the effects on consumption and capital accumulation are not conclusive.
2. The Model
2.1. Environment
Time is discrete. Consider an overlapping generation model for , where each individual lives for two periods
, where each individual lives for two periods
 i.e., the young who works, consumes and saves and the old who consumes. At each time
i.e., the young who works, consumes and saves and the old who consumes. At each time
 individuals are born and the population is grown at a rate of
individuals are born and the population is grown at a rate of
 Thus it is satisfied that
Thus it is satisfied that
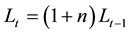 and
and
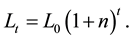 Because the individuals live for two periods, at time
Because the individuals live for two periods, at time
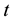 there are
there are
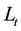 individuals who are in their first stage of life, i.e., young and
individuals who are in their first stage of life, i.e., young and
 individuals who are in their second stage. Each agent is endowed with
individuals who are in their second stage. Each agent is endowed with
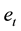 efficient unit of labor when young and earns income of
efficient unit of labor when young and earns income of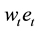 , where
, where
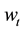 is the market determined wage rate. When the agent is old, he consumes private saving from the first period, together with social security benefit. There is no labor income in the second period. The financial income at the second period from private saving is
is the market determined wage rate. When the agent is old, he consumes private saving from the first period, together with social security benefit. There is no labor income in the second period. The financial income at the second period from private saving is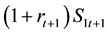 , where
, where
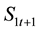 is the saving of young made at time
is the saving of young made at time
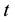 for the next period and
for the next period and
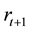 is the market determined interest rate. Let
is the market determined interest rate. Let
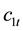
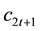
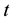
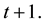

Social Security System
There is a government who implements a generic social security system financed by a payroll tax of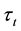
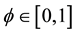
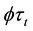

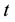


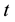
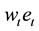
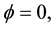
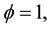
2.2. Household’s Optimization
Suppose that young households at time

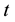
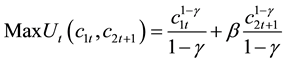
subject to

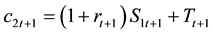
with
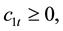


The second budget constraint shows that old households live on both private saving
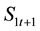
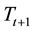
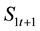
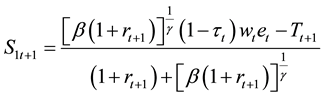
with

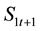
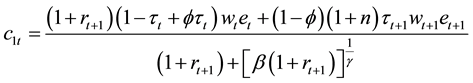
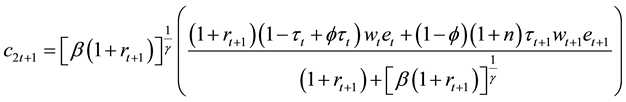
This is the solution to the household maximization problem. Before we get equilibrium with production sector, we want to look for the immediate effect of
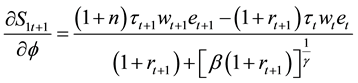
That is,
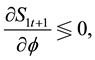
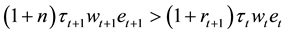
saving by the young households increases. If all the rates are fixed over short period of time, this simply tells that when
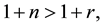
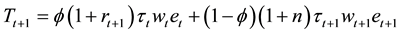
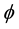
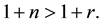
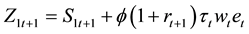
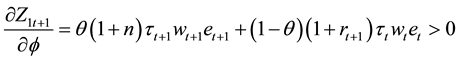
with
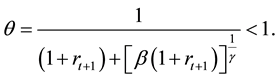
creases total saving, outweighing the possible decrease in private saving. Likewise as shown in Equation (10), the effect on consumption has the opposite direction and thus if
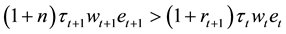
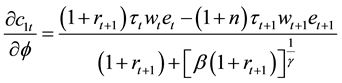
which is greater or lower than zero depending on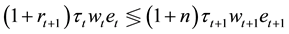
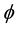
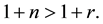
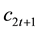


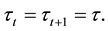
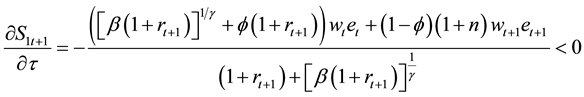
This implies that given fundedness intensity, as public saving and transfer increase, the young household’s incentive for personal saving decreases. Similarly
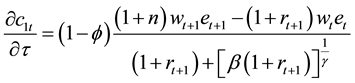
Thus

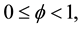
gives higher consumption among young agents when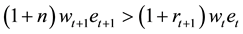
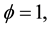
on consumption:
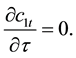

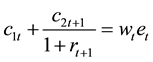
2.3. Technology and Perfect Foresight Equilibrium
We assume that the production technology is the same as in the Ramsey model8 and CRS with Inada condition is satisfied. For simplicity, let us assume that there is no technological progress. Specifically let the functional form of the technology be
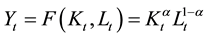
Competitive market equilibrium induces each factor price to be paid out its marginal productivity.
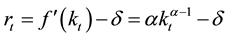
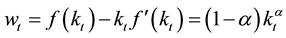
where
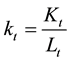

brium. In the model there are two channels of saving: private saving by households and public saving through payroll tax. The capital stock at t+1 is the amount saved by young individuals at period t plus the amount invested at
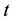
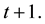
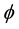

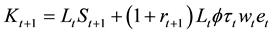
where the saving for time

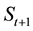
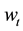
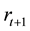
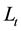
pression in capital per labor,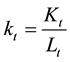
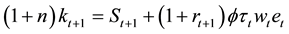
Substituting
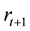
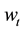
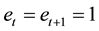
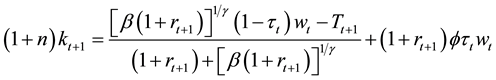
where
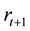


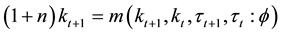
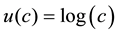

Before we study long run result through steady states from this equation, we want to revisit the question regarding the effect of

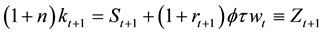
where
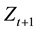

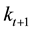
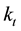
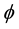

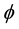


Then each of the partial derivatives is represented by the notation of
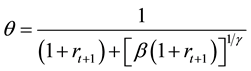
lows. Keep in mind that
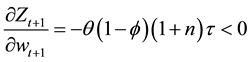
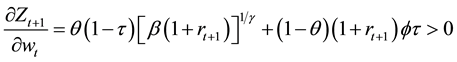
Given a value of fundedness intensity
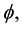
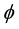
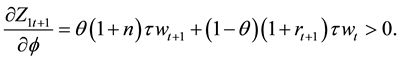
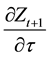
are not deterministic.
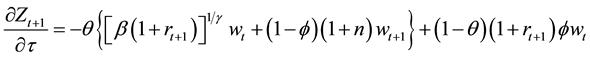
This shows that an increase in tax reduces private saving but increases public saving. The overall direction depends on the relative strength. Even more complicated effect comes from the interest rate change due to trade-
off between income and substitution effects, as well as lifecycle wealth change. That is,
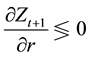
interest rate increases, given fundedness intensity, it increases publicly saved amounts through
come and substitution effects in an inter-temporal choice when there is an increase in the price, i.e.,
Together with these, it is also true that
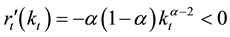
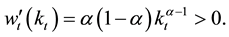
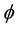
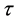
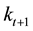
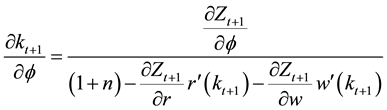


Because it is satisfied that
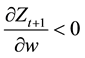
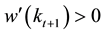

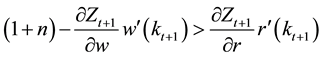
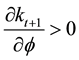
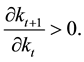
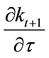

biguous.
3. Long-Run Equilibrium
In this section, we explore the long-run effect of transition toward more funded system by analyzing the change of variables at steady states. We start with the law of motion in Equation (19) steady states and analyze the effect of parameter change on the main variables studied above. Because of the implicit relation among variables, the Equation (19) does not generate closed form solutions for steady states. However, given a specific value of

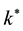
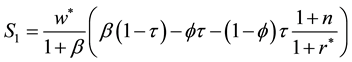


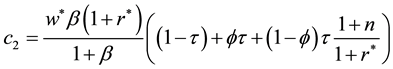
where
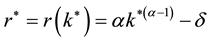

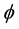
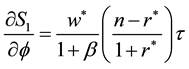
It is straight forward that given steady state wage rate and interest rate, higher fundedness intensity increases private saving if the population growth rate is greater than the steady state net return to capital. Likewise if pop-
ulation growth rate is lower than the net return, then the saving decreases:
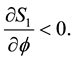
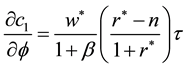
To see the effect of

motion is an implicit function of capital and fundedness intensity, we need to obtain this through implicit differentiation: from Equation (19), the partial derivative w.r.t.
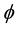
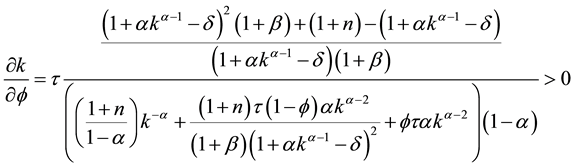
for positive net rate because
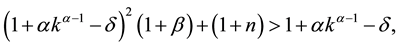

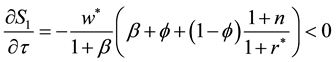
Regardless of intensity level, a higher payroll tax induces lower private saving in the long run. For the direction of consumption from tax rate is
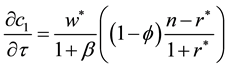
which is positive if
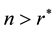
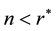


system, it is true that
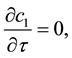
ing. Overall, the effect on consumption is not conclusive. Finally, for the effect of capital accumulation, we again use implicit differentiation to get
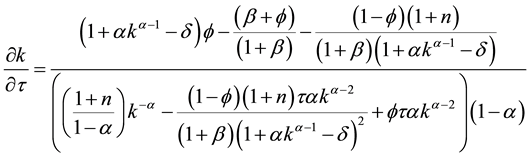
The result is ambiguous. However, for the case of
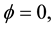

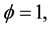
Comparison
In this subsection, we specifically compare the three social security systems, PAYG, Partially Funded and Fully Funded, in terms of the three main variables at steady states. For this comparison, it is necessary to set the initial steady states of each system at the same level:
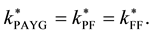
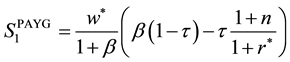

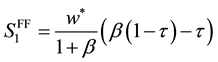
Because the first terms in each of the equations are identical, we can focus only on the second terms: because
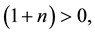
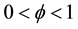
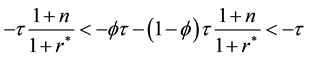
implying
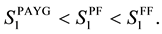
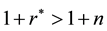
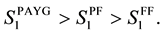

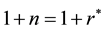
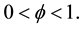

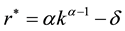
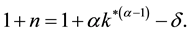

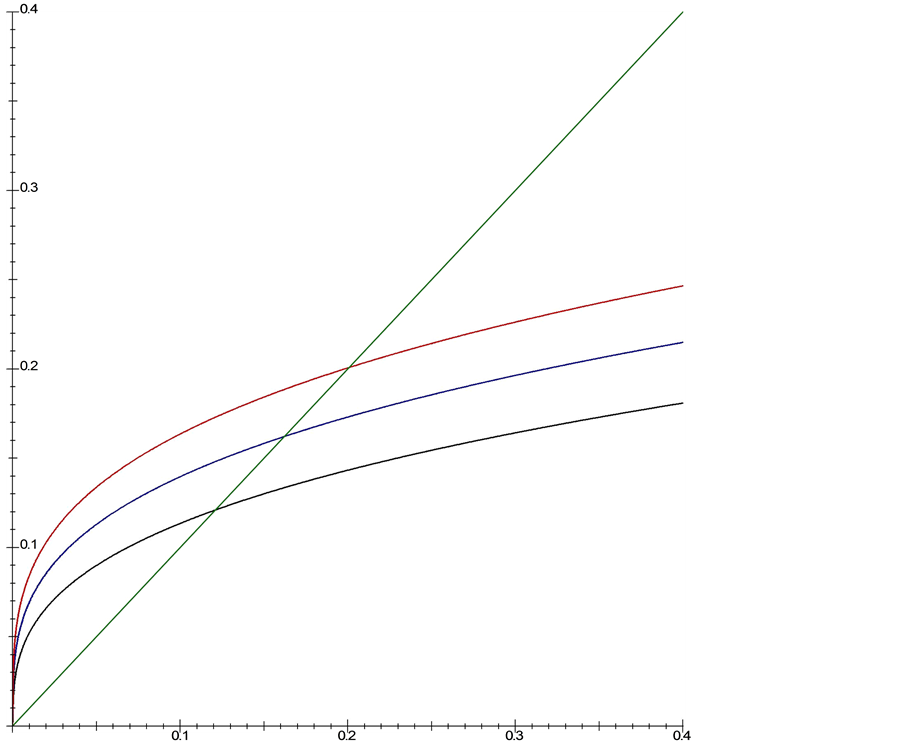
Next is the capital accumulation. Because of the interdependence of many variables, it may not be possible to get the direct comparison of steady state capital level among the different systems. Instead we want to demonstrate this numerically. Thus for the parameters of
The capital level in graph appeals to the intuitive notion that fully funded social security would give an eco- nomy a higher incentive to accumulate capital. Finally, we want to compare the welfare of the households in each system. Because we assume log utility and this function is monotonic in consumption, the first period consumption determines the relative value of the utility. From Equation (30), we obtain the relationship among the steady state consumption profiles of the three social security plans. It may be convenient to describe both the PAYG consumption and Partially Funded consumption in term of the one in the Fully Funded system. Thus we have
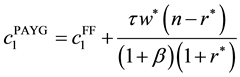
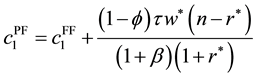
Therefore, at steady states, if
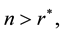
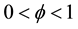
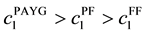
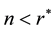



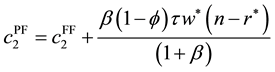
Figure 1. Steady state capital: the red curve is from
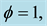
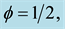
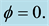
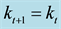
This implies that if the long term population growth rate is higher than the steady state net return to capital, then because the PAYG consumption in both periods is greater than the one in Fully Funded, PAYG utility is greater than the Fully Funded utility12, i.e.,
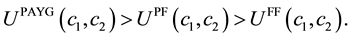
4. Conclusion
This paper develops a model of a unified social security system by which different social security plans are re- presented via certain degrees of fundedness and analyzes the inter-generational distribution of consumption and saving in general equilibrium. This paper specifically examines the effect of transition toward more funded system on capital accumulation. The result shows that as we move toward more funded system, the capital accumulation tends to increase as the total saving from both private and public savings increases. Only if the income effect from interest rate change is so strong to make the total saving decreases severely, then the more funded system may not produce this outcome. Also increase in the intensity of fundedness increases saving but decreases consumption, when population growth rate is greater than the net return to capital. This paper derives closed form solutions and demonstrates the direct effect of parameter change on many variables under different social security plans: given a partially funded plan, an increase in tax rate increases public saving but decreases private saving unambiguously, while the effect on consumption and capital accumulation are not conclusive.
References
- Feldstein, M. (2005) Structural Reform of Social Security. Journal of Economic Perspectives, 19, 33-55. http://dx.doi.org/10.1257/0895330054048731
- Kunze, L. (2012) Funded Social Security and Economic Growth. Economics Letters, 115, 180-183. http://dx.doi.org/10.1016/j.econlet.2011.11.032
- Kaganovich, M. and Zilcha, I. (2012) Pay-As-You-Go or Funded Social Security? A General Equilibrium Comparison. Journal of Economic Dynamics & Control, 36, 455-467. http://dx.doi.org/10.1016/j.jedc.2011.03.015
- Attanasio, O., Kitao, S. and Violante, G. (2007) Global Demographic Trends and Social Security Reform. Journal of Monetary Economics, 54, 144-198. http://dx.doi.org/10.1016/j.jmoneco.2006.12.010
- Aubuchon, C.P., Conesa, J.C. and Garriga, C. (2011) A Primer on Social Security Systems and Reforms. Federal Reserve Bank of St. Louis Review, 93, 19-35.
- Geanakoplos, J. and Zeldes, S. (2008) Reforming Social Security with Progressive Personal Accounts. NBER Working Paper No. 13979.
- Gonzalez-Eiras, M. and Niepelt, D. (2008) The Future of Social Security. Journal of Monetary Economics, 55, 197- 218. http://dx.doi.org/10.1016/j.jmoneco.2007.10.005
- De La Croix, D. and Michel, P. (2002) A Theory of Economic Growth: Dynamics and Policy in Overlapping Generations. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511606434
- Diamond, P. and Orszag, P.R. (2005) Saving Social Security. Journal of Economic Perspectives, 19, 11-32. http://dx.doi.org/10.1257/0895330054048722
- Jimeno, J.F., Rojas, J.A. and Puente, S. (2008) Modelling the Impact of Aging on Social Security Expenditures. Economic Modelling, 25, 201-224. http://dx.doi.org/10.1016/j.econmod.2007.04.015
- Hines, J.R. and Taylor, T. (2005) Short Falls in the Long Run: Predictions about the Social Security Trust Fund. Journal of Economic Perspectives, 19, 3-9. http://dx.doi.org/10.1257/0895330054048759
- Pecchenino, R.A. and Utendorf, K.R. (1999) Social Security, Social Welfare and the Aging Population. Journal of Population Economics, 12, 607-623. http://dx.doi.org/10.1007/s001480050116
- Lambrecht, S., Michel, P. and Vidal, J.-P. (2005) Public Pensions and Growth. European Economic Review, 49, 1261- 1281. http://dx.doi.org/10.1016/j.euroecorev.2003.09.009
Appendix
Steady States in Closed Form
The closed form solutions of steady states are obtained from the law of motion (19), setting
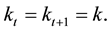
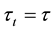
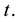
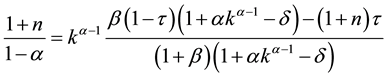
By rearranging, the closed form solution is obtained by
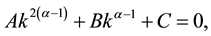
The steady state is obtained at the capital level of

Under the Fully-Funded social security system where
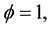
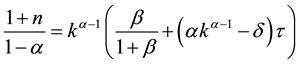
Rearranging to get

Thus we get the following closed form solution:
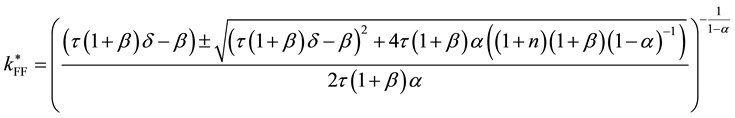
NOTES
1Regarding social security with other consideration such as aging population, see Pecchenino and Utendorf, and others [4] - [12] .
2Regarding the relationship between the size of an unfunded public pension system and economic growth, see Lambrecht, Michel, and Vidal [13] .
3The government is assumed to be in balanced budget each time.
4By this, it is satisfied that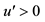
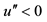
5We may want to use the term public saving for
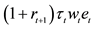
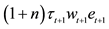
6This implies we are getting the transition effect from a less funded system to more funded one in partial equilibrium.
7The intertemporal budget constraint is
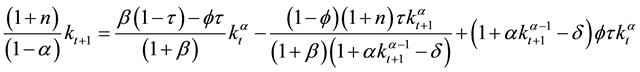
8The Ramsey model implies a representative firm in a decentralized economy with profit maximization of the following:
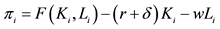
9This is because
10This implies
11
12