Theoretical Economics Letters
Vol.04 No.08(2014), Article ID:50869,11 pages
10.4236/tel.2014.48092
Preference Intensity in Positional Voting
Esther Mata-Pérez1, Annick Laruelle2,3, Ricardo Martínez4, Giovanni Ponti1,5
1Departamento de Fundamentos del Análisis Económico, Universidad de Alicante, Alicante, Spain
2Departamento de Fundamentos del Análisis EconómicoI, Universidad del País Vasco (UPV/EHU), Bilbao, Spain
3IKERBASQUE—Basque Foundation for Science, Bilbao, Spain
4Departamento de Economía y Estadística, Universidad de León, León, Spain
5Dipartimento di Economia e Finanza, LUISS Guido Carli, Roma, Italy
Email: giuba@ua.es
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 9 August 2014; revised 2 September 2014; accepted 6 October 2014
ABSTRACT
We report a laboratory experiment on strategic manipulation in positional rules, by which individuals are asked to elicit a complete ranking over 3 alternatives. The prominent rule in this set is the so-called Borda Count, but our experiment also considers other rules in which we increase the score associated to the second-best candidate and vary the monetary prizes in case of a victory of the latter (“preference intensity”). Our results suggest that, as standard game-theoretic logic would suggest, when the intermediate scores and prizes increase, strategic manipulation is reduced. We also see that group size affects the likelihood of strategic manipulation in a non-linear fashion, and mostly depends on how the intermediate score is manipulated. Furthermore, rule efficiency increases with group size (i.e., as the probability of being pivotal decreases) and with both the intermediate scores and prizes.
Keywords:
Strategic manipulation, Borda Count, positional voting, Experimental Economics

1. Introduction
Strategy proofness, or non-manipulability, is a very desirable property for a voting mechanism, as it requires that no individual gets a benefit from misrepresenting her “true” preferences. We know from Gibbard [1] and Satterth Waite [2] that there is no voting mechanism—other than the dictatorial one—that is strategy-proof when voters are allowed to submit any ranking of candidates and every candidate has the chance to be elected at least once. Notwithstanding, the extent of manipulability for specific voting rules is essentially an empirical matter. By the same token, it should also be checked empirically if (and how) strategic manipulation affects the allocation efficiency induced by the voting rule.
The aim of this paper is to contribute to this literature by designing and conducting an experiment on a popular family of voting rules, called positional, which are used to select one out of multiple (i.e., more than two) alternatives. A positional rule requires voters to assign decreasing scores from the best to the worst alternative. The alternative collecting the highest cumulative score wins the contest, with ties resolved by a random draw.
The possibilities of strategic manipulation have been studied both theoretically (Ludwin [3] , Kube and Puppe [4] ) and experimentally. The experimental papers closest to ours are those of Forsythe et al. [5] and Bassi [6] , who focus on the comparison among Borda Count, plurality voting and approval voting rules. In our experiment, a voting committee of a variable size (2, 4, or 8 voters, respectively) has to select one out of three alternatives, A, B, or C. The committee’s individual preferences are equally split into two alternative profiles: half of the voters prefers A to B, and half of the voters prefers B to A, while C corresponds to the worst option for everybody. In all voting rounds, subjects are asked to submit a full ranking over the three available options. In our experiment that consists of four treatments, we study how strategic manipulation is affected by i) grour size; ii) the intermediate score (i.e., the score associated with the second option in the ranking) and, most importantly; by iii) the monetary prize voters get when the second most preferred candidate wins (this is what we label as “preference intensity”). By the first treatment condition, we are able to compare, with the same game-form, Borda-type mechanisms with a voting scheme closer to anti-plurality voting. By the latter condition, we manipulate the incentives for strategic manipulation. As we explain in Appendix A, standard game-theoretic reasoning predicts a reduction in strategic voting as the intermediate score and prize increase (as the opportunity costs of sincere voting are reduced). However, the effect (and direction) of an increase in the group size in subjects’ willingness to vote strategically is uncertain, besides the simple observation that, as group size grows, the likelihood of being pivotal decreases, which, in turn, may reduce the incentive for strategic manipulation (Duffy and Tavits [7] )1.
The remainder of the paper is arranged as follows. Section 2 describes our experimental environment, while Section 3 summarizes our main findings. Here we report that strategic manipulation varies across treatments according with standard game-theoretic reasoning, as we just defined. We also detect (see Section 3.4) that efficiency (measured by the relative frequency of outcomes in which the last-best outcome C does not win the contest) is increasing with both group size and the intermediate score, alongside what common sense would also predict for sincere voting (as strategic voting, even more when the intermediate prize is high, increases the likelihood of option C winning the election). By contrast, we also see that size effects are comparatively low, and also vary with preference intensity, decreasing (increasing) strategic manipulation when the value of the intermediate prize is low (high), respectively. Finally, Section 4 concludes, followed by Appendices reporting a standard game-theoretic analysis of our game-forms and the experimental instructions.
2. Design
2.1. Sessions
We run 5 sessions at the Laboratory of Theoretical and Experimental Economics (LaTEx), of the Universidad de Alicante. A total of 120 students (24 per session) were recruited among the undergraduate population of the Universidad de Alicante. The experimental sessions were computerized. Instructions were provided by a self-paced, interactive computer program that introduced and described the experiment; subjects were also provided with a written copy of the instructions2.
2.2. Game-Form
The experimental protocol mimics voting of small committees of 2, 4 or 8 players. Players have to rank, simultaneously and independently, a set of three alternatives A, B and C. The protocol assigns 1 (α) [0] points to the best (intermediate) [worst] alternative, respectively. The score of the intermediate option,
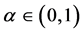 defines a positional mechanism, ranging from plurality rule (α = 0); Borda count (α =1 /2); to anti-plurality voting (α = 1). The sum of scores over all players is computed for each alternative, and the alternative receiving the largest amount of points wins the voting game. In case of a tie between two or three candidates for the highest score, the winner is determined through a uniform random draw.
defines a positional mechanism, ranging from plurality rule (α = 0); Borda count (α =1 /2); to anti-plurality voting (α = 1). The sum of scores over all players is computed for each alternative, and the alternative receiving the largest amount of points wins the voting game. In case of a tie between two or three candidates for the highest score, the winner is determined through a uniform random draw.
Preferences for a candidate are artificially induced by different monetary prizes; 1 (x) [0] points to the first (second) [third] best alternative. The monetary payoff associated with the second best,
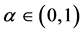 ,
,
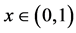 is our second treatment variable, which we label as preference intensity.
is our second treatment variable, which we label as preference intensity.
Appendix A reports a standard game-theoretic analysis of our experimental treatments, by evaluating all Nash equilibria that survive the iterative deletion of weakly dominated strategies of the 2-player versions of our voting protocol, as a function of our parameter pair,
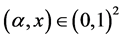 There we see that 1) symmetric sincere voting is never an equilibrium; 2) strategic voting (i.e., placing the worst candidate second) belongs to the support of all equilibria and corresponds to the unique symmetric equilibrium when α < 1/2; and 3) when α and x grows, individual incentives for strategic manipulation are reduced, in that the game is strategically equivalent to an anti-coordination game whose equilibria require one player playing sincerely, while the other playing strategically3.
There we see that 1) symmetric sincere voting is never an equilibrium; 2) strategic voting (i.e., placing the worst candidate second) belongs to the support of all equilibria and corresponds to the unique symmetric equilibrium when α < 1/2; and 3) when α and x grows, individual incentives for strategic manipulation are reduced, in that the game is strategically equivalent to an anti-coordination game whose equilibria require one player playing sincerely, while the other playing strategically3.
2.3. Treatments
A realization of the pair (α, x) defines a (between-subject) experimental treatment. We run five sessions under four different treatments, TR1 to TR4 (two sessions in case of TR2), parametrized as follows: TR1 = (0.5, 0.25), TR2 = (0.5, 0.5), TR3 = (0.5, 0.75), TR4 = (0.75, 0.5). In words: α = 0.5 corresponds to the Borda Count, where α = 0.75 approaches anti-plurality voting (which corresponds to α = 1, i.e., discarding the least preferred option).
2.4. Matching
In each session, subjects are randomly divided into 3 matching groups (cohorts) of 8, with subjects from different cohorts never interacting with each other throughout the session. In each session, subjects play 40 rounds of one treatment of the voting game. Within each round t = 1, ..., 40, group size within a cohort is randomly de-
termined. Let perio
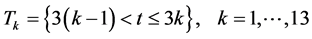 be the subsequence of the kth 3 rounds. Within each
be the subsequence of the kth 3 rounds. Within each
period
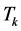 subjects experience each possible group size
subjects experience each possible group size
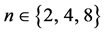 with the sequence being different for each cohort, to keep under control the time distance between two rounds characterized by the same value of n. As for preference distribution, exactly half of the subjects receives the highest prize if either A or B wins, while a victory of C is associated with a zero payoff for all. Given this design feature, in what follows we shall define the type of a player, A or B, depending on the identity of her preferred option. The same preferences distribution is maintained in all groups and for all sizes. Player type, A or B, is fixed during all the session. This specific matching protocol is publicly announced at the beginning of the experiment.
with the sequence being different for each cohort, to keep under control the time distance between two rounds characterized by the same value of n. As for preference distribution, exactly half of the subjects receives the highest prize if either A or B wins, while a victory of C is associated with a zero payoff for all. Given this design feature, in what follows we shall define the type of a player, A or B, depending on the identity of her preferred option. The same preferences distribution is maintained in all groups and for all sizes. Player type, A or B, is fixed during all the session. This specific matching protocol is publicly announced at the beginning of the experiment.
2.5. Financial Rewards
All monetary payoff in the experiment are expressed in Spanish pesetas (€1 is about 166 pesetas). Subjects receive 1000 pesetas just to show up, to which they sum up all their cumulative earnings throughout the 40 rounds of the experiment. As for payment, the payoff parametrization of Section 2.2 is multiplied by 100. Average earnings in the experiment were about € 12, for experimental sessions lasting for approximately 45 minutes.
3. Results
3.1. Aggregate play
Table 1 reports average frequency of strategy use across treatments.
As Table 1 shows, frequencies of sincere and strategic votes are much higher than those of all other strategies combined, which, in what follows, will be considered as a “residual strategy”. We also notice that strategy ma-nipulation is the highest in Borda Count, especially in TR1 and TR2, when the intermediate prize is compara
Table 1. Average frequency of strategy use disaggregated for treatments.
tively low. This is perfectly in line with the game-strategic analysis reported in Appendix A.
Figure 1 tracks the evolution of strategic behavior across periods.
As Figure 1 shows, strategic manipulation grows with time, this effect being stronger in the Borda Count treatments (TR1 to TR3), and within this set, the lower is the intermediate prize (i.e., TR1 through TR3, when the opportunity cost of manipulating is lower, see Appendix A). These results are in line with the finding of Bassi (2014), who detects higher manipulation in the case of the Borda Count with respect to approval voting (the rule which is closer to our “high intermediate prize”, T4). In this respect, Figure 1 also shows that, when strategic conditions are more favorable (above all, in TR1 and TR2), we detect a strong learning effect in favor of strategic manipulation.
3.2. Individual behavior
In light of the aggregate data presented in Section 3.1, Table 2 shows the estimates of a panel data logit regression (with random individual effects) where the dependents variables, STRAT, SINC and OTHER, are binary variables indicating whether an individual voted sincerely, strategically or chose an action different from strategic or sincere, respectively. We include in the set of regressors our treatment variables, α and x, together with the group size and the voting round. Except for the latter, all regressors are dummies (i.e., we allow for non-linear relations between our regressors and the dependent variables).
As Table 2 shows, strategic voting increases (decreases) with time (α and x), respectively. As for the latter, this result is consistent with the theoretical analysis of Appendix A, in that subjects’ likelihood to play strategically seems aligned to a great extent with the strategic incentives by which strategic manipulation pays off. We also see that this tendency gets stronger as time proceeds.
The “size effect” deserves a separate discussion. As Table 2 shows, moving from 2 to 4 players boosts strategic manipulation significantly—this in contrast with the commonsense argument we proposed in the introduction. By contrast, moving from 4 to 8 has the opposite effect, so that the 8-player dummy is no longer significant4.
This (somewhat puzzling) result requires further investigation. To this aim, Figure 2 shows the “box plots” representing the distribution of subjects’ relative frequencies of strategic behavior across the four treatment conditions, disaggregated for group size5.
As Figure 2 shows, strategic behavior has a more pronounced positive (negative) trend in T3 (T2), respectively, although seems negligible in all four treatment conditions. This preliminary conclusion is reinforced by looking the estimates of Table 3, where we estimate the probability of strategic play is estimated by way of a random-effect logit regression for each (between-subject) treatment, maintaining group size and period as common regressors.
The estimates of Table 3 show that group effects strongly depend on preference intensity, in that the lower is
Figure 1. Evolution of aggregate behavior disaggregated for treatment and group size.
Figure 2. Distributions of strategic play (averaged across subjects), disaggre- gated for treatment and group size.
x—theoretically, the best condition for strategic manipulation—the higher is the tendency of subjects to play sincerely when group size increases. By contrast, no group significant group effect emerges when x = 0.5, where the case of x = 0.75 is characterized by a significant increase—specifically, moving from n = 2 to n = 4—of strategic manipulation.
Table 2. Logit regressions.
Robust standard errors in parentheses, clustered at cohort level. *** p < 0.01, ** p < 0.05, * p < 0.1.
Table 3. Logit regressions.
Robust standard errors in parentheses, clustered at cohort level. *** p < 0.01, ** p < 0.05, * p < 0.1.
3.3. Efficiency
Lehtinen [11] claims, by way of numerical simulations, that strategic voting in the case of positional voting mechanisms is welfare increasing and that it is less welfare increasing when the second-placed utilities for the second-best candidates are midway between the best and the worst, i.e. intensity of preferences matter.
In the specific parametrization we use, with an equal split between type A and type B players, and uniform payoff across types (see Appendix A), a natural measure for ex-post efficiency can be considered as the relative likelihood of the worst available option, C, winning the contest6. To this aim, for each voting game, we define a variable, EFF index, which takes the value of 1 if A or B win (or tie), 2/3 if there is a tie between all candidates, 1/2 if C wins with either A or B, and 0 if C wins alone.
Figure 3 tracks the evolution of our efficiency index, disaggregated for treatment and group size. As Figure 3 shows, efficiency seems to decrease with time (i.e., when strategic behavior increases), especially when n = 2. On the other hand, group size seems to have a significant impact on efficiency: although it does not seem to directly impact the overall rate of sincere play, it seem crucial in avoiding the coordination failure associated with strategic play, i.e., the associated likelihood for the last-best to be selected.
By analogy with previous analysis, in Table 4 we estimate a (random-effect) ordered log it by which our effi-
Figure 3. Evolution of EFFindex, disaggregated for treatment and group size.
Table 4. Orderedlogit regressions of EFF index. Robust standard errors in parentheses, clustered at cohort level.
Robust standard errors in parentheses, clustered at cohort level. *** p < 0.01, ** p < 0.05, * p < 0.1.
ciency index is regressed against our common set of explanatory variables.
Table 4 reports two regressions, one using the entire dataset, the other only considering the evidence for the Borda Count (i.e., excluding TR4). The estimations of Table 4 confirm that efficiency falls with time, and grows with α x and n. In other words, 1) Lehtinen’s (2007) is not supported by our data, while 2) our commonsense conjecture, although does not seem to hold when looking at individual behavior, works with efficiency: as the group goes large, the likelihood of inefficient outcomes falls.
4. Conclusion
Paraphrasing Jean-Charles De Borda’s famous quote, our experiment indicates that positional voting rules make subjects rather prone to behave “dishonestly”, shaping their elicited ranking to strategic considerations. As our results show, the textbook game-theoretic analysis of our game-forms is sufficient to explain much of subjects’ variability in behavior across treatments, at least once the usual amount of noise, typical of experimental data has been accounted for. We also report a non-linear size effect, also typical of other experimental environments (take Selten [8] or Huck et al. [9] for example), which surely calls for further investigation, so it is the case for the robustness of our results under different parametrizations and most crucial preference distributions.
Acknowledgments
We thank Max Ferraresi and Andrea Succi for their precious research assistance. The usual disclaimers apply. Financial support from the Spanish Ministries of Education and Science and Economics and Competitiveness (SEJ 2007-62656 and ECO2012-34928, ECO2011-29355, and ECO2011-29230), MIUR (PRIN 20103S5RN3\_ 002), Generalitat Valenciana (Research Projects Gruposo3/086 and PROMETEO/2013/037), Junta de Andalucía (SEJ5980 and SEJ4941), and Instituto Valenciano de Investigaciónes Económicas (IVIE) is gratefully acknowledged.
References
- Gibbard, A. (1973) Manipulation of Voting Schemes: A General Result. Econometrica, 41, 587-601. http://dx.doi.org/10.2307/1914083
- Satterthwaite, M. (1975) Strategy-Proofness and Arrow’s Conditions: Existence and Correspondence Theorems for Voting Procedures and Social Welfare Functions. Journal of Economic Theory, 10, 187-217. http://dx.doi.org/10.1016/0022-0531(75)90050-2
- Ludwin, W.G. (1978) Strategic Voting and the Borda Method. Public Choice, 33, 85-90. http://dx.doi.org/10.1007/BF00123946
- Kube, S. and Puppe, C. (2009) (When and How) Do Voters Try to Manipulate?: Experimental Evidence from Borda Elections. Public Choice, 139, 39-52. http://dx.doi.org/10.1007/s11127-008-9376-9
- Forsythe, R., Rietz, T., Myerson, R. and Weber, R. (1996) An Experimental Study of Voting Rules and Polls in Three- Candidate Elections. International Journal of Game Theory, 25, 355-383. http://dx.doi.org/10.1007/BF02425262
- Bassi, A. (2014) Voting Systems and Strategic Manipulation: An Experimental Study. Journal of Theoretical Politics, Online First. http://dx.doi.org/10.1177/0951629813514300
- Duffy, J. and Tavits, M. (2008) Beliefs and Voting Decisions: A Test of the Pivotal Voter Model. American Journal of Political Science, 52, 603-618. http://dx.doi.org/10.1111/j.1540-5907.2008.00332.x
- Selten, R. (1973) A Simple Model of Imperfect Competition, Where 4 Are Few and 6 Are Many. International Journal of Game Theory, 2, 141-201. http://dx.doi.org/10.1007/BF01737566
- Huck, S., Normann, H.T. and Oechssler, J. (2004) Two Are Few and Four Are Many: Number Effects in Experimental Oligopolies. Journal of Economic Behavior & Organization, 53, 435-446. http://dx.doi.org/10.1016/j.jebo.2002.10.002
- Fischbacher, U. (1999) z-Tree: Zurich Toolbox for Ready-Made Economic Experiments. Experimental Economics, 10, 171-178. http://dx.doi.org/10.1007/s10683-006-9159-4
- Lehtinen, A. (2007) The Borda Rule Is Intended Also for Dishonest Men. Public Choice, 133, 73-90. http://dx.doi.org/10.1007/s11127-007-9178-5
Appendix A. Theory
Two voters, A and B, vote on three candidates: (A, B, C) for a single seat. Each voter, simultaneously and independently, allocates to each candidate a score from the set {1, α, 0}. We can represent a pure strategy by the triplet (a, b, c) where a is the score attributed to candidate A, b to candidate B and c to candidate C. There are six possible strategies: (1, α, 0), (α, 1, 0), (1, 0, α), (α, 0, 1) (0, α, 1), (0, 1, α) for positional voting whenever α ≠ 0, 1. For the plurality and the anti-plurality rules the set of strategies reduces to three: {(1, 0, 0), (0, 1, 0), (0, 0, 1)} for the plurality rule and {(1, 1, 0), (0, 1, 1), (1, 0, 1)} for the anti-plurality rule, respectively. To determine the winner, the score of the candidates are added and the candidate with the largest score is the winner. In case of ties among the candidates with the largest score, a uniform random draw selects the identity of the winner.
Player A prefers candidate A to candidate B and candidate B to candidate C and receives a payoff of 1 if candidate A is chosen, x if candidate B is elected and 0 if candidate C is chosen. Player B prefers candidate B to candidate A and candidate A to candidate C, with payoff 1 if B is chosen, x if A is chosen and 0 if C is chosen. In case of ties, i.e. when at least two candidates are chosen, the expected payoff is the average of the payoffs obtained with the elected candidates (for instance if candidates A and B are chosen, the payoff is (1 + x)/2 for both players). Note that we assume 0 < x < 1.
We say that a player votes sincerely if she allocates scores according to her preference profile: 1 to her preferred candidate, α to the second preferred candidate and 0 to the third preferred candidate. We say that a player votes strategically if she allocates 1 to her preferred candidate, α to the third preferred candidate and 0 to the second preferred candidate. Note that, in case of the plurality rule (α = 0), there is no difference between strategic and sincere voting.
The value of α determines the winner and, therefore, the payoffs. In what follows, we shall apply as solution concept the set of pure strategy Nash equilibria which survive the iterated deletion of weakly dominated strategies. Let us represent the payoff matrix when player A is the row player and player B is the column player. First, let us consider the extreme cases, whenever α = 0 or 1.
Case 1. α = 0 (plurality rule).
The sincere strategy dominates the other two strategies. The pair of strategies (sincere, sincere) constitutes an equilibrium in dominant strategies.
Case 2. α = 0 (antiplurality rule).
The strategy that consists of giving 0 to the most preferred candidate (the third strategy) is weakly dominated by sincere voting. If we eliminate this strategy for both player, the remaining game is an anti-coordination game with two asymmetric equilibria. To put it differently, in each pure strategy equilibrium of the reduced game that is obtained by the iterated deletion of weakly dominated strategies one player votes sincerely while the other votes strategically.
Case 3. 0 < α < 1.
where (s, t), (y, z) and (u, v) depend on the parameter α as follows
From the table it can be seen that the stategies that allocate a smaller score to the most preferred candidate than to the least preferred candidate are always weakly dominated by strategies reversing the scores for the most and least preferred candidates. That is, for player A strategy (0, α, 1) is weakly dominated by (1, α, 0), strategy (α, 0, 1) is weakly dominated by (1, 0, α), and strategy (0, 1, α) is weakly dominated by (α, 1, 0), strategy. The last three rows and the last three columns correspond to these weakly dominated strategies that can be eliminated in a first round. Once these strategies are eliminated the third row and the third columns become respectively weakly dominated by the sincere strategy. Eliminating this strategy we obtain the 2 × 2 game strategically corresponding to:
Whose equilibria are as follows:
1) α < 1/2 : (strat, strat).
2) α = 1/2: x ≤ 1/2 (strat, strat); x > 1/2, (strat, sinc) U (sinc, strat).
3) α > 1/2: (strat, sinc) U (sinc, strat).
Appendix B. Experimental instructions (translated from Spanish)
Welcome to the experiment!
This experiment is intended to study how people behave when voting.
We are only interested in average voting behavior, not in your particular voting behavior. Don’t think we expect you to vote in any particular way.
But, on the other hand, the money you earn during the experiment depends on your vote.
You will find instructions explaining how the experiment works and how to use the computer in the subsequent screens.
Please, do not speak to your neighbors and keep quiet during the entire experiment. If you need help, please, raise your hand and wait in silence, we will come to your booth as soon as possible.
How to raise money
First of all, you will receive 1000 pesetas just for participating to the experiment.
You will play 40 rounds of a voting protocol. In each round, you will be matched with other participants in this room, and each member of your matching group will have to cast a vote. How much you earn depends on your vote and on the votes of the other participants in your matching group.
You could earn money in each round (vote). Your total profit for a given session will be the sum of your profits in each round of the session.
By the end of the experiment you will receive the sum of profits for each session, besides your show up fee of 1000 pesetas.
The voting protocol
Three candidates, A, B and C, stand for an election. You and the rest of participants will be the electorate in this experiment. The computer has assigned you a letter, either A or B. This letter appears in the right corner of your screen and represents your player type.
There are two types of players: player A and player B.
Player A (her favorite candidate is A).
If candidate A wins the voting round she gets 100 pesetas. If candidate B wins the voting round she gets x pesetas. If candidate C wins the voting round she gets 0 pesetas.
Player B (her favorite candidate is B).
If candidate B wins the voting round she gets 100 pesetas. If candidate A wins the voting round she gets x pesetas. If candidate C wins the voting round she gets 0 pesetas.
Observe that when candidate C wins the voting round both players receive nothing.
Important: you will have the same player type during all the experiment.
The voting protocol (II)
Remember that you and the rest of the people in your matching group will decide the result of the voting in each round.
The number of people in each matching group will change in each of the T rounds. The number of people in each group will be two (2), four (4) or eight (8). We will let you know the size of your group at the beginning of each round.
At the beginning of each round the computer randomly selects how many people will be in your group and who will be part of it.
The number of players of each type will be the same in all groups at all times. If the group consists of two people, there will be 1 type A player and 1 type B player. If the group consists of four people, there will be 2 type A player and 2 type B player. If the group consists of eight people, there will be 4 type A player and 4 type B player.
The people to whom you are matched will change in each round but there will always be the same number of type A and type B players.
Remember that your player type will not change during the experiment.
How to vote
You have to assign a score to each candidate. The scores you can assign to the candidates are the following: 1 point, α points and 0 points. Thus, you will give 1 point to one of the candidates, α points to another candidate and 0 points to the third candidate.
Voting results
The rest of people in your group will also vote by assigning scores to candidates. By the end of each vote (round), the computer will compute the total amount of points each candidate received. The candidate with the highest score is the winner of the election. In case of two or three candidates receiving the same amount of points there will be a tie.
Your profit in each round depends on the winning candidate.
If just one candidate wins the voting round, your payoff for that round will be:
In case of a tie you will receive the expected monetary payoff:
Summing up
The computer will randomly select your player type, either A or B. This will be your type during all the experiment.
You will vote T times (rounds). In each round, the computer will randomly selects the rest of your group members. The size of the group can be two, four or eight (including you).
In each round you and your group mates will vote assigning scores to candidates A, B and C. Your votes and the votes of your group mates will determine your monetary profit.
NOTES
1Notice that we cannot directly apply group size effects in the same way as in the literature on Cournot games(Selten [8] , Huck et al. [9] ), where, as the numbers of firm increases, the underlying equilibrium structure moves in the direction of increasing competition (and increasing instability of collusive behavior). In the context of positional voting, the (anti)coordination structure we identify in Appendix A in the case of 2 players, basically carries through for larger group sizes, with the basic difference that coordination is made more difficult as it involves a larger number of players.
2The experiment was programmed and conducted with the software z-Tree (Fischbacher [10] ).
3This is exactly the reason whywe did not run sessions with α < 0.5. As we explain in Appendix A, this is the case in which strategic voting dominates all other strategies and the game becomes trivial.
4The point estimate for the difference between group size 4 and 8 reveals that the change in voting behavior when group size increases from 4 to 8 is not significant (p-value = 0.393).
5The boxes show 50% of the total observations (from the 25% to the 75% percentile). Adjacent lines trace the first upper and lower adjacent values, while points denote outliers. The line within the box denotes the median. The solid lines connect the means of the two distributions.
6See Appendix B.










