Theoretical Economics Letters
Vol.4 No.6(2014), Article
ID:47303,9
pages
DOI:10.4236/tel.2014.46061
Trade, Technology, Income Distribution and Growth
Hernando Zuleta, Luiza Pogorelova
Economics Department, Universidad de los Andes, Bogotá, Colombia
Email: h.zuleta@uniandes.edu.co
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 April 2014; revised 25 May 2014; accepted 23 June 2014
Abstract
The standard Hecksher-Ohlin model predicts that trade liberalization leads to a decline in the rate of return of the scarce factor of production. However, the empirical evidence of the falling labor share in some developing countries contrasts with the theory. We show that if a simple change in technology is introduced into the standard model, conditions exist for the rate of return of the scarce factor of production to increase. In particular, the price of the exported good and the amount of capital the country owns can serve as determinants whether the rate of return of the abundant factor will increase.
Keywords
Biased Technological Change, International Trade, Heckscher-Ohlin Model, Factor Income Shares, Economic Growth

1. Introduction
It has been documented that in different countries all across the world labor shares have been going down for the last decades (see Blanchard [1] , Jones [2] , Glyn [3] , Bental and Demougin [4] and Zuleta [5] among others). Bai and Qian [6] investigate the decline in labor share in China for the period 1995-2007 after its stable previous growth. Harrison [7] investigates the effect of globalization on labor shares and claims that labor shares in developing countries fell over the 1960 to 1997 period. This evidence of falling labor shares in developing countries contrasts with the predictions of the Heckscher-Ohlin theory.
Theoretical technology-related explanations have been offered for such a change in factor income shares. For example, Zuleta [8] and Peretto and Seater [9] model the change in factor shares as being induced by endogenous technological progress, which leads, depending on the parameters and initial conditions, to the reduction or full elimination of non-reproducible factors of production (e.g. unskilled labor).
Similar to the previous literature we relate relative supplies of factors, technology and trade. However, we use a different setting. In particular, we consider a general production function and we refer to reproducible factors in general and not only to skilled labor. In this setting, we explain why trade may increase the income share of scarce factors and connect the behavior of human capital shares to economic growth. We show that trade liberalization in a developing economy can cause labor saving innovation, which, in its turn, increases the return to reproducible factors and fosters economic growth.
We consider an economy with two goods, A and B, two factors of production, one reproducible and one not reproducible, and two technologies for the production of good A, α and β, α being more capital intensive. For ease of presentation, we denote the factors by K (capital) and L (labor) respectively. The production of good B is relatively labor intensive. The choice of technology is costless and depends on the capital-labor ratio of the country, k. We assume that in the state of autarky the economy is relatively capital-scarce and chooses technology β. In these circumstances, trade opening increases the capital-labor ratio of sector A up to a point where it induces a switch in production technology from β to α. In this case, contrary to the original Heckscher-Ohlin model, the return to the scarce factor (capital) may increase after trade liberalization. Finally, the increase in the human capital share may be accompanied by economic growth because it augments the return to human capital as well as the incentives to invest.
We conclude that the effects of international trade depend on the human capital abundance of the economy. Given the international prices of final goods, for very labor abundant economies international trade does not induce technological changes and, for this reason, the standard results of the H-O model hold. However, in relatively labor abundant economies, international trade may induce technological changes. For this group of economies, the labor income share may go down and the return to human capital may increase.
2. The Model
2.1. Production
The production function of good B is:
 (1)
(1)
For the production of good A firms can choose either technology α or β (α > β):
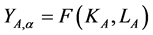 (2)
(2)
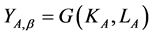 (3)
(3)
The functions ,
, 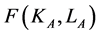 and
and 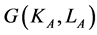 exhibit the usual assumptions1. Technology
exhibit the usual assumptions1. Technology  is more capital intensive than technology
is more capital intensive than technology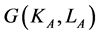 :
:
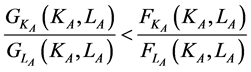 (4)
(4)
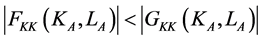 (5)
(5)
 (6)
(6)
Producers of good A choose the technology which maximizes output given  and
and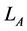 :
:
If  then producers choose
then producers choose , otherwise they choose
, otherwise they choose 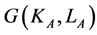 .
.
We assume constant returns to scale so this condition can be rewritten as follows:
If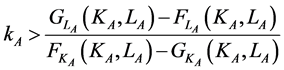 , then firms choose
, then firms choose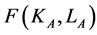 , otherwise they choose
, otherwise they choose  , where
, where . Equations (5) and (6) imply that the right hand side of the condition above is a decreasing function of
. Equations (5) and (6) imply that the right hand side of the condition above is a decreasing function of . Result 1 is a direct implication of these assumptions.
. Result 1 is a direct implication of these assumptions.
Result 1: There exists a critical level 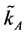 such that if
such that if  then producers of good A choose the technology α, and if
then producers of good A choose the technology α, and if 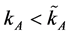 then producers of good A choose the technology β.
then producers of good A choose the technology β.
In other words, firms choose technologies α and β for high and low levels of the sector A capital-labor ratio respectively.
2.2. Factor Markets
Assuming perfect competition, factor mobility and normalizing the price of good A to one,  , we find
, we find
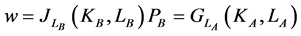 (7)
(7)
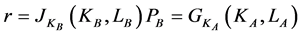 (8)
(8)
where 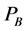 is the price of good B.
is the price of good B.
Result 2: In equilibrium  can be expressed as a function of
can be expressed as a function of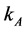 ,
,  , where
, where  and
and .
.
The production of good A is more capital intensive so result 2 also implies that output per worker in sector B can be expressed as a function of output per worker in sector A:  where
where .
.
From Equations (7) and (8), the price of good B can be written as
 (9)
(9)
Result 3 follows directly from Equation (9).
Result 3: In equilibrium,  can be expressed as a function of
can be expressed as a function of ,
,  where
where 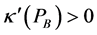 and
and .
.
From results 2 and 3 it follows that 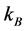 can be expressed as a function of
can be expressed as a function of ,
,  where
where  and
and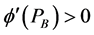 .
.
2.3. Consumption
In a dynamic setting, consumers maximize their lifetime utility subject to the budget constraint:
 where a is the amount of assets owned by the representative consumer, r is the interest rate, w is the wage and η is the discount factor. From the first order conditions we find
where a is the amount of assets owned by the representative consumer, r is the interest rate, w is the wage and η is the discount factor. From the first order conditions we find
 (10)
(10)
 (11)
(11)
2.4. Autarky Equilibrium
In equilibrium, the configuration of prices (PB, w and r), consumption (CA and CB), and output (YA and YB) are such that consumers maximize utility, producers maximize profits and no international trade takes place.
In steady state, assuming no depreciation, in the autarkic equilibrium CA = YA and CB = YB, so from Equation (11),
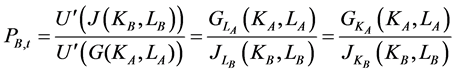 (12)
(12)
Result 4 follows directly from Equation (12):
Result 4: In the autarkic equilibrium the ratio of outputs 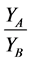 can be expressed as a function of the price level of sector B,
can be expressed as a function of the price level of sector B, 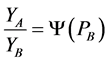 where
where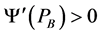 .
.
From result 4 it follows that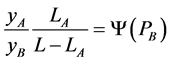 . Therefore,
. Therefore,
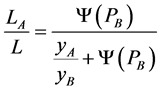 (13)
(13)
Equation (13) together with results 2 and 3 implies that, in the autarkic equilibrium, the ratio of labor allocated to sector A can be expressed as a function of the capital-labor ratio of sector A:
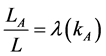 .
.
Proposition 1: Starting with the labor intensive technology β, there is a critical capital-labor ratio  such that if
such that if  then producers of good A choose the technology α.
then producers of good A choose the technology α.
The proof is presented in the appendix.
Here as in the H-O model, the more capital abundant the economy, the higher is the relative output of the capital abundant sector A, the wage and the higher is the relative price of the labor abundant sector PB. The difference from the H-O model is that when the economy is very capital abundant the capital-labor ratio of sector A is high enough to generate incentives for the firms to adopt the capital intensive technology α. As we stated before, we assume that the economy is labor abundant, so the domestic price of good B is lower than the international price and the producers of good A chose the labor intensive technology β.
2.5. A Graphical Representation
Figure 1 illustrates the autarkic equilibrium. It is an extension of the textbook illustration of the Stolper-Samuelson Theorem2. The right hand side of the figure shows the relation between capital-labor ratio and wage-interest rate ratio for goods A and B. Given that the production of good A is more capital intensive, for any ratio of factor prices the capital-labor ratio is higher for sector A. Now, producers of sector A can choose between technology α and technology β and technology α is more capital intensive. As stated in result 1, producers of good A choose technology α if the capital-labor ratio is higher than  and technology β if the capital-labor ratio is lower than
and technology β if the capital-labor ratio is lower than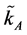 . For this reason, the relation between factor prices and the capital-labor ratio of sector A is the one described by the bold line. Similarly, the relation between the price of good B and the ratio of factor prices depends on the technology in use. If sector A uses the more capital intensive technology, ceteris paribus, the demand for labor is relatively lower and the demand for capital is relatively higher and, for this reason, given the price p, the wage-interest rate ratio is relatively lower.
. For this reason, the relation between factor prices and the capital-labor ratio of sector A is the one described by the bold line. Similarly, the relation between the price of good B and the ratio of factor prices depends on the technology in use. If sector A uses the more capital intensive technology, ceteris paribus, the demand for labor is relatively lower and the demand for capital is relatively higher and, for this reason, given the price p, the wage-interest rate ratio is relatively lower.
In autarky, the capital-labor ratio of the economy determines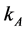 ,
, 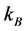 and p. If
and p. If 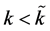 then the capital-labor ratio of the economy is such that under autarky
then the capital-labor ratio of the economy is such that under autarky 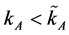 and
and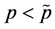 . Therefore, the wage-interest rate ratio is lower than
. Therefore, the wage-interest rate ratio is lower than  .
.
From Figure 1 we also see that, if 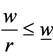 then
then  and the labor intensive technology is used
and the labor intensive technology is used . Similarly, if
. Similarly, if  then
then  and the capital intensive technology is used. However, if
and the capital intensive technology is used. However, if  then either technology can be used and both p and
then either technology can be used and both p and  may take two different values.
may take two different values.
2.6. Multiple Equilibria
Assumption 1 imposes a restriction on the initial technology. Now, if the conditions of the economy are such that

Figure 1. Factor abundance, prices and technology in the closed economy.
initially the technology used by producers of good A is the capital intensive technology, then in equilibrium factor prices are given by
 (7’)
(7’)
 (8’)
(8’)
And, in the same way that we found results 2 and 3 when the initial technology was labor intensive, we find now results 5 and 6.
Result 5: In equilibrium  can be expressed as a function of
can be expressed as a function of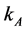 ,
, 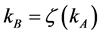 where
where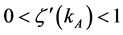 , and
, and  for every
for every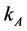 .
.
Result 6: In equilibrium, 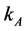 can be expressed as a function of PB,
can be expressed as a function of PB,  where
where ,
,  and
and 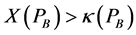 for every
for every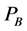 .
.
Finally, proposition 2 follows from the previous results.
Proposition 2: Starting with the capital intensive technology α, there is a critical capital-labor ratio  such that if
such that if 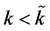 then producers of good A choose the technology β.
then producers of good A choose the technology β.
The proof is presented in the appendix.
Corollary 1: If 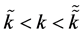 then there are two equilibria: one where producers of good A choose the technology
then there are two equilibria: one where producers of good A choose the technology 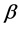
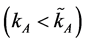 and
and  and the other where producers of good A choose the technology
and the other where producers of good A choose the technology 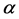
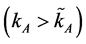 and
and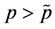 .
.
Proof: It follows directly from propositions 1 and 2.
Corollary 1 implies that if  and the autarkic equilibrium is such that
and the autarkic equilibrium is such that  and
and  then an exogenous increase in the price of good B may direct the economy to the equilibrium where
then an exogenous increase in the price of good B may direct the economy to the equilibrium where . Under this new equilibrium, the technology α is used and the wage-interest rate ratio is lower than in the initial equilibrium.
. Under this new equilibrium, the technology α is used and the wage-interest rate ratio is lower than in the initial equilibrium.
In general, when a relatively labor abundant economy switches from autarky to free trade there is an “exogenous” increase the in relative price of the labor intensive good. Therefore, international trade may generate a labor saving technological change and a reduction in the wage-interest rate ratio. However, international trade may generate labor saving technological change and a reduction in labor shares even if the capital-labor ratio is such that there is only one equilibrium and the chosen technology is labor intensive, namely,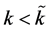 . The following sessions deal with this case. In other words, assumption 1 holds for the rest of the paper.
. The following sessions deal with this case. In other words, assumption 1 holds for the rest of the paper.
Assumption 1: In the autarkic steady state the capital-labor ratio of the domestic economy is such that, the equilibrium is unique and technology β is used, so the production function of good A is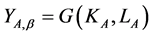 , namely,
, namely,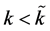 .
.
2.7. Trade
Given that the economy is labor abundant, opening the economy leads to an exogenous increase in 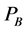 and the economy exports good B.
and the economy exports good B.

Now, if the increase in 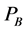 is big enough then international trade may generate a change of technology. We formalize this result in proposition 3.
is big enough then international trade may generate a change of technology. We formalize this result in proposition 3.
Proposition 3: There exists a critical price level 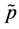 such that, if
such that, if 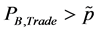 then after the domestic economy starts trading with the foreign economy, the domestic economy switches to technology α in the production of good A.
then after the domestic economy starts trading with the foreign economy, the domestic economy switches to technology α in the production of good A.
Proof: From result 1 it follows that there exists a critical capital-labor ratio 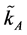 such that, if
such that, if 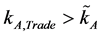 then after the domestic economy starts trading, the economy switches to technology α in the production of good A.
then after the domestic economy starts trading, the economy switches to technology α in the production of good A.
From result 3 it follows that there exists a price level 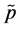 such that
such that . Q.E.D.
. Q.E.D.
Proposition 4: Holding relative prices constant, if the economy switches to technology α in the production of good A then  and
and .
.
Proof: From Equations (2) to (5) it follows that, given , the adoption of the technology α increases the marginal productivity of capital and reduces the marginal productivity of labor. From Equation (9) it follows that after the adoption of the new technology the factors of production should be reallocated increasing the capital-labor ratio of sector A and decreasing the capital-labor ratio of sector B. Q.E.D If the capital-labor ratio of the domestic economy is close to the critical level
, the adoption of the technology α increases the marginal productivity of capital and reduces the marginal productivity of labor. From Equation (9) it follows that after the adoption of the new technology the factors of production should be reallocated increasing the capital-labor ratio of sector A and decreasing the capital-labor ratio of sector B. Q.E.D If the capital-labor ratio of the domestic economy is close to the critical level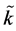 , then with a small increase in
, then with a small increase in 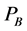 the economy switches to technology α. If the distance between technologies α and β is big then the effect of the technological change may be stronger than the effect of the increase in the relative price of good B.
the economy switches to technology α. If the distance between technologies α and β is big then the effect of the technological change may be stronger than the effect of the increase in the relative price of good B.
Proposition 5: If the capital-labor ratio of the economy is high enough, then there exists a critical price level 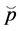 such that, if
such that, if 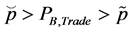 then after the domestic economy starts trading with the foreign economy the wage-interest rate ratio decreases.
then after the domestic economy starts trading with the foreign economy the wage-interest rate ratio decreases.
The proof is presented in the appendix.
Proposition 6: If the capital-labor ratio of the economy is high enough, then there exists a critical price level  such that, if
such that, if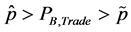 , then after the domestic economy starts trading with the foreign economy the interest rate increases.
, then after the domestic economy starts trading with the foreign economy the interest rate increases.
The proof is presented in the appendix.
Corollary: If the capital-labor ratio of the economy is high enough then there exists a critical price level 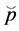 such that, if
such that, if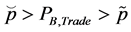 , then after the domestic economy starts trading with the foreign economy, the rate of economic growth increases.
, then after the domestic economy starts trading with the foreign economy, the rate of economic growth increases.
From Equation (11), when the interest rate increases, the growth rate of consumption grows and the savings rate has to increase as well, leading to faster capital accumulation and economic growth. This result also holds outside the steady state as long as consumption depends positively on output.
2.8. A Graphical Representation of the Open Economy
Figure 2 illustrates the trade equilibrium. When the economy starts trading the price p is determined in the international market and, given the labor abundance of the economy, it goes up. In principle, following the increase in p, the factor prices and the capital ratio of both sectors grow. However, the final result on relative factor prices depends on the capital-labor ratio of the economy and the international price of good B.
Note that, as stated in proposition 3, if 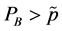 then after the domestic economy starts trading,
then after the domestic economy starts trading, 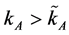 and the domestic economy switches to technology α in the production of good A. Now, when the technology changes, holding the rest constant,
and the domestic economy switches to technology α in the production of good A. Now, when the technology changes, holding the rest constant, 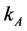 also grows (from Aβ to Aα) but this change implies that there must be a flow of factors between sector B and sector A reducing
also grows (from Aβ to Aα) but this change implies that there must be a flow of factors between sector B and sector A reducing  as stated in proposition 4.
as stated in proposition 4.
2.8.1. When the Standard Result of the H-O Model Holds
Consider the case of an economy where the capital labor ratio is such that ,
,  and
and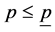 . In this case, any increase in the price of good B generates an increase in the wage-interest rate ratio regardless of the technological choice of producers of good A.
. In this case, any increase in the price of good B generates an increase in the wage-interest rate ratio regardless of the technological choice of producers of good A.
Next, consider the case when the international price is higher than  . In this case, there is technological change and the wage-interest rate ratio after trade is higher than
. In this case, there is technological change and the wage-interest rate ratio after trade is higher than  , namely higher than its autarkic level.
, namely higher than its autarkic level.

Figure 2. Prices and technology in the open economy.
2.8.2. When the Standard Result of the H-O Model Does Not Hold
Now, consider the case where  and the international price is lower than
and the international price is lower than  . International trade generates an increase in price p which, in its turn, produces an increase in the capital-labor ratio for both sectors and triggers a change in the technology of sector A. This change in technology generates a flow of factors reducing the capital labor-ratio in sector B. Therefore, the change in p has a positive effect on
. International trade generates an increase in price p which, in its turn, produces an increase in the capital-labor ratio for both sectors and triggers a change in the technology of sector A. This change in technology generates a flow of factors reducing the capital labor-ratio in sector B. Therefore, the change in p has a positive effect on , but the technological change has a negative effect. If the change in prices is relatively small, and the change in technology is big, then the net effect is a decrease in the wage-interest rate ratio.
, but the technological change has a negative effect. If the change in prices is relatively small, and the change in technology is big, then the net effect is a decrease in the wage-interest rate ratio.
Figure 2 illustrates this case. In the autarkic equilibrium the capital-labor ratio of sector A is ![]() and the price of good B is p0 (very close to
and the price of good B is p0 (very close to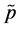 ). When the economy starts trading, the price of good B becomes PB,Trade (also close to
). When the economy starts trading, the price of good B becomes PB,Trade (also close to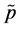 ) and technology changes. The change in price is small but the change in
) and technology changes. The change in price is small but the change in  produced by the technological change is big and, therefore, the net effect of the wage-interest rate ratio is negative.
produced by the technological change is big and, therefore, the net effect of the wage-interest rate ratio is negative.
This result depends on the assumptions we made about the production function. We assume that both factors of production are essential, diminishing marginal productivity of factors and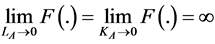 . For this reason, the imported good is also domestically produced. However, the increase in the price of the exported good under factors mobility generates a raise in the capital-labor ratio, which may trigger an unskilled laborsaving technological change.
. For this reason, the imported good is also domestically produced. However, the increase in the price of the exported good under factors mobility generates a raise in the capital-labor ratio, which may trigger an unskilled laborsaving technological change.
3. Conclusions
Over the recent decades the inability of the standard HO model to explain the declining labor shares and the rising skill premium in developing countries after trade liberalization has given motivation to some substantial theoretical work. Continuing this effort, we put together the globalization question and biased innovations theory and introduce a change in technology into the standard Hecksher-Ohlin model to find that the rate of return of the scarce factor of production will not necessarily decline after trade liberalization takes place.
We find conditions under which the rate of return of the scarce factor of production increases. In particular, the price of the exported good and the amount of capital the country owns can serve as determinants whether the rate of return of the abundant factor will rise. Given the international prices of final goods, we find that the effects of international trade depend on the capital abundance of the economy. For very labor abundant economies international trade does not induce technological changes and, for this reason, the standard results of the H-O model hold. However, for relatively labor abundant economies which capital labor ratio is close to one, international trade induces technological changes. Within this group of economies, in the least labor abundant ones, the labor income share goes down and the return to capital may increase. In addition, we show that, for these economies, the savings rate increases after the trade liberalization, leading to faster economic growth.
References
- Blanchard, O.J. (1997) The Medium Run. Brookings Papers on Economic Activity, 16, 89-158. http://dx.doi.org/10.2307/2534687
- Jones, C.I. (2003) Growth, Capital Shares, and a New Perspective on Production Functions. Version 1.0. http://www.stanford.edu/~chadj/alpha100.pdf
- Glyn, A. (2007) Explaining Labor’s Declining Share of National Income. UNCTAD, Intergovernmental Group of Twenty Four, G-24, Policy Brief No. 4.
- Bental, B. and Demougin, D. (2010) Declining Labor Shares and Bargaining Power: An Institutional Explanation. Journal of Macroeconomics, 32, 443-456.
http://dx.doi.org/10.1016/j.jmacro.2009.09.005 - Zuleta, H. (2012) Variable Factor Shares, Measurement and Growth Accounting. Economics Letters, 114, 91-93. http://dx.doi.org/10.1016/j.econlet.2011.09.026
- Bai, C. and Qian, Z. (2010) The Factor Income Distribution in China: 1978-2007. China Economic Review, 21, 650-670. http://dx.doi.org/10.1016/j.chieco.2010.08.004
- Harrison, A. (2002) Has Globalization Eroded Labor’s Share? Some Cross-Country Evidence. University of California at Berkeley and NBER, Berkeley.
- Zuleta, H. (2008) Factor Saving Innovations and Factor Income Shares. Review of Economic Dynamics, 11, 836-851. http://dx.doi.org/10.1016/j.red.2008.02.002
- Peretto, P. and Seater, J.J. (2013) Factor-Eliminating Technical Change. Journal of Monetary Economics, 60, 459-473. http://dx.doi.org/10.1016/j.jmoneco.2013.01.005
- Krugman, P. and Obstfeld, M. (2008) International Economics: Theory and Policy. 7th Edition, Addison Wesley, Boston.
Appendix
Proof of Proposition 1:
Claim 1: Under autarky, in equilibrium,  can be expressed as a function of the capital-labor ratio of the economy:
can be expressed as a function of the capital-labor ratio of the economy: 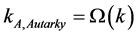 where
where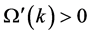 .
.
Capital and labor are allocated between the two sectors so,
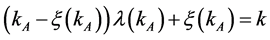 (14)
(14)
Define 
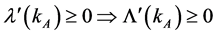 (15)
(15)
Suppose that 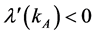 and consider that
and consider that 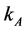 grows. Then
grows. Then  grows but
grows but  decreases, so LB and KB grow. But then YB must be growing, YA decreasing, and PB decreasing, implying that
decreases, so LB and KB grow. But then YB must be growing, YA decreasing, and PB decreasing, implying that 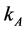 and
and 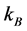 are decreasing which contradicts the initial assumption. The analogous argument can be done for the case where
are decreasing which contradicts the initial assumption. The analogous argument can be done for the case where 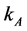 decreases. Therefore,
decreases. Therefore, 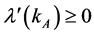 and
and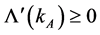 .
.
Finally we can define .
.
Claim 1 follows from equation (15) together with results 2 and 4.
Claim 2: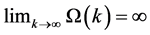 .
.
It follows directly from result 2 and Equation (14).
Proposition 1 follows directly from claims 1 and 2 and result 1. Q.E.D.
Proof of Proposition 2:
Claim 1: When the technology used is capital intensive, in equilibrium 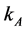 can be expressed as a function of the capital-labor ratio of the economy:
can be expressed as a function of the capital-labor ratio of the economy: where
where 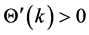 and
and  for every k.
for every k.
Claim 2: 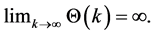
Proposition 2 follows directly from claims 1 and 2 and results 5 and 6. Q.E.D.
Proof of Proposition 5:
Claim 1: Given the technologies 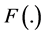 and
and  there exists a critical capital-labor ratio
there exists a critical capital-labor ratio 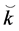 such that if
such that if
 then
then 
From Equation (4) it follows that 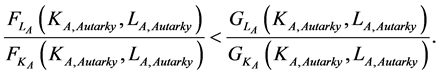
The two sides of the inequality are increasing in k. Therefore, there exists an 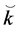 such that
such that 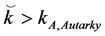 and
and
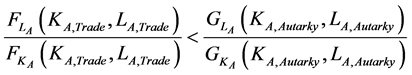 for any
for any .
.
Claim 2: There exists a critical price level 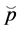 such that, if
such that, if , then after trade opening the capitallabor ratio in the production of good A,
, then after trade opening the capitallabor ratio in the production of good A,  , is such that
, is such that .
.
Result 3 implies that 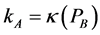 where
where  is continuous and monotonically increasing. Therefore, there exists a
is continuous and monotonically increasing. Therefore, there exists a  such that, if
such that, if  then
then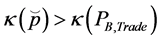 .
.
Claim 3: If the capital-labor ratio of the economy k is high enough then .
.
Proposition 1 implies 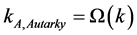 where
where .
.
While 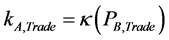 and
and  is exogenous.
is exogenous.
Therefore, we can define the function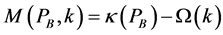 , where
, where ,
, 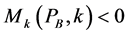 and
and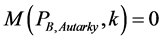 .
.
Now, choose an arbitrary small number ε and choose 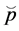 in such a way that
in such a way that 
Note that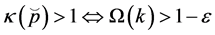 . Therefore,
. Therefore, .
.
From claims 1, 2 and 3, it follows that if 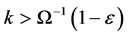 then there exists a critical price level
then there exists a critical price level  such thatif
such thatif , then after the domestic economy starts trading with the foreign economy
, then after the domestic economy starts trading with the foreign economy ![]() decreases.
decreases.
Proof of Proposition 6:
NOTES

1Positive and diminishing returns to factors, constant returns to scale, essentiality and two of the Inada conditions hold. Consistently, the elasticity of substitution between K and L is finite and strictly positive.

2See Krugman and Obstfeld .

