ABSTRACT

Under the circumstances of the most recent and still undergoing severe economic recession in Greece, the question arises on the role of uncertainty as regards the country’s growth prospects. In order to assess the potential impact of real uncertainty on economic growth, this paper investigates the bidirectional link between output growth and real uncertainty for the case of Greece. We use quarterly GDP data covering the time period from 1975 to mid-2013, and so include the most recent period of still undergoing recession. We apply an extended GARCH-M model to be able to directly and simultaneously examine both directions of dependence between output growth and real uncertainty. We find that a negative and significant relation exists in both ways, hence providing a tool for policies in order to speed up economic recovery.

Keywords:Real Uncertainty; Output Growth; GARCH; Greece

1. Introduction

The most recent world economic crisis and especially the developments within the Euro area regarding the stability of the common currency and the sustainability of economic growth as a whole and in individual member countries, once again forced all participants in economic activity to pay particular attention to uncertainty conditions and their potential impact on economic growth. Greece presents a clear example for the role that uncertainty can overtake in driving down expectations, enhancing negative spillover effects and hindering the recovery of the growth process. In theoretical terms, the issue of the role of real uncertainty with reference to economic growth relates to the question on the link between theories of the variability of the business cycle and economic growth¹. The earlier dichotomization which traditionally characterized related macroeconomic analysis before the early 1980’s was later questioned by several theories. Such theories allowed for a relation between growth and the volatility of economic fluctuations², and hence, provided the framework for such a link, even though without being conclusive as to its kind. Empirical evidence, which was called upon to resolve the theoretical inconclusiveness issue, is mostly characterized by controversial findings as to the existence and the sign of the investigated link, often even with reference to one and the same country. In light of these considerations, and particularly against the background of the necessity to provide certainty conditions in Greece in order to return to positive growth, the present work attempts to investigate the existence and kind of a potential link between growth and real uncertainty, using Greek GDP data³. The aim of this study is to focus on a potential bidirectional link and include the most recent period of recession, with the motivation and originality of the present paper consisting in the fact that the underlying relationship remains an unresolved empirical issue⁴. The bidirectional relationship between growth and real uncertainty, proxied by output growth uncertainty is examined by applying an extended GARCH-M model. The time period covered begins in 1975 and ends in mid-2013, hence including the recent years of recession, which has not yet ended. The provided evidence reinforces the existence of a link between growth and real uncertainty for the case of Greece, with both directions of dependence being negative, offering a potential mechanism for enhancing the process of economic recovery. The remainder of the paper is organized as follows. Section 2 offers a review of related theoretical approaches and summarizes some empirical evidence. Section 3 presents the empirical methodology underlying the analysis, and Section 4 describes the data used and offers the results for the case of Greece. The final section concludes.

2. Theoretical Approaches and Empirical Evidence

The emergence of theoretical approaches postulating a link between output growth and output growth volatility (uncertainty) has been related to the growing belief in the concept that business cycle theory and growth theory should not be treated separately. With the focus being more on potential determinants of growth, the relation under investigation runs mainly from real uncertainty to output growth. The economic mechanisms involved in approaches anticipating such a relationship justify both a positive and negative link, resulting in the lack of a consensus with regard to the kind of the underlying association⁵. At the same time, theory can also give rise to the reverse direction of dependence, namely to an impact of output growth on real uncertainty—mostly via mechanisms involving the channel of inflation and inflation uncertainty⁶—being again consistent with either a positive or a negative relation. Still, as a whole and as Lee [7] points out, the literature on the potential causal effect of output growth on its volatility remains rather sparse. Table 1 provides a summarized reference to related theories, the investigated direction and resulting findings. With theory being inconclusive about the kind of association between output growth and real uncertainty, empirical applications are called upon to solve the puzzle. But again, the provided evidence is mixed, leaving the issue unresolved, on empirical grounds as well. As indicated in Table 2, the derived empirical results, based either on cross-section, panel or time series data, different data frequencies and various empirical methodologies, support either a positive, or a negative link, or even suggest the independence between output growth and its uncertainty⁷. The ambiguity holds as to both directions of dependence.

3. Empirical Methodology

The focus of the present paper is to examine the bidirectional relationship between output growth and real uncertainty for the case of Greece in order to enrich the very limited existing evidence and since the ambiguity in the related empirical literature offers space for further investigation of the issue. The targeted investigation requires at first an accurate quantification of a proxy for real uncertainty and, in addition, a suitable methodology to account for the issue of endogeneity (see Fang, Miller and Lee [12], Fang and Miller [13] and Badinger [14]). Note that, with the intention to focus on real uncertainty, proxied by output growth uncertainty, we do not include additional effects entering through nominal uncertainty, which may arise via inflation uncertainty.

On the basis of all the above considerations, the GARCH methodology (Engle [15], Engle and Bollerslev [16]) appears to be ideally suited for the current application to Greece⁸, since it allows taking into account the aspect of heteroskedasticity, while it makes feasible the simultaneous estimation of various simple or more enriched structures of the conditional mean and variance equations. Most importantly, it enables the estimation of the time-varying conditional variance of a stochastic process, in our case the unpredictable innovations in output growth, providing a measure that corresponds closely to the notion of uncertainty, which is the underlying concept. At the same time, the application of an extended GARCH model allows the joint investigation of

¹Note the finding by Blackburn and Pelloni [29] that depending on the source of stochastic fluctuation, namely according to whether real or nominal shocks predominate, the relation between output growth and its variability may be positive or negative.

¹The respective evidence for the US is mixed, while no such evidence is found for Japan. ²In distinguishing between ex post (based on the historical data) and ex ante (variance derived from survey data) empirical approaches for quantifying uncertainty according to Lensink et al. [40], Kneller and Young [5] provide a summary of empirical findings. Note, that the reference to the summary results offered by Kneller and Young focus on significant coefficients only. The authors further indicate that variations in the results seem to be confined to the ex post measures of volatility. ³Note that the authors attribute the strong differentiation of their results for Italy regarding the negative effect of real uncertainty on growth from the respective ones provided by Fountas and Karanasos [49], Fountas and Karanasos [6] and Fountas, Karanasos and Kim [31] for Italy to the different sample periods and methodological approaches applied. ⁴The authors use the iterated cumulative sum of squares (ICSS) algorithm to correct for structural change in the variance of output growth. Note that Fang and Miller [13] find no significant effect for Japan running in either direction, after correcting for outliers and structural shifts. ⁵The authors also conclude that the effect of variability on growth differs depending on the included lag of the variability measure.

the respective bidirectional link via 1) the incorporation of the in-mean term (M-term, Engle, Lilien and Robins [17]) in the conditional mean equation and 2) the impact of output growth on output growth uncertainty through the inclusion of lagged output growth in the conditional variance equation. Note that, as Fang et al. [12] and Fang and Miller [13] indicate, if output growth is a determinant of its volatility but not included in the conditional variance equation, then the estimated model on the basis of the GARCH-M type methodology may suffer from misspecification in variance. The enriched model entailing several advantages, which makes feasible the simultaneous examination of both directions of the link between real uncertainty and output growth, is expressed by the following structure,

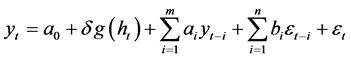(1)

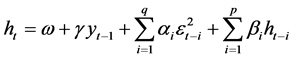(2)

where which is given by Equation (1) stands for output growth, , with corresponds to the innovation in the mean for the output growth process with zero mean and its time-varying conditional variance equaling, described by Equation (2), and by the process being identically and independently distributed with zero mean and unit variance. The conditional mean Equation (1), which is expressed as an ARMA process, is augmented by a function 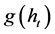of the conditional variance term, providing the framework for the direct investigation of the impact of real uncertainty on output growth. Most commonly, the respective functional form is given by the conditional variance itself, the conditional standard deviation or the logarithm of the conditional variance. The conditional variance equation, which is expressed as a GARCH 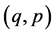process— namely as a function of past squared innovations and past values of the conditional variance—is extended by the lagged output growth term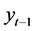. This allows the simultaneous investigation of the impact of output growth on real uncertainty, i.e., the examination of the reverse direction of the underlying relation⁹.

4. Data and Empirical Results

In this application to Greece, we use seasonally adjusted quarterly real Greek GDP data¹⁰ covering a time period of almost forty years—including the most current period of recession, which has not yet ended—namely the period from the first quarter of 1975 to the second quarter of 2013. To obtain GDP growth, we calculate differences in logarithms of GDP. We proceed with testing for stationarity, by applying the Augmented Dickey-Fuller test to the original GDP series, the log of the GDP series and the GDP growth series. As illustrated by the obtained ADF statistics and p-values¹¹, the null of a unit root cannot be rejected in the first two cases, whereas it is clearly rejected for the growth series, indicating stationarity for the transformed GDP growth series. On the basis of the Akaike Information criterion (AIC) we select the ARMA-GARCH-M model, including the conditional mean and the conditional variance equations, that best fits the Greek data. Estimations are carried out using the BerndtHall-Hall-Hausman [18] (BHHH) maximization algorithm. To ensure the robustness to departures from normality, the Bollerslev-Wooldridge [19] robust quasimaximum likelihood standard errors are obtained. The coefficient estimates for the selected ARMA-GARCH-M model are reported in Table 3, together with residual diagnostics. Note that the variance term itself is used in the conditional mean equation and also that the GARCH (1,1) order has proven to be a sufficient lag structure. The provided Ljung-Box statistics for the standardized squared residuals indicate no further second order serial correlation, while the ARCH LM test statistics indicate no remaining conditional heteroskedasticity. These statistics imply that there is no statistically significant evidence of misspecification¹². The estimation results which are presented in Table 3 offer important evidence on the relation between economic growth and real uncertainty for Greece. In the first equation, the estimate of the corresponding coefficient on, namely , implies a negative and statistically significant effect of output growth uncertainty on output growth, suggesting that higher output growth uncertainty leads to lower output growth in Greece. In the second equation, and as indicated by the negative and statistically significant estimate of the respective coefficient on lagged output growth, namely 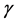, lower output growth uncertainty may result from higher output growth. Note that this result may be explained by the effect of output growth via the inflation channel, as outlined in Section 2¹³. To check for the sensitivity of the results and test their robustness, we also estimate our model using alternative forms of function, which enters the conditional mean equation, such as the condi

Notes: Bollerslev-Wooldridge robust standard errors are reported in parentheses. Asterisk denotes coefficient significance at the 5% level. Ljung-Box Q-statistics (Q²-statistics) are reported for 4thand 8th-order serial correlation in the standardized (squared standardized) residuals. 4th and 8th order ARCH LM test statistics are reported with probabilities in parentheses.

tional standard deviation and the logarithm of the conditional variance¹⁴, instead of the conditional variance term. In both cases, the results confirm the kind of the detected relation running from real uncertainty to output growth through negative, even though statistically insignificant, coefficients. Furthermore, we estimate the selected model without the GARCH term in the mean equation, the lagged output term in the variance equation and without both terms. In none of these cases, the obtained values of the AIC are lower than the respective value for the selected extended model. Finally, we conduct coefficient diagnostic tests, where the statistics from the Wald test lead to rejection of the null hypothesis that the coefficients on the output growth uncertainty term in the conditional mean equation and the lagged output growth term in the conditional variance equation individually and/or jointly equal zero. Overall, the above findings imply, in accordance with evidence in the related empirical literature for several countries, that, for the case of Greece, it is important to consider the bidirectional relationship between output growth and output growth uncertainty. Hence, our findings point to the necessity to investigate not only the effect of output uncertainty on growth but also the opposite direction, and as a whole do not support the dichotomy between economic growth and real uncertainty.

5. Conclusion

Following the more recent trend in macroeconomics of connecting the analyses of the business cycle and economic growth, and given the asserted role of uncertainty in hindering and retarding economic recovery in Greece, in this paper, we attempt to empirically investigate the existence of a link between real uncertainty and economic growth. Against the backdrop of lacking sufficient evidence on the potential bidirectional dependence for the case of Greece, we rely on an extended GARCH-M model, which is constructed so as to enable the simultaneous examination of the two directions of dependence. Most importantly, we include the most recent time period of recession (which has not yet ended for the Greek economy) in order to take into account changes that followed the last especially long period of expansion, which had started in 1993 and ended in 2008. The detected significant effects in both directions offer clear justification for the necessity to consider business cycle analysis side by side with the analysis of growth. At the same time, the provided evidence suggests that in the case of Greece real uncertainty negatively affects growth, while growth appears also to be a negative determinant of real uncertainty. These findings appear to be particularly significant for economic policy in the country aiming at exiting from the recession and securing a stable path towards robust growth conditions. They indicate that the ascertained relationships can work in favor of promoting growth strategies through the function of the spiral “reduced real uncertainty leads to higher economic growth and higher economic growth leads to lower real uncertainty”.

REFERENCES

NOTES

¹According to Friedman’s model of the business cycle, deviations of output from its natural rate are due to price misperceptions which are activated by monetary shocks. Changes in the growth rate of output do not arise from such deviations, but instead depend on real factors, such as technology.

²A measure of volatility can include predictable, unpredictable (variance of innovations) or both kinds of changes in growth. It is argued (for example, Ramey and Ramey ) that measuring the variance of innovations corresponds more closely to proxying the notion of uncertainty, which is indeed the variable of interest in most of the related theoretical approaches.

³We rely here on the notion of uncertainty by focusing on the unpredictable changes in growth (see also Section 3).

⁴There is to our knowledge a lack of similar evidence on the case of Greece, since, the only detailed individual application for Greece is that by Chapsa ) (see Section 2) which is, however, differentiated in terms of methodology, data and time period covered.

⁵As Blackburn and Kneller and Young indicate, different kinds of relation can emerge depending on the mechanisms generating technological progress or the origin of the shocks.

⁶Note that in many cases, the considerations are based on the assumption of a positive relation between inflation and inflation uncertainty. However, as Fountas et al. indicate, the effect of inflation on inflation uncertainty is theoretically also ambiguous.

⁷Independence between output growth and variability (uncertainty), lending support to the separation of business cycle and growth analyses is suggested, for example, by Speight , who reexamines (building upon the analysis of Caporale and McKiernan the link for the UK, Fountas et al. for Japan and Fang and Miller for the US, after controlling for structural changes in variance via the ICSS algorithm (focusing on the effect of the Great Moderation).

⁸Note that in their study for Greece, Chapsa investigate the relation between real uncertainty and output growth, within the framework of the analysis of the dynamic linkages between output growth and macroeconomic uncertainty, including both real and nominal uncertainty. By using the estimated uncertainty variables of interest via GARCH models, the relations under investigation are examined on the basis of a VAR specification. In the present paper, however, we use the GARCH methodology, instead of the two-step procedure, as a more direct approach for the simultaneous estimation of real uncertainty and analysis of the effects of interest.

⁹Note that the non-negativity of the parameters of Equation (2), , and, is sufficient to ensure a well-defined variance process. Also, the issue of persistence of shocks to the variance can be referred to, by investigating whether current information remains important for forecasts of the conditional variance for long (or all) horizons on the basis of the sum of the and coefficients. A value of the respective sum close (or equal) to unity implies high persistence (or an IGARCH process). The IGARCH process is referred to as a process integrated in variance. See Engle and Bollerslev who use this specific expression to classify models characterized by an approximate unit root in the autoregressive polynomial.

¹⁰Greek GDP data are used since they are assumed to best describe aggregate economic activity in Greece, while other indicators such as Industrial Production are not that comprehensive and representative of total activity.

1⁴Note the remarks by Speight and Fountas et al. on some caveats with regard to the use of the logarithmic transformation and its interpretation.