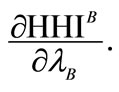Theoretical Economics Letters
Vol. 2 No. 3 (2012) , Article ID: 21502 , 9 pages DOI:10.4236/tel.2012.23057
Collusion Sustainability with Multimarket Contacts: Revisiting HHI Tests
LAMETA UMR 5474, Montpellier, France
Email: edmond.baranes@univ-montp1.fr
Received March 13, 2012; revised April 15, 2012; accepted May 17, 2012
Keywords: Collusion; Multimarkets; HHI
ABSTRACT
Our paper focuses on the relationship between market concentration and collusion sustainability in a framework of multimarket contacts. We consider two independent and symmetric markets in which a subset of firms are active in both markets. When firms are able to transfer market power from one market to another, firms have strong incentives to collude even in a highly competitive market. This result is relevant for competition policy since assessing market concentration using HHI index could be misleading in some situations.
1. Introduction
Competition policy traditionally distinguishes between market structures and market behaviors. Concerning the control of market structures, competition authorities focus on the degree of market concentration. For this reason, many concentration indexes have been built as HHI or concentration ratio as CR1, CR3 and so on. Among them, the Hirschmann Herfindhal Index (HHI) is certainly the most used on market reports. Concerning the control of market behaviors, an academic literature focuses on the distortive behaviors.1
However, a few works have study the link between both kinds of market control although it seems that they show strong interactions. It is nevertheless essential to underline these links between market structures and market behaviors in the implementation of competition policy.
In a simple model of price competition repeated game, it can be shown that a decrease in the number of firms facilitates collusion. This standard result states that little concentrated market structures entails weaker incentives to collude. Consequently, using concentration indexes seems not to be in contradiction with the control of behaviors in markets.
Nevertheless, some works have moderated this result. In some cases, highly concentrated market structures can give strong collusion incentives. For example, it is shown in [2] that mergers reduce incentives to collude among firms in the industry. In a similar setting of dynamic price competition with capacity constraints, [3] show that collusion incentives are low when the market is highly concentrated or in the contrary when the number of firms is very important. Last, [4] show that collusion is more difficult to sustain when concentration creates asymmetries in production capacities. In that case, increasing HHI index induces sometimes strong incentives to collude.
Our paper studies the relationship between market concentration and collusion sustainability in the framework of multimarket contacts literature (in [5]). In this setting, one can show that collusion transfers can be made from a market to another when some firms are active in both considered markets: i.e. they are in “multimarket contacts”. In this case, even in a highly competetive market, firms could get incentives to collude if they are also supplying customers in less competitive markets. This result is relevant for competition policy since measuring concentration with HHI index could be misleading. It may not encompass the behavioral dimension of competition, especially when multimarket contacts are a key feature of the industry.2
Our paper is organized as follows. In Section 2, we present the model and the benchmark case without multimarket contact. In Sections 3 and 4 multimarket contacts among firms are introduced; in this framework, we analyze if tacit collusion could be transferred from a market to another. Section 5 concludes and gives some implications of results in terms of competition policy. Proofs of Lemma and Propositions are given in an Appendix.
2. Model
2.1. Basic Assumptions
We model two independents markets (A and B) with an identical demand. Goods supplied on these markets are supposed to be homogeneous. Supply is provided by  symmetric firms in market A, and
symmetric firms in market A, and  in B. Without loss of generality, we assume market B to be always less concentrated than market A that is
in B. Without loss of generality, we assume market B to be always less concentrated than market A that is . In this industry, it exists a subset of k firms (
. In this industry, it exists a subset of k firms (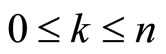 ) which are active on both markets: we refer to them as multimarket contacts firms. This configuration means that these firms supply the good in both markets A and B.
) which are active on both markets: we refer to them as multimarket contacts firms. This configuration means that these firms supply the good in both markets A and B.
As it is standard in the analysis of tacit collusion (see [7]), we consider an infinitely repeated Bertrand price competition game. The punishment strategy for a given firm corresponds to trigger strategy consisting in a reversion to a static competitive equilibrium. We denote 
 , the individual profit gained from a punishment strategy for all active firms in market h. We denote
, the individual profit gained from a punishment strategy for all active firms in market h. We denote  individual collusion profit. The determination of
individual collusion profit. The determination of 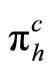 generally depends on the way the collusive agreement is reached as well as on various factors. Last,
generally depends on the way the collusive agreement is reached as well as on various factors. Last, 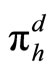 represents the individual profit gained from deviating from the collusive agreement and corresponds here to the monopolist outcome in market h, we denote
represents the individual profit gained from deviating from the collusive agreement and corresponds here to the monopolist outcome in market h, we denote . One can thus determine a threshold for the discount factor denoted
. One can thus determine a threshold for the discount factor denoted 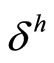 such as:
such as:
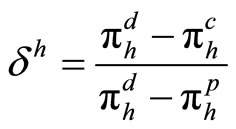
 (1)
(1)
Whenever3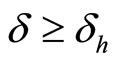 , collusion is sustainable in market
, collusion is sustainable in market . Hereafter, we will consider that market conditions (demand, costs and so on) in markets A and B are identical, one can write
. Hereafter, we will consider that market conditions (demand, costs and so on) in markets A and B are identical, one can write .
.
2.2. Collusion Incentives without Multimarket Contact
As a benchmark, we study collusion incentives in the case where multimarket contacts are not possible i.e.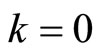 . Because of symmetry among firms, individual collusive profits are just given by an equal sharing of the monopolistic outcome that is
. Because of symmetry among firms, individual collusive profits are just given by an equal sharing of the monopolistic outcome that is  and
and . Then using Equation (1), the critical discount factors in both markets are given by:
. Then using Equation (1), the critical discount factors in both markets are given by:
 (2)
(2)
One can easily link up the incentives to collude (i.e. ) to the market concentration degree traditionally measured by the Hirschman-Herfindhal Index (HHI)4. In this benchmark case, this index for each market is:
) to the market concentration degree traditionally measured by the Hirschman-Herfindhal Index (HHI)4. In this benchmark case, this index for each market is:
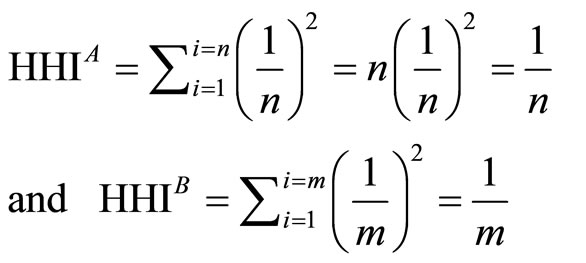
Then we can write thresholds for the discount factor as simple linear functions of the respective HHI in each market that is:

It does appear an inverse relationship between the value of these thresholds and HHI’s. Clearly on a given market, the lower HHI is, the less sustainable collusion is.
Collusion is then sustainable in both markets if and only if the discount factor 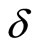 in the industry is such that
in the industry is such that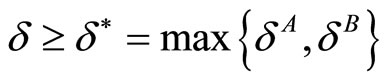 . We call the maximum value for these discount factors as the critical discount factor. In that case, with
. We call the maximum value for these discount factors as the critical discount factor. In that case, with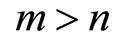 , the sustainability condition in both markets boils down to
, the sustainability condition in both markets boils down to 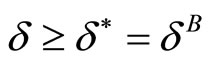 .
.
Remark 1. Without multimarket contact among firms, the HHI test is not conflicting with the analysis of tacit collusion.
A competitive market structure (i.e. a weak HHI level) is linked with pro-competitive behaviors (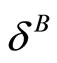 is high). This is the conventional wisdom in the field of competetion policy.
is high). This is the conventional wisdom in the field of competetion policy.
In the following, we study market structures with multimarket contacts and we analyze how such contacts could increase incentives for firms to collude.
3. Multimarket Contacts and “Business as Usual”
In this section, we analyze collusion incentives in the industry in the case where some firms ( ) are active in both markets A and B. Here, we consider that coordination to a given collusive agreement allows firms to keep their customers with respect to the competitive (Bertrand) equilibrium. As a result in case of collusion, market shares are assumed to be “frozen”: firms “in contact” in both markets does not modify the market sharing. In short, a “business as usual” principle applies.
) are active in both markets A and B. Here, we consider that coordination to a given collusive agreement allows firms to keep their customers with respect to the competitive (Bertrand) equilibrium. As a result in case of collusion, market shares are assumed to be “frozen”: firms “in contact” in both markets does not modify the market sharing. In short, a “business as usual” principle applies.
Now we have to distinguish three thresholds for the discount factor according to the type of firm. The factor  corresponds to active firms in the single-market A and
corresponds to active firms in the single-market A and  corresponds to those active in the single-market B. Last
corresponds to those active in the single-market B. Last  represents the discount factor for
represents the discount factor for  active firms in both markets. Using again relation (1), we obtain easily thresholds for the discount factor for firms without multimarket contact
active firms in both markets. Using again relation (1), we obtain easily thresholds for the discount factor for firms without multimarket contact 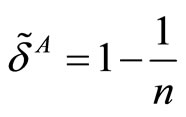 and
and .
.
To determine this threshold for each firm in contact in both markets A and B, the “business as usual” assumption leads to define each firm’s collusive profit as the sum of collusive profits on each market. This is due to the fact that market shares remain at their egalitarian competitive levels ( or
or ). The total collusive profits are then given by
). The total collusive profits are then given by
 . Furthermoreeach firm’s deviation profit equals twice the monopoly profit that is
. Furthermoreeach firm’s deviation profit equals twice the monopoly profit that is  Hence:
Hence:

As seen in the Section 2, it is easy to write this factor as a function of HHI’s in both markets A and B:

We find also the same kind of inverse relation that was previously established between the discount factor and the HHI calculated in each market. One can directly find that5 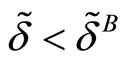 as soon as
as soon as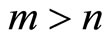 . In that case, the critical discount factor (i.e.
. In that case, the critical discount factor (i.e. ) is clearly
) is clearly . Therefore, collusion is sustainable in both markets A and B if6
. Therefore, collusion is sustainable in both markets A and B if6 .
.
Remark 2. When “business as usual” applies, multimarket contacts do not constitute a structural factor making easier collusive agreements.
This remark is directly linked to the “business as usual” assumption. Indeed since no direct link exists between markets7, collusion transfers from market A towards B can only occur if active firms in both markets give incentives for “single-market firms” to collude. Such incentives could be developed if market sharing in case of collusive agreements is modified. In that case, we have to enlarge the framework of our paper relaxing the “business as usual” assumption.
4. Multimarket Contacts and Collusion Transfers
We eliminate now the assumption of market shares freeze in order to allow active firms in both markets to transfer their collusive power from a market to another. Firstly, this leads us to define new collusive market shares; secondly, this allows calculating the critical discount factor in that case.
4.1. Sustainable Market Shares and Critical Discount Factors
We denote now  and
and  collusive market shares (resp. in market A and B) for a firm in contact in both markets. These shares are then defined by:
collusive market shares (resp. in market A and B) for a firm in contact in both markets. These shares are then defined by:
 (3)
(3)
where 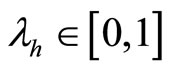 with
with  This definition of market shares simply explains that a given firm which is in contact on several markets can be encouraged to reduce his market share (from
This definition of market shares simply explains that a given firm which is in contact on several markets can be encouraged to reduce his market share (from  to
to  and/or from
and/or from  to
to ) in order to increase collusion incentives for other firms. For instance in market A, the gap between
) in order to increase collusion incentives for other firms. For instance in market A, the gap between  and
and  represents the opportunity cost that an active firm in both markets has to bear in order to increase the incentives for other firms to collude.
represents the opportunity cost that an active firm in both markets has to bear in order to increase the incentives for other firms to collude.
The individual collusive market share  for a single-market firm in market A (without contact), is defined by the linear equation
for a single-market firm in market A (without contact), is defined by the linear equation 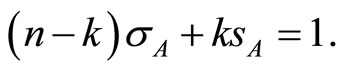 Solving it in
Solving it in
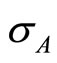 yields
yields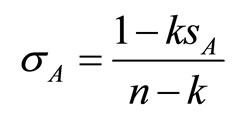 . Symmetrically, we obtain
. Symmetrically, we obtain  for a single-market firm in B.
for a single-market firm in B.
As in Section 3, we obtain the threshold for the discount factor for active firms in each single market  (denoted
(denoted ) as well as for active firms in both markets (
) as well as for active firms in both markets ( ). The new definition of market shares, in Equation (3), modifies these thresholds: they do not only depend on market structures (n and m) but also on the number of active firms in both markets (k). Using relation (1), the threshold for the discount factor for active firms in the single-market A is then given by:
). The new definition of market shares, in Equation (3), modifies these thresholds: they do not only depend on market structures (n and m) but also on the number of active firms in both markets (k). Using relation (1), the threshold for the discount factor for active firms in the single-market A is then given by:

The expression of this threshold depends on the value of . Using Equation (3) one can rewrite it as a function of the market A structure (n):
. Using Equation (3) one can rewrite it as a function of the market A structure (n):
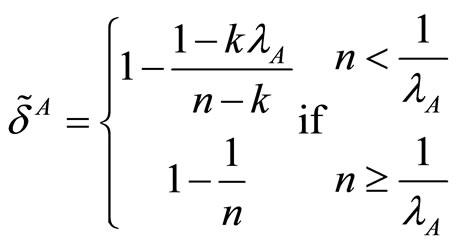 (4)
(4)
The threshold for the discount factor for active firms in the single-market B is defined in the same way but is a function of the market B structure (m):
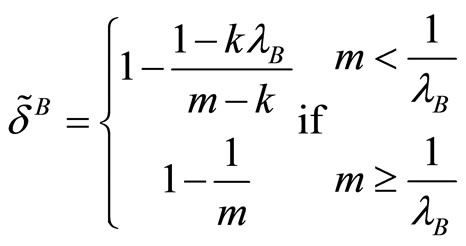 (5)
(5)
Finally, for firms with multimarket contacts, the threshold for the discount factor writes:
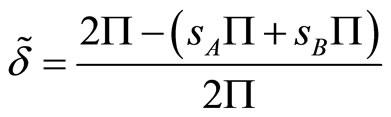
It takes different values according to the definition in Equation (3) of market shares 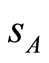 and
and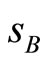 . Indeed, we have to differentiate between situations where the market shares are “frozen” on a given single market (A or B) and situations where they are simultaneously “frozen” in both markets. More precisely, this threshold rewrites:
. Indeed, we have to differentiate between situations where the market shares are “frozen” on a given single market (A or B) and situations where they are simultaneously “frozen” in both markets. More precisely, this threshold rewrites:
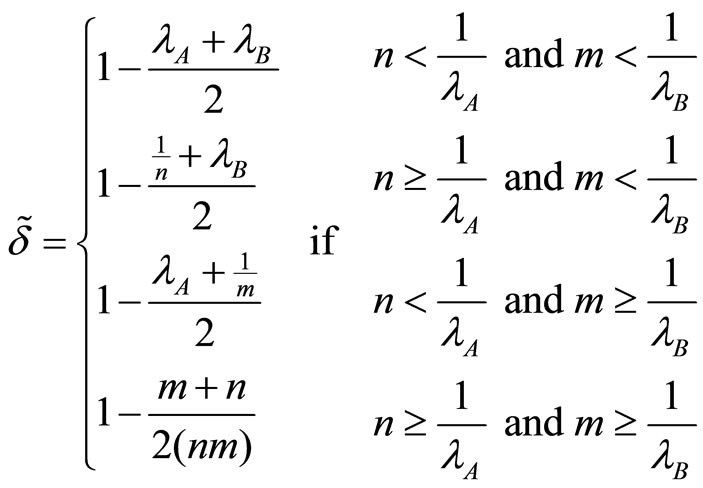 (6)
(6)
4.2. Critical Discount Factors
In order to determine the sustainability conditions in both markets, it is sufficient to analyze the corresponding critical discount factor denoted  and defined by
and defined by
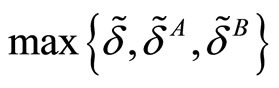 . Without loss of generality, we proceed the analysis assuming
. Without loss of generality, we proceed the analysis assuming .8
.8
Lemma 1. With multimarket contacts, collusion is sustainable in both markets if 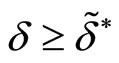 where
where  is defined as:
is defined as:
 (7)
(7)
where

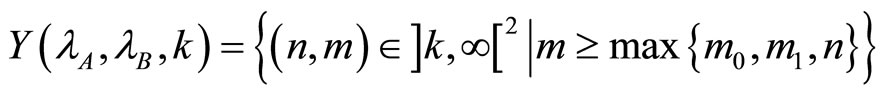
with 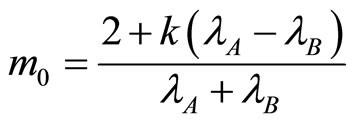 and
and .
.
For each type of firms (with and without contacts), we have defined thresholds ,
, 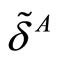 and
and 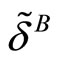 for the discount factor. They allow studying incentives to collude for each type of firms that depend on the values of parameters
for the discount factor. They allow studying incentives to collude for each type of firms that depend on the values of parameters .
.
Intuitively, active firms in the single-market A have more incentives to collude. They are active in the most concentrated market, so the gain derived from a deviation strategy is relatively lower than for firms supplying singlemarket B (less concentrated): the deviation profit is the same ( ) whereas collusion profits are decreasing with the number of firms.
) whereas collusion profits are decreasing with the number of firms.
On the other hand, for active firms in the single-market B and for firms with multimarket contacts, the analysis of the incentives to collude is not so obvious. Figure 1 summarizes this analysis in the plane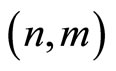 . More precisely, it represents critical discount factors in the plane
. More precisely, it represents critical discount factors in the plane  as defined in Lemma 1. In this figure, one can see the values of parameters for which active firms in both markets—respectively without contact in market B—have stronger incentives to deviate (area
as defined in Lemma 1. In this figure, one can see the values of parameters for which active firms in both markets—respectively without contact in market B—have stronger incentives to deviate (area ) respectively area
) respectively area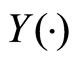 .
.
Within area , market B is relatively weakly competitive (
, market B is relatively weakly competitive ( ). In that case, the market B share which is supplied by active firms in both markets does not depend directly on the number of active firms in this market since
). In that case, the market B share which is supplied by active firms in both markets does not depend directly on the number of active firms in this market since . Incentives to collude for these firms (i.e.
. Incentives to collude for these firms (i.e.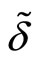 ) are therefore independent of the intensity of competition in this market. However, incentives for firms without contact in market B does depend on m through their market share given by
) are therefore independent of the intensity of competition in this market. However, incentives for firms without contact in market B does depend on m through their market share given by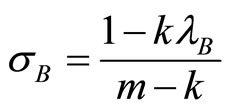 .
.
For a given k, the incentives to collude are higher for active firms in the single-market B and increase with the concentration of market (low value of m). Consequently, for a low level of concentration in market B ( ), the active firms in both markets have strongest incentives to deviate. Within area X, collusion is then sustainable as
), the active firms in both markets have strongest incentives to deviate. Within area X, collusion is then sustainable as . However, as soon as market A is very competitive (
. However, as soon as market A is very competitive ( ), this area vanishes.
), this area vanishes.
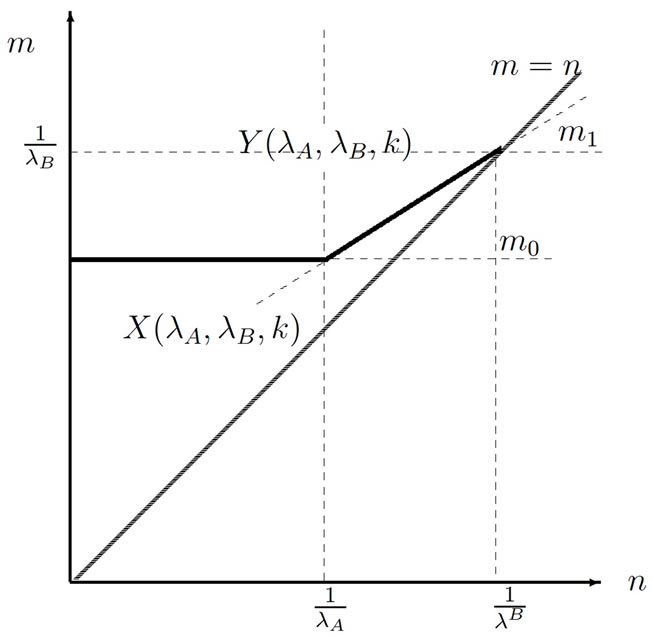
Figure 1. Analysis of collusion transfers.
In area Y, two situations have to be distinguished. First, when market B remains concentrated (i.e. ), the incentives to deviate for active firms in both markets are independent from the corresponding market structure (i.e.
), the incentives to deviate for active firms in both markets are independent from the corresponding market structure (i.e. ). Second, as market B becomes more competitive (
). Second, as market B becomes more competitive ( ), the share of market B supplied by firms with contacts in both markets corresponds to the situation where
), the share of market B supplied by firms with contacts in both markets corresponds to the situation where 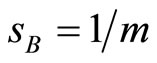 i.e. a freeze of market shares. In that case, their incentive to collude is now linked to the structure of market B. Within this area Y, collusion is sustainable as soon as
i.e. a freeze of market shares. In that case, their incentive to collude is now linked to the structure of market B. Within this area Y, collusion is sustainable as soon as .
.
A simple comparative statics with respect to the number of firms with multimarket contacts (k) allows to state the following result.
Proposition 1. The number of firms with multimarket contacts is a structural factor facilitating collusion in both markets.
When the number of firms with multimarket contacts (k) is increasing, the area X is expanding but the area Y is reducing since the frontier 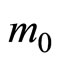 is moving upward. In this case, the share of firms that are supplying in both markets is very high and the number of
is moving upward. In this case, the share of firms that are supplying in both markets is very high and the number of 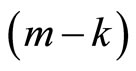 active firms in the single market B is very low; in that case, their benefit from a deviation is diminishing since their collusion profit is growing. One can also underline that the critical discount factor decreases with the number of active firms in both markets. Parameter k can be considered therefore as a structural factor facilitating collusion in markets9. This critical threshold decreases as a function of k. As the number of firms with contacts in both markets is relatively high, it becomes constant with respect to k since it is equal to
active firms in the single market B is very low; in that case, their benefit from a deviation is diminishing since their collusion profit is growing. One can also underline that the critical discount factor decreases with the number of active firms in both markets. Parameter k can be considered therefore as a structural factor facilitating collusion in markets9. This critical threshold decreases as a function of k. As the number of firms with contacts in both markets is relatively high, it becomes constant with respect to k since it is equal to .
.
4.3. Collusion Transfers
Now we make the comparison between both critical discount factors in two previous frameworks: the situation where some firms are active in both markets (i.e. ) and the benchmark case without multimarket contact (
) and the benchmark case without multimarket contact (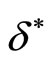 defined in Section 2).
defined in Section 2).
Figure 2 synthesizes the analysis of the critical discount factors and shows the area (depending on the parameter values) in which the existence of multimarket contacts is a structural factor facilitating collusion transfers from the less concentrated market (i.e. market A ) to the more concentrated market (B).
In this figure, one can distinguish three areas denoted ,
, 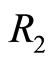 and
and  according to the values of parameters. Within locus
according to the values of parameters. Within locus  and
and , multimarket contacts do not increase the incentives for firms to collude. In both regions, the critical discount factor threshold does not decrease with the number of active firms in both markets:
, multimarket contacts do not increase the incentives for firms to collude. In both regions, the critical discount factor threshold does not decrease with the number of active firms in both markets:
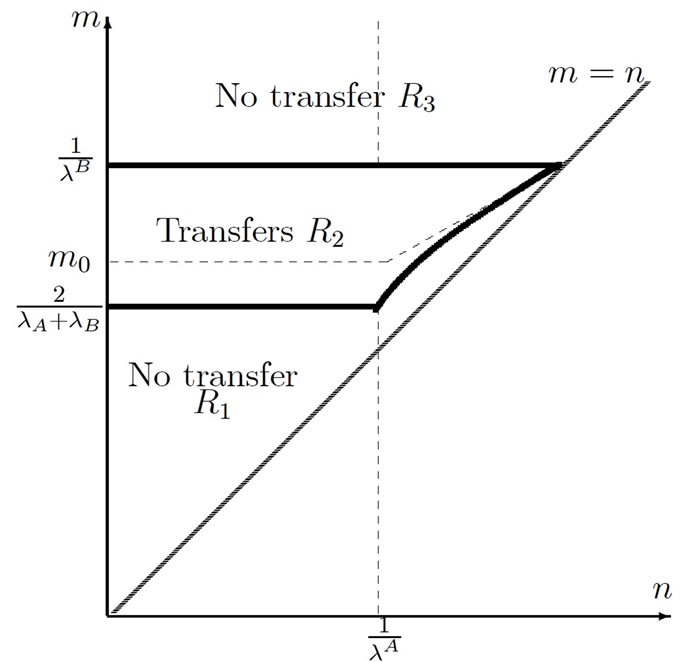
Figure 2. Regions for the critical discount factor.
 . In the area
. In the area , presence of firms with contacts in both markets entails more incentives for firms to collude in market A and also in market B. One can precise these results when market B becomes more competitive (m increases with n being fixed).
, presence of firms with contacts in both markets entails more incentives for firms to collude in market A and also in market B. One can precise these results when market B becomes more competitive (m increases with n being fixed).
As market B is relatively concentrated ( )we have
)we have 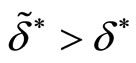 (in area
(in area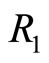 ): no collusion transfer occurs. Indeed initially, without multimarket contact, the critical discount factor is already very low. Active firms in market B have thus strong incentives to collude since collusion profits are shared between few firms. In that case, transferring collusion is too costly for active firms in both markets since they should give up a too large market share in market A but also in market B. In this situation, active firms in both markets make collusion less sustainable since
): no collusion transfer occurs. Indeed initially, without multimarket contact, the critical discount factor is already very low. Active firms in market B have thus strong incentives to collude since collusion profits are shared between few firms. In that case, transferring collusion is too costly for active firms in both markets since they should give up a too large market share in market A but also in market B. In this situation, active firms in both markets make collusion less sustainable since .
.
When market B is less concentrated
( ), our results show that firms with contacts in both markets are able to transfer collusion on this market:
), our results show that firms with contacts in both markets are able to transfer collusion on this market:  (area
(area ). We distinguish between two situations according to values of m: 1) whenever
). We distinguish between two situations according to values of m: 1) whenever 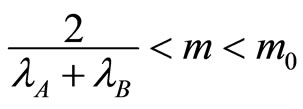 and 2) whenever
and 2) whenever

In the case 1)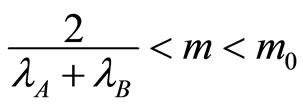 , market B becomes less concentrated. Individual collusion profits for active firms in this market are relatively low. In that case, the critical discount factor is defined using the incentive constraint for firms with multimarket contacts. These firms are then able to transfer collusion at a lower cost giving up a relatively small part of their market share. On the other side, if 2)
, market B becomes less concentrated. Individual collusion profits for active firms in this market are relatively low. In that case, the critical discount factor is defined using the incentive constraint for firms with multimarket contacts. These firms are then able to transfer collusion at a lower cost giving up a relatively small part of their market share. On the other side, if 2) , the critical discount factor in the multimarket contacts framework is defined using the incentive constraint for active firms in the single-market B (
, the critical discount factor in the multimarket contacts framework is defined using the incentive constraint for active firms in the single-market B ( ).
).
Within the area , market B is very competitive (
, market B is very competitive ( ); active firms in this market have then initially a low market share that is
); active firms in this market have then initially a low market share that is . It is then impossible to transfer collusion since de facto firms with contacts cannot concede an additional part of their market share.
. It is then impossible to transfer collusion since de facto firms with contacts cannot concede an additional part of their market share.
One can summarize the previous discussion using Figure 3 which represents the variation of the critical discount factor as a function of m when market A is weakly competitive ( ).
).
In this figure, the thick line represents the critical threshold  for which a collusion transfer is made. More precisely, for n and
for which a collusion transfer is made. More precisely, for n and 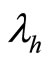 given, the figure shows the market B structure for which firms with multimarket contacts are able to transfer collusion.
given, the figure shows the market B structure for which firms with multimarket contacts are able to transfer collusion.
We can now state the following proposition concerning the impact of market-B concentration on the incentives to collude for firms in market A.
Proposition 2. When market A is weakly competitive ( ), more concentration in market B can reduce incentives to collude for firms in market A.
), more concentration in market B can reduce incentives to collude for firms in market A.
This proposition states a relevant result for competition policy. Usually, more market concentration leads to more incentives to collude. Here we show that a reverse result may hold: with multimarket contacts, a weakly competitive adjacent market (A here) relax incentives to collude for firms competing in others markets (as B).
The intuition of this result is simple. In order to transfer collusion, firms with multimarket contacts have to give up a significant part of their respective market share for firms without contact. Then firms with multimarket contacts may give up a small market share as collusion profits for single-market firms are low10. In that case, firms with contacts are able to transfer collusion easily. For example, to transfer collusion towards market B (i.e. 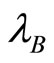 high), collusion profits for active firms in single market B must be weak; this is the case when these firms are numerous (
high), collusion profits for active firms in single market B must be weak; this is the case when these firms are numerous ( high). The idea is obvious: ability for firms to transfer collusion depends on their ability to give up market shares that depends on the value of
high). The idea is obvious: ability for firms to transfer collusion depends on their ability to give up market shares that depends on the value of  or on the number of firms (
or on the number of firms ( ) without contact in market B.
) without contact in market B.
Moreover, one can note that within the “transfer area” , the difference between both critical factors denoted
, the difference between both critical factors denoted  is not a monotonic function of m. When the market B structure is not very competitive
is not a monotonic function of m. When the market B structure is not very competitive
( ), the gap
), the gap 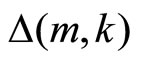 is increasing in m.
is increasing in m.
In that case, incentives to transfer collusion increase when market B becomes more competitive. On the other hand, as market B is sufficiently competitive
( ), incentives to transfers collusion reverse: they decrease with the number of active firms in market
), incentives to transfers collusion reverse: they decrease with the number of active firms in market

Figure 3. Collusion transfers as a function of m.
B. Hence, it exists a degree of market concentration in market B for which incentives to transfer collusion reach a maximum level, i.e. when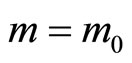 . Last, one can see that this value
. Last, one can see that this value 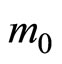 is increasing in the number of firms with contacts in both markets (i.e. k). Figure 4 illustrates how the gap
is increasing in the number of firms with contacts in both markets (i.e. k). Figure 4 illustrates how the gap  varies with m and k.
varies with m and k.
We see in Figure 4 that when k is growing ( ), incentives to transfer collusion are higher for more competitive market B:
), incentives to transfer collusion are higher for more competitive market B: 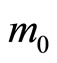 is increasing with k. Moreover, one can note that maximum incentives (corresponding to a market structure
is increasing with k. Moreover, one can note that maximum incentives (corresponding to a market structure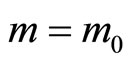 ) are increasing in k.
) are increasing in k.
So far, we have just considered low level of competition in market A (low level of n). When market A is more competitive ( ) and market
) and market  is weakly concentrated (
is weakly concentrated (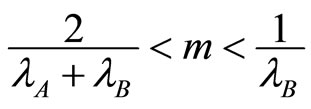 ), concentration of market A entails more collusive behaviors for firms in market B.
), concentration of market A entails more collusive behaviors for firms in market B.
4.4. HHI Test and Collusion with Multimarket Contacts
In order to analyze the link between incentives to collude and the degree of market concentration in the situation where k firms are active in both markets, we first calculate the concentration indexes HHI for each area ,
, 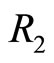 and
and 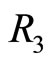 depicted in Figure 3.
depicted in Figure 3.
Hence in those areas, HHI for each market writes:

On the one hand, on can see clearly that  are decreasing functions11 of each
are decreasing functions11 of each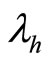 . On the other hand, using relation (7) in Lemma 1, we can see that
. On the other hand, using relation (7) in Lemma 1, we can see that  is an increasing function of
is an increasing function of  whereas
whereas 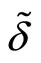 is a decreasing function of
is a decreasing function of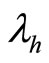 ,
, . Hence, it follows that
. Hence, it follows that  is a
is a

Figure 4. Collusion transfers: sensitivity analysis.
decreasing function of  but
but  is an increasing function of HHI in markets A and B.
is an increasing function of HHI in markets A and B.
In the configuration where market A is weakly competitive ( ), we just have proved the following proposition.
), we just have proved the following proposition.
Proposition 3. When market B is few concentrated
 , a low HHI level in market A or B corresponds to a market structure which facilitates collusion.
, a low HHI level in market A or B corresponds to a market structure which facilitates collusion.
This result reverses the established link between collusion sustainability and index of market concentration (see remarks 1 and 2). In the Proposition 3, we show that the analysis of the market structure (HHI test) could generate results in contradiction with results of the analysis of firm’s behaviors (collusion test). In particular, whenever , the critical discount factor (which would be the correct but unobservable collusion test) increases whereas HHI decreases. This reflects the situation where more competitive markets A or B could strengthen incentives to collude for some firms in these markets.
, the critical discount factor (which would be the correct but unobservable collusion test) increases whereas HHI decreases. This reflects the situation where more competitive markets A or B could strengthen incentives to collude for some firms in these markets.
5. Conclusions
In this paper, we show how the relationship between market concentration and collusive behaviors can be modified when firms are active on several independent markets (firms with multimarket contacts). It turns out that in particular market configurations, the well-known HHI test can generate results opposite to those obtained with the analysis of market behaviors, particularly the control of collusion.
Concerning the competition policy, three interesting results are underlined. First, the presence of active firms in both markets can increase incentives to collude. In that case, the concentration index HHI would be calculated on larger relevant markets. It is therefore necessary to analyze other geographical markets on which firms are active in order to control there is no collusion transfers from a geographic market to another. Second, the entrance of a firm in a market allows to improve concentration index and to decrease the HHI value. This entrance is therefore very favorable from a structural point of view. However, if this new firm is also active in a more concentrated market, her entrance in the more competitive market would increase incentives for other firms to collude. Indeed, this active firm in both markets could give up market shares on her new market in order to incite other firms to collude. In that case, the entrance of a firm (decrease of HHI) could give more incentives to collude and could be therefore harmful. Third, the process of concentration on a market can question previous collusive agreements and therefore can be favorable in terms of competition policy. More precisely, if the HHI value is increasing on the more competitive market, active firms in both markets can have more difficulties to incite other firms to collude. In this context, for a coherent competetion policy, it is better to analyze the relative levels of market concentration on which firms are active and not only absolute HHI level on each independent relevant market. Such a coherent analysis would allow controlling the structure of market linked to the control of collusive behaviors of firms.
REFERENCES
- M. Ivaldi, B. Jullien, P. Rey, P. Seabright and J. Tirole, “The Economics of Tacit Collusion,” IDEI Working Paper, No. 186, Report for DG Competition, European Commission, 2003,.
- C. Davidson and R. Deneckere, “Horizontal Mergers and Collusive Behavior,” International Journal of Industrial Organization, Vol. 2, No. 2, 1984, pp. 117-132.
- W. A. Brock and J. Scheinkman, “Price Setting Supergames with Capacity Constraints,” Review of Economic Studies, Vol. 52, No. 3, 1985, pp. 371-382. doi:10.1016/S0014-2921(01)00099-X
- O. F. Compte, F. Jenny and P. Rey, “Capacity Constraints, Mergers and Collusion,” European Economic Review, Vol. 46, No. 1, 2002, pp. 1-29.
- B. D. Bernheim and M. D. Whinston, “Multimarket Contact and Collusive Behavior,” Rand Journal of Economics, Vol. 21, No. 1, 1990, pp. 1-26.
- F. Domanico, “Concentration in the European Electricity Industry: The Internal Market as Solution?” Energy Policy, Vol. 35, No. 10, 2007, pp. 5064-5076. doi:10.1016/j.enpol.2007.04.014.
- J. W. Friedman, “A Non Cooperative Equilibrium for Supergames,” Review of Economic Studies, Vol. 28, 1971, pp. 1-12.
Appendix
Proof of Lemma 1. From relation (7) in the text we know that  Let us define three difference
Let us define three difference
 and
and
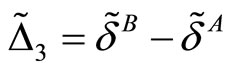 and study them according to
and study them according to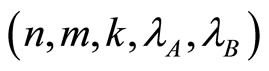 .
.
First, suppose that 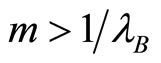 and
and  then we turn back in the situations of Sections 2 and 3 where
then we turn back in the situations of Sections 2 and 3 where
 for
for  then
then  and
and . This implies
. This implies 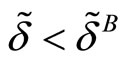 and
and hence
hence 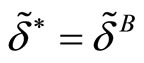 so we have
so we have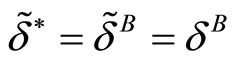 . Second, suppose that
. Second, suppose that  then from Equations
then from Equations
(4) to (6) in the text, we have 1) 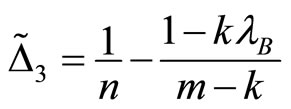 which is bounded below by
which is bounded below by . Thus
. Thus 
and the sign of  is of no relevance here.
is of no relevance here.
2) , moreover
, moreover 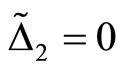 when
when 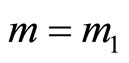 where
where 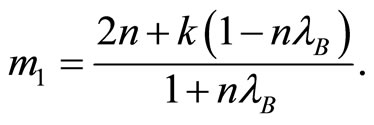 This value
This value 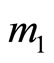 is an increasing concave function of n which takes values
is an increasing concave function of n which takes values
 if
if  and
and 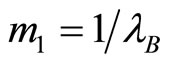 if
if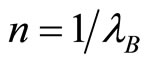 . Last as
. Last as ,
, 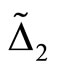 is monotonic and decreasing in m, so
is monotonic and decreasing in m, so 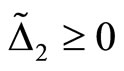 when
when
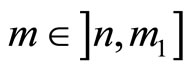 and when
and when  then
then 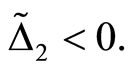 To sum up
To sum up 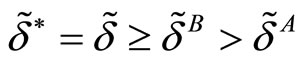 if
if 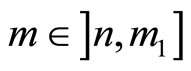 and
and
 if
if . Third if
. Third if
 then again using Equations (4)-(6):
then again using Equations (4)-(6):
1)  is again bounded below by
is again bounded below by , so
, so  and studying
and studying 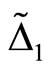 is useless but 2)
is useless but 2) . Hence
. Hence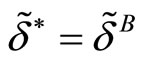 .
.
Last if  and
and 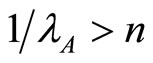 then 1)
then 1)
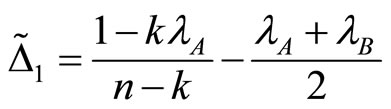 is decreasing in n and is zero for
is decreasing in n and is zero for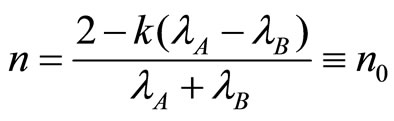 . Moreover
. Moreover 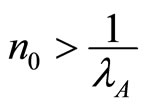 since
since
 Consequently
Consequently  that is
that is ; 2)
; 2)  is decreasing in m and is zero for
is decreasing in m and is zero for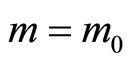 , but
, but  since
since . Hence
. Hence  if
if 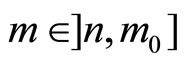 and
and 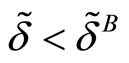 if
if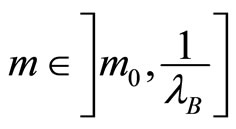 ; 3)
; 3)
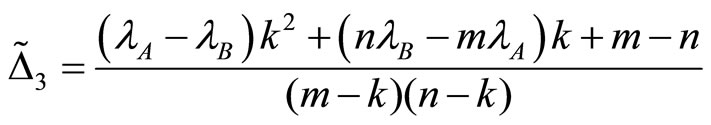 is monotone increasing in m and is zero for
is monotone increasing in m and is zero for
 where
where 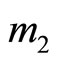 is increasing in n and take the values
is increasing in n and take the values 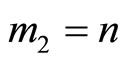 if
if 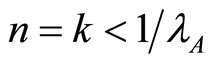 and
and
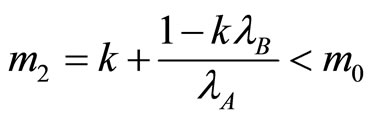 if
if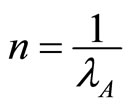 . Hence
. Hence 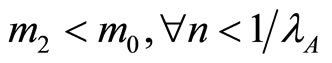 and thus
and thus 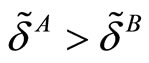 if
if  and
and  if
if . In summary 1) if
. In summary 1) if  then
then ; 2) if
; 2) if
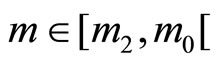 then
then 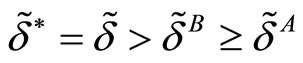 and 3) if
and 3) if 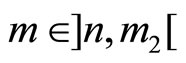 then
then .
.
As a result of these developments:  if
if 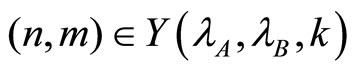 where
where

and  if
if

Proof of Proposition 2. We just have to show that the low boundary of the subset  that is
that is
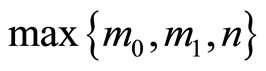 is an increasing function of k. We see that
is an increasing function of k. We see that 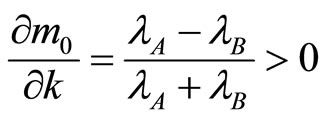 and
and  in their respective definition domains (see above).
in their respective definition domains (see above).
Collusion Transfers. We have to give the sign of the difference  .
.
1) Assume that  and
and 
(a) If  and
and 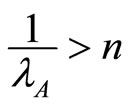 then
then  is decreasing in m and is equal to zero for
is decreasing in m and is equal to zero for 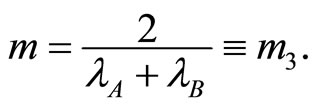 Moreover, we have
Moreover, we have 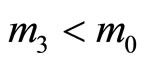 since
since 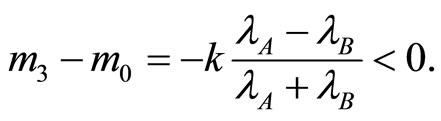 In that case,
In that case,  if
if . (b) If
. (b) If  and
and 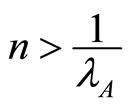 then
then 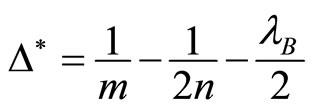 is decreasing in m and is equal to zero when
is decreasing in m and is equal to zero when  We have therefore
We have therefore 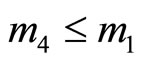 since
since 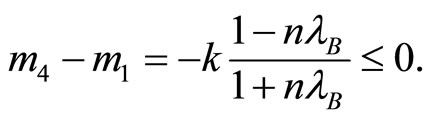 Moreover, if
Moreover, if  then
then  and if
and if  then
then . In that case,
. In that case,  if
if .
.
One can define the area  as a subset
as a subset  such that
such that
 .
.
2) Assume that  and
and . (a) If
. (a) If and
and 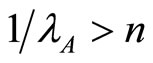 then
then
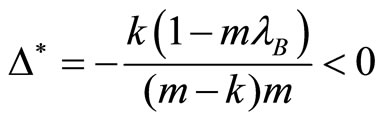 in that case
in that case . Idem if
. Idem if
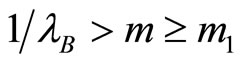 and
and . We can define area
. We can define area  as a subset of
as a subset of  such that
such that
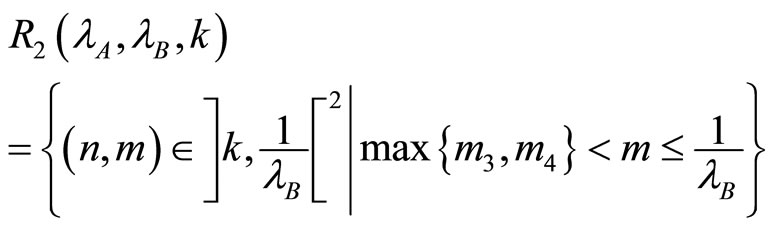
(b) If 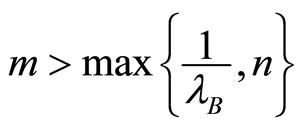 then
then 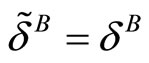 and
and 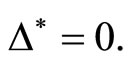
This allows to define the area , subset of
, subset of 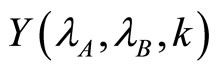 so that
so that

Study of  in locus
in locus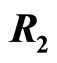 . We denote in the text
. We denote in the text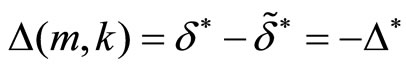 . If
. If  and if
and if  then, we shown above that:
then, we shown above that:
• For ,
, 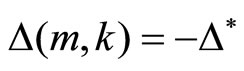 is increasing in m.
is increasing in m.
However 
• For ,
, 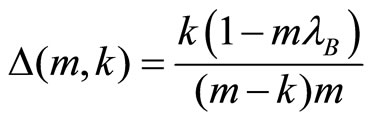 is decreasing in m since
is decreasing in m since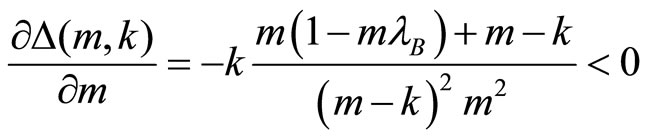 . Moreover
. Moreover 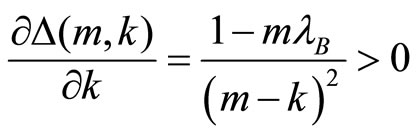 and we show that
and we show that .
.
Proof of Proposition 3. According to the text, if 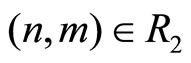
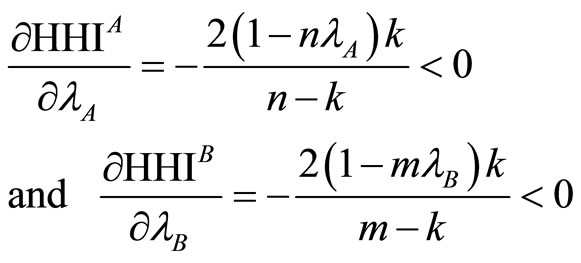
Moreover, if  then
then  is an increasing function of
is an increasing function of 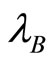 since
since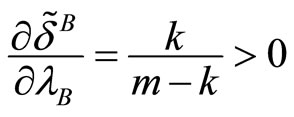 . On the other side,
. On the other side, 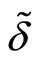 is a decreasing function of
is a decreasing function of  and
and 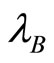 since
since 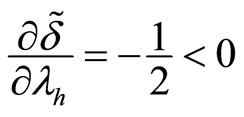 for
for .
.
NOTES
1See for example the survey on collusive behaviors in [1].
2An interesting empirical paper [6] focuses on this relationship between European electricity market concentration and collusive behaviors using multimarket contacts framework.
3Here 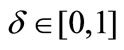 represents the common discount factor in both markets.
represents the common discount factor in both markets.
4HHI is calculated by squaring the market share of each firm competing in the market and summing.
5Indeed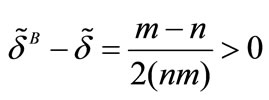 .
.
6It is important to underline that collusion sustainability in all markets does only depend on the degree of concentration in the market B.
7Demands in markets A and B are totally independents.
8On the same way, one can obtain the same type of results in the case where  and
and .
.
9In a sense this result strengthens the classical result stating that multimarket contacts facilitate collusion. See for example [1].
10This collusion profit decreases with the number of these firms.
11Indeed  and analogically for
and analogically for