ABSTRACT

This paper presents a simple model of monopolistic competition in a North-South world. The North introduces new goods that the South takes over when the goods become old. The new goods are more technology-intensive than the old goods because innovation requires more efforts than imitation. In the literature, the world distribution of income favors the country that produces a greater range of variety. However, in this model, the South’s catching up in terms of the range of variety is not a threat to the North’s status quo. It is the difference in technology intensity that determines their relative wage.

1. Introduction

It is well documented that technological change reshapes the pattern of trade and then the distribution of world income. Dornbusch, Fischer, and Samuelson [1] employed a Ricardian model in the case of a continuum of goods to demonstrate that the relative wage is basically determined by the range of variety in which a country has a comparative advantage. An increase in efficiency in the production of a given range of products makes a country better off by giving it a larger share of world income and consumption.1 Another thread of the literature is the product cycle model, where development of technology leads to new products rather than to an improvement in efficiency. Vermon [3] argued that a new product is first introduced and produced in a developed country because of its larger market. Furthermore, the newly-innovated product requires intense communication between producers and consumers to satisfy unfulfilled needs. Since only the developed country is endowed with sufficient technological capabilities to fulfill those needs, the new product will not be located in the less developed country that has a wage advantage until the product becomes mature.

Nevertheless, would the product cycle, driven by innovation and technology transfer, affects the distribution of world income? To address this issue, Krugman [4] developed a general-equilibrium model of product cycle under perfect competition, where products are innovated and imitated at exogenous rates. He argued that the relative wage of the developed country depends on the range of product variety that it can produce but the less developed country cannot. The developed country must continually innovate; otherwise, the less developed country’s imitation may suppress the developed country’s innovation, thus lowering the North’s real income in absolute terms.

The literature, as referred to above, both conclude that the world distribution of income favors the country that generates a greater range of product varieties. Instead, by drawing heavily from Krugman’s [4] model, I incorporate a monopolistic competition framework in his model, where innovation of new goods needs more lump-sum efforts while imitation requires fewer such efforts, such that new goods are of high technology intensity while the old goods are of low technology intensity. Furthermore, I incorporate Romer’s [5] model to endogenize the innovation and imitation. Surprisingly, in this model, the capability of the less developed country to take over a greater range of variety is not a threat to the status quo. It is the difference in technology intensity that determines the relative wage.

2. The Model

In a world of North and South with monopolistic competition, there is only one factor of production, labor, and all goods are assumed to be produced by the same cost function. All the goods are innovated in the North, but are gradually transferred to the South with a time lag. Suppose that product varieties that remained in the North are referred to as “new” goods, while 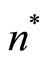product varieties that have been transferred to the South are referred to as “old” goods. We represent the total number of product varieties as.

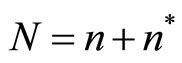All goods, whether new or old, are assumed to enter demand symmetrically. All consumers share the same utility function

(1)

where 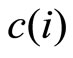is the consumption of the ith good. In addition to product varieties, as in Krugman’s [4] model, there is also a latent demand for as yet unproduced new goods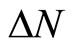, which enters the utility function in the same way as the 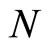product varieties did.

In this paper, I assume that labor supply in each country grows at an exogenous rate. The population growth of the North triggers innovation of new goods, while the population growth of the South speeds up the process of technology transferring in relation to the old goods. Each of the new goods requires a lump-sum cost of innovation, 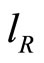, while each of the old goods requires a lump-sum cost of imitation,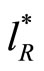. The cost of innovation is referred to as research and development (R & D) cost, while the cost of imitation is referred to as technology transfer cost. It is reasonable to assume 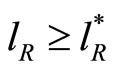because imitation should require less efforts than innovation.

The cost functions for the new and old goods are, respectively, as

(2)

where and represent the labor employed in the manufacturing sector for the North and South, respectively. Here, denotes consumption of a Northern good and 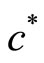consumption of a Southern good. The total labor supply in the North and in South are given by and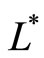, respectively.

The price of each good is then given by

(3)

where and 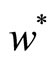are the wage rates of the North and South, respectively. Assume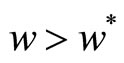. The utility function in Equation (1) implies that the relative demand will depend only on prices:

(4)

Demand for labor in each country will equal labor demand for each good times the number of goods, so the relative demand for labor can be expressed as

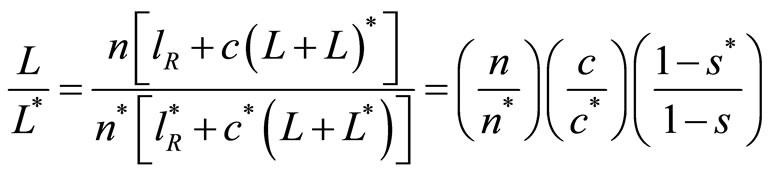(5)

where 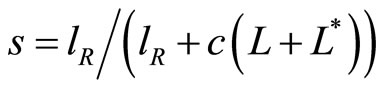denotes technology intensity of the North and that of the South, respectively. It turns out that we obtain an expression for the relative wage of

(6)

In contrast to the literature (e.g., Krugman, [4]), the relative wage of the North not only depends on the relative importance of newly-developed products which the North can produce but the South cannot, but also on the relative technology-intensity of the North to the South. That is, the greater the difference in technology intensity, the greater the difference in relative wage of the North to the South. This is the first implication in this model.

3. Innovation, Technology Transfer, and Technology Intensity

This current model deviates away from Krugman’s [4] model further in the design of innovation function. By contrast, I borrow Romer’s model [5] and assume that innovation is proportional to not only the number of products already in existence, but also to the number of R & D workers employed:

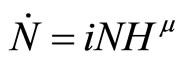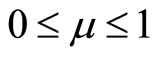, , (7)

where is a positive innovation parameter and 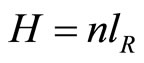represents the total employment in the R & D sector in the North. Similar to Romer’s model, both the R & D and manufacturing sectors grow at the same rate as population growth in each country. At this moment, the technology intensity in each country remains unchanged. In Equation (7), 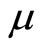is a country-specific parameter indicating how R & D workers are efficiently employed. That is, a country has a good management and the efficient allocation of research activities tends to generate more innovation. Jones [2] referred to this as the “stepping on toes” effect (i.e., that duplication of the R & D effort is more likely when there are too many persons engaged in it).

Additionally, the parameter 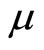also captures whether an economy has well-protected intellectual property rights. It is widely acknowledged that innovation is encouraged if intellectual property rights are well protected (e.g., Jones, [2]), wherein entrepreneurs are more willing to invest in R & D and unveil their innovations in the form of patent applications. Protection of intellectual property ends up encouraging innovation. Without loss of generality, let measure the innovation environment of a country in order to capture all of the exogenous technology shocks that affect the efficiency of innovation in this paper.

Krugman [4] argued that process of technology transfer turns new goods, which are a Northern monopoly, into old goods, following a way of radioactive decay. That is, the innovative goods would remain new for some fixed period, as if they were patented. Gradually, the South takes over the goods from the North:

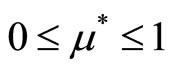, , (8)

where 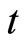denotes a positive imitation parameter and 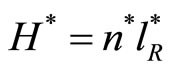represents the total employment in the R & D sector of the South. Again, following Romer’s model [5], I presume that technology transfer is also proportional to the number of southern workers that are devoted to technology transfer. Note that it is feasible to argue that the North is superior in terms of patent protection and is more efficient than the South in the employment of the R & D works, such that.

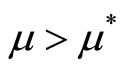The rate of change in new goods will be the difference between the rate of innovation and the rate of technology transfer:

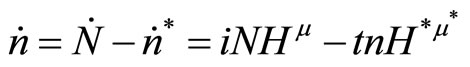(9)

Let denote the relative share of new goods. Then we have

(10)

Suppose, at an initial time, the total employment of R&D workers is given by 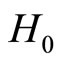and for the North and South, respectively. Assume further that the population growth rates are and for the North and South, respectively. We should have 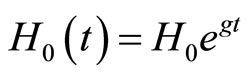and 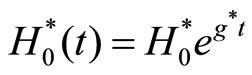at time t for the North and South, respectively. Let’s rewrite the relative share of new varieties in a dynamic form as

.

The system of innovation and imitation will tend toward an equilibrium if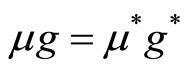. That is, if

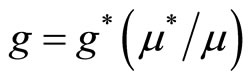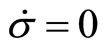, we obtain in equilibrium and. Obviously, the relative share of new varieties in the North remains unchanged even if the South has a higher population growth rate than the North as while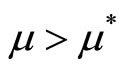. Consequently, the relative wage between the North and the South in Equation (6) remains unchanged.

If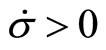, the relative share of new varieties becomes larger. On the contrary, if, the relative share of old varieties becomes larger. In either case, the relative wage remains unchanged as implied in Equation (6) because the change in variety (i.e.,) will be fully offset by the change in labor growth (i.e.,).

Krugman [4] argued that the North’s higher wage depends on the quasi rents from the Northern monopoly of new goods, so that the North’s relative wage crucially depends on its relative supply of new goods (). However, in this current model, the North can maintain its real income in absolute terms regardless of whether the South’s imitation suppresses the North’s innovation such that. Instead, the relative share of product varieties is irrelevant to the relative wage of the North to that of the South. It is the difference in technology intensity that determines their wage inequality in this current paper.

4. Conclusion

I have extended Krugman’s [4] general equilibrium model of product cycle in a monopolistic competition form to show that the greater the difference in technology intensity, the greater the difference in relative wage of the North to the South. This model also shows that the relative share of product varieties is irrelevant to their relative wage, implying that technology transferring is welfare improving for both countries. It is because that, the lower wage cost in the South is translated into lower product prices, the real wage of the both countries on these transferred goods then increases. Furthermore, innovation of new varieties adds to utility in Equation (1), improving is welfare to the world as well.

REFERENCES

NOTES

¹Jones [2] tried to apply the Heckscher-Ohlin model to demonstrate the possibility that technical change might result in an improvement in the quality of commodities instead of factor efficiency.