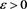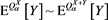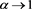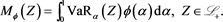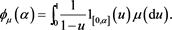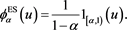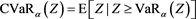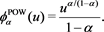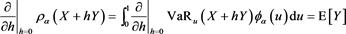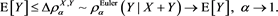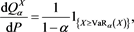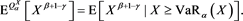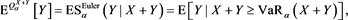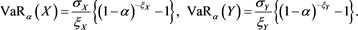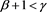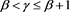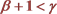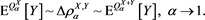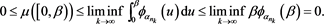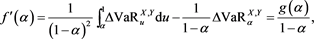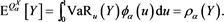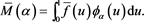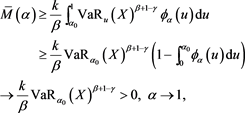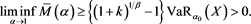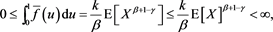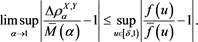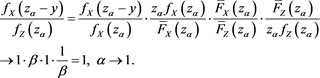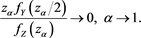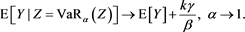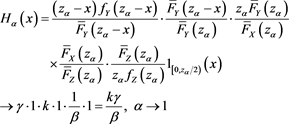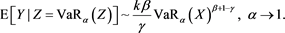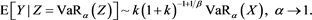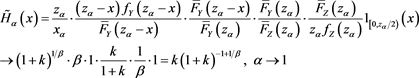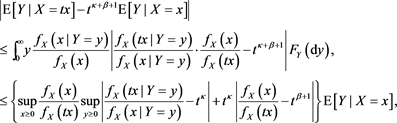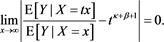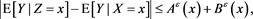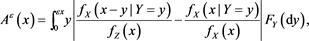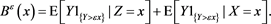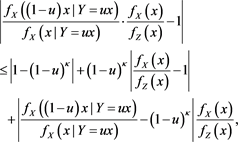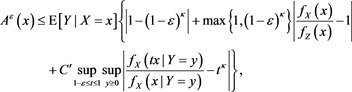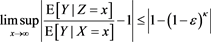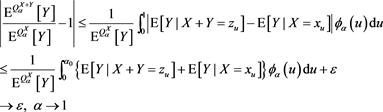Journal of Mathematical Finance
Vol.08 No.01(2018), Article ID:82779,30 pages
10.4236/jmf.2018.81015
Asymptotic Analysis for Spectral Risk Measures Parameterized by Confidence Level
Takashi Kato
Association of Mathematical Finance Laboratory (AMFiL), Tokyo, Japan
Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 21, 2018; Accepted: February 25, 2018; Published: February 28, 2018
ABSTRACT
We study the asymptotic behavior of the difference as , where is a risk measure equipped with a confidence level parameter , and where X and Y are non-negative random variables whose tail probability functions are regularly varying. The case where is the value-at-risk (VaR) at a, is treated in [1] . This paper investigates the case where is a spectral risk measure that converges to the worst-case risk measure as . We give the asymptotic behavior of the difference between the marginal risk contribution and the Euler contribution of Y to the portfolio . Similarly to [1] , our results depend primarily on the relative magnitudes of the thicknesses of the tails of X and Y. Especially, we find that is asymptotically equivalent to the expectation (expected loss) of Y if the tail of Y is sufficiently thinner than that of X. Moreover, we obtain the asymptotic relationship as , where is a constant whose value likewise changes according to the relative magnitudes of the thicknesses of the tails of X and Y. We also conducted a numerical experiment, finding that when the tail of X is sufficiently thicker than that of Y, does not increase monotonically with a and takes a maximum at a confidence level strictly less than 1.
Keywords:
Spectral Risk Measures, Quantitative Risk Management, Asymptotic Analysis, Extreme Value Theory, Euler Contribution

1. Introduction
The purpose of this paper is to investigate the asymptotic behavior of the difference
(1.1)
as , where X and Y are fat-tailed random variables (loss variables) and is a family of risk measures. The case where is an a-percentile value-at-risk (VaR), has been treated in [1] , where it was shown that the asymptotic behavior of drastically changes according to the relative magnitudes of the thicknesses of the tails of X and Y (the definition of the VaR is given in (2.1) in the next section). In this paper, we study a progressive case in which is given as a parameterized spectral risk measure, and we obtain similar results as in [1] . In particular, we find that if X and Y are independent and if the tail of X is sufficiently fatter than that of Y, then converges to the expected value as whenever are spectral risk measures converging to a risk measure of the worst case scenario. That is, whenever
(1.2)
for each loss random variable Z in some sense. Our result does not require any specific form for , implying that this property is robust. Furthermore, assuming some technical conditions for the probability density functions of X and Y, we study the asymptotic behavior of the Euler contribution, defined as
(1.3)
(see Remark 17.1 in [2] ), and show that is asymptotically equivalent to as . Here, is a constant determined according to the relative magnitudes of the thicknesses of the tails of X and Y.
We now briefly review the financial background for this study. In quantitative financial risk management, it is important to capture tail loss events by using adequate risk measures. One of the most standard risk measures is the VaR. The Basel Accords, which provide a set of recommendations for regulations in the banking industry, essentially recommend using VaR as a measure of risk capital for banks. VaRs are indeed simple, useful, and their values are easy to interpret. For instance, a yearly 99.9% VaR calculated as
means that the probability of a risk event with a realized loss larger than
is 0.1%. In other words, an amount  of risk capital is sufficient to prevent a default with 99.9% probability. The meaning of the amount
of risk capital is sufficient to prevent a default with 99.9% probability. The meaning of the amount  is therefore easy to understand. However, VaRs are often criticized for their lack of subadditivity (see, for instance, [3] [4] [5] and [6] ). VaRs do not reflect the risk diversification effect.
is therefore easy to understand. However, VaRs are often criticized for their lack of subadditivity (see, for instance, [3] [4] [5] and [6] ). VaRs do not reflect the risk diversification effect.
The expected shortfall (ES) has been proposed as an alternative risk measure that is coherent (in particular, subadditive) and tractable, with the risk amount at least that of the corresponding VaR. Note that there are various versions of ES, such as the conditional value-at-risk (CVaR), the average value-at-risk (AVaR), the tail conditional expectation (TCE), and the worst conditional expectation (WCE). These are all equivalent under some natural assumptions (see [4] [7] [8] , and [9] ). It should be noted that the Basel Accords have also considered recently the adoption of ESs as a minimal capital requirement, in order to better capture market tail risks (see for instance [10] and [11] ).
A spectral risk measure (SRM) has been proposed as a generalization of ESs, in [3] . SRMs are characterized by a weight function 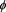 that represents the significance of each confidence level for the risk manager. SRMs are equivalent to comonotonic law-invariant coherent risk measures (see Remark 1 in the next section).
that represents the significance of each confidence level for the risk manager. SRMs are equivalent to comonotonic law-invariant coherent risk measures (see Remark 1 in the next section).
VaRs and ESs as risk measures depend on a confidence level parameter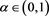 . We let
. We let 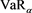 (resp.,
(resp.,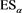 ) denote the VaR (resp., ES) with confidence level a. When a is close to 1, the values of
) denote the VaR (resp., ES) with confidence level a. When a is close to 1, the values of  and
and 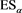 are increasing without bound as in (1.2). The parameter a corresponds to the risk aversion level of the risk manager. Higher values of a indicate that the risk manager is more risk-averse and evaluates the tail risk as more severe.
are increasing without bound as in (1.2). The parameter a corresponds to the risk aversion level of the risk manager. Higher values of a indicate that the risk manager is more risk-averse and evaluates the tail risk as more severe.
In this paper, we consider a family 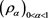 of SRMs parameterized by the confidence level a. We make a mathematical assumption that intuitively implies situation (1.2) and investigate the asymptotic behaviors of (1.1) and (1.3) as
of SRMs parameterized by the confidence level a. We make a mathematical assumption that intuitively implies situation (1.2) and investigate the asymptotic behaviors of (1.1) and (1.3) as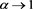 , when the tail probability function of X (resp., Y) is regularly varying with index
, when the tail probability function of X (resp., Y) is regularly varying with index 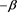 (resp.,
(resp., ). Our main theorem asserts that the asymptotic behaviors of (1.1) and (1.3) strongly depend on the relative magnitudes of
). Our main theorem asserts that the asymptotic behaviors of (1.1) and (1.3) strongly depend on the relative magnitudes of  and
and . Note that our results include the case
. Note that our results include the case , the inclusion of which was discussed as a future task in [1] .
, the inclusion of which was discussed as a future task in [1] .
The rest of this paper is organized as follows. In Section 2, we prepare the basic settings and introduce the definitions for SRMs based on confidence level. In Section 3, we give our main results. We numerically verify our results in Section 4. Finally, Section 5 summarizes our studies. Throughout the main part of this paper, we assume that X and Y are independent. The more general case where X and Y are not independent is studied in Appendix 1. All proofs are given in Appendix 2.
2. Preliminaries
Let 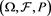 be a standard probability space and let
be a standard probability space and let  denote a set of non-negative random variables defined on
denote a set of non-negative random variables defined on . For each
. For each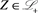
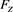
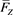
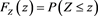



Note that 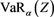

We now introduce the definition of SRMs.
Definition 1
1) A Borel measurable function 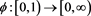
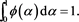
2) A risk measure 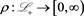


Remark 1 SRMs are law-invariant, comonotonic, and coherent risk measures. However, as shown in [12] [13] , and [14] , if 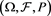


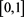
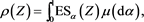
for each
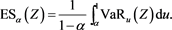
Moreover, such a 
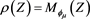
Here, it is easy to see that 
meaning that 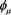
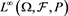
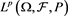
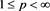
Next, we introduce a family 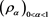
Definition 2 Let 

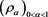
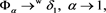
where 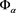
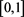
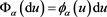

Condition (2.5) formally implies (1.2). Indeed, if 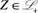

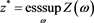
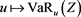
where we recognize
Lemma 1 Relation (2.5) is equivalent to
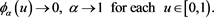
We now give some examples of CLBSRMs.
Example 1. Expected Shortfalls
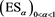
It is easy to see that (2.5) does hold. Indeed, for any bounded continuous function f defined on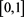
due to the bounded convergence theorem. Equivalently, we can also check that 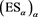

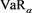
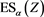
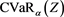
(see [8] for details).
Example 2. Exponential/Power SRMs
An admissible spectrum f corresponding to an SRM 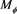
The exponential utility function is a typical example of tractable utility functions
where p denotes the profit-and-loss (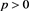
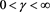
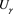



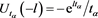
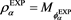
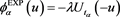
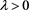
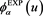
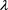
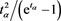
Note that the theoretical validity of the above method is still unclear. Other methods to adequately construct SRMs from exponential utility functions have been discussed in [18] [19] , and [20] , but no definite answer has been reached. In particular, it is pointed out in [18] that there exists no general consistency between expected utility theory and SRM-decision making. In any case, we can easily verify that 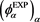

Similarly to the above, an SRM 
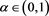
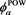
We can also verify that 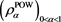
We now introduce some notations and definitions used in asymptotic analysis and extreme value theory.
Let f and g be positive functions defined on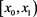
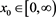
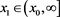

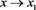
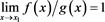

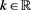

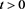
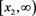
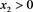
3. Main Results
Our main purpose is to investigate the property of (1.1) for a CLBSRM 

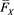
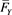

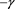



for some
In [1] , we study the asymptotic property of (1.1) as 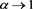

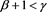




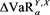

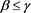

Let 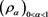

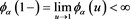
for each
for each

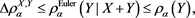
where 


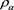
Our main purpose in this section is to investigate in detail the asymptotic behavior of
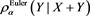

[C1] X and Y are independent.
[C2] There is some 

density function 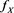
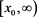

[C3] The function 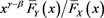
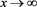
Let us adopt the notation
for
Theorem 1 Assuming [C1]-[C3], 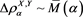

Formally, assertions (i)-(iii) of Theorem 4.1 in [1] are the same as the assumptions of Theorem 1, by setting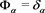
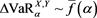
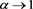
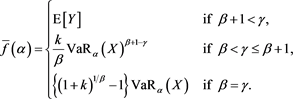
Theorem 1 justifies the following relation:
Note that condition [C3] is not required for Theorem 1 when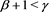
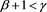
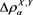
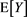
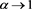
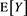
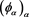
Theorem 2 Assume [C1] and [C3]. Moreover, assume that
[C4] X and Y have positive, continuous, and ultimately decreasing density functions 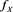

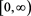
Under these assumptions, 



Theorems 1 and 2 together imply that if X and Y are independent, and if 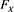

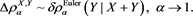
Note that 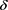
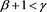
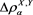
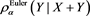
Note that 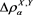

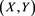
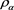
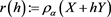
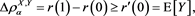
where the last equality in the above relation is obtained from (5.12) in [24] ,

and
due to the dominated convergence theorem. Therefore, if
In Section 4, we numerically verify the above relation. Note that we can also verify a version of Assumption (S) under [C4].
Remark 2
1) If 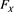
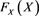
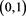

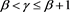
where 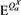
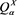
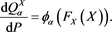
Note that we have
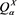
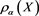
where 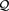
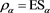
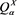
and therefore
Until the end of Remark 2, we assume that 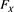

2) We can relax the independence condition [C1] so that X may weakly depend on Y within the negligible joint tail condition (see Remark A.1 in [1] ). In this case, under some additional assumptions such as [A5] and [A6] in [1] , we can make the same assertion as in Theorem 1, where the value 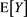
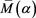
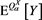

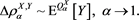
Indeed, our proof in Appendix 2 also works by applying Theorem A.1 in [1] instead of Theorem 4.1. Note that we need some additional condition to have that

(see Proposition 3 in Appendix 2).
3) As mentioned in Appendix A.1 of [1] , we can get another version of Theorem A.1 by switching the roles of 
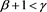

and then (by the same proof as Theorem 1 with (3.13))
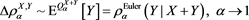
under some assumptions. Here, 
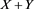

because 
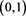
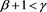
Note that if
which is known as the component CVaR (also known as the CVaR contribution) and widely used, particularly in the practice of credit portfolio risk management (see for instance [25] [26] , and [27] ).
4. Numerical Analysis
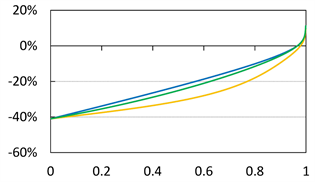
In this section, we numerically investigate the behavior of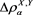
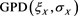
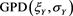




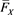
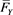
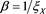

(see (5.2) in [1] ). Also note that 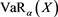

We numerically compute
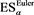
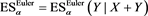

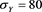

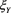
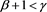

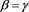
Case 1)
We set 
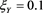

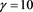

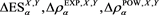
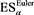
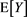
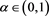

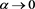
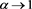
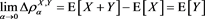
holds because
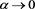
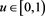
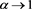

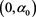
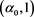

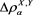
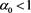
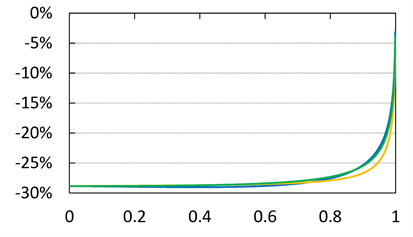
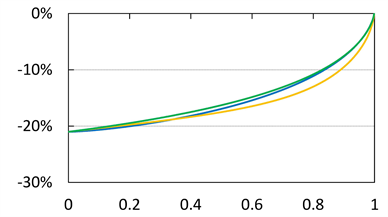
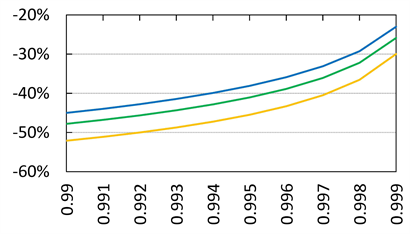
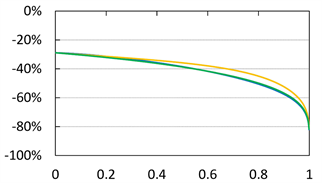
Figure 2 shows the relation between 

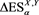
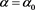
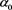
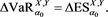
Indeed, we have the following result.
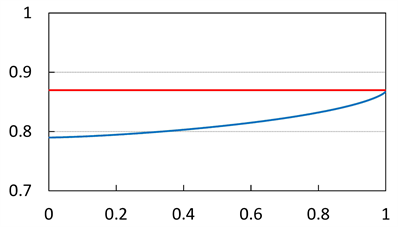
Proposition 1 If there is a unique solution 
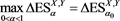
Note that unlike the case of SRMs, 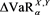

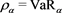
Figure 1. Graphs of 


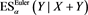
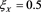
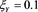
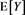
Figure 2. Graphs of 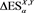
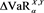
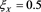
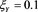
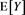

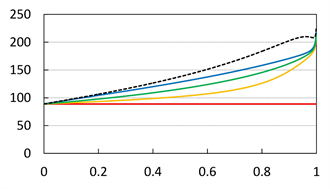
Case 2)
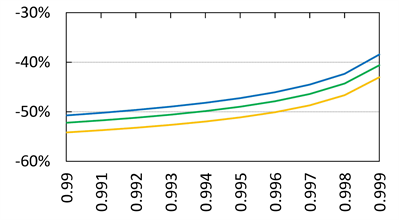
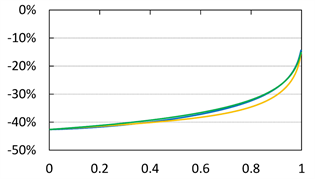
Figure 3 shows the approximation errors, defined as

with 

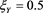

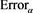
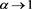
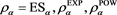
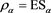

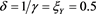

By contrast, the convergence speed of 

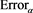
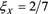
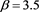
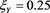

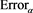
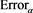
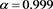
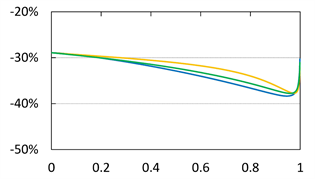
Case 3)
Finally, we look at the case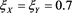

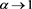
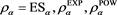
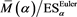

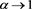
Similarly to Case 2), the convergence speed of 
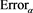
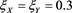
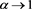

5. Concluding Remarks
In this paper, we have studied the asymptotic behavior of the difference between 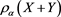
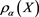
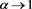
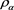

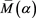
Figure 3. Approximation errors defined by (4.4) with 




Figure 4. 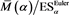

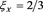

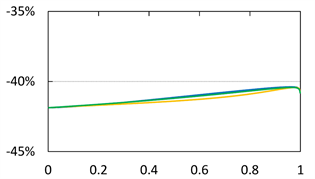
Figure 5. Approximation errors defined by (4.4) with 
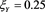

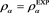
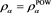
Figure 6. Approximation errors defined by (4.4) with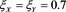


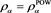
Figure 7. 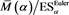
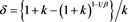
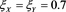
Figure 8. Approximation errors defined by (4.4) with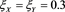

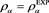

of the thicknesses of the tails of X and Y. In particular, for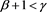
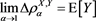
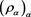

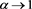
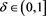
Our numerical results in the case 

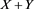
Our results essentially depend on the assumption that X and Y are independent. However, the dependence structure of the loss variables X and Y plays an essential role in financial risk management. The case of dependent X and Y for 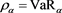
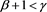

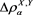
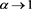
Cite this paper
Kato, T. (2018) Asymptotic Analysis for Spectral Risk Measures Parameterized by Confidence Level. Journal of Mathematical Finance, 8, 197-226. https://doi.org/10.4236/jmf.2018.81015
References
- 1. Kato, T. (2017) Theoretical Sensitivity Analysis for Quantitative Operational Risk Management. International Journal of Theoretical and Applied Finance, 20, 23 p. https://doi.org/10.1007/PL00011399
- 2. Tasche, D. (2008) Capital Allocation to Business Units and Sub-Portfolios: The Euler Principle. In: Resti, A., Ed., Pillar II in the New Basel Accord: The Challenge of Economic Capital, Risk Books, London, 423-453.
- 3. Acerbi, C. (2002) Spectral Measures of Risk: A Coherent Representation of Subjective Risk Aversion. Journal of Banking & Finance, 26, 1505-1518. https://doi.org/10.1016/S0378-4266(02)00281-9
- 4. Acerbi, C. and Tasche, D. (2002) Expected Shortfall: A Natural Coherent Alternative to Value at Risk. Economic Notes, 31, 379-388. https://doi.org/10.1111/1468-0300.00091
- 5. Embrechts, P. (2000) Extreme Value Theory: Potential and Limitations as an Integrated Risk Management Tool, Derivatives Use. Trading & Regulation, 6, 449-456.
- 6. Tasche, D. (2002) Expected Shortfall and Beyond. Journal of Banking & Finance, 26, 1519-1533. https://doi.org/10.1016/S0378-4266(02)00272-8
- 7. Acerbi, C., Nordio, C. and Sirtori, C. (2001) Expected Shortfall as a Tool for Financial Risk Management. Preprint. https://arxiv.org/pdf/cond-mat/0102304.pdf
- 8. Acerbi, C. and Tasche, D. (2002) On the Coherence of Expected Shortfall. Journal of Banking & Finance, 26, 1487-1503. https://doi.org/10.1016/S0378-4266(02)00283-2
- 9. Artzner, P., Delbaen, F., Eber, J.-M. and Heath, D. (1999) Coherent Measures of Risk. Mathematical Finance, 9, 203-228. https://doi.org/10.1111/1467-9965.00068
- 10. Basel Committee on Banking Supervision (2012) Fundamental Review of the Trading Book. Press Release, Bank for International Settlements. http://www.bis.org/publ/bcbs219.pdf
- 11. Basel Committee on Banking Supervision (2016) Minimum Capital Requirements for Market Risk. Press Release, Bank for International Settlements. http://www.bis.org/bcbs/publ/d352.pdf
- 12. Föllmer, H. and Schied, A. (2016) Stochastic Finance: An Introduction in Discrete Time. 4th Edition, De Gruyter. https://doi.org/10.1515/9783110463453
- 13. Jouini, E., Schachermayer, W. and Touzi, N. (2006) Law Invariant Risk Measures Have the Fatou Property, In: Kusuoka, S. and Yamazaki, A., Eds., Advances in Mathematical Economics, 9, 49-71, Springer, Japan. https://doi.org/10.1007/4-431-34342-3_4
- 14. Kusuoka, S. (2001) On Law-Invariant Coherent Risk Measures. In: Kusuoka, S. and Maruyama, T., Eds., Advances in Mathematical Economics, 3, 83-95, Springer, Japan. https://doi.org/10.1007/978-4-431-67891-5_4
- 15. Shapiro, S. (2013) On Kusuoka Representation of Law Invariant Risk Measures. Mathematics of Operations Research, 38, 142-152. https://doi.org/10.1287/moor.1120.0563
- 16. Pflug, G.Ch. and Römisch, W. (2007) Modeling, Measuring and Managing Risk. World Scientific Publishing Co., London. https://doi.org/10.1142/6478
- 17. Cotter, J. and Dowd, K. (2006) Extreme Spectral Risk Measures: An Application to Futures Clearinghouse Margin Requirements. Journal of Banking & Finance, 30, 3469-3485. https://doi.org/10.1016/j.jbankfin.2006.01.008
- 18. Brandtner, M. and Kürsten, W. (2017) Consistent Modeling of Risk Averse Behavior with Spectral Risk Measures: Wächter/Mazzoni Revisited. European Journal of Operational Research, 259, 394-399. https://doi.org/10.1016/j.jbankfin.2006.01.008
- 19. Sriboonchitta, S., Nguyen, H.T. and Kreinovich, V. (2010) How to Relate Spectral Risk Measures and Utilities. International Journal of Intelligent Technologies and Applied Statistics, 3, 141-158. https://doi.org/10.6148/IJITAS.2010.0302.03
- 20. Wächter, H.P. and Mazzoni, T. (2013) Consistent Modeling of Risk Averse Behavior with Spectral Risk Measures. European Journal of Operational Research, 229, 487-495. https://doi.org/10.1016/j.ejor.2013.03.001
- 21. Dowd, K., Cotter, J. and Sorwar, G. (2008) Spectral Risk Measures: Properties and Limitations. Journal of Financial Services Research, 34, 61-75. https://doi.org/10.1007/s10693-008-0035-6
- 22. Bingham, N.H., Goldie, C.M. and Teugels, J.L. (1989) Regular Variation. Cambridge University Press, Cambridge.
- 23. Embrechts, P., Klüppelberg, C. and Mikosch, T. (1997) Modelling Extremal Events, Springer, Berlin. https://doi.org/10.1007/978-3-642-33483-2
- 24. Tasche, D. (2000) Risk Contributions and Performance Measurement, Working Paper. https://pdfs.semanticscholar.org/2659/60513755b26ada0b4fb688460e8334a409dd.pdf
- 25. Andersson, F., Mausser, H., Rosen, D. and Uryasev, S. (2001) Credit Risk Optimization with Conditional Value-at-Risk Criterion. Mathematical Programming Series B, 89, 273-291. https://doi.org/10.1007/PL00011399
- 26. Kalkbrener, M., Kennedy, A. and Popp, M. (2007) Efficient Calculation of Expected Shortfall Contributions in Large Credit Portfolios. Journal of Computational Finance, 11, 1-43. https://doi.org/10.21314/JCF.2007.162
- 27. Puzanova, N. and Düllmann, K. (2013) Systemic Risk Contributions: A Credit Portfolio Approach. Journal of Banking & Finance, 37, 1243-1257. https://doi.org/10.1016/j.jbankfin.2012.11.017
- 28. McNeil, A.J., Frey, R. and Embrechts, P. (2005) Quantitative Risk Management. Princeton University Press, Princeton.
- 29. Bingham, N.H., Goldie, C.M. and Omey, E. (2006) Regularly Varying Probability Densities, Publications de l’Institut Mathematique, 80, 47-57. https://doi.org/10.2298/PIM0694047B
Appendix 1. A Short Consideration of the Dependent Case
Here, we briefly investigate the asymptotic behavior of 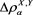
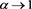

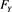
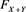

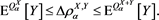
Note that (A.1) holds for general SRM 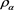
1.1. Comonotonic Case
We consider the case where X and Y are comonotone. In other words, they are perfectly positively dependent (see Definition 4.82 of [12] and Definition 5.15 in [28] ). In this case, the following proposition is straightforwardly shown.
Proposition 2 If X and Y are comonotone, then
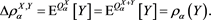
This proposition implies that when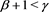

1.2. Additional Numerical Analysis
Similarly to Section 4, we assume that 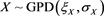


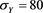


for a copula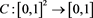
1) The Gaussian copula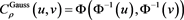
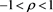
2) The Gumbel copula
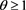
3) The countermonotonic copula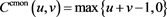
where 
normal distribution (for more details on the copulas, see, for instance, Chapter 5 of [28] ). The parameters 



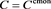
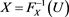
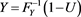
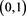
Figure A1 summarizes the results with 


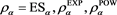
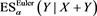
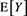
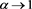
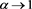
Figure A2 shows the graphs of the relative errors defined by (4.4) with 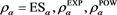

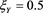

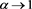
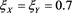

Figure A1. Graphs of 
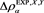

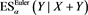
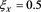
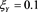
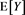
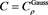
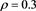

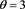

Figure A2. Approximation errors defined by (4.4) with 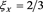


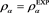
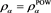
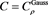

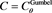
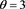
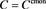
Note that the above findings are consistent with the comonotonic case (Proposition 2).
1.3. Theoretical Result in the Case
We describe the following conditions.
[C5] For each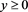
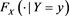
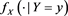
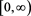
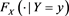
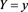


[C6] There is a 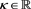


Figure A3. Approximation errors defined by (4.4) with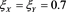


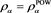
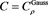
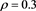
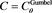
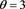
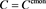
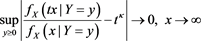
for each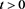
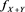
[C7] It holds that
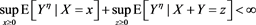
for some
Conditions [C5]-[C7] strongly correspond to conditions [A5]-[A6] in [1] . It should be noted that the index parameter 
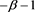

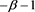
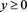
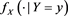
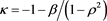
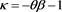
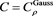


Using a similar argument as in the proof of the uniform convergence theorem (Theorem 1.2.1 in [22] ), together with the continuity of 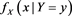
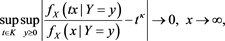
for each compact set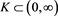
We now introduce the following result.
Theorem 3 Assume [C5]-[C7] and (3.12). If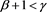
This theorem claims that both (3.11) and (3.14) are true under some conditions, even when X and Y are dependent.
Appendix 2. Proofs
\Proof of Lemma 1. Assume (2.5). Fix any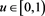

Because 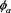
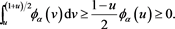
Combining (B.1) with (B.2), we have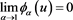
Conversely, if we assume (2.6), then Prokhorov’s theorem implies that for
each increasing sequence 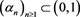
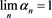
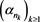

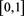
weakly converges to 

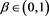
This immediately leads us to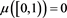
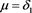
Proof of Proposition 1. Let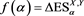
where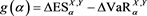
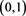

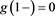
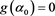

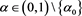
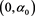
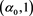
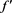
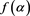
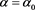
Proof of Proposition 2. Because 
Here, we see that 
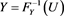

and thus
Similarly, because
and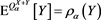
2.1. Proof of Theorem 1
We first state some propositions and prove them. For this, let 
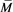
Proposition 3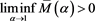
Proof. If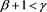
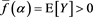
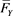
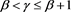
where 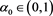

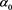

Proposition 4
Proof. If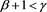
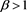

because of
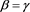
Corollary 1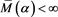
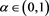
Proof. This follows from (3.2) and Proposition 4.
Proof of Theorem 1. Let
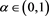
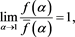
by virtue of Theorem 4.1(i)-(iii) in [1] . Moreover, (B.3) immediately implies
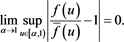
Furthermore, it holds that
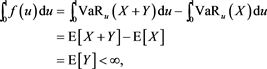
hence 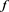
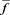
Temporarily fix any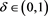

Similarly, we have
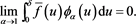
Additionally, we have

where

By (B.8) and (B.9), we have
Combining this with (B.6) and Proposition 3, we arrive at
Because 
2.2. Proof of Theorem 2
Let 
Lemma 2 
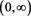
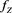
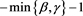
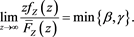
Proof. Continuity and positivity are obvious. By [C4] and Theorem 1.1 in [29] , we see that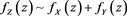
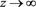
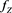
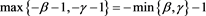
Let 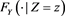
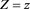
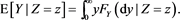
Proposition 5 It holds that
Proof. For each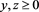
which implies our assertion.
Note that (B.11) and Proposition 5 lead to

Proposition 6 If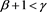
Proof. Let
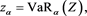
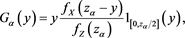
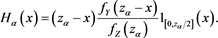
Then, we see that
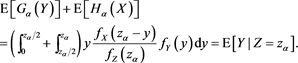
Therefore, we need to show that
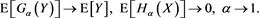
First, we show that
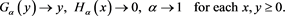
Using (B.10), Lemmas A.1 and A.3 in [1] , and Proposition A3.8 in [23] , we obtain
Furthermore, we observe that

and that the function 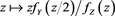
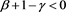
Now, (B.18) is obvious.
Next, we observe that
Because 
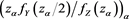
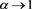
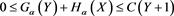
for some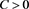
Proposition 7 If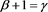
Proof. Let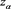


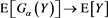
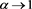

due to [C3], (B.10), Proposition A3.8 in [23] , Proposition 3.1(i) in [1] , and Lemmas A.1 and A.3 in [1] . Moreover, we have (B.19), and the right-hand side of this inequality converges to 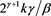


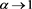
Proposition 8 If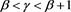
Proof. Let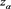
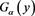
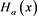
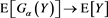

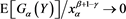
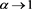
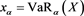
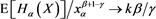
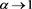
Proposition 9 If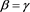
Proof. Similarly to the proof of Proposition 8, we need to show only that
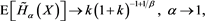
where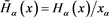

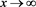

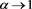
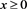
by [C3], (B.10), Proposition A3.8 in [23] , and Lemma A.3 in [1] . Moreover, we have
and thus we obtain (B.21) by applying the dominated convergence theorem.
Proof of Theorem 2. We can verify that the random vector 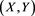

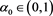

where we denote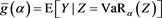
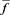
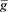
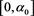
where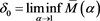
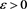
2.3. Proof of Theorem 3
First, note that condition [C5] immediately implies [C2] with 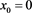
Second, note that by [C6], Proposition 3.1(i) in [1] (see also Remark 3.2 therein) and Proposition A3.8 in [23] , we have (B.10) and
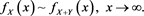
To prove Theorem 3, we give the following three propositions.
Proposition 10 
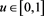
Proposition 10 is obtained by an argument similar to the proof of Lemma 5.3 in [24] , using the implicit function theorem.
Proposition 11 The function 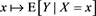
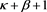
Proof. Fix any
and therefore, using [C5], we arrive at
Proposition 12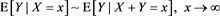
Proof. Fix any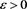
where we denote 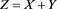
By [C7] and the Chebyshev inequality, we get
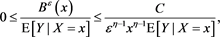
for some

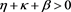
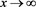
Moreover, we see that
Here, we observe that
for each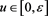
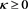

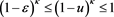
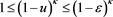
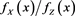
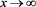
for some
Now we arrive at
by using (A.5) and (B.23). Because 
Proof of Theorem 3. First, note that Proposition 10 guarantees that
where 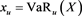

Then, fix any
Thus, there is an 
Therefore, we have
by virtue of (3.12). Because