ABSTRACT

We study the free boundary problem of the American type of options. We consider a continuous dividend paying put option and provide a much simpler way of approximating the option payoff and value. The essence of this study is to apply geometric techniques to approximate option values in the exercise boundary. This, being done with the nature of the exercise boundary in mind, more accurate results are guaranteed. We define a transformation (map) from a unit square to the free boundary. We then examine the transformation and its properties. We take a linear case for a transformation as well as a nonlinear case which would be more fitting for option values. We consider stochasticity (an Ito process) as we define this transformation and this yields better approximations for option values and payoffs. We also numerically compute optimal option prices by using the same transformation. We finally demonstrate that our transformation performs better than most semi-analytic results.

Keywords:

Option Pricing, American Put Option, Free Boundary, Payoff, Stochastic Interpolation

1. Introduction

Option pricing is one of the major areas of Mathematical Finance and has over the years generated a series of interesting problems. Among the many questions that still exist in this area, the analytic valuation of American options remains key as one of the most outstanding. About half a century ago, one of the most fundamental results in option pricing was put forth by Black & Scholes in their seminal paper. The results of this paper have gone on to be embraced as the dogma of option pricing [1] . Regardless of the type of options, the available measures are in a way either directly or indirectly related to Black & Scholes equation (sometimes known as Black-Scholes-Merton equation). Nevertheless, the pricing of options put forward by Black & Scholes does not perfectly suit the American type of options. This has triggered scholars to search for appropriate pricing measures for the American type of options. American call options have relatively been handled and pricing strategies developed as compared to the put options. American calls on stock with proportional dividends were treated as a free boundary problem by [2] [3] after [4] had also addressed a related problem. If the asset does not pay dividends, early exercise on American calls is useless [2] since they would then be yielding the same as their European equals. Moreover even with discrete dividends, American calls can still be valued by using analytic expressions [5] . In [6] , they provided an analytic characterization for a non-dividend paying put option. The problem that remains is the valuation of put dividend paying options. Analytic pricing representations have been independently supplied by [7] . The papers [7] [8] are so far the most popular among the analytic characterizations but unfortunately none of them does solve the analytic valuation developed therein. [8] put forward results on optimal stopping and the put option and decomposed the price of the option as the price of the European equal and the premium [7] [9] , the latter in a way bettering the work of [10] . The lower and upper bounds for the American option prices are provided in [11] . A version of Monte Carlo methods for pricing American options that is claimed to perform better than the already existing one has been put forward in [12] . The study of the free boundary for American butterfly options is done in [13] . The pricing of American options with the help of front fixing finite differences which is quite a better scheme has been handled in [14] . However, it still underestimates the prices at certain instances. Quite a variety of the recent literature on American option valuation have been about trying to study the properties of the free boundary, at least to the authors, and those that attempt to price the options tend to provide quite interesting and yet somewhat hard algorithms. This necessitates the need for an article that does not concentrate on the properties of the free boundary but attempts to look into the free boundary itself with an aim of acquiring approximates not only at specific times (as most papers have demonstrated) but in a general case (at all times) and with a straight forward approximation algorithm. This work is intended to develop an easier way of approximating option values, which can be applied easily in the market. This article is divided into four sections.

The first section introduces the problem, followed by a section that details the study of an American put option (the only case we consider in this work). In section 3, we handle the transformation. We derive both the linear and non-linear cases of the transformation having also defined some parts of the free boundary. The next section follows with numerical simulations which attempt to envisage the reliability of our results. The last section discusses the results before we sum it up with suggestions for further work in this line.

2. Model Set up

In this section we dig in depth information about the features of the American put option as well as its price.

Let us now study the desirable properties of the put price. These are the ones on which we base to justify the reliability of our transformation in the preceding sub section as well as move on to carry out simulation of the same in the forth coming section 4. First, we note that the price 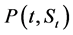of an American put option is given by;

(1)

where

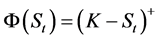(2)

Now some of the desirable properties about this price are such that;

・ For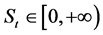, 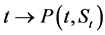is increasing.

・ Also for, 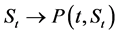is non-increasing and convex, of course this is as a result of the monotone and convex nature of Phi

・ ,

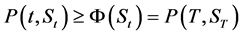
Now we need to summarize all we have done in the preceding subsection into a theorem. This is a standard theorem and it puts forward the restriction on the fact that the value of an American put option is at least the value of its European counterpart.

Theorem 1. For any market, if the risk-free rate r is positive, then for every,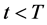

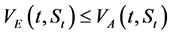(3)

where and 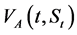are the values of the European and American put options respectively.

This theorem is clearly reflected by the decomposition of the American option value into the European option value as well as the early exercise premium. Since the premium can at worst be zero but not negative, this establishes the theorem 1 as can be seen from the Figure 1. Now first we recognize that the pay off for the American option is always greater than that of its European counterpart. This is explained by the fact that the American option payoff can be decomposed into two terms (see [7] [8] [9] ), a non-negative term (usually referred to as the premium) and the other being the European payoff of the American option counterpart. Nevertheless, this reward comes with a price to pay in terms of risk as an American option is more risky than the European counterpart. However, as risk theory suggests, higher rewards always come with highly risky investments. So in that case well as the American option carries a better payoff than the European, it also carries a higher risk which may scare away risk-averse investors as is always the case.

3. The Transformation

We now embark on establishing a transformation for the optimal boundary. We define

this transformation from a unit square a set 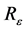whose area we approximate using quadrature numerical integration techniques. The area of 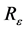is, here, analogous to the measure of the disjoint sets 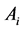and thus we can easily evaluate the American option using the value equation supplied in literature. Here, we evaluate for the put option as the call option can also be equally evaluated or rather employ the put-call parity relationship. We also consider the value equation supplied in Kim, 1990 (p. 560). Notice that

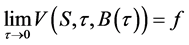(4)

being the option value and the pay off f is given by;

(5)

whenever. This basically explains that the option value is always going to lie within some value from the payoff. In brief, we can say it as the option value cannot exceed the payoff of the option otherwise the option is not worth anything then. Having noticed that the option value is at most the option payoff, we now analytically define some parts of the free boundary. This is intended in mathematically explaining why (and how) the option value is at most the option payoff. So set

(6)

and also not that

Now the standard American put option valuation equation is given by;

(7)

And

Set then;

Again, set

(8)

and 7 is satisfied.

Lets again set to be defined by;

(9)

and 7 is satisfied and thus

where. Set also that

(10)

and 7 is satisfied. The optimal exercise boundary is and the free boundary is the set given by;

(11)

Recall that; for;. Now

where Now consider the coordinates and the curve with a trajectory given by the definition, the curve of, can be somewhat like as in Figure 2 below.

The aim is to locate and the area of is given by;

(12)

The next question now is how to compute or express. We approximate through employing the Gaussian quadrature method of integration on a unit square.

3.1. Quadrature Approximation of Area (R_e)

In this sub section, we apply quadrature techniques to obtain an approximate for the area of. Quadrature approximation has merits such as the ease with which it can be applied as well as its accuracy. Still the fact that all nodes lie within the interior of the main interval guarantees that even integrals with functions that tend to infinite value at one end of the interval can be handled (of course given that the integral is defined there). Recall that

(13)

and computing the value of the integral, we employ the Gaussian quadrature approximation technique.

(14)

and where

(15)

and now we notice that for, we have that

and

and hence

Consequently with increase in the n value, there will be an increase in the terms on the expansion thus increasing accuracy. So then recall the Equation (12) which is;

which is the required exercise boundary i.e.

(16)

Now having obtained the area of the co-domain of our desired transformation, we now move on to establish this transformation from a unit square to the set whose area has been computed in the preceding sub section. This transformation is designed in way that it ought to satisfy some conditions especially at the grid bounds of the unit square. Other values within the square can be consequently computed with reference to the bound values using any mathematically efficient numerical scheme as shall be seen in section 4. We define the transformation to be

such that

(17)

and on the boundaries of the unit square, it is clear that

(18)

So a transformation that satisfies both of these Equations (17) and (18) would be our appropriate result to use in the analytic approximation of the option optimal prices alongside their corresponding optimal times.

3.2. The Linear Transformation

Now note that;

and also that is the piece of the transformation that evaluates values on the x-axis of the unit square. Hence we have the values as depicted in Table 1 and interpolating these results linearly in x yields;

Consequently, a similar expression can be obtained for various other values of y provided they are assumed constant and only x varying. In general, the transformation for values along the x-axis of the unit square is given by;

(19)

And also for the second piece of the transformation i.e. in the y-direction we apply interpolation. However here we note that the varies on two indices i and the x concurrently since the optimal value would have to depend on the optimal times that is in an economically meaningful sense. Having taken that into consideration, we use the following Table 2 and on linearly interpolating

Also, a similar expression can be obtained for various other values of x provided they are assumed constant and only y varying. hence in general, the transformation for values along the y-axis of the unit square is given by;

(20)

In a summary, the transformation would then be defined as in the next proposition which is one of the major results of this work.

Proposition 2. Linear transformation

Define by

where is a unit square, then is a bijection.

in this case represents the optimal times as represents the optimal value of the option at node i whose location is geometrically.

Proof. The first part of the proof is to prove that is one-to-one and the second is to prove that it is onto. Consider the associated vector transformation of , say i.e.

Notice that

hence is one-to-one. So we now prove that is onto. Now, for every, there exists a point for which we have that

Hence is onto. Therefore being onto as well as one-to-one implies that is a bijection.

3.3. The Nonlinear Transformation

Now, we have a linear transformation that could be used to approximate the payoff values of the option over time. Nevertheless, we remark that the approximations from it would be too inaccurate as option payoffs are known not to be linear over time otherwise. It is rather evident that option prices and their corresponding pay-offs follow Ito processes and not log normal processes (even though the two are somewhat related). So we need to consider this in the approximation of payoff values from the bound values of the same. We thus employ techniques borrowed from the area of stochastic interpolation1; the type of interpolation in which we approximate functional values for random (stochastic) data; with some modifications so as to suit our problem here. Consider an Ito process

(21)

where is the drift term (also called the mean of the process) and is the volatility, is the standard Wiener process and is the price of the underlying asset on which the option is written. Since we have to consider the variation of the point (optimal times) whose payoff value we seek from both ends, we propose a method that takes this into consideration and there after demonstrate its accuracy as it proves to be better than most known. Consider and and that we wish to know the optimal payoff corresponding to time, the technique below can help swipe away the high variations and approximate an appropriate value. This technique is basically given by;

(22)

where

(23)

the log-normal probability density function. Using the technique given in Equation (22), we can reliably approximate the payoff values and thus define a transformation from the unit square using this approximation. So then we now organize the preceding results into a proposition which follows right away.

Proposition 3. Nonlinear transformation

Suppose the price of an underlying asset for a given American put option follows an Ito process, then the option pay off can be approximated by the transformation

where

(24)

and is a unit square. in this case are the optimal times as are the optimal value of the option at node i whose location is geometrically and the optimal exercise boundary.

Proof. Notice that the proof can be done in the very exact way as in proposition (2) with a change of into a stochastic representation now. Never the less, we provide a heuristic one here. Suppose the hypothesis in proposition 3 holds, then we prove that this transformation is indeed a better approximation compared to the previous one. Consider the extreme points and, the the probability that we appro- ximate and obtain the functional value for is and the functional value is such that

from the start of the interval. Also from the interval end it would then be given as;

Hence from either end; we have that

So the task remains to demonstrate that our results concur with this in all ways. But before embarking on that we desire to note some properties of a good approximation for the put price that we can perhaps look out for from our results.

4. Numerical Results

In this section we show the numerical results of this work. We numerically compute optimal option prices from the transformation. We also compare the results of our transformation with some of the powerful known analytic approximations. Now we proceed to derive and demonstrate the numerical approximations of the method in sub section 3 and the exercise boundary is obtained graphically depicted in Figure 3

Now for the exercise boundary plot, as the stock price grows over time there is at first a gradual expansion in the size of the exercise region with a concurrent reduction in the

holding region. Also at about, the expansion of the exercise region starts to

grow at an exponential rate. Now we next study a 3D plot of option prices against stock prices over time. This is depicted in Figure 4. This plot clearly informs us of the various

relationships among these three. Notice that the structure of the exercise boundary (region) is depicted along the x-axis (time) of this plot which is analogous to the structure obtained for the exercise boundary plot which is graphed as stock prices over time.

Also notice that the shape of the variation of the payoff for an American option is also reflected here in (Option prices axis) over time. This, in a nut shell is a plot that summarizes all the plots into one. So all conclusions made regarding the other previous two plots still hold under Figure 5.

5. Discussion & Conclusion

Here, we have provided a far much simpler way of approximating option values as well as payoffs basing on a unit square. Most approximation techniques provided in literature tend to be sophisticated and somewhat cumbersome at specific times of the option. However, our method stays put in regard to application throughout the entire life of the option. We have demonstrated that an option value can be approximated through basing on the unit square to acquire far better accurate results. This beats most approximation techniques already in existence. This method also exceeds others in terms of simplicity of application coupled with accuracy of results. The major objective of this work has been achieved as it was majorly providing an easier way of approximating the payoff by using a transformation from a unit square to the exercise boundary. This has been superfluously achieved. The transcendence of our method is evidenced by the fact that when approximating payoffs, one works within a known set, the unit square. Moreover, our method can easily be run on a computer and the average running time is

so minimal. Further work may be needed to be done in this area to improve the results such as considering better and more efficient non-linear approximation (interpolation) schemes such as ordinary kriging, universal kriging. Notice that considering these approximation schemes would better the results (in terms of accuracy) as variance is minimized. However, such methods were beyond the scope of this work.

Acknowledgements

We thank African Union for the support towards this research.

Cite this paper

Katende, R., Seck, D. and Ngare, P. (2016) On the Location of a Free Boundary for American Options. Journal of Mathematical Finance, 6, 930- 943. http://dx.doi.org/10.4236/jmf.2016.65062

References

NOTES

¹first introduced by [15] .