Journal of Mathematical Finance
Vol.2 No.1(2012), Article ID:17617,8 pages DOI:10.4236/jmf.2012.21015
Variational Form of Classical Portfolio Strategy and Expected Wealth for a Defined Contributory Pension Scheme
1Department of Mathematics, University of Benin, Benin City, Nigeria
2Department of Mathematics, University of Ibadan, Ibadan, Nigeria
Email: {nkekicharles2003, crnwozo}@yahoo.com
Received October 26, 2011; revised December 10, 2011; accepted December 18, 2011
Keywords: Variational form; Classical portfolio strategy; Expected wealth; Defined contribution; Pension scheme; Pension plan member; Inter-temporal hedging terms; Stochastic salary
ABSTRACT
This paper examines the variational form of classical portfolio strategy and expected terminal wealth for a Pension Plan Member (PPM) in a Defined Contribution (DC) Pension scheme. The flows of contributions made by PPM are invested into a market that is characterized by a cash account and a stock. It was assumed that the growth rate of salary of PPM is a linear function of time. The present value of PPM’s future contribution process was obtained. The optimal portfolio processes with inter-temporal hedging terms that offset any shocks to the stochastic cash inflows were established. The expected value of PPM’s terminal wealth was obtained.
1. Introduction
This paper considers the variational form of classical portfolio strategy and expected terminal wealth for a DC pension scheme. It was assumed that the salary and risky asset are driven by a standard geometric Brownian motion. The growth rate of salary of PPM is assumed to be a linear function of time. A non-linear partial differential equation was derived and then, the optimal portfolio values for the PPM were determined using power utility function. In this paper, we focus on studying the optimal portfolio strategy based on a classical model: geometric Brownian motion model as in equation (2). While in [1] and [2], they are using an optimal portfolio strategy based on the non-Gaussian models. They constructed optimal portfolios of variance swaps based on a variance Gamma correlated model. The portfolios of the variance swaps are optimized based on maximizing the distorted expectation given the index of acceptability.
In related literature, [3] examined the rationale, nature and financial consequences of two alternative approaches to portfolio regulations for the long term institutional investor sectors of life insurance and pension funds. [4] considered the deterministic life styling (the gradual switch from equities to bonds according to preset rules) which is a popular asset allocation strategy during the accumulation phase of a defined contribution pension plans which is designed to protect the pension funds from a catastrophic fall in the stock market just prior to retirement. They shown that this strategy, although easy to understand and implement can be highly suboptimal. [5] developed a model for analyzing the ex ante liquidity premium demanded by the holder of an illiquid annuity. The annuity is an insurance product that is similar to a pension savings account with both an accumulation and decumulation phase. They computed the yield needed to compensate for the utility welfare loss, which is induced by the inability to re-balance and maintain an optimal portfolio when holding an annuity. [6-8] considered the optimal design of the minimum guarantee in a defined contribution pension fund scheme. They studied the investment in the financial market by assuring that the pension fund optimizes its retribution which is a part of the surplus, which is the difference between the pension fund value and the guarantee. [9] studied optimal investment strategy for a defined contributory pension plan. They adopted dynamic optimization technique. [10] considered optimal portfolio strategies with minimum guarantee and inflation protection for a DC pension scheme. [11] studied the optimal portfolio and strategic lifecycle consumption process in a defined contributory pension plan.
The remainder of this paper is organized as follows. In Section 2, we present the financial market models, Section 3, presents the present value of the expected flow of future discounted premiums process. We also establish in this section, the dynamics of the values of wealth of the PPM. In Section 4, we present the valuation of PPM’s wealth process. In Section 5, we present the optimization process and portfolio value of a PPM in pension scheme. Section 6, presents the expected wealth for a PPM up to terminal period. Section 7 presents a special case of optimal portfolio selection problem. Finally, Section 8 concludes the paper.
2. Problem Formulation
The Brownian motion 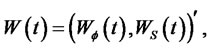
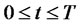 is a 2-dimensional process, defined on a given probability space
is a 2-dimensional process, defined on a given probability space  where
where  is the real world probability measure and
is the real world probability measure and 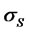 and
and 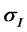 are the volatility of stock and volatility of inflation with respect to changes in
are the volatility of stock and volatility of inflation with respect to changes in  and
and , respectively.
, respectively.  is the appreciation rate for stock. Moreover,
is the appreciation rate for stock. Moreover,  and
and 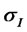 are the volatilities for the stock and inflation respectively, referred to as the coefficients of the market and are progressively measurable with respect to the filtration
are the volatilities for the stock and inflation respectively, referred to as the coefficients of the market and are progressively measurable with respect to the filtration  We assume that the investor faces a market that is characterized by a risk-free asset (cash account) and risky asset, all of whom are tradeable. In this paper, we allow the stock price to be correlated to inflation. Also, we correlated the cash inflows to stock market risk. The dynamics of the underlying assets are given by (1) and (2)
We assume that the investor faces a market that is characterized by a risk-free asset (cash account) and risky asset, all of whom are tradeable. In this paper, we allow the stock price to be correlated to inflation. Also, we correlated the cash inflows to stock market risk. The dynamics of the underlying assets are given by (1) and (2)
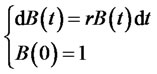 (1)
(1)
 (2)
(2)
where,
 is the nominal interest rate,
is the nominal interest rate,
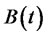 is the price of the riskless asset at time
is the price of the riskless asset at time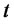 ,
,
 is the stock price process at time
is the stock price process at time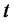 Therefore, (2) can be rewritten as
Therefore, (2) can be rewritten as
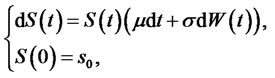 (3)
(3)
where, 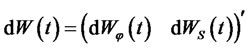 and
and  .
.
It is assume that the market is complete; therefore there exists a unique market price of risk 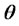 satisfying
satisfying
 .
.
The salary of the PPM is assume to follow the dynamics
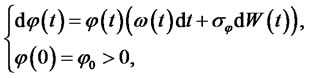 (4)
(4)
where,  ,
,  is the volatility caused by the source of inflation,
is the volatility caused by the source of inflation, 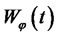 and
and  is the volatility caused by the source of uncertainty arises from the stock market,
is the volatility caused by the source of uncertainty arises from the stock market,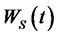 . We assume that the growth rate of the salary of PPM is linear and satisfies
. We assume that the growth rate of the salary of PPM is linear and satisfies 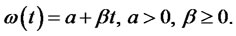
![]() may be seen as expected yearly growth of salary and
may be seen as expected yearly growth of salary and 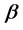 as effect of economic growth or welfare of the PPM.
as effect of economic growth or welfare of the PPM.
Therefore, the flow of contributions of the PPM is given by  where
where ![]() is proportion of PPM salary he/she is contributing into the scheme.
is proportion of PPM salary he/she is contributing into the scheme.
We now define the following exponential process which we assume to be Martingale in 
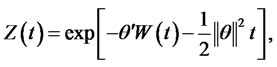
which will be useful in the next section.
Let 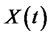 be the wealth process and
be the wealth process and  the portfolio process, that is the proportion of wealth invested in stock at time
the portfolio process, that is the proportion of wealth invested in stock at time . Then,
. Then, 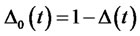 is the proportion wealth invested in the riskless asset at time
is the proportion wealth invested in the riskless asset at time . We now have the following definition:
. We now have the following definition:
Definition 1: the portfolio process ![]() is said to be selffinancing if the corresponding wealth process
is said to be selffinancing if the corresponding wealth process 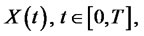 satisfies
satisfies
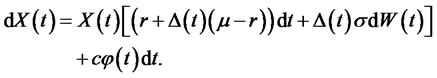 (5)
(5)
3. The Expected Value of Future Contribution of a PPM
Definition 2: the present value of expected future contribution process is defined as
 , (6)
, (6)
where 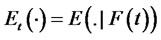 is the conditional expectation with respect to the Brownian filtration
is the conditional expectation with respect to the Brownian filtration 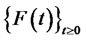 and
and  is the stochastics discount factor which adjusts for nominal interest rate and market price of risks.
is the stochastics discount factor which adjusts for nominal interest rate and market price of risks.
Theorem 1 tells us that the present value of expected future contribution process, then proportional to the instanttaneous contribution process 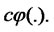
Definition 3: a portfolio process is said to be admissible if the corresponding wealth process 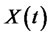 satisfies
satisfies
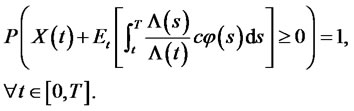
Theorem 1: let 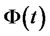 be the present value of expected future contribution (PVFC) process, then
be the present value of expected future contribution (PVFC) process, then
 (7)
(7)
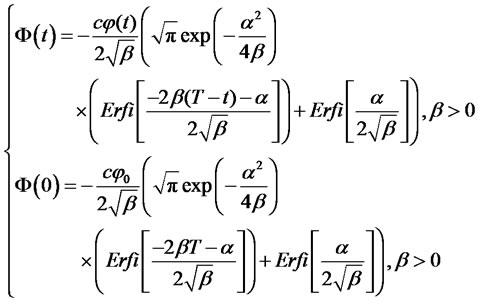 (8)
(8)
 (9)
(9)
where, 
Proof: by definition,
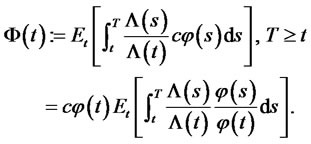
The processes  and
and ![]() are geometric Brownian motions. It therefore follows that
are geometric Brownian motions. It therefore follows that 
is independent of . Hence,
. Hence,
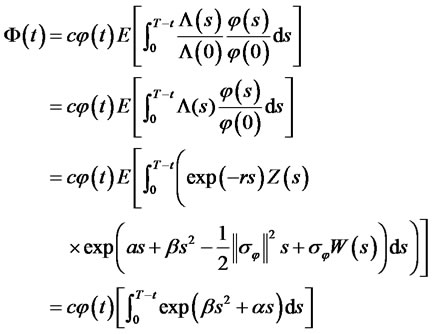
where, 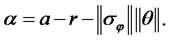
Therefore,

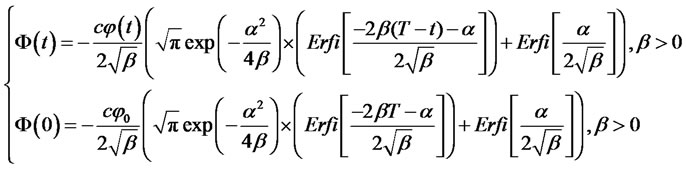

Numerical Example 1: setting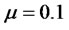 ,
, 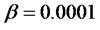 ,
, 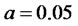 ,
,  ,
, 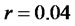 ,
, 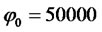 ,
,  ,
, 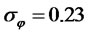 ,
, 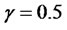 ,
,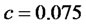 . Mathematica 6.0 was used for the plotting.
. Mathematica 6.0 was used for the plotting.
In this paper, we consider the case of 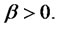 For the case of
For the case of 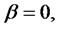 see [4,7,10-12].
see [4,7,10-12].
Lemma 1: the dynamics of the present value of future contribution process is given by
 (10)
(10)
where,
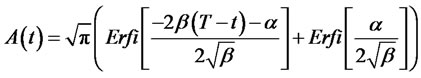

Proof: taking differential of both sides of (8), we obtain the following:
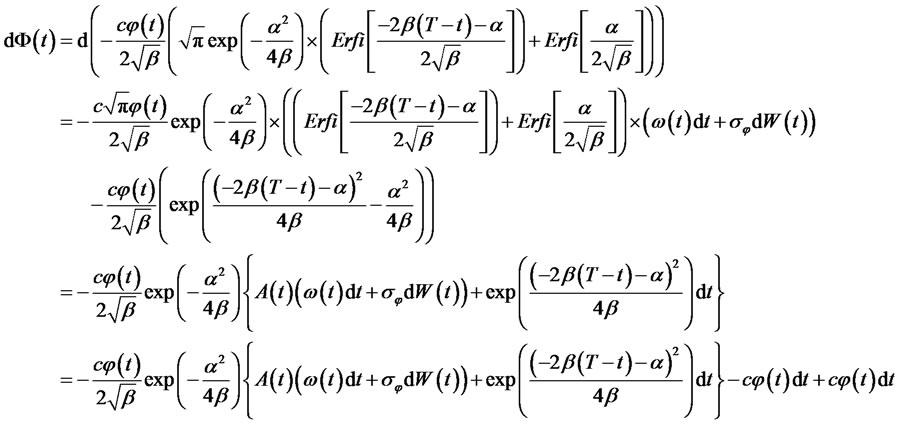
Therefore,

where,

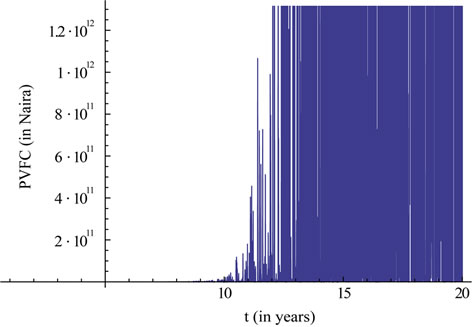
Figure 1. The present value of PPM’s future contributions. The expected today value of PPM’s contributions is obtained as 49,890 Naira. From the Figure 1, observed that the expected future contribution is highly volatile. This is because there is high rate of inflation. This, to a great extent will reduce the value of PPM’s benefits at retirement.
4. Valuation of PPM’s Wealth Process
Definition 2: the value of PPM’s wealth 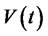 at time
at time  is the sum of PPM’s wealth
is the sum of PPM’s wealth 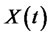 and the present value of expected future contribution process,
and the present value of expected future contribution process,  at time
at time  that is,
that is,
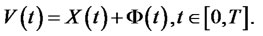 (11)
(11)
Finding the differential of both sides of (11) and substituting (5) and (10), we obtain
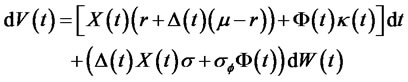 (12)
(12)
5. The Optimization Process and Portfolio Value of a PPM
In this section, we consider the optimal portfolio process for the IC. We define the general value function
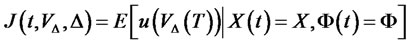 where
where 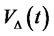 is the path of
is the path of  given the portfolio strategy
given the portfolio strategy![]() . Define
. Define  to be the set of all admissible portfolio strategy that are
to be the set of all admissible portfolio strategy that are 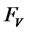 - progressively measurable, and let
- progressively measurable, and let 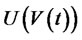 be a concave function in
be a concave function in 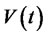 such that
such that
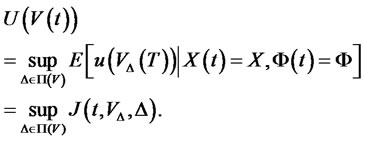
Then 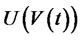 satisfies the HJB equation
satisfies the HJB equation
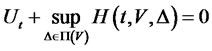 (13)
(13)
subject to: 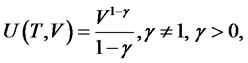
where,

Finding the partial derivative of  with respect to the optimal control
with respect to the optimal control  and setting it to zero, we obtain
and setting it to zero, we obtain
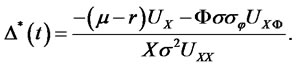 (14)
(14)
Substituting (14) into (13), we obtain the HJB equation
 (15)
(15)
Let 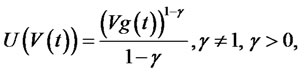 be the solution to the HJB equation (15), then,
be the solution to the HJB equation (15), then,
![]()
![]()
![]()
![]()
![]()
![]()
Substituting the partial derivatives above into (15), we obtain
 (16)
(16)
Again, substituting the partial derivatives into (14), we obtain
 (17)
(17)
Therefore, the portfolio value in the riskless asset is obtain as
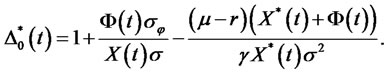 (18)
(18)
Numerical Example 2:
Setting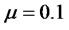 ,
, 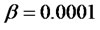 ,
, 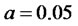 ,
,  ,
,  ,
, 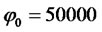 ,
, 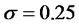 ,
, 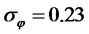 ,
, 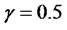 ,
, 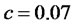 , we found that the optimal portfolio in stock at retirement to be 1.92 and in cash account to be −0.92.
, we found that the optimal portfolio in stock at retirement to be 1.92 and in cash account to be −0.92.
6. Expected Wealth for a PPM
In other to determine the expected wealth of the PPM at time t, we find the mathematical expectation of (12) as follows:
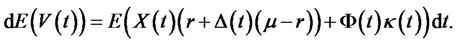
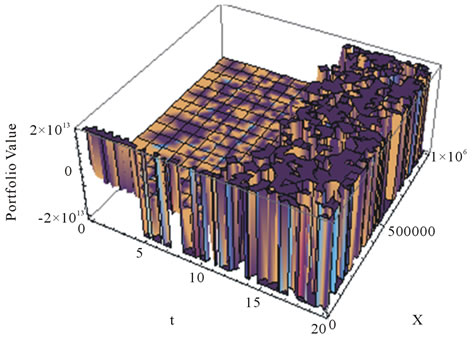
Figure 2. Portfolio value in stock. It has an optimal portfolio value after 20 years to be 1.92. This implies that more funds should be borrowed from cash account and then, invests in stock market.
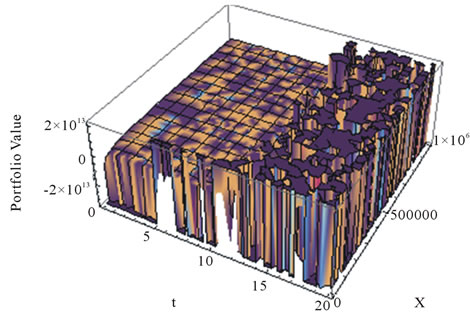
Figure 3. Portfolio value in cash account. It has an optimal portfolio value after 20 years to be −0.92. This implies that no fund should keep in cash account at the optimal level and that all fund should remain in stock market.
For simplicity, we set , so that
, so that
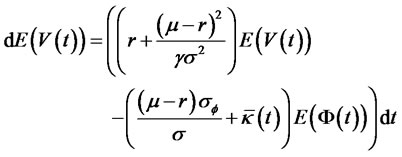

 (19)
(19)
where,
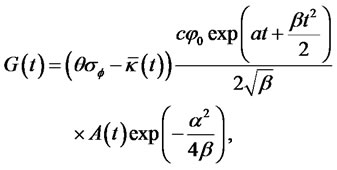
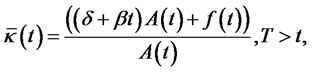
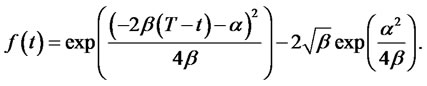
Integrating both sides of (19), we obtain
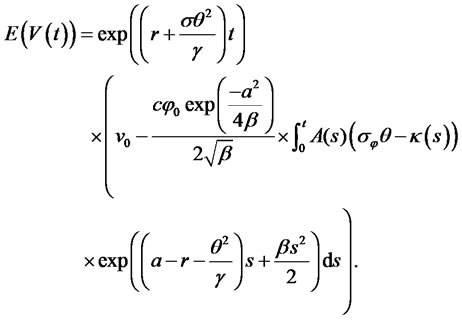 (20)
(20)
At  we have
we have
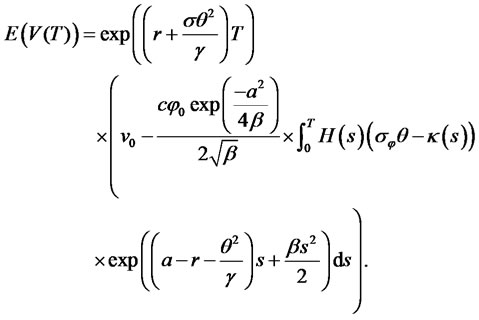 (21)
(21)
Numerical Example 3: in this numerical example, we illustrate the expected value of a PPM’s wealth up to retirement.
In figure 4, we set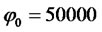 ,
,  ,
, 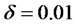 ,
,  ,
, 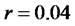 ,
, 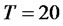 ,
, 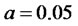 ,
, 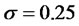 ,
,
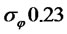 ,
, 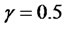 ,
,  and MATLAB was used for the plotting. It was found that at final time
and MATLAB was used for the plotting. It was found that at final time![]() , the
, the

Figure 4. Expected value of wealth of a PPM.
expected value of PPM’s wealth is 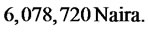
7. Discussion
In Figure 1, we found that the expected present value of PPM’s contributions is obtained as 49,890 Naira. We also observed that the expected future contribution is highly volatile. This is because there is high rate of inflation. In Figure 2, we found that the optimal portfolio value after 20 years to be 1.92. This implies that more funds should be borrowed from cash account and then, invests in stock market. In Figure 3, we found that the optimal portfolio value after 20 years to be –0.92. This implies that no fund should be kept in cash account at the optimal level and that all fund should remain in stock market. Figure 4 shows the expected value of PPM’s wealth up to 20 years and is obtained as 6,078,720 Naira.
8. Special Case c = 0
If we set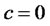 , we obtain the usual portfolio selection problem, provided that
, we obtain the usual portfolio selection problem, provided that . In that case, we have
. In that case, we have
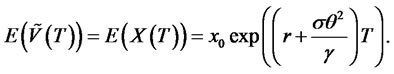
Corollary: assume that an investor intends to invest a wealth of  for the time horizon
for the time horizon 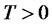 in a financial market as in section (1) and wealth equation (5). Assume that the investor maximizes the expected utility of final wealth at time
in a financial market as in section (1) and wealth equation (5). Assume that the investor maximizes the expected utility of final wealth at time 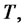 then,
then,
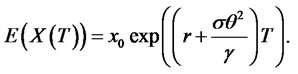 (22)
(22)
Observed that the ratio of the expected value of PPM’s terminal wealth to the expected usual portfolio selection problem is obtain as

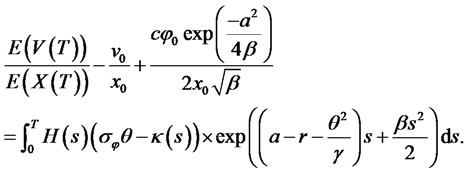
Substituting (23) into (21), we obtain
 (24)
(24)
where,


(24) shows that the expected final wealth of the PPM’s can be expressed as a function of the expected value of the usual portfolio selection problem (22).
If we set 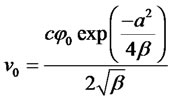 and
and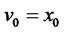 for the purpose of analysisthen,
for the purpose of analysisthen,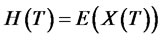 .
.
Therefore, (24) becomes
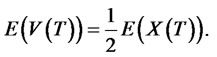 (25)
(25)
If 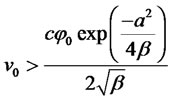 and
and 
then,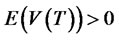 .
.
If  and
and 
then,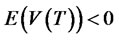 .
.
9. Conclusion
This paper considered the variational form of classical portfolio strategy and expected terminal wealth for a Pension Plan Member (PPM) in a Defined Contribution (DC) Pension scheme. The present value of PPM’s future contribution process was established and numerical ressults were given. The optimal portfolio processes with inter-temporal hedging terms that offset any shocks to the stochastic cash inflows were obtained. The expected value of PPM’s terminal wealth and numerical results were established.
REFERENCES
- L. Cao and Z. F. Guo, “Optimal Variance Swaps Investments,” IAENG Journals, Vol. 41, No. 4, 2011, Article ID IJAM_41_4_07.
- L. Cao and Z. F. Guo, “Delta Hedging through Deltas from a Geometric Brownian Motion Process,” Proceedings of International Conference on Applied Financial Economics, London, 30 June-2 July, 2011.
- P. E. Davis, “Portfolio Regulation of Life Insurance Companies and Pension Funds,” Oxford University Press, Oxford, 2000. http.//www.oecd.org/dataoecd/30/39/2401884.pdf.
- A. J. G. Cairns, D. Blake and K. Dowd, “Stochastic Lifestyling: Optimal Dynamic Asset Allocation for Defined Contribution Pension Plans,” Journal of Economic Dynamics & Control, Vol. 30, No. 5, 2006, pp. 843-877. doi:10.1016/j.jedc.2005.03.009
- S. Brawne, A. M. Milevsky and T. S. Salisbury, “Asset Allocation and the Liquidity Premium for Illiquid Annuities,” The Journal of Risk and Insurance, Vol. 70, No. 3, 2003, pp. 509-526. doi:10.1111/1539-6975.t01-1-00062
- G. Deelstra, M. Grasselli and P. Koehl, “Optimal Design of the Guarantee for Defined Contribution Funds,” 2002. http://www.amazon.com/Optimal-design-guarantee-defined-contribution/dp/B000RQY19I.
- G. Deelstra, M. Grasselli and P. Koehl, “Optimal Investment Strategies in the Presence of a Minimum Guarantee,” Insurance: Mathematics and Economics, Vol. 33, No. 1, 2003, pp. 189-207. doi:10.1016/S0167-6687(03)00153-7
- G. Deelstra, M. Grasselli and P. Koehl, “Optimal Design of the Guarantee for Defined Contribution Funds,” Journal of Economics Dynamics and Control, Vol. 28, No. 2, 2004, pp. 2239-226.
- C. R. Nwozo and C. I. Nkeki, “Optimal Investment Strategy for a Defined Contributory Pension Plan in Nigeria Using Dynamic Optimization Technique,” Studies in Mathematical Sciences, Vol. 2, No. 2, 2011, pp. 43-60.
- C. R. Nwozo and C. I. Nkeki, “Optimal Investment and Portfolio Strategies with Minimum Guarantee and Inflation Protection for a Defined Contribution Pension Scheme,” Studies in Mathematical Sciences, Vol. 2, No. 2, 2011, pp. 78-89.
- C. R. Nwozo and C. I. Nkeki, “Optimal Portfolio and Strategic Consumption Planning in a Life-Cycle of a Pension Plan Member in a Defined Contributory Pension Scheme,” IAENG Journals, Vol. 41, No. 4, 2011, Article ID IJAM_ 41_4_03.
- A. Zhang, R. Korn and C. O. Ewald, “Optimal Management and Inflation Protection for Defined Contribution Pension Plans,” Worker Paper, University of St. Andrews, 2007. http://mpra.ub.uni-muenchen.de/3300/1/MPRA_paper_3300.pdf

