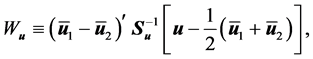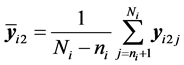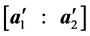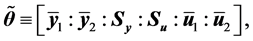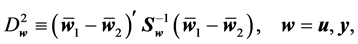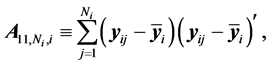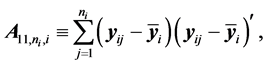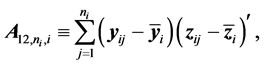Open Journal of Statistics
Vol.06 No.01(2016), Article ID:63883,14 pages
10.4236/ojs.2016.61015
A Comparison of Two Linear Discriminant Analysis Methods That Use Block Monotone Missing Training Data
Phil D. Young1, Dean M. Young2, Songthip T. Ounpraseuth3
1Department of Information Systems, Baylor University, Waco, TX, USA
2Department of Statistical Science, Baylor University, Waco, TX, USA
3Department of Biostatistics, University of Arkansas for Medical Sciences, Little Rock, AK, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 January 2016; accepted 23 February 2016; published 26 February 2016
ABSTRACT
We revisit a comparison of two discriminant analysis procedures, namely the linear combination classifier of Chung and Han (2000) and the maximum likelihood estimation substitution classifier for the problem of classifying unlabeled multivariate normal observations with equal covariance matrices into one of two classes. Both classes have matching block monotone missing training data. Here, we demonstrate that for intra-class covariance structures with at least small correlation among the variables with missing data and the variables without block missing data, the maximum likelihood estimation substitution classifier outperforms the Chung and Han (2000) classifier regardless of the percent of missing observations. Specifically, we examine the differences in the estimated expected error rates for these classifiers using a Monte Carlo simulation, and we compare the two classifiers using two real data sets with monotone missing data via parametric bootstrap simulations. Our results contradict the conclusions of Chung and Han (2000) that their linear combination classifier is superior to the MLE classifier for block monotone missing multivariate normal data.
Keywords:
Linear Discriminant Analysis, Monte Carlo Simulation, Maximum Likelihood Estimator, Expected Error Rate, Conditional Error Rate

1. Introduction
We consider the problem of classifying an unlabeled observation vector 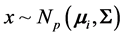 into one of two distinct multivariate normally distributed populations
into one of two distinct multivariate normally distributed populations ,
, 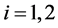 , when monotone missing training data are present, where
, when monotone missing training data are present, where 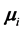 and
and 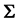 are the
are the  population mean vector and common covariance matrix, respec- tively. Here, we re-compare two linear classification procedures for block monotone missing (BMM) training data: one classifier is from [1] , and the other classifier employs the maximum likelihood estimator (MLE).
population mean vector and common covariance matrix, respec- tively. Here, we re-compare two linear classification procedures for block monotone missing (BMM) training data: one classifier is from [1] , and the other classifier employs the maximum likelihood estimator (MLE).
Monotone missing data occur for an observation vector 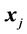 when, if
when, if  is missing, then
is missing, then 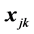 is missing for all
is missing for all . The authors [1] claim that their “linear combination classification procedure is better than the substitution methods (MLE) as the proportion of missing observations gets larger” when block monotone missing data are present in the training data. Specifically, [1] has performed a Monte Carlo simulation and has concluded that their classifier performs better in terms of the expected error rate (EER) than the MLE sub- stitution (MLES) classifier formulated by [2] as the proportion of missing observations increases. However, we demonstrate that for intra-class covariance training data with at least small correlations among the variables, the MLES classifier can significantly outperform the classifier from [1] , which we refer to as the C-H classifier, in terms of their respective EERs. This phenomenon occurs regardless of the proportion of the variables missing in each observation with missing data (POMD) in the training data set.
. The authors [1] claim that their “linear combination classification procedure is better than the substitution methods (MLE) as the proportion of missing observations gets larger” when block monotone missing data are present in the training data. Specifically, [1] has performed a Monte Carlo simulation and has concluded that their classifier performs better in terms of the expected error rate (EER) than the MLE sub- stitution (MLES) classifier formulated by [2] as the proportion of missing observations increases. However, we demonstrate that for intra-class covariance training data with at least small correlations among the variables, the MLES classifier can significantly outperform the classifier from [1] , which we refer to as the C-H classifier, in terms of their respective EERs. This phenomenon occurs regardless of the proportion of the variables missing in each observation with missing data (POMD) in the training data set.
Throughout the remainder of the paper, we use the notation  to represent the matrix space of all
to represent the matrix space of all  matrices over the real field
matrices over the real field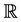 . Also, we let the symbol
. Also, we let the symbol 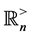 represent the cone of all
represent the cone of all 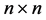 positive definite matrices in
positive definite matrices in


The author [3] has considered the problem of missing values in discriminant analysis where the dimension and the training-sample sizes are very large. Additionally, [4] has examined the probability of correct classi- fication for several methods of handling data values that are missing at random and use the EER as the criterion to weigh the relative quality of supervised classification methods. Moreover, [5] has examined missing obser- vations in statistical discrimination for a variety of population covariance matrices. Also, [6] has applied re- cursive methods for handling incomplete data and has verified asymptotic properties for the recursive methods.
We have organized the remainder of the paper as follows. In Section 2, we describe the C-H classifier, and we describe the MLES linear discriminant procedure when the training data from both classes contain identical BMM data patterns. In Section 3, we describe and report the result of Monte Carlo simulations that examine the differences in the estimated EERs of the C-H and MLES classifiers for various parameter configurations, training-sample sizes, and missing data sizes and summarize our simulation results graphically. In Section 4, we compare the C-H and MLES linear classifiers using a parametric bootstrap estimator of the EER difference (EERD) on two actual data sets. We summarize our results and conclude with some brief comments in Section 5.
2. Two Competing Classifiers for BMM Training Data
2.1. The C-H Classifier for Monotone Missing Data
Suppose we have two 

where
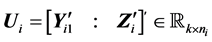
denotes the 





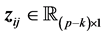

where
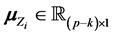




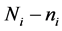



The authors [1] have derived a linear combination of a discriminant function composed from complete data and a second discriminant function determined from BMM data. The C-H classifier uses Anderson’s linear dis- criminant function (LDF) for the subset of complete data

where 
are the complete-data sample mean and complete-data sample covariance matrix, respectively. They also use Anderson’s LDF for the data



with

where
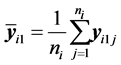
denotes the sample mean for the first 
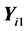
denotes the sample mean for the first k features of the latter 
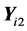
is the pooled sample covariance matrix for the incomplete training data (4), where

The authors [1] have proposed the linear combination statistic
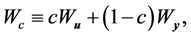
where


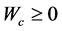
and into

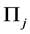




with
Also,

where 








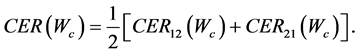
If
then, for (8), the EER of misclassifying an unlabeled observation vector 



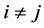
In choosing c in (7), [1] have utilized the fact that the CER and EER will depend on the Mahalanobis distance for the complete and partial training observations and the corresponding training-sample sizes, 


will be large. While 








to determine the linear combination classification statistic (7).
2.2. A Maximum Likelihood Substitution Classifier for Monotone Missing Training Data
The authors [7] have derived an MLE method for estimating parameters in a multivariate normal distribution with BMM data. The estimator of 
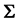
Below, we state the MLEs for two multivariate normal distributions having unequal means and a common covariance matrix with identical BMM-data patterns in both training samples.
Theorem. Let 



and

Also, let
and
where






respectively, where

and

with

and
where




Proof: A proof is alluded to in [8] .
The MLES classification statistic is
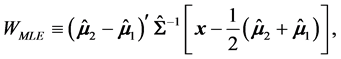
where


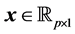





and into
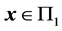
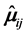
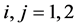
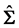
where
where

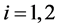
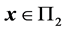
where 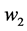



Hence, the overall expected error rate is
3. Monte Carlo Simulations
The authors [1] claim that “it can be shown that the linear combination classification statistic is invariant under nonsingular linear transformations when the data contain missing observations” and assume this invariance is also true for the MLES classifier. While their assertion might be true for the C-H classifier, it is not necessarily true for the MLE classifier. Because [1] do not consider covariance structures with moderate to high correlation, their results are biased toward the C-H classifier. Here, we show that the MLES classifier can considerably outperform the C-H classifier, depending on the degree of correlation among the variables with missing data and the variables without missing data.
Next, we present a description and results of a Monte Carlo simulation we have performed to evaluate the EERD between the MLE and C-H classifiers for two multivariate normal configurations, 
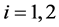

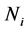
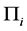
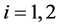
is the intraclass covariance matrix where 
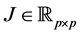
The simulation was performed in SAS 9.2 (SAS Institute In., Cary, NC, USA) using the RANDNORMAL command in PROC IML to generate 10,000 training-sample sets of size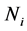



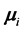

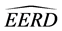
where 

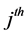


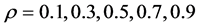
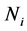


The relationship between p and r was fixed at 

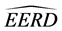


Lastly, we chose 

and 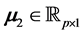

with 








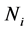
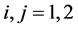
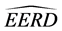





Figure 1, Figure 2 illustrate that the 


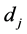











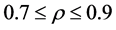

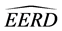



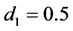
The MLES classifier especially outperformed the C-H classifier when 




Table 1. Dimensions and sample sizes for the Monte Carlo simulation.
Figure 1. Graphs of the 


Mahalanobis distance when 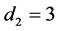


As we used a large number of simulation iterations, we obtained

the grid of parameter vectors considered in the simulation. Thus, the relatively small estimated standard errors also support our claim that 


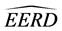
In summary, the simulation results indicated that the MLES classifier became increasingly superior to the C-H classifier as the correlation magnitude among the features with no missing data and the features with BMM data increased.
We remark that the standard errors for the 
We also performed a second Monte Carlo simulation whose results are not presented here. In this simulation, all fixed parameter values were equivalent to those of the first simulation except for 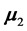


Figure 2. Graphs of the 


4. Two Real-Data Examples
4.1. Bootstrap Expected Error Rate Estimators for the C-H and MLE Classifiers
In this section, we compare the parametric bootstrap estimated ERRs of the C-H and MLES classifiers for two real-data sets each having two approximate multivariate normal populations with different population means and equal covariance matrices. First, we define the bootstrap ERR estimator for the C-H classifier,



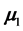






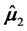
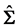

that is generated from




for
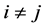






Also, conditioning on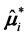


where 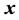







and given
where
Thus, assuming equal a priori probabilities of belonging to
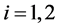

Hence, the estimated parametric bootstrap EERD for the C-H and MLES classifiers is
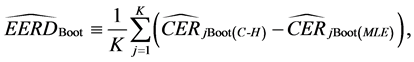
where j denotes the 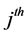

4.2. A Comparison of the C-H and MLE Classifiers for UTA Admissions Data
The first data set was supplied by the Admissions Office at the University of Texas at Arlington and imple- mented as an example in [1] . The two populations for the UTA data are the Success Group for the students who receive their master’s degrees (






Also, the common estimated correlation matrix for the UTA data is

We remark that only one sample correlation coefficient in the last column of (28) has a magnitude exceeding 0.50, which reflects relatively low correlation among the four features without BMM data with the one feature having BMM data.
To estimate EERD for the C-H classifier (8) and the MLES classifier (19) for the UTA Admissions data, we determine



Table 2. UTA Admissions office.
and 

and
for the means of 

Subsequently, we obtained 
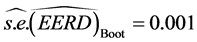
4.3. A Comparison of the C-H and MLE Classifiers on the Partial Iris Data
The second real-data set on which we compare the C-H and MLES classifiers is a subset of the well-known Iris data, which is one of the most popular data sets applied in pattern recognition literature and was first analyzed by R. A. Fisher (1936). The data used here is given in Table 3.
The University of Irvine Machine Learning Repository website provides the original data set, which contains 150 observations (50 in each class) with four variables: X1 = sepal length (cm), X2 = sepal width (cm), X3 = petal length (cm), and X4 = petal width (cm). This data set has three classes: Iris-setosa (





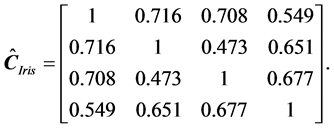
Table 3. Partial iris data.
In (29), all estimated correlation coefficients in the last column had a magnitude greater than 0.50, which reflects a moderate degree of correlation among the features



For the Iris subset data, which can be found in Table 3, we used 10,000 bootstrap iterations, 

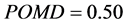

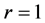


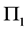

and
respectively, with common covariance matrix
For the parametric bootstrap estimate for 
the subset of the Iris data set, we obtained 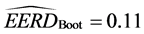

that
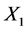

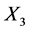
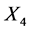
5. Conclusions
In this paper, we have considered the problem of supervised classification using training data with identical BMM data patterns for two multivariate normal classes with unequal means and equal covariance matrices. In doing so, we have used a Monte Carlo simulation to demonstrate that for the various parameter configurations considered here, 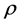


We also have compared the MLE and C-H classifiers on two real training-data sets using 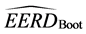
Cite this paper
Phil D.Young,Dean M.Young,Songthip T.Ounpraseuth, (2016) A Comparison of Two Linear Discriminant Analysis Methods That Use Block Monotone Missing Training Data. Open Journal of Statistics,06,172-185. doi: 10.4236/ojs.2016.61015
References
- 1. Chung, H.-C. and Han, C.-P. (2000) Discriminant Analysis When a Block of Observations Is Missing. Annals of the Institute of Statistical Mathematics, 52, 544-556.
- 2. Bohannon, T.R. and Smith, W.B. (1975) Classification Based on Incomplete Data Records. ASA Proceeding of Social Statistics Section, 67, 214-218.
- 3. Jackson, E.C. (1968) Missing Values in Linear Multiple Discriminant Analysis. Biometrics, 24, 835-844.
http://dx.doi.org/10.2307/2528874 - 4. Chang, L.S. and Dunn, O.J. (1972) The Treatment of Missing Values in Discriminant Analysis—1. The Sampling Experiment. Journal of the American Statistical Association, 67, 473-477.
- 5. Chang, L.S., Gilman, A. and Dunn, O.J. (1976) Alternative Approaches to Missing Values in Discriminant Analysis. Journal of the American Statistical Association, 71, 842-844.
http://dx.doi.org/10.1080/01621459.1976.10480956 - 6. Titterington, D.M. and Jian, J.-M. (1983) Recursive Estimation Procedures for Missing-Data Problems. Biometrika Trust, 70, 613-624.
http://dx.doi.org/10.1093/biomet/70.3.613 - 7. Hocking, R.R. and Smith, W.B. (2000) Estimation of Parameters in the Multivariate Normal Distribution with Missing Observations. Journal of the American Statistical Association, No. 63, 159-173.
- 8. Anderson, T.W. and Olkin, I. (1985) Maximum-Likelihood Estimation of the Parameters of a Multivariate Normal Distribution. Linear Algebra and Its Applications, 70, 147-171.
http://dx.doi.org/10.1016/0024-3795(85)90049-7 - 9. Fisher, R.A. (1936) The Use of Multiple Measurements in Taxonomic Problems. Annals Eugenics, 7, 179-188.
http://dx.doi.org/10.1111/j.1469-1809.1936.tb02137.x