Received 25 July 2015; accepted 27 December 2015; published 30 December 2015

ABSTRACT

The paper introduces a new Frequentist model averaging estimation procedure, based on a stacked OLS estimator across models, implementable on cross-sectional, panel, as well as time series data. The proposed estimator shows the same optimal properties of the OLS estimator under the usual set of assumptions concerning the population regression model. Relatively to available alternative approaches, it has the advantage of performing model averaging ex-ante in a single step, optimally selecting models’ weight according to the MSE metric, i.e. by minimizing the squared Euclidean distance between actual and predicted value vectors. Moreover, it is straight- forward to implement, only requiring the estimation of a single OLS augmented regression. By exploiting ex-ante a broader information set and benefiting of more degrees of freedom, the proposed approach yields more accurate and (relatively) more efficient estimation than available ex-post methods.

Keywords:

Model Averaging; Model Uncertainty

1. Introduction

The Classical Linear Regression Model (CLRM) is grounded on a basic set of assumptions concerning its specification and distributional properties of control variables and error term. In this respect, under what is usually held as Assumption 1, the population regression model is required to be linear in the parameters, and control variables are all known and included in the model. However, the latter correct specification assumption may not always be appropriate in Economics; for instance, there may be more than a single set of variables, i.e. more than a single candidate model, which can be employed in estimation, also when economic theory has clear-cut implications for the causal linkage of interest.

Consider the relationship linking y to x, when both variables can be measured in different ways, i.e. when there exist 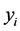and, ,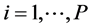; then, in principle, up to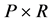, different models can be estimated.¹

Two solutions have so far been proposed in the literature to the above model selection problem. On the one hand, by maintaining the assumption of correct specification, a single model out of the 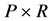candidates can be selected according to various specification strategies (see [2] for a general account; see also [3] for recent developments in model selection). Alternatively, all of the models can be estimated, and a weighted average across models computed ex-post for the parameters of interest. In the latter case, the assumption of correct specification does not have necessarily to be maintained.

Several model averaging procedures have been proposed in the literature, making use of either Bayesian or Frequentist procedures (see [4] [5] ). Admittedly, relatively to Bayesian, the Frequentist approach to model averaging is fairly underdeveloped. The current paper then aims at filling this gap in the literature, by proposing an ex-ante, mean square error-optimal model averaging procedure. The proposed procedure is grounded on a stacked OLS estimator across models, implementing model averaging ex-ante in a single step, optimally selecting models’ weight according to the MSE metric, i.e. by minimizing the squared Euclidean distance between actual and predicted value vectors. Moreover, it is straightforward to compute, only requiring the estimation of a single OLS augmented regression. By exploiting a broader information set ex-ante, i.e. by making use of all the available information jointly, and benefiting of more degrees of freedom, the proposed estimator then yields more accurate and (relatively) more efficient estimation than available ex-post methods. Extension to other estimation frameworks, i.e. GIVE or GMM, is also straightforward.

The rest of the paper is organized as follows. In Section 2, the proposed approach is illustrated by means of a simple example. Then, the econometric methodology is outlined in full in Section 3, while Section 4 deals with its statistical properties. Finally Section 5 concludes.

2. Ex-Ante Model Averaging: An Example

For sake of clarity, consider the following bivariate example

(1)

where the dependent variable y is a linear function of the independent variable x. The endogenous variable y can then be alternatively measured by 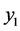and, while the independent variable x by 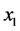and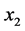. In what fol-

lows we assume that the other usual properties of the CLRM hold, i.e., , ,

, is a stationary and ergodic process, of zero mean for simplicity; the regressors and the residuals

are at least contemporaneously orthogonal, i.e.; the residuals are conditionally homoskedastic and non serially correlated,).²

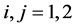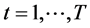Four consistent estimates of the parameter of interest are then obtained, i.e., , , , by means of OLS estimation of each of the four available alternative models

(2)

Ex-post model averaging then yields a robust consistent estimate of, by computing a weighted average of the four available estimates, , , , with weights determined according to Bayesian or Frequentist approaches.

For instance, within a Frequentist model averaging approach [2] , one has

(3)

where the weights can be computed by means of information criteria as in [6] , setting

(4)

where is the Akaike or Schwarz-Bayes information criterion for model. Other approaches are also available, based on Mallow's criterion [7] or cross-validation [8] .

On the other hand, the proposed model averaging strategy is single-step and implemented by means of an augmented regression model using all the available data jointly. It then requires the construction of the auxiliary dependent () and independent () variables, by appropriately stacking the actual data and in single column vectors.

With reference to the set of models in (2), consider the stacked model obtained from their union, i.e.

(5)

where, and are vectors,

;, , , , are vectors containing the observations on, and, respectively.

Alternatively, the regression model can be written as

(6)

The stacked OLS problem is then stated as

(7)

yielding, after some algebra

(8)

or

(9)

where

(10)

(11)

with.

The ex-ante model averaging or stacked OLS estimator of is then equivalent to its ex-post counterpart, with weights determined according to the relative variation of the candidate regressors.

Moreover, consistent OLS estimation of from the generic th disjoint model yields

(12)

while the stacked estimator is

(13)

Hence, the stacked OLS estimator of is equivalent to the arithmetic mean, across models, of the disjoint OLS estimators of.

Issues related to the (relative) efficiency of the stacked OLS estimator and the gain in terms of higher degrees of freedom are discussed below.

3. Ex-Ante Model Averaging by Stacking

Consider the regression function

(14)

and suppose that P candidate dependent variables are available, i.e., where, , is a column vector of observations.

For simplicity, three cases for the specification of the design matrix are considered:

1) The case of a single design matrix for the K regressors, , where is a vector and.

2) The case of R candidates for one of the K regressors in the model, ordered first for simplicity, i.e., , , yielding up to R different design matrices.

3) The case of R candidates for each of the K regressors in the model, yielding up to different design matrices,.

3.1. The Case of a Single Design Matrix

In case 1. Up to P models could be estimated, i.e.

(15)

Their union yields the stacked model

(16)

where is a vector of observations on the P available candidate dependent variables, obtained by stacking the P column vectors on top of one other; is the joint design matrix obtained by staking P times the matrix on top of itself, i.e., is the vector of parameters, and is the vector of residuals, obtained by stacking the P column vectors on top of one other. Hence, the sample size of the stacked model is.

Disjoint OLS estimation of the pth generic model in (15) yields (see [9] )

(17)

while for the variance, in large samples

(18)

The Ex-Ante Model Averaging Estimator

Ex-ante model averaging is obtained by OLS estimation of the stacked model in (16), yielding

(19)

(20)

The linkage between ex-ante and ex-post model averaging can then be gauged by noting that (19) can be stated as

(21)

where,.

Hence, in this case, ex-ante OLS model averaging is equivalent to ex-post arithmetic model averaging across the P disjoint OLS estimators.

Similarly for

(22)

which also is the arithmetic average, across the P available models, of the disjoint estimators.

3.2. The Case of Multiple Design Matrices

In the case of multiple design matrices, up to G regression models can be computed, with in case 2. and in case 3., i.e.

(23)

The disjoint OLS estimator for the generic th model, , , in (23)

(24)

is

(25)

while for the variance, in large samples

(26)

On the other hand, the union of the above disjoint models yields the stacked model

(27)

where is the vector of parameters, is the vec-

tor collecting the P vectors, , which are then stacked on top of one other G times, is the vectorization operator, is the Kronecker product and a unitary vector.³

By denoting the matrix obtained by stacking the G candidate design matrices on top of one another, is then the design matrix yield by staking P times the matrix on top of itself, i.e.. Finally, is a vector of residuals. Hence, the sample size of the stacked model is.

The stacked OLS estimator is then computed as

(28)

(29)

3.2.1. The Case of a Single Candidate Dependent Variable

For sake of simplicity, consider first the case where; hence, , , and the design matrix in the stacked model is

The stacked OLS estimator in (28) can then be stated

(30)

where

Denote, yielding, , and so on. By substitution in (30), it follows

(31)

Using matrix inversion rules⁴, one has

(32)

where

By substitution in (31), it follows

(33)

where.

Optimal ex-ante weights, contained in the matrices, , are then computed by taking into account all the information available on the various candidate regressors, being proportional to their relative variation. In fact, multiplying both sides of (32) by, one has

and therefore.

Moreover, given, one has

Hence, is the arithmetic average, across the available G models, of the disjoint estimators.

3.2.2. The Case of Multiple Candidate Dependent Variables

Consider now the case in which more than single candidate dependent variable is available, i.e.. The stacked OLS estimator in (28) is then

(34)

where again.

Moreover, denote, i.e., , and so on; by substitution in (34), one then has

(35)

By recalling that, where, by substitution in (35) one eventually has

(36)

where, as for the previous case,.

The optimal ex-ante weights, contained in the matrices, , are again computed by taking into account all the information available on the various candidate regressors and are proportional to their relative variation. Averaging is then performed across all possible models which can be estimated according to the P candidate dependent variables.

Moreover,

(37)

Then, ex-ante model averaging estimation of the variance is computed as the arithmetic average, across all the models, of the disjoint estimators.

4. Statistical Properties

Assume that the properties of the classical linear regression model hold, i.e.:

1) The population regression function is linear in the K parameters, i.e..

2) is a candidate stationary and ergodic process,;,;

is a vector of regressors (belonging to the rth design matrix) at observation t,;.

3) The regressors are at least contemporaneously orthogonal to the residuals, i.e., where is the residual from the generic prth model at observation t.

4) Any of the design matrices has rank equal to K with probability 1, with a finite, symmetric, invertible, positive semidefinite matrix.

5) The conditional variance covariance matrix of the residuals is a scalar identity matrix, i.e.

, implying that the residuals are conditionally homoskedastic and non serially correlated,).

Under the above assumptions (even relaxing the conditional homoskedasticity property), the disjoint OLS estimator in (25) and in (26) is consistent and asymptotically normal (see [9] ). The same properties hold for the stacked OLS estimator. Proofs for the most general case are reported below; results for the intermediate cases can be straightforwardly derived from those provided, by setting or.

4.1. Large Sample Properties

In so far as, it follows for in (36)

since by ergodic stationarity, where is a finite and non singular matrix and

.

Moreover, in so far as, it follows for in (37)

Under properties 1. to 5., by means of a CLT (see [9] ), one also has

leading to

The asymptotic distribution of then follows

as well as its feasible form

In the case of conditional heteroskedasticity, it would be straightforward to prove that

and

with feasible form

where.

The relative efficiency of the stacked over the disjoint OLS estimator can be established by comparing their asymptotic variances, i.e. and. One then has

(38)

which is a finite, symmetric, positive semidefinite matrix, as and, both finite, and

is a finite, symmetric, positive semidefinite matrix by construction (is real and of full column rank for any r).

Finally, the gain in terms of degrees of freedom yield by the stacked over the disjoint OLS estimator is equal to. In fact, by recalling that the number of degrees of freedom of the residual term is equal to the rank of the annihilator matrix (see [9] ), the gain yield by stacked over disjoint OLS estimation can be established by comparing the rank of the annihilator matrix in the two cases

which is of rank equal to as

and

which is of rank as

The increase in degrees of freedom yield by stacked over disjoint OLS estimation is then

4.2. Small Sample Properties

If the stronger assumption of strict exogeneity is made in 3. above, i.e., the disjoint OLS estimators in (25) and are also (conditionally and unconditionally) BLUE, i.e. best un-

biased and efficient (within the class of linear estimators) (see [9] ).⁵ Moreover, if the assumption of conditional Normality of the error term is added, i.e., OLS is (conditionally and unconditionally) BUE, i.e. best unbiased (within the class of linear and non linear estimators), as well as (conditionally and unconditionally) normally distributed

(39)

where is a finite, nonsingular, symmetric, positive semidefinite matrix of rank.

The above properties can also be established for the stacked OLS estimator, in the same way as for the disjoint OLS estimator (see [9] ), yielding

(40)

with a finite, nonsingular, symmetric, positive semidefinite matrix of rank, and feasible form

where.

Then, by comparing the conditional variances of and, one has again

(41)

as for the asymptotic case. Moreover,

(42)

which similarly is a finite, symmetric and positive semidefinite matrix by construction.

Finally, the gain in terms of degrees of freedom yield by stacked over disjoint OLS estimation is again, as already shown for the asymptotic case.

5. Conclusion

The paper introduces an ex-ante model averaging approach, requiring the estimation of a single augmented model obtained from the union of all the possible candidate models, rather than their disjoint estimation. In this framework, optimal weights are implicitly computed according to the MSE metric, i.e. by minimizing the squared Euclidean distance between actual and predicted value vectors, and are proportional to the relative variation of the regressors. By exploiting ex-ante all the available information on the various candidate set of variables, and relying on more degrees of freedom, it then leads to more accurate and (relatively) more efficient estimation than available ex-post methods. Moreover, the proposed estimator shows the same optimal properties of the disjoint OLS estimator, under the usual set of assumptions concerning the population regression model. While the method is proposed to be used within the OLS estimator framework, extension to GIVE and GMM is straightforward. We point to [1] for an empirical application using OLS and GMM estimation.

Acknowledgements

The author is grateful to the referees for their comments. This project has received funding from the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement no. 3202782013-2015. The flowers are supported by the branches/The trunk supports the branches/The roots support the trunk/But we do not see the roots (Mitsuo Aida).

Cite this paper

ClaudioMorana,11, (2015) Model Averaging by Stacking. Open Journal of Statistics,05,797-807. doi: 10.4236/ojs.2015.57079

References

NOTES

¹In Economics, the above situation is not unusual. For instance, be y a measure of income distribution inequality and x the degree of financial development of a country; in the latter case, the Gini Index, net or gross, or top-to-bottom income distribution quantile ratios (top to bottom 1% or 10%) would all be valid candidate dependent variables; moreover, concerning financial deepening, the GDP share of liquidity (M2 or M3), stock market capitalization, or credit to the private sector, might be alternatively employed (see [1] ).

²t is not necessarily a temporal index; applications to cross-sectional data are as viable as to time series.

³Hence,

⁴Given matrices A and C, non singular and of proper dimensions for their sum, it holds

⁵The usual caveat concerning the efficiency of applies, as no linear unbiased estimator of achieves the Cramer-Rao Lower Bound, which is obtained by the biased ML estimator.