American Journal of Operations Research
Vol.3 No.1A(2013), Article ID:27562,28 pages DOI:10.4236/ajor.2013.31A021
Prediction and Optimization of System Quality and Risks on the Base of Modelling Processes
1Research Institute of Applied Mathematics and Certification, Moscow, Russia
2Gubkin Russian State University of Oil and Gas, Moscow, Russia
3Research Institute of Applied Mathematics and Certification, Moscow, Russia
4Institute of Informatic Problems of the Russian Academy of Sciences, Moscow, Russia
5Scientific & Technical Center “NAOPRO”, Moscow, Russia
Email: akostogr@gmail.com, lgrig@gubkin.ru, george.icie@gmail.com, andrey.nistratov@gmail.com, vk@aatv.ru
Received November 19, 2012; revised December 18, 2012; accepted January 14, 2013
Keywords: Analysis; Model; Quality; Prediction; Reliability; Risk; Safety; Software Tools; System Engineering
ABSTRACT
The paper is concerned with the development and application of the original probability models and supporting them software tools to predict and optimize quality and risks for complex systems. The examples demonstrate possibilities to use modeling results from different application spheres and to go in making decision “from a pragmatical filtration of information to generation of the proved ideas and effective decisions”.
1. Introduction
Today system processes for different conditions and threats are the main objects for improvement of system operation. The goal of this work is to propose models, methods, and software tools well-tested in practice, to predict and optimize quality and risks as applied to newly developed and currently operated manufacture, power generation, transport, engineering, information, control and measurement, food storage, quality assurance and security systems. Presented work covers logically closed contour: “system requirements—supporting mathematical models to estimate processes and system operation— ways to optimize quality and risks”. Thereby the answers on system engineering questions—“Is expected quality achievable?”, “Can be the system requirements met?”, “How much safe are those or others scenarios?”, “What about the real risks, profits and possible damages?”, “What choice in system architecture is rational?”, “What analyzed variants and decision are more effective and why?”, “What rational measures should lead to estimated effect without waste expenses, when, by which controllable and uncontrollable conditions and costs?” etc.— can be substantiated quantitatively. The answers may be received before critical events (not only after these events). As demonstration 10 practical examples are investigated and explained, the detailed ‘hardware’ of the work (including dozens of models), other hundreds examples and routine comments are gathered at [1-12] and on site www.mathmodels.net.
Why you should trust to the results of prediction by the offered models? In other words how models adequacy is substantiated? Though any answer to these questions won’t be irrefragable for a certain system we shall try to formulate our arguments (experience readers understand that any model needs in similar arguments).
Argument 1. The fact is that while shaping models all mathematical results are initially drawn in the integral form. As input data are somehow connected with time after choosing probability distribution functions (PDF) characterizing these data there were selected the gammadistribution and the Erlang’s distribution. Mathematicians know that these distributions approximate sums of positively distributed random variables well. Every temporary data are as a matter of fact such a sum of compound time expenses. Studies of regularities (for example, [13-18]) have shown that extremes are achieved on bounds of these distributions, i.e. of exponential and deterministic (discrete) distributions. Thus, real values will be somewhere between lower and upper estimations. The results reflect pessimistic value for following using.
Argument 2. As a basis of our models the probability theory and the theory of regenerative processes (i.e. recurring processes) are used. Proofs of basic theoretical results are received, for example, by [14-15]. If to return in the 70-s of the last century we may remember the boom of mathematical modelling, defining calls flow reliable and time-probabilistic characteristics. The boom passed and appeared the reliability theory, the queuing theory and a variety of models, which proved themselves to be effective. There are created standards and other normative documents regulating system methodical evaluations on the basis of these models. Nowadays these models are widely used and trusted because they produce reliable results confirmed in the course of time. It is worth to remind that these created theories and models are based on the probability theory and the theory of regenerative processes. Some the offered models are the classical models of the 70-s improved and developed to meet the requirements of the present time. The other models [1-12] are created on the basis of the limit theorem for regenerative processes developed in the 70-80-s in Moscow State University.
Argument 3. Skilled analysts know that if a probabilistic analytical model is incorrect then if input data are changed in the range from –¥ to +¥ there are always errors appearing either in infraction the probability theory laws or in illogic of dependencies behavior (most probably on the bounds of possible values) or in impossibility of obtained effects physical explanation. Bounds of input data in the offered software tools are assigned in the range from –¥ to +¥ (more precisely from milliseconds to 108 years). Ten-years testing of models including beta testing by different independent companies raise confidence in software tools algorithmic correctness.
Argument 4. As far as possible any designer tends to use several models of different authors. If results of different models use are not divergent a designer begins to trust not only to results but also to the models. Comparison of results of the presented software tools with results of other models use proved their high adequacy (concerning computations of reliability and time-probabilistic characteristics, the other models don’t have analogues).
These arguments are supported by correct results of hundreds deep researches and technical solutions corresponding theory and practice.
The offered software tools are an original Russian creation patented. They have been presented at seminars, symposiums, conferences, ISO/IEC working groups and other forums since 2000 in Russia, Australia, CanadaChina, Finland, France, Germany, Kuwait, Luxembourg, Poland, Serbia, Ukraine, the USA, etc. The software tools were awarded by the Golden Medal of the International Innovation and Investment Salon and the International Exhibition “Intellectual Robots”, acknowledged on the World’s fair of information technologies CeBIT in Germany, noted by diplomas of the Hanover Industrial Exhibition and the Russian exhibitions of software. The offered technology of modelling through the Internet has been acknowledged as the best project-2007 by the National Association of Innovations and Developments of Information Technologies of Russia.
2. Review and Analysis of System Processes
As a result of analyzing practice approaches to safety (to industrial, fire, radiating, nuclear, chemical, biological, transport, ecological systems, safety of buildings and constructions, information security) we made the next conclusions-see Figure 1 [7-12].
For the spheres of industrial, fire, radiating, nuclear, aviation safety in which already there were numerous facts of tragedies-requirements to admissible risks are expressed quantitatively at probability level and qualitative at level of necessary requirements to the initial materials, used resources, protective technologies and operation conditions. Generally risk estimations from one sphere do not use in others spheres because of methods and metrics for risk analysis are different, interpretations are not identical in spite of processes are logically similar.
For the spheres of chemical, biological, transport, ecological safety, safety of buildings and constructions, information security, including the conditions of terrorist threats—requirements to admissible risks are set mainly at qualitative level in the form of requirements to performance. The analytical methods for quantitatively risk analysis are in creating yet. The term “Admissible risk” can’t be defined because of one depend on methods. Experience from other spheres is missing.


Figure 1. Comparison results to risk estimations.
To improve essentially this situation the offered way includes mathematical models and applicable technologies to predict, analyze and optimize quality and risks for complex systems.
Existing practices for providing system quality and safety were reviewed and analyzed (including approaches of system standards ISO 9001, ISO/IEC 15288, IEC 60300, 61508, CMMI etc.).
As a result of reviewing: all organizations need adequate knowledge to solve the problems, but only some part from them uses modelling complexes; used models are highly specialized, input and calculated metrics are adhered strongly to specificity of systems; existing modelling complexes have been created within the limits of concrete systems and as a rule are very expensive for adaptation to other conditions. In general case prediction and optimization of quality and risks should be founded on the mathematical modelling of system processes. Really, any process is a repeated sequence of consuming time and resources for outcome receiving in all application areas. The moments for any activity beginning and ending are, in mathematical words, random events on time line. Moreover, there exists the general property of all process architectures. It is a repeated performance for majority of timed activities (evaluations, comparisons, selections, controls, analysis etc.) during system life cycle—for example see on Figures 2 and 3 the problems that are due to be and can be solved by the mathematical modelling of processes according to ISO/IEC 15288 “System engineering. Processes of system life cycle”. The summary of the analysis is the next. Probability estimations of identical processes from one sphere do not use in other spheres because of methodologies are different, interpretations are not identical. The methods for quantitative quality and risk analysis on probability level are in creating stage yet. As consequence probability estimations are not comparable, experience from different spheres is missing, a universal objective scale of measurement is not established yet. Moreover the terms “Acceptable quality” and “Admissible risk” should be defined on probability scale level only in dependence on corresponding methods.
It does not allow to solve the main problems of a substantiation of system requirements to processes parameters

Figure 2. The problems that are due to be and can be solved by mathematical modelling of processes.
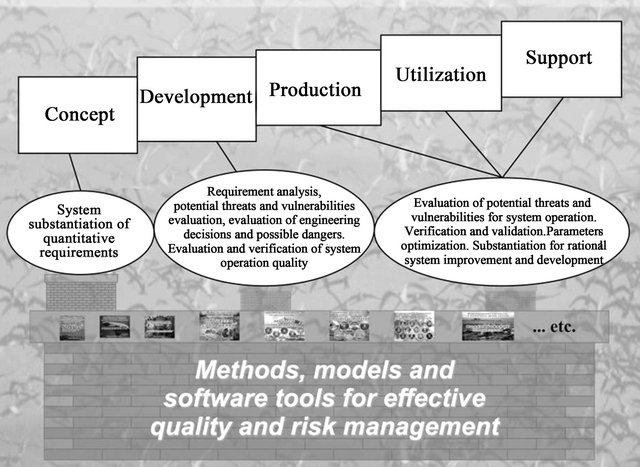
Figure 3. System engineering problems in life stages.
of information gathering and analysis, control, monitoring and counteraction measures at restrictions, and also to confirm about efficiency of the prevent measures to provide quality and safety in different spheres.
This work focuses on the way for using universal metrics in a system processes: probabilities of success or failure during a given period for an element, subsystem, system. Calculation of these metrics within the limits of the offered probability space built on the basis of the theory for random processes, allows to predict quality and risks on an uniform probability scale, quantitatively to prove comprehensive levels of acceptable quality and admissible risks from “precedents cases”. The prediction of risks can use widely transportation safety monitoring data and statistics. In general case a probabilistic space  for the evaluation of system operation processes should be proposed, where:
for the evaluation of system operation processes should be proposed, where: —is a limited space of elementary events; B—a class of all subspace of
—is a limited space of elementary events; B—a class of all subspace of  -space, satisfied to the properties of s-algebra; P—a probability measure on a space of elementary events
-space, satisfied to the properties of s-algebra; P—a probability measure on a space of elementary events  Because,
Because, 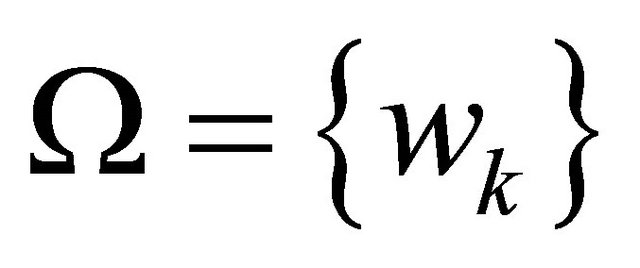 is limited, there is enough to establish a reflection
is limited, there is enough to establish a reflection 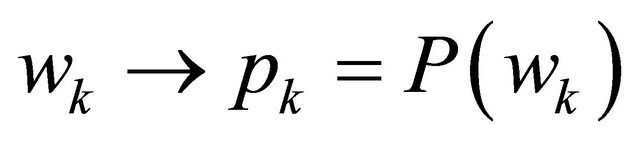 like that
like that 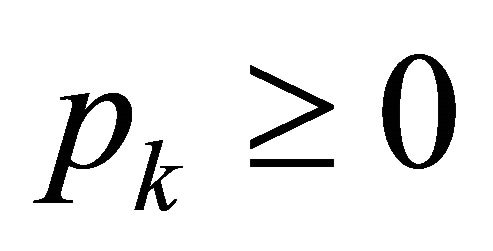 and
and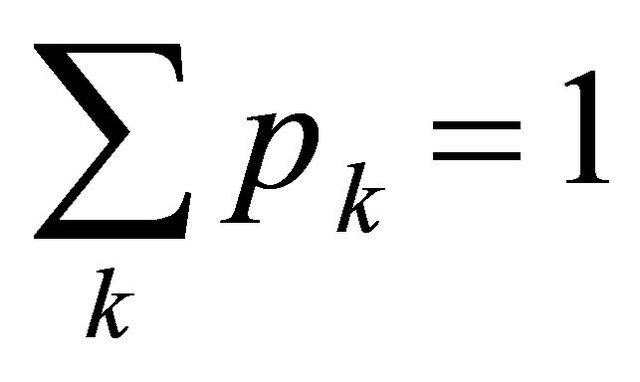 .
.
3. Example of Modelling Processes
3.1. The Models and Software Tools to Analyze Information System Processes
The example of creating models and technologies to predict quality and risks is modelling software Complex for Evaluation of Information Systems Operation Quality, patented by Rospatent No. 2000610272 (CEISOQ+) [1- 3].
Requirements to Information Systems (IS) operation depend on SYSTEM purposes and general purpose of IS operation, real conditions (including potential threats), available resources, information sources facilities and communication requirements (see Figure 4). This is the logical basis to create universal mathematical models to estimate the reliability and timeliness of information producing, the completeness, validity and confidentiality of the used information from users’ point of view [1-3].
The idea of estimating IS operation quality appeared as a result of studying potential threats to output information (see Figure 5 and example of modelling protection processes against dangerous influences in subsection 3.2).

Figure 4. The place and the purpose of information system in a SYSTEM.
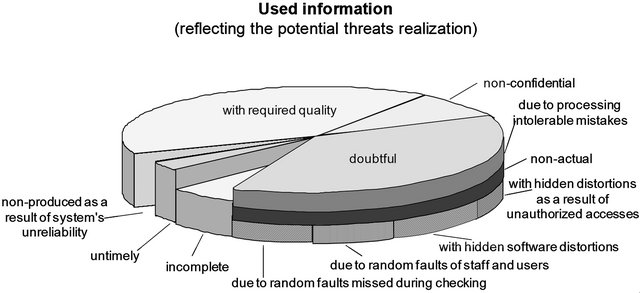
Figure 5. Potential threats to output information according to general purpose of IS operation.
The created CEISOQ+ allows to simplify and to spread the use of the next mathematical models: of functions performance by a system in conditions of unreliability of components; complex of calls processing; of entering into IS current data concerning new objects of application domain; complex of information gathering from sources; of information analysis; of dangerous influences on a protected system; of an unauthorized access to system resources. CEISOQ+ may be applied for solving such system problems appearing in IS life cycle as: substantiation of quantitative system requirements to hardware, software, users, staff, technologies; requirements analysis; estimation of project engineering decisions and possible danger; detection of bottle-necks; investigation of problems concerning potential threats to system operation and information security; testing, verification and validation of IS operation quality; rational optimization of IS technological parameters; substantiation of plans, projects and directions for effective system utilization, improvement and development.
3.2. Example of Modelling Protection Processes against Dangerous Influences
Nowadays at system development and utilization an essential part of funds is spent on providing system protection from various dangerous influences able to violate system integrity (these may be failures, defects events, “human factors” events, terrorists attacks, etc.).
There are examined two general technologies of providing protection from dangerous influences in different transportation spheres: proactive diagnostic of system integrity1 (technology 1) and security monitoring when system integrity is checked at every shift change of operators (technology 2).
Technology 1 is based on proactive diagnostics of system integrity. Diagnostics are carried out periodically. It is assumed that except diagnostics there are also included means of necessary integrity recovery after revealing of danger sources penetration into a system or consequences of negative influences. Integrity violations detecting is possible only as a result of diagnostics, after which system recovery is started. Dangerous influences on system are acted step-by step: at first a danger source penetrates into a system and then after its activation begins to influence. System integrity is not considered to be violated before a penetrated danger source is activated. A danger is considered to be realized only after a danger source has influenced on a system. The essence of protecting process architecture for the first technology is illustrated by Figure 6. The cases 1, 4 illustrate dangerous influences. The cases 2, 3, 5 illustrate secure system operation during period Treq.2
Technology 2, unlike the previous one, implies that operators alternating each other trace system integrity between diagnostics. In case of detecting a danger source an operator is supposed to remove it recovering system integrity (ways of danger sources removing are analogous to the ways of technology 1). A penetration of a danger source is possible only if an operator makes an error but a dangerous influence occurs if the danger is activated before the next diagnostic. Otherwise the source will be detected and neutralized. Errorless operator’s actions provide a neutralization of a danger source trying to penetrate into a system. When operators alternate a diagnostic and recovery of lost integrity is held.
For all technologies availability of means of danger sources total-lot detecting and existence of ways of violated system integrity total-lot recovery may seem to be a very high requirement. Nonetheless, a system which can’t check and recover its integrity (if it needs) is a very vulnerable and knowingly doomed system.
The probability of safe system operation within the assigned period may be estimated as a result of use the next mathematical models. Risk to lose safety is an addition to 1 (assumption: for all time input characteristic the probability distribution functions (PDF) exist).
There are possible the next variants: variant 1—the assigned period Treq. is less than established period between neighboring diagnostics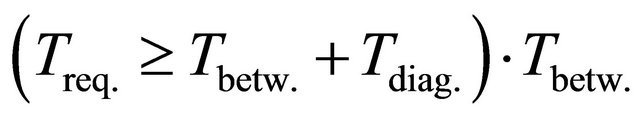 ; variant 2— the assigned period Treq. is more than or equals to established period between neighboring diagnostics Treq ≥ (Tbetw. + Tdiag.)∙Tbetw..—is the time between the end of diagnostic and the beginning of the next diagnostic (Tbetw. = const); Tdiag.—is the diagnostic time (Tbetw. = const)∙ Wpenetr(t)—is the PDF of time between neighboring influences for penetrating a danger source; Wactiv.(t)—is the PDF of activation time of a penetrated danger source; A(t) is the PDF of time between operator’s error; Treq.—is the required period of system operation for prediction.
; variant 2— the assigned period Treq. is more than or equals to established period between neighboring diagnostics Treq ≥ (Tbetw. + Tdiag.)∙Tbetw..—is the time between the end of diagnostic and the beginning of the next diagnostic (Tbetw. = const); Tdiag.—is the diagnostic time (Tbetw. = const)∙ Wpenetr(t)—is the PDF of time between neighboring influences for penetrating a danger source; Wactiv.(t)—is the PDF of activation time of a penetrated danger source; A(t) is the PDF of time between operator’s error; Treq.—is the required period of system operation for prediction.
Statement 1. Under the condition of independence of considered characteristics the probability of dangerous influence absence within the assigned period Treq. for the variant 1 of technology 1 is equal to
![]() (1)
(1)
where *—is the convolution sign.
Statement 2. Under the condition of independence for considered characteristics the probability of dangerous influence absence within the assigned period Treq. for the variant 2 of technology 1 is equal to
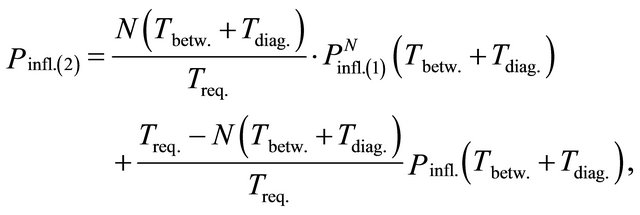
where
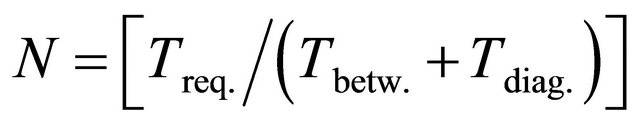 —is the integer part.
—is the integer part.
Statement 3. Under the condition of independence for considered characteristics the probability of dangerous influence absence within the assigned period Treq. for the

Figure 6. Abstract formalization for technology 1.
variant 1 of technology 2 is equal to
 (2)
(2)
Statement 4. Under the condition of independence of considered characteristics the probability of dangerous influence absence within the assigned period Treq. for the variant 2 of technology 2 is equal to
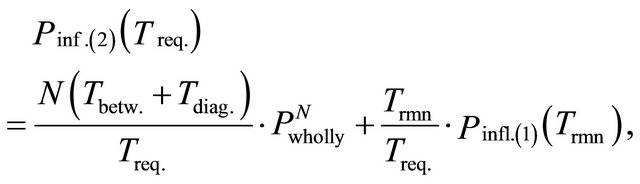
Pwholly—is the probability of dangerous influence absence within the assigned period Treq., and 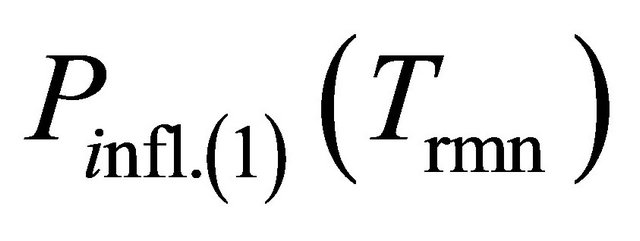 is defined above, but one is calculated not for all period Treq., only for the remainder time
is defined above, but one is calculated not for all period Treq., only for the remainder time
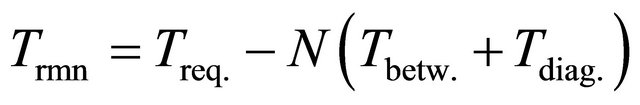 .
.
The final clear analytical formulas for modelling are received by convolution of (1) and Lebesque-integration of (2) expression with due regard to Statements 1-4.
3.3. The Idea of Modelling Complex Processes
The idea of modelling complex processes consists in the following. Any process represents a set of the works which are carried out with any productivity at limitations for resources and conditions. This amount of works is characterized by expenses of resources (cost, material, human), accordingly works can be executed for different time with various quality. For every system the terms “quality” and “safety” should be formal defined. And conditions are characterized by a set of random factors influencing processes. From the point of view of probability theory and the theory of regenerating processes it is possible to put formally, that all processes on macro-and micro-levels are cyclically repeated. If to assume, that number of recurrences of such processes is very large we can speak theoretically about probability of any events which can occur. The mean time characteristics of processes, frequency characteristics of any events and characteristics, connected in due course are used as input. Probabilities of “success” during a given time of prediction are final or intermediate results of modelling. Risks of failures are an addition to 1. They are used as evaluated output.
Thus the main proposition, implemented in the offered models, concludes the next: all amounts of works, characteristics of their performance, possible events and other inputs are interpreted as expense of time which can be reflected on a timeline. Probability metrics on the introced limited space of elementary events are calculated by the rule of the probability theory.
Correct integration of probability metrics for complex processes are based on a combination and development of models [4-12]. For a complex estimation of the sysms with parallel or consecutive structure existing models can be developed by usual methods of probability theory. For this purpose in analogy with reliability it is necessary to know a mean time between violations of integrity for each of element (similarly mean time between neighboring failures in reliability (MTBF), but in application to violation of quality, safety etc. For unrenowal objects this is mean time to the first failure). Let’s consider the elementary structure from two independent series elements that means logic connection “AND” (Figure 7, left), or parallel elements that means logic connection “OR” (Figure 7, right).


Figure 7. Illustration of system, combined from series (left) or parallel (right) elements
Let’s PDF of time between violations of i-th element integrity as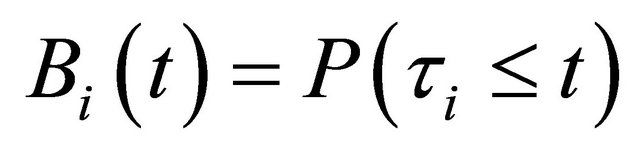 , then:
, then:
1) time between violations of integrity for system comned from consecutively connected independent elents is equal to a minimum from two times τi: failure of 1st or 2nd elements (i.e. the system goes into a state of violated integrity when either 1st, or 2nd element integty will be violated). For this case the PDF of time between violations of system integrity is defined by expression
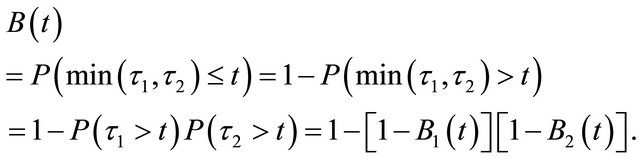 (3)
(3)
2) time between violations of integrity for system combined from parallel connected independent elements (hot reservation) is equal to a maximum from two times τi: failure of 1st or 2nd elements (i.e. the system goes into a state of violated integrity when both 1st and 2nd element integrity will be violated). For this case the PDF of time between violations of system integrity is defined by expression
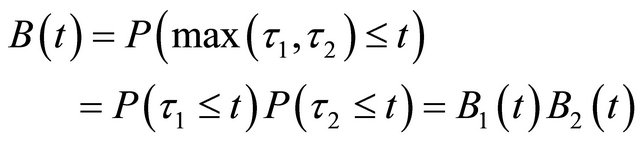 (4)
(4)
Applying recurrently expressions (3)-(4), it is possible to receive PDF of time between violations of integrity for any complex system with parallel and/or consecutive structure (in an assumption of independence). The illustration of threats, periodic control, monitoring and recovery of integrity for combined subsystems of estimated system is reflected on Figure 8.
Many models are applicable to the system presented as one element. The main output of such system modelling is probability of providing system integrity or violation of system integrity during the given period. If a probability for all points Тgiven. from 0 to ∞ will be calculated, a trajectory of the PDF (or analogy of PDF) for each combined element depending on threats, periodic control, monitoring and recovery of integrity is automatically synthesized. The known kind of this PDF allows to define mean time of providing integrity or between violations of system integrity for every system element by traditional methods of mathematical statistics.
Thus, there is possible an integration of metrics on the level of a PDF of permanent system integrity time or violation of system integrity (or analogy of PDF). And it is the base for quality and risk prediction.
3.4. Some Examples of Original Software Tools to Predict Quality and Risks
The next complex for modelling system life cycle processes “MODELLING OF PROCESSES”, patented by Rospatent No. 2004610858, supports more than 100 models and includes multi-functional software tools—see Figure 9 [7-12].
Complex “MODELLING OF PROCESSES” includes multi-functional software tools for evaluation of Agreement (models and software tools “Acquisition”, “Supply”), Enterprise (models and software tools “Environment Management”, “Investment Management”, “Life Cycle Management”, “Resource Management”, “Quality Management”), Project (models and software tools “Project Planning”, “Project Assessment”, “Project Control”, “Decision-making”, “Risk Management”, “Configuration Management”, “Information Management”) and Technical Processes (models and software tools “Requirements Definition”, “Requirements Analysis”, “Architectural Design”, “Human Factor”, “Implementation”, “Integration”, “Verification”, “Transition”, “Validation”, “Operation”, “Maintenance”, “Disposal” tools)—see Figures 10-13 (one separate box is an implementation of one or more mathematical models [1-12]).
The one from last implementations is the “Complex for evaluating quality of production processes” (patented by Rospatent No. 2010614145)—Figure 14.
The offered models help to answer the system engineering questions (see Figures 2-5) by estimations of quality and risks. The effect from implementation in system life cycle is commensurable with expenses for its creation (see Figure 15 and www.mathmodels.net).
Thereby necessary attributes of the offered innovative approach to improve system processes are above formed. Traditional approaches consist as a matter of fact in a pragmatical filtration of the information. In the decisions the responsible person, making decision, is guided firstly by the own experience and the knowledge and the advices of those persons of a command to whom trusts. Intuitively forming ideas which seem correct, this person chooses only that information which proves idea. The denying information is often ignored and more rare— leads to change of initial idea. This approach can be explained from the facts that at absence or limitation of used models it is difficult to investigate at once many ideas for short time. The presented models, methods and software tools, reducing long time of modelling (from several days, weeks and months to few seconds and minutes) change this situation cardinally.
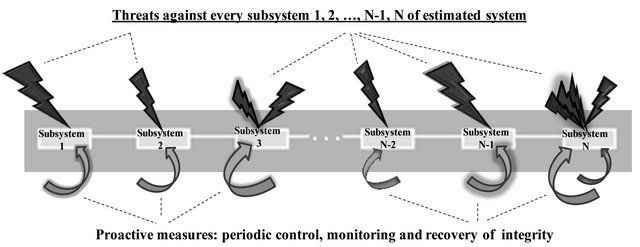
Figure 8. Threats, control, monitoring and recovery for combined subsystems (series elements).

Figure 9. Complexes for modelling system processes.

Figure 10. Software tools for evaluation of agreement processes.

Figure 11. Software tools for evaluation of enterprise processes.
The offered innovative approach is at the beginning substantiation of the system requirements, purposefully capable to lead to a success. Further, the responsible person, equipped by a set of necessary mathematical models and their software tools possibilities to predict quality and risks, is powered for generation of the proved ideas and effective decisions. These decisions are physically clear because of using accessible and operative analysis and optimization of processes in system life cycle. The offered approach allows to go “from a pragmatical filtration of information to generation of the proved ideas and effective decisions”.
The use of created methods to analyze and optimize system processes allows to optimize quality and risks in practice of system engineering.
4. Optimization of System Quality and Risks
Classical examples of optimization generally are maximization of a prize (profit, a degree of quality or safety, etc.) at limitations on expenses or minimization of expenses at limitations on an admissible level of quality

Figure 12. Software tools for evaluation of project processes.

Figure 13. Software tools for evaluation of technical processes.


Figure 14. Subsystems of the “complex for evaluating quality of production processes”.

Figure 15. The offered way is the use of created methods to analyze and optimize system processes.
and/or safety. In a life cycle of systems criteria and limitations vary. The statement of problems for system analysis includes definition of conditions, threats and estimation a level of critical measures. As probability parameters give higher guarantees in estimations of a degree of achieving purposes in comparison with average value at a choice it is recommended to use probability as the cores. And evaluated mean time characteristics (for example the mean time between violations of admissible system operation reliability) are auxiliary. For examplethere are applicable the next general formal statements of problems for system optimization:
1) on the stages of system concept, development, production and support: system parameters, software, technical and management measures (Q) are the most rational for the given period if on them the minimum of expenses (Zdev.) for creation of system is reached

at limitations on probability of an acceptable level of quality 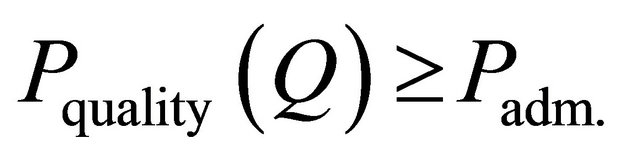 and expenses for operation
and expenses for operation
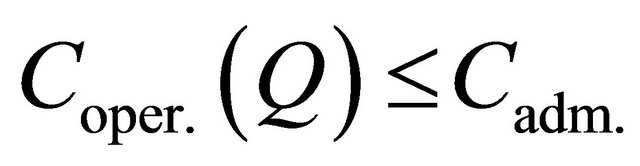 and under other development, operation or maintenance conditions;
and under other development, operation or maintenance conditions;
2) on operation stage: system parameters, software, technical and management measures (Q) are the most rational for the given period of operation if on them the maximum of probability of providing acceptable system operation quality is reached

at limitations on probability of an acceptable level of quality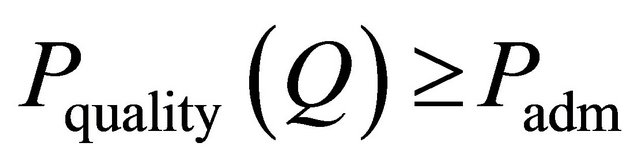 . and expenses for operation
. and expenses for operation
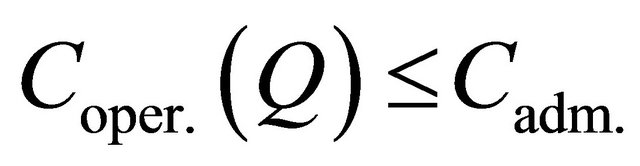 and under other operation or maintenance conditions. System parameters, software, technical and management measures (Q) are as a rule vectors of input—see examples below.
and under other operation or maintenance conditions. System parameters, software, technical and management measures (Q) are as a rule vectors of input—see examples below.
These statements may be identically transformed into problems of expenses or risk minimization or retention in different limitations. For example for security services it is necessary to provide safety of object, process or system up to the mark. In this case the criterion of a minimum of expenses at limitations on an admissible risk level of dangerous influence on system contrary to counteraction measures or a minimum of risk of dangerous influence at limitations on expenses are possible. There may be combination of formal statements in system life cycle.
The purposed order for use the developed formal approach to analyze and optimize quality and risks is illustrated by Figure 16.
When analyst use this approach he’d like for several minutes to formalize a problem, perform mathematical modelling, analyze system processes in different conditions, choose the most rational variant and prepare analytical report. Such possibilities exist: an analyst should perform mathematical modelling by the Internet versions of the some offered models—see Figure 17.
The analytical report forms automatically and includes a formalization of analyst’s problem, input, results of mathematical modelling in pictures (as demonstrated

Figure 16. The purposed approach to analyze and optimize quality and risks.

Figure 17. Mathematical modelling by the Internet versions.
above in examples), analysis of system processes behaviour for different conditions, choice of the most rational variant and recommendations”.
It is virtual outsourcing of high system analysis on the base of the offered mathematical models. The purpose is to give to analysts an opportunity of accessible and cheap high technology of studying complex processes in life cycle of estimated systems. This work has begun, the first models are accessible (see www.mathmodels.net).
An application of the offered methodology [1-12 etc.] covers the predictions of probabilities of “success”, risks and related profitability and expenses. This helps to solve well-reasonly the next problems in system life cycle: analysis of system use expediency and profitability, selecting a suitable suppliers, substantiation of quality management systems for enterprises, substantiation of quantitative system requirements to hardware, software, users, staff, technologies; requirements analysis, evaluation of project engineering decisions, substantiation of plans, projects and directions for effective system utilization, improvement and development; evaluation of customer satisfaction in system design & development and possible dangers, detection of bottle-necks; investigation of problems concerning potential threats to system operation including protection against terrorists and information security; verification and validation system operation quality, investigation rational conditions for system use and ways for optimization etc.
5. Some Examples of Solving Problems of System Engineering
Examples 1-9 are presented from simply to complex and based on real input for some operating systems. Example 10 is artificial hypothetic system as a combination of the systems from examples 1-9.
Example 1 (“Human factor”). Let the problem solution depends on joint but independent actions of 5 people. Let each of 4 specialists make 1 error a month and the 5th inexperienced person makes 1 error a day. System recovery time after an error equals to 30 minutes. It is required to evaluate faultlessness of such group’s actions within a week.
Approach to solution. Integral computation results by CEISOQ+ reveal that the probability of faultless joint actions of the first 4 skilled specialists within a 40-hours workweek equals to 0.80 but the low-quality work of the 5th unexperienced member mocks the whole group work. Indeed, the probability of faultless actions decreases to 0.15 (see Figure 18). The question is lawful—what MTBF an worker should possess to provide a faultlessness of the actions with probability 0.99 within 8 hours of the working day? According to calculations the MTBF not less than 850 working hours is acceptable. It is 106 times (!) more than 8-hours working day.
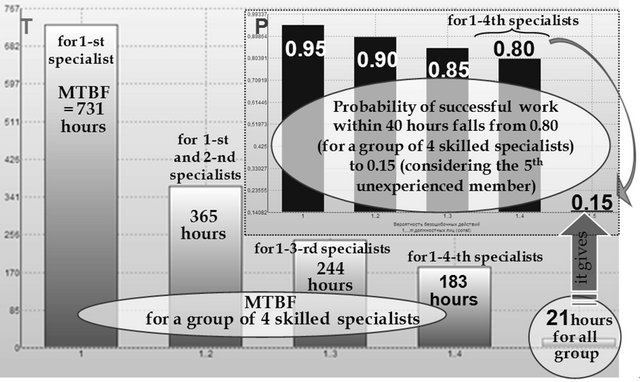
Figure 18. Analysis of human factor.
Example 2 (Efficiency of non-destroying control). Let’s consider two competing enterprises which are suppliers of pipes for transportation of production and guided in their quality management system (QMS) by various technical politics. The first of these enterprises, guided by an innovative way of development with rational application of modern information technologies, effectively uses (as believed) existing innovations for quality control. The second company uses cheaper and out-of-date technologies, keeping competitiveness on the market at the expense of it. At the enterprises various methods of non-destroying control are applied to revealing defects.
The first enterprise acquires input production from suppliers after quality control by all recommended methods of non-destroying control (acoustic, magnetic, optical, radiating, radio wave, thermal, electromagnetic etc.) that is confirmed by test reports and certificates on ISO 9001 and on output production. As a result for total controllable production in 100,000 units per a month (for example, production tons, running meters etc.) the part of possible defects before control is 5%, a frequency of errors during the control is no more than 2 defects in a year (these are the latent defects not revealed by existing methods or passed at the control).
The second enterprise is satisfied by certificate on ISO 9001. And only radio wave method of non-destroying control is used by the suppliers. It allows to reveal such defects, as stratifications and deviations on a thickness in metal products (i.e. no more than 10 % of possible defects). At the expense of it the part of possible defects before the control is already 20%, moreover, at the control defects of moulding (slag and flux inclusions, shrinkable bowls, gas bubbles, cracks, etc.), defects of processing by pressure (internal and superficial cracks, ruptures, tempers, dents, etc.), defects of heat treatment (overheats, hardening and hydrogen cracks, etc.) are missed. Totally about 30 defects per a year are possible.
Omitting questions of profits, it needs to compare technical politics of these enterprises by a risk of mistaken analytical conclusion within a month.
Approach to solution. Input and results of control processes are on Figure 19.
The comparative analysis of the received dependences has shown: the risk of mistaken analytical conclusions for 1st enterprise is 0.15, and for 2nd one—0.92 (!); if the volume of controllable production is changed from 50,000 to 200,000 units per a month the risk increases for 1st enterprise from 0.08 to 0.58, and for 2nd one—from 0.71 to 0.96; the increase in a part of possible defects twice essentially does not influence value of risk (i.e. efficiency of applied technologies of the control depends essentially on other parameters, in particular from frequency of possible errors); if frequency of possible errors increases twice than the risk increases for 1st enterprise from 0.08 to 0.28, and for 2nd one—from 0.71 to 0.99.
Conclusion: for 1st enterprise the risk of mistaken analytical conclusions at level 0.15 after the control within a month can be recognized as acceptable. The 2nd enterprise supplies frankly defected production (probability nearby 0.9) that will negatively affect further at system operation.
Example 3 (Errors during a use of SCADA system). The control towers use SCADA system (supervisory control and data acquisition) for making decision. Wrong interpretation may be caused by errors of dispatcher
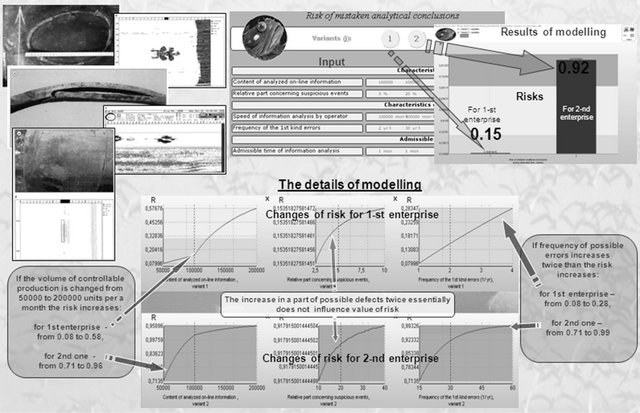
Figure 19. Comparative estimation of efficiency of non-destroying control.
personnel, which can miss important information or turn harmless information into dangerous one, fails of SCADA system. Let’s consider a control station receiving information from the SCADA system. The information flow is measured in some conventional units and the information flow is of 100 units per hour. The total information contains not more than 1% of data related to potentially dangerous events. Taking into account automatic data analysis we suppose the speed of event interpretation to be near 30 sec per information unit. In this case 100 information units will be processed during 50 min. At that the frequency of errors for the whole dispatcher shift on duty, including fails of the SCADA system itself is about 1 error per year according to statistical data. The task is to estimate the risk of mistaken analyticcal conclusion for a time period of 1 hour, during one dispatcher shift turn of 8 hours, 1 month, 1 and 10 years.
Approach to solution. The analysis of modelling by the software tools “Complex for evaluating quality of production processes” shows (see Figure 20) that for short time periods such as one shift turn or even for a month the risk of mistaken analytical conclusion is small enough (0.00076 and 0.07 accordingly). But when the time period grows the risk increases and becomes 0.565 for a year and almost unity (0.9998) during time period of 10 years. This means that during a month the probability for errors of dispatcher personal or SCADA system fails to occur is very small and their operation will be almost faultless. But for a more long time period such as a year is considered 1 - 2 errors of dispatcher personal or system SCADA fails will occur for certain.
Considering high reliability of SCADA system and according to “precedent” principle the level 0.07 for the risk of mistaken analytical conclusion during a month can be defined as admissible.
Example 4 (Efficiency of counteraction measures against risks in pipes manufacture and use). It needs to compare efficiency of counteraction measures against risks for two different companies that are responsible for systems of pipes manufacture and use.
Approach to solution. A solution can be based on comparisons of risks to lose efficiency during 2 years and 15 years of companies operation.
Let’s the 1st system is characterized by measures: 1st measure—QMS at the supplier; 2nd measure—production quality check by all recommended kinds and methods of control within a year and improvement of times in 3 years; 3rd measure—the control by SCADA-system; 4th measure—remote sounding with preservation of efficiency within the days, carried out once a week; 5th measure—annual local inspections with preservation of efficiency within a month; 6th measure—integrated inspections of 1 times in 5 years with preservation of efficiency within a month; 7th measure—electrochemical
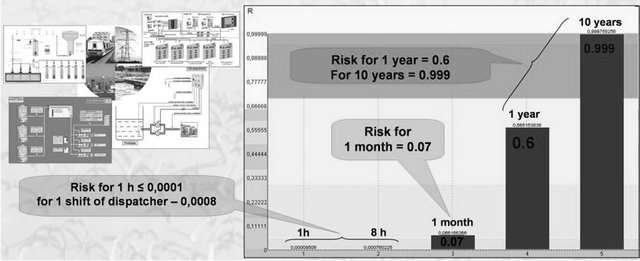
Figure 20. Results of modelling a SCADA-system.
protection of pipelines and means of telemechanics.
Let’s the 2nd system is characterized by measures: 1st measure—QMS at the supplier; 2nd measure-the control by SCADA-system; 3rd measure—helicopter inspection and regular radiographic methods of the analysis with preservation of efficiency within the days, carried out once a week; 4th measure-annual local inspections with preservation of efficiency within a month; 5th measureintegrated inspections of 1 times in 5 years with presservation of efficiency within a month; 6th measure—electrochemical protection of pipelines and means of telemechanics.
Results show high degree of efficiency for both companies: 0.11 - 0.25 during 2 years, 0.21 - 0.38 during 15 years. These results, compared with results from other spheres [7-12] considering “precedent cases” (see also examples of this paper), proves: the level of risks 0.11 for 2 years and 0.25 for the period 15 years can be recognized as “admissible”.
Example 5 (Preservation of foods quality). Prediction and optimization of system quality is demonstrated on an example of modelling processes that are peculiar for grain storage. Quality of the grain supplied on longtime storage, decreases because of influences of dangerous biological, chemical and physical factors. Let’s estimate the possible period before such moment of time when storing grain begin to loss required quality, and also expediency of introduction of continuous monitoring of grain quality.
Approach to solution is based on the use of the subsystem “Risk evaluation. Risk of uncontrollable development of situations” of the software tools “Complex for evaluating quality of production processes”. The list of dangerous factors (threats), controllable parameters and proactive actions at grain storage in real conditions is resulted in Table 1 [19].
The cleared, dry and non-contaminated grain may be stored lost-free some years. However, the insects which are present in granaries and round them, occupy grain and breed. For example, every 2 months rice weevil increases in the number at 15 - 45 times at temperature from 20˚С to 25˚С. If in batch of wheat in weight 1000 tons contamination reaches 16 bugs on 1 kg of grain, losses are expected more than 5 %. The grain polluted by wreckers and products of their vital functions (excrements, dead bodies, uric acid, etc.), becomes toxic. It cannot be used for the food purposes. Therefore we will consider security of grain from insects, believing within the example, that exactly the main dangers are from them.
Let’s a frequency of latent occurrence of critical situations during hot months is often not less than 1 time a day (i.e. every day at air temperature above 12˚С infection or the further damage of grain is possible). Our consideration: at 12˚C - 15˚С a duration of insects development (for example, weevil) is 141 - 376 days, and in a laying from 300 to 600 eggs a cycle of development is 1.5 - 2 months. In the conditions of cooling of grain below a temperature threshold of insects development (more low than 10.2˚С) their pairing, eggs putting off and development of all stages stop. Insects become inactive and almost do not eat. Long stay of insects at such temperature leads to their slow extinction. Besides, humidity maintenance at a level of 13% - 15% also promotes extinction of insects.
Thus, input for modelling is defined: frequency of latent occurrence of critical situations—from 1 time a day to 1 time a week; mean time of danger source activation—1.5 months; time between diagnostics of system integrity (analysis of temperature and humidity)—
Table 1. The list of dangerous factors, controllable parameters and proactive measures at grain storage.
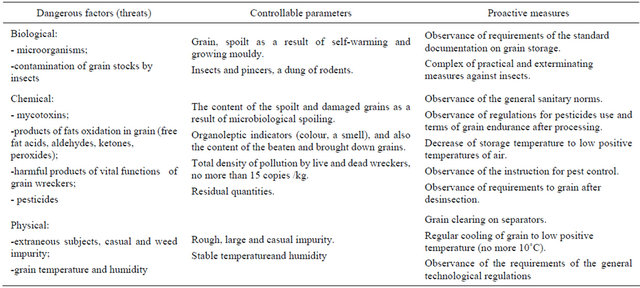

Figure 21. Comparisons of risks to lose efficiency.
1 hour; duration of diagnostic, including recovery time— 1 hour.
It is enough to predict a risk of uncontrollable development of situations with grain storage. The results of modelling for the period from 1 year to 6 years have shown the following.
If a frequency of latent occurrence of critical situations is 1 - 2 times a day, risk of uncontrollable development of situations within a year will grow from 0.28 to 0.47, and during 2-years period it can exceed 0.5—see Figure 22 left.
These results can be interpreted so: if storage conditions daily promote occurrence of insects, then for a 1 - 2 years grain quality loss is possible at the same degree as preservation of quality. Thus the next conclusion is right: the accepted conditions of grain storage in a granary leads to inadmissible damages. For prevention such danger scenario the following basic requirements [19] should be performed: a smell unusual for grain should not be felt; isolation from dampness and from penetration of subsoil waters should be provided; grain-elevator should not have unfixed vertical and horizontal joints; doors should be densely closed, floors and walls should be smooth, without cracks, roofs—in a serviceable condition; fixtures should be protected by protective caps with grids; inlet of active ventilation should be densely closed preventing a penetration of an atmospheric precipitation, etc.
Performance of these requirements conducts to decrease a frequency of latent occurrence of critical situations in granaries. Further we will answer the question-what about risk in conditions of more rare occurrences of critical situations? And, on the contrary, what the level of a frequency of latent occurrence of critical situations can be considered as admissible for granaries?
Results of modelling show: if frequency of latent occurrence of critical situations will be 1 - 2 times a week, risk of uncontrollable development of situations within a year will grow from 0.05 to 0.09, i.e. the risk decreases in 5 - 7 times! (Against the level from 0.28 to 0.47), and within 6 years risk will make 0.25 - 0.43 (it is better, than risk within a year when frequency of latent occurrence of critical situations is 1 - 2 times a day!)—see Figure 22 right. These results can be interpreted so: if storage conditions prevent from occurrence of insects with the frequency more often, than once a week, probability of preservation of grain quality within 3 - 6 years exceeds probability of quality loss in 3 - 5 times!
The results of modelling are quantitatively confirmed by results of long-term researches of the Russian Research Institute of Grain [19]. According to these researches experimental batches of grain wheat met to standard requirements of class grain has been kept within 6 years without deterioration in dry, cleared and the cooled condition. Moreover, the received values of risk can define admissible quality for grain storage. Indeed, new recommended result is: the admissble risk of uncontrollable development of situations should not exceed 0.10 for 1 year and 0.25 for 6 years of grain storage. It is comparable with the results of example 4 concerning other sphere of models applications.
Example 6 (Estimation of control and monitoring for
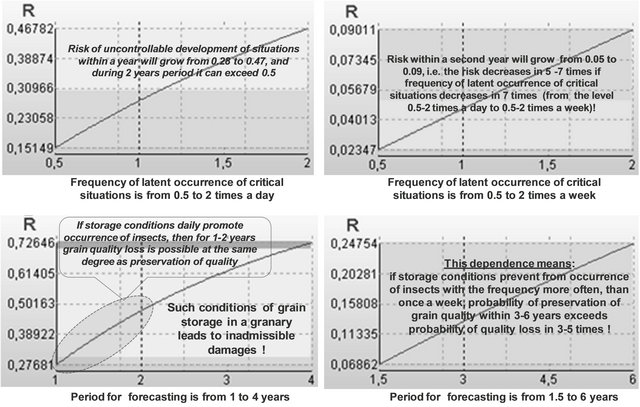
Figure 22. Some detail results of modelling and analysing.
railroad tracks). Geological, ecological, technical, mechanical, information and other factors can impact on system operation. From a general point of view these factors can be divided in the following groups: pressure on the railroad tracks from surrounding soils, lateral earth movements; soil erosion and vegetation impact (for example, in jungle area); thermal effects; slope instability of the railroad tracks right-of-way; defects or deformations in the railroad tracks; the failures of integration; mechanical bumps etc.
After an analysis of the accident statistics we can assume the main characteristics to have following values: the frequency of critical situations is 3 events per year, the mean time of situation evolution before damaging is 1 hour. The railroad tracks integrity is confirmed on the central control station once in a day while the dispatcher shifts are changed. The system integrity control includes the monitoring of information from SCADA system and other automatic facilities such as data from leak detection integrated system, intelligent electronic devices and others. Duration of integrity control is 1 hour on average. A dispatcher can misunderstand the results of monitoring of the pipeline condition and do not start actions to control critical situation opportunely as required. Taking into account dispatcher personnel training degree and automatic decision support on the statistics we assume the mean time between mistakes for the shift of monitoring to be 1 week or more. The task is to estimate the risk of uncontrolled situation evolution for a time period of 1 month, 1 year, and 10 years in give conditions.
Approach to solution. Input data are determined for evaluation the risk during a time period of 1 month (columns 1, 4), 1 year (columns 2, 5), and 10 years (columns 3, 6); for easy recoverable critical situations with time period of integrity control and recovery of 1 hour (columns 1-3) and for severe critical situations with time period of integrity control and recovery of 10 days (columns 4-6). Results of analysis see on Figure 23.
The risk of uncontrolled situation evolution is high enough (more than 0.6 during a year). To decrease the risk the mean time between mistakes for the dispatcher personnel should be increased, the time of carrying out control and repairing damages should be shorten to several days or even hours.
Example 7 (Reliability of engineering equipment for enterprise objects). Let prediction of operation reliability of computer-aided engineering equipment against usual non-automated engineering equipment is needed for the stages “Concept” and “Development”. An estimated object (for instance, the center of information processing and storage) includes power supply subsystem, an air conditioning subsystem, supported by 2 sources of an uninterrupted supply and a server, supported by 1 source of an uninterrupted supply and disks for information storage, supported also by 2 sources of an uninterrupted supply. In turn, the power supply subsystem includes the switchboards, supporting by 2 sources of an uninterrupted supply. All listed above engineering equipment is supported by 2 engine-generating installations.
Approach to solution. Within the example two subsystems are allocated (see Figure 24): subsystem 1—the city power supply formalized as basic and reserve subsystems; subsystem 2—an object fragment. It is supposed, that reliability of the object operation during given period is provided, if “AND” in 1st subsystem “AND” in 2nd subsystem there will be no power supply infringements.
The analysis of modelling shows, that, at estimated technology of the control, monitoring and integrity recovery the MTBF for computer-aided engineering
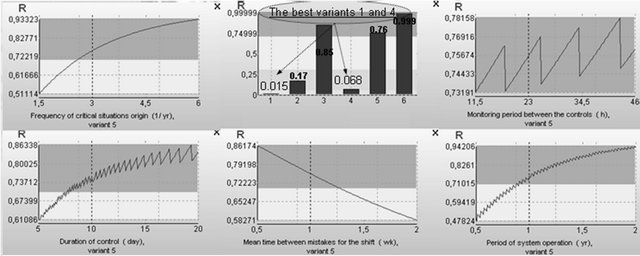
Figure 23. Dependency of the risk for 1 year as input data varying in the range of -50% +100% (variant 5: period of integrity control and recovery =10 days).
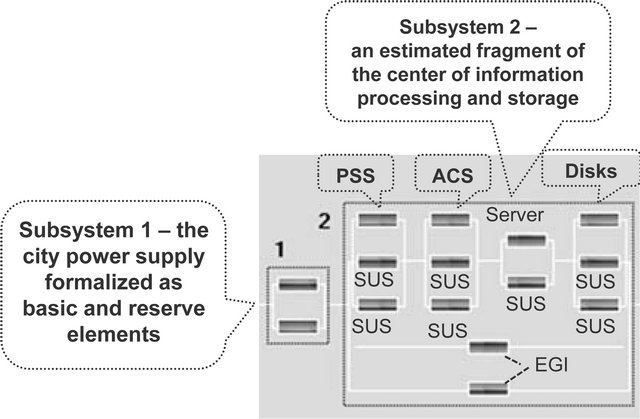
Figure 24. Logic model (PSS—power supply subsystem, ACS—air conditioning subsystem, SUS—source of an uninterrupted supply, EGI—engine-generating installation).
equipment will equal to 42219 hours. The probability of reliable object operation within a year equals to 0.828. In turn, for usual non-automated engineering equipment (there is no the monitoring implemented for computeraided engineering equipment) efficiency characterized by estimations on Figure 25.
For usual non-automated engineering equipment the MTBF will make 16,196 hours (it is at 2.44 time less, than for computer-aided engineering equipment that uses monitoring), and the probability of reliable object operation within a year equals to 0.649 (at 1.26 time less, than for computer-aided engineering equipment). Moreover, without automation for 2 years the probability of at least one failure (0.52) exceeds probability of reliable operation (0.48). Against this the probability of reliable object operation within 2 years for computer-aided engineering equipment is more at 1.5 times and will not fall low than 0.7. Attention, please, results are comparable with the results of examples 4-6 concerning other spheres of models applications.
Example 8 (the estimations of flights safety before and after 09/11) [3-4,10-11]. From the modelling point of view a flying airplane is a protected system operating in conditions of threats to its integrity during the flight. What about risk to lose complex safety before and after 09/11? And what about efficiency of additional measures for counteractions?
Approach to solution. For the existing before 09/11 safety system consisted the next main barriers: pass and inter-object modes in aerodromes and centers of air traffic control; preflight examination and control of passengers and their luggage during the registration; preflight examination before boarding; a lock-up door to the cockpit; an on-line warning about a highjacking (this barrier is critical if terrorists try to hide the fact of highjacking).
The results of modelling are the next: before 09/11 in Russia and the USA the risk to lose complex safety against trained terrorists estimated about 0.47 - 0.48, i.e. every second prepared terrorist act comes true. The bottlenecks were a weak protection of a cockpit and absence of active opposing measures on board an airplane (see Figure 26).
How the level of the safety may be increased by measures, listed on Figure 27? As in a cabin may be accomplices able to repeat the high-jacking after an additional preparing there must be provided ways of compulsory keeping of suspicious passengers on their seats till the emergency landing. All the listed measures seem to be effective but how effective are they quantitatively? It is impossible to make a variety of natural experiments. We use the offered mathematical models.
Analysis of modelling results has shown, that after implementation of the described measures the integrated risk to lose complex safety of flight during 5 hours of flight against terrorist threats is equal to 0.000004. And if duration of threats will be increased to 5 days the risk raises from 0.000004 to 0.002. The last can be commented by the next interpretation: safety will be achieved in 998 cases from thousand hypothetical terrorist attacks. Even taking into account an essential error of initial scenarios and preconditions it is an obvious indicator of high efficiency of additional safety measures according to “precedent” principle! Still it is not a victory. It is clear that the first failures will make terrorists to analyze their causes and find new bottlenecks of the safety system thus continuing the counteraction. This counteraction will be ended when there are taken proactive measures which effectiveness is based on modelling.
Example 9 (Protection against an unauthorized access). We will consider the approach to an estimation of IS protection against an unauthorized access (UAA) and information confidentiality. A resources protection from UAA is a sequence of barriers. If a violator overcomes these barriers he gets access to IS information and/or software resources. In the Table 2 there are shown supposed characteristics of barriers and mean time of their overcoming by a specially trained violator (real values of such characteristics may be drawn as a result of actual tests or use of other models). It is required to estimate IS protection against UAA.
Approach to solution. The analysis of computed dependencies (see Figure 28 left) shows the next. The barriers 1-3 will be overcome with the probability equal to 0.63. However, monthly password changing for barriers 4-6 allows to increase the protection probability from 0.37 to 0.94 but the level of IS protection (the first six barriers) is still low. The introducing of 7-9 barriers is useless because it does not practically increase the level of IS protection. The use of cryptography allows to increase the level of IS protection to 0.999. This is probability for all time of IS operation (i.e. about 20 - 30 years). It is possible to establish a conclusion, that with the use
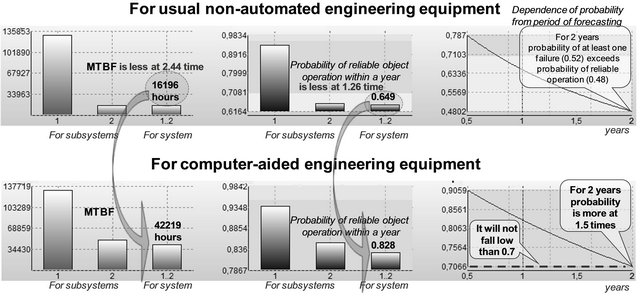
Figure 25. Results of modelling engineering equipment.

Figure 26. Risk to lose complex safety against terrorists.
of cryptographic devices the achieved protection level exceeds similar level of reliability and safety for processes from examples above. But according to “precedent” principle this level of protection can’t be recommended as high for every cases.
Let’s look on example condition more widely. The violator is interested in certain IS resources during a given period of time. This period is called the period of objective confidentiality. Let’s information confidentiality should be provided within 7 days. Figure 28 (right) shows how this period influences on protection: in comparison with the results above the use of the first 5 barriers provides confidentiality during 7 days on the level 0.98 which is more higher than protection by the 9 barriers
Table 2. Input for modeling.
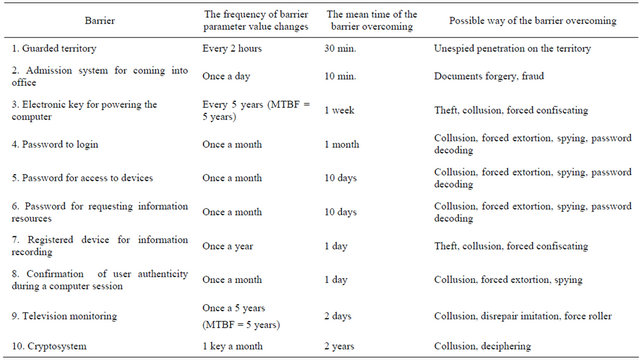
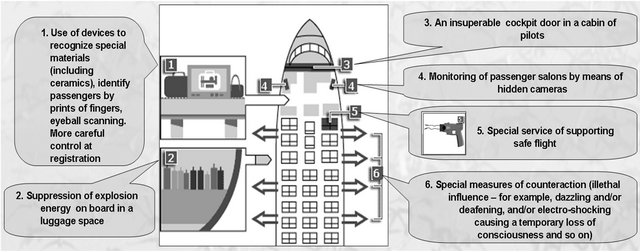
Figure 27. Additional measures for counteractions.
(0.946—see Figure 28 left); the use of all the 10 barriers provides the required confidentiality on the level 0.99997. It eliminates the customer’s risk in providing system protection. It explains the role of a considered period of objective confidentiality. Its consideration allows to understand, that real protection of resources during 7 days is essentially higher—0.99997 against 0.999!
And what about safety of complex system, including head subsystem and two used subsystems 2 and 3 (see Figure 29)? A frequency of threats is no more than 1 time at hour, average time for system recovery is no more than 30 minutes. It is required to predict quantitatively the level of safety within month and year system operation and to reveal its bottlenecks.
Results of modelling are reflected on Figure 30. With monitoring and control within a month all barriers are overcame with probability 0.9, and within a year—with probability 0.43. Without monitoring and control these probabilities decrease to level 0.83 and 0.29 accordingly. Monitoring is ineffective for example conditions.
Following recommendations are obvious: for safe system operation it is expedient, that all subsystems are
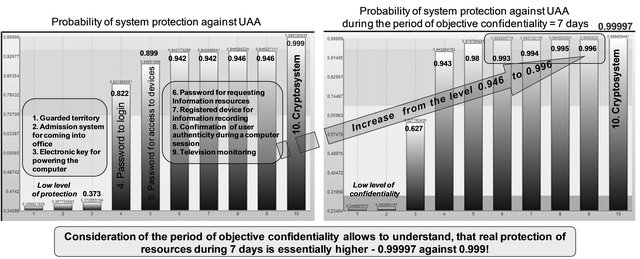
Figure 28. Comparison of protection levels.
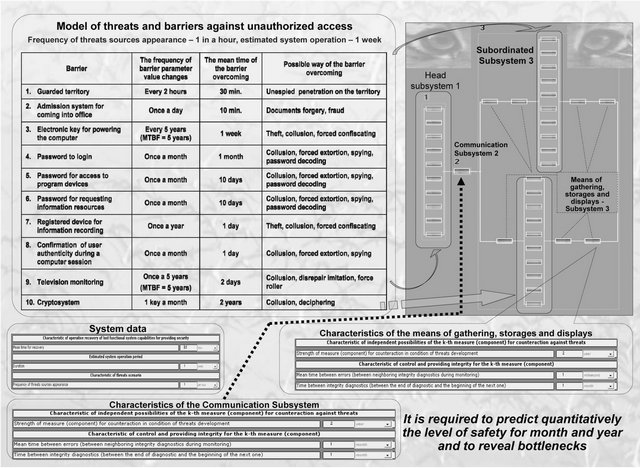
Figure 29. Input for modelling complex safety.
strong equally. The technology of safety maintenance in emergency case is necessary. Recommendations are supported by the offered mathematical models.
Example 10 (Predicts of risks for complex multipurpose system). Let’s consider a hypothetic multipurpose system which formally composed from functional system—similar, for instance, to system of non-destroying control, pipes manufacture and use or foods presservation (from examples 2, 4 and 5), gathering and data processing system (similar to SCADA-system from example 3), system of control and monitoring for railroad tracks (from example 7), system of engineering equipment for enterprise object (from example 7), system of protection against UAA (from example 9). “The human factor” is considered in the parameters of control, monitoring and integrity recovery measures for corresponding elements. It is supposed, that a required integrity of system is not lost, if during given time a required integrity is not lost by all subsystems: “AND” by 1st subsystem, “AND” by 2nd subsystem, ××דAND” by the last 6th subsystem (the logic illustrated by Figure 31). It is required to predict risk to lose integrity during years of system operation and estimate the measures of risk management, including the periodic control and, where it is possible, continuous monitoring of integrity of components.
Approach to solution. The input for subsystems 1-6 is described in examples 2-7, 9. The general results of complex prediction of risk are reflected by Figure 32. Analysis of results shows, that integrated risk to lose system integrity of system within operational 2 years is 0.27. And for subsystems 1-6 this risk differs from 0.01 to 0.12.
The dependence of integrated risk on time of predicttion (from 1 to 4 years) is reflected by Figure 33. Analysis of results shows, that the integrated risk to lose system integrity is changing from 0.11 to 0.67 (with using of measures of the periodic control and where it is possible, monitoring of elements operation).
The general logic proposition is right for a given period of prediction: as a rule, the risk to lose system integrity increases in depending on increasing time period. But there are the features demanding a logic explanation. Serrated and nonmonotonic character of dependence on Figure 33 is explained by the periodic diagnostics of elements, monitoring presence or absence and their quantitative values (see subsection 3.2). Let’s remind: for every monitored element a penetration of a danger source and its activation is possible only if an operator-monitor makes an error but a dangerous influence occurs if the danger is activated before the next diagnostic. Otherwise the source will be detected and neutralized. Immediately after element diagnostic the risk decreases because dur-
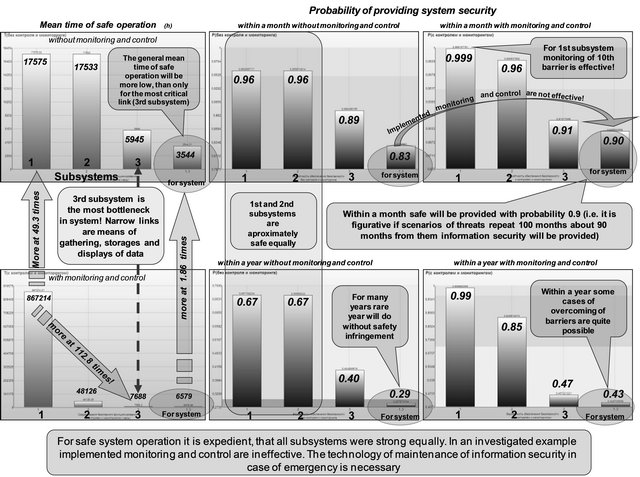
Figure 30. The results of prediction and analysis.
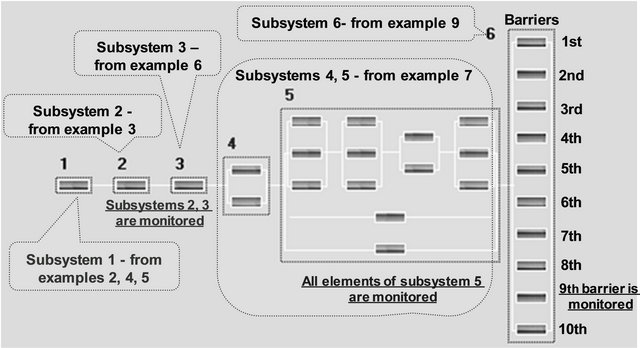
Figure 31. The results of prediction and analysis.
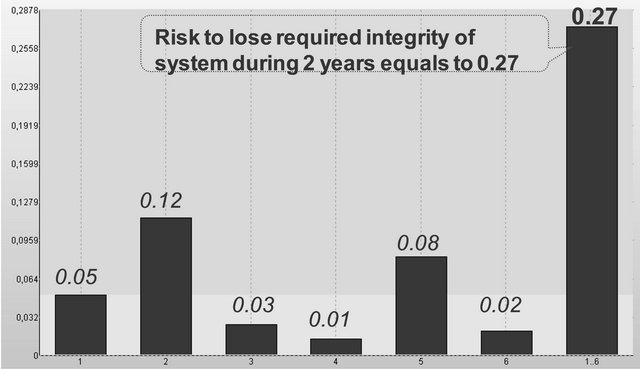
Figure 32. Risk to lose integrity for multipurpose system.
ing diagnostic all dangers are detected and neutralized and at the beginning of a period after diagnostic dangerous influences don’t have enough time to accumulate and be activated. Nonetheless, there is a lack of protection accumulated for the previous full periods that’s why the risk doesn’t decrease to 0 for every element. By the middle of a period between neighboring diagnostics there is an increase of the calculated risk because new danger sources can begin to influence. Moreover, for the longer period of prediction monitoring possibilities are weaken, thereby the moment of operator error comes nearer. And, if on timeline the following diagnostic does not come yet, risk increases. Similar effects paradoxes are explained— for example, that risk to lose integrity during 2.96 years (0.58) is more, than risk during more long time—3.12 years, 58 days longer (0.57). One more effect of modelling: if to do prediction not for 2.04 years, and for 2 weeks longer (2.08 years, i.e. 2% longer period) the expected risk to lose system integrity increases from 0.28 to 0.36. This is higher on 28%! These results of modelling

Figure 33. Integrated risk to lose integrity of system within operational 1 - 4 years.
should serve as a substantiation for development of predicting counter-measures to optimize quality and risks by criterias of Section 4. Indeed, on the basis of a rational choice of parametres for technologies of the control, monitoring and integrity recovery an optimization of processes offered in the work is possible.
6. Conclusion
The presented models, methods and software tools, allowing to predict quality and risks according to system requirements of standards, are real levers to analyze processes in system life cycle. The criteria for optimization are maximization of a prize (profit, a degree of quality or safety, etc.) at limits on expenses or minimization of expenses at limits on a comprehensible degree of quality and-or safety or their combination. As a result of adequate modelling more deep and extend knowledge of system operation allows the customer to formulate well-reasoned system requirements. And it is rational to developer to execute them without excessive expenses of resources, and to the user—as much as possible effectively to implement in practice the incorporated power of system. The investigated practical examples demonstrated models possibilities to use principle of “precedent cases” for definition the justified levels of acceptable quality and admissible risks. For complex systems the proposed results help to answer the questions “What rational measures should lead to estimated effect without waste expenses, when, by which controllable and uncontrollable conditions and costs?” and allow to go “from a pragmatical filtration of information to generation of the proved ideas and effective decisions”. The effect from implementation in system life cycle is commensurable with expenses for system creation.
REFERENCES
- A. I. Kostogryzov, A. V. Petuhov and A. M. Scherbina, “Foundations of Evaluation, Providing and Increasing Output Information Quality for Automatized System,” Voorushenie. Politica. Konversija, Moscow, 1994.
- A. I. Kostogryzov, “Software Tools Complex for Evaluation of Information Systems Operation Quality (CEISOQ),” Proceedings of the 34th Annual Event of the Government Electronics and Information Association (GEIA), Engineering and Technical Management Symposium, Dallas, 2000, pp.63-70.
- M. M. Bezkorovainy, A. I. Kostogryzov and V. M. Lvov, “Modelling Software Complex for Evaluation of Information Systems Operation Quality CEISOQ. 150 Problems of Analysis and Synthesis and Examples for Their Solutions,” 2nd Edition, Voorushenie. Politica. Konversija, Moscow, 2002.
- A. I. Kostogryzov and G. A. Nistratov, “Standardization, Mathematical Modelling, Rational Management and Certification in the Field of System and Software Engineering (80 Standards, 100 Mathematical Models, 35 Software Tools, More than 50 Practical Examples),” 2nd Edition, Voorushenie. Politica. Konversija, Moscow, 2005
- A. I. Kostogryzov and G. A. Nistratov “100 Mathematical Models of System Processes According International Standards Requirements,” Transaction of the XXV International Seminar on Stability Problems for the Stochastic Models, Maiority, 20-24 September 2005, pp. 196-201
- A. Kostogryzov, G. Nistratov and N. Kleshchev, “Mathematical Models and Software Tools to Support an Assessment of Standard System Processes,” Proceedings of the 6th International SPICE Conference on Process Assessment and Improvement (SPICE-2006), Luxembourg, 2006, pp. 63-68
- A. Kostogryzov and G. Nistratov, “Mathematical Models and Software Tools for Analyzing System Quality and Risks According to Standard Requirements,” Proceedings of the 6th International Scientific School, Modelling and Analysis of Safety and Risk in Complex Systems (MASR), Saint-Petersburg, RUSSIA, 4-8 July, 2006, pp. 155-163.
- A. I. Kostogryzov and P. V. Stepanov, “Innovative Management of Quality and Risks in Systems Life Cycle,” Voorushenie. Politica. Konversija, Moscow, 2008.
- L. I. Grigoriev, V. Ya. Kershenbaum and A. I. Kostogryzov, “System Foundations of the Management of Competitiveness in Oil And Gas Complex,” National Institute of Oil and Gas, Moscow, 2010.
- A. Kostogryzov, V. Krylov, A. Nistratov, G. Nistratov, V. Popov and P. Stepanov, “Mathematical Models and Applicable Technologies to Predict, Analyze and Optimize Quality and Risks for Complex Systems,” Proceedings of the 1st International Conference on Transportation Information and Safety (ICTIS 2011), 30 June-2 July 2011, Wuhan, pp. 845-854.
- A. Kostogryzov, G. Nistratov and A. Nistratov, “Some Applicable Methods to Analyze and Optimize System Processes in Quality Management,” In: T. Aized, Ed., Total Quality Management and Six Sigma, InTech, 2012, pp. 127-196, http://www.intechopen.com/books/total-quality-management-and-six-sigma/some-applicable-methods-to-analyze-and-optimize-system-processes-in-quality-management
- A. Kostogryzov G. Nistratov and A. Nistratov, “Applicable Technologies to Predict, Analyze and Optimize Reliability and Risks for Complex Systems,” Journal of Polish Safety and Reliability Association, SSARS, Vol. 3, No. 1, 2012, pp. 1-14.
- W. Feller, “An Introduction to Probability Theory and Its Applications,” Wiley, Hoboken, 1971.
- B. V. Gnedenko, et al., “Priority Queueing Systems,” Мoscow State University, Moscow, 1973.
- G. P. Klimov, “Probability Theory and Mathematical Statistics,” Мoscow State University, Moscow, 1983.
- J. Martin, “System Analysis for Data Transmission,” IBM System Research Institute, Prentice Hall, Inc., Englewood Cliffs, 1972.
- L. Kleinrock, “Queueing Systems,” John Wiley & Sons, New York, 1976.
- V. F. Matweev and V. G. Ushakov, “Queuing Systems”, Мoscow State University, Moscow, 1984.
- L. I. Machikhina, L. V. Alexeeva and L. S. L’vova, “Scientific Foundations of Food Grain Safety during Storage and Processing,” DeLi Print, Moscow, 2007.
NOTES
1Note. System integrity is defined as such system state when system purposes are achieved with the required quality.
2Note. It is supposed that used diagnostic tools allow to provide necessary system integrity recovery after revealing of danger sources penetration into a system or consequences of influences.

