Int. J. Communications, Network and System Sciences, 2010, 3, 213-252
doi:10.4236/ijcns.2010.33031 blished Online March 2010 (http://www.SciRP.org/journal/ijcns/). Pu
Advances in MIMO Techniques for Mobile
Communications—A Survey
Farhan Khalid, Joachim Speidel
Institute of Telecommunications, University of Stuttgart, Stuttgart, Germany
Received December 2, 2009; revised January 5, 2010; accepted Febr uary 6, 2010
Abstract
This paper provides a comprehensive overview of critical developments in the field of multiple-input multi-
ple-output (MIMO) wireless communication systems. The state of the art in single-user MIMO (SU-MIMO)
and multiuser MIMO (MU-MIMO) communications is presented, highlighting the key aspects of these
technologies. Both open-loop and closed-loop SU-MIMO systems are discussed in this paper with particular
emphasis on the data rate maximization aspect of MIMO. A detailed review of various MU-MIMO uplink
and downlink techniques then follows, clarifying the underlying concepts and emphasizing the importance of
MU-MIMO in cellular communication systems. This paper also touches upon the topic of MU-MIMO ca-
pacity as well as the promising convex optimization approaches to MIMO system design.
Keywords: Multiple-Input Multiple-Output (MIMO), Multiuser MIMO, Wireless Communications, Beam-
forming, Diversity, Precoding, Capacity
1. Introduction
Multiple-input multiple-output (MIMO) wireless systems
employ multiple transmit and receive antennas to in-
crease the transmission data rate through spatial multi-
plexing or to improve system reliability in terms of bit
error rate (BER) performance using space-time codes
(STCs) for diversity maximization [1]. MIMO systems
exploit multipath propagation to achieve these benefits,
without the expense of additional bandwidth. More re-
cent MIMO techniques like the geometric mean decom-
position (GMD) technique proposed in [2] aim at com-
bining the diversity and data rate maximization aspects
of MIMO in an optimal manner. These advantages make
MIMO a very attractive and promising option for future
mobile communication systems especially when com-
bined with the benefits of orthogonal frequency-division
multiplexing (OFDM) [3,4].
The capacity of an M  N single-user MIMO (SU-
MIMO) system with M transmit and N receive antennas,
in terms of the spectral efficiency i.e. bits per second per
Hz, is given by [1]
2
log detH
N
CM
 


 


IHH



(1)
where H is the N  M MIMO channel matrix and ρ is the
signal to noise ratio (SNR) at any receive antenna. Equa-
tion (1) assumes that the M information sources are un-
correlated and have equal power. Expressed in terms of
the eigenvalues, Equation (1) can be written as [1]
2
1
log 1
m
i
i
CM









(2)
where λi represent the nonzero eigenvalues of HHH or
HHH for N ≤ M and M < N respectively and m = min(M,
N). Therefore, MIMO systems are capable of achieving
several-fold increase in system capacity as compared to
single-input single-output (SISO) systems by transmit-
ting on the spatial eigenmodes of the MIMO channel.
Equation (2) also shows that the performance of
MIMO systems is dependent on the channel eigenvalues.
Very low eigenvalues indicate weak transmission chan-
nels which may make it difficult to recover the informa-
tion from the received signals. Optimal power allocation
based on the water-filling algorithm can be used to maxi-
mize the system capacity subject to a to tal transmit pow-
er constraint. Water-filling provides substantial capacity
gain when the eigenvalue spread, i.e., the cond ition num-
ber λmax/λmin is sufficiently large.
The MIMO concept becomes even more attractive in
multiuser scenarios where the network capacity can be
increased by simultaneously accommodating several users

F. KHALID ET AL. 214
without the expense of valuable frequency resources.
This paper is arranged as follows: Section 2 provides
an overview of the current wireless standards which sup-
port MIMO technologies. Sections 3 and 4 include de-
tailed discussion and performance analysis of various
important SU-MIMO and multiuser MIMO (MU-MIMO)
techniques respectively that are proposed for the next
generation wireless communication systems. In-depth
description of several MU-MIMO uplink and downlink
schemes is given in Section 4 followed by a brief discus-
sion of the MU-MIMO capacity. Section 5 provides an
overview of convex optimization which has become an
important tool for designing optimal MIMO beamform-
ing systems. Section 6 concludes this work and identifies
the areas for future research.
2. Current Implementation Status
There has been a lot of research on MIMO systems and
techniques. MIMO-O FDM WLAN products based on the
IEEE 802.11n standard are already available. The IEEE
802.16 wireless MAN standard known as WiMAX also
includes MIMO features. Fixed WiMAX services are
being offered by operators worldwide. Mobile WiMAX
networks based on 802.16e are also being deployed
while 802.16m is under development. IEEE 802.20 mo-
bile broadband wireless access (MBWA) standard is also
being formulated which will have complete support for
mobility including high-speed mobile users e.g., on train
networks. For other applications like cellular mobile com-
munications which supports both voice and data traffic,
MIMO systems are yet to be deployed. However, the
3GPP’s long term evolution (LTE) is under development
and adopts MIMO-OFDM, orthogonal frequency-divi-
sion multiple access (OFDMA) and single-carrier frequ-
ency-division multiple access (SC-FDMA) transmission
schemes. The following text presents a more detailed dis-
cussion of the various technical aspects of these stand-
ards and technologies.
2.1. IEEE 802.11n Wi-Fi
The IEEE 802.11n WLAN standard incorporates MIMO-
OFDM as a compulsory feature to enhance data rate. Ini-
tial target was to achieve data rates in excess of 100 Mb/s
[5]. However, current WLAN devices based on 802.11n
Draft 2.0 a re capable of ac hi eving thro ug h put u p t o 30 0 Mb/s
utilizing two spatial streams in a 40 MHz channel in the
5 GHz band [6].
Initially, there were two main proposals one form the
WWiSE consortium and the other from the TGnSync
consortium competing for adoption by the IEEE 802.11
TGn. However, another proposal by the Enhanced Wire-
less Consortium (EWC) was finally accepted as the first
draft for IEEE 802.11n [7].
The IEEE 802.11n standard proposes the use of the
legacy 20 MHz channel and also an optional 40 MHz
channel. The available modulation schemes include
BPSK, QPSK, 16-QAM and 64-QAM [5,6]. Convolu-
tional coding with different code rates is specified and
use of low-density parity-check (LDPC) codes is also
supported [5,8]. The MIMO techniques adopted include
both spatial multiplexing and diversity techniques.
Open-loop MIMO (OL-MIMO) techniques which do not
require channel state information (CSI) at the transmitter
seem to have been preferred [9]. Non-iterative linear
minimum mean square error (LMMSE) detection has
primarily been considered so as to minimize the com-
plexity associated with MIMO detection while ensuring
reasonably good performance [10].
Spatial spreading mentioned in [11] is an open-loop
MIMO spatial multiplexing technique where multiple
data streams are transmitted such that the diversity is
maximized for each of the streams. The MIMO diversity
techniques introduced in the standard include space-time
block coding (STBC) and cyclic shift diversity (CSD)
which extend the range and reception of 802.11n devices.
In addition, conventional receiver spatial diversity tech-
niques like maximum ratio combining (MRC) are also
specified. Transmit beamforming is also specified as an
optional feature [6]. The Cisco Aironet 1250 series ac-
cess point based on 802.11 n draft 2.0 supports op en-loop
transmit beamforming [12].
802.11n draft 2.0 specifies a maximum of 4 spatial
streams per channel. Thus, a maximum throughput of
600 Mb/s can be achieved by using 4 spatial streams in a
40 MHz channel. In addition to spatial multiplexing and
doubled channel bandwidth, more efficient OFDM with
shorter guard interval (GI) and new medium access con-
trol (MAC) layer enhancements (e.g. closed-loop rate
adaptation [13]) have also contributed to the increased
throughput of 802.11n [6].
2.2. IEEE 802.16 WiMAX
The IEEE 802.16 worldwide interoperability for micro-
wave access (WiMAX) is a recently developed wireless
MAN standard that employs MIMO spatial multiplexing
and diversity techniques. In addition to fixed WiMAX,
the IEEE 802.16e Mobile WiMAX standard has also
been developed and was approved in December 2005
[14]. Fixed WiMAX networks have already been de-
ployed around the world and Mobile WiMAX deploy-
ments have also started.
802.16e-2005 is basically an amendment to the
802.16-2004 stand ard for fixed WiMAX with addition of
new features to support mobility. 802.16e specifies the
2–6 GHz frequency band for mobile applications and the
2–11 GHz band for fixed applications (The single-carrier
WirelessMAN-SC PHY specification for fixed wireless

F. KHALID ET AL. 215
access however specifies the 10–66 GHz frequency band
[15].). It also specifies a license-exempt band between
5–6 GHz. A cellular network structure is specified with
support for handoff s and mobile users moving at vehicu-
lar speeds are also supported, thus enabling mobile wire-
less internet access [14,16].
In addition to single carrier transmission, the standard
specifies OFDM transmission scheme with 128, 256, 512,
1024 or 2048 subc arrier s. Both TDD and FDD duplex ing
is specified while the multiplexing/multiple access
schemes include OFDMA in addition to burst TDM/
TDMA. However, scalable OFDMA is specified in all
mobile WiMAX profiles as the physical layer multiple
access technique. The various channel bandwidths speci-
fied in the standard include 1.25, 1.75, 3.5, 5, 7, 10, 8.75,
10, 14 and 15 MHz. WiMAX supports adaptive modula-
tion and coding schemes. The supported modulation
schemes include BPSK, QPSK, 16-QAM and 64-QAM
[14,16]. Optional 256-QAM support is provided in the
WirelessMAN-SCa PHY [15]. Convolutional codes at
rate1/2, 2/3, 3/4 or 5/6 are specified as mandatory for
both uplink and downlink. In addition, convolutional
turbo codes, repetition codes, LDPC and concatenated
Reed-Solomon convolutional code (RS-CC ) are specified
as optional. The supported data rates range from 1 Mb/s
to 75 Mb/s [14,16].
IEEE 802.16e supports both open-loop and closed-
loop MIMO. Open-loop MIMO techniques include spa-
tial multiplexing (SM) and space-time coding (STC)
[14,17,18]. 802.16e includes support for up to four spa-
tial streams and therefore a maximum of 4  4 MIMO
configuration [14,18]. STC is based on the Alamouti
scheme (also STBC) and is also called space-time trans-
mit diversity (STTD). It is an optional feature and may
be used to provide higher order transmit diversity on the
downlink [14].
In closed-loop MIMO, full or partial CSI is available
at the transmitter through feedback. Eigenvector steering
is employed to approach full capacity of the MIMO
channel and water filling can be used to maximize
throughput by allocating power in an optimal manner
[9,19]. IEEE 802.16e supports closed-loop MIMO pre-
coding for SM and also closed-loop STC [14,17]. How-
ever, closed-loop MIMO is not yet su ppor ted in the latest
WiMAX Forum Wave 2 profiles [18]. Another MIMO
mode called “collaborative spatial multiplexing” is also
specified where two subscriber stations (SS), each hav-
ing a single antenna, use the same subchannel for uplink
transmission in order to increase the throughput [14,15,
17,20].
The adaptive antenna systems (AAS) supported in
802.16e also include closed-loop adaptive beamforming,
which us es feed back fro m the S S to the b ase sta tion (BS )
to optimize the down link transmission [14,15,18].
IEEE 802.16 Task Group m (TGm) has also been set
up to develop the IEEE 802.16m standard which will
enable interoperability between WiMAX and 3GPP’s
Long Term Evolution (LTE) standard for next genera-
tion mobile communications [21,22]. 802.16m is ex-
pected to support high-speed mobile wireless access (up
to 350 km/h) and peak data rates of over 300 Mb/s us-
ing 4  4 MIMO [22].
2.3. IEEE 802.20 MBWA
The IEEE 802.20 working group was established to
draft the IEEE 802.20 Mobile Broadband Wireless Ac-
cess (MBWA) standard which is also nicknamed as
MobileFi. IEEE 802.20 proposes a complete cellular
structure and is designed and optimized for mobile data
services at speeds up to 250 km/h. However, it can also
support voice services due to very low transmission
latency of 10–30 ms (better than the 25–40 ms for
802.16e). User data rates in excess of 1 Mb/s can be
supported at 250 km/h [23–25].
MBWA is designed to operate in the licensed bands
below 3.5 GHz [24,25]. 2.5 MHz to 20 MHz of up-
link/downlink transmission bandwidth can be allocated
per cell [25]. For a bandwidth of 5 MHz, peak aggregate
data rate of around 16 Mb/s can be supported in the
downlink [23,24] which obviously would be much
greater for higher bandwidths.
The transmission scheme is based on OFDM, with
OFDMA used for downlink transmission while both
OFDMA and code-division multiple access (CDMA) are
specified for the uplink. Rotational OFDM is specified as
an optional scheme. The standard supports both FDD and
TDD operation. The supported modulation schemes in-
clude QPSK, 8-PSK, 16-QAM and 64-QAM. Support of
hierarchical (layered) modulation involving the superpo-
sition of two modulation schemes is also included for
broadcast and multicast services. The specified FEC
coding schemes include convolutional codes, turbo codes
and LDPC codes [25 ].
Various MIMO schemes are also supported. STTD
(based on STBC) and SM are specified for SU-MIMO
transmission, utilizing up to 4 transmit antennas. STTD
is particularly important for high speed mobile access.
Two different stream multiplexing schemes namely sin-
gle codeword (SCW) and multiple codeword (MCW)
may be employed for MIMO transmission. These sche-
mes also support closed-loop MIMO downlink transmis-
sion with rank adaptation. Both schemes utilize linear
precoding at the BS for transmit beamforming based on
the feedback of a suitable precoding matrix from the user
equipment’s (UE’s) codebook to the BS. The standard
also supports MU-MIMO or space-division multiple ac-
cess (SDMA) transmission in the downlink which in-
volves multiuser scheduling and precoding at the BS
depending upon the feedback of the preferred precoding
matrix index and differential channel quality indicator
Co pyright © 2010 SciRes. IJCNS

F. KHALID ET AL. 216
(CQI) reports from the UEs [25].
The IEEE 802.20 standard was supposed to be avail-
able in 2006 but was delayed du e to lack of support from
some of the key vendors and the political turmoil within
the standards forum [23]. However, it was finally ap-
proved in June 2008 and made available by the end of
August 2008 [25].
2.4. 3GPP LTE
The 3rd generation partnership project’s (3GPP) long
term evolution (LTE) project is aimed at developing a
new mobile communications standard for gradual migra-
tion from 3G to 4G. LTE physical layer is almost near
completion. It specifies an OFDM based system with
support for MIMO. Downlink transmission is based on
OFDMA while SC-FDMA is used for the uplink due to
its low PAPR characteristics. It supports both TDD and
FDD operation. A packet switching architecture is speci-
fied for LTE [26,27].
LTE supports scalable bandwidths of 1.25, 2.5, 5, 10
and 20 MHz. Peak data rates of 100 Mb/s and 50 Mb/s
are supported in the downlink and the uplink respectively,
in 20 MHz channel. The standard specifies full perform-
ance within a cell up to 5 km radius and slight degrada-
tion from 5–30 km. Operation up to 100 km may be pos-
sible. It also supports high-speed mobility with high per-
formance at speeds up to 120 km/h while the E-UTRAN
(Evolved Universal Terrestrial Radio Access Network
i.e., LTE’s RAN) should be able to maintain the con nec-
tion up to 350 km/h, or even up to 500 km/h. LTE also
specifies very low latency operation with control plane
(C-plane) latency of < 50-100ms and user p lane (U-plane)
latency of < 10 ms [27,28].
The single-user MIMO techniques supported include
STBC and SM. Closed-loop multiple codeword (MCW)
SM with codebook based precoding and with support for
cyclic delay diversity (CDD) is specified. A maximum of
two downlink spatial streams are specified. LTE also
supports MU-MIMO in the downlink as well as in the
uplink. Closed-loop transmit diversity using MIMO
beamforming with rank adaptation is also supported . The
supported antenna configurations for the downlink in-
clude 4  2, 2  2, 1  2 and 1  1 whereas 1  2 and 1  1
configurations are supported in the uplink [27,29,30].
However, multiple UE antennas in the uplink may be
supported in future.
3. Single-User MIMO Techniques
Various open-loop and closed-loop SU-MIMO tech-
niques are discussed in the following text along with
performance analysis and compariso n. Some of the tech-
niques mentioned herein have already been adopted for
the current standards while other advanced methods are
likely candidates for the next generation wireless sys-
tems.
3.1. V-BLAST
The vertical Bell Laboratories Layered Space-Time (V-
BLAST) [31] is one of the very first open-loop spatial
multiplexing MIMO systems which has been practically
demonstrated to achieve much higher spectral efficien-
cies than SISO systems, in rich scattering environments.
In V-BLAST, a single data stream is demultiplexed into
multiple substreams which are mapped on to symbols
and then transmitted through multiple antennas. Inter-
substream coding is not employed in V-BLAST, how-
ever channel coding can be applied to the individual sub-
streams for reduction of bit error rate (BER). CSI in a
V-BLAST system is available at the receiver only by
means of channel estimation. Figure 1 shows the simple
block di agram of a V-BLAST system.
V-BLAST detection can be accomplished by using
linear detectors like zero-forcing (Z F) or mini mum me an
square error (MMSE) detector along with symbol can-
cellation (also called successive interference cancella-
tion). Symbol cancellation is a nonlinear technique
which enhances the detection performance by subtracting
the detected components of the transmit vector from the
received symbol vector [31]. This technique, however, is
prone to error propagation.
The QR decomposition of the MIMO channel matrix
can be used to represent the ZF nulling in V-BLAST
[2]. Assuming a frequency-flat fading MIMO channel,
the corresponding sampled baseband received signal for
a V-BLAST system with M transmit and N receive an-
tennas (M ≤ N) is therefore given by
H




yHxn
QRxn (3)
where Q is an N  M unitary matrix with orthonormal
columns, R is a M  M upper triangular matrix, x is the
transmitted signal and n represents the noise vector. The
Figure 1. V-BLAST system block diagram [31].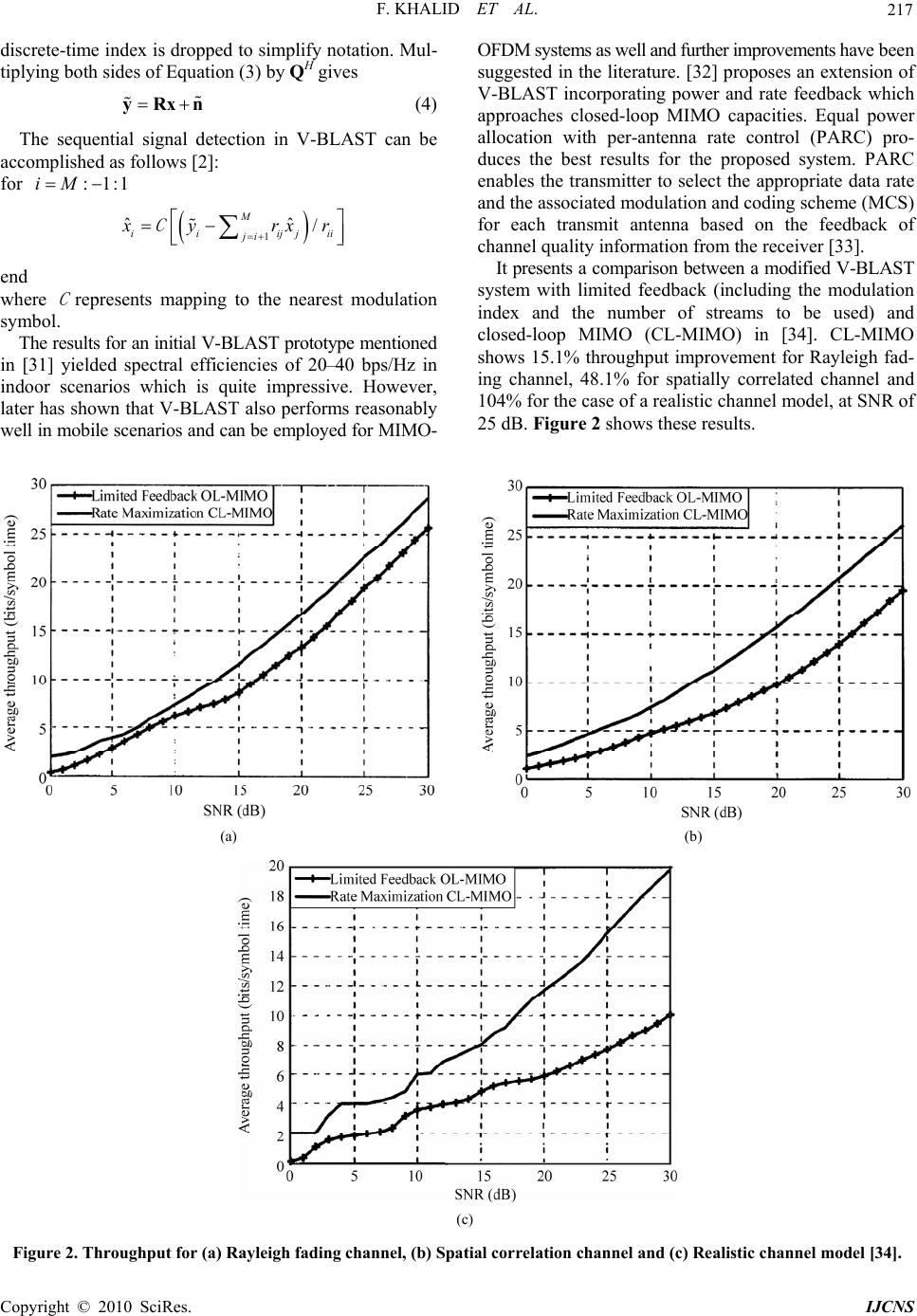

F. KHALID ET AL. 217
ii
discrete-time index is dropped to simplify notation. Mul-
tiplying both sides of Equation (3) by QH gives
yRxn
  (4)
The sequential signal detection in V-BLAST can be
accomplished as follows [2]:
for :1:1iM

1
ˆˆ
/
M
ii ijj
ji
x
yrx







C r



end
where represents mapping to the nearest modulation
symbol.
C
The results for an initial V-BLAST prototype mentioned
in [31] yielded spectral efficiencies of 20–40 bps/Hz in
indoor scenarios which is quite impressive. However,
later has shown that V-BLAST also performs reasonably
well in mobile scenarios and can be employed for MIMO-
OFDM system s as well and furt her impro vements ha ve been
suggested in the literature. [32] p roposes an extension of
V-BLAST incorporating power and rate feedback which
approaches closed-loop MIMO capacities. Equal power
allocation with per-antenna rate control (PARC) pro-
duces the best results for the proposed system. PARC
enables the transmitter to select the appropriate data rate
and the associated modulation and coding scheme (MCS)
for each transmit antenna based on the feedback of
channel quality information from the receiver [33].
It presents a comparison between a mod ified V-BLAST
system with limited feedback (including the modulation
index and the number of streams to be used) and
closed-loop MIMO (CL-MIMO) in [34]. CL-MIMO
shows 15.1% throughput improvement for Rayleigh fad-
ing channel, 48.1% for spatially correlated channel and
104% for the case of a realistic channel model, at SNR of
25 dB. Figure 2 shows these results.
(a) (b)
(c)
Figure 2. Throughput for (a) Rayleigh fading channel, (b) Spatial cor rel ation channe l and (c ) Realistic c hannel model [34].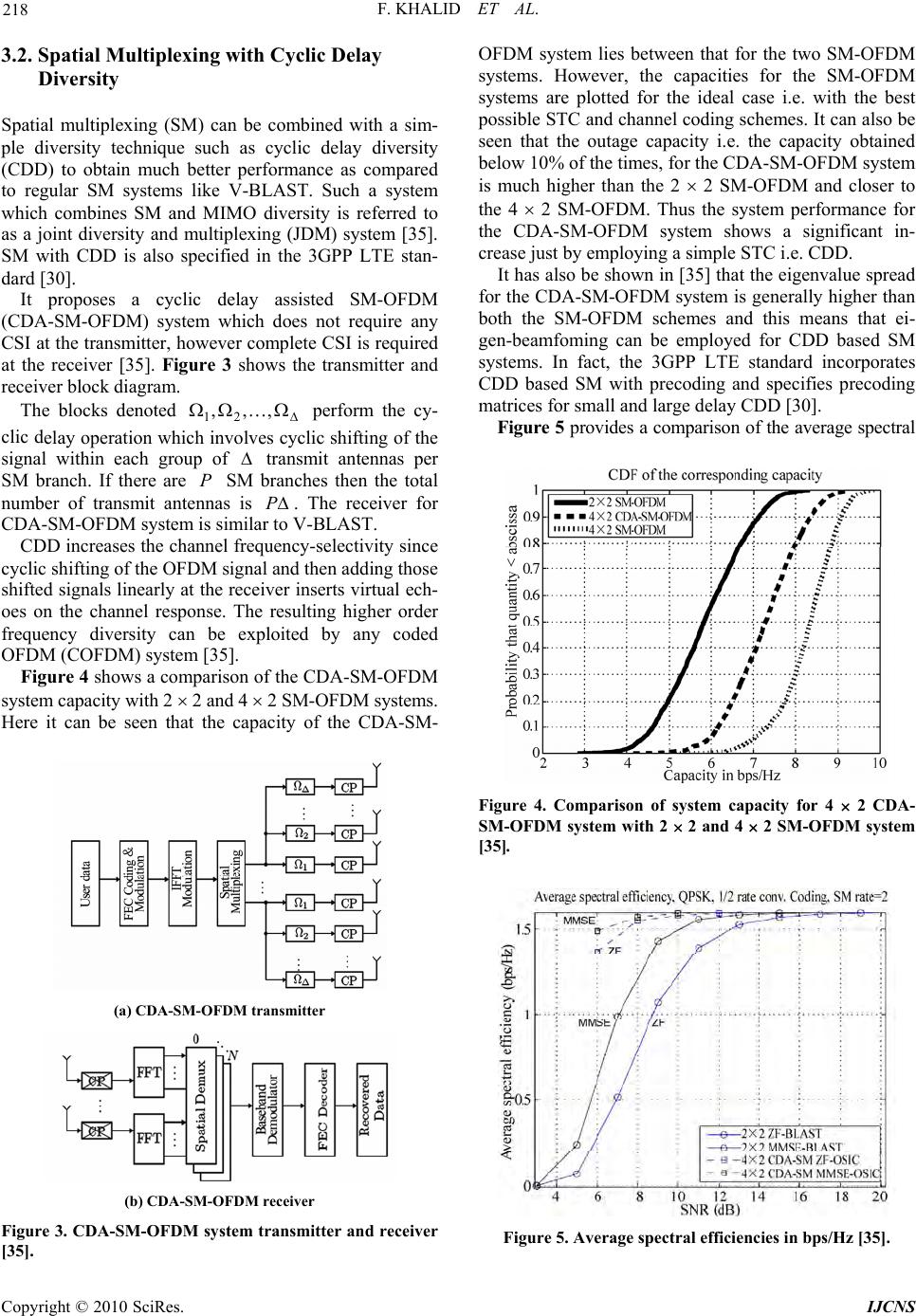

F. KHALID ET AL. 218
3.2. Spatial Multiplexing with Cyclic Delay
Diversity
Spatial multiplexing (SM) can be combined with a sim-
ple diversity technique such as cyclic delay diversity
(CDD) to obtain much better performance as compared
to regular SM systems like V-BLAST. Such a system
which combines SM and MIMO diversity is referred to
as a joint diversity and multiplexing (JDM) system [35].
SM with CDD is also specified in the 3GPP LTE stan-
dard [30].
It proposes a cyclic delay assisted SM-OFDM
(CDA-SM-OFDM) system which does not require any
CSI at the transmitter, however complete CSI is required
at the receiver [35]. Figure 3 shows the transmitter and
receiver block diagram.
The blocks denoted perform the cy-
clic delay operation which involve s cyclic shifting of the
signal within each group of

 ,,, 21

transmit antennas per
SM branch. If there are
P
SM branches then the total
number of transmit antennas is 
P
. The receiver for
CDA-SM-OFDM system is similar to V-BLAST.
CDD increases the channel frequency-selectivity since
cyclic shifting of the OFDM signal and then adding those
shifted signals linearly at the receiver inserts virtual ech-
oes on the channel response. The resulting higher order
frequency diversity can be exploited by any coded
OFDM (COFDM) system [35].
Figure 4 shows a comparison of the CDA-SM-OFDM
system capacity with 2  2 and 4  2 SM-OFDM systems.
Here it can be seen that the capacity of the CDA-SM-
(a) CDA-SM-OFDM transmitter
(b) CDA-SM-OFDM receiver
Figure 3. CDA-SM-OFDM system transmitter and receiver
[35].
OFDM system lies between that for the two SM-OFDM
systems. However, the capacities for the SM-OFDM
systems are plotted for the ideal case i.e. with the best
possible STC and channel coding schemes. It can also be
seen that the outage capacity i.e. the capacity obtained
below 10% of the times, for the CDA-SM-OFDM system
is much higher than the 2  2 SM-OFDM and closer to
the 4  2 SM-OFDM. Thus the system performance for
the CDA-SM-OFDM system shows a significant in-
crease just by employing a simple STC i.e. CDD.
It has also be shown in [35] that the eigenvalue spread
for the CDA-SM-OFDM system is generally higher than
both the SM-OFDM schemes and this means that ei-
gen-beamfoming can be employed for CDD based SM
systems. In fact, the 3GPP LTE standard incorporates
CDD based SM with precoding and specifies precoding
matrices for small and large delay CDD [30].
Figure 5 provides a comparison of the average spectral
Figure 4. Comparison of system capacity for 4  2 CDA-
SM-OFDM system with 2  2 and 4  2 SM-OFDM system
[35].
Figure 5. Average spectral efficiencies in bps/Hz [35].

F. KHALID ET AL. 219
efficiencies of 2  2 SM-OFDM systems and 4  2
CDA-SM-OFDM systems for a low user mobility indoor
WLAN scenario. Here it can be seen that the 4  2
CDA-SM-OFDM systems provide much higher spectral
efficiencies at low SNR values.
3.3. Singular Value Decomposition Based MIMO
Precoding
Singular value decomposition (SVD) based MIMO pre-
coding is a closed-loop MIMO scheme where the pre-
coding filter at the transmitter is designed by taking the
SVD of the MIMO channel matrix H.
[36] provides an analysis of the classical SVD based
MIMO precoding scheme, SVD based precoding with
ZF equalization, SVD based precoding with MMSE
equalization and also an improved SVD based precoding
technique. All of these schemes are analyzed with realis-
tic channel knowledge at the transmitter. Figure 6 shows
the block diagram of the SVD based MIMO-OFDM
transmitter and receiver.
3.3.1. Classical SVD Precoding and Equalization
In SVD based techniques, the channel matrix of a
MIMO system with transmit antennas and
receive antennas, is decomposed as
H
t
Nr N
H
HUDV (5)
where and are unitary matrices
while
rt
NN
U
tt
NN
tt
NN
V

D is a diagonal matrix consisting of the
ordered s i ngular v alues .
i
d
The classical SVD approach utilizes matrix for
precoding at the transmitter. The columns of matrix
are the eigenvectors of
V
i
v
V
H
HH . The received signal is
given by

rHVsn (6)
where is a vector of information symbols
si
s
and
is the noise vector correspond ing to an additive white
Gaussian noise (AWGN) process with variance
n2
n

for
each element. At the receiver, matrix
H
U is employed
for equalization and the detected signal vector is given
by
HH H
HH H
H
 


y
UrUHVs Un
UUDVVs Un
yDsUn
(7)
Each individual received signal can be written as
iii
ydsn

i

 (8)
(a)
(b)
Figure 6. SVD based MIMO-OFDM system (a) Transmitter and (b) Receiver [36].
Co pyright © 2010 SciRes. IJCNS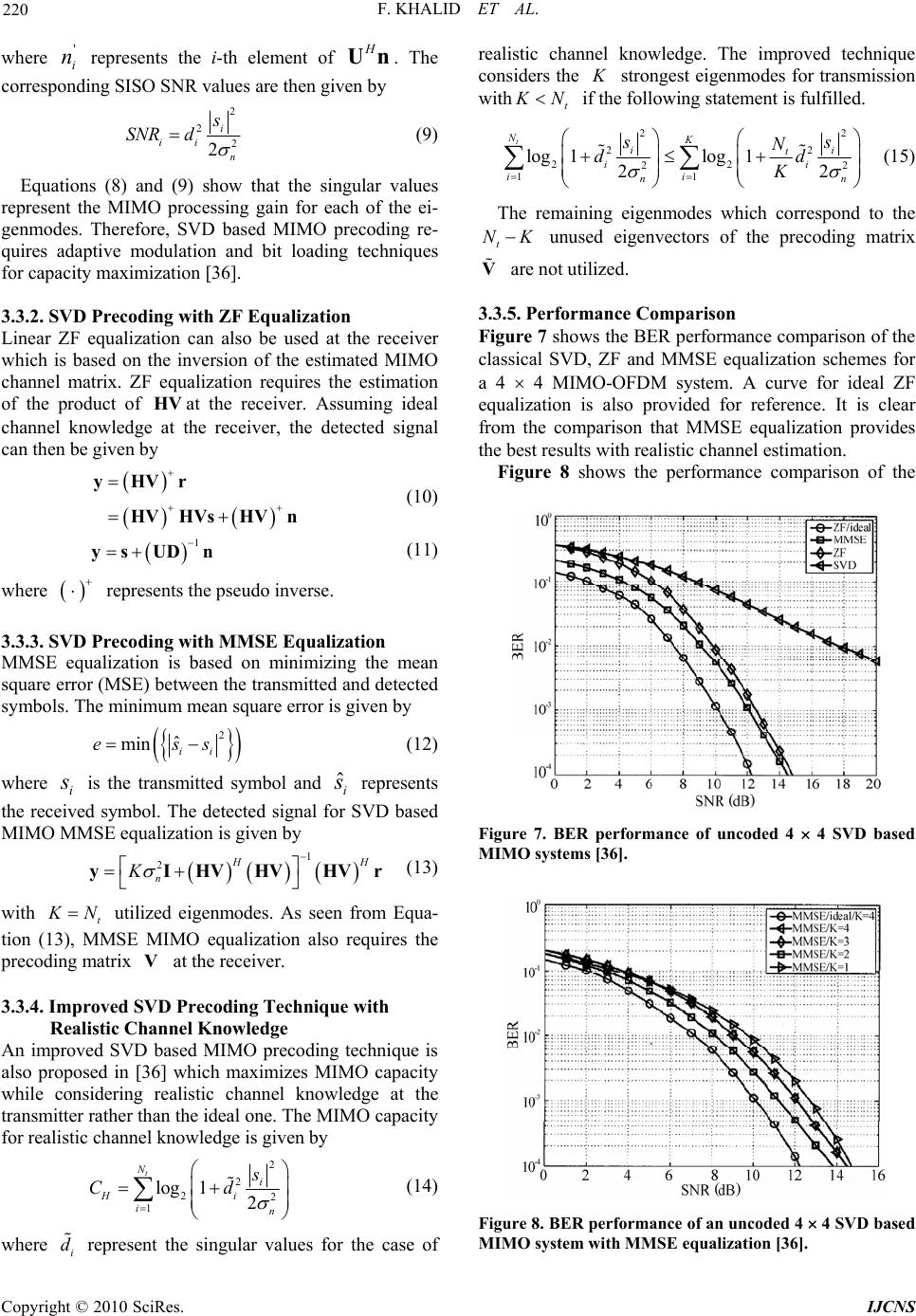

F. KHALID ET AL. 220
where represents the i-th element of
'
i
n
H
Un. The
corresponding SISO SNR values are then given by
2
2
2
2
i
ii
n
s
SNR d

 (9)
Equations (8) and (9) show that the singular values
represent the MIMO processing gain for each of the ei-
genmodes. Therefore, SVD based MIMO precoding re-
quires adaptive modulation and bit loading techniques
for capacity maximization [36].
3.3.2. SVD Precoding with ZF Equalization
Linear ZF equalization can also be used at the receiver
which is based on the inversion of the estimated MIMO
channel matrix. ZF equalization requires the estimation
of the product of at the receiver. Assuming ideal
channel knowledge at the receiver, the detected signal
can then be given b y
HV

 




yHVr
HVHVsHV n

(10)

1
ys UDn
(11)
where represents the pseudo inverse.



3.3.3. SVD Precoding with MMSE Equalization
MMSE equalization is based on minimizing the mean
square error (MSE) between the transmitted and detected
symbols. The minimum mean square error is given by


2
ˆ min ii ess

H
(12)
where is the transmitted symbol and represents
the received symbol. The detected signal for SVD based
MIMO MMSE equalization is given by
i
sˆi s

1
2H
n
K 




y
IHV HVHVr
(13)
with t
K
N utilized eigenmodes. As seen from Equa-
tion (13), MMSE MIMO equalization also requires the
precoding matrix at the receiver. V
3.3.4. Improved SVD Precoding Technique with
Realistic Channel Knowledge
An improved SVD based MIMO precoding technique is
also proposed in [36] which maximizes MIMO capacity
while considering realistic channel knowledge at the
transmitter rather than the ideal one. The MIMO capacity
for realistic channel knowledge is given by
2
2
22
1
log 12
t
Ni
Hi
in
s
Cd








(14)
where represent the singular values for the case of
realistic channel knowledge. The improved technique
considers the
i
d

K
strongest eigenmodes for transmission
with t
K
N

if the following statement is fulfilled.
22
22
22
22
11
log 1
t
Nlog 1
22
K
ii
t
ii
ii
nn
ss
N
dd
K



 
 
 
 
 


(15)
The remaining eigenmodes which correspond to the
t
NK

unused eigenvectors of the precoding matrix
are not utilized. V

3.3.5. Performance Comparison
Figure 7 shows the BER performance comparison of the
classical SVD, ZF and MMSE equalization schemes for
a 4  4 MIMO-OFDM system. A curve for ideal ZF
equalization is also provided for reference. It is clear
from the comparison that MMSE equalization provides
the best results with realistic channel estimation.
Figure 8 shows the performance comparison of the
Figure 7. BER performance of uncoded 4  4 SVD based
MIMO systems [36].
Figure 8. BER performance of an uncoded 4  4 SVD based
MIMO system with MMSE equalization [36].

F. KHALID ET AL. 221
MMSE equalization scheme with different values of
(utilized eigenmodes) for an uncoded 4  4 MIMO sys-
tem with realistic channel knowledge at the transmitter.
The BER curve for the case of ideal channel knowledge
is also provided. The MMSE equalization scheme pro-
vides the best performance for = 2 utilized eigen-
modes selected according to Equation (15).
K
K
3.4. Geometric Mean Decomposition (GMD)
Based MIMO
GMD based MIMO [2] is also a closed-loop joint trans-
ceiver design scheme which aims at optimally combining
the benefits of MIMO diversity and spatial multiplexing.
This technique utilizes the GMD of the MIMO channel
matrix for precoder and equalizer design when the CSI is
available at both the transmitter and the receiver. It is
also applicable to MIMO-OFDM systems.
GMD calculation algorithm in [2] starts from the SVD
of the channel matrix which is given according to
Equation (5) H
H
HUDV
The GMD is then given by
H
H
RR
H
HUURVV
QRP (16)
where and are semi-unitary matrices, P being
the linear precoder at the transmitter.
Q P
K
K

R is an
upper triangular matrix whose diagonal elements are the
geometric mean of the
K
nonzero singular values of
. The GMD scheme thus decomposes the MIMO
channel into identical parallel subchannels which makes
the symbol constellation selection and the overall system
design much simpler. GMD can also be seen as an ex-
tended QR decomposition.
H
GMD MIMO can be implemented with the V-BLAST
receiver and also with the zero-forcing dirty paper pre-
coder (ZFDP). The V-BLAST technique has been dis-
cussed earlier in the text. The ZFDP technique also in-
volves sequential nulling and cancellation but at the
transmitter and utilizes CSI at the transmitter only.
The ZFDP scheme combines QR decomposition and
“dirty paper” precoding. The QR decomposition for
ZFDP is given by
HHQR
 (17)
The sampled baseband received signal is then given by
HH
yRQxn
  (18)
Substituting we have xQx

H
yRxn
 (19)
Let be the transmitted symbol vector then
should satisfy
1K
s
x



diag H Rs Rx

 (20)
where the left-hand side represents the element-wise
multiplication of the diagonal elements of with the
elements of . The solution to Equation (20) is then
R

s


1diag
H
xR Rs

 (21)
The ZFDP scheme, unlike V-BLAST, does not suffer
from the error propagation problem. However, due to the
matrix inversion in Equation (21) the norm of can be
significantly amplified resulting in increased transmitter
power consumption. This problem can be resolved by
using the Tomlinson-Harashima precoder to restrict the
transmit signal level within acceptable limits [2].
x

3.4.1. Combining GMD with V-BLAST and ZFDP
The GMD-VBLAST scheme can be implemented begin-
ning with the GMD of the channel matrix,
H
HQRP.
The information symbol vector is then encoded by
the linear precoder resulting in the transmit signal
s
P

xPs. The resulting signal at the receiver is then given
by


y
QRsn (22)
which can be decoded simply by using the V-BLAST
receiver. GMD-ZFDP scheme can be also be imple-
mented in a similar way. The resulting
K
independent
and identical subchannels are given by
; 1,,
iHii
yxni   K (23)
where
H

represent the subchannel gain and are in fact
the identical diagonal elements of the matrix [2]. R
3.4.2. Performance
Some simulation results from [2] depicting the perform-
ance of GMD based MIMO schemes are presented in the
following text, assuming independent identically distrib-
uted (i.i.d) Rayleigh flat fading channels. Figure 9 shows
a comparison of the capacity of GMD-MIMO with oth er
schemes for 4  4 MIMO configuration. The informed
transmitter (IT) curve corresponds to the Shannon chan-
nel capacity when CSI is available at both the transmitter
and the receiver while the uninformed transmitter (UT)
curve corresponds to the channel capacity when CSI is
not available at the transmitter. MTM and MMD are both
linear precoder design schemes for linear transceivers.
MTM is based on the minimization of the trace of the
MSE matrix while MMD minimizes the maximum di-
agonal elements of the MSE matrix resulting in near-
optimal performance. Clearly, GMD outperforms both
MTM and MMD at high SNR and approaches optimal
capacity. The capacity loss of GMD at low SNR is due to
Co pyright © 2010 SciRes. IJCNS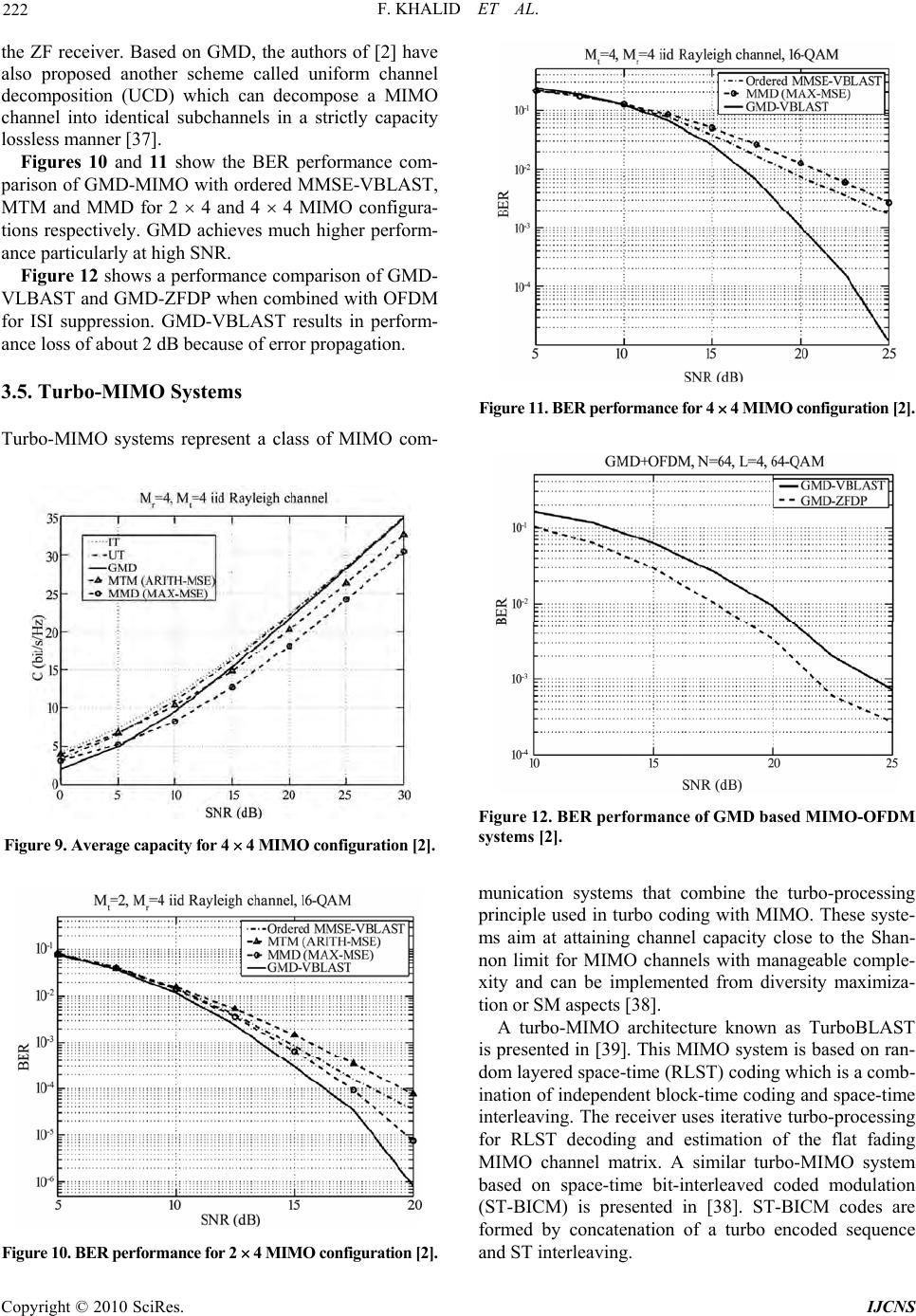

F. KHALID ET AL. 222
the ZF receiver. Based on GMD, the authors of [2] have
also proposed another scheme called uniform channel
decomposition (UCD) which can decompose a MIMO
channel into identical subchannels in a strictly capacity
lossless manner [37].
Figures 10 and 11 show the BER performance com-
parison of GMD-MIMO with ordered MMSE-VBLAST,
MTM and MMD for 2  4 and 4  4 MIMO configura-
tions respectively. GMD achieves much higher perform-
ance particularly at high SNR.
Figure 12 shows a performance comparison of GMD-
VLBAST and GMD-ZFDP when combined with OFDM
for ISI suppression. GMD-VBLAST results in perform-
ance loss of about 2 dB because of error propagation.
3.5. Turbo-MIMO Systems
Turbo-MIMO systems represent a class of MIMO com-
Figure 9. Average capacity for 4  4 MI MO configuration [2].
Figure 10. BER performan ce for 2  4 MI MO co nfigurat ion [2].
Figure 11. BER performan ce for 4  4 MI MO co nfigurat ion [2].
Figure 12. BER performance of GMD based MIMO-OFDM
systems [2].
munication systems that combine the turbo-processing
principle used in turbo coding with MIMO. These syste-
ms aim at attaining channel capacity close to the Shan-
non limit for MIMO channels with manageable comple-
xity and can be implemented from diversity maximiza-
tion or SM aspects [38].
A turbo-MIMO architecture known as TurboBLAST
is presented in [39]. This MIMO system is based on ran-
dom layered space-time (RLST) coding which is a comb-
ination of independent block-time coding and space-time
interleaving. The receiver uses iterative turbo-processing
for RLST decoding and estimation of the flat fading
MIMO channel matrix. A similar turbo-MIMO system
based on space-time bit-interleaved coded modulation
(ST-BICM) is presented in [38]. ST-BICM codes are
formed by concatenation of a turbo encoded sequence
and ST interleaving.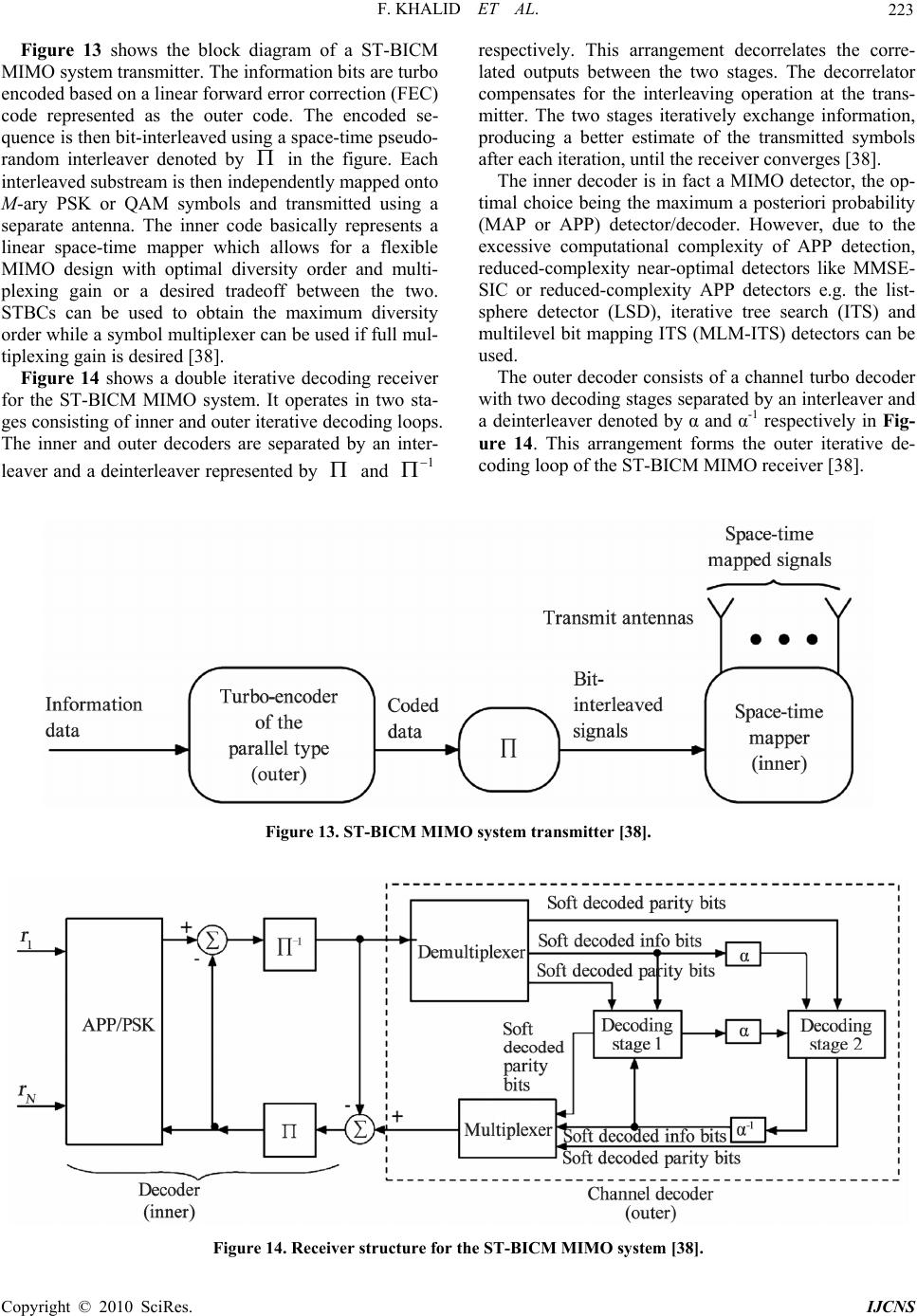

F. KHALID ET AL. 223
Figure 13 shows the block diagram of a ST-BICM
MIMO system transmitter. The information bits are turbo
encoded based on a linear forward error correction (FEC)
code represented as the outer code. The encoded se-
quence is then bit-interleaved using a space-time pseudo-
random interleaver denoted by in the figure. Each
interleaved substream is then independently mapped onto
M-ary PSK or QAM symbols and transmitted using a
separate antenna. The inner code basically represents a
linear space-time mapper which allows for a flexible
MIMO design with optimal diversity order and multi-
plexing gain or a desired tradeoff between the two.
STBCs can be used to obtain the maximum diversity
order while a symbol multiplexer can be used if full mul-
tiplexing gain is desired [38].

Figure 14 shows a double iterative decoding receiver
for the ST-BICM MIMO system. It operates in two sta-
ges consisting of inner and outer iterative decoding loops.
The inner and outer decoders are separated by an inter-
leaver and a deinterleaver represented by and 1


respectively. This arrangement decorrelates the corre-
lated outputs between the two stages. The decorrelator
compensates for the interleaving operation at the trans-
mitter. The two stages iteratively exchange information,
producing a better estimate of the transmitted symbols
after each iteration, until the receiver converges [38].
The inner decoder is in fact a MIMO detector, the op-
timal choice being the maximum a posteriori probability
(MAP or APP) detector/decoder. However, due to the
excessive computational complexity of APP detection,
reduced-complexity near-optimal detectors like MMSE-
SIC or reduced-complexity APP detectors e.g. the list-
sphere detector (LSD), iterative tree search (ITS) and
multilevel bit mapping ITS (MLM-ITS) detectors can be
used.
The outer decoder consists of a channel turbo decoder
with two decoding stages separated by an interleaver and
a deinterleaver denoted by α and α-1 respectively in Fig-
ure 14. This arrangement forms the outer iterative de-
coding loop of the ST-BICM MIMO receiver [38].
Figure 13. ST-BICM MIMO system transmitter [38].
Figure 14. Receiver structure for the ST-BICM MIMO system [38].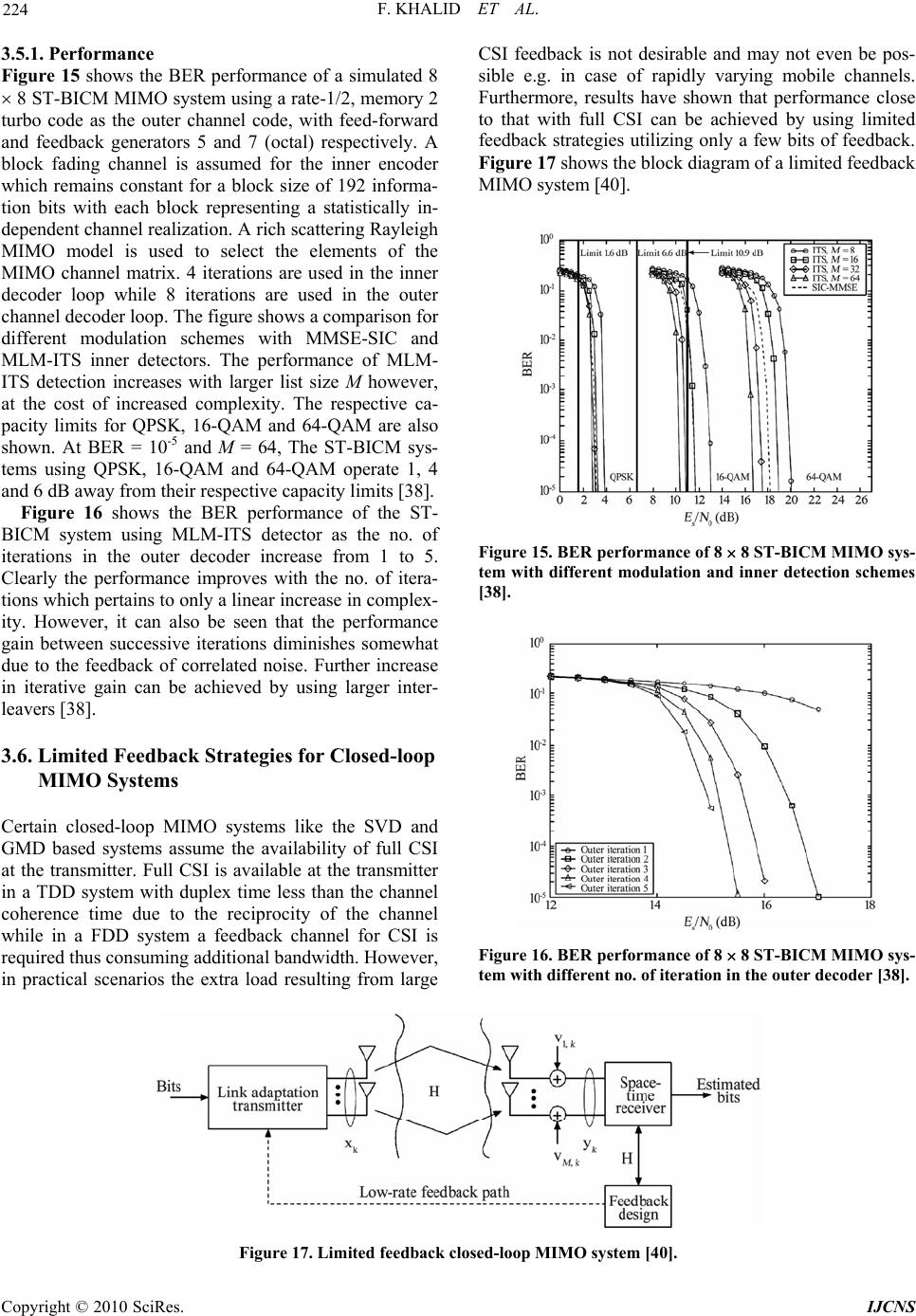

F. KHALID ET AL. 224
3.5.1. Performance
Figure 15 shows the BER performance of a simulated 8
 8 ST-BICM MIMO system using a rate-1/2, memory 2
turbo code as the outer channel code, with feed-forward
and feedback generators 5 and 7 (octal) respectively. A
block fading channel is assumed for the inner encoder
which remains constant for a block size of 192 informa-
tion bits with each block representing a statistically in-
dependent channel realization. A rich scattering Rayleigh
MIMO model is used to select the elements of the
MIMO channel matrix. 4 iterations are used in the inner
decoder loop while 8 iterations are used in the outer
channel decoder loop. The figure shows a comparison for
different modulation schemes with MMSE-SIC and
MLM-ITS inner detectors. The performance of MLM-
ITS detection increases with larger list size M however,
at the cost of increased complexity. The respective ca-
pacity limits for QPSK, 16-QAM and 64-QAM are also
shown. At BER = 10-5 and M = 64, The ST-BICM sys-
tems using QPSK, 16-QAM and 64-QAM operate 1, 4
and 6 dB away from their respective capacity limits [38].
Figure 16 shows the BER performance of the ST-
BICM system using MLM-ITS detector as the no. of
iterations in the outer decoder increase from 1 to 5.
Clearly the performance improves with the no. of itera-
tions which pertains to only a linear increase in complex-
ity. However, it can also be seen that the performance
gain between successive iterations diminishes somewhat
due to the feedback of correlated noise. Further increase
in iterative gain can be achieved by using larger inter-
leavers [38].
3.6. Limited Feedback Strategies for Closed-loop
MIMO Systems
Certain closed-loop MIMO systems like the SVD and
GMD based systems assume the availability of full CSI
at the transmitter. Full CSI is available at the transmitter
in a TDD system with duplex time less than the channel
coherence time due to the reciprocity of the channel
while in a FDD system a feedback channel for CSI is
required thus consuming additional bandwidth. However,
in practical scenarios the extra load resulting from large
CSI feedback is not desirable and may not even be pos-
sible e.g. in case of rapidly varying mobile channels.
Furthermore, results have shown that performance close
to that with full CSI can be achieved by using limited
feedback strategies utilizing only a few bits of feedback.
Figure 17 shows the block diagram of a limited feedback
MIMO system [40].
Figure 15. BER performance of 8  8 ST-BICM MIMO sys-
tem with different modulation and inner detection schemes
[38].
Figure 16. BER performance of 8  8 ST-BICM MIMO sys-
tem with different no. of iteration in the outer decoder [38].
Figure 17. Limited feedback closed-loop MIMO system [40].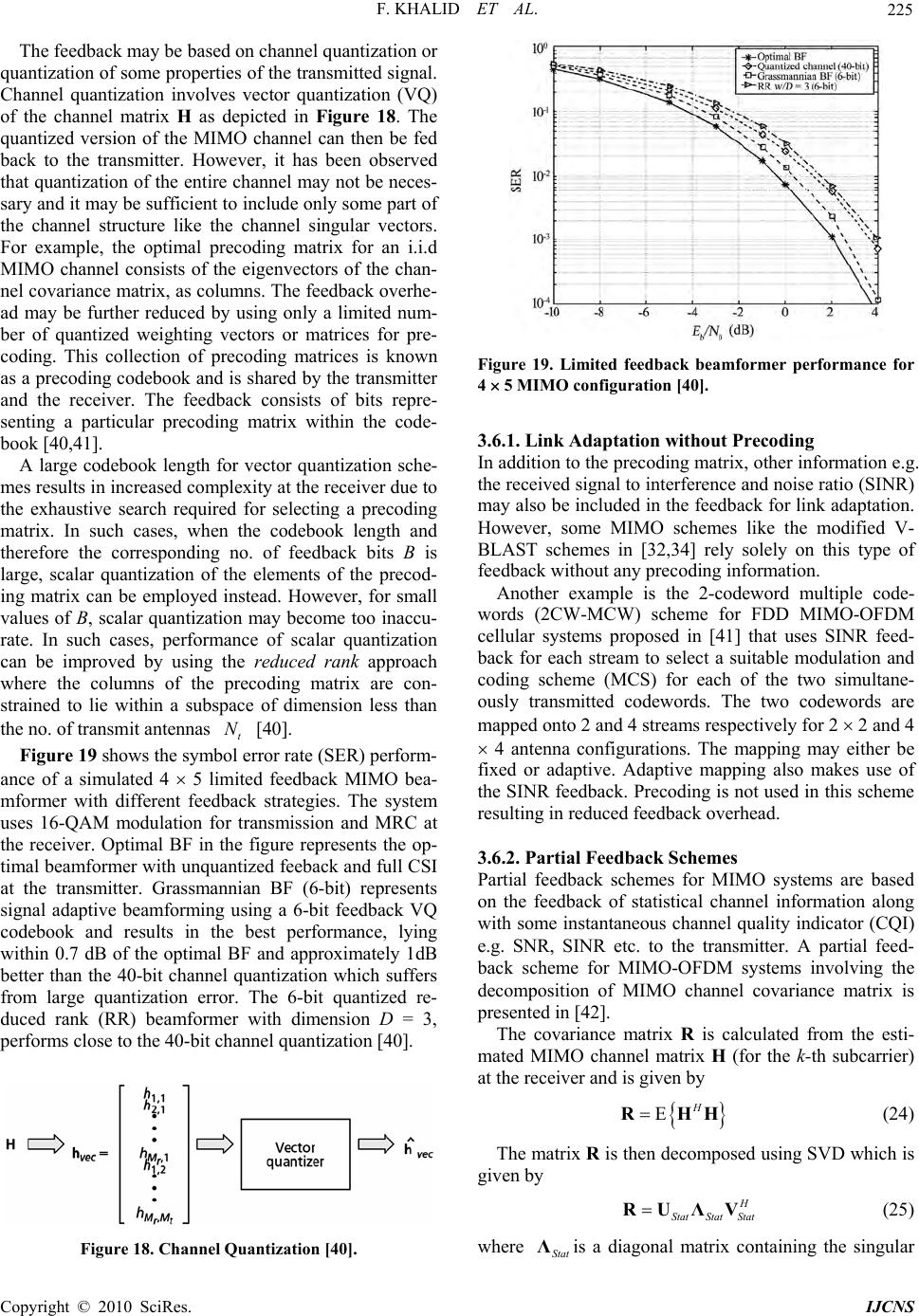

F. KHALID ET AL. 225
The feedback may be based on channel quantization or
quantization of some properties of the transmitted signal.
Channel quantization involves vector quantization (VQ)
of the channel matrix H as depicted in Figure 18. The
quantized version of the MIMO channel can then be fed
back to the transmitter. However, it has been observed
that quantization of the entire channel may not be neces-
sary and it may be sufficient to include only some part of
the channel structure like the channel singular vectors.
For example, the optimal precoding matrix for an i.i.d
MIMO channel consists of the eigenvectors of the chan-
nel covariance matrix, as columns. The feedback overhe-
ad may be further reduced by using only a limited num-
ber of quantized weighting vectors or matrices for pre-
coding. This collection of precoding matrices is known
as a precoding codebook and is shared by the transmitter
and the receiver. The feedback consists of bits repre-
senting a particular precoding matrix within the code-
book [40,41].
A large codebook length for vector quantization sche-
mes results in increased complexity at the receiver due to
the exhaustive search required for selecting a precoding
matrix. In such cases, when the codebook length and
therefore the corresponding no. of feedback bits B is
large, scalar quantization of the elements of the precod-
ing matrix can be employed instead. However, for small
values of B, scalar quantization may become too inaccu-
rate. In such cases, performance of scalar quantization
can be improved by using the reduced rank approach
where the columns of the precoding matrix are con-
strained to lie within a subspace of dimension less than
the no. of transmit antennas [40].
t
N
Figure 19 shows the symbol error rate (SER) perform-
ance of a simulated 4  5 limited feedback MIMO bea-
mformer with different feedback strategies. The system
uses 16-QAM modulation for transmission and MRC at
the receiver. Optimal BF in the figure represents the op-
timal beamformer with unquantized feeback and full CSI
at the transmitter. Grassmannian BF (6-bit) represents
signal adaptive beamforming using a 6-bit feedback VQ
codebook and results in the best performance, lying
within 0.7 dB of the optimal BF and approximately 1dB
better than the 40-bit channel quantization which suffers
from large quantization error. The 6-bit quantized re-
duced rank (RR) beamformer with dimension D = 3,
performs close to the 40-bit channel quantization [40].
Figure 18. Channel Quantization [40].
Figure 19. Limited feedback beamformer performance for
4  5 MIMO configuration [40].
3.6.1. Link Adaptation without Precoding
In addition to the precoding matrix, other information e.g.
the received signal to interference and noise ratio (SINR)
may also be included in the feedback for link adaptation.
However, some MIMO schemes like the modified V-
BLAST schemes in [32,34] rely solely on this type of
feedback without any precoding information.
Another example is the 2-codeword multiple code-
words (2CW-MCW) scheme for FDD MIMO-OFDM
cellular systems proposed in [41] that uses SINR feed-
back for each stream to select a suitable modulation and
coding scheme (MCS) for each of the two simultane-
ously transmitted codewords. The two codewords are
mapped onto 2 and 4 streams respectively for 2  2 and 4
 4 antenna configurations. The mapping may either be
fixed or adaptive. Adaptive mapping also makes use of
the SINR feedback. Precoding is not used in this scheme
resulting in reduced feedback overhead.
3.6.2. Partial Feedback Schemes
Partial feedback schemes for MIMO systems are based
on the feedback of statistical channel information along
with some instantaneous channel quality indicator (CQI)
e.g. SNR, SINR etc. to the transmitter. A partial feed-
back scheme for MIMO-OFDM systems involving the
decomposition of MIMO channel covariance matrix is
presented in [42].
The covariance matrix R is calculated from the esti-
mated MIMO channel matrix H (for the k-th subcarrier)
at the receiver and is given by


EH RHH (24)
The matrix R is then decomposed using SVD which is
given by
H
StatStat Stat
RUΛV (25)
where is a diagonal matrix containing the singular
Stat
Λ
Co pyright © 2010 SciRes. IJCNS

F. KHALID ET AL. 226
values while and are unitary matrices. The
feedback includes the matrix and the column
vectors of for power allocation and spatial proc-
essing (precoding) at the transmitter [42].
Stat
U
Stat
Stat
V
Stat
Λ
V
Figure 20 shows the block diagram of a TR
NN

MIMO-OFDM system based on this partial feedback
scheme which transmits spatial streams using
OFDM subcarriers. The received signal vector for the
k-th subcarrier is given by
S
N
HQAx
T
N
C
N
y = (26)
where x is the transmit data vector, H is the MIMO
channel matrix for the k-th subcarrier, A is a diagonal
matrix with diagonal elements determined by the
matrix feedback for power allocation to the active
spatial streams, and the
S
N
St
Λat
S
N

matrix Q represents a
spatial processing transformation which maps the spatial
streams to the transmit antennas. The Q matrix is con-
structed from the vectors of received at the trans-
mitter via feedback and is used to maximize the received
energy for each transmitted spatial stream. This enables
Stat
V
maximum ratio transmission (MRT) and SVD beam-
forming along with tracking of spatial variations of the
MIMO channel [42].
The MIMO channel covariance and the corresponding
channel singular values do not vary rapidly with time
even at vehicular speeds around 100 km/h [42]. This
greatly reduces the feedback load on the system and
makes this closed-loop MIMO-OFDM system suitable
for mobile environments.
Figures 21 and 22 show the simulated frame error rate
(FER) performance of the proposed MIMO-OFDM sys-
tem in comparison with open-loop SM and perfect CSI
feedback MIMO-OFDM systems, for 2  2 and 4  4
MIMO configurations respectively. The figures include
FER performance curves for QPSK and 64-QAM modu-
lation in a low speed mobile scenario using the ITU PB
channel profile with vehicular speeds of 3 km/h. The
OFDM scheme is based on 512-point FFT with 15 sub-
channels for data transmission each consisting of 20 con-
tinuous subcarriers, for a total bandwidth of 5 MHz. The
frame duration is about 0.5ms. Turbo coding is employed
for FEC and MMSE detection is used at the receiver.
Figure 20. MIMO-OFDM system with partial feedback [42].
Figure 21. FER performance for coded 2  2 MIMO con-
figuration [42].
Figure 22. FER performance for coded 4  4 MIMO con-
figuration [42].

F. KHALID ET AL. 227
Equal power allocation is used for the open-loop SM
system while water-filling is used for the closed-loop
systems. Ideal channel knowledge is assumed at the re-
ceiver for all systems and antenna correlations are not
considered [42].
As seen from the results, the proposed system operates
quite close to the perfect CSI feedback system and shows
substantial performance gain over the open-loop system.
The small performance loss in comparison with the per-
fect feedback system is primarily due to the quantization
error associated with limited feedback [42].
Efficient feedback reconstruction algorithms for im-
provement of the closed-loop transmit diversity scheme
constituting the mode 1 of 3GPP’s wideband code-divi-
sion multiple access (WCDMA) 3G standard are pre-
sented in [43]. These algorithms efficiently reconstruct
the beamforming weights at the transmitter while con-
sidering the effect of feedback error. Performance results
for vehicular speeds up to 100 km/h are provided. The
proposed techniques are applicable to closed-loop MI-
MO diversity systems and may possibly be extended to
4G systems.
In [44], the optimal MIMO precoder designs for fre-
quency-flat and frequency-selective fading channels are
presented, assuming partial CSI at the transmitter con-
sisting of transmit and receive correlation matrices. The
elements of transmit and receive correlation matrices are
determined from the respective transmit and receive an-
tenna spacing and angular spread. It is shown that from
the capacity maximization perspective, the optimal pre-
coder for a frequency-flat fading channel is an ei-
gen-beamformer. On the other hand, the optimal pre-
coder for a frequency-selective fading channel repre-
sented by L uncorrelated effective paths consists of P + L
parallel eigen-beamformers where P is an arbitrary value
depending on the no. of vectors in a transmission data
block [44].
A closed-loop limited feedback MIMO scheme called
multi-beam MIMO (MB-MIMO) is proposed in [45] for
3GPP LTE E-UTRA downlink. MB-MIMO employs
multiple fixed beams at the base station (Node B) to
transmit multiple data streams. The no. of beams and
data streams to be used are adaptively selected using a
codebook at the UE. The selected precoding vectors or
beam indices constituting a precoding matrix are then fed
back to the Node B. The MB-MIMO scheme can adap-
tively switch between MIMO SM and transmit beam-
forming (Tx-BF) modes. Tx-BF is used if a single beam
is selected and SM is used if multiple beams are selected.
The proposed scheme eliminates the need for a hard-
ware calibrator (HW-CAL) at Node B that was required
for a previously proposed MB-MIMO implementation.
HW-CAL compensates the phase variations caused by
RF components and was needed to align the phase con-
dition of each transmit antenna element for maximizing
the transmit beamforming gain. The proposed scheme
uses a larger codebook based on an extended precoding
matrix which includes phase terms that can be controlled
to align the phase condition of the 4 node B antenna
elements. This results in high beamforming gain even
without HW-CAL. However, 4 additional bits or a total
of 8 bits are required for feedback, which is still a small
number.
3.7. MIMO over High-Speed Mobile Channels
Open-loop MIMO diversity techniques like STC and
space frequency coding (SFC) are appropriate choices
for high-speed mobile channels that vary rapidly with
time. In such scenarios, maintaining a reliable link be-
comes the foremost priority rather than maximizing sys-
tem throughput.
High-speed mobile channels undergo fast fading whi-
ch may cause time variation of the fading channel within
an OFDM symbol period. This results in the loss of sub-
channel orthogonality and leads to interchannel interfer-
ence (ICI) due to the distribution of leakage signals over
other OFDM subcarriers. The error floor associated with
ICI increases with the speed of the mobile terminal [46].
An improved MIMO-OFDM technique for high-speed
mobile access in cellular environments is proposed in
[46]. This technique reduces ICI and provides diversity
gain as well as noise averaging even for highly correlated
channels. ICI is reduced by transmitting weighted data
on adjacent subcarriers. The weights are selected such
that the mean ICI power is minimized. The adopted
weight selection procedure however results in subopti-
mal weights. Diversity gain in [46] is achieved by using
space-frequency block coding (SFBC) which is based on
Alamouti code but the coding is applied in frequency
domain i.e. to OFDM subcarriers rather than to OFDM
symbols in time domain [47]. Figure 23 shows the data
assignment scheme for the 2  1 SFBC-OFDM system,
without the weighting factors. The transmit data is as-
signed to subcarrier groups each consisting of two adja-
cent subcarriers, as shown in the figure.
Instead of SFBC, other diversity techniques such as
STBC, space-frequency trellis coding (SFTC), maximal-
Figure 23. Data assignment scheme for ICI reduction in 2 
1 SFBC-OFDM system [46].
C
opyright © 2010 SciRes. IJCNS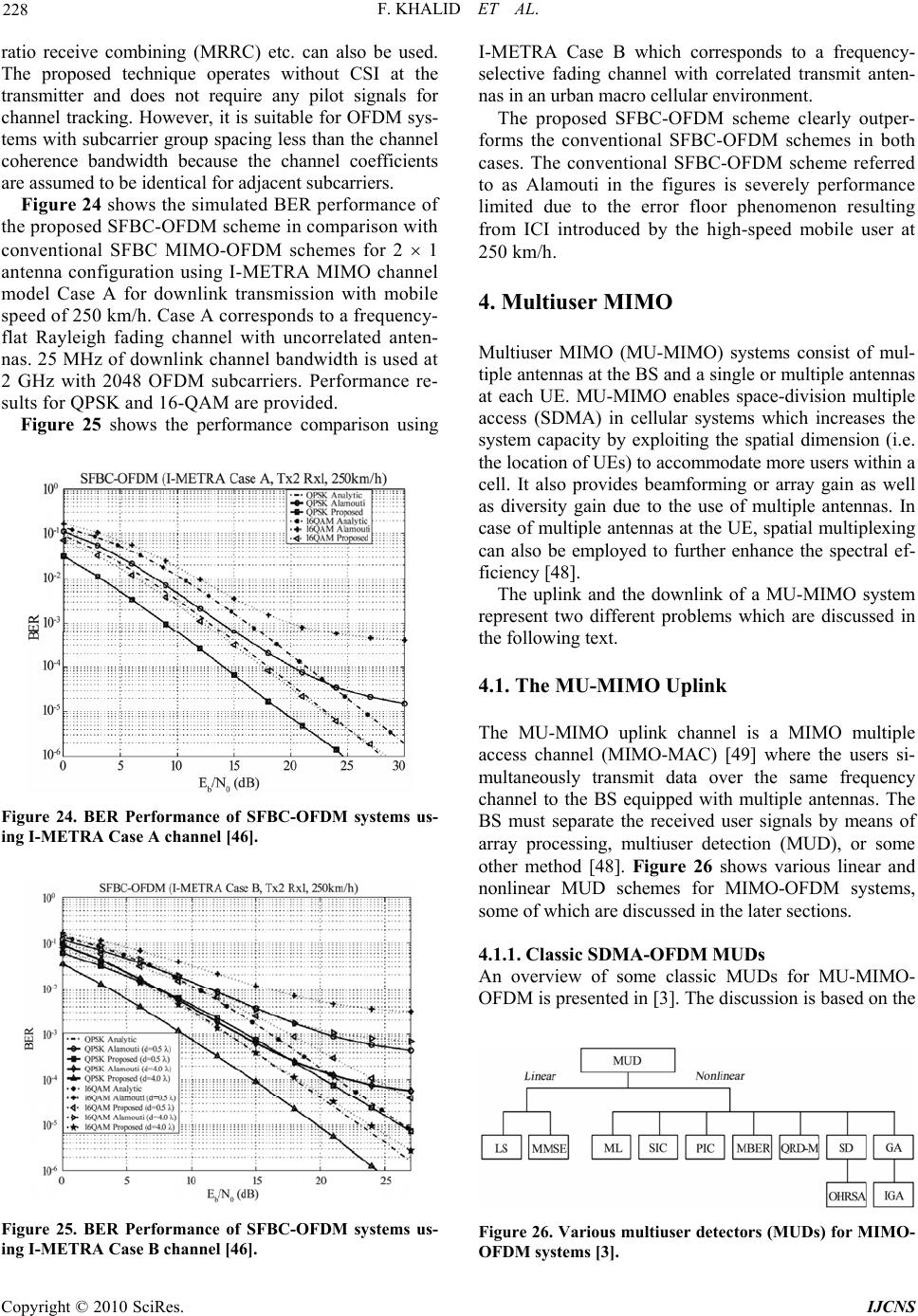

F. KHALID ET AL. 228
ratio receive combining (MRRC) etc. can also be used.
The proposed technique operates without CSI at the
transmitter and does not require any pilot signals for
channel tracking. However, it is suitable for OFDM sys-
tems with subcarrier group spacing less than the channel
coherence bandwidth because the channel coefficients
are assumed to be identical for adjacent subcarriers.
Figure 24 shows the simulated BER performance of
the proposed SFBC-OFDM scheme in comparison with
conventional SFBC MIMO-OFDM schemes for 2  1
antenna configuration using I-METRA MIMO channel
model Case A for downlink transmission with mobile
speed of 250 km/h. Case A corresponds to a frequency-
flat Rayleigh fading channel with uncorrelated anten-
nas. 25 MHz of downlink channel bandwidth is used at
2 GHz with 2048 OFDM subcarriers. Performance re-
sults for QPSK and 16-QAM are provided.
Figure 25 shows the performance comparison using
Figure 24. BER Performance of SFBC-OFDM systems us-
ing I-METRA Case A channel [46].
Figure 25. BER Performance of SFBC-OFDM systems us-
ing I-METRA Case B channel [46].
I-METRA Case B which corresponds to a frequency-
selective fading channel with correlated transmit anten-
nas in an urban macro cellular environment.
The proposed SFBC-OFDM scheme clearly outper-
forms the conventional SFBC-OFDM schemes in both
cases. The conventional SFBC-OFDM scheme referred
to as Alamouti in the figures is severely performance
limited due to the error floor phenomenon resulting
from ICI introduced by the high-speed mobile user at
250 km/h.
4. Multiuser MIMO
Multiuser MIMO (MU-MIMO) systems consist of mul-
tiple antennas at the BS and a single or multiple antennas
at each UE. MU-MIMO enables space-division multiple
access (SDMA) in cellular systems which increases the
system capacity by exploiting the spatial dimension (i.e.
the location of UEs) to accommodate more users within a
cell. It also provides beamforming or array gain as well
as diversity gain due to the use of multiple antennas. In
case of multiple antennas at the UE, spatial multiplexing
can also be employed to further enhance the spectral ef-
ficiency [48].
The uplink and the downlink of a MU-MIMO system
represent two different problems which are discussed in
the following text.
4.1. The MU-MIMO Uplink
The MU-MIMO uplink channel is a MIMO multiple
access channel (MIMO-MAC) [49] where the users si-
multaneously transmit data over the same frequency
channel to the BS equipped with multiple antennas. The
BS must separate the received user signals by means of
array processing, multiuser detection (MUD), or some
other method [48]. Figure 26 shows various linear and
nonlinear MUD schemes for MIMO-OFDM systems,
some of which are discussed in the later sections.
4.1.1. Classic SDM A -OF DM MUDs
An overview of some classic MUDs for MU-MIMO-
OFDM is presented in [3]. The discussion is based on the
Figure 26. Various multiuser detectors (MUDs) for MIMO-
OFD M sys tems [3].

F. KHALID ET AL. 229


uplink MIMO SDMA-OFDM system model of Figure
27 where each of the L UEs uses a single transmit an-
tenna while the BS is equipped with P antennas.
the AWGN signal has zero mean and variance
p
n2
n

.
The channel transfer functions


l
p
H
are assumed to be
independent, stationary, complex Gaussian distributed
processes with zero mean and unit variance.
The complex-valued P  1 received signal vector at
the BS antenna array for the k-th subcarrier of the n-th
OFDM symbol is given by The classic MUD schemes [3] are discussed in the fol-
lowing text.
x=Hs+n (27) 1) MMSE MUD:
where s is the L  1 transmitted signal vector, n is the P
 1 AWGN noise vector and H is the P  L channel
transfer function matrix consisting of L column vectors,
each containing the transfer functions for a particular UE.
Therefore, H ca n be represe nted as
  12
,,,
L

 HHH H (28)
where

12
,,,, 1,,
T
llll
P
H
HH l



HL (29)
Figure 28 shows the schematic diagram of a MMSE
SDMA-OFDM MUD. The multiuser signals received at
each BS antenna are multiplied by a complex-valued
array weight


l
p
w and then summed up . The superscript
l represents a particular user which means that a separate
set of weights is used for detection of each user’s signal.
The combiner output is subtracted from a user
specific reference signal known at the BS and the
UE, resulting in an error signal . The error signal is
used for weight estimation according to the MMSE crite-
rion. The steepest descent algorithm can be used in this
regard for stepwise weight adjustment for each subcarrier
of each user. The performance of the MMSE MUD im-
proves as the no. of antenn as P in the BS antenna array is
increased and degrades when the no. of users increase.
()yt
()rt
()єt
is a P  1 vector whose eleme nts are the cha nnel tran sfer
functions for the transmission paths between the transmit
antenna of the l-th UE and the P BS antennas.
It is assumed that the complex signal


l
s
transmitted
by the l-th user has zero mean and variance 2
l

while
Figure 27. Uplink MIMO SDMA-OFDM system model with single antenna at each UE [3].
Figure 28. MMSE SDMA-OFDM MUD [3].

F. KHALID ET AL. 230
2) Successive Interference Cancellation (SIC) MUD:
The successive interference cancellation (SIC) MUD
enhances the MMSE MUD using SIC. For each subcar-
rier, the detection order of the users is arranged accord-
ing to their estimated total received signal power at the
BS antenna array and the strongest user’s signal with the
least multiuser interference (MUI) is detected using the
MMSE MUD. The detected user signal is then subtracted
from the composite multiuser signal and the next strong-
est user is detected by the same procedure. This process
continues till the detection is completed for all users. SIC
results in high diversity gain at the MMSE combiner,
which mitigates the effects of MUI as well as channel
fading. The SIC MUD is also effective in near-far sce-
narios that result from inaccurate power control. How-
ever, it is prone to errors in power classification of user
signals and also to interuser error propagation. Figure 29
shows the BER performance comparison of MMSE
MUD and SIC MUD (M-SIC with M = 2) for an SDMA-
OFDM scenario with four single-antenna UEs and a
four-antenna BS antenna array using QPSK modulation.
The indoor short wireless asynchronous transfer mode
(SWATM) channel model is used.
3) Parallel Interference Cancellation (PIC) MUD:
The PIC MUD does not require any power classifica-
tion of the received user signals. The detection procedure
consists of two iterations for all subcarriers. In the first
iteration, MMSE detection is used to estimate all user
signals

l
y
from the received composite multiuser sig-
nal vector x. In case of channel encoded transmission, all
user signals must be decoded, sliced, channel encoded
Figure 29. BER performance of MMSE MUD and SIC
MUD [3].
again and also remodulated onto subcarriers. In the sec-
ond detection iteration, signal vectors for all L us-
ers are reconstructed and an estimate

l
x

 k
y
 of each user
signal is generated by subtracting the signal vectors


,
llk

x
 of all other users followed by MMSE com-
bining. The estimated user signals are then channel de-
coded and sliced. The PIC MUD scheme is also vulner-
able to interuser error propagation.
4) Maximum Likelihood (ML) MUD:
The ML MUD employs the ML detection principle to
find the most likely transmitted user signals through an
exhaustive search. It provides the optimal detection per-
formance but also has the highest complexity of any
other MUD. For an OFDM-SDMA system with L simul-
taneous users, the ML MUD produces the estimated L  1
symbol vector consisting of the most likely trans-
mitted symbols of the L users for a particular OFDM
subcarrier, as given by
ML
ˆ
s
2
ML
ˆarg min
L


s
sx


M
Hs
(30)
where M L is a set containing trial vectors, m being
the no. of bits per symbol depending on the modulation
scheme used resulting in constellation points.
Therefore, the computational complexity of the ML
MUD increases exponentially with the no. of users L
thus making it prohibitive for practical implementation.
2mL
2m
5) Sphere Decoding (SD) aided MUD:
SD-aided MUDs use SD for reduced-complexity ML
multiuser detection with near-optimal performance. SD
reduces the ML search to within a hypersphere of a cer-
tain radius around the received signal. The radius of this
search sphere determines the complexity of the MUD.
Various SD algorithms have been proposed in literature
like the complex-valued SD (CSD) and multistage SD
(MSD) which significantly reduce the complexity by
reducing the required search radius [3].
4.1.2. Layered Space-Time MUD
A V-BLAST based MUD scheme referred to as layered
space-time MUD (LAST-MUD) is presented in [50] for
CDMA uplink. This scheme is somewhat similar to the
SIC MUD since V-BLAST detection also incorporates
SIC.
Figure 30 shows the layered space-time MU-MIMO
system block diagram. Here the single antenna users are
arranged in G groups each containing M users for a total
of
K
GM

. The UEs within each group are treated
as the multiple transmit antennas of a V-BLAST system.
The users within each group share the same unique
spreading code which distinguishes the groups from one
another. Therefore, out of the K total spreading codes,
only G are unique. The N  K random spreading matrix
consisting of K length N code vectors is denoted by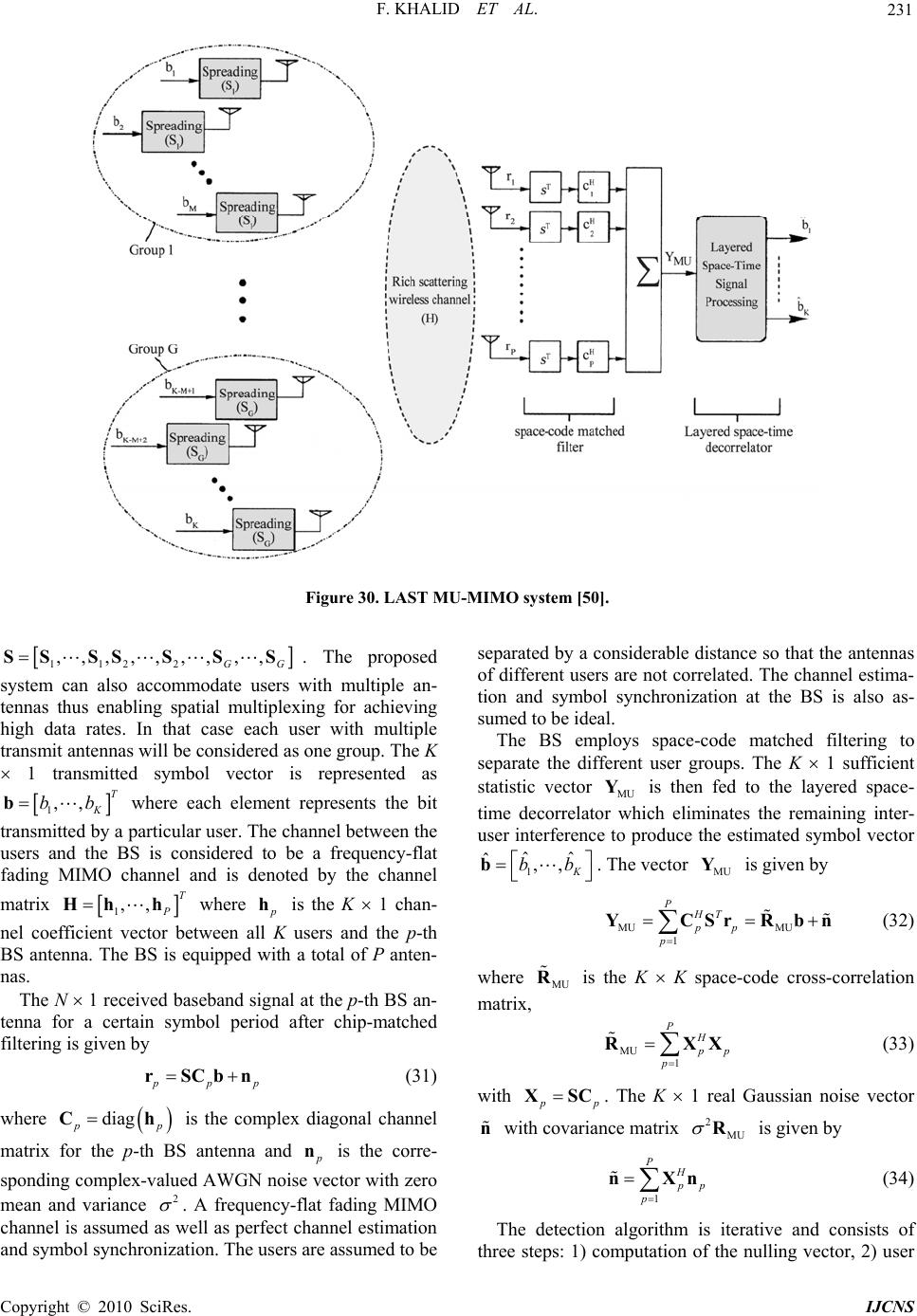

F. KHALID ET AL. 231
Figure 30. LAST MU-MIMO system [50].


112 2
,,,,,,,,,
G
SSSSSSS

1,, T K
bbb

1,,T P
Hhh
G
. The proposed
system can also accommodate users with multiple an-
tennas thus enabling spatial multiplexing for achieving
high data rates. In that case each user with multiple
transmit antennas will be considered as one group. The K
 1 transmitted symbol vector is represented as
where each element represents the bit
transmitted by a particular user. The channel between the
users and the BS is considered to be a frequency-flat
fading MIMO channel and is denoted by the channel
matrix where
p
h is the K  1 chan-
nel coefficient vector between all K users and the p-th
BS antenna. The BS is equipped with a total of P anten-
nas.
Co pyright © 2010 SciRes. IJCNS
The N  1 received baseband signal at the p-th BS an-
tenna for a certain symbol period after chip-matched
filtering is given by
pp
rSCbn
p
p
h
(31)
where is the complex diagonal channel
matrix for the p-th BS antenna and

diag
p
C
p
n is the corre-
sponding co mplex-valued AWGN noise vector with zero
mean and variance 2

. A frequency-flat fading MIMO
channel is assumed as well as perfect channel estimation
and symbol synchronization. The users are assumed to be
separated by a considerable distance so that the antennas
of different users are not correlated. The channel estima-
tion and symbol synchronization at the BS is also as-
sumed to be ideal.
The BS employs space-code matched filtering to
separate the different user groups. The K  1 sufficient
statistic vector is then fed to the layered space-
time decorrelator which eliminates the remaining inter-
user interference to produce the estimated symbol vector
MU
Y
1
ˆˆ ˆ,,
K
bb





b. The vector is given by
MU
Y
MU MU
1
PHT
pp
p



YCSrRb

n (32)
where is the K  K space-code cross-correlation
matrix, MU
R

MU 1
PH
p
p
p
 RX
X (33)
with
p
p

XSC. The K  1 real Gaussian noise vector
with covariance matrix is given by
n
2MU
 R
1
PH
p
p
p
 nXn  (34)
The detection algorithm is iterative and consists of
three steps: 1) computation of the nulling vector, 2) user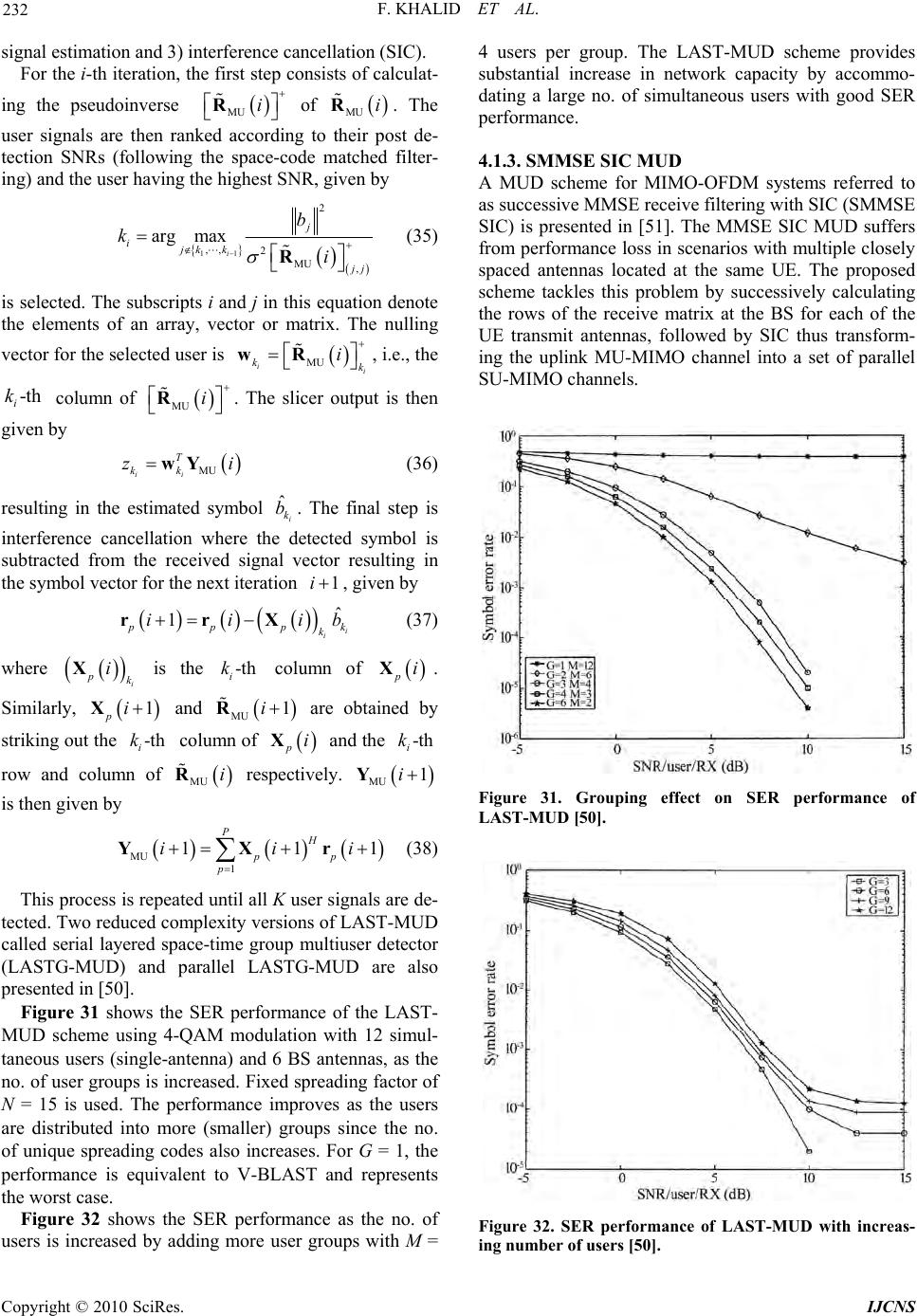

F. KHALID ET AL. 232
signal estimation and 3) interference cancellation (SIC).
For the i-th iteration, the first step consists of calculat-
ing the pseudoinverse of

MU i


R



MU iR
. The
user signals are then ranked according to their post de-
tection SNRs (following the space-code matched filter-
ing) and the user having the highest SNR, given by



11
2
,, 2MU ,
arg max
i
j
ijk k
j
j
b
ki





R
 (35)
is selected. The subscripts i and j in this equation denote
the elements of an array, vector or matrix. The nulling
vector for the selected user is , i.e., the
column of . The slicer output is then
given by

MU
ii
kk
i

 wR





i
-th
i
k

MU i


R


MU
ii
T
kk
zwY (36)
resulting in the estimated symbol . The final step is
interference cancellation where the detected symbol is
subtracted from the received signal vector resulting in
the symbol vector for the next iteration , given by
ˆi
k
b
1i
 

ˆ
1i
i
p
pp
k
iii rrX
k
b

(37)
where is the column of


i
pk
iX-th
i
k


piX
-th
i
k
.
Similarly, and are obtained by
striking ou t the column of and the
row and column of respectively.

piX
i
k
 
1
-th

1

p
X
MU iR


i

i
MU
R



MU 1i

Y
is then given by
 
MU 1
11
PH
pp
p
ii

 

YXr

1i (38)
This process is repeated until all K user signals are de-
tected. Two reduced complexity versions of LAST-MUD
called serial layered space-time group multiuser detector
(LASTG-MUD) and parallel LASTG-MUD are also
presented in [50].
Figure 31 shows the SER performance of the LAST-
MUD scheme using 4-QAM modulation with 12 simul-
taneous users (single-antenna) and 6 BS antennas, as the
no. of user groups is increased. Fixed spreading factor of
N = 15 is used. The performance improves as the users
are distributed into more (smaller) groups since the no.
of unique spreading codes also increases. For G = 1, the
performance is equivalent to V-BLAST and represents
the worst case.
Figure 32 shows the SER performance as the no. of
users is increased by adding more user groups with M =
4 users per group. The LAST-MUD scheme provides
substantial increase in network capacity by accommo-
dating a large no. of simultaneous users with good SER
performance.
4.1.3. SMMSE SIC MUD
A MUD scheme for MIMO-OFDM systems referred to
as successive MMSE receive filtering with SIC (SMMSE
SIC) is presented in [51]. The MMSE SIC MUD suffers
from performance loss in scenarios with multiple closely
spaced antennas located at the same UE. The proposed
scheme tackles this problem by successively calculating
the rows of the receive matrix at the BS for each of the
UE transmit antennas, followed by SIC thus transform-
ing the uplink MU-MIMO channel into a set of parallel
SU-MIMO channels.
Figure 31. Grouping effect on SER performance of
LAST-MUD [50].
Figure 32. SER performance of LAST-MUD with increas-
ing number of users [50].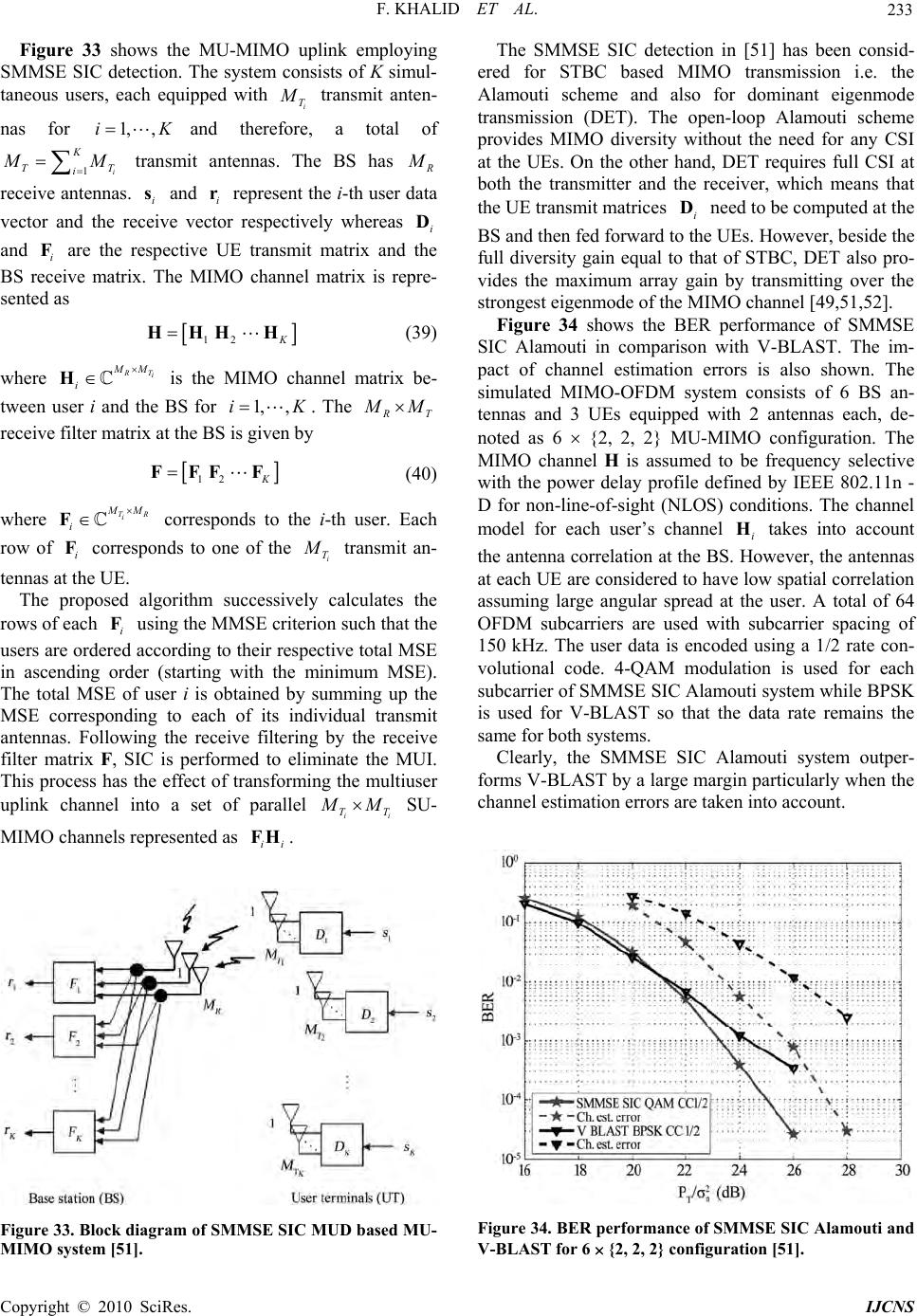

F. KHALID ET AL. 233
Figure 33 shows the MU-MIMO uplink employing
SMMSE SIC detection. The system consists of K simul-
taneous users, each equipped with i
T
M
transmit anten-
nas for and therefore, a total of 1, ,i
i
T
K
1
K
T
i
M
M

 transmit antennas. The BS has
R
M
receive antennas. and represent the
i-th user data
vector and the receive vector respectively whereas
and are the respective UE transmit matrix and the
BS receive matrix. The MIMO channel matrix is repre-
sented as
i
si r
i
D
i
F


12
K
HHH H (39)
where
R
Ti
MM
i

H is the MIMO channel matrix be-
tween user i and the BS for 1, ,iK

. The
R
T
M
M

receive filter matrix at the BS is given by

12

K
FFFF (40)
where TR
i
M
M
i

F
i
F
corresponds to the i-th user. Each
row of corresponds to one of the i
T
M
transmit an-
tennas at the UE.
The proposed algorithm successively calculates the
rows of each using the MMSE criterion such that the
users are ordered according to their respective total MSE
in ascending order (starting with the minimum MSE).
The total MSE of user i is obtained by summing up the
MSE corresponding to each of its individual transmit
antennas. Following the receive filtering by the receive
filter matrix F, SIC is performed to eliminate the MUI.
This process has the effect of transforming the multiuser
uplink channel into a set of parallel
i
F
i
Ti T
M
M SU-
MIMO channels represented as .
ii
FH
Figure 33. Block diagram of SMMSE SIC MUD based MU-
MIMO system [51].
The SMMSE SIC detection in [51] has been consid-
ered for STBC based MIMO transmission i.e. the
Alamouti scheme and also for dominant eigenmode
transmission (DET). The open-loop Alamouti scheme
provides MIMO diversity without the need for any CSI
at the UEs. On the other hand, DET requires full CSI at
both the transmitter and the receiver, which means that
the UE transmit matrices need to be computed at the
BS and then fed forward to the UEs. However, beside the
full diversity gain equal to that of STBC, DET also pro-
vides the maximum array gain by transmitting over the
strongest eigenmode of the MIMO channel [49,51,52].
i
D
Figure 34 shows the BER performance of SMMSE
SIC Alamouti in comparison with V-BLAST. The im-
pact of channel estimation errors is also shown. The
simulated MIMO-OFDM system consists of 6 BS an-
tennas and 3 UEs equipped with 2 antennas each, de-
noted as 6  {2, 2, 2} MU-MIMO configuration. The
MIMO channel H is assumed to be frequency selective
with the power delay profile defined by IEEE 802.11n -
D for non-line-of-sight (NLOS) conditions. The channel
model for each user’s channel takes into account
the antenna correlation at the BS. However, the antennas
at each UE are considered to have low spatial correlation
assuming large angular spread at the user. A total of 64
OFDM subcarriers are used with subcarrier spacing of
150 kHz. The user data is encoded using a 1/2 rate con-
volutional code. 4-QAM modulation is used for each
subcarrier of SMMSE SIC Alamouti system while BPSK
is used for V-BLAST so that the data rate remains the
same for both systems.
i
H
Clearly, the SMMSE SIC Alamouti system outper-
forms V-BLAST by a large margin particularly when the
channel estimation errors are taken into account.
Figure 34. BER performance of SMMSE SIC Alamouti and
V-BLAST for 6  {2, 2, 2} configuration [51].
Co pyright © 2010 SciRes. IJCNS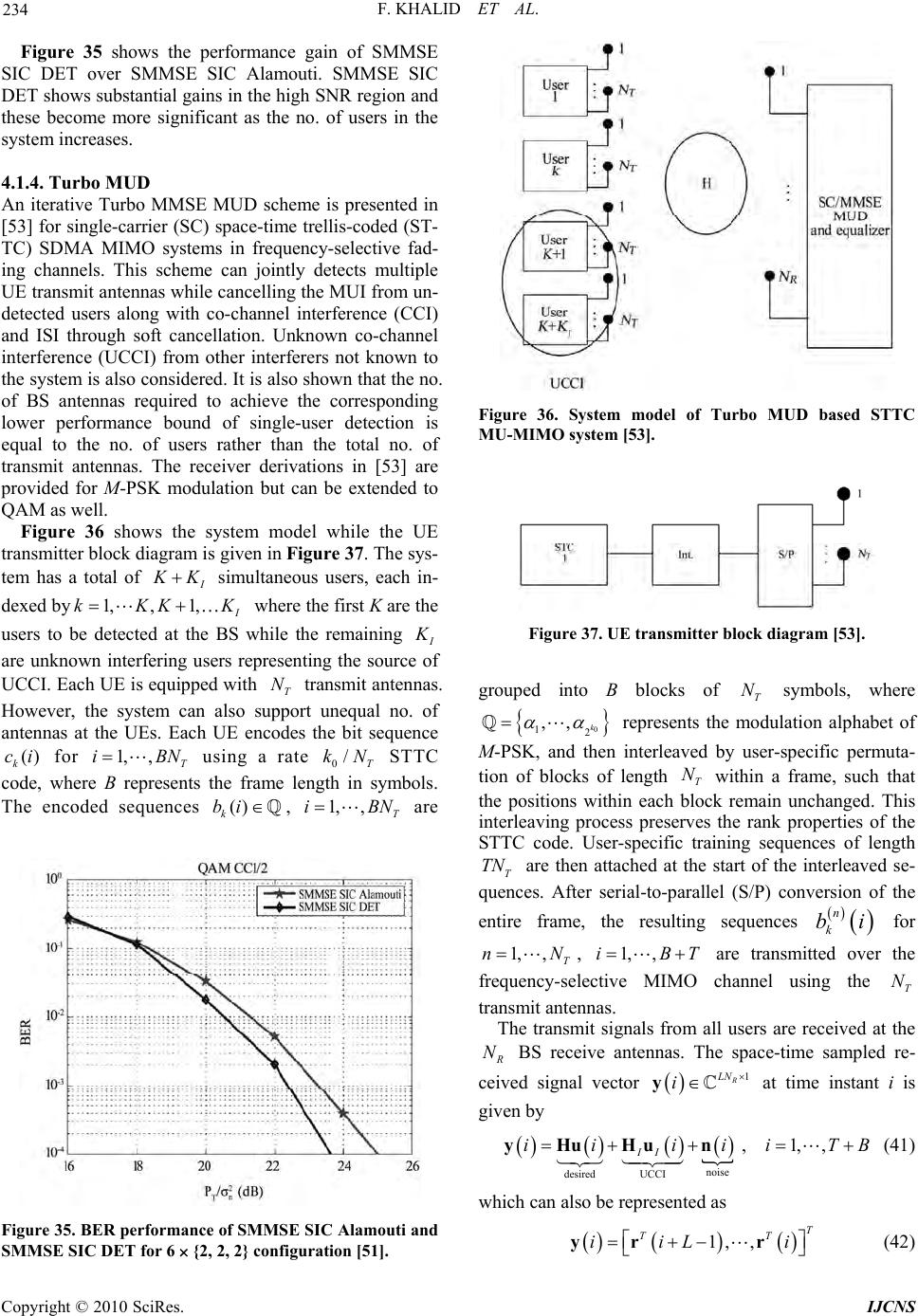

F. KHALID ET AL. 234
Figure 35 shows the performance gain of SMMSE
SIC DET over SMMSE SIC Alamouti. SMMSE SIC
DET shows substantial gains in the high SNR region and
these become more significant as the no. of users in the
system increases.
4.1.4. Turbo MUD
An iterative Turbo MMSE MUD scheme is presented in
[53] for single-carrier (SC) space-time trellis-coded (ST-
TC) SDMA MIMO systems in frequency-selective fad-
ing channels. This scheme can jointly detects multiple
UE transmit antennas while cancelling the MUI from un-
detected users along with co-channel interference (CCI)
and ISI through soft cancellation. Unknown co-channel
interference (UCCI) from other interferers not known to
the system is also considered. It is also shown that the no.
of BS antennas required to achieve the corresponding
lower performance bound of single-user detection is
equal to the no. of users rather than the total no. of
transmit antennas. The receiver derivations in [53] are
provided for M-PSK modulation but can be extended to
QAM as well.
Figure 36 shows the system model while the UE
transmitter block diagram is given in Figure 37. The sys-
tem has a total of
I
K
K
, 1,
simultaneous users, each in-
dexed by1,
I
kKKK where the first K are the
users to be detected at the BS while the remaining
I
K
are unknown interfering users representing the source of
UCCI. Each UE is equipped with transmit antennas.
However, the system can also support unequal no. of
antennas at the UEs. Each UE encodes the bit sequence
for using a rate STTC
code, where B represents the frame length in symbols.
The encoded sequences , are
T
N

()
k
ci 1,i
()
k
bi
,T BN 0/T kN
1, ,iT BN
Figure 35. BER performance of SMMSE SIC Alamouti and
SMMSE SIC DET for 6  {2, 2, 2} configuration [51].
Figure 36. System model of Turbo MUD based STTC
MU- MIMO syst em [53].
Figure 37. UE transmitter block diagram [53].
grouped into B blocks of symbols, where
T
N


0 12
,,k  
T
TN
represents the modulation alphabet of
M-PSK, and then interleaved by user-specific permuta-
tion of blocks of length within a frame, such that
the positions within each block remain unchanged. This
interleaving process preserves the rank properties of the
STTC code. User-specific training sequences of length
are then attached at the start of the interleaved se-
quences. After serial-to-parallel (S/P) conversion of the
entire frame, the resulting sequences
T
N




n
k
bi
for
1,, T nN

, 1, ,iBT

 are transmitted over the
frequency-selective MIMO channel using the
transmit antennas. T
N
The transmit signals from all users are received at the
R
N BS receive antennas. The space-time sampled re-
ceived signal vector


1
R
LN
i y at time instant i is
given by







noise
desired UCCI
, 1,,
II
ii iiiTB

 yHuHu n

T
(41)
which can also be represented as
 
1, ,T
T
iiL i





yr r (42)

F. KHALID ET AL. 235
where each vector

1
R
N
i

r consists of
R
N eleme-
nts ,

m
ri 1, ,
R
mN representing the received sig-
nal sample after matched filtering at the m-th receive ant-
enna and L is the no. of paths of the frequency-selective
MIMO channel. The channel matrix


21
RT
KN LLN


H
has the structure

  
1, ,, ,1
1, ,, ,1
T
TTT
T
TTT
IIII
iiLi iL
iiLi iL

  







ubb b
ubbb


(45)
 

01)
01
L
L
 





HH 0
H
0H H

 

where the vectors


1
T
KN
i b and

1
IT
KN
Ii

b
are given b y


















11
11
11
11
,, ,,
,, ,,
TT
TT
II
T
NN
KK
T
NN
IKKKK KK
ibi bibibi
ibi bib ib i
 







b
b


)
(43)
Each element

R
T
NKN
l H is given by (46)

















11
1,1 1,1,1,1
11
1, 1,,,
T
T
RR R
N
KK
N
NNKN KN
hl hlhlhl
l
hl hl hl hl






H
 
   
 
T
N
N
T
R









1
R
LN
i

n
2
is the AWGN vector with covariance ma-
trix

I.
The Turbo receiver block diagram is shown in Figure 38.
For the k-th user, the receiver first associates the signals
from the user’s transmit antennas to sets
of equal size such that the antennas
T
N
0
n
0
/
T
Nn
1, 0 ,nn


represent the first set and so on. The training sequence


iu, 1,i,T

 is used to obtain an estimate of
the channel matrix H. The UCCI-plus-noise covariance
matrix R is then estimated. The estimate for the first it-
eration is given by
ˆ
H
(44)
where represents the complex gain for the l-th
path between the n-th transmit antenna of user k and the
m-th BS receive antenna. The channel matrix
corresponding to UCCI has a similar
structure as H, and consi sts of matrices

,
n
km
hl
RIT
LNKN


21L
IH


R
IT
NKN
Il
H.
The vectors




211
T
KN L
i


u and



211
IT
KN L
Ii


u
consist of the respective transmit sequences




n
k
bi of
the desired and the unknown users, and are expressed as
 

 

1
1
ˆˆˆ
T

H
i
iiii
T
 

RyHuyHu (47)
Figure 38. Block diagram of the iterative Turbo multiuser receiver [53].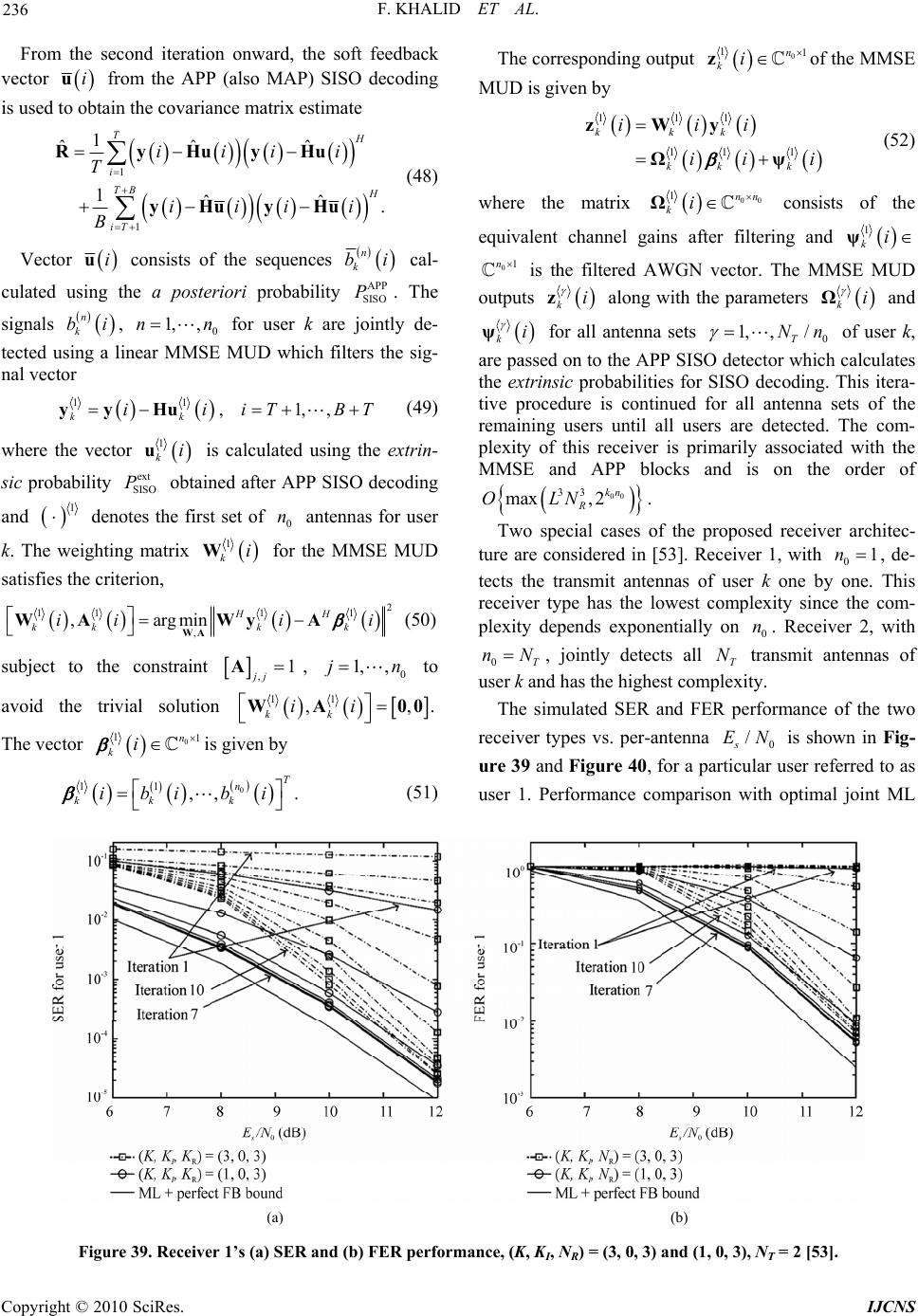

F. KHALID ET AL. 236
From the second itera
ve tion onward, the soft feedback ctor

iu from the APP (also MAP) SISO decoding
is used to obtain the covariance matrix estimate
 

 

 

 

1
1
1
ˆˆˆ
TH
1ˆˆ
.
i
TB
H
iT
iiii
T
iiii
B



 
 


RyHuyHu
yHuyHu
(48)
Vector

iu consists of the sequences




n
k
bi cal-
cuing lated usthe a posteriori probability The
signals
APP
SISO
P.



n
bi, 1, ,nn for user k are y de-
tected ulin MUD which filters the sig-
nal vector
k0jointl
sing a ear MMSE
 
1
y1 ,1,,
kk
iiiTBT y Hu (49)
where the vector

1
kiu is calculated using the extrin-
obt
sic probability ex
Pained after APP SISO decoding
and

t
SISO
1
 denohe first set of n antennas for user
k. Thighting matrix
tes t0
e we


1iW f the MMSE MUD
satisfies the criterion,
kor
 
2
11
 11
,
,argmin
HH
kkk k
iii i

WA
WAWyA  (50)
subject to the constraint


,1 jjA, to
avoid the trivial solution
0
1, ,jn
  
11
,
kk
ii



WA 00 ,.
The vector

0
11 n
i   is give
kn by





0
11,,.
T
n
kk k
ibi bi

  
The corresponding output

0
1
k
z1
n
i of the MMSE
MUD is given by

(51)
  
  
11
11 1
kkk
kk k
iii
ii i


y
Ωψ 
(52)
where the matrix
1
zW


00
1nn
ki
Ω consists of the
equivalent channel gains after filtering and


1i
k

ψ
01n

 is the filtered AWGN vector. The MMS
ts
E MUD
outpu


ki

z along with the parameters


ki

Ω and


ki

ψ antenna sets 1, ,/Nnfor all0T

ser k,
ed on to the APP SISO calculates
the extrinsic probabilities for SISO decoding. This itera-
tive procedure is continued for all antenna sets of the
remaining users until all users are detected. The com-
plexity of this receiver is primarily associated with the
MMSE and APP blocks and is on the order of
of u
are pass detector which




00
33
max ,2kn
R
OLN .
Two special cases of the proposed receiver architec-
ture are considered in [53]. Receiver 1, with 01n

, de-
tects the transmit antennas of user k one by ones
receiver type has the lowest complexity since the com-
plexity depends exponentially on 0 n. Receiver 2, with
0T
nN
. Thi

, jointly detects all T N tnsmit antennas of
d has the highest compity.
The simulated SER and FER perfor
ra
user k anlex
mance of the two
re
ticular
ceiver types vs. per-antenna 0 /
s
EN is shown in Fig-
ure 39 and Figure 40, for a par user referred to as
user 1. Performance comparison with optimal joint ML
(a) (b)
Figure 39. Receiver 1’s (aI R1, 0, 3), NT = 2 [53]. ) SER and (b) FER performance, (K, K, N) = (3, 0, 3) and (

F. KHALID ET AL.
237
detection

of all T N antennas of user 1 followed by
MAP SISO decodi assuming perfect feedback (FB), is
also provided. The results are provided for 1 and 10 it-
erations for

,, 3,0,3
IR
KK N and for 1 and 7 it-
erations for with 2N trans-
mit antennas p
ng
,,KK
user.

1,0,3
IR
N
er K,
T
I
K
and
R
N r e prthe no.
of desired users, unknownterferer (UCCI) and BS
receive antennas. QPSK modulation is used for transmis-
sion and frequency-selective fading is assumed with L =
5 uncorrelated Rayleigh distributed paths. For a suffi-
cient no. of iterations, both receivers perform reasonably
esent
n is
igh SNR
ws the SER and FER performance of the
tw
close to the ML receiver, particularly in the h
region. Receiver 2 shows slightly better performance
than receiver 1.
Figure 41 sho
o receivers for

 
,, 2,1,3
IR
KK N with 2
T
N

transmit antennas pesingle t
antenna for the unknown interferer (UCCI) i.e. 1
I
N
r desired user and a ransmit

.
Two cases of signal-to-UCCI interference ratio (Se
considered. For SIR = 3 dB, the signal transmitted from
UCCI’s antenna is assumed to have the same power as
that of the signal from one antenna of the desired user
whereas, for SIR = 0 dB, UCCI’s antenna transmits at
IR) ar
(a) (b)
Figure 40. Receiver 2’s (a) SERI R, 3), NT = 2 [53]. and (b) FER performance, (K, K, N) = (3, 0, 3) and (1, 0
(a) (b)
Figure 41. Receiver 1’s and 2’s I R, NT = 2, NI = 1 [53]. (a) SER and (b) FER performance, (K, K, N) = (2, 1, 3)
Co pyright © 2010 SciRes. IJCNS

F. KHALID ET AL. 238
twice the
ithm (GA) Assisted MUDs ry of
transmit power of a desired user’s antenna. The
performance of both receivers is obviously better for the
3 dB SIR case. However, the UCCI has a considerable
impact on performance and more iterations are needed to
achieve a reasonably low SER or FER. The performance
will degrade further in case of multiple UCCI antennas
and also as the UCCI sources i.e. the no. of unknown
interferers increase.
.1.5. Genetic Algor4
Genetic algorithms (GAs) are based on the theo
evolution’s concept of survival of the fittest, where the
genes from the fittest individuals of a species are passed
on to the next generation through the process of “natural
selection”. When applied to MUDs, an “individual” repr-
esents the L-dimensional MUD weight vector corre-
sponding to the L users. These MUD weights are then
optimized using GA by genetic operations of “mating”
and “mutation” to get a new generation of individuals i.e.
the MUD weights. The initial “population” (MUD
weights) is typically obtained from the MMSE solution
which is retained throughout the GA search process as an
alternate solution in case of poor conve rgence [3].
Considering the SDMA-OFDM system model of Fig-
ure 27 with a single transmit antenna at each UE and P
receive antennas at the BS, the ML-based decision metric
or objective function (OF) for a GA-assisted MUD cor-
responding to the p-th receive antenna can be written as

2
ppp
xsHs

(53)
where p
x
is the received symbol corresponding to the
p-th BS antenna for a specific OFDM subcarrier and
p
H is the p-th row of the channel transfer function ma-
trix H. The estimated symbol vector of the L users cor-
responding to the p-th BS antenna is then given by


 GA
ˆarg min
pp



ss


s (54)
The combined decision metric for the P receive an-
tennas can therefore be written as
 
2
1
P
 

ss

p
p
xHs

(55)
Therefore, the decision rule for the GA-assisted MUD
is to find an estimate GA
ˆ
s of the L  1 transmitted sym-
bol vector such that


sΩ is minimized [3].
Review and analy various GA-assistedsis of MUDs is
provided in [3] for the SDMA-OFDM uplink consisting
of a single transmit antenna at each UE. Figure 42 shows
the schematic diagram of the SDMA-OFDM uplink sys-
tem based on the concatenated MMSE-GA MUD. The
concatenated MMSE-GA MUD uses the MMSE estimate
1
MMSE
ˆ
L

sof the transmitted symbol vector of the L
users as initial information for the GA. MMSE
ˆ
s is given
by
MMSE MMSE
ˆH
sW x (56)
e wherMMSE
P
L

W is the M
ressed as
MSE MUD weight ma-
trix, exp


1
2
MMSE Hn


HHI H (57) W
Figure 42. SDMA-OFDM uplink system based on concatenated MMSE-GA MUD [3].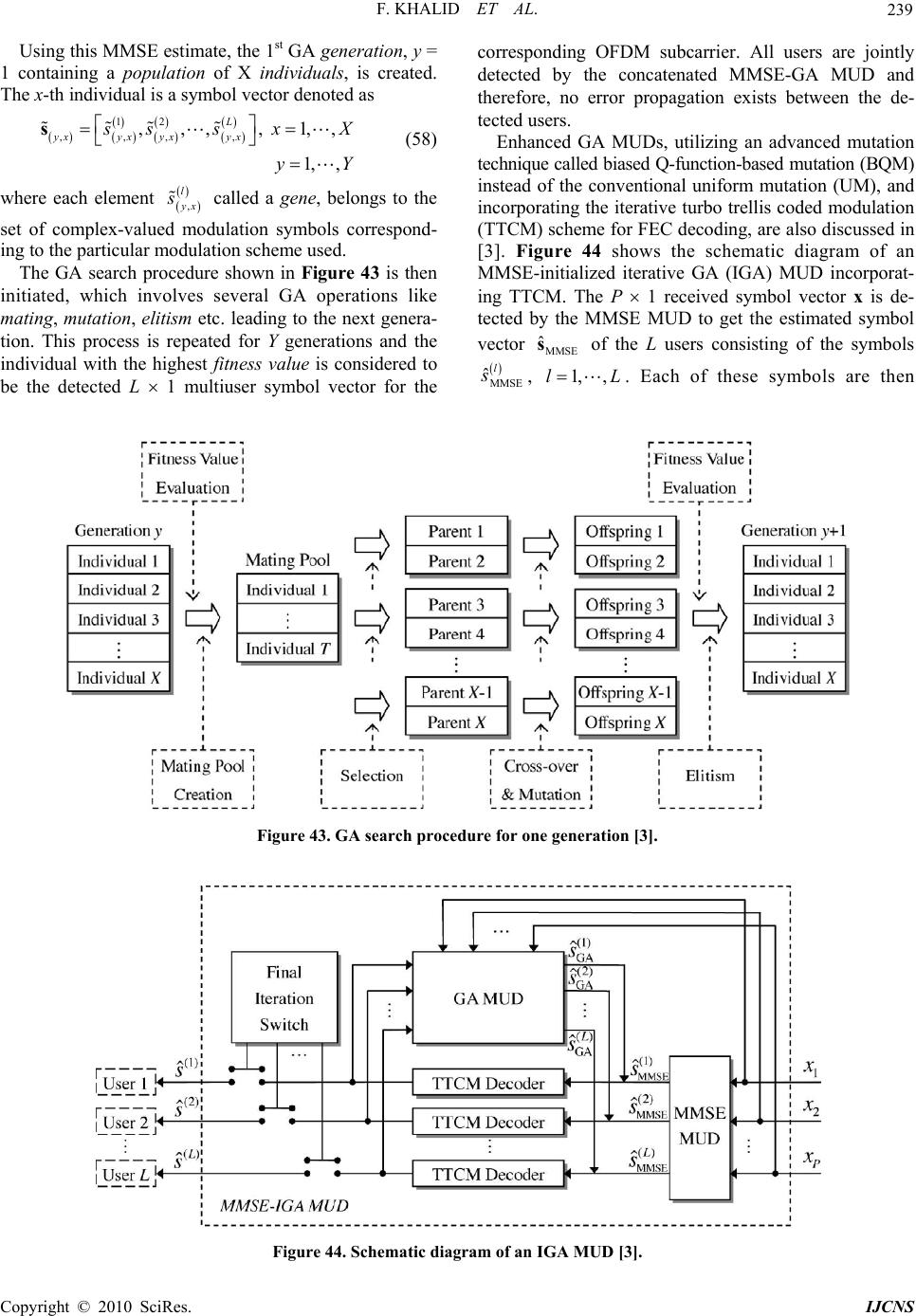

F. KHALID ET AL.
239
Using this MMS
1 E estimate, the 1st GA generation, y = containing a population of X individuals, is created.
The x-th individual is a symbol vector denoted as
  12
,,, ,1,,
L
  
,, ,,
1, ,
yx yx yx yx
s
ssxX

s
 

y

 Y
(58)
where each element


,
l
yx
s
 called a gene, belongs to the
d mo
43 is then
in
users are jointly
A MUDs, utilizing an advanced mutation
te
set of complex-valuedulation symbols correspond-
ing to the particular modulation scheme used.
The GA search procedure shown in Figure
itiated, which involves several GA operations like
mating, mutation, elitism etc. leading to the next genera-
tion. This process is repeated for Y generations and the
individual with the highest fitness value is considered to
be the detected L  1 multiuser symbol vector for the
corresponding OFDM subcarrier. All
detected by the concatenated MMSE-GA MUD and
therefore, no error propagation exists between the de-
tected users.
Enhanced G
chnique called biased Q-function-based mutation (BQM)
instead of the conventional uniform mutation (UM), and
incorporating the iterative turbo trellis coded modulation
(TTCM) scheme for FEC decoding, are also discussed in
[3]. Figure 44 shows the schematic diagram of an
MMSE-initialized iterative GA (IGA) MUD incorporat-
ing TTCM. The P  1 received symbol vector x is de-
tected by the MMSE MUD to get the estimated symbol
vector MMSE
ˆ
s of the L users consisting of the symbols


ˆl
s, ,L. Each of these symbols are then
MMSE 1,l
Figure 43. GA search procedure for one generation [3].
Figure 44. Schematic diagram of an IGA MUD [3].
Co pyright © 2010 SciRes. IJCNS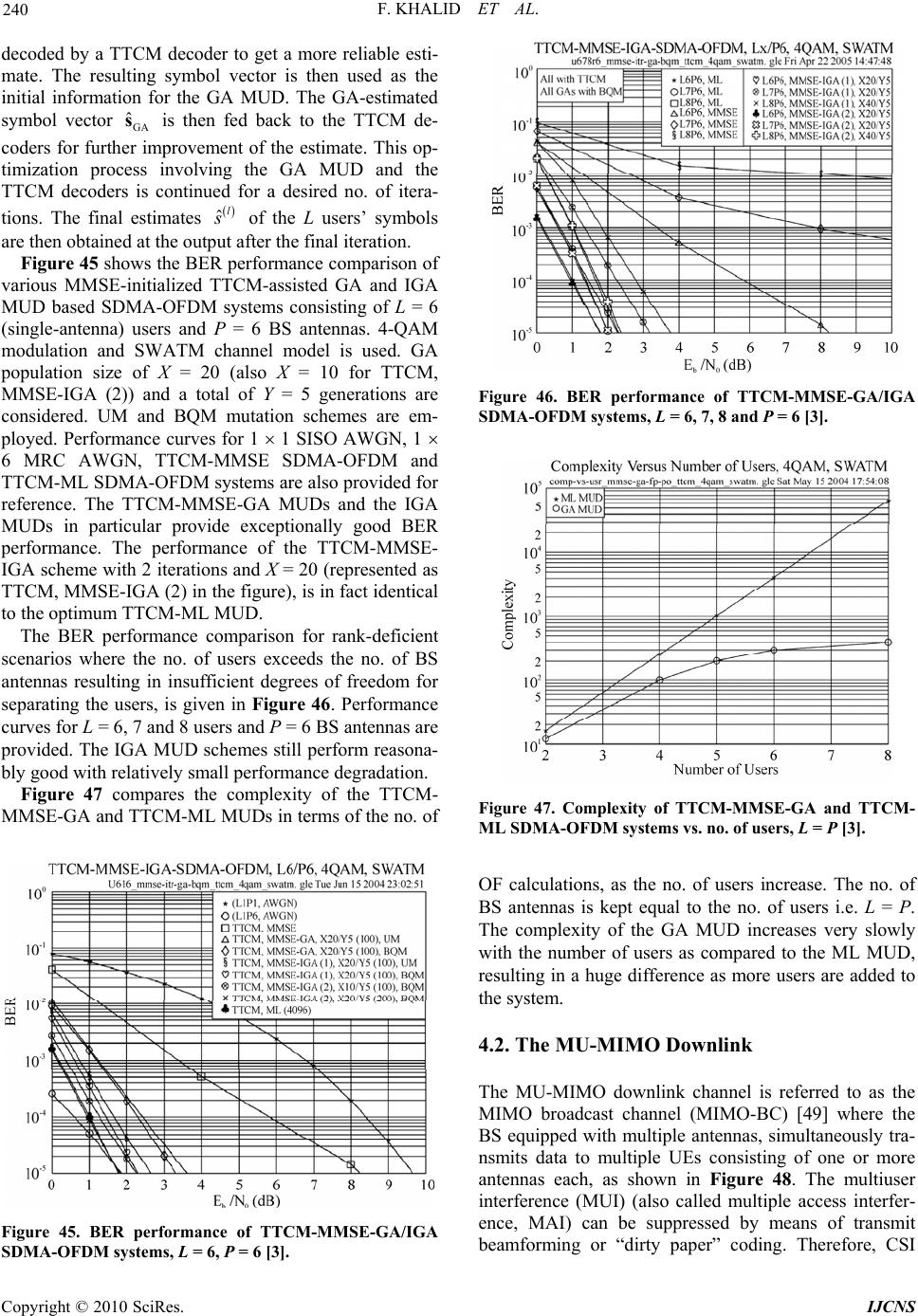

F. KHALID ET AL. 240
ecoded by a TTCM decoder to gedt a more reliable esti-
mate. The resulting symbol vector is then used as the
initial information for the GA MUD. The GA-estimated
symbol vector GA
ˆ
s is then fed back to the TTCM de-
coders for furtheprovement of the estimate. This op-
timization process involving the GA MUD and the
TTCM decoders is continued for a desired no. of itera-
tions. The final estimates
r im


ˆl
s
of the L users’ symbols
are then obtained at the outpafter the final iteration.
Figure 45 shows the BER performance comparison
ut of
va
on for rank-deficient
sc
M
rious MMSE-initialized TTCM-assisted GA and IGA
MUD based SDMA-OFDM systems consisting of L = 6
(single-antenna) users and P = 6 BS antennas. 4-QAM
modulation and SWATM channel model is used. GA
population size of X = 20 (also X = 10 for TTCM,
MMSE-IGA (2)) and a total of Y = 5 generations are
considered. UM and BQM mutation schemes are em-
ployed. Performance curves for 1  1 SISO AWGN, 1 
6 MRC AWGN, TTCM-MMSE SDMA-OFDM and
TTCM-ML SDMA-OFDM systems are also provided for
reference. The TTCM-MMSE-GA MUDs and the IGA
MUDs in particular provide exceptionally good BER
performance. The performance of the TTCM-MMSE-
IGA scheme with 2 iterations and X = 20 (represented as
TTCM, MMSE-IGA (2) in the fig ure), is in fact identical
to the optimum TTCM-ML MUD.
The BER performance comparis
enarios where the no. of users exceeds the no. of BS
antennas resulting in insufficient degrees of freedom for
separating the users, is given in Figure 46. Performance
curves for L = 6, 7 and 8 users and P = 6 BS antennas are
provided. The IGA MUD schemes still perform reasona-
bly good with relatively small performance degradation.
Figure 47 compares the complexity of the TTCM-
MSE-GA and TTCM-ML MUDs in terms of the no. of
Figure 46. BER performance of TTCM-MMSE-GA/IGA
SDMA-OFDM systems, L = 6, 7, 8 and P = 6 [3].
Figure 47. Complexity of TTCM-MMSE-GA and TTCM-
ML SDMA-OFDM systems vs. no. of users, L = P [3].
= P.
he complexity of the GA MUD increases very slowly
O downlink channel is referred to as the
C) [49] where the
simultaneously tra-
OF calculations, as the no. of users increase. The no. of
BS antennas is kept equal to the no. of users i.e. L
T
with the number of users as compared to the ML MUD,
resulting in a huge difference as more users are added to
the system.
4.2. The MU-MIMO Downlink
he MU-MIMT
MIMO broadcast channel (MIMO-B
S equipped with multiple antennas,B
nsmits data to multiple UEs consisting of one or more
antennas each, as shown in Figure 48. The multiuser
interference (MUI) (also called multiple access interfer-
ence, MAI) can be suppressed by means of transmit
beamforming or “dirty paper” coding. Therefore, CSI
Figure 45. BER performance of TTCM-MMSE-GA/IGA
SDMA-OFDM systems, L = 6, P = 6 [3].

F. KHALID ET AL. 241
nlink systems where each UE is equ-
ped with a single receive antenna. As the name sug-
es the inverse of the channel
feedback from each user is required for precoding at the
BS. Various linear and nonlinear precoding techniques
for MU-MIMO downlink systems are discussed in the
following text.
4.2.1. Channel Inve rsion
Channel inversion is a linear precoding technique for
MU-MIMO dow
ip
gests, channel inversion us
matrix for precoding to remove the MUI, as illustrated in
Figure 49.
Assuming that the no. of receive antennas
R
T
M
M

,
the no. of transmit antennas, ZF precoding can be used
for this purpose. The 1
T
M transmitted signal vector is
then give n by

1
H


xHd
HH d
(59)

H
H
where d is the vector of data symbols to be precoded and
is the pseudoinverse of the

H
R
T
M
M channel ma-
dimension utrix H. Vector d can have anyp to the rank
of H [48]. The i-th column of the prefiltering or precod-
ing matrix ZF P is given by [49]


ZF, 2
i
i
i


h p
h
(60)
where


i

h is the i-th column of
received signal vector can be expresse

H. The combined
d as
Figure 48. The MU-MIMO downlink [48].

ydw (61)
where w is the noise vector. Therefore, ZF precoding is
only suitable for low-noise or high transmit power sce-
narios [4 8 ].
MMSE precoding, also called “regularized” channel
inversion provides a better alternative. In this case, the
transmitted signal vector is given by


1
HH


xH HHI d (62)
where

is the loading factor. For a MU-MIMO
downlink system with total transmit power T
P and K
simultaneous /T
K
P


users, maximizes the SINR at
th
Block diagonalization (BD) or block chan
which was first proposed in [54], is a ge
e receivers [48].
4.2.2. Block Diagonalization nel inversion,
neralization of
channel inversion to multi-antenna UEs [48]. BD also
requires the total no. of receive antennas
R
M
to be less
than or equal to the no. of transmit antennas T
M
i.e.
R
T
M
M

.
Consider the system model of Figure 50. The system
ers each havingconsists of K simultaneous us re-
i
R
M
ceive antennas for 1,, iK

 such that the total no. of
receive antennas 1i
K
R
R
i
M
M

. The combined chan-
nel matrix
R
T
M
M

H is given by
T
TTT
12 K





HHHH 63) (
where
R
T
i
M
M
i

H represents the MIMO channel
from the T
M
BS antennas to user i. The coined
precoding matrix
mb
T
M
S


Pcan be expressed as 


12
K
PPPP
(64)
Ti
M
S
i

P
Figure 49. Channel inversion [48].
where is the precoding matrix for the
user,
i-th
R
SM

is th
i
M
e total no. of transmitted data streams
and iR
S

is th
eds
e
nal. To this de-
fined as
no. of data streams transmitted to
user i. P ne to be selected in such a way that HP be-
comes block diagois end, a matrix i H

Figure 50. System model for MU-MIMO downlink trans-
mission [55].
Co pyright © 2010 SciRes. IJCNS

F. KHALID ET AL. 242


ns all but the i-th user’s channel matrix.
herefore, lies in the null space of and consists
of unitary column vectors which are obtained by the
SVD of en by
111
TT TT
iiiK 

 HH HHH

(65)
which contai
T
Ti P
i, giv
i
H

H

 
10
H
iiii i

 HUDV V
 ( 6) 6
The rightmos t Ti
M
L singular vectors


0TTi
M
ML
i


V

space oform the null an orthogonal basis for f i H

where i L
 is the rank of i
H
. The product


0
ii
HV
 with
dimensions

i
R
Ti
M
ML
 represents e equivalent
channel matrix for user i after eliminating the MUI. Thus,
BD transforms the MU
th
m into a -MIM

Ti
O downlink syste
set of K parallel i
R
M
LM
 SU-M
Using SD,
IMO systems.
V


0
ii
 can HV be expressed as

010
H
i
iiii i







0
HVV V
00

where i is an ii LLdiagonal matrix, ag i L
to be the ran
D
U (67)
ssumin
k of
D


0
ii
HV
. The product of


0
i
V
 and the
first i L singular vectors
 1
i
V produces an orthogonal
basis of dimensionnt the transmission
vectors which maxiation rate for the i-th
user while elig the MUI. Therefore,
i L a
mize t
atin
er i
nd re
he inf
consists
prese
orm
min ecodi
matrix for usof
the prng
i
P




01
ii
VV

e diagonal ele
with
l power allocation is
ap
priate power scaling. ah m
[54,56
im
ords, the transmit power
f user i is optimized in such a manner that it does not
wever, interference
pro-
ents of
ly
Optim
ng tachieved by water-filling, usi
the mats i D and can either be implemented global
to maximize the overall information rate of the system or
on a per-user basis,57].
4.2.3. Successive Optization
Successive optimization (SO) [54,56,57] is a successive
precoding algorithm which addresses the power control
problem in BD where capacity loss occurs due to the
nulling of overlapping subspaces of different users. First,
an optimum ordering of the users is determined like in
case of V-BLAST detection. The precoding matrix for
each user is then designed in a successive manner so that
it lies in the null space of the channel matrices of the
previous users only. In other w
rice
o
interfere with users 1, ,1i. Ho
with the successive users is allowed. The combined
channel matrix for the previous 1i users can be writ-
ten as
121
ˆT
TTT
ii 





HHH H (68)
and its SVD is given by
  10
ˆˆˆˆˆ
H
iiii i





HUDV V (69)


0
ˆi
V contains the ˆ
Ti
M
L

rightmost singular vectors
where ˆi L is the rank iThe precoding matrix i P
that lies in the null space of ˆi His then determined as
of ˆ H.


0
ˆ
i
' PV
ii
for som
4.2.4. Dirty Paper Coding
nonlinear precoding technique
and is based on the concept introduced by Costa [58]
where the AWGN channel is modifi
ference which is known at the transmitter. This concept
is anting on d
rrty
writing on clean
In addityss, e.g. the GMD-
FDP scheme mentioned in Subsection 3.4, dirty paper
MU-MIMO downlink trans-
position of the channel ma-
tri
P e choice of i' P.
Dirty paper coding is a
ed by adding inter-
alogous to “wriirty paper” where the writ-
ing is the desired signal and the dirt represents the inter-
ference. Since the transmitte knows where the “dirt” or
interference is, writing on di paper is the same as
paper [48].
ion to SU-MIMO stem
Z
coding is also applicable to
mission. In a MU-MIMO downlink system, CSI feed-
back from the users is available at the BS and it can fig-
ure out the interference produced at a particular user by
the signals meant for other users. Therefore, dirty paper
coding can be applied to each user’s signal at the BS so
that the known interfere nce fr om other users is avoide d.
Various dirty paper coding techniques for the MU-
MIMO downlink are discussed in [48]. A well-known
approach is to use QR decom
x, given by

HLQ, where L is a lower triangular
matrix and Q is a unitary matrix.
H
Q is then used for
transmit precoding which results in the effective channel
L. Therefore, the first user does not see any interference
from the other users and no further processing of its sig-
nal is required at the BS. However, each of the subse-
quent users sees interference from the preceding users
and dirty paper coding is applied to eliminate this known
interference.
Another technique called vector precoding jointly pre-
codes the users’ signals rather than applying dirty paper
coding to the usals individually. The vector pre-
coding technique is shown in Figure 51. The desired
signal vector d is offset by a vector l of integer values
and this operation is followed by channel inversion, re-
sulting in the transmitted signal x, given by
ers’ sign


1


xHdl (70)
where the vector l is chosen to minimize the power of x,
i.e.

F. KHALID ET AL. 243
Figure 51. Vector precoding [48].


1
argmin 

Hd
'
'
l
ll (71)
The signal received at the k-th user is expressed as
kkkk
yd lw


here represents the Gaussian noise. A modulo
applied to remove t
given by
(72)
wk w
operation is then he offset k l, as
 
mod mod
kkkk
ydlw

k
d

mod
k
w

 

(73)

Regularized vector precoding is a modification of
vector precoding which uses regularized (MMSE) han-
nel invers
transmitte
c
ion in place of simple channel inversion. The
d signal vector is then given by



1
HH



xHHHIdl 
w
(74)
here the vector l is chosen to minimize the norm of x
and /T
K
P

. Dirty paper coding techniques based on
vector precoding approach the sum capacity of the
MU-MIMO downlink channel, which is defined as the
maximum system throughput achieved by maximizing
the sum of the information rates of all the us
Figure 52ers [48]. shows the performance comparison of vari-
Figure 52. Performance comparison of various channel
inversion and dirty paper co ding te c hnique s [48].
ous channel inversion and dirty paper coding techniques
for uncoded MU-MIMO downlink transmission with
10
T
M

BS transmit antennas and single-
antenna UEs, using QPSK modulation. Th vector pre-
ues clearly outperform the others at high
r, regularized channel inversion performs
even better than regularized vector precoding in the low
SNR region. A possible reason for the performance loss
of regularized vector precoding at low SNR is the use of
a finite cubical lattice in this algorithm [48]. Use of dif-
ferent lattice strategies may result in improved perform-
ance.
4.2.5. Tomlinson-Harashima Precoding
Tomlinson-Harashima precoding (THP) is a nonlinear
precoding technique originally developed for SISO sys-
tems for temporal pre-equalization of ISI and is equiva-
lent to moving the decision feedback part of the decision
feedback equalizer (DFE) to the transmitter [59]. How-
ever, THP can also be applied to MU-MIMO downlink
systems for MUI mitigation in the spatial domain.
T
10
R
M
e
coding techniq
SNR. Howeve
Two MU-MIMO downlink transmission schemes util-
izing THP are described in [57]. The first one called SO
THP combines SO and THP to improve performance by
eliminating residual MUI. SO THP involves successive
BD, reordering of the users and finally,HP. Figure 53
shows the block diagram of the SO THP system (taken
from [57] with a slight notational change). Here P repre-
sents the combined precoding matrix for all users gener-
ated by SO, given by Equation 64. H is the channel mat-
rix and D represents the combined demodulation (receive
filtering) matrix. The lower triangular feedback matrix B
is generated in the last step and is used for THP. In order
to generate matrix B, the users are first arranged in the
reverse order of precoding and then the lower diagonal
Figure 53. SO THP system block diagram [57].

F. KHALID ET AL. 244
ngular
va
s at the transmitter. Detailed description of SO THP is
provided in [60].
The other scheme called MMSE THP [61] combines
MMSE precoding and THP to eliminate the MUI below
the main diagonal of the equivalent combined channel
matrix. MMSE THP is an iterative precoding technique.
The users are first arranged according to some optima
orderi alcu-
equivalent combined channel matrix (which includes
precoding and demodulation) is calculated, with si
lues on the main diagonal. The elements in each row
of this matrix are then divided by the corresponding sin-
gular values to obtain the feedback matrix B. The order
in which THP precoding is applied to the users’ data
streams is opposite to the order in which their precoding
matrices are generated. Therefore, THP precoding starts
with the data stream of the first user whose precoding
matrix 1 P was generated last.
Use of THP results in increased transmit power and
for this reason, a modulo operator is introduced at the
transmitter and the receiver so that the constellation
points are kept within certain boundaries. At the receiver,
each data stream is divided by the corresponding singular
value before applying the modulo operator, which en-
sures that the constellation boundaries remain the same
a
l
ng criterion and the precoding matrix P is c
lated column by column starting from the last user K.
The i-th column of P corresponding to the i-th user is
obtained using the coresponding i rows (first i rows for
user K) of the channel matrix H according to the MMSE
criterion, given by

1
T
H
H
M


PHHIH (75)
where

2
,
tr
R
n
M
T
P
HH T
P

   
PxxP
T
P represents the total transmit power, x is the data
vector to be transmitted and 2
n

represents the variance
of the zero-mean circularly symmetric c omplex Gaussian
(ZMCSCG) noise. THP is then applied to eliminate the
MUI seen by the i-th user from the previous 1i

users.
Figure 54 compares the 10% outage capacity of SO THP
and MMSE THP schemes for a MU-MIMO downlink
system consisting of 4 single-antenna users and 4 BS
transmit antennas, denoted as {1, 1, 1, 1}  4 antenna
configuration. Results for ZF channel inversion and a
{2, 2}  4 TDMA system are also provided.
4.2.6. Successive MM SE Pre coding
The Successive MMSE (SMMSE) precoding scheme
proposed in [57] addresses the problem of performance
degradation associated with MMSE precoding when clo-
sely spaced receive antennas are used, like in case of
multi-antenna UEs. SMMSE involve
culating the columns of the combine
re each column represents a beamforming vector
to a particular receive antenna.
Consider the system model of Subsection7 where
each of the K users is equipped with
s successively cal-
d precoding matrix
P, whe
corresponding 3.
i
R
M
receive an-
tennas for 1, ,iK

 and i P represents the precoding
matrix for the i-th user consisting of i
R
M
columns,
each corresponding to a receive antenna. For the j-th
receive antenna of the i-th user, the matrix


j
i
H is de-
fined as

,111
T
jTTT T
iijii K 





HhH HHH (76)
where ,
T
ij
h represents the j-th row of the i-th user’s
channel matrix i H. The correspond ing colu mn of i P is
then calculated using the MMSE criterion and is equal to
e first column of the matrix
th







1
,T
H
H
jj j
ijiiMi


PHHIH (77)
All columns of i P are calculated in this manner and
this process is repeated for all users to obtain the com-
bined precoding matrix P. After precoding, the equiva-
lent combined channel matrix is given by
R
R
M
M

HP 
which is block diagonal for high SNR values, resulting in
ligh
a ing
or Daxim
applied th
rop
set of K SU-MIMO channels. Therefore, any SU-
MIMO technique e.g. eigen-beamformfor capacity
maximization for mum diversity and array
gain can be the i-t user’s equivalent channel
matrix ii HP. SMMSE precoding has stly higher
complexity than BD [57]. A reduced complexity version
called per-user SMMSE (PU-SMMSE) is posed in
[62].
ET
o
Figure 54. 10% outage capacity of SO THP and MMSE
THP f or {1, 1, 1, 1}  4 configuration [57].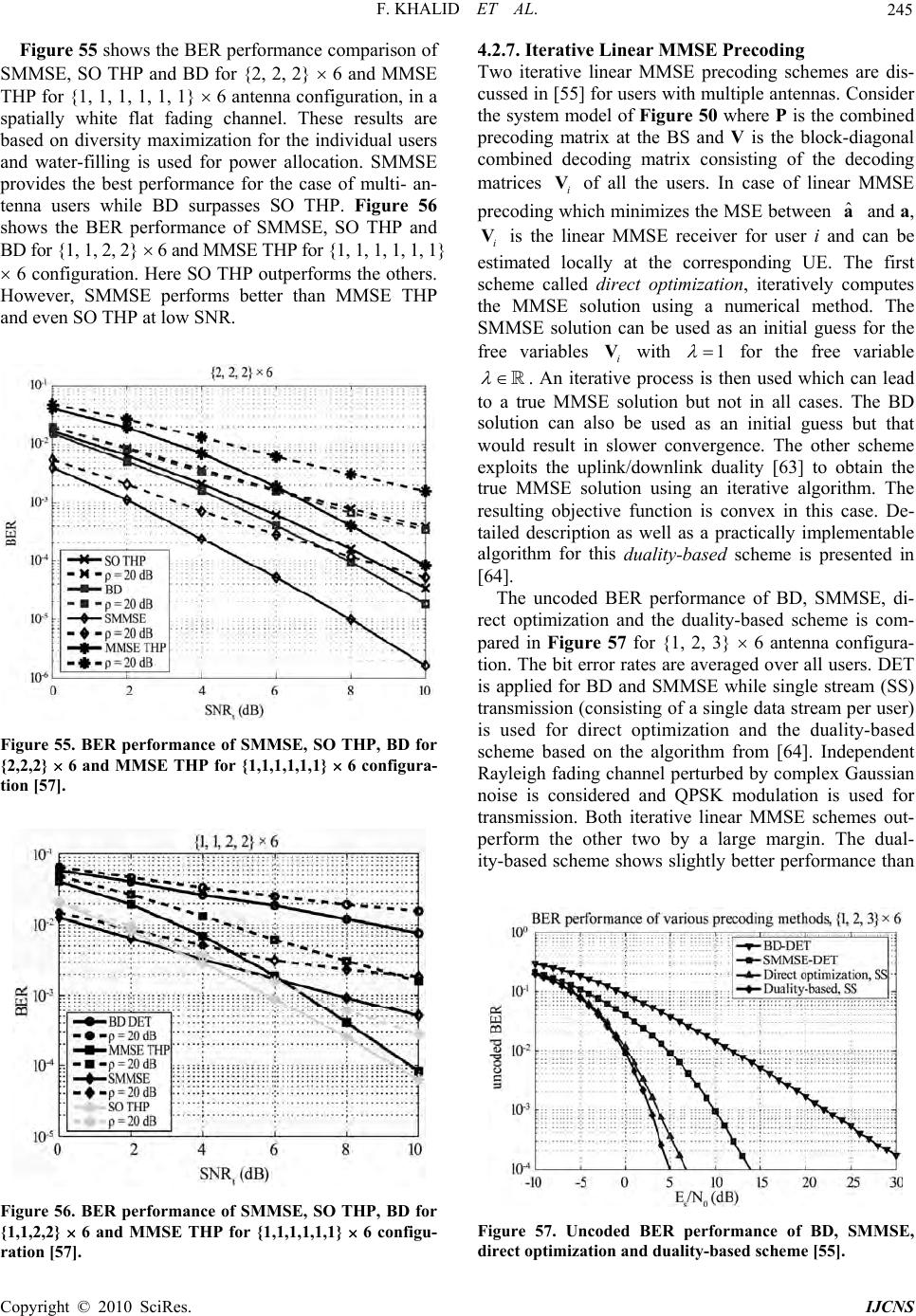

F. KHALID ET AL.
245
es the best performance for the case of multi- an-
tenna users while BD surpasses SO THP. Figure 56
hows the BER performance of SMMSE, SO THP and
BD for {1, 1, 2, 2}  6 and MMSE THP for {1, 1, 1, 1, 1, 1}
 6 configuration. Here SO THP outperforms the others.
However, SMMSE performs better than MMSE THP
and even SO THP at low SNR.
Figure 55 shows the BER performance comparison of
SMMSE, SO THP and BD for {2, 2, 2}  6 and MMSE
THP for {1, 1, 1, 1, 1, 1}  6 antenna configuration, in a
spatially white flat fading channel. These results are
based on diversity maximization for the individual users
and water-filling is used for power allocation. SMMSE
provid
s
Figure 55. BER performance of SMMSE, SO THP, BD for
{2,2,2}  6 and MMSE THP for {1,1,1,1,1,1}  6 configura-
tion [57].
Figure 56. BER performance of SMMSE, SO THP, BD for
{1,1,2,2}  6 and MMSE THP for {1,1,1,1,1,1}  6 configu-
ration [57].
4.2.7. Iterative Linear MMSE Precoding
Two iterative linear MMSE precoding schemes are dis-
cussed in [55] for users with multiple antennas. Consider
the system model of Figure 50 where P is the combined
precoding matrix at the BS and V is the block-diagonal
combined decoding matrix consisting of the decoding
matrices of all the users. In case of linear MMSE
precodinich minimizes the MSE between and a,
is the linear MMSE receiver for user i ad can be
ated locally at the corresponding UE. Te first
edirect optimization, iteratively computes
using a numerical me. The
SMMSE soltion can be used as an initial guess for the
with
i
V
g wh
called
the MMSE solution
u
variables
ˆ
a
n
h
thod
i
V
estim
schem
free i V1

 for the free variable


. An iterative process is then used which can lead
to a true MMSE solution but not in all cases. The BD
he uplink/downlink duality [63] to obtain the
ue MMSE solution using an iterative algorithm. The
resulting objective function is convex in this case. De-
tailed description as well as a practically implementable
algorithm for this duality-based scheme is presented in
[64].
The uncoded BER performance of BD, SMMSE, di-
rect optimization and the duality-based scheme is com-
pared in Figure 57 for {1, 2, 3}  6 antenna configura-
tion. The bit error rates are averaged over all users. DET
is applied for BD and SMMSE while single stream (SS)
transmission (consisting of a single data stream per user)
is used for direct optimization and the duality-based
scheme based on the algorithm from [64]. Independent
Rayleigh fading channel perturbed by complex Gaussian
noise is considered and QPSK modulation is used for
transmission. Both iterative linear MMSE schemes out-
perform the other two by a large margin. The dual-
ity-based scheme shows slightly better performance than
solution can also be used as an initial guess but that
would result in slower convergence. The other scheme
exploits t
tr
Figure 57. Uncoded BER performance of BD, SMMSE,
direct optimization and duality-based scheme [55].
Co pyright © 2010 SciRes. IJCNS

F. KHALID ET AL. 246
on iffere
conve
interesting MU-MIMO downlink transmission scheme
ased solely on instantaneous channel norm feedback is
proposed in [65]. MU-MIMO configuration with multi-
ple base station (BS) antennas and a single antenna at
each UE is considered. The proposed scheme can pro-
vide high multiuser diversity gain by optimizing resource
allocation at the BS while simply utilizing the instanta-
neous channel norm feedback from the UEs.
Figure 59 shows the operatio n of the propo sed system
at the transmitter (BS). The BS initially transmits or-
thogonal pilot signals on all transmit antennas which are
used by each UE to estimate the received signal energy
i.e. the squared norm of the channel vector given by
direct optimizati. This dnce is due to the non-
x objective function used for direct optimization
which occasionally causes the optimization routine to
undesired minima. BD provides the worst performance
because of the zero-forcing constraint.
Figure 58 shows the coded BER performance of these
precoding schemes. A rate 1/2 turbo code is used for
error correction. OFDM based transmission is considered
where the precoding is applied on a per-subcarrier basis.
The ITU Vehicular A channel model is used. Direct op-
timization and the duality-based scheme provide almost
identical performance in this case, far better than BD and
SMMSE.
4.2.8. Partial CSI Feedback
Transmit precoding for downlink MU-MIMO transmis-
sion requires CSI feedback from the users. However,
feedback information consisting entirely of the current
state of the channel may not be accurate enough in case
of rapidly varying channels. Downlink transmission sche-
mes that utilize partial CSI consisting of long-term cha-
nnel statistics along with some instantaneous channel
information like SNR, SINR etc. provide a solution to
this problem while reducing the feedback overhead. An
b
Figure 58.
optimization an
Figure 59. System operation at the transmitter [65].
2
kk
 h (78)
where k h represents the channel vector for the k-th UE
from the  UEs scheduled for transmission. k

is cate-
gorized as channel gain information (CGI) in [65]. This
quantity is then fed back to the BS. The BS estimates the
long-term channel statistics including the channel mean
and the channel covariance matrix, defined as


ˆE|
kkk

hh (79)


ˆE|
H
kkkk

Qhh (80)
This slow varying statistical information is referred to
as channel distribution information (CDI). The CGI feed -
back along with the CDI is used to estimate the SINR
and the optimized beamforming weight vectors for each
of the UEs scheduled for transmission. The SINR for
user k is estimated as


2
\
ˆ
SINR H
kkk
kH
iki k
ik




wQw
wQw


(81)
where is the corresponding beamforming vector,
is the MMSE estimate of the sig-
nce power ratio (SIR)
k
w
ˆ
H
i k
wQ
-inter
k
ˆki i
 w
nal-to fere
and
HH
kiik ki
whh w

is the AWGN power.
The actual data transmission to the scheduled users
then begins. Another set of users can later be scheduled
to achieve better fairness and this process goes on until
the CGI becomes outdated. At this point, BS transmits
the pilot signals again and the whole process is repeated.
simultaneous
users for MU-MIMO downlink transmission with accep-
table performance. The performance degrades in rank-
deficient scenarios and also when the users are spatially
correlated. In case of multi-antenna users, the no. of us
ers en
sser. In practical situations, the BS would generally
erve a larger no. of user
support. Therefore, an eff
du
4.2.9. Multiuser Scheduling
The BS can only support a limited no. of
-
that can be supported simultaneously becomes ev
le
ss than it can simultaneously
icient scheduling algorithm is
required to select the group of users that will be spatially
multiplexed by the BS at a certain time and frequency.
The scheling algorithm should avoid grouping spa-
tially correlated users and maximize system performance
while maintaining fairness toward all users. Fairness
Coded BER performance of BD, SMMSE, direct
d duality-based scheme [55].

F. KHALID ET AL. 247
mit to the
strong users only and the wea
[59]. A fair scheduling schem
weakest-normalized-subchannel-fir
ing proposed in [66] enhances the c
of
ty of a MU-MIMO system is ex-
pressed in terms of the sum capacity (or sum-rate capac-
ity) of the broadcast channel. As mentioned ea
sum capacity represents the maximum achievable system
throughput and is defined as the maximum sum of the
k i
60 illustrates th
a MU-MIMO coff between the
s, depending on the shape
ensures that all users are served including those with
weak channels. Otherwise, the BS will transwhere H is the channel matrix, xx
R is the transmit sig-
nal covariance matrix, nn R is covariance matrix of the
additive ZMCSCG noise with variance 2
n

and P
represents the total transmit power. The sum capacity is
obtained by iteratively computing the best transmit co-
variance matrix xx R for a given noise covariance and
then computing the least favorable noise covariance ma-
trix nn R for the given transmit covariance. It is also
shown that decision-feedback precoding or dirty paper
ker ones will be ignored
e called the strongest-
st (SWNSF) schedul-
overage and capacity
MU-MIMO systems while requiring only a limited
amount of feedb ac k.
4.3. MU-MIMO Capacity
The maximum capacico
n total transmit
power constraint. The DPC achievable rate region for the
case of multi-antenna users is formulated in [67] and i
also discussed in [69]. Further research work is required
on the capacity of fading MIMO broadcast channels.
channels co
cis
ding is the optimal precoding strategy capable of
achieving the sum capacity. In [68], it has been proved
that the capacity region of the Gaussian MIMO-BC with
single-antenna users is equivalent to the dirty paper cod-
ing (DPC) rate region under a certai
rlier, the
downlinnformation rates of all the users [48]. Figure
e capacity region and the sum capacity of
hannel with two users. Clearly, achieving
the sum capacity requires some trade
capacities of the individual user
of
s
the capacity region.
It has been shown in [67] that the sum capacity of a
Gaussian MIMO broadcast channel with an arbitrary no.
of BS transmit antennas and multi-antenna users, is the
saddle-point of a minimax problem and (assuming
eal-valued signals) is given by [49,67] r


The capacity of MIMO-MAC nstitutes a
relatively simple problem. The capacity of any MAC
is given as the convexlosure of the union of rate
regions corr esponding to every produ ct input dtribution




1
K
pu pu satisfying certain user-by-user power
constraints, where 1N
k
u is the k-th user’s trans-
mitted signal. Hoer, the convex hull operation is not
required for the Gaussian MIMO-MAC and only the
Gaus inputs need to be considered. This can be writ-
wev
sian

2
,Tr( )
0,
min max log
2det n
kk
BC P
C




xx
nn nn
xx nn
R
RR nn
R
(82)
det HHR HR
1
ten as [69]



g 1, ,
H
iii
iSSK 


1
0,Tr
,,
;1
iii
K
H
MAC Pi i
iS
RR
CR
 
:
lo
2






 




IHQ H (83)


QQ
PH


where


1,, K
PPP represents the set of transmit
powers corresponding to each of the K users,

de-
notes the determinant and i R, i Q and i H represent
the rate vector, spatial covariance matrix and the channel
matrix respectively for the i-th user. A general expres-
sion for the capacity regions of fading MAC channels is
also given in [69].
ptimization
Convex optimization methods provide a powerful set of
tools for solving optimization problems expressed in
convex form. However, most engineering problems are
not convex
5. Convex O
when directly formulated and need to be re-
formulated in a convex form in order to apply convex
optimization. Two methods are commonly used for this
reformulation. The first method is to use a change of
Figure 60. The capacity region and sum capacity of a two-
user MU-MIMO channel [48].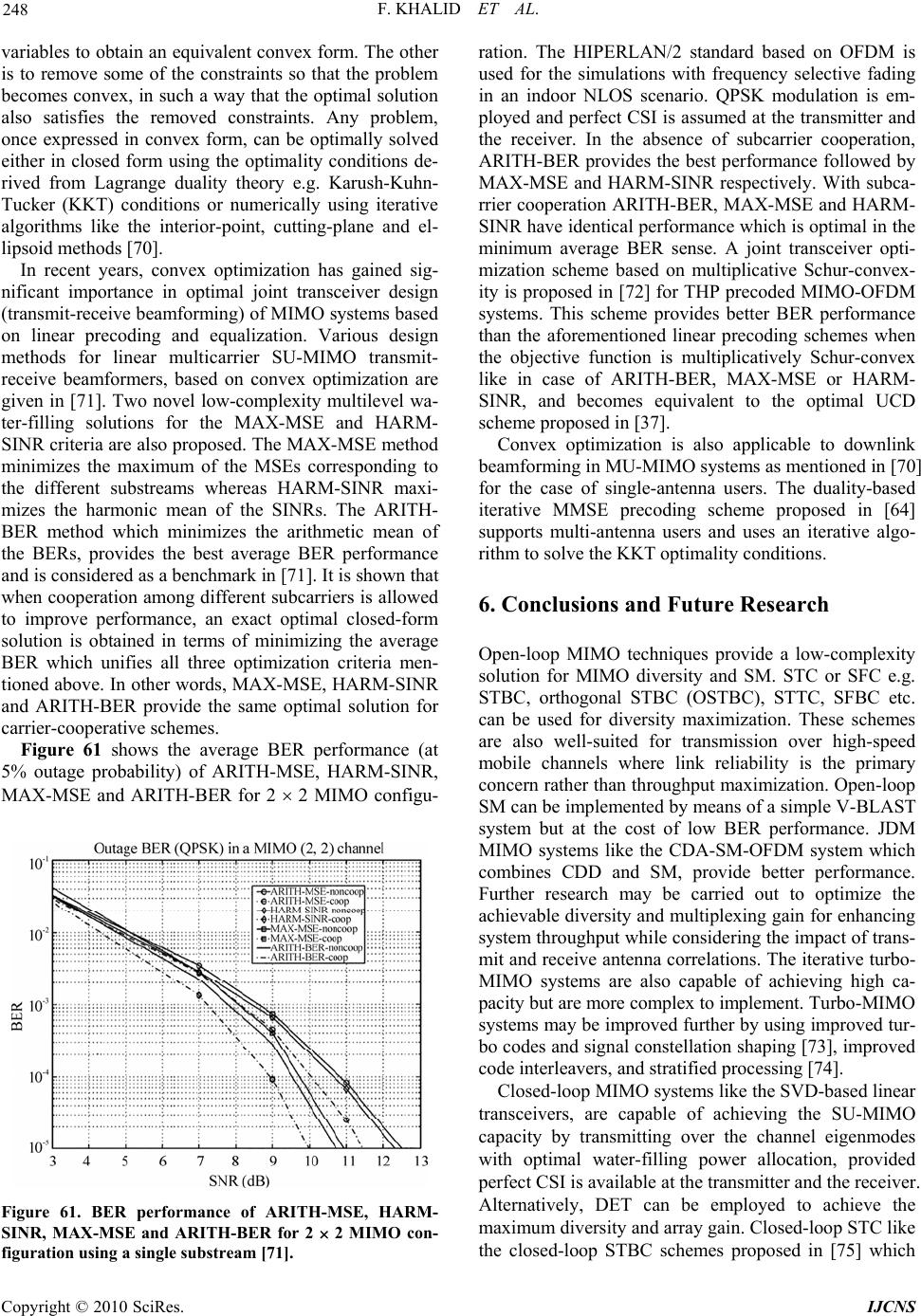

F. KHALID ET AL. 248
variables to obtain an equivalent convex form. The other
is to remove some of the constraints so that the problem
becomes convex, in such a way that the optimal solution
also satisfies the removed constraints. Any problem,
once expressed in convex form, can be optimally solved
either in closed form using the optimality conditions de-
rived from Lagrange duality theory e.g. Karush-Kuhn-
ucker (KKT) conditions or numerically using iterative
algorithms like the interior-point, cutting-plane and el-
lipsoid methods [70].
In recent years, convex optimization has gained sig-
nificant importance in optimal joint transceiver design
(transmit-receive beamforming) of MIMO systems based
on linear precoding and equalization. Various design
methods for linear multicarrier SU-MIMO transmit-
receive beamformers, based on convex optimization are
given in [71]. Two novel low-complexity multilevel wa-
ter-filling solutions for the MAX-MSE and HARM-
SINR criteria are also proposed. The MAX-MSE method
minimizes the maximum of the MSEs corresponding to
the different substreams whereas HARM-SINR maxi-
mizes the harmonic mean of the SINRs. The ARITH-
BER method which minimizes the arithmetic mof
oration am
ave
oimi
s the average BER performance (at
ARITH-MSE, HARM-SINR,
or 2  2 MIMO configu-
T
ean
the BERs, provides the best average BER performance
and is considered as a benchmark in [71]. It is shown that
peowhen cong different subcarriers is allowed
to improve performance, an exact optimal closed-form
solution is obtained in terms of minimizing the rage
BER which unifies all threeptzation criteria men-
tioned above. In other words, MAX-MSE, HARM-SINR
and ARITH-BER provide the same optimal solution for
carrier-cooperative schemes.
Figure 61 show
% outage probability) of 5
MAX-MSE and ARITH-BER f
Figure 61. BER performance of ARITH-MSE, HARM-
SINR, MAX-MSE and ARITH-BER for 2  2 MIMO con-
figuration using a single substream [71].
rrier cooperation ARITH-BER, MAX-MSE and HARM-
SINR have identical performance which is optimal in the
minimum average BER sense. A joint transceiver opti-
mization scheme based on multiplicative Schur-convex-
ity is proposed in [72] for THP precoded MIMO-OFDM
systems. This scheme provides better BER performance
than the aforementioned linear precoding schemes when
the objective function is multiplicatively Schur-convex
like in case of ARITH-BER, MAX-MSE or HARM-
SINR, and becomes equivalent to the optimal UCD
scheme proposed in [37].
Convex optimization is also applicable to downlink
beamforming in MU-MIMO systems as mentioned in [70]
for the case of single-antenna users. The duality-based
iterative MMSE precoding scheme proposed in [64]
supports multi-antenna users and uses an iterative algo-
rithm to solve the KKT optimality conditions.
6. Conclusions and Future Research
ration. The HIPERLAN/2 standard based on OFDM is
used for the simulations with frequency selective fading
in an indoor NLOS scenario. QPSK modulation is em-
ployed and perfect CSI is assumed at the transmitter and
the receiver. In the absence of sub
ARITH-BER provides the best performance followed by
MAX-MSE and HARM-SINR respectively. With subca-
an be used for diversity maximization. These schemes
are also well-suited for transmission over high-speed
mobile channels where link reliability is the primary
concern r ather than throu ghput maximization. Op en-loop
SM can be implemented by means of a simple V-BLAST
system but at the cost of low BER performance. JDM
MIMO systems like the CDA-SM-OFDM system which
combines CDD and SM, provide better performance.
Further research may be carried out to optimize the
achievable diversity and multiplexing gain for enhancing
system throughput wh ile considering the impact of trans-
mit and receive antenna correlations. The iterative turbo-
MIMO systems are also capable of achieving high ca-
pacity but are more complex to implement. Turbo-MIMO
systems may be improved further by using improved tur-
bo codes and signal constellation shaping [73], improved
code interleavers, and stratified processing [74].
nel eigenmodes
carrier cooperation,
Open-loop MIMO techniques provide a low-complexity
solution for MIMO diversity and SM. STC or SFC e.g.
STBC, orthogonal STBC (OSTBC), STTC, SFBC etc.
c
Closed-loop MIMO systems like the SVD-based linear
transceivers, are capable of achieving the SU-MIMO
capacity by transmitting over the chan
with optimal water-filling power allocation, provided
perfect CSI is available at the transmitter and the receiver.
Alternatively, DET can be employed to achieve the
maximum diversity and array gain. Closed-loop STC like
the closed-loop STBC schemes proposed in [75] which

F. KHALID ET AL.
249
perform-
provides
tems. The
igher complexity Turbo-MUD scheme achieves better
le com-
pl
support more than two transmit antennas, also provide
diversity maximization. The GMD-MIMO scheme de-
composes the MIMO channel into identical subchannels
and attempts to combine MIMO diversity and SM in an
optimal manner. MAX-MSE, HARM-SINR and
ARITH-BER methods based on convex optimization
provide optimal average BER performance for multi-
stream transmission when subcarrier cooperation is al-
lowed. However, the GMD and convex optimization
approaches assume the availability of full CSI at the
transmitter and the receiver which is not always the case
e.g. in rapidly changing mobile channels. Therefore, the
performance of these schemes with imperfect feedback
needs to be evaluated for practical implementation. Use
of convex optimization methods for designing optimal
linear transceivers utilizing partial CSI also need to be
investigated.
For the MU-MIMO uplink, the LAST-MUD scheme
ased on V-BLAST detection provides goodb
ance for CDMA systems. The SMMSE MUD
acceptable performance for MIMO-OFDM sys
h
performance and can jointly detect the transmit antennas
of each multi-antenna user. Use of different turbo detec-
tion strategies, joint detection of all users and extension
to multicarrier systems may be investigated in future.
The GA-assisted MUDs, particularly the TTCM-assisted
IGA-MUD provide near-ML detection performance for
SDMA-OFDM systems and also perform reasonably
well in certain rank-deficient scenarios. The complexity
is high but increases slowly with the no. of users as
compared to the ML-MUD. GA-assisted MUDs can also
incorporate joint channel estimation and symbol detec-
tion. Future research work may include extending the
GA-assisted MUD schemes to support multi-antenna
users and development of more efficient GAs to reduce
system complexity. Use of artificial intelligence (AI)
techniques like the radial basis function (RBF) based
artificial neural networks (ANNs) should also be ex-
plored for multiuser detection.
Coming to the MU-MIMO downlink, SMMSE pre-
coding performs reasonably well with manageab
exity. The nonlinear dirty paper coding techniques are
capable of achieving the sum capacity of Gaussian mul-
tiuser channels with single-antenna users. The iterative
linear MMSE techniques like direct optimization and the
duality-based scheme which uses convex optimization,
provide excellent uncoded and coded BER performance
for single stream transmission. Further research is re-
quired to develop MU-MIMO downlink transmission
schemes capable of supporting SM for individual
multi-antenna mobile users. Transmission schemes based
on partial CSI which require minimal CSI feedback from
the users represent the most suitable choice for practical
implementation. Convex optimization tools might be
useful in designing joint transmit-receive beamforming
systems less prone to errors resulting from imperfect CSI.
Research efforts are also needed for developing efficient
multiuser scheduling schemes that maintain fairness to
the users while minimizing the loss of system capacity.
Determining the sum capacity and capacity regions for
fading MU-MIMO downlink channels with multi-an-
tenna users is als o an area for future research.
Accurate channel estimation is of prime importance in
MIMO communications. Channel estimation errors may
result in severe performance degradation. Therefore,
research efforts are continuing for further improvements
in this domain. A broadband wireless transmission tech-
nique called orthogonal frequency- and code-division
multiplexing (OFCDM) [76] has recently gained promi-
nence as a better alternative to OFDM. OFCDM readily
supports MIMO techniques and extensive research
would be required to realize the full potential of MIMO-
OFCDM systems.
7. References
[1] D. Gesbert, M. Shafi, D.-S. Shiu, P. J. Smith, and A.
Naguib, “From theory to practice: An overview of MIMO
space-time coded wireless systems,” IEEE Journal on
Selected Areas in Communications, Vol. 21, No. 3, pp.
281–302, April 2003.
[2] Y. Jiang, J. Li, and W. W. Hager, “Joint transceiver de-
sign for MIMO communications using geometric mean
decomposition,” IEEE Transactions on Signal Processing,
Vol. 53, No. 10, pp. 3791–3803, October 2005.
[3] M. Jiang and L. Hanzo, “Multiuser MIMO-OFDM for
next-generation wireless systems,” Proceedings of the
IEEE, Vol. 95, No. 7, pp. 1430–1469, July 2007.
[4] K. W. Park, E. S. Choi, K. H. Chang, and Y. S. Cho, “An
MIMO-OFDM technique for high-speed mobile chan-
nels,” in Proceedings of Vehicular Technology Confer-
ence, Vol. 2, pp. 980–983, April 2003.
[5] M. S. Gast, “802.11 wireless networks: The definitive
guide,” 2nd edition, O’Reilly, April 2005.
[6] Wi-Fi Alliance, “WiFi CERTIFIED™ 802.11n draft 2.0:
Longer-range, faster-throughput,multimedia grade WiFi®
networks,” 2007. http://wi-fi.org/whiteppaper_80211n_
draft2_technical.php.
[7] FierceBroadbandWireless, “IEEE approves EWC 802.11n
as first draft,” 24 January 2006. http://www. fiercebroad-
bandwireless.com/story/ieee-approves-ewc-802-11n-as-
first-draft/2006-01-25.
[8] Y. Sun, M. Karkooti, and J. Cavallaro, “High throughput,
parallel, scalable LDPC encoder/decoder architecture for
OFDM systems,” in Proceedings of IEEE Workshop on
Circuits and Systems, pp. 225–228, October 2006.
[9] H. N. Niu and C. Ngo, “Diversity and multiplexing
switching in 802.11n MIMO systems,” in Proceedings of
40th Asilomar Conference on Signals, Systems and Com-
Co pyright © 2010 SciRes. IJCNS

F. KHALID ET AL. 250
put sys-
ss Mesh Networks, in Proceedings of 2nd
IEEE Workshop on Wireless Mesh Networks (WiMesh
47, 25–28 September 2006.
2.16e™-2005 and IEEE Std 802.16™-
ation in licensed bands and Corri-
October
ireless
works.com.
2005.
10932.00&id=1213544.
d
upporting ve-
-03), “Evolved universal
TS 36.211 V8.1.0 (2007-11), “Evolved universal
G. D. Golden, and R.
dings of 1998 URSI International
” in Proceedings
R. Prasad,
April 2007.
puters (ACSSC ’06), pp. 1644–1648, 29 October–1 No-
vember 2006.
[10] P. Kim and K. M. Chugg, “Capacity for suboptimal re-
ceivers for coded multiple-input multiple-out
tems,” Vol. 6, No. 9, pp. 3306–3314, September 2007.
[11] S. Abraham, A. Meylan, S. Nanda, “802.11n MAC de-
sign and system performance,” in Proceedings of IEEE
International Conference on Communications (ICC 2005),
Vol. 5, pp. 2957–2961, 16–20 May 2005.
[12] Cisco Aironet 1250 Series Access Point Q&A. http://www.
cisco.com/en/US/prod/collateral/wireless/ps5678/ps6973/
ps8382/prod_qas0900aecd806b7c82.html.
[13] S. Kim, S.-J. Lee, and S. Choi, “The impact of IEEE
802.11 MAC strategies on multi-hop wireless mesh net-
works,” Wirele
[27]
2006), pp. 38–
14] IEEE Std 80[2004/Cor 1-2005 (Amendment and Corrigendum to IEEE
Std 802.16-2004), “IEEE standard for local and metro-
politan area networks Part 16: Air Interface for fixed and
mobile broadband wireless access systems amendment 2:
Physical and medium access control layers for combined
fixed and mobile oper
gendum 1,” 28 February 2006.
[15] IEEE Std 802.16™-2004, “IEEE standard for local and
metropolitan area networks Part 16: Air interface for
fixed broadband wireless access systems,” 1
2004.
[16] J. G. Andrews, A. Ghosh, and R. Muhamed, “Fundamen-
tals of WiMAX: Understanding broad-band w
A. Va
networking,” Prentice Hall, 2007.
[17] I. Kambourov, “MIMO aspects in 802.16e WiMAX
OFDMA,” WiMAX Tutorial, Siemens PSE MCS RA 2,
22 November 2006.
[18] Nokia Siemens Networks, “Advanced antenna systems
for WiMAX.” http://www.nokiasiemensnet
[19] S. Nanda, R. Walton, J. Ketchum, M. Wallace, and S.
Howard, “A high-performance MIMO OFDM wireless
LAN,” IEEE Communications Magazine, Vol. 43, No. 2,
pp. 101–109, February
[20] Agilent Technologies, “Mobile WiMAX 802.16 Wave 2
Features.” http://www.home.agilent.com/agilent/editorial.
jspx? action=downl oad& cc=US&lc= eng &ckey=1213544
&nid=-536902344.5369
[21] IEEE C802.16m-07/069, “Draft IEEE 802.16m evalua-
tion methodology document,” IEEE 802.16 Broadband
Wireless Access Working Group, 2007.
[22] WiMAX Forum®, “Deployment of Mobile WiMAX™
Networks by Operators with Existing 2G & 3G Net-
works,” 2008. http://www.wimaxforum.org/technology/
downloads/deployment_of_mobile_wimax. pdf.
[23] C. Ribeiro, “Bringing wireless access to the automobile:
[36]
A comparison of Wi-Fi, WiMAX, MBWA, and 3G,” 21st
Computer Science Seminar, 2005.
[24] B. M. Bakmaz, Z. S. Bojković, D. A. Milovanović, an
M. R. Bakmaz, “Mobile broadband networking based on
IEEE 802.20 standard,” in Proceedings of 8th Interna-
tional Conference Telecommunications in Modern Satel-
lite, Cable and Broadcasting Services (TELSIKS 2007),
pp. 243–246, 26–28 September 2007.
[25] IEEE Std 802.20™-2008, “IEEE standard for local and
metropolitan area networks Part 20: Air interface for mo-
bile broadband wireless access systems s
hicular mobility–physical and media access control layer
specification,” 29 August 2008.
[26] 3GPP TS 36.201 V8.1.0 (2007-11), “LTE physical layer
– general description (Release 8),” 3GPP TSG RAN,
2007.
J. Zyren, “Overview of the 3GPP long term evolution
physical layer,” White Paper, Freescale Semiconductor,
Inc., 2007.
[28] 3GPP TR 25.913 V7.3.0 (2006-03), “Requirements for
evolved UTRA (E-UTRA) and evolved UTRAN
(E-UTRAN) (Release 7),” 3GPP TSG RAN, 2006.
[29] 3GPP TS 36.300 V8.4.0 (2008
terrestrial radio access (E-UTRA) and evolved universal
terrestrial radio access network (E-UTRAN); Overall de-
scription; Stage 2 (Release 8),” 3GPP TSG RAN, 2008.
[30] 3GPP
terrestrial radio access (E-UTRA); Physical channels and
modulation (Release 8),” 3GPP TSG RAN, 2007.
[31] P. W. Wolniansky, G. J. Foschini,
lenzuela, “V-BLAST: An architecture for realizing
very high data rates over the rich-scattering wireless
channel,” in Procee
Symposium Signals, Systems, and Electronics, pp.
295–300, 29 September–2 October 1998.
[32] S. T. Chung, A. Lozano, and H. C. Huang, “Approaching
eigenmode BLAST channel capacity using V-BLAST
with rate and power feedback,” in Proceedings of IEEE
VTC 2001 Fall, Vol. 2, pp. 915–919, 7–11 October 2001.
[33] Q. P. Cai, A. Wilzeck, C. Schindler, S. Paul, and T. Kai-
ser, “An exemplary comparison of per antenna rate con-
trol based MIMO-HSDPA receivers,” in Proceedings of
13th European Signal Processing Conference (EUSIPCO
2005), 4–8 September, 2005.
[34] R. Gowrishankar, M. F. Demirkol, and Z. Q. Yun,
“Adaptive modulation for MIMO systems and throughput
evaluation with realistic channel model,
of 2005 International Conference on Wireless Networks,
Communications and Mobile Computing, Vol. 2, pp.
851–856, 13–16 June 2005.
[35] M. I. Rahman, S. S. Das, E. de Carvalho, and
“Spatial multiplexing in OFDM systems with cyclic delay
diversity,” in Proceedings of IEEE Vehicular Technology
Conference, pp. 1491–1495, 22–25
H. Busche, A. Vanaev, and H. Rohling, “SVD based
MIMO precoding and equalization schemes for realistic
channel estimation procedures,” Frequenz Journal of
RF-Engineering and Telecommunications, Vol. 61, No.

F. KHALID ET AL. 251
decomposition
ommunications,” IEEE
lathurai and S. Haykin, “Turbo-BLAST for wire-
ctober 2002.
2, No.
-
ptember 2007.
25 April 2007.
ations: An International
Vol. 42,
aardt, “Improved diversity on the
. Elvira, J. Via, D. Ramirez, J. Perez, J.
s Communications and
ber
th
“Efficient
Speech, and Signal
tschick, “MMSE ap-
7–8, pp. 146–151, July–August 2007.
[37] Y. Jiang and J. Li, “Uniform channel for uplink of multi-user MIMO systems,” in Proceedings of
European Conference on Wireless Technology ’05, pp.
113–116, 3–4 October 2005.
[52] I. Santamaria, V
MIMO communications,” in Proceedings of 38th Asilo-
mar Conference on Signals, System, and Computers,
7–10 November 2004.
[38] S. Haykin, M. Sellathurai, Y. de Jong, and T. Willink,
“Turbo-MIMO for wireless c
Iban
Communications Magazine, Vol. 42, No. 10, pp. 48–53,
October 2004.
[39] M. Sel
less communications: Theory and experiments,” IEEE
Transactions on Signal Processing, Vol. 50, No. 10, pp.
2538–2546, O
[40] D. J. Love, R. W. Heath Jr., W. Santipach, and M. L.
Honig, “What is the value of limited feedback for MIMO
channels,” IEEE Communications Magazine, Vol. 4
Netw
10, pp. 54–59, October 2004.
[41] Y. Yuda, K. Hiramatsu, M. Hoshino, and K. Homma, “A
study on link adaptation scheme with multiple code
words for spectral efficiency improvement on OFDM 2002
MIMO systems,” IEICE Transactions on Fundamentals,
Vol. E90A, No. 11, pp. 2413–2422, November 2007.
[42] Z. G. Zhou, H. Y. Yi, H. Y. Guo, and J. T. Zhou, “A par-
tial feedback scheme for MIMO systems,” in Proceedings
of WiCom 2007, pp. 361–364, 21–25 September 2007.
[43] A. Heidari, F. Lahouti, and A. K. Khandani, “Enhancing
closed-loop wireless systems through efficient feedback
reconstruction,” IEEE Transactions on Vehicular Tech-
nology, Vol. 56, No. 5, pp. 2941–2953, Se
[44] H. R. Bahrami and T. Le-Ngoc, “MIMO precoding struc-
tures for frequency-flat and frequency-selective fading
channels,” in Proceedings of 1st International Conference
on Communications and Electronics (ICCE ’06), pp.
193–197, 10–11 October 2006.
[45] M. Tsutsui and H. Seki, “Throughput performance of
downlink MIMO transmission with multi-beam selection
using a novel codebook,” in Proceedings of IEEE VTC
2007-Spring, pp. 476–480, 22–
[46] K. W. Park and Y. S Cho, “An MIMO-OFDM technique
for high-speed mobile channels,” IEEE Communications
Letters, Vol. 9, No. 7, pp. 604–606, July 2005.
[47] A. A. Hutter, S. Mekrazi, B. N. Getu, and F. Platbrood,
“Alamouti-based space-frequency coding for OFDM,”
Wireless Personal Communic
[60]
Journal, Vol. 35, No. 1–2, pp. 173–185, October 2005.
[48] Q. H. Spencer, C. B. Peel, A. L. Swindlehurst, and M.
Haardt, “An introduction to the multi-user MIMO
downlink,” IEEE Communications Magazine,
No. 10, pp. 60–67, October 2004.
[49] A. Paulraj, R. Nabar, and D. Gore, “Introduction to
space-time wireless communications,” Cambridge, UK,
Cambridge University Press, 2003.
[50] S. Sfar, R. D. Murch, and K. B. Letaief, “Layered
space-time multiuser detection over wireless uplink sys-
tems,” IEEE Transactions on Wireless Communications,
Vol. 2, No. 4, July 2003.
[51] V. Stankovic and M. H
ez, R. Eickoff, and F. Ellinger, “Optimal MIMO
transmission schemes with adaptive antenna combining
in the RF path,” in Proceedings of 16th European Signal
Processing Conference (EUSIPCO 2008), 25–29 August
2008.
[53] N. Veselinovic, T. Matsumoto, and M. Juntti, “Iterative
MIMO turbo multiuser detection and equalization for
STTrC-coded systems with unknown interference,”
EURASIP Journal on Wireles
orking, Vol. 2004, No. 2, pp. 309–321, 2004.
[54] Q. Spencer and M. Haardt, “Capacity and downlink
transmission algorithms for a multi-user MIMO channel,”
in Proceedings of 36th Asilomar Conference on Signals,
Systems, and Computers, pp. 1384–1388, Novem
.
[55] B. Bandemer, M. Haardt, and S. Visuri, “Linear MMSE
multi-user MIMO downlink precoding for users wi
multiple antennas,” in Proceedings of IEEE 17th Interna-
tional Symposium on Personal, Indoor and Mobile Radio
Communications (PIMRC’06), pp. 1–5, 11–14 September
2006.
[56] Q. H. Spencer, A. L. Swindlehurst, and M. Haardt,
“Zero-forcing methods for downlink spatial multiplexing
in multiuser MIMO channels,” IEEE Transactions on
Signal Processing, Vol. 52, No. 2, pp. 461–471, February
2004.
[57] V. Stankovic and M. Haardt, “Multi-user MIMO down-
link precoding for users with multiple antennas,” in Pro-
ceedings of 12th Wireless World Research Forum (WWRF),
Toronto, ON, Canada, November 2004.
[58] M. Costa, “Writing on dirty paper,” IEEE Transactions
on Information Theory, Vol. 29, pp. 439–441, May 1983.
[59] V. Stankovic, M. Haardt, and G. D. Galdo,
multi-user MIMO downlink precoding and scheduling,”
in Proceedings of 1st IEEE International Workshop on
Computational Advances in Multi-Sensor Adaptive
Processing, pp. 237–240, 13–15 December 2005.
V. Stankovic and M. Haardt, “Successive optimization
Tomlinson-Harashima precoding (SO THP) for multi-
user MIMO systems,” in Proceedings of IEEE Interna-
tional Conference on Acoustics,
Processing (ICASSP), Philadelphia, PA, USA, March
2005.
[61] M. Joham, J. Brehmer, and W. U
proaches to multiuser spatio-temporal Tomlinson-Hara-
shima precoding,” in Proceedings of 5th International
ITG Conference on Source and Channel Coding (ITG
SCC’04), pp. 387–394, January 2004.
[62] M. Lee and S. K. Oh, “A per-user successive MMSE
precoding technique in multiuser MIMO systems,” in
Proceedings of IEEE VTC 2007-Spring, pp. 2374–2378,
22–25 April 2007.
Co pyright © 2010 SciRes. IJCNS

F. KHALID ET AL. 252
zghani, M. Joham, R. Hunger, and W. Utschick,
IEEE Transactions on Wireless Communications,
ten, Y. Steinberg, and S. Shamai, “The c
reas in Communications, Vol. 21, No. 5
ommunications, edited by
or multicarrier MIMO chan-
en Brink, “Achieving near-ca-
er 2003.
, pp. 765–769, August 2005.
[63] M. Schubert, S. Shi, E. A. Jorswieck, and H. Boche,
“Downlink sum-MSE transceiver optimization for linear
multi-user MIMO systems,” in Proceedings of 39th Asi-
lomar Conference on Signals, Systems, and Computers,
pp. 1424–1428, October 2005.
[64] A. Me
“Transceiver design for multi-user MIMO systems,” in
Proceedings of ITG/IEEE Workshop on Smart Antennas
(WSA 2006), March 2006.
[65] D. Hammarwall, M. Bengtsson, and B. Ottersten, “Ac-
quiring partial CSI for spatially selective transmission by systems: A unified approach to transceiver optimization
based on multiplicative Schur-convexity,” IEEE Transac-
tions on Signal Processing, Vol. 56, No. 8, August 2008.
[73] B. M. Hochwald and S. t
instantaneous channel norm feedback,” IEEE Transac-
tions on Signal Processing, Vol. 56, No. 3, March 2008.
[66] C.-J. Chen and L.-C. Wang, “Enhancing coverage and
capacity for multiuser MIMO systems by utilizing sched-
uling,”
Vol. 5, No. 5, May 2006.
[67] W. Yu and J. M. Cioffi, “Sum capacity of Gaussian vec-
tor broadcast channels,” IEEE Transactions on Informa-
tion Theory, Vol. 50, No. 9, September 2004.
[68] H. Weingarapac-[75] S. Lambotharan and C. Toker, “Closed-loop space time
block coding techniques for OFDM broadband wireless
access systems,” IEEE Transactions on Consumer Elec-
tronics, Vol. 51, No. 3
ity region of the Gaussian MIMO broadcast channel,” in
Proceedings of ISIT 2004, 27 June–2 July 2004.
[69] A. Goldsmith, S. A. Jafar, N. Jindal, and S. Vishwanath,
“Capacity limits of MIMO channels,” IEEE Journal on
Selected A, pp. [76] Y. Zhou, T.-S. Ng, J. Wang, K. Higuchi, and M. Sawa-
hashi, “OFCDM: A promising broadband wireless access 684–702, June 2003.
[70] D. P. Palomar, A. Pascual-Iserte, J. M. Cioffi, and M. A.
Lagunas, “Convex optimization theory applied to joint
transmitter-receiver design in MIMO channels,” Space-
Time Processing for MIMO C
A. B. Gershman and N. D. Sidiropoulos, Chichester, Eng-
land, Wiley, 2005.
[71] D. P. Palomar, J. M. Cioffi, and M. A. Lagunas, “Joint
tx-rx beamforming design f
nels: A unified framework for convex optimization,”
IEEE Transactions on Signal Processing, Vol. 51, No. 9,
September 2003.
[72] A. A. D’Amico, “Tomlinson-Harashima precoding in MIMO
pacity on a multiple-antenna channel,” IEEE Transactions
on Communications, Vol. 51, No. 3, pp. 389–399, March
2003.
[74] M. Sellathurai and G. Foschini, “A stratified diagonal
layered space-time architecture: Information theoretic and
signal processing aspects,” IEEE Transactions on Signal
Processing, Vol. 51, No. 11, pp. 2943–2954, Novem b
technique,” IEEE Communications Magazine, Vol. 46,
No. 3, March 2008.