J. Service Science & Management, 2010, 3: 143-149
doi:10.4236/jssm.2010.31018 Published Online March 2010 (http://www.SciRP.org/journal/jssm)
143
Allocating Collaborative Profit in
Less-than-Truckload Carrier Alliance
Peng Liu1, Yaohua Wu1*, Na Xu2
1School of Control Science and Engineering, Shandong University, Jinan, China; 2School of Business, Shandong Jian-zhu University,
Jinan, China; *Corresponding Author.
Received September 21st, 2009; revised November 5th, 2009; accepted December 20th, 2009.
ABSTRACT
International Financial Crisis has made the less-than-truckload (LTL) industry face with severe challenges of survival
and development. More and more small and medium-sized LTL carriers choose to collaborate as the potential savings
are large, often in the range 5–15%. A key question is how to distribute profits/savings among the participants. Since
every LTL carriers are guided by their own self-interests and their contributions to the collaboration are quite different,
the proposed allocation method should be a collectively and individually desirable solution. In this paper, we firstly
analyze the profit oppo rtunities from collaboration and present mecha nisms to realize these benefits by two illustrative
examples. Based on the co operative gam e theory, we formula te the LTL co llabo ration game and discuss the well-kn own
profit allocation concepts including Proportional Allocation, Shapley value and Nucleolus. We then propose a new
al-location method named Weighted Relative Savings Model (WRSM) which is in the core and minimizes the maximum
difference between weighted relative sa vings among the participants. Simulation resu lt for real-life instances shows the
effectiveness of WRSM.
Keywords: Cooperative Game, Profit Allocation, Collaborative Transportation
1. Introduction
International Financial Crisis causes a huge decrease in
transportation requests and has made less-than-truckload
(LTL) segment of the trucking industry face with severe
challenges of survival and development. Under this cir-
cumstance, horizontal collaboration becomes a good
choice for small and medium-sized LTL carriers. In the
collaborative alliance, a number of complementary trans-
portation resources from the participants could be inte-
grated and thus more profits could be gained for every
participant compared with their stand-alone operation.
The potential cost savings from collaboration are often
range from 5% to 15%.
Although the benefits from collaboration are appeal-
ing, the key question is how to distribute the collabora-
tive profits among every participant to ensure the estab-
lishment and sustainability of the alliance and realize
the potential of collaboration. Since every participant is
guided by their own self-interests and their contribu-
tions to the collaboration are quite different, the pro-
posed allocation method should be a collectively and
individually desirable solution [1]. The challenge is to
design mechanisms that are fair, reasonable and easy-
to-implement. We will show that the proposed Weight-
ed Relative Savings Model (WRSM) satisfies all these
requirements.
The remainder of the paper is organized as follows. In
Section 2, we analyze the opportunity to increase every
LTL carrier’s profit through collaboration and present
two illustrative examples to demonstrate the mechanisms
to realize these benefits. In Section 3, based on the coop-
erative game theory, we formulate the LTL collaborative
game and discuss the well-known profit allocation con-
cepts. We then propose a new solution method called
Weighted Relative Savings Model (WRSM) which is in
the core and minimizes the maximum difference between
the weighted relative savings among the participants.
Simulation result for real-life instances is presented and
analyzed in Section 4 to show the effectiveness of
WRSM.
2. Profit Opportunities from Collaboration
The construction of LTL carriers’ alliance will enable the
formulation of collaborative transportation system. In
this section, we will analyze the profit opportunities of
this system.

Allocating Collaborative Profit in Less-than-Truckload Carrier Alliance 144
2.1 Collaborative Transportation System
As it is shown in Figure 1, the collaborative transporta-
tion system is a kind of system in which all participants
share the network and transportation resources.
E denotes Terminal Point (TP) which is the boundary
point of the carrier’s business coverage. N denotes
Switch Point (SP), through which the cargos transport to
the carrier’s adjacent business point. W denotes Ex-
change Point (EP) where two or more collaborative car-
riers in the alliance exchange their cargos and transport
the exchanged cargos to their own business point. S
de-notes Shared Point (SDP) which is shared by two or
more collaborative carriers in the alliance. From the sys-
tem–wide point of view, transportation network and
re-sources are shared among all the LTL carriers in the
alliance through EP and SDP which expand the business
scope of every participant.
Resource sharing will help to build more reasonable
transportation plans to better utilize vehicles, reduce
travel time, unloaded distance and lower the total trans-
portation cost effectively.
2.2 Benefits of Collaboration
Cruijssen and Salomon [2] analyze the effect of collabo-
ration for an entire coalition and show, using a case study
that cost savings may range from 5 to 15% and can be
even higher. Ergun et al. [3] note that shippers can re-
duce their “hidden costs” by cooperating, partly due to
higher utilization of their less-than-truckload loading and
asset repositioning capabilities. In the time-constrained
lane covering problem, the savings range is from about
5.5 percent to a little over 13 percent, where the savings
tend to be larger when the size of the instance is larger.
[4] Krajewska and Kopfer [5] show that, using a case
study, cooperation between the two carriers yields a 10%
reduction in the number of vehicles and a 12.46% reduction
in routing cost. In practice, after forming collaborative part-
nerships with others in the Nistevo Network, Georgia-
Figure 1. Collaborative transportation system
Pacific’s percentage of empty movements decreased
from 18% to 3%, which corresponds to $11,250,000
savings yearly [6].
We demonstrate the potential benefits of LTL carrier
collaboration with the following two examples.
1) Backhauling
Consider a network with three cities and two carriers A
and B. We assume that the cost of traveling between two
cities is the same for both carriers and, for simplicity,
that there is no difference in cost between traveling
loaded or empty. We further assume that carrier A has a
contract in place to serve lane (2, 1), (1, 3) and that car-
rier B has a contract in place to serve lane (3, 2). The cost
C and freight F of each lane in the network and other
relevant information are given in Figure 2, where a
dashed line represents repositioning (or empty travel).
Without collaboration, carrier A and B operate indi-
vidually and the corresponding profit of them are
Profit A = F21 + F13 – C21 – C13 – C32 = 1300
Profit B = F32 – C32 – C23 = 400
As it is shown in Figure 3, if carrier A and carrier B
collaborate and carrier A serve lane (3, 2) instead of car-
rier B, they significantly increase their total profit to
2100 by reducing two empty trips. Assume that the profit
allocation rate is 0.75, then the new profit become 1575
for carrier A and 525 for carrier B. Carrier A and B in-
crease their profits by 21% and 31% respectively.
Through collaboration, carrier A reduces its empty trip
and fully utilizes the truck while carrier B does not need
to transport the cargos. But they both gain more benefits
since the total repositioning cost is much lower.
Figure 2. Network information and transportation requests
Figure 3. Collaboration betwee n carrier A and B

Allocating Collaborative Profit in Less-than-Truckload Carrier Alliance 145
2) Lane/Request Exchanging
Consider a network with four cities and two carriers A
and B. We assume that the cost of traveling between two
cities is the same for both carriers and, for simplicity,
that there is no difference in cost between traveling
loaded or empty. We further assume that carrier A has a
contract in place to serve lane (2, 1), (1, 3), (3, 4) and
that carrier B has a contract in place to serve lane (4, 3),
(3, 2). The cost C and freight F of each lane in the
net-work and other relevant information are given in
Figure 4, where a dashed line represents repositioning (or
empty travel).
Without collaboration, carrier A and B operate indi-
vidually and the corresponding profits are 1900 for car-
rier A and 1000 for carrier B.
We assume that the existing contracts are not long term
contractual agreements so can potentially be exchanged
between the carriers [1]. As it is shown in Figure 5, if car-
rier A and carrier B collaborate and exchange lanes (3, 4)
and (3, 2), the corresponding profits are 2100 for carrier A
and 1200 for carrier B. Carrier A and B increase their
profits by 10.5% and 20% respectively.
Through collaboration, the optimal set of cycles cov-
ering the contract lanes are assigned to each carrier.
Empty travels are greatly reduced and total profits are
redistributed between carrier A and carrier B.
Figure 4. Network information and transportation requests
Figure 5. Collaboration betwee n carrier A and B
3. Profit Allocation Problem
Cooperative game theory provides a natural framework
for the profit allocation. There are a set of papers that
join the transportation related profit or cost allocation
problems and cooperative game theory.
Sakawa et al. [7] discuss the production and transpor-
tation profit and cost allocation based on nucleolus in the
fuzzy environment and shows, using actual data, the
usefulness of fuzzy programming and the effectiveness
nucleolus allocation. Sanchez-Soriano et al. [8] study the
core of the transportation games, prove the nonemptiness
of the core for these games and provide some results
about the relationship between the core and the dual op-
timal solutions of the underlying transportation problem.
Sanchez-Soriano et al. [9] study the cost allocation of the
integrated transportation services provided by Alacant
University for students, formulate the problem as tree
buses game, propose the aggregated egalitarian solution
concept and show it is the core of the game. Engevall et
al. [10] formulate the traveling salesman game and vehi-
cle routing game, discuss nucleolus, TSP nucleolus, TSP
demand weighted nucleolus, Shapley value and τ value
respectively. Matsubayashi et al. [11] study a cost alloca-
tion problem arising from hub-spoke network systems
and show that, if the demand across the system has a
block structure and the fixed cost is high, allocating the
cost proportional to the flow that an agent generates be-
longs to the core. Ozener [1] study the cost allocation in
the collaborative transportation procurement network and
discuss the truckload carrier’s collaboration. Krajewska
et al. [5] study the profit sharing problem among carriers
in the horizontal collaboration, discuss the possibilities of
sharing these profit margins fairly among the partners,
apply the Shapley value to determine a fair allocation of
the problem and present numerical results for real-life
and artificial instances.
These papers in general study the existing profit or
cost allocation methods with well-studied properties from
cooperative game theory and present the computational
results for such allocations. However, to the best of our
knowledge, there is no literature on profit allocation for
LTL collaborative transportation problem that considers
both the relative cost savings and contribution differences,
which are very important in the contractual agreement
negotiation of the collaboration. In this section, we will
search for a new profit allocation method that satisfies
these requirements based on the well-known solution
concepts from cooperative game theory.
3.1 Problem Definitions and Assumptions
We formulate the profit allocation for LTL collaborative
transportation problem as a co-operative game


,Nv.

Allocating Collaborative Profit in Less-than-Truckload Carrier Alliance 146

1, 2,...,2Nnn is called the grand coalition
which denotes all collaborative carriers.

vS is the
characteristic function which assigns to each possible
coalition of carriers

SS N a numerical value to be
interpreted as the cost savings realized by the carriers in
coalition S.

i
y
iN is the profit/cost savings allo-
cated to carrier i.

1, 2,..., n
Yyyy is the profit allocation.
It is assumed that all carriers have the opportunity to
form and cooperate in coalition. When coalition S coop-
erates, the total cost

cS is generated and we have
   
,
iS
vSc icSSN


 (1)
Below we discuss some of the most commonly used
profit allocation properties from cooperative game theory.
A profit allocation method that splits the total profit

vN among the carriers iN is said to be efficient
or budget balanced, that is()
i
iN
yvN


.
A profit allocation is said to be individual rational if
no carrier gains less than its “stand alone profit/cost sav-
ing”, which equals to zero. Mathematically, this property
is expressed as({ }),
i
yvi iN.
The core of the game is defined as those profit alloca-
tions

1, 2,..., n
Yyyy that satisfy the conditions
(),
i
iS
yvSSN


 (2)
()
i
iN
yvN


 (3)
That is, no single carrier or coalition of carriers would
be better off if they decide to opt out and collaborate only
among themselves. A profit allocation in the core is said
to be stable.
For each coalition S and a given profit allocation

1, 2,..., n
Yyyy, we can compute the excess
(,) (),
i
iS
eY SyvSSN


 (4)
which expresses the difference between the sum of the
profits allocated to its members and the total profit of a
coalition. For a given profit allocation, the vector of all
excesses can be thought of as a measure of how far the
profit allocation is from the core. If a profit allocation is
not in the core, at least one excess is negative.
3.2 Well-known Profit Allocation Concepts
3.2.1 Proportional Allocation
In practice, the most commonly used solution is to dis-
tribute the collaborative profit/cost savings of the grand
alliance


vN among the carriers equally, weighted
with each carrier’s stand alone cost. This is expressed as


,
ii
y
rvN iN

 (5)
where i
r is equal to



  
iN
ci ci

.
Although this method is easy to understand, easy to
show and easy to compute, it is not stable from a coop-
erative game theoretic point of view since a participant
will pay, possibly, more than when operating alone [1].
3.2.2 Shapley Value
A well-known cost allocation method is the Shapley
Value, which is defined for each player as the weighted
average of the player’s marginal contribution to each
subset of the collaboration [12]. Shapley Value can be
interpreted as the average marginal contribution each
member would make to the grand coalition if it were to
form one member at a time [13]. Mathematically,
Shapley Value is expressed as



 


!1! \,
!
iiS
ns s
yvSvSiiN
n





where s denotes the number of carriers in coalition S.
Shapley Value is the unique allocation method to sat-
isfy three axioms: dummy, additivity and equal treatment
of equals. Although Shapley Value may return cost allo-
cations in the core for some instances, there are many
instances where allocations based on Shapley Value are
not stable [1].
3.2.3 Nucleolus
Nucleolus, introduced by Schmeidler [14], is the cost
allocation that lexicographically minimizes the maximal
excess, the difference between the total allocated profit to
a subset and the stand alone cost of that subset, over all
the subsets of the collaboration. Mathematically, it is
expressed as

..( ),
()
({})
i
iS
i
iN
i
M
inimize
styv SSSNS
yvN
yvi iN











The nucleolus exists and is unique. However it does not
take into account each carrier’s contributions to the coa-
lition and the relative cost savings.
3.3 Weighted Relative Savings Model
As discussed above, the existing solutions are not always
stable, which keeps the sustainability of the LTL col-
laboration, and different to show that some participants
can gain more if they contribute more and all participants
have a similar relative profit or cost savings. In a nego-

Allocating Collaborative Profit in Less-than-Truckload Carrier Alliance 147
tiation situation it would be beneficial to have an initial
allocation where the relative savings are as similar as
possible for all participants.
We therefore propose the Weighted Relative Savings
Model (WRSM) which is completely new and motivated
by finding a stable allocation that minimizes the maxi-
mum difference between relative savings among the par-
ticipants and also reflects the contribution difference.
The relative savings of carrieriis expressed as


i
yci . Thus, the difference in relative savings be-
tween two participants i and j is equal to
   
j
iy
y
cicj
 (6)
The contribution to the collaboration depends on the
distribution of power among freight carriers, on their
level of interdependency and willingness to make com-
promises, and on the market within which the freight
carriers operate [5]. Following the ideas of the Shapley
Value, we define the contribution of carrier i to the
grand coalition as
 
 
\,
iS
vSvSii N


 (7)
In order to reflect the contribution difference, we mod-
ify the relative savings by adding the contribution ratio
weight i

which is expressed as
  

  

\
1\
iS
i
iNiS
vSvS i
vSvS i




 

 (8)
The weighted relative savings of carrieriis then equal
to



ii
yci   and the difference in relative savings
between two participants i and
j
is equal to




j
j
ii y
y
cicj


 (9)
The Weighted Relative Savings Model (WRSM) is the
following LP problem which we need to solve to find the
allocation.




.. ,
()
()
jj
ii
i
iS
i
iN
Minimize f
y
y
s
tfijN
cic j
yvS SN
yvN









The first constraint set is to measure the difference
between all participants’ weighted relative savings. The
variable
f
is used in the objective function to minimize
the maximum difference. The other two constraint sets
ensure that the allocation is in the core and thus stable.
We add a minimum penalized slack in the constraints
defining the core. In the case the core is empty we pro-
pose to use the epsilon-core or alternatively seek the
maximal number of players present in a game for which
the core exists. However, how this subgroup of players
should be selected remains to be studied in future research.
Compared with the Proportional Allocation and the
Shapley Value, this allocation is stable. Since the objec-
tive is a combination between participants and considers
the relative savings and the contribution difference, this
model is not a weighted nucleolus. In the literature of this
field, we have not been able to find an allocation method
with similar objective. Therefore, to the best of our
knowledge, this allocation concept is new.
4. Simulation Result and Analysis
In order to show the effectiveness of the method we pro-
pose, we compare the Weighted Relative Savings Model
(WRSM) with Proportional Allocation, Shapley Value
and Nucleolus based on the existing test instances in [5].
Table 1 presents the instances used in our test and re-
lated calculations. There are three carriers in the grand
coalition and the optimal number of vehicles and cost of
each subset of the grand coalition is calculated according
to the transportation requests in the sub-coalition [5].
Cost Savings of Coalition is calculated using (1). Con-
tribution to the Grand Coalition is calculated using (7)
and Contribution Ratio Weight is calculated using (8)
respectively.
Table 2 shows the results for test instances and the
comparison among Proportional Allocation, Shapley
Value, Nucleolus and WRSM. For each allocation con-
cept, Cost Savings allocated to carrier is calculated ac-
cording to the related definitions and algorithms dis-
cussed above. Net Cost equals to Stand-alone Cost minus
Cost Savings.
These results show clearly that it is indeed worth pool-
ing the LTL carriers’ transportation resources through
collaboration to serve customer requests. The cost sav-
ings is range from 7.3% to 18.7%.
Although the Proportional Allocation and Shapley
Value is stable using our test instances, carrier C will not
agree with those allocation methods since he contributes
more to the grand coalition but gains the same relative
savings as carrier A and B in Proportional Allocation and
the smallest savings in Shapley Value allocation. The
Nucleolus, which divides the cost savings equally among
three carriers, does not take into account the contribution
difference among the three and may be rejected by any of
them. WRSM which is in the core and considers both
relative savings and contribution difference makes the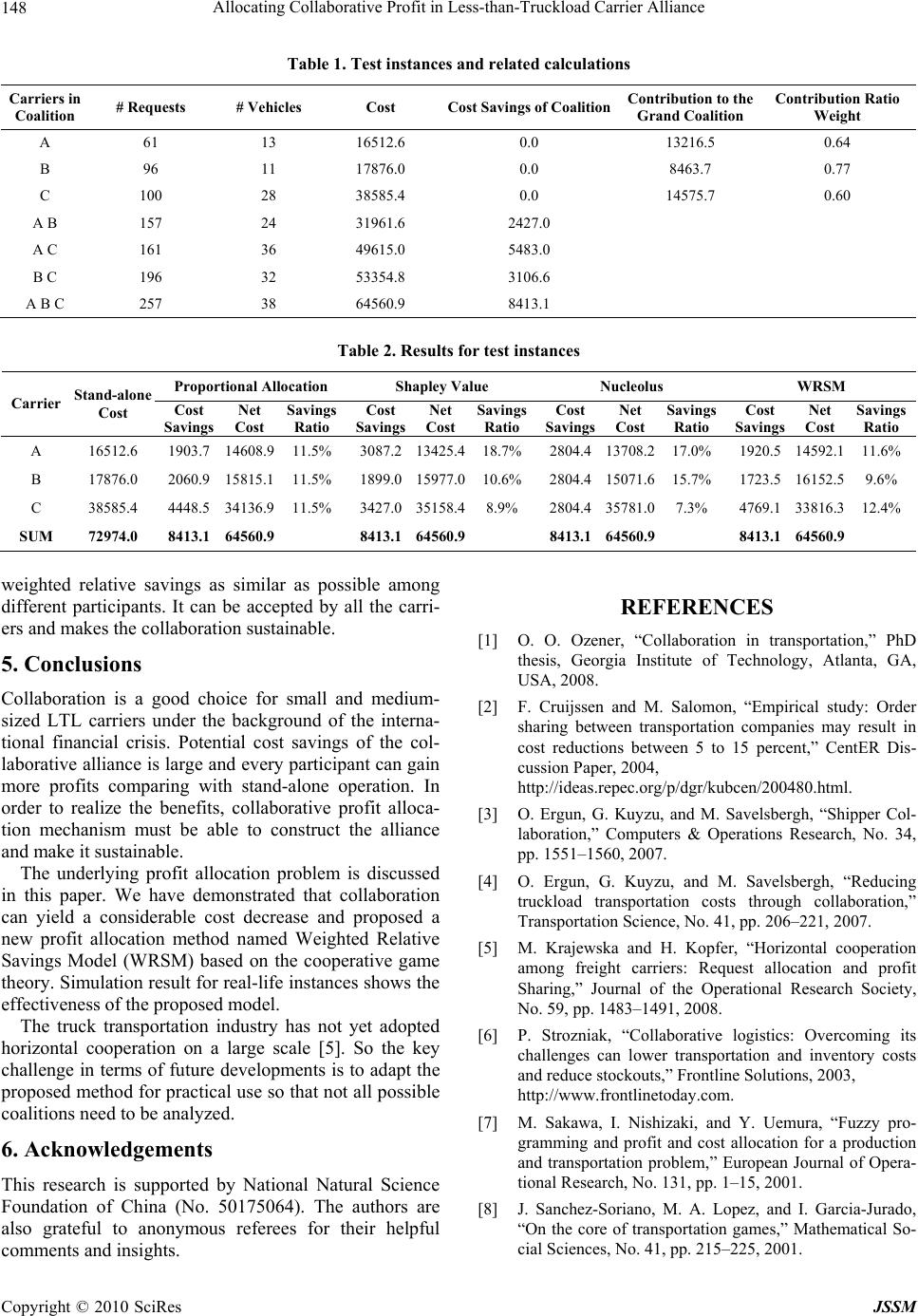

Allocating Collaborative Profit in Less-than-Truckload Carrier Alliance 148
Table 1. Test instances and related calculations
Carriers in
Coalition # Requests # Vehicles Cost Cost Savings of CoalitionContribution to the Grand Coalition Contribution Ratio Weight
A 61 13 16512.6 0.0 13216.5 0.64
B 96 11 17876.0 0.0 8463.7 0.77
C 100 28 38585.4 0.0 14575.7 0.60
A B 157 24 31961.6 2427.0
A C 161 36 49615.0 5483.0
B C 196 32 53354.8 3106.6
A B C 257 38 64560.9 8413.1
Table 2. Results for test instances
Proportional Allocation Shapley Value Nucleolus WRSM
Carrier Stand-alone
Cost Cost
Savings Net Cost Savings Ratio Cost Savings Net Cost Savings Ratio Cost Savings Net Cost Savings Ratio Cost Savings Net Cost Savings Ratio
A 16512.6 1903.7 14608.9 11.5% 3087.213425.418.7% 2804.413708.217.0% 1920.5 14592.111.6%
B 17876.0 2060.9 15815.1 11.5% 1899.015977.010.6% 2804.415071.615.7% 1723.5 16152.59.6%
C 38585.4 4448.5 34136.9 11.5% 3427.035158.48.9% 2804.435781.07.3% 4769.1 33816.312.4%
SUM 72974.0 8413.1 64560.9 8413.164560.9 8413.164560.9 8413.1 64560.9
weighted relative savings as similar as possible among
different participants. It can be accepted by all the carri-
ers and makes the collaboration sustainable.
5. Conclusions
Collaboration is a good choice for small and medium-
sized LTL carriers under the background of the interna-
tional financial crisis. Potential cost savings of the col-
laborative alliance is large and every participant can gain
more profits comparing with stand-alone operation. In
order to realize the benefits, collaborative profit alloca-
tion mechanism must be able to construct the alliance
and make it sustainable.
The underlying profit allocation problem is discussed
in this paper. We have demonstrated that collaboration
can yield a considerable cost decrease and proposed a
new profit allocation method named Weighted Relative
Savings Model (WRSM) based on the cooperative game
theory. Simulation result for real-life instances shows the
effectiveness of the proposed model.
The truck transportation industry has not yet adopted
horizontal cooperation on a large scale [5]. So the key
challenge in terms of future developments is to adapt the
proposed method for practical use so that not all possible
coalitions need to be analyzed.
6. Acknowledgements
This research is supported by National Natural Science
Foundation of China (No. 50175064). The authors are
also grateful to anonymous referees for their helpful
comments and insights.
REFERENCES
[1] O. O. Ozener, “Collaboration in transportation,” PhD
thesis, Georgia Institute of Technology, Atlanta, GA,
USA, 2008.
[2] F. Cruijssen and M. Salomon, “Empirical study: Order
sharing between transportation companies may result in
cost reductions between 5 to 15 percent,” CentER Dis-
cussion Paper, 2004,
http://ideas.repec.org/p/dgr/kubcen/200480.html.
[3] O. Ergun, G. Kuyzu, and M. Savelsbergh, “Shipper Col-
laboration,” Computers & Operations Research, No. 34,
pp. 1551–1560, 2007.
[4] O. Ergun, G. Kuyzu, and M. Savelsbergh, “Reducing
truckload transportation costs through collaboration,”
Transportation Science, No. 41, pp. 206–221, 2007.
[5] M. Krajewska and H. Kopfer, “Horizontal cooperation
among freight carriers: Request allocation and profit
Sharing,” Journal of the Operational Research Society,
No. 59, pp. 1483–1491, 2008.
[6] P. Strozniak, “Collaborative logistics: Overcoming its
challenges can lower transportation and inventory costs
and reduce stockouts,” Frontline Solutions, 2003,
http://www.frontlinetoday.com.
[7] M. Sakawa, I. Nishizaki, and Y. Uemura, “Fuzzy pro-
gramming and profit and cost allocation for a production
and transportation problem,” European Journal of Opera-
tional Research, No. 131, pp. 1–15, 2001.
[8] J. Sanchez-Soriano, M. A. Lopez, and I. Garcia-Jurado,
“On the core of transportation games,” Mathematical So-
cial Sciences, No. 41, pp. 215–225, 2001.

Allocating Collaborative Profit in Less-than-Truckload Carrier Alliance 149
[9] J. Sanchez-Soriano, N. Llorce, A. Meca, and E. Molina,
“An integrated transport system for Alacant’s students,”
Annals of Operations Research, No. 109, pp. 41–60,
2002.
[10] S. Engevall, M. Gothe-Lundgren, and P. Varbrand, “The
heterogeneous vehicle-routing game,” Transportation
Science, No. 38, pp. 71–85, 2004.
[11] N. Matsubayashi, M. Umezawa, Y. Masuda, and H. Ni-
shino, “A cost allocation problem arising in hub–spoke
network systems,” European Journal of Operational Re-
search, No. 160, pp. 821–838, 2005.
[12] L. S. Shapley, “A value for n-person games,” Annals of
Mathematical Studies, No. 28, pp. 307–317, 1953.
[13] H. P. Young, “Cost allocation: Methods, principles, ap-
plications,” European Journal of Operational Research,
No. 27, pp. 254–255, 1986.
[14] D. Schmeidler, “Nucleolus of a characteristic function
game,” Siam Journal on Applied Mathematics, No. 17, pp.
1163–1170, 1969.