Intelligent Information Management, 2010, 2, 149-158
doi:10.4236/iim.2010.22018 Published Online February 2010 (http://www.scirp.org/journal/iim)
On the Mechanism of CDOs behind the Current
Financial Crisis and Mathematical Modeling
with Lévy Distributions
Hongwen Du1, Jianglun Wu2, Wei Yang3
1School of Finance and Economics, Hangzhou Dianzi University, Hangzhou, China
2Department of Mathematics, Swansea University, Swansea, UK
3Department of Mathematics, Swansea University, Swansea, UK
Abstract
This paper aims to reveal the mechanism of Collateralized Debt Obligations (CDOs) and how CDOs extend
the current global financial crisis. We first introduce the concept of CDOs and give a brief account of the de-
velopment of CDOs. We then explicate the mechanism of CDOs within a concrete example with mortgage
deals and we outline the evolution of the current financial crisis. Based on our overview of pricing CDOs in
various existing random models, we propose an idea of modeling the random phenomenon with the feature
of heavy tail dependence for possible implements towards a new random modeling for CDOs.
Keywords: Collateralized Debt Obligations (CDOs), Cashflow CDO, Synthetic CDO, Mechanism, Financial
Crisis, Pricing Models, Lévy Stable Distributions
Collateralized debt obligations (CDOs) were created in
1987 by bankers at Drexel Burnham Lambert Inc. Within
10 years, the CDOs had become a major force in the
credit derivatives market, in which the value of a deriva-
tive is “derived” from the value of other assets. But
unlike some fairly straightforward derivatives such as
options, calls, and Credit Default Swaps (CDSs), CDOs
are not “real”, which means they are constructs, and
sometime even built upon other constructs. CDOs are
designed to satisfy different type of investors, low risk
with low return and high risk with high return.
In early 2007, following the burst of the bubble of
housing market in the United States, losses in the CDOs
market started spreading. By early 2008, the CDO crisis
had morphed into what we now encountered the world-
wide financial crisis. CDOs are at the heart of the crisis
and even extend the crisis.
1. Introduction to CDOs
Collateralized Obligations (COs) are promissory notes
backed by collaterals or securities. In the market for COs,
the securities can be taken from a very wide spectrum of
alternative financial instruments, such as bonds (Col-
lateralized Bond Obligations, or CBO), loans (Co-
llateralized Loan Obligations, or CLO), funds (Coll-
ateralized Fund Obligations, or CFO), mortgages
(Collateralized Mortgage Obligations, or CMO) and oth-
ers. And frequently, they source their collaterals from a
combination of two or more of these asset classes.
Collectively, these instruments are popular referred to as
CDOs, which are bond-like instruments whose cashflow
structures allocate interest income and principal repay-
ments from a collateral pool of different debt instruments
to a prioritized collection of CDO securities to their
investors. The most popular life of a CDO is five years.
However, 7-year, 10-year, and to a less extent 3-year
CDOs now trade fairly actively.
A CDO can be initiated by one or more of the
followings: banks, non-bank financial institutions, and
asset management companies, which are referred to as
the sponsors. The sponsors of a CDO create a company
so-called the Special Purpose Vehicle (SPV). The SPV
works as an independent entity and is usually bankruptcy
remote. The sponsors can earn serving fees, adminis-
tration fees and hedging fees from the SPV, but otherwise
has no claim on the cash flow of the assets in the SPV.
According to how the SPV gains credit risks, CDOs
are classified into two kinds: cashflow CDOs and syn-

H. W. DU ET AL. 150
thetic CDOs. If the SPV of a CDO owns the underlying
debt obligations (portfolio), that is, the SPV obtains the
credit risk exposure by purchasing debt obligations (eg.
bonds, residential and commercial loans), the CDO is
referred to as a cashflow CDO, which is the basic form
in the CDOs market in their formative years. In contrast,
if the SPV of a CDO does not own the debt obligations,
instead obtaining the credit risk exposure by selling
CDSs on the debt obligations of reference entities, the
CDO is referred to as a synthetic CDO; the synthetic
structure allows bank originators in the CDOs market to
ensure that client relationships are not jeopardized, and
avoids the tax-related disadvantages existing in cashflow
CDOs. The following graph (Figure 1) illustrates a
construction of a cashflow CDO.
After acquiring credit risks, SPV sells these credit ris-
ks in tranches to investors who, in return for an agreed
payment (usually a periodic fee), will bear the losses in
the portfolio derived from the default of the instruments
in the portfolio. Therefore, the tranches holders have the
ultimate credit risk exposure to the underlying reference
portfolio.
Tranching, a common characteristic of all securisa-
tions, is the structuring of the product into a number of
different classes of notes ranked by the seniority of in-
vestor's claims on the instruments assets and cashflows.
The tranches have different seniorities: senior tranche,
the least risky tranche in CDOs with lowest fixed interest
rate, followed by mezzanine tranche, junior mezzanine
tranche, and finally the first loss piece or equity tranche.
A CDO makes payments on a sequential basis, depen-
ding on the seniority of tranches within the capital struc-
ture of the CDO. The more senior the tranches investors
are in, the less risky the investment and hence the less
they will be paid in interest. The way it works is fre-
quently referred to as a “waterfall” or cascade of cash-
flows. We well give a specific illustration in Section 3.
In perfect capital markets, CDOs would serve no pur-
pose; the costs of constructing and marketing a CDO
would inhibit its creation. In practice, however, CDOs
address some important market imperfections. First, ban-
ks and certain other financial institutions have regulatory
capital requirements that make it valuable for them to
securitize and sell some portion of their assets, reducing
the amount of (expensive) regulatory capital that they
must hold. Second, individual bonds or loans may be
illiquid, leading to a reduction in their market values.
Securitization may improve liquidity, and thereby raise
the total valuation to the issuer of the CDO structure.
In light of these market imperfections, at least two
classes of CDOs are popular: the balance-sheet CDO and
the arbitrage CDO. The balance-sheet CDO, typically in
the form of a CLO, is designed to remove loans from the
Figure 1.Cashflow colateralised mortgage obligation.

H. W. DU ET AL. 151
balance sheets of banks, achieving capital relief, and
perhaps also increasing the valuation of the assets thr-
ough an increase in liquidity. An arbitrage CDO, often
underwritten by an investment bank, is designed to cap-
ture some fraction of the likely difference between the
total cost of acquiring collateral assets in the secondary
market and the value received from management fees
and the sale of the associated CDOs structure.
2. The Development of CDOs
Although a market for CMOs—the forerunner of modern
CDOs—was taking shape in the US market by the early
1980s, the market for CDOs is generally believed to date
back to the late 1980s and the rapid revolution of CDOs
is very much a story of the 1990s.
By the late 1990s, the structure of the international
market for CDOs of all kinds was becoming characte-
rized by a number of conspicuous and interrelated trends.
Firstly, issuance volume was rising exponentially, as was
understanding and acceptance of the CDO technique. Se-
condly, the cross-border investment flowing into CDOs
were rising steeply. Thirdly, more and more asset classes
were being used as security for COs. Finally, in 1999 and
2000 the concept of the COs was popularised across
continental Europe with strikingly high speed and, mean-
while, changes to legislation and regulation were emer-
ging as important sources of support for new issuance in
the CDOs market in Europe.
In 2000 CDOs were made legal and at the same time
were prevented from being regulated, by the Commodity
Futures Modernization Act, which specifies that products
offered by banking institutions could not be regulated as
futures contracts. It lies at the root of America's failure to
regulate the debt derivatives that are now threatening the
global economy. By 2000 and 2001 globally, the most
important determinant of increasing volumes in the CDO
market was the explosive growth in the market for credit
derivatives in general and for CDS in particular, which
paved the way for an equally explosive expansion of the
market for synthetic CDOs. Thereafter, the volume of
traditional cashflow CDOs has been eclipsed by syn-
thetic products.
The process of increasing diversification in the CDO
market has began in 2002. An example of such diver-
sification is the so-called CDOs of CDOs (CDOs squar-
ed): a portfolio of CDOs is assembled, tranched, and sold
to investors. Other exotic CDO products include CDOs
of funds (CFO), and CDOs of equity default swaps
(CDOs of EDS), forward starting CDOs, options on
CDO tranches, leverage super senior CDOs, and bespoke
CDOs.
CDOs were originally static portfolios where the un-
derlying names rarely changed and the static CDOs po-
ssess the advantage that they call for minimal resources
in terms of management expertise and time and reduce
costs involved in trading. However, when they declined
in value, investors were unable to do anything to reverse
that decline as credit quality began to deteriorate. There-
fore, actively managed CDOs were rapidly gaining in
popularity. The growth of managed products, however,
was also helped by the growing maturity of the CDO
market and by the increasing number of managers with
proven experience in managing credit in general and
credit derivatives in particular.
3. The Mechanism of CDOs
In this section, we try to describe the mechanism of
CDOs in a vivid, therefore not so rigorous, way. We
simplify the collaterals as mortgages. Then the process to
create a CDO can be seen in the following manner:
investment banks buy mortgages and then pool them into
Mortgage Backed Securities (MBSs) with different ra-
tings. Financial institutions seeking new markets pur-
chase these MBSs, pool them with other similarly rated
MBSs and sometimes derivatives, and then issue new
securities. This process of buying mortgages, creating
MBSs, and packaging these MBSs into CDOs is desi-
gned to apportion credit risk to those parties who are
willing to take it on.
First of all, we have a CDO manager who decides to
create a CDO. He/She has a bottle (SPV). In order to fill
the bottle, he/she can buy collaterals (anything he/she
wants: the loans, credit card debt and student loans). For
example, let us assume the collaterals are $1b mortgages
paying interest rate of 10%. Then $1m credit-linked no-
tes (CLNs) with par value $1k are issued based on the
underlying collaterals portfolio.
Secondly, we may regard its capital structure as a
4-layer pyramid of wine glasses over a tray. Each layer
(tranche) has different seniority. Into these glasses are the
CLNs rated according to their riskiness. On the top layer
is the senior tranche with 400k AAA-rated CLNs, the
least risky tranche with lowest fixed interest rate 6%,
followed by mezzanine tranche with 200k AA-rated
CLNs paying fixed interest rate 7%, junior mezzanine
tranche with 200k BBB-rated CLNs paying fixed interest
rate 10%, and equity tranche with 200k CLNs with
highest risk. Investors will get paid, at each payment day,
at corresponding interest rates of tranches they are in-
volved in.
At the payment day, because these mortgages are pay-
ing interest, the cork of the bottle pops off with much
pressure. The money then flows out on the top and into
the pyramid of the glasses. If all of the mortgages are
paying interest, i.e., there is no default, the interest would
sum up to $100m. Because the senior tranche is the least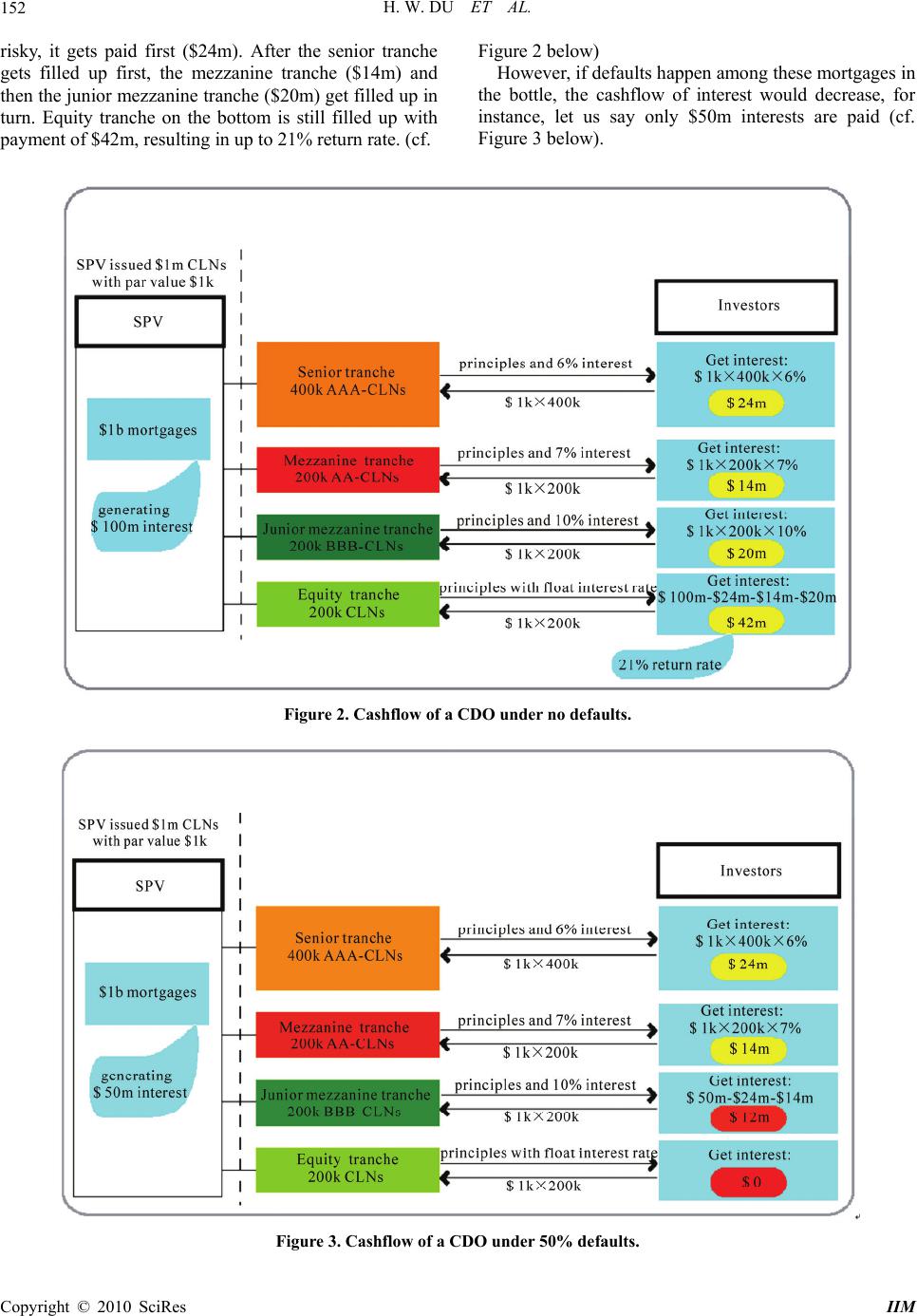

H. W. DU ET AL. 152
risky, it gets paid first ($24m). After the senior tranche
gets filled up first, the mezzanine tranche ($14m) and
then the junior mezzanine tranche ($20m) get filled up in
turn. Equity tranche on the bottom is still filled up with
payment of $42m, resulting in up to 21% return rate. (cf.
Figure 2 below)
However, if defaults happen among these mortgages in
the bottle, the cashflow of interest would decrease, for
instance, let us say only $50m interests are paid (cf.
Figure 3 below).
Figure 2. Cashflow of a CDO under no defaults.
Figure 3. Cashflow of a CDO under 50% defaults.

H. W. DU ET AL. 153
In this situation, the senior tranche still gets paid in
full first ($24m); mezzanine tranche get paid $14m; yet
the junior mezzanine tranche only gets paid $12m gene-
rating 6% return rate less then 10% as expected; nothing
can be paid to the equity tranche holders.
If we complicate the situation further by thinking of
another manager who also decides to create a CDO.
Instead of filling the bottle with mortgages, he decides to
fill with these MBSs (the first CDO). The second
manager then takes the glasses from the bottom layer
(equity tranche) in the previous CDO. In the boom, it
will be no problem whenever everyone is paying their
mortgages in the first bottle and these glasses are ge-
nerating payment in payment day. Both pyramids of
glasses are full.
However, with 50% defaults, the bottom glasses in the
first pyramid are not filled up. At payment day of the
second CDO, the cork pops off and generates zero. In
this case, even nothing is filled at the top glasses of the
second CDO, they are still rated AAA, as if they were
safe as the original assets. In the situation that housing
market persists weak and people default or stop paying
mortgages, there will be less and less money come out
from the first bottle into the pyramid of glasses, and less
and less money these AAA highly rated securities in the
second CDO would make. Thousands of millions of
dollars have been invested into this kind of secondary
CDOs.
Similarly, a third CDO can be created, which repa-
ckage MBSs in the first and second CDO. Then, a fourth,
a fifth, , and so on. We can easily imagine the much more
complicated situation if we refer to the volume of the
CDOs market. Many investment banks are involved in
the enormous web by the CDOs contracts.
This is the right problem. Investors have packed a lot
of funds with these securities which are now not paying
anything and liable never to pay anything again. Many
financial situations start to teeter because of being tied in
numbers of contracts. They cannot unravel these deals.
One failure in the web starts to drag down the rest of the
system and suck people down in the end. Nobody knows
how big it is, how far it is and who are actually involved.
We only find out whenever a company began to collapse,
suddenly, the second finds itself was dragged with it and
then the third, the forth and so on. That's the situation we
are exactly in today.
4. The Current Financial Crisis
The current unprecedented financial crisis started from
the US subprime mortgage financial crisis, and spreaded
and accelerated by the securitisation of subprime mort-
gages into credit derivatives, especially into kinds of
CDOs. As the crisis develops, the real economy has been
been obviously seen severely affected since late 2008.
Alongside the stock bubble of mid-1990s, the US
housing bubble grew up and began to burst in early 2007
as the building boom led to so much over-supply that
house prices could no longer be supported, which evo-
lved into the so-called US subprime mortgage financial
crisis.
The over expansion of credit in US housing market led
to losses by financial institutions. Initially the companies
affected were those directly involved in home cons-
truction and mortgage lending such as the Northern Rock
and Countrywide Financial. Take Northern Rock, a ma-
jor British bank, as an example. It raises most of the
money, which it provides for mortgages via the whole-
sale credit market, primarily by selling the debt on in the
form of bonds. Following the widespread losses made by
investors in the subprime mortgage market, these banks
and investors have become wary of buying mortgage
debt, including Northern Rock's. The highly leveraged
nature of its business led the bank to request security
from the Bank of England. News of this lead to investors
panic and a bank run in mid-September 2007. Northern
Rock's problems proved to be an early indication of the
severe troubles that would soon befall other banks and
financial institutions.
The crisis then began to affect general availability of
credit to non-housing related businesses and to large
financial institutions not directly connected with mor-
tgage lending. It is the “securitisation” process, which
spreads the current crisis. Many subprime mortgages
were securitised and sold to investors using asset-backed
securities (ABSs). It has been estimated that 54% of
subprime mortgages were securitised in 2001 and this
rose to 75% in 2006 [1]. At the heart of the portfolios of
many financial institutions were investors whose assets
had been derived from bundled home mortgages.
In early 2007, when defaults were rising in the mor-
tgage market, New York's Wall Street began to feel the
first tremors in the CDOs world. Hedge fund managers,
commercial and investment banks, and pension funds, all
of which had been big buyers of CDOs, found them-
selves landed in trouble, as many CDOs included deri-
vatives that were built upon mortgages—including risky,
subprime mortgages. More importantly, the mathematical
models that were supposed to protect investors against
risk weren’t working. The complicating matter was that
there was no market on which to sell the CDOs. CDOs
are not traded on exchanges and even not really stru-
ctured to be traded at all. If one had a CDO in his/her
portfolio, then there was not much he/she could do to
unload it. The CDO managers were in a similar bind. As
fear began to spread, the market for CDOs' underlying
assets also began to disappear. Suddenly it was impo-
ssible to dump the swaps, subprime-mortgage derivatives,
and other securities held by the CDOs.

H. W. DU ET AL. 154
In March 2008, slightly more than a year after the first
indicator of troubles in the CDO market, Bear Stearns,
which was one of Wall Street's biggest and most pres-
tigious firms and which had been engaged in the secu-
ritisation of mortgages, fell prey and was acquired by JP
Morgan Chase through the deliberate assistance from the
US government. By the middle of 2008, it became clear
that no one was safe; everyone—even those who had
never invested in anything—would wind up paying the
price. On September 15, 2008, the 158 year-old Lehman
Brothers filed for Chapter 11 bankruptcy protection. The
collapse of Lehman Brothers is the largest investment
bank failure since Drexel Burnham Lambert in 1990 and
triggered events that seemed unthinkable a year before:
the high volatility of worldwide financial institutions,
massive state-funded bailouts of some of the world's
leading financial institutions and the disappearance of
investment banks.
The 94 year-old Merrill Lynch accepted a purchase
offer by Bank of America for approximately US$ 50
billion, a big drop from a year-earlier market valuation of
about US$ 100 billion. A credit rating downgrade of the
large insurer American International Group (AIG) led to
a rescue agreement on September 16, 2008 with the
Federal Reserve Bank for a $ 85 billion dollar secured
loan facility, in exchange for a warrants for 79.9% of the
equity of AIG. Even, in January 2009, HBOS, a banking
and insurance group in UK, was taken over by Lloyds
TSB Banking Group.
The crisis is now much far beyond the virtual economy,
the real economy has been severely affected. The global
economy is in the midst of a deep downturn. The dra-
matic intensification of the financial crisis has generated
historic declines in consumer and business confidence,
steep falls in household wealth, and severe disruptions in
credit intermediation.
In the last quarter of 2008, industrial production has
fallen precipitously across both advanced and emerging
economies, declining by some 15%–20% and merchan-
dise exports have fallen by some 30%–40%, at an annual
rate. Official figures show that the Britain industrial
production dived at record speed, underlying how hard
the global downturn has hit producers and exporters:
manufacturing outputs dropped by 2.9% in January, 2009,
taking annual rate of decline to 12.8%, which is the
biggest decline since January, 1981; broader industrial
productions, including mining and utilities, are now also
falling at an annual rate of 11.4%, again the worst since 1981.
Labor markets are weakening rapidly, particularly in
those advanced economies. In February, 2009, the US
unemployment rate rose to 8.1%, the highest in more
than 25 years and more layoffs are on the way; the
Britain unemployment rate rose to 6.3%, up 1.1% on
2008, and the Euro unemployment rate rose to 8.2%, the
highest level in over 2 years.
Despite production cut-backs by OPEC, oil prices
have declined by nearly 70% since their July 2008 peak.
Similarly, metals prices are now around 50% below their
March 2008 peaks. Food prices have eased 35% from
their peak, reflecting not only deteriorating global cyc-
lical conditions, but also favorable harvests.
Clearly, the global economy faces a contraction in ov-
erall Gross Domestic Product (GDP) for the first time
since the Second World War, as claimed by Dominique
Strauss-Kahn, the head of the International Monetary
Fund (IMF).
5. Mathematical Challenges in Modeling the
Mechanism of CDOs
The investment banks presented CDOs as investments in
which, actually, the key factors were not the underlying
assets, rather the use of mathematical calculations to
create and distribute the cash flows. In other words, the
basis of a CDO was not a mortgage, a bond or even a
derivative, but the metrics and algorithms of quants and
traders. In particular, the CDO market skyrocketed in
2001 with the invention of a formula called the Gaussian
Copula, which made it easier to price CDOs quickly. But
what seemed to be the great strength of CDOs—complex
formulas that protected against risk while generating
high returns—turned out to be flawed.
Normally financial institutions do not trade instru-
ments unless they have satisfactory models for valuing
them. What is surprising about the financial crisis is that
financial institutions were prepared to trade senior
tranches of an ABS (i.e., an asset-backed security) or an
ABS CDO (an instrument in the synthetic CDOs market)
without a model [1]. The lack of a model makes risk
management almost impossible and causes problems
when the instrument ceases to be rated. Because models
were not developed, the key role of correlation in valuing
ABSs and (particularly) ABS CDOs was not well
understood. Many investors and analysts assumed that
CDOs were diversified, and hence made less risky, due
to the large number of individual bonds that might
underlie a given deal. In fact, the investments within the
CDOs turned out to be more highly correlated than
expected.
Pricing a CDO is mainly to find the appropriate spread
for each tranche and its difficulty lies in how to estimate
the default correlation in formulating models that fit
market data. With the empirical evidence of the existence
of mean reversion phenomena in efficient credit risk
markets, mean-reverting type stochastic differential
equations are considered (cf. e.g. [2]). In addition, the
CDOs market has seen the phenomenon of heavy tail
dependence in a portfolio, which draws the attention to
use modeling with heavy tail phenomenon as a feature.
Besides, the efficiency in calibrating pricing models to

H. W. DU ET AL. 155
market prices should be paid much attention. A well-
calibrated and easily implemented model is the right
goal.
The market standard model is the so-called one factor
Gaussian copula model. Its origins can be found in [3,4].
The assumptions of the one factor Gaussian copula
model about the characteristics of the underlying
portfolio simplify the analytical derivation of CDOs
premiums but are not very realistic. Thereafter more and
more extensions have been proposed to pricing CDOs:
homogeneous infinite portfolio is extended to homogen-
eous finite portfolio, and then to heterogeneous finite
portfolio which represents the most real case; multi-
factor models are considered other than one factor model;
Gaussian copula is replaced by alternative probability
distribution functions; the assumptions of constant defau-
lt probability, constant default correlation and determi-
nistic loss given default are relaxed and stochastic ones
are proposed which incorporate dynamics into pricing
models.
In one line of thinking, to relax the assumption of
Gaussian distribution in the one factor Gaussian copula
model, student-t copula [5–12], double-t copula [13,14],
Clayton copula [12,15–20], Archimedian copula [21,22],
Marshall Olkin copula [23–26] are studied. And default
correlations are made stochastic and correlated with the
systematic factor in [27,28] to relax the assumption that
default correlations are constant through time and
independent of the firms default probabilities. Hull and
White propose the implied copula method in [29].
In the other line of thinking, many stochastic processes
are applied in CDOs pricing models to describe the de-
fault dependence. Markov chains are used to represent
the distance to default of single obligor (eg. [30,31]). Then
correlation among obligors is introduced with nonrecom-
bining trees [30] or via a common time change of affine
type [31].
Some researchers include jumps in CDOs pricing mo-
del. Duffie and Garleanu [32], for example, propose an
approach based on affine processes with both a diffusion
and a jump components. To improve tractability, Chapo-
vsky, Rennie and Tavares [33] suggest a model in which
default intensities are modeled as the the sum of a
compensated common random intensity driver with trac-
table dynamics (e.g. the Cox-Ingersoll-Ross model (or
CIR model in short) with jumps) and a deterministic
name-depended function.
Motivated by the possibility that price processes could
be pure jump, several authors have focused their att-
ention on pure jump models in the Lévy class. Firstly, we
have the Normal Inverse Gaussian (NIG) model of
Barndorff-Nielsen [34], and its generalisation to the
generalised hyperbolic class by Eberlein, Keller, and
Prause [35]. Kalemanova, Schmid and Werner [36] and
Guégan and Houdain [37] work with NIG factor model.
Secondly, we have the symmetric Variance Gamma (VG)
model studied by Madan and Seneta [38] and its asy-
mmetric extension studied by Madan and Milne [39],
Madan, Carr, and Chang [40]. Baxter [41] introduces the
B-VG model where has both a continuous Brownian
motion and a discontinuous variance—Gamma jump
terms. Finally, we have the model developed by Carr,
Geman, Madan, and Yor (acronym: CGMY) [42], which
further generalises the VG model. Most of these models
are special cases of the generic one-factor Lévy model
supposed in [43]. Lévy models bring more flexibility into
the dependence structure and allow tail dependence.
Besides default dependence, the recovery rate is also
an important variable in pricing CDOs. Empirical reco-
very rate distributions in [44] have high variance and the
certainty with which one can predict recovery is quite
low. One undisputed fact about recovery rates is that
average recovery rates tend to be inversely related to
default rates: in a bad year, not only are there many
defaults, but recoveries are also low. The loss process
models involve the development of a model for the
evolution of the losses on a portfolio. Graziano and
Rogers [45] provide semi-analytic formulas via Markov
chain and Laplace transform techniques which are both
fast and easy to implement. In [46], Schoenbucher deri-
ves the loss distribution of the portfolio from the tran-
sition rates of an auxiliary time-inhomogeneous Markov
chain and stochastic evolution of the loss distribution is
obtained by equipping the transition rates with stochastic
dynamics. Other loss process can be found in [47] where
discuss a dynamic discrete-time multi-step Markov loss
model and in [48] where loss follows a jump process.
6. Modeling Heavy Tail Phenomena by Lévy
Distributions
From the mathematical view point, we see the highly
complexity and chaotic dynamics in the system of CDOs,
and, especially, the phenomenon of heavy tail depend-
ence. In literatures, researchers have investigated quite a
lot of models in pricing CDOs, but seldom incorporate
Lévy stable distributions to represent the heavy tail
dependence in the modeling. In this final section, we
shall explicate and suggest an idea about applying Lévy
stable distributions in pricing CDOs.
Historically, the application of probability distribu-
tions in mathematical modeling for the real world
problems started with the use of Gaussian distributions to
express errors in measurement. Concurrently with this,
mathematical statistics emerged. The mean of a Gaussian
distribution traditionally represents the most probable
value for the actual size and the variance of it is related
to the errors of the measurement. The whole distribution
is in fact a prediction which is easy to check, since it was

H. W. DU ET AL. 156
developed for probability distributions which can be well
characterized by their first two moments.
Other probability distributions have appeared in
mathematical modeling where the mean and variance can
not well represent the process. For example, it is
well-known that all moments, of the lognormal distribu-
tion are finite but . This fact shows that a lot of weight is
in the tail of the distribution where rare but extreme
events can occur. This phenomenon is the so-called
heavy tail dependence phenomenon and is exactly the
one observed in the market for CDOs.
Moreover, probability distributions with infinite mo-
ments are also encountered in the study of critical ph-
enomena. For instance, at the critical point one finds
clusters of all sizes while the mean of the distribution of
clusters sizes diverges. Thus, analysis from the earlier
intuition about moments had to be shifted to newer no-
tions involving calculations of exponents, like e.g. Lya-
punov, spectral, fractal etc., and topics such as strange
kinetics and strange attractors have to be investigated.
It was Paul Lévy who first grappled in-depth with
probability distributions with infinite moments. Such
distributions are now called Lévy distributions. Today,
Lévy distributions have been expanded into diverse areas
including turbulent diffusion, polymer transport and
Hamiltonian chaos, just to mention a few. Although
Lévy's ideas and algebra of random variables with
infinite moments appeared in the 1920s and the 1930s (cf.
[49,50]), it is only from the 1990s that the greatness of
Lévy's theory became much more appreciated as a
foundation for probabilistic aspects of chaotic dynamics
with high entropy in statistical analysis in mathematical
modelling (cf. [51,52], see also [53,54]). Indeed, in
statistical analysis, systems with highly complexity and
(nonlinear) chaotic dynamics became a vast area for the
application of Lévy processes and the phenomenon of
dynamical chaos became a real laboratory for developing
generalizations of Lévy processes to create new tools to
study nonlinear dynamics and kinetics. Following up this
point, Lévy type processes and their influence on long
time statistical asymptotic will be unavoidably encountered.
As a flavor on this aspect, let us finally give a brief
account for modelling the risk with Lévy processes
within the framework of the intensity based models.
Relative to the copula approach, intensity based mo-
dels has the advantage that the parameters have econo-
mic interpretations. Furthermore, the models, by nature,
deliver stochastic credit spreads and are therefore well-
suited for the pricing of CDOs tranches. In the intensity
based model, default is defined as the first jump of a pure
jump process, and it is assumed that the jump process has
an intensity process. More formally, it is assumed that a
non-negative process λ exists such that the process
{}{ }
0
():11( )
t
ts
M
ts





is a martingale. And the default correlation is generated
through dependence of firms' intensities on the common
factor.
Following Mortensen [55], we assumes that default of
obligor is modelled as the first jump of a Cox process
with a default intensity composed of a common and an
idiosyncratic component in the following way
()() ()
iic i
taXtXt



where ai>0 is a constant and Xc and Xi are independent
Lévy processes. Namely, the two independent processes
Xc and Xi are of the following form
00 1
01
() ()
[(,)()]
(, )
ctcc
t
cc c
x
t
cc
x
Xt Wt
x
Ndsdx dsdx
xNds dx










and
00 1
01
() ()
[(,) ()]
(, )
iiic
t
ii i
x
t
ii
x
Xtt Wt
x
Ndsdx dsdx
xNds dx










where mean values θc, θi and volatilities are constants, σc,
σi>0 are constants, Wc(t), Wi(t) ane independent
Brownian motions on (Ω, Ғ, P; { Ғt}t≥0); Nc(t, A), Ni(t, A)
are defined to be the numbers of jumps of process Xc, Xi
with size smaller than A during time period t. For fix A,
Nc(t, A), Ni(t, A) are Poisson processes with intensity
μc(A), μi(A) respectively.
Based on these assumptions, we may calculate marg-
inal default probability, joint default probability and the
characteristic function of the integrated common risk
factor to get the expression of expected tranche losses.
Finally, we may get the tranche spreads of CDOs. We
will realize this aim in our forthcoming work towards the
concrete mathematical modelling.
7. Conclusions
In this paper, we start with detailed explanation of the
mechanism of CDOs and discuss the mathematical cha-
llenge in modelling the complexity systems arising from
CDOs. We link the feature of CDOs with heavy tail
phenomenon and then propose to use Lévy process, in
particular Lévy stable process, to model risk factors in
pricing CDO tranche spreads.
ds
Our paper shows Lévy stable distribution may capture
the feature of high default dependence among CDOs'
underlying portfolio.

H. W. DU ET AL. 157
8. Acknowledgments
We would like to thank Claire Geleta of Deutsche Bank
Trust Company Americas at Los Angeles for useful
conversation regarding to CDOs. We also thank the
referee for constructive comments on our previous ma-
nuscript.
9. References
[1] J. Hull, “The credit crunch of 2007: What went wrong?
Why? What lessons can be learned?” Working Paper,
University of Toronto, 2008.
[2] J. L.Wu and W. Yang, “Pricing CDO tranches in an
intensity-based model with the mean-reversion app-
roach,” Working Paper, Swansea University, 2009.
[3] O. Vasicek, “Probability of loss on a loan portfolio,”
Working Paper, KMV (Published in Risk, December
2002 with the title Loan Portfolio Value), 1987.
[4] D. X. Li, “On default correlation: A Copula approach,”
Journal of Fixed Income, Vol. 9, No. 4, pp. 43–54, 2000.
[5] L. Andersen, J. Sidenius, and S. Basu, “All your hedges
in one basket,” Risk, pp. 67–72, 2003.
[6] S. Demarta and A. J. McNeil, “The t copula and related
copulas,” International Statistical Review, Vol. 73, No. 1,
pp. 111–129, 2005.
[7] P. Embrechts, F. Lindskog, and A. McNeil, “Modelling
dependence with Copulas and applications to risk mana-
gement,” In Handbook of Heavy Tailed Distributions in
Finance, edited by S. Rachev, Elsevier, 2003.
[8] R. Frey and A. J. McNeil, “Dependent defaults in models
of portfolio credit risk,” Journal of Risk, Vol. 6, No. 1, pp.
59–92, 2003.
[9] A. Greenberg, R. Mashal, M. Naldi, and L. Schloegl,
“Tuning correlation and tail risk to the market prices of
liquid tranches,” Lehman Brothers, Quantitative Research
Quarterly, 2004.
[10] R. Mashal and A. Zeevi, “Inferring the dependence stru-
cture of financial assets: Empirical evidence and imp-
lications,” Working paper, University of Columbia, 2003.
[11] R. Mashal, M. Naldi, and A. Zeevi, “On the dependence
of equity and asset returns,” Risk, Vol. 16, No. 10, pp.
83–87, 2003.
[12] L. Schloegl and D. O’Kane, “A note on the large homo-
geneous portfolio approximation with the student-t Co-
pula,” Finance and Stochastics, Vol. 9, No. 4, pp. 577–
584, 2005.
[13] J. Hull and A. White, “Valuation of a CDO and an n-th to
default CDS without Monte Carlo simulation,” Journal of
Derivatives, Vol. 12, No. 2, pp. 8–23, 2004.
[14] A. Cousin and J. P. Laurent, “Comparison results for
credit risk portfolios,” Working Paper, ISFA Actuarial
School, University of Lyon and BNP-Paribas, 2007.
[15] P. Schönbucher and D. Schubert, “Copula dependent
default risk in intensity models,” Working Paper, Bonn
University, 2001.
[16] J. Gregory, and J. P. Laurent, “I will survive,” Risk, Vol.
16, No. 6, pp. 103–107, 2003.
[17] E. Rogge and P. Schönbucher, “Modelling dynamic port-
folio credit risk,” Working Paper, Imperial College, 2003.
[18] D. B. Madan, M. Konikov, and M. Marinescu, “Credit
and basket default swaps,” The Journal of Credit Risk,
Vol. 2, No. 2, 2006.
[19] J. P. Laurent and J. Gregory, “Basket default swaps,
CDOs and factor copulas,” Journal of Risk, Vol. 7, No. 4,
pp. 103–122, 2005.
[20] A. Friend and E. Rogge, “Correlation at first sight,” Eco-
nomic Notes, Vol. 34, No. 2, pp. 155–183, 2005.
[21] P. Schönbucher, “Taken to the limit: Simple and not-
so-simple loan loss distributions,” Working Paper, Bonn
University, 2002.
[22] T. Berrada, D. Dupuis, E. Jacquier, N. Papageorgiou, and
B. Rémillard, “Credit migration and basket derivatives
pricing with copulas,” Journal of Computational Finance,
Vol. 10, pp. 43–68, 2006.
[23] D. Wong, “Copula from the limit of a multivariate binary
model,” Working Paper, Bank of America Corporation,
2000.
[24] Y. Elouerkhaoui,. “Credit risk: Correlation with a diffe-
rence,” Working Paper, UBS Warburg, 2003.
[25] Y. Elouerkhaoui, “Credit derivatives: Basket asympto-
tics,” Working Paper, UBS Warburg, 2003.
[26] K. Giesecke, “A simple exponential model for dependent
defaults,” Journal of Fixed Income, Vol. 13, No. 3, pp.
74–83, 2003.
[27] L. Andersen and J. Sidenius, “Extensions to the Gaussian
copula: Random recovery and random factor loadings,”
Journal of Credit Risk, Vol. 1, No. 1, pp. 29–70, 2005.
[28] L. Schloegl, “Modelling oorrelation skew via mixing
Copula and uncertain loss at default,” Presentation at the
Credit Workshop, Isaac Newton Institute, 2005.
[29] J. Hull and A. White, “Valuing credit derivatives using an
implied copula approach,” Journal of Derivatives, Vol. 14,
No. 2, pp. 8–28, 2006.
[30] C. Albanese, O. Chen, A. Dalessandro, and A. Vidler,
“Dynamic credit correlation modeling,” Working Paper,
Imperial College, 2005.
[31] T. R. Hurd and A. Kuznetsov, “Fast CDO computations in
affine Markov chains models,” Working Paper, McMaster
University, 2006.
[32] D. Duffie and N. Gârleanu, “Risk and valuation of
collateralized debt obligations,” Financial Analysts Jour-
nal, Vol. 57, No. 1, pp. 41–59, 2001.
[33] A. Chapovsky, A. Rennie and P. A. C. Tavares, “Sto-
chastic intensity modeling for structured credit exotics,”
Working paper, Merrill Lynch International, 2006.

H. W. DU ET AL. 158
[34] O. E. Barndorff-Nielsen, “Processes of normal inverse
Gaussian type,” Finance and Stochastics, Vol. 2, No. 1, pp.
41–68, 1998.
[35] E. Eberlein, U. Keller and K. Prause, “New insights into
smile, mispricing and value at risk,” Journal of Business,
Vol. 71, No. 3, pp. 371–406, 1998.
[36] A. Kalemanova, B. Schmid and R. Werner, “The Normal
Inverse Gaussian distribution for synthetic CDO pricing,”
Journal of Derivatives, Vol. 14, No. 3, pp. 80–93, 2007.
[37] Guégan and Houdain, “Collateralized debt obligations
pricing and factor models: A new methodology using
Normal Inverse Gaussian distributions,” Note the rech-
erche IDHE-MORA, ENS Cachan, No. 007-2005, 2005.
[38] D. B. Madan and E. Seneta, “The Variance Gamma (V.G.)
model for share market returns,” Journal of Business, Vol.
63, No. 4, pp. 511–24, 1990.
[39] D. B. Madan and F. Milne, “Option pricing with V.G.
martingale components,” Mathematical Finance, Vol. 1,
No. 4, pp. 39–55, 1991.
[40] D. B. Madan, P. Carr and E. C. Chang, “The variance
gamma process and option pricing,” European Finance
Review, Vol. 2, No. 1, pp. 79–105, 1998.
[41] M. Baxter,. “Lévy process dynamic modeling of single-
name credits and CDO tranches,” Working Paper, Nomu-
ra International, 2006.
[42] P. Carr, H. Geman, D. Madan, and M. Yor, “The fine
structure of asset returns: An empirical investigation,”
Journal of Business, Vol. 75, No. 2, pp. 305–332, 2002.
[43] H. Albrecher, S. A. Landoucette, and W. Schoutens, “A
generic one-factor Lévy model for pricing synthetic
CDOs,” In: Advances in Mthematical Fiance, R. J. Elliott
et al. (eds.), Birkhäuser, Boston, 2007.
[44] Gupton and Stein, “Losscalc: Moody's model for pre-
dicting loss given default(LGD),” Working Paper, Moody’s
Investor sevices, 2002.
[45] G. Graziano and L. C. G. Rogers, “A dynamic approach to
the modeling of correlation credit derivatives using
markov chains,” Working Paper, University of Cambridge,
2005.
[46] P. Schönbucher, “Portfolio losses and the term structure
of loss transition rates: A new methodology for the pri-
cing portfolio credit derivatives,” Working Paper, ETH
Zurich, 2006.
[47] M. Walker, “Simultaneous calibration to a range of
portfolio credit derivatives with a dynamic discrete-time
multi-step loss model,” Working Paper, University of
Toronto, 2007.
[48] F. Longstaff and A. Rajan, “An empirical analysis of the
pricing of collateralized debt obligations,” Journal of
Finance, Vol. 63, No. 2, pp. 529–563, 2008.
[49] P. Lévy, “Calcul des probabilités,” Gauther-Villars, 1925.
[50] P. Lévy, “Théorie de l'addition des variables aléatoires,”
Gauther-Villars, 1937.
[51] G. Samorodnitsky and M. S. Taqqu, “Stable non-Gau-
ssian random processes: Stochastic models with infinite
variance,” Chapman and Hall/CRC, Boca Raton, 1994.
[52] M. F. Shlesinger, G. M. Zaslavsky, and U. Frisch (Eds.),
“Lévy flights and related topics in physics,” Lecture
Notes in Physics, Vol. 450, Springer-Verlag, Berlin, 1995.
[53] B. Mandelbrot, “The Pareto-Lévy law and the distribution
of income,” International Economic Review, Vol. 1, pp.
79–106, 1960.
[54] V. M. Zolotarev, “One-dimensional stable distributions,”
American Mathematical Society, R. I. Providence, 1986.
[55] A. Mortensen, “Semi-analytical valuation of basket credit
derivatives in intensity-based models,” Journal of Deri-
vatives, Vol. 13, No. 4, pp. 8–26, 2006.