Intelligent Information Management, 2010, 2, 80-89
doi:10.4236/iim.2010.22010 Published Online February 2010 (http://www.scirp.org/journal/iim)
A Nonlinear Control Model of Growth,
Risk and Structural Change
P. E. Petrakis, S. Kotsios
National and Kapodistrian University of Athens, Athens, Greece
Abstract
Uncertainty is perceived as the means of removing the obstacles to growth through the activation of Knig-
htian entrepreneurship. A dynamic stochastic model of continuous-time growth is proposed and empirically
tested, including equilibrating and creative entrepreneurial activity. We find that uncertainty affects economic
growth and the rate of return, and causes structural changes in portfolio shares for the two types of entrepre-
neurial events. Structural change depends mainly on the intertemporal rate of substitution, productivity ratios,
and finally intersectoral difference in return and risk.
Keywords: Growth, Risk, Entrepreneurship, Structural Change
1. Introduction
This paper examines the relationship between growth and
risk through structural change. Structural change is ana-
lyzed through the examination of growth, since it relates
to entrepreneurship and uncertainty. Uncertainty is treated
as the means of removing barriers to growth through the
activation of Knightian entrepreneurship.
We assume that growth is the result of equilibrating
and creative entrepreneurial events. Equilibrating entre-
preneurial events (adaptive behaviour) are the most
common ones and bring demand and supply to an equi-
librium [1]. On the other hand, creative entrepreneurial
events (innovative Schumpeterian behaviour) are those
that result from the creation of new (innovative) products
and services.
Considering structural change issues prompts discus-
sion of ‘why industries grow at different rates and which
industries come to have an increasing weight in the total
output while others decline and eventually wane’ [2]. In
search for an answer, researchers usually bring up dif-
ferences in income elasticities of domestic demand, sup-
plyside productivity differences, or different productivity
growth rates, which is the result of selection mechanisms
within the general evolutionary process [2–10]. Changes
in the relationship between intersectoral conditions of
risk and return are believed to have implications for
structural changes and economic growth. Thus, risk and
uncertainty are examined in the framework of structural
change and economic growth. Intuitively one can expect
to find a causal relationship between uncertainty and
structural change. However, this has not yet been verified
using a growth structural change model.
A dynamic stochastic model of continuous-time growth
is proposed, including two basic types of entrepreneurial
events, based on the work of Turnovsky [11]. It includes
three distinct ‘crucial’ individual concepts: growth rates,
portfolio shares, and rates of return. Thus, our analysis
includes the performance indexes (growth rates), ‘incen-
tives’ (rates of returns) and ‘results’ (portfolio shares) of
entrepreneurial behaviour. This paper therefore contrib-
utes to the analysis of uncertainty, entrepreneurship, and
risk. It also contributes to the analysis of structural change
patterns with regards to risk.
The rest of the paper is organized as follows. In Sec-
tion 2 of the paper the sustainable growth conditions are
discussed. Section 3 provides a short literature review on
structural change. In Section 4 we introduce the model
and its implications. Section 6 concludes.
2. Sustainable Growth and Uncertainty
The purpose of this study is to establish a theoretically
acceptable relationship between growth and uncertainty
taking into consideration the role of entrepreneurship.
The argument runs as follows: uncertainty activates en-
trepreneurship, which stimulates social capital and in-
fluences growth. Thus, the focus is on the relationship
between growth, entrepreneurship, and uncertainty. Social
capital is the common ground where entrepreneurship
and uncertainty operate. Do the above dynamics work
towards the elimination of obstacles to sustainable growth?

P. E. PETRAKIS ET AL. 81
Lucas [12] rearranges the neoclassical model and es-
tablishes that our attention should be on human capital
and its externalities on labour (L). Romer [13,14] aug-
ments this theory, arguing that additional investment in
research could result in increasing returns through
knowledge spillover embodied in human capital. What is
important here is alertness ([15], i.e. the ‘know- ledge’ of
where to find market data [16]). The process of finding
entrepreneurial opportunities relates to the stock of
knowledge (social capital) inherent in everyday life ex-
perience [17].
Yu [17], utilising a) Kirzner’s [14] theory of entrepre-
neurial discovery, b) Schumpeter’s [18] two types of
economic responses (extraordinary and adaptive), and c)
the Austrian theory of institutions as building blocks,
constructs an entrepreneurial theory of institutional change
and social capital accumulation. Yu [17,19], as well as
other researchers in the field, do not use the concept of
social capital as an alternative for institutions. However,
social capital as defined by Westlund and Bolton [20] is
greatly comparable to the concept of institutions, as de-
scribed in Yu [17,19]. The process of institutional change
is the continuous interaction between entrepreneurial
exploitation and exploitation of opportunities [21]. Insti-
tutions (stores of knowledge) emerge as a consequence
of the attempt to reduce structural (as opposed to neo-
classical static) uncertainty. Therefore, entrepreneurship
expands institutional development and social capital ac-
cumulation. Evidently in this process there are second-
round effects. Social capital accumulation boosts entre-
preneurship through externalities. These externalities
promote the distribution of information and generate
asymmetric information. At the same time, institutions
reinforce entrepreneurial alertness and the process of
discovering new entrepreneurial opportunities [19]. Thus,
entrepreneurship increases social capital. Thus entrepre-
neurship affects growth positively through social capital
accumulation.
According to Brouwer [22], in Knight’s [23] view, true
uncertainty is the only source of profits because they
vanish as soon as change becomes predictable, or they
become costs if uncertainty is hedged. Brouwer [22]
shows that diminishing returns to investment in innova-
tion can be avoided with the use of Knightian uncertainty.
This can be achieved through R&D cooperation; that is,
by creating social capital through R&D networks. We
can therefore suggest that uncertainty makes perpetual
innovation more likely. Thus, growth and uncertainty are
positively related. Knight [23] supports that rates of re-
turn on entrepreneurial investment vary around an aver-
age, and it is the relative entrepreneurial ability that is
rewarded.
Entrepreneurs also create a great deal of uncertainty
through Schumpeterian innovation, which creates confu-
sion in the market. A lack of entrepreneurship indicates
an over-reliance on old structures, interpretations, and
understandings [17]. Thus, entrepreneurial activation is
positively related with uncertainty.
From the above analysis, we can conclude that entre-
preneurship and uncertainty are related, with the latter
positively affecting entrepreneurship. Therefore, growth
and uncertainty are related, with the latter positively af-
fecting growth.
Montobbio [2], in his critical and concentrated litera-
ture review, presents three main trends stemming from
studies on structural change:
a) Endogenous growth models assess the determinants
of aggregate growth in a multi-sectoral economy [14,24]
but they incur difficulties in explaining major processes
of structural change.
b) Industry life-cycle models examine growth, matur-
ity and decline [25] but do not address 1) demand pres-
sures and 2) the relationship between growth and sector
that decline.
c) The supply and demand side factors approach seems
to attract most of the recent work done in the field.
The supply side was first proposed by Schumpeter
[18]. Kuznets [6] also stressed the importance of differ-
ent impact of 1) technological innovations and 2) a se-
lection mechanism based on competitive advantage.
Pasinetti [9,10] demonstrates that growth rates depend on
productivity rates. Montobbio [2] shows aggregate pro-
ductivity growth can be achieved without technological
change at the firm level.
This paper follows the supply and demand side factors
approach to structural change. The model includes basic
characteristics of the supply side, especially the influence
of uncertainty, productivity, and social capital and net-
works on the portfolio shares. In addition, in takes into
account the intertemporal elasticity of substitution. It
evidently shows how growth and structural change can
be achieved simultaneously, without the use of further
assumptions.
3. The Model of Growth, Creative
Equilibrating Events and the Role of
Uncertainty
The preceding analysis sets the basis for the introduction
of a representative agent model based on three funda-
mental concepts: economic growth, and the two types of
entrepreneurial events, including their basic characteris-
tics. Obviously, this points to a stochastic growth model,
which will include stochastic capital accumulation, capi-
tal return specification, and consumer utility maximisa-
tion procedures. The model is based on Turnovsky’s [11]
stochastic growth model with an entrepreneurial event.
We consider an economy, where the household and
production sectors are consolidated. The representative
agent consumes output over the period ),( dttt

at a
non-stochastic rate. Cdt
The agent distributes his resources between the two
types of entrepreneurial events. This means that he func-

P. E. PETRAKIS ET AL. 82
tions within an environment of perfect information, with
no costs or limitations regarding the initiation of a crea-
tive or equilibrating event.
The two types of entrepreneurial events influence
growth rates in different ways. In particular:
a) The role of creative vs. equilibrating events, with
regards to the accumulated flow of output over the period
, is rather different (see description of Equation
(3) below).
),( dttt
b) The two types of entrepreneurial activities face dif-
ferent technologies. Each activity adds to the total pro-
duction flow in the same way.
Each agent maximizes expected lifetime utility captured
by a standard concave utility function:



0
0)( dteCUEbt with and (1) 0)( CU ''' 0)( CU
subject to the stochastic accumulation equation,
CdtdYdKdKec  (2)
where:
c
K
= stock of physical capital devoted to creative en-
trepreneurial events at time t;
e
K
= stock of physical capital devoted to equilibrating
events at time t;
dY = flow of output (from both entrepreneurial events)
over the period ).,( dttt
The initial stocks of capital are given by and .
c
K0
e
K0
4. The Mechanics of Growth, Risk an
Structural Change
This section outlines the model. Subsection 4.1 gives the
model’s assumptions; 4.2 is concerned with the stochas-
tic process; 4.3 analyzes the determinants of risk; 4.4
summarizes the findings concerned with the growth
process; last, 4.5 examines the portfolio shares and the
rates of return. Finally, Table 1 presents the findings of
our theoretical analysis.
4.1. The Model’s Assumptions
Besides the basic assumptions, which are:
a) Linearity in production equations;
b) Individuals are risk averse, which implies that
01

, i.e. relatively large elasticity of intertemporal
substitution.
The model adopts the following two additional hy-
potheses:
c) ; i.e. the rate of return on creative entrepre-
neurial events is larger than that of equilibrating events;
ec rr
d) and ; the risk of equilibrating
and creative entrepreneurial events is greater than the
covariance of risk between the two types of events. This
hypothesis is based on the fundamental principle of
portfolio structuring according to which the risk of each
portfolio component is greater than the total portfolio
risk. In other words, since the agent is risk averse, it al-
ways makes sense to reduce risk by composing portfolios
that include both types of entrepreneurial events.
,
2
cee
 cec  
2
e) We assume that the production functions are linear
in their components; that is, that and,
where
e
ee
YK  c
cc
YK  
ce


,
e
the TFP variables in the two production
technologies respectively. There is no a priori reason to
assume thatc



; thus the model does not necessarily
assume heterogeneity of the sectors (firms) in terms of
productivity. However, for simplicity reasons the two
productivities are different in notation. The consequences
of identical intersectoral productivity values will be ex-
amined later.
Output is assumed to be generated from capital thro-
ugh the following stochastic process:
ccee
ce
dyKHdyKH
dtKFdtKFtdY
)()(
)()()(

 (3)
Equation (3) has the following interpretation: the
change in total output depends on deterministic events
and stochastic episodes stemming from equilibrating and
creative entrepreneurial activity. () ()
ce
F
KFK
ccee dyKHdyK)()( 
repre-
sent the deterministic effects of creative and equilibrating
events respectively, whereas repre-
sent the stochastic events in each category of entrepre-
neurship.
H
The stochastic terms in the production function are
based on two crucial assumptions: 1),
)( i KH ,iec

is constant and the shocks enter the production function
additively, 2) or , where the dist-
urbances are proportional to the aggregate capital stock,
thus entering the production function in a multiplicative
way. The assumptions regarding the stochastic distur-
bance terms are crucial for obtaining tractable, closed-
form solutions to the optimisation problem.
ii hKKH )( ,iec
Stochastic disturbances of creative events are additive
to the model. Equilibrating events, however, enter the
model in a multiplicative function. Thus, according to
this specification, equilibrating events are assumed to
depend on the existing level of capital, whereas creative
events are independent of the stock of capital.
Total capital stock held by the representative agent is

P. E. PETRAKIS ET AL. 83
denoted in the following way:
WKKKce (4)
with the corresponding portfolio shares being
,1
ec
ece
K
K
nnn
WW

(5)
From relationship (5) we see that
, , 1
ec
ece
KnKKnKnn
c
,
where are the corresponding portfolio shares.
ce nn,
4.2. The Stochastic Processes
Capital (K) follows a continuous time stochastic process:
, dKKdt Kdk

   (6)
where
K
C
K
KF  )(
 is the growth rate of capital and
denotes a stochastic component. The properties of
this stochastic component are:
dk
()0Edk

and
, dtdkK
2
)  Var(2
2
2
2
yK
K
H
 
 The rate of return on capital occupied in equilibrat-
ing entrepreneurship is determined through the following
stochastic process:
ee
dRr dtdu
e
(7)
The variance of the stochastic part of (7) is given by
2
()
ee
Var dudt  
Stochastic real rate of return on capital occupied in
creative events is described through a similar stochastic
process:
cc c
dRr dtdu (8)
With the variance of the stochastic part being equal to
.
2
()
cc
Var dudt  
The deterministic parts and denote the
rates of return on the two types of capital. The stochastic
parts are normally distributed with
dtredtrc
( 0)

duE and
. They represent the risks that the agent
undertakes when he employs capital on equilibrating and
creative entrepreneurship.
dtduVar u
2
)(  
4.3. The Determinants of Risk
Theorem 4.3.1: The following relations hold:
22222
,
eeK cc
2
K

   (9)
(Proof available upon request)
Theorem 4.3.1 suggests that the two levels of risk as-
sociated with entrepreneurial equilibrating and creative
events are directly dependent upon the corresponding
productivity ratio. They are also directly related to the
stochastic part of capital accumulation, described by the
variance. This is consistent with economic intuition since
it implies that economies with small capital accumulation
variance (i.e. low density business cycles) are character-
ized by low levels of entrepreneurial risk. The positive
relationship between entrepreneurial risk and productiv-
ity is also an anticipated outcome since according to
theorem 4.3.1 entrepreneurial risk, and thus the rate of
return, has a positive relationship with productivity.
4.4. The Growth Process
The functional form portraying the relationship between
individual entrepreneurial risk and the growth rate of
capital, establishes the mechanism and the necessary
conditions through which the two types of risk influence
the rate of growth in our model. In order to address these
two issues we introduce the following optimisation
problem:



0
0
1
max dteCE bt
C


(10)
s.t.
KdzKdtdK




(11)
In other words, we want to maximise the expected value
of the following utility function
bt
eCCU  


1
)( , 1

(12)
where C is the agent’s consumption and b is the dis-
count rate.
The following result plays an essential role in the study
of the comparative statics.
Theorem 4.4.1: In equilibrium the following hold:
2
2
11 (1
2e
e

 

)



 ,
2
2
11 (1)
2c
c

 





 
(13)
(Proof available upon request)
The effect of entrepreneurial risk on growth depends on
the intertemporal elasticity of substitution. When large
(i.e. 1


) the effect of risk on growth is positive. When
1

then the effect is negative. This effect also depends
on the reciprocal of productivity ratio, where the larger

P. E. PETRAKIS ET AL. 84
the productivity the smaller its influence on growth. This
fact is demonstrated in the following theorem:
Theorem 4.4.2: The following inequalities are valid:
0 ,022 





ce




(14)
Moreover, in both cases, entrepreneurial risk has a direct
relationship with the aggregate capital stock and an in-
verse relationship with productivity. The greater the
quantity of aggregate capital, the larger the influence of
risk on growth. On the other hand, the larger the produc-
tivity in the economy, the weaker the influence of risk on
growth. In other words the greater the average ratio in the
economy, the greater is the risk influence, as the financial
theory suggests. On the other hand, the larger the produc-
tivity in the economy is, the smaller the effect of risk on
growth. Different sector productivity levels imply differ-
ences on their impact on growth. Thus, if ce


, that is
the productivity ratio in the equilibrating sector is greater
than the productivity ratio in the creative sector, then if
risk increases (decreases) by the same amount in both
sectors, the impact on growth will be smaller (larger) for
the equilibrating events vs. the creative events.
4.5. Portfolio Shares and Rates of Return of
Entrepreneurial Events
By using the stochastic accumulation equation we have
successively shown:
CdtdYdYCdtdYdK ce  (15)
Dividing by we get

() ()
ec
ec
ec eecc
ec
eee eccc c
ee cceeccee cc
dKdYdYC dt
KKKK
dYdYCC
nndtndRn dRdt
KKK K
C
rn dtn durn dtn dudt
K
C
r nr ndtn dundur nr ndtdk
KK
 
  

 
  
 
 
C
(16)
with, . We can easily prove that the variance
of this stochastic process satisfies the relation
1ce nn
cececceeK nnnn
 2
22222  (17)
where ce

is the covariance of .
ce
This is a standard portfolio construction statement. As
dRdR and
we have already seen above, the variances of equilibrat-
ing and creative events are connected with the covari-
ance of the ce

with the basic relation of
and
cee
 
2
cec
 
2
The original optimisation problem is transformed to
c
00
C, n,e
1
max , 1
bt
nECedt


 
 (18)
s.t.
dkdt
K
C
nrnr
K
dK
ccee 





 (19)
with
1

ce nn (20)
cececceeK nnnn
 2
22222 (21)
Theorem 4.5.1: The first-order conditions for the opti-
misation problem can be written as follows
2
1/( 1)
1
()(1)
2
() 1
ee ccK
brnrn



 
 



(22)
1











K
C





K
rnncceecc  ))(1( 2






K
rnnececee  ))(1( 2


1

ecnn


where Cnn ce



,,
C
are the maximum achieved values of
, and nn ce,,

is the Lagrange multiplier, related to
the equation 1


e
n
c
n.
(Proof available upon request)
These above equations describe the solution of our op-
timisation problem. For the sake of the appearances, in
the next paragraphs we will omit the hat symbol. The
reader should keep in mind that we refer to the optimal
values. Let us now assume that the quantities
cece are functions of . Differentiating the abo-
ve equations, (proof on request), with respect to , we
get:
rrnn ,,, 2
e

2
e

,
)(2
)1( 2
2ec
e
e
e
rr
nn







(24)
)(2
)1( 2
2ec
e
e
c
rr
nn







(25)
)(2
)()1(
)1(
222
2ec
ceee
e
e
e
rr
n
n
r








(26)
)(2
)()1( 222
2ec
ccee
e
c
rr
nr







(27)

P. E. PETRAKIS ET AL. 85
Accordingly for the special case where the quantities
are considered as functions of the variable
, we get:
cece rrnn ,,,
2
c

,
)(2
)1( 2
2ec
c
c
e
rr
nn







(28)
)(2
)1(
2
2ec
c
c
c
rr
nn







(29)
)(2
)()1( 222
2ec
ceec
c
e
rr
nr




 

(30)
)(2
)()1(
)1(
222
2ec
ccec
c
c
c
rr
n
n
r








(31)
From the comparative statics presented above we con-
clude that there are three variables that play a significant
role: 1) the difference between the rates of return on the
two entrepreneurial activities, which is reciprocal to the
degree of structural change, 2) the intertemporal elastic-
ity of substitution, which is directly related to structural
change, and 3) the existing portfolio share, which has a
strong impact because of the exponent. The larger the
difference between the two rates of return (creative vs.
equilibrating activities), the smaller the effect of struc-
tural change is expected to be. It is also noted that the
larger the intertemporal rate of substitution, the larger the
value of return (1

) and thus, the larger the extent of
structural change. Finally, the greater the portfolio share,
the larger the effect of entrepreneurial risk on portfolio
shares will be.
The involvement of portfolio share on structural
change requires further elaboration. The influence of
existing portfolio shares refers to the concept of network
effects and social capital accumulation. The larger the
portfolio shares, the greater the effects on entrepreneurial
activity, the larger is the social capital employed in the
production function, and the greater the influences on
sectoral growth.
Regarding the impact of entrepreneurial risk on the
rates of return, the analysis becomes more complicated.
The factors mentioned above still play a significant role,
as in the case of portfolio shares. In addition, there are
two more terms which appear to affect this relationship.
These are the difference for the equilibrating
events and the difference for the creative
events. In both cases, the central principle of portfolio
construction holds. That is, the risk involved in equili-
brating and creative entrepreneurial events is greater than
the covariance between the two types of risk. The greater
the magnitude of these differences the larger the degree
to which risk affects the rates of return.
cee
 
2
ce
 2
c

We are now ready to obtain our next results:
Theorem 4.5.2:
If then
ecrr 
0 ,022 





e
c
e
enn

(32)
0 ,022 





c
c
c
enn

(33)
Proof: Obvious from the above formulas and the fact
that 01



.
These results are particularly interesting regarding the
impact of risk on portfolio shares in the two entrepreneu-
rial activities. Due to the difference in the rates of return
between creative and equilibrating events, the higher
level of risk involved in creative events directs total en-
trepreneurial activity more towards equilibrating activi-
ties than creative ones. The opposite also holds. So the
level of risk essentially determines the nature of the en-
trepreneurial activity adopted (creative-equilibrating). In
the case where both types of risk are in high levels, one
should expect equilibrating entrepreneurship to dominate
creative entrepreneurship. This fact will also have a posi-
tive effect on economic growth. This result influences
the intertemporal elasticity of substitution, making agents
more willing to give up consumption stemming from the
equilibrating sector rather than the creative sector. As a
matter of fact, the two conditions, rc > re and γ < 1,
should coincide if the particular type of structural change
takes place. If one of the above two relationships changes
direction, then one condition could offset the other. Thus,
for a steady-state situation, the larger the reward of crea-
tive entrepreneurship the less the required intertemporal
elasticity of substitution.
Finally, we test the relationship between entrepreneu-
rial risk and the economy’s growth rate, without distin-
guishing between the two types of entrepreneurship. In
essence, we accept that
Theorem 4.5.3: If and
then:
ecrr ceccee
  22 ,
0
2
e
c
r

,0
2




e
e
r

(34)
Proof: Obvious from the above formulas and the fact
that 01



.
Theorem 4.5.4: If and
then:
ecrr ceccee
 22 ,
0?
2
c
c
r

,0
2
c
e
r
 




(35)
Proof: Obviously by the above formulas and the fact
that 01



.

P. E. PETRAKIS ET AL. 86
Theorem 4.5.5: If 1

we have at the equilibrium:
0
2


K


(36)
Proof: Indeed, from equation (37) we have:
1
22 2
1
1(1) 0
2K
CbK KK
KK
 









(37)
which means that
0)1(
2
1
2





K (38)
Thus it is proved that risk and growth are positively
related.
Table 1 presents the findings from the preceding
analysis. We concentrate on the results regarding the
effect of both types of entrepreneurial events on growth
rate, portfolio shares, and rates of return.
a) The effect of a change in equilibrate risk
In equilibrating events, risk has a positive relationship
with the corresponding rate of return. In turn, it has a
negative relationship with the rate of return of the equili-
brating events. In this case, the portfolio share of equili-
brating entrepreneurial events will increase against the
portfolio share of creative events and eventually the
growth rate will increase. Otherwise, a decrease in equ-
ilibrating entrepreneurship risk, decreases the rate of
return and the portfolio share of equilibrating events. The
total growth rate in this case will fall.
b) The effect of a change in creative risk
An increase (decrease) in the risk of a creative entre-
preneurial event will increase (decrease) the correspond-
ing rate of return while having the opposite effect on the
rate of return of an equilibrating event. However the in-
crease (decrease) in the risk of a creative event will
shrink the corresponding portfolio share and will in-
crease (decrease) the portfolio share of equilibrating
events. Eventually, the total rate of growth will increase
(decrease). The above comments hold when the creative
risk influences positively the rate of return of creative
events.
c) How the portfolio share of creative entrepreneurial
events could be increased
Evidently, any kind of increase in risk will increase
the portfolio share of equilibrating events. Then the ques-
tion arises regarding the conditions that need to hold in
order for the portfolio share of creative events to increase.
Two mutually exclusive conditions can provide the con-
ditions for the creative portfolio share to be increased.
The first is that the rate of return of creative events is less
than the rate of return of equilibrating events. In other
words, the creative sector expands when the risk be-
comes smaller than the level of the risk of equilibrating
events. The second refers to the intertemporal elasticity
of substitution. The lower its value, the larger the portfo-
lios share of the creative events. This last result should
be evaluated in the light of the fact that the model pin-
points the direction in the change of the basic variables
as we depart from the equilibrium point and for very
small changes. Thus, an increase in the high (by defini-
tion) risk of creative events reduces their portfolio share.
d) The question of possible uniformity of growth
Equations (24–25) and (26–31) imply that uniform
growth can be achieved when the existing portfolios of
the two entrepreneurial events are equal. Since this is a
rare situation, we conclude that risk will exercise
non-uniform influences on the different portfolio shares.
5. Conclusions
This paper explores the fundamental growth question
regarding which forces and under what conditions the
obstacles to sustainable growth can be removed. The
answer focuses on the role of uncertainty. The outcome
of the analysis underlines the fact that uncertainty affects
growth and structural change. In turn, structural change
impacts growth, if the agent follows the basic principles
of portfolio construction.
6. References
[1] P. Petrakis, “Entrepreneurship and growth: Creative and
equilibrating events,” Small Business Economics, Vol. 9
No. 5, pp. 383–402, 1997.
[2] F. Montobbio, “An evolutionary model of industrial
growth and structural change,” Structural Change and
Economic Dynamics, No.13, pp. 387–414, 2002.
[3] W. J. Baumol, “Macroeconomics of unbalanced growth:
The anatomy of urban crisis,” American Economic Re-
view 57, pp. 415–426, 1967.
[4] W. J. Baumol, S. A. B. Blackman, and E. N. Wolff, “Un-
balanced growth revisited: Asymptotic stagnancy and
new evidence,” American Economic Review, No. 75, pp.
806–817, 1985.
[5] S. Kuznets, “Economic growth and nations: Total output
and production structure,” Cambridge University Press,
Cambridge, 1971.
[6] S. Kuznets., “Economic development, the family and income
distribution. selected essays,” Cambridge University Press,
Cambridge, 1988.
[7] J. S. Metcalfe, “Evolutionary economics and creative
destruction,” Routledge, London, 1998.
[8] J. S. Metcalfe, “Restless capitalism: Increasing returns
and growth in enterprise economics,” Mimeo, CRIC,
Manchester, March 1999.
[9] L. Passinetti, “Structural change and economic growth: A
theoretical essay on the dynamics of the wealth of nations,”

P. E. PETRAKIS ET AL. 87
Cambridge University Press, Cambridge, 1981.
[10] L. Passinetti, “Structural change and economic dynam-
ics,” Cambridge University Press, Cambridge, 1993.
[11] S. J. Turnovsky, “Methods of macroeconomic dynamics,”
MIT Press, Cambridge, 2000.
[12] R. J. Lucas, “On the mechanics of economic develop-
ment,” Journal of Monetary Economics, No. 22, pp. 3–42,
January 1988.
[13] P. M. Romer, “Increasing returns and long-run growth,”
Journal of Political Economy, Vol. 94, No. 5, pp. 1002–
1037, 1986.
[14] P. M. Romer, “Endogenous technological change,” Jour-
nal of Political Economy, Vol. 98, No. 5, pp. S71–102, 1990.
[15] I. M. Kirzner, “Competition and Entrepreneurship,” Uni-
versity of Chicago Press, Chicago, 1973.
[16] R. G. Holcombe, “Entrepreneurship and economic grow-
th,” Quarterly Journal of Austrian Economics, Vol. 1, No.
2, pp. 45–62, Summer 1998.
[17] T. F. L. Yu, “Entrepreneurial alertness and discovery”
Review of Austrian Economics, Vol. 14, No. 1, pp. 47–63,
2001a.
[18] J. Schumpeter, “The instability of capitalism,” The Eco-
nomic Journal, No. 38, pp. 361–386, Vol. 123, No. 2, pp.
297–307, 1928.
[19] T. F. L. Yu, “An entrepreneurial perspective of institu-
tional change,” Constitutional Political Economy, Vol. 12,
No. 3, pp. 217–236, 2001b.
[20] H. Westlund and R. Bolton, “Local social capital and
entrepreneurship,” Small Business Economics, No.21, pp.
77–113, 2003.
[21] G. Dosi and F. Malebra, “Organizational learning and
institutional embeddedness. In: Organization and strategy
in the evolution of the enterprise,” Macmillan, London,
pp. 1–24, 1996
[22] M. Brouwer, “Entrepreneurship and uncertainty: innova-
tion and competition among many,” Small Business Eco-
nomics, Vol. 15, No. 2, pp. 149–160, 2000.
[23] F. H. Knight, “Risk, uncertainty and profit,” Houghton
Mifflin, New York, 1921.
[24] P. Aghion and P. Howitt, “Endogenous growth theory,”
MIT Press, Cambridge, 1998.
[25] D. Audretch, “An empirical test of the industry life cy-
cle,” Welwirtschaftliches Archiv,1987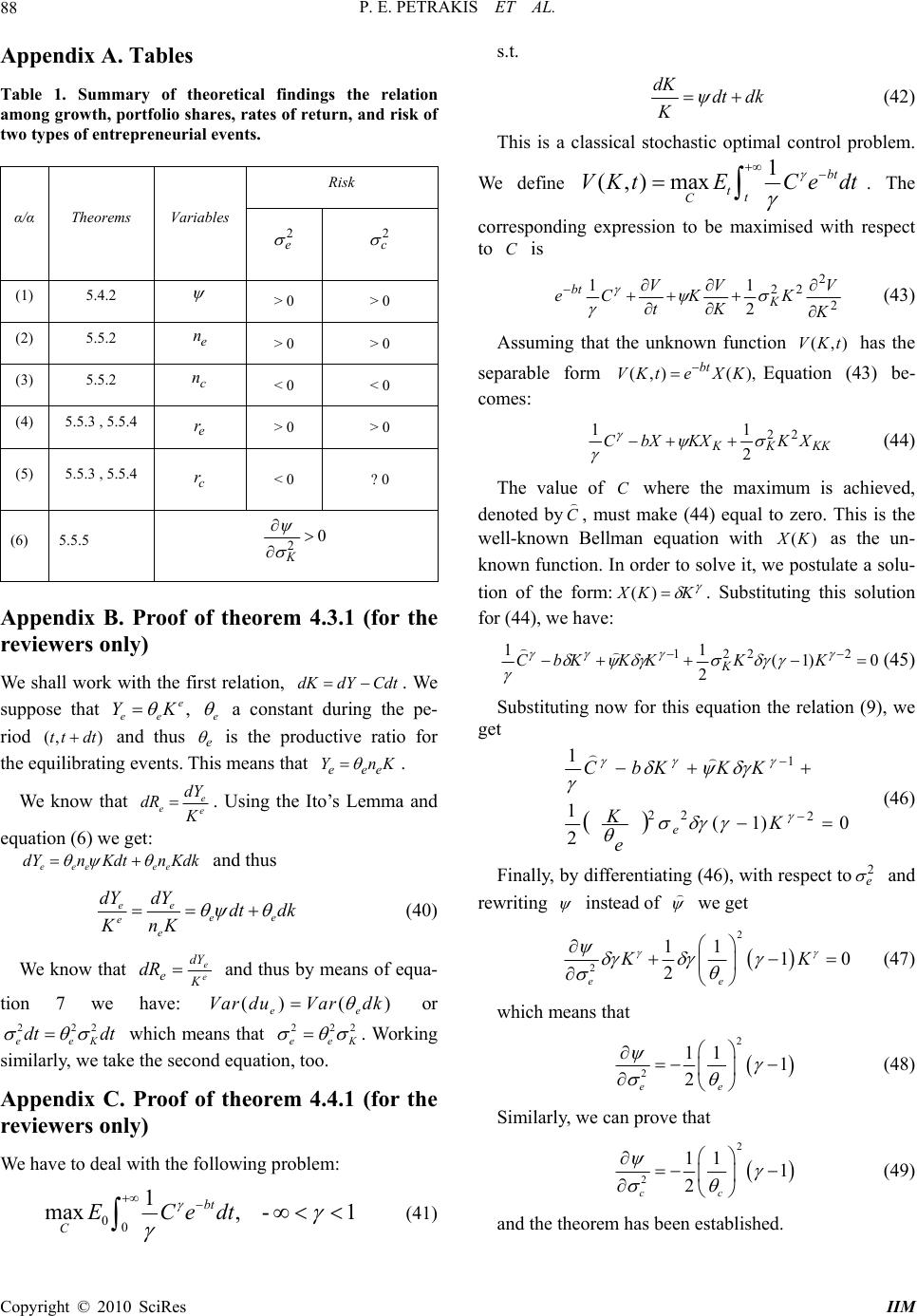

P. E. PETRAKIS ET AL. 88
Appendix A. Tables
Table 1. Summary of theoretical findings the relation
among growth, portfolio shares, rates of return, and risk of
two types of entrepreneurial events.
Risk
α/α Theorems Variables
2
e
 2
c

(1) 5.4.2

> 0 > 0
(2) 5.5.2 e
n > 0 > 0
(3) 5.5.2 c
n < 0 < 0
(4) 5.5.3 , 5.5.4 e
r > 0 > 0
(5) 5.5.3 , 5.5.4 c
r < 0 ? 0
(6) 5.5.5 0
2


K


Appendix B. Proof of theorem 4.3.1 (for the
reviewers only)
We shall work with the first relation, CdtdYdK

. We
suppose that ,
e
ee
YK
e

 
e

a constant during the pe-
riod and thus is the productive ratio for
the equilibrating events. This means that
),( dttt 
KnY eee

.
We know that e
ee
dY
dR
K
. Using the Ito’s Lemma and
equation (6) we get:
eee ee
dYnKdtn Kdk    and thus
ee
ee
e
e
dY dYdt dk
nKK
   (40)
We know that e
e
K
dY
e
dR  and thus by means of equa-
tion 7 we have: () (
ee
Var duVardk)


222
eeK
or
which means that
222
eeK
dt dt  

 . Working
similarly, we take the second equation, too.
Appendix C. Proof of theorem 4.4.1 (for the
reviewers only)
We have to deal with the following problem:
 
0
01- ,
1
max 


dteCEbt
C
(41)
s.t.
dK dt dk
K
  (42)
This is a classical stochastic optimal control problem.
We define   t
bt
t
CdteCEtKV


1
max),( . The
corresponding expression to be maximised with respect
to is C
2
2
22
2
11
K
V
K
K
V
K
t
V
Ce K
bt













(43)
Assuming that the unknown function has the
separable form Equation (43) be-
comes:
),( tKV
),(),( KXetKV bt 
KKKK XKKXbXC 22
2
11



 (44)
The value of where the maximum is achieved,
denoted byC
C

, must make (44) equal to zero. This is the
well-known Bellman equation with as the un-
known function. In order to solve it, we postulate a solu-
tion of the form:. Substituting this solution
for (44), we have:
)(KX

 KK )X(
0)1(
2
11 2221  



KKKKKbCK


(45)
Substituting now for this equation the relation (9), we
get
  0)1(
2
1
1
2
22
1










K
e
K
KKKbC
e


(46)
Finally, by differentiating (46), with respect to and
rewriting
2
e


instead of


we get

2
2
11 1
2e
e
KK

 



0



 (47)
which means that

2
2
11 1
2e
e









 
(48)
Similarly, we can prove that

2
2
11 1
2c
c









 
(49)
and the theorem has been established.

P. E. PETRAKIS ET AL. 89
Appendix D. Proof of theorem 4.5.1 (for the
reviewers only)
These equations determine the optimal values:
 ,,, cenn
K
C as functions of . Furthermore,
substituting once more, the values we got above, for the
relation (53) and cancelling the term we take the
Bellman equation:
KKK XX ,
ebt
We have to solve the following optimisation problem.
c
00
C,n ,
1
max , 1
e
bt
nECedt



  
 (50)
0
2
1
)(
1
22


















KKK
Kccee
XK
KX
K
C
nrnrKbXC






(55)
s.t.
dkdt
K
C
nrnr
K
dK
ccee 





 (51)
with
1 ce nn where denotes optimised value. To solve the Bellman
equation we postulate a solution of the form
, where the coefficient δ can be determined.
Substituting this into the Bellman equation and the equa-
tions (54), we perform some manipulations:

 KKX )(
cececceeK nnnn
 2
22222 (52)
This is a classical stochastic optimal control problem;
to solve it we shall follow Turnovsky [11]. The corre-
sponding Lagrangian expression to be maximised is:
2
1/(1)
1
()(1)
2
() 1
ee ccK
brnrn



 
 



(22)
]1[
2
1
1
2
2
22
ecK
ccee
bt
nn
K
V
K
K
V
K
K
C
nrnr
t
V
e


















(53)
1











K
C

We assume now that the unknown function, has
the separable form, we substitute this
value into (53) and we put then, the partial derivatives of
the resulting expression, with respect to the variables
equal to zero. We shall take:
),( tKV
)(),( KXetKV bt 
,,,, 
ce nnC




K
rnn cceecc  ))(1(2






K
rnnececee  ))(1(2


1

ecnn


1
0)(
0)(
22
22
1





ce
KKceceeKe
KKceeccKc
K
nn
XKnnKXr
XKnnKXr
XC



(54)
and the theorem has been established.