J. Software Engineering & Applications, 2008, 1: 8-12
Published Online December 2008 in SciRes (www.SciRP.org/journal/jsea)
1
A Bioinformatics-Inspired Adaptation to Ukkonen’s Edit
Distance Calculating Algorithm and Its Applicability
Towards Distributed Data Mining
Bruce Johnson
University of Tennessee 1508 Middle Drive Knoxville, TN 1-865-974-3461
Received November 25
th
, 2008; revised November 29
th
, 2008; accepted December 1
st
, 2008.
ABSTRACT
Edit distance measures the similarity between two strings (as the minimum number of change, insert or delete
operations that transform one string to the other). An edit sequence s is a sequence of such operations and can be used
to represent the string resulting from applying s to a reference string. We present a modification to Ukkonen’s edit
distance calculating algorithm based upon representing strings by edit sequences. We conclude with a demonstration of
how using this representation can improve mitochondrial DNA query throughput performance in a distributed
computing environment.
Keywords: Bioinformatics-Inspired Adaptation, Calculating Algorithm, Data Mining
1. Introduction
Let ∑ be a finite alphabet and let ∑
*
denote the collection
of finite strings over ∑. Edit distance is a means of
measuring similarity between a target and reference string
in ∑
*
by computing the minimum number of change, insert,
or delete edit operations that transform one string into
another. The edit distance is a metric [1] and is a means of
measuring the similarity between two strings [2].
Wagner and Fischer presented one of the first
algorithms for calculating edit distance [3]. Ukkonen
improved upon Wagner and Fischer’s algorithm (using
potentially less time and space) [4,5]. However, a
significant performance bottleneck in Ukkonen’s
algorithm is calculating the length of a longest common
prefix (which we refer to as the degree of agreement)
between two strings.
Let alphabet ∑
d
= {a, c, g, t}. ∑
d
can be regarded as
representing the molecules adenine, cytosine, guanine
and thymine respectively. These molecules are
collectively known as nucleotides. When covalently
bonded together, these molecules become a polymer
called a polynucleotide. Two polynucleotides can
produce the well-known double helix shape of DNA. The
determination of the order in which the nucleotides are
covalently bonded together in a polynucleotide is called
sequencing. The act of sequencing yields a string since
each nucleotide in the given polynucleotide maps to one
of the members of ∑
d
.
The mitochondria are organelles found throughout
eukaryotic cells. They are responsible for the production
of adenosine triphosphate (ATP), the primary currency
by which a cell’s energy needs are trafficked [6].
Mitochondria possess DNA (mtDNA). This mtDNA is
ultimately responsible for the production of the proteins
which regulate the mitochondrion and produce ATP.
We define an mtDNA string to be the string that results
from sequencing one of the polynucleotides that comprise
mtDNA. Anderson et al. [7] were the first scientists
responsible for sequencing a human’s mtDNA. The mtDNA
string they produced is a standard reference and is now
known as the Cambridge Reference Sequence (CRS).
Mitochondrial DNA is the subject of much research by
forensic scientists because it has features that aid them in
their identification of an individual [8].
1) It is widely distributed throughout a given cell
2) It is always inherited from a child’s mother
3) It is conservative, i.e., the edit distance between the
CRS and a target mtDNA string is very small in
comparison to their lengths.
The first feature means that intact mtDNA can likely
be extracted from some piece of human detritus such as
hair or fingernails.
The second feature means that it is likely that the
mtDNA possessed by maternally related individuals is
the same. This feature is particularly advantageous for
individuals who seek to determine whether the remains of
a body belong to their sibling.
With regard to the third feature, we will show that
since mtDNA is conservative, the performance of the
longest common prefix calculation for Ukkonen’s edit
distance calculating algorithm can be improved by
representing strings as edit sequences. We will show how
this feature can improve mtDNA query throughput
performance in a distributed computing environment.
2. Preliminaries
2.1 Definitions
We begin by defining edit operations (to streamline
exposition, they may be referred to simply as operations).

A Bioinformatics-Inspired Adaptation to Ukkonen’s Edit Distance Calculating Algorithm 9
and Its Applicability Towards Distributed Data Mining
A nontrivial change operation has the form of ac σ and
acts on string α = α
0
… α
l
(provided 0≤a≤l ) to produce
β = β
0
… β
l
where
α
α
σ
β
β
=
≠



=i
i
i
i
if
fi
,
,
In other words, symbol α
a
at (address) a is changed to
symbol σ .
An insert operation has the form of ai σ and acts on string α
= α
0
… α
l
(provided 0≤a≤l ) to produce β = β
0
… β
l+1
where
α
α
α
σ
α
β
＞if
if
＜if
,
,1
,
i
i
i
a
i
i
i
=





=
−
In other words, symbol σ has been inserted into string
α at address a.
A delete operation has the form of ad and acts on string α
= α
0
… α
l
(provided 0≤a≤l) to produce β = β
0
… β
l-1
where
α
α
α
α
β
＞if
＜if
,
1
,
i
i
i
i
i



=
+
In other words, symbol α
a
has been deleted from string α .
A sequence of edit operations is referred to as an edit
sequence. The concatenation of edit sequence s with t is
denoted s|t.
Given edit operation e, the function &() returns e’s
address, (i.e. &(ad ) = a), the function τ() returns e’s type
(i.e. τ (ai σ ) =i) and the function δ() returns the symbol to
be inserted or changed, i.e. δ(ac σ ) = σ .
A change operation e is called trivial (with respect to α )
if it acts as the identity function on α (i.e. e ( α ) = α ). To
indicate that is trivial (when is understood) it may be
written as at σ .
The notation [expression] is defined as
falseisexpif
trueisexpif
,0
,1
][exp ression
ression
ression 


=
Given strings α , β ∈ ∑
*
, an edit sequence s taking α to
β (i.e. s( α ) = β ) is produced by Wagner and Fischer’s
algorithm [1]. Their algorithm-which we refer to as WF -
first proceeds by calculating a (n+1) × (m+1) distance
matrix D as follows (where | α | = n and | β | = m).
otherwise
0
0
),],[min(1
,
,
1,,,1111,1
,
=
=





≠−+
=
−−−−−−
iif
jif
DDD
j
i
D
jijijiji
ji
βα
Next, an edit sequence s (transforming α into β ) is
obtained by the recursive function S
S(∅) = ε
S(D) = e | S(D′)
where ∅ denotes the empty matrix (0 rows, 0 columns),
ε denotes the empty edit sequence, and D′ is either the
result of removing the last D (if case 1 applied),
removing the last column from D if case 2 applied or
removing both the last row and last column from D (if
case 3 or 4 is applied).
4case
3case
2case
1case
otherwise
1if
1if
1if
)1(
)1(
)1(
,
1,1,
1,,
,1,
1
1
1
'
'
'
−−
−
−
−
−
−
+=
+=
+=







−
−
−
=
mnmn
mnmn
mnmn
n
m
m
DD
DD
DD
tm
cm
im
md
e
α
β
β
Given edit sequence s = S transforming α into β , the
function r (s, α , β ) returns the reduced edit sequence s
r
(with respect to α ). Example: let s = e
0
e
1
e
2
e
3
e
4
e
5
= 0tg
1tt 2d 2ig 3tt 4ct. Then, s
r
= r (s, α , β ) = e
0′
e
1′
e
2′
= 2d 2ig
4ct. Note that
1) 0′=2, 1′=3 and 2′=5
2) both s and s
r
map α to β
3) s
r
uses the minimum number of edit operations to
transform α to β
Edit sequence s = S(D) has the following properties.
1) No edit sequence mapping α to β is shorter than r(s,
α , β ).
2) Addresses of edit operations found in s are nondec-
reasing.
3) If e
j
is a delete edit operation in s, then &(e
j
)=
&(e
j+1
).
4) If e
j
is an insert or change edit operation in s, then
e
j + 1
has an address that differs from e
j
by one.
2.2 Characteristics of Reduced and Non-reduced
Edit Sequences
Given edit sequence s, define 〈s〉 by
Given s
r
( α ) = β the length of β can be recovered by
| β | = α + 〈s〉
Let ρ
t
be a subsequence of s consisting of trivial
change operations, maximal with respect to containment,
such that the addresses of successive members differ by
one. Such a subsequence ρ
t
is called a trivial change
queue. Example: s =0ta 1tc 2ia 3ct 4tt; ρ
t
= 0ta 1tc.
Let ρ
c
be a subsequence of s consisting of nontrivial
change operations, maximal with respect to containment,
such that the addresses of successive members differ by
one. Such a subsequence ρ
c
is called a nontrivial change
queue. Example: s = 0ca 1cc 2ia 3ct 4tt; ρ
c
= 0ca 1cc.
Let ρ
i
be a subsequence of s consisting of insert
operations, maximal with respect to containment, such
that the addresses of successive members differ by one.
Such a subsequence ρ
i
is called an insert queue. Example:
s = 0ia 1ic 2ca 3ct 4tt; ρ
i
= 0ia 1ic.
Let ρ
d
be a subsequence of s consisting of delete
operations, maximal with respect to containment, such
that the addresses of successive members do not differ.
Such a subsequence ρ
d
is called a delete queue. Example:
s = 0d 0d 0t t 1ca; ρ
d
= 0d 0d.
The length of a change or insert queue ρ = e
y
… e
z
is
given by | ρ | = &(e
z
)-&(e
y
) + 1.
2.3 Recovering Elements of s Using s
r
= r(s, α
αα
α , β
ββ
β )
Given s
r
= r(s, α , β ), we can recover the trivial change
queues removed from s while producing s
r
. We will first

10 A Bioinformatics-Inspired Adaptation to Ukkonen’s Edit Distance Calculating Algorithm
and Its Applicability Towards Distributed Data Mining
consider how to find the locations and then the symbols
associated with trivial change queues.
A trivial change queue ρ
t
may be a prefix, a suffix or
neither a prefix nor a suffix of s
r
. In order to find the
addresses of members of ρ
t
, there are three cases to
consider.
Case 1: Queue ρ
t
= e
k
… e
l
is a prefix of s
r
:
Queue ρ
t
is a prefix of s
r
if &(e
0′
) > 0. Furthermore, k =
&(e
k
) = 0 and l = &(e
l
) = &(e
0′
) - 1.
Case 2: Queue ρ
t
= e
k
… e
l
is a suffix of s
r
:
Queue ρ
t
is a suffix of s
r
if the last edit operation, e
m ′
,
in s
r
has address &(e
m′
) < n = |β| - 1. Furthermore, k = m ′
+ 1, &(e
k
) = &(e
m ′
) + [τ (e
m′
) ≠ d ], &(e
l
) = n and l = m′ +
(&(e
l
) – &(e
m ′ + 1
) + 1).
Case 3: Queue ρ
t
= e
k
… e
l
is neither a prefix nor a
suffix of s
r
:
Queue ρ
t
is neither a prefix nor a suffix of s
r
if the
consecutive edit operations e
j ′
and e
(j+1)′
in s
r
have
addresses &(e
j′
) < &(e
(j+1)′
) – [τ(e
j′
) = d ]. Furthermore, k
= j′ + 1 and l = ( j+1)′ – 1 where &(e
k
) = &(e
j ′
) + [τ(e
j ′
) =
d] and &(e
l
) = &(e
(j+1)′
) – 1.
Now that we know how to find the addresses of
members of trivial change queues, we need to find their
symbols. Given s
r
= r(s, α , β ). Let cell D
i,j
have a
column whose address is that of a trivial change
operation. Let function ni( j) return the number of insert
edit operations in s
r
whose addresses are less than j. Let
function nd( j) return the number of delete edit operations
in s
r
whose addresses are less than or equal to j. In order
to find the symbols in trivial change queues, we
discovered that nd( j) – ni( j) = i – j.
Since nd( j) – ni( j) = i – j it follows that α
i
= α
j + nd(j) –
ni(j)
. If e = at α
i
then we can say that e = at α
j + nd(j) – ni(j)
.
Since the address of e is equal to the column j labeled by
D
i,j
, we can say that e = jt α
j + nd(j) – ni(j)
. Hence, given α and
s
r
, we can acquire the address and symbol associated with
each trivial change operation in s.
Given element β
x
, let t
r
= Partition (s
r
, x) return edit
sequence t
r
whose elements are comprised of those
elements of s
r
whose addresses are greater than or equal
to x. Let e = GetOp(s
r
, y) return the first edit operation
found in s
r
whose address is greater than or equal to y.
Let ρ
t
be a trivial change queue, the following
pseudocode ρ
t
= Recover(s
r
, x) shows the procedure for
finding trivial change queues in s
r
. The code is initialized
by a call to Partition (s
r
, x).
ρ
t
= Recover (t
r
, x)
1. e = GetOp(t
r
, x)
2. if (e == e
0′
&& &(e
0′
) > 0) //Case 1
2.1. k = 0
2.2. l = &(e
l
)
2.3. return ( ρ
t
= e
k
… e
l
)
3. if (e == e
m′
&& &(e
m′
) < n = |β| - 1) //Case 2
3.1. k = m′ + 1
3.2. l = m′ + (&(e
l
) – &(e
m ′ + 1
) + 1)
3.3. return ( ρ
t
= e
k
… e
l
)
4. if (e==e
j ′
&& &(e
j ′
)<&(e
(j+1)′
)–[τ(e
j ′
) == d ]) //Case 3
4.1. k = j′ + 1
4.2. l = ( j+1)′ – 1
4.3. return ( ρ
t
= e
k
… e
l
)
5. return ∅
3. Calculating the Degree of Agreement
Using Edit Sequences
3.1 Motivation for Using Reduced Edit Sequences
At this point, it is productive to ask why we care about
reduced edit sequences. Let reference string α be the
CRS, target strings β and γ be mtDNA strings and let s
r1
=r (s
1
, α , β ) and s
r2
= s (s
2
, α , γ ). Edit sequences s
r1
and
s
r2
(and reference string α ) can be used as a means of
representing β and γ , respectively. This is significant
because large, conservative target strings are represented
by edit sequences that are substantially smaller. Hence,
calculating the edit distance between β and γ by using α ,
s
r1
and s
r2
, may lead to a more efficient utilization of
distributed computing resources for calculating edit
distance by increasing network throughput. Furthermore,
using α , s
r1
and s
r2
can afford forensic experts seeking to
find a match for an mtDNA string the ability to store and
carry large numbers of mtDNA sequences.
3.2 Our Algorithm
Let β and γ be target strings of lengths m and n,
respectively. Let s
r1
= r (s
1
, α , β ) and s
r2
= s (s
2
, α , γ )
and let (0≤x
1
≤m-1) and (0≤x
2
≤n-1). We want to know the
length of the longest common prefix of the substrings β
x1
… β
m - 1
and γ
x2
… γ
n-1
(i.e. the degree of agreement
between β and γ ). We will now consider how the degree
of agreement between β and γ can be calculated using
reduced edit sequences that represent β and γ by
examining how our algorithm deals with the different
types of edit operations that comprise our edit sequences
used to represent our strings.
Case 1: x
1
or x
2
is the address of a member of a delete
queue.
In this case, we do not have any symbols to compare;
hence, we will simply traverse to the end of the
respective queues.
Case 2: x
1
and x
2
are the addresses of members of
trivial change queues ρ
1
and ρ
2
, respectively.
Let l
1
be the last member of ρ
1
and let l
2
be the last
member of ρ
2
. Let e
1
be a member of ρ
1
and let e
2
be a
member of ρ
2
where e
1
=x
1
cα
w
, e
2
=x
2
cα
y
, w=x
1
+nd
1
(x
1
)
–ni
1
(x
1
) and y=x
2
+nd
2
(x
2
) – ni
2
(x
2
). If w = y, then δ((x
1
+ n)
tα
w + n
) = δ((x
2
+ n)tα
y + n
) for 0 ≤ n ≤ min(g, h), where g =
|{e
1
… l
1
}| and h = |{e
2
… l
2
}|. Hence, the degree of
agreement will be min(g, h).
Case 3: x
1
and x
2
are the addresses of members of ρ
1
and ρ
2
, respectively and neither ρ
1
nor ρ
2
are trivial
change queues nor delete queues.
Let e
j
and e
k
be members of ρ
1
and ρ
2
respectively, and
let &(e
j
) = x
1
and &(e
k
) = x
2
. Let e
y
and e
z
be the last
members of queues ρ
1
and ρ
2
, respectively. Let r be the
degree of agreement between β and γ . We compare the
symbols associated with these queues sequentially using
the following loop.
1. r = 0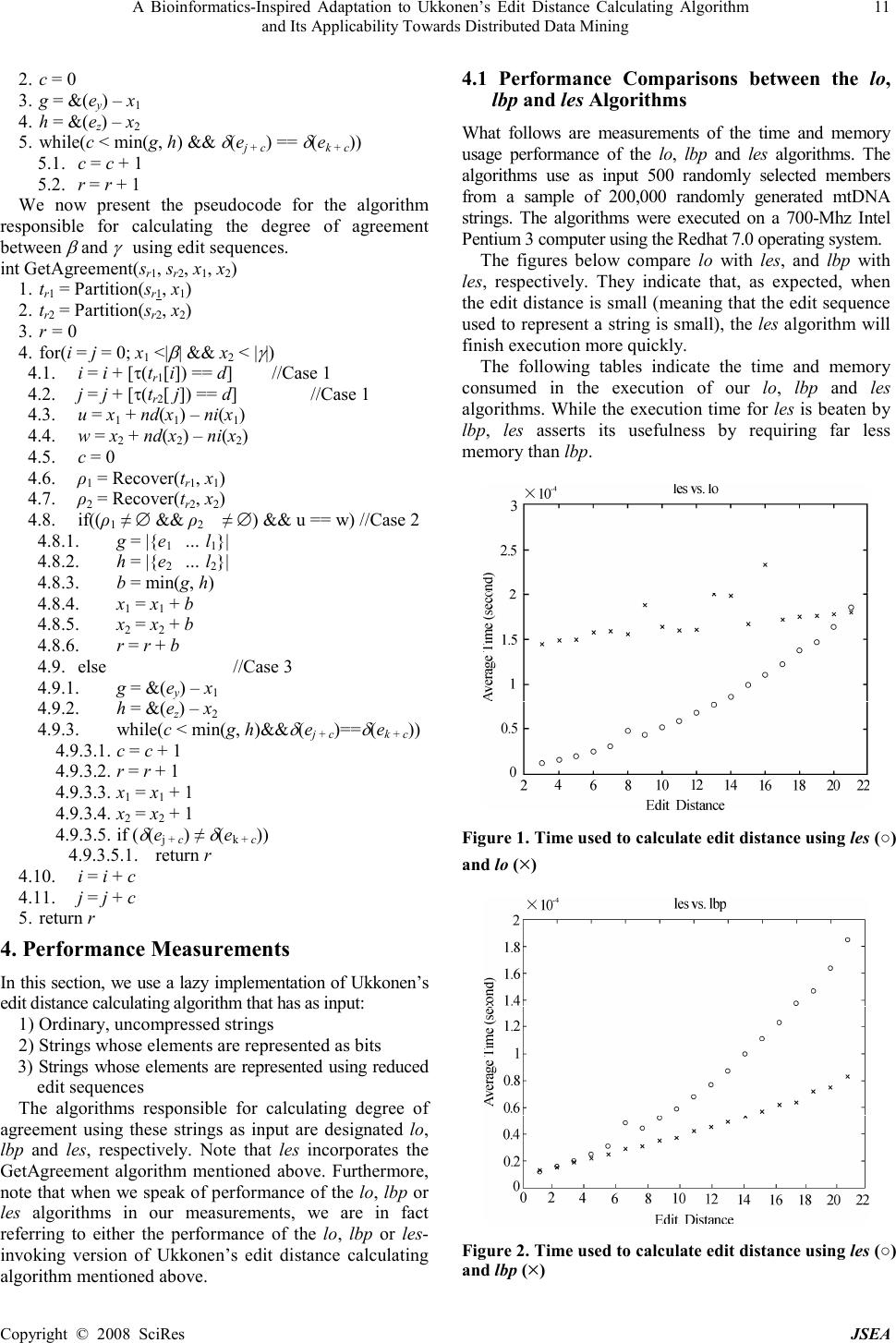

A Bioinformatics-Inspired Adaptation to Ukkonen’s Edit Distance Calculating Algorithm 11
and Its Applicability Towards Distributed Data Mining
2. c = 0
3. g = &(e
y
) – x
1
4. h = &(e
z
) – x
2
5. while(c < min(g, h) && δ (e
j + c
) == δ (e
k + c
))
5.1. c = c + 1
5.2. r = r + 1
We now present the pseudocode for the algorithm
responsible for calculating the degree of agreement
between β and γ using edit sequences.
int GetAgreement(s
r1
, s
r2
, x
1
, x
2
)
1. t
r1
= Partition(s
r1
, x
1
)
2. t
r2
= Partition(s
r2
, x
2
)
3. r = 0
4. for(i = j = 0; x
1
<| β | && x
2
< | γ |)
4.1. i = i + [τ(t
r1
[i]) == d] //Case 1
4.2. j = j + [τ(t
r2
[ j]) == d] //Case 1
4.3. u = x
1
+ nd(x
1
) – ni(x
1
)
4.4. w = x
2
+ nd(x
2
) – ni(x
2
)
4.5. c = 0
4.6. ρ
1
= Recover(t
r1
, x
1
)
4.7. ρ
2
= Recover(t
r2
, x
2
)
4.8. if((ρ
1
≠ ∅ && ρ
2
≠ ∅) && u == w) //Case 2
4.8.1. g = |{e
1
… l
1
}|
4.8.2. h = |{e
2
… l
2
}|
4.8.3. b = min(g, h)
4.8.4. x
1
= x
1
+ b
4.8.5. x
2
= x
2
+ b
4.8.6. r = r + b
4.9. else //Case 3
4.9.1. g = &(e
y
) – x
1
4.9.2. h = &(e
z
) – x
2
4.9.3. while(c < min(g, h)&& δ (e
j + c
)== δ (e
k + c
))
4.9.3.1. c = c + 1
4.9.3.2. r = r + 1
4.9.3.3. x
1
= x
1
+ 1
4.9.3.4. x
2
= x
2
+ 1
4.9.3.5. if ( δ (e
j + c
) ≠ δ (e
k + c
))
4.9.3.5.1. return r
4.10. i = i + c
4.11. j = j + c
5. return r
4. Performance Measurements
In this section, we use a lazy implementation of Ukkonen’s
edit distance calculating algorithm that has as input:
1) Ordinary, uncompressed strings
2) Strings whose elements are represented as bits
3) Strings whose elements are represented using reduced
edit sequences
The algorithms responsible for calculating degree of
agreement using these strings as input are designated lo,
lbp and les, respectively. Note that les incorporates the
GetAgreement algorithm mentioned above. Furthermore,
note that when we speak of performance of the lo, lbp or
les algorithms in our measurements, we are in fact
referring to either the performance of the lo, lbp or les-
invoking version of Ukkonen’s edit distance calculating
algorithm mentioned above.
4.1 Performance Comparisons between the lo,
lbp and les Algorithms
What follows are measurements of the time and memory
usage performance of the lo, lbp and les algorithms. The
algorithms use as input 500 randomly selected members
from a sample of 200,000 randomly generated mtDNA
strings. The algorithms were executed on a 700-Mhz Intel
Pentium 3 computer using the Redhat 7.0 operating system.
The figures below compare lo with les, and lbp with
les, respectively. They indicate that, as expected, when
the edit distance is small (meaning that the edit sequence
used to represent a string is small), the les algorithm will
finish execution more quickly.
The following tables indicate the time and memory
consumed in the execution of our lo, lbp and les
algorithms. While the execution time for les is beaten by
lbp, les asserts its usefulness by requiring far less
memory than lbp.
Figure 1. Time used to calculate edit distance using les (○)
and lo ( × )
Figure 2. Time used to calculate edit distance using les (○)
and lbp (
× )

12 A Bioinformatics-Inspired Adaptation to Ukkonen’s Edit Distance Calculating Algorithm
and Its Applicability Towards Distributed Data Mining
4.2 Query throughput Performance Comparisons
in a Distributed Computing Environment
Using the lo, lbp and les Algorithms
A query is defined as an mtDNA string submitted by a
client to a server. Query satisfaction is defined as the
determination of which mtDNA strings residing on a
server fall within an edit distance threshold of the query.
Query throughput is defined as the number of edit
distance calculations performed in a second while
satisfying a query. The following tables provide
performance measurements in terms of query strings
submitted per second and queries satisfied per second for
the lo, lbp and les algorithms in a LAN and WAN
distributed computing environment. The algorithms used
as input 200,000 randomly generated mtDNA strings.
The queries were transmitted on a 1GB LAN where each
network node was a 3.2-Ghz Intel Pentium 4 computer
using the Debian GNU/Linux 3.1 operating system. The
queries were also transmitted on a 54MB wireless WAN
where the client and server were 2.2-Ghz and 2.4-Ghz
Table 1. Time consumption (microseconds)
les lbp lo
Average 79 43 172
Minimum 12 13 145
Maximum 185 83 234
Table 2. Memory consumption (bytes)
les lbp lo
Average 337.6 8494 33777
Minimum 300 8494 33777
Maximum 372 8494 33777
Table 3. LAN throughput performance (strings
submitted/second)
les lbp lo
Average 3.3e4 1.2e3 310
Minimum 2.9e4 1.1e3 295
Maximum 3.5e4 1.3e3 326
Table 4. LAN query throughput performance
les lbp lo
Average 1.7e4 1.2e3 310
Minimum 5.8e3 1.1e3 295
Maximum 3.4e4 1.3e3 326
Table 5. WAN throughput performance (strings
submitted/second)
les lbp lo
Average 9.1e3 353 88
Minimum 7.8e3 340 84
Maximum 9.6e3 362 92
Table 6. WAN query throughput performance
les lbp lo
Average 9.1e3 353 88
Minimum 7.8e3 340 84
Maximum 9.6e3 362 92
Intel Pentium 4 computers, respectively, and were each
using the Windows XP operating system. Network
performance was measured using Jperf 2.0 [9].
We see that when queries are submitted in a distributed
computing environment, the les algorithm can accept
more query strings transmitted and therefore allows our
les algorithm to achieve greater query throughput than
either the lbp or les algorithms.
5. Conclusions
This decade has witnessed three major disasters-the 9/11
attacks, the Indian Tsunami and hurricane Katrina. In the
wake of such disasters, identifying people who have
perished is of paramount importance.
The usefulness of the les algorithm is asserted by the
fact that it consumes far less memory than competing
algorithms lo and lbp. This means that greater information
throughput may be achieved on a network and thus
greater use of distributed computational resources is
facilitated.
Moreover, this means that forensic experts can store
far more mtDNA sequences using the les algorithm than
they could if they were using the mtDNA strings required
by lo or lbp algorithms. Having the ability to store a huge
number of mtDNA sequences by forensic experts could
prove to be a boon by those forensic experts charged with
the duty of identifying the remains of people after a
major disaster. Having the ability to draw from a vast
database of mtDNA strings increases the likelihood that a
match can be made between the mtDNA collected and
the mtDNA stored in a database.
6. Acknowledgements
We would like to thank Dr. Michael Vose for his kind
mentorship and guidance.
REFERENCES
[1] M. D. Vose, “A formal analysis of edit distance,” UT CS
Technical Report ut-cs-04-517, February 2004.
[2] R. O. Duda and P. E. Hart, Pattern Classification (2nd ed.).
Wiley Interscience, 2000.
[3] A. Wagner and M. I. Fischer, “The string-to-string
correction problem,” Journal of the ACM, 21(1) (Jan.
1974), pp. 168-173, 1974.
[4] E. Ukkonen, “Algorithms for approximate string matching,”
International Control 64, pp. 100-118, 1985.
[5] E. Ukkonen, “On approximate string matching,” International
Conference Fundamentals of Computation Theory, Lecture
Notes in Computer Science, pp. 158:487-495, 1983.
[6] N. Campbell and J. Reese, Biology (6th ed.), Addison
Wesley, 1997.
[7] S. Anderson, et al., “Sequence and organization of the
human mitochondrial genome,” Nature, 290(5806) (April
9, 1981), pp. 457-265, 1981.
[8] K. L. Monson, et al., “The mtDNA population database:
An integrated software and database resource for forensic
comparison,” Forensic Science Communications, 4(2),
April 2002. DOI=http://www.fbi.gov/hq/lab/fsc/
backissu/april2002/miller1.htm.
[9] http://iperf.sourceforge.net.