Journal of Biomedical Science and Engineering
Vol.7 No.8(2014), Article
ID:47356,9
pages
DOI:10.4236/jbise.2014.78059
A Sleep Scoring System Using EEG Combined Spectral and Detrended Fluctuation Analysis Features
Amr F. Farag1,2*, Shereen M. El-Metwally1, Ahmed A. Morsy1
1Department of Biomedical Engineering, Cairo University, Cairo, Egypt
2Department of Biomedical Engineering, Shorouk Higher Institute of Engineering, El-Shorouk, Egypt
Email: *msc.afawzy@gmail.com, shereen.elmetwally@yahoo.com, amorsy@ieee.co
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 28 May 2014; accepted 15 June 2014
ABSTRACT
Most of sleep disorders are diagnosed based on the sleep scoring and assessments. The purpose of this study is to combine detrended fluctuation analysis features and spectral features of single electroencephalograph (EEG) channel for the purpose of building an automated sleep staging system based on the hybrid prediction engine model. The testing results of the model were promising as the classification accuracies were 98.85%, 92.26%, 94.4%, 95.16% and 93.68% for the wake, non-rapid eye movement S1, non-rapid eye movement S2, non-rapid eye movement S3 and rapid eye movement sleep stages, respectively. The overall classification accuracy was 85.18%. We concluded that it might be possible to employ this approach to build an industrial sleep assessment system that reduced the number of channels that affected the sleep quality and the effort excreted by sleep specialists through the process of the sleep scoring.
Keywords:Automated Sleep Staging, Detrended Fluctuation Analysis (DFA), Decision Tree, Multi-Layer Perceptron (MLP)

1. Introduction
Sleep is defined as a desired state of unconsciousness. The science of sleep investigation began to catalog the unique and varying texture of this state over the past 75 years. Standard metrics were needed to characterize what could be observed. After many germinal studies, a consensus for manual sleep assessment has evolved. A standardized method for characterizing normal sleep was published in 1968 by Allan Rechtschaffen and Anthony Kales [1] . Since then, this method has been considered the golden standard for sleep assessment.
In 2009, the American Academy of Sleep Medicine (AASM) set the AASM manual for the scoring of sleep and associated events [2] . Sleep scoring classifies sleep into stages that correspond to certain brain activities. According to the AASM standard, sleep is divided into 5 stages, the awake stage (WK), the rapid eye movement (REM), and three non-rapid eye movements (NREM) sleep sub-stages (NREMS1, NREMS2, and NREMS3) that describe the depth of sleep.
Both R&K and AASM manuals were originally developed to facilitate manual sleep scoring, not to be used in automated sleep scoring systems. Sleep assessment specialists exert considerable effort and time in the scoring of a single subject record. These manuals provide a subjective method for sleep scoring which may lead to inconsistent results. In a study that involved eight European sleep laboratories, the overall level of agreement in the scoring of the five sleep stages was only 76.8% [3] .
In the past few decades, many studies aimed to develop automated sleep scoring systems. Various automated systems differ in the extracted features, classification engines, or the bio-signals that these systems are based on. Spectral analysis features have the longest tradition in the analysis of sleep bio-signal due to the capability to quantify the different frequency contents of the signal similar to visual analysis [4] . The spectral features of sleep bio-signals could be calculated using FFT [5] -[7] and autoregressive models [8] [9] .
Many studies in the last decade switched from the conventional methods of spectral analysis to time-frequency analysis, and particularly using the Wavelets Transform [10] -[12] . Other feature extraction techniques include relative power band [8] , Harmonic parameter (Hjorth parameter) [8] [13] , K-means clustering based features [14] and detrended fluctuation analysis (DFA) of the raw EEG signals [15] [16] .
Detrended fluctuation analysis (DFA) is a widely used technique for the detection of long-range autocorrelation in non-stationary and noisy time series [15] . The advantage of DFA over conventional methods is that it avoids the spurious detection of apparent long-range correlations that are artifacts of non-stationarity [17] . Previous studies indicate that DFA power law exponents of EEG signals changes significantly with various sleep stages [18] . In our previous study, we concluded that the DFA of the extracted brain waves changes significantly with various sleep stage [19] .
The field of machine intelligence provides a broad range of classification engines that were recently employed in designing reliable automatic sleep staging algorithms. The Multi-layer perceptron (MLP) classification engine with back propagation training was used in [7] [9] [20] . Rule-based, decision trees, random forests, and fuzzy classifiers were also applied and showed to be reliable techniques for automated sleep assessment [5] [21] -[23] .
Decision trees are one of the most successful and popular classification engines in automated sleep assessment [22] . A classification decision tree is a hierarchical non-parametric model for supervised learning. One of the advantages of decision trees over other classification engines is its superior interpretability [24] .
The main goal of this study is to develop an accurate automated sleep scoring engine with clinically acceptable performance using only a single EEG channel. The motivation of the work is to facilitate the use of such engine in home-based devices requiring minimal complexity and maximal convenience and ease of use. Even at the clinic-based setting, a single channel engine can improve the polysomnography experience of the patient, which helpsto obtain better clinical diagnosis. In this study, we employed a hybrid classification engine used over a combination of DFA features of filtered EEG brain waves components and a number of derived spectral features.
2. Material and Methods
2.1. Data Set Description and Acquisition
22 healthy subjects aged 20 - 32 underwent one overnight polysomnographic recording which comprised EEG signal acquisition (4 channels, Ag/AgCl electrodes placed according to the 10 - 20 International System referred to linked earlobes: C3, C4, F3, F4). Recordings were carried out using Alice Polysomnographic System (Respironics, Inc.) The records were initially scored by a sleep specialist according to AASM rules. The data was divided into two groups for training and validation of the algorithm. The first group consisted of 12 subjects and the second group consisted of 10 subjects.
In this study, the sleep EEG (C3A2 Lead) was selected for classification. 10 minutes for each sleep stage were extracted from the records of the first group. Each 10 minute EEG record was labeled by its sleep stage; WK, REM, NREMS1, NREMS2, and NREMS3. The total length of isolated data set is 600 minutes composed of 120 min for each sleep stage. These data records were used in the training of the classifier model.
2.2. Algorithm
The block diagram for the proposed algorithm is shown in Figure 1. The proposed algorithm was tested using Matlab (MathWorks, Inc., Natick, Massachusetts, United States) Signal Processing toolbox and Weka (Waikato Environment for knowledge analysis, University of Waikato, Hamilton, New Zealand). In the following, a detailed description of the system block diagram is given.
2.3. DFA Features Extraction
2.3.1. Signal Processing
The EEG isolated data were introduced to the filter bank shown in Figure 2 to extract the known brain waves: Delta, Theta, Alpha and Beta waves. The EEG signals training set was segmented to 30 sec segments using a Hamming window of 3000 samples length applied to each segment to compensate for truncation errors and edge mismatches.
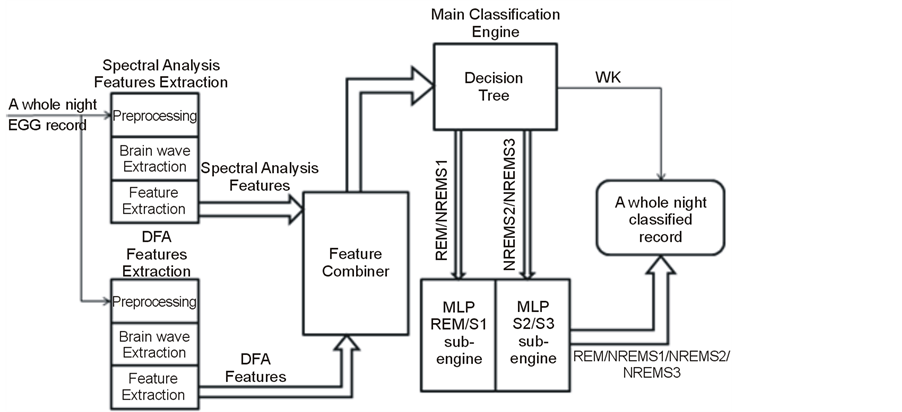
Figure 1. The block diagram of the system algorithm.
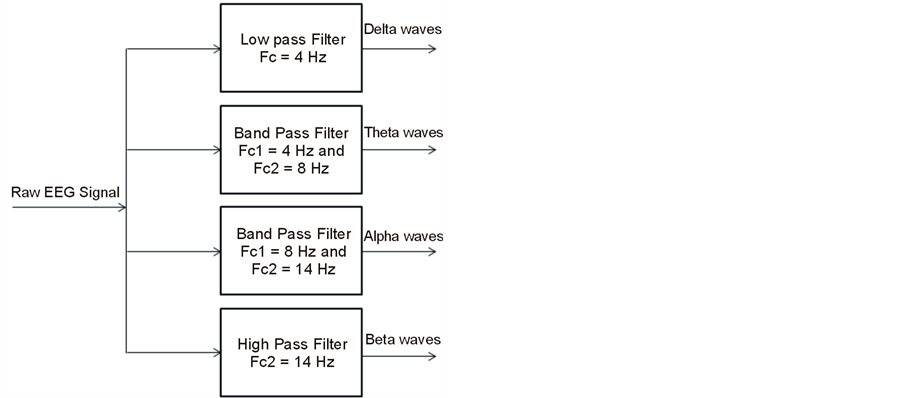
Figure 2. Brain waves filter bank.
2.3.2. Detrended Fluctuation Analysis
DFA reveals the properties of non-stationary time series by calculating the scaling exponents which index the long-range power-law correlations. The DFA scaling exponent was computed for the segmented raw EEG signal and its filtered brain waves of length 30 seconds. The DFA procedure [17] [25] consists of 4 steps:
Step 1: Determine the “profile” of the data series of length N and a mean τ.
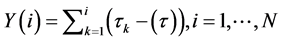 (1)
(1)
where  represents the integration of the EEG time series τk.
represents the integration of the EEG time series τk.
Step 2: we divide 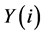 into Nt = int(N/t) non-overlapping segments of equal length t. Since the length N of the series is often not a multiple of the considered time scale t, a short part at the end of the profile may remain. In order not to disregard this part of the series, the same procedure is repeated starting from the opposite end. Thereby, 2Nt segments are obtained altogether.
into Nt = int(N/t) non-overlapping segments of equal length t. Since the length N of the series is often not a multiple of the considered time scale t, a short part at the end of the profile may remain. In order not to disregard this part of the series, the same procedure is repeated starting from the opposite end. Thereby, 2Nt segments are obtained altogether.
Step 3: Calculate the local trend for each of the segments by a least-square fit of the data. Then determine the variance
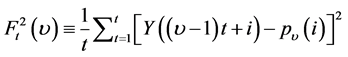 (2)
(2)
for each segment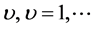 , Nt. Here,
, Nt. Here, 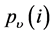 is the fitting polynomial in segment υ. Linear, quadratic, cubic, or higher order polynomials can be used in the fitting procedure (conventionally called DFA1, DFA2, DFA3,…..).
is the fitting polynomial in segment υ. Linear, quadratic, cubic, or higher order polynomials can be used in the fitting procedure (conventionally called DFA1, DFA2, DFA3,…..).
Step 4: Average over all segments and take the square root to obtain the fluctuation function.
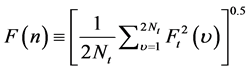 (3)
(3)
The logarithm of 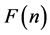 is then plotted as a function of the logarithm of the time scale n. The slope, α, of the plot of Log2(F(n)) versus Log2(n) is called the scaling or self-similarity exponent. A time series shows self-similarity when this plot will display a linear scaling region and slope α > 0.5. This exponent is 0.5 for white noise, where the values of the time series are completely uncorrelated, when the exponent is α < 0.5, power-law anti-correlation is present.
is then plotted as a function of the logarithm of the time scale n. The slope, α, of the plot of Log2(F(n)) versus Log2(n) is called the scaling or self-similarity exponent. A time series shows self-similarity when this plot will display a linear scaling region and slope α > 0.5. This exponent is 0.5 for white noise, where the values of the time series are completely uncorrelated, when the exponent is α < 0.5, power-law anti-correlation is present.
In order to determine how 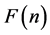 depends on the time scale n, steps 2 to 4 were repeated 30 times with different time scales between n = 4 and 3000. The long range auto-correlation properties of the raw sleep EEG signal and the filtered brain waves for each sleep stage were investigated separately using DFA.
depends on the time scale n, steps 2 to 4 were repeated 30 times with different time scales between n = 4 and 3000. The long range auto-correlation properties of the raw sleep EEG signal and the filtered brain waves for each sleep stage were investigated separately using DFA.
2.4. Spectral Features Extraction
2.4.1. Signal Processing
The isolated EEG data was introduced to a filter bank as the one shown in Figure 2 to extract the brain waves. The brain waves were segmented using a one second hamming window (100 samples length) to compensate for truncation errors and edge mismatches. The one-second window is selected in order to assume that the signal is stationary within the window length for accurate spectrum estimation. Zero padding was then used to enhance the frequency resolution.
2.4.2. Spectral Analysis
Using Matlab, Welch’s power spectrum density was calculated for each segmented sleep brain wave. The sum of the power spectrum values (e.g. sum(Delta)) was calculated for Delta, Theta, Alpha and Beta brain waves and the sum of the 4 sums (sum(Delta, Theta, Alpha, Beta)) was also calculated. Then, the relative power for each of these brain waves was calculated as follows:
P-delta = sum(Delta)/sum(Delta, Theta, Alpha, Beta) (4)
P-theta = sum(Theta)/sum(Delta, Theta, Alpha, Beta) (5)
P-alpha = sum(Alpha)/sum(Delta, Theta, Alpha, Beta) (6)
P-beta = sum(Beta)/sum(Delta, Theta, Alpha, Beta) (7)
Using the power spectrum sum of each frequency range, the following features and ratios were extracted: Alpha wave index (AWI), Theta wave index (TWI), and Slow wave index (SWI):
AWI = P-alpha/(P-delta + P-theta) (8)
TWI = P-theta/(P-alpha + P-delta) (9)
SWI = P-delta/(P-theta + P-alpha) (10)
This yields a 7-elements feature vector for a 1-second segment and 30 × 7 features matrix for each 30-seconds brain wave epoch.
2.5. Features Combination
The main challenge in combining spectral and detrended fluctuation analysis features was that the spectral features were computed for 1 second segments while the DFA features were computed for the whole 30 second epoch. This yields 30 spectral features set and single DFA features set per sleep epoch. Therefore, each DFA feature was replicated 29 times for each epoch. This resulted in a features matrix of dimensions 36,000 × 11.
Each raw represents 11 features computed for a 1-second EEG epoch. These 11 features include: DFA-Alpha, DFA-Beta, DFA-Delta, DFA-Theta, P-Alpha, P-Beta, P-Delta, P-Theta, AWI, TWI and SWI. The total number of epochs that the combined feature matrix represents is 1200 epochs divided into 240 epochs for each sleep stage.
2.6. Decision Tree Classifier
In this study, we employed a Decision Tree Classifier. A classification tree is a hierarchal data structure implementing divide and conquer strategy. It is composed of internal decision nodes and terminal leaves. The construction of a tree given a training data is called tree induction.
Recently many methods were developed for tree induction. C4.5 algorithm is one of the most popular algorithms of tree induction. It employs the following steps [26] [27] :
• Discretization of continuous attributes: for effective classification, some continuous valued attributes must be discretized.
• Attribute selection: information gain of each attribute is calculated, the attribute with the highest information gain is selected for the instant node split.
• Pruning: to prevent the over fitting for the training data, the decision tree must be pruned.
In this work, each input instance represents a 1 second sleep EEG record. The C4.5 algorithm is employed for tree induction using Weka classification software package. The resulting tree consisted of 63 leaves with a maximum depth of 17 levels. The decision tree classifier accuracy was improved using Multi-layer perceptron (MLP) sub-classifier as will be discussed in next section.
2.7. MLP Sub-Engines
MLP classifiers are special types of artificial neural networks (ANN) where the nodes are set in successive layers; input layer, hidden layer and output layer. Two MLP sub-classifiers were employed in this work to reduce the main classifier (decision tree) confusion error. One MLP classifier was dedicated to reduce the confusion between REM and NREMS1 sleep stages, while the other one was dedicated for confusion between NREMS2 and NREMS3 sleep stages.
The MLP sub-classifiers were modeled using Weka classification software package with sigmoid and pureline functions for model nodes. The classifiers were trained using the training data that the main classifier has been able to classify correctly in an adaptive pattern. The classifiers were trained using the back propagation algorithm [28] .
3. Results and Discussion
The isolated EEG records were used to build and train a decision tree classifier model that distinguish between WK, REM, NREMS1, NREMS2 and NREMS3 sleep stages. Hence, the model was tested using the total data of the testing group combined with the data of the validation group (22 subjects EEG sleep records). Table 1 illustrates the confusion matrix for the decision tree classifier; representing the prediction capability of the algorithm for each class. The diagonal elements represent the sensitivity of the algorithm to each sleep stage.
The system performance measures including the accuracy and specificity for each sleep stage are listed in Table2 Table 3 shows the system confusion vectors computed by adding the off-diagonal confusion values in Table 1 for all sleep stages pairs. Based on the results shown in Table 3, two sub-engines were employed to reduce or eliminate the top two confusion vector elements after the main decision tree classifier application. The complete elimination of the top two confusions could improve the overall accuracy dramatically.
The systems overall accuracy was improved to be 87.62%. The improved confusion matrix is shown in Table4 The effect of the sub-engines is shown by the confusions in bold font. The REM/NREMS1 confusion was reduced to 27% while the NREMS2/NREMS3 was reduced to 16%.
Other feature combination methods were tested in order to compare to the DFA features of the EEG spectral components combination with the spectral analysis features. The other features tested include: DFA computed for the raw EEG signal, DFA computed for the filtered EEG waves, and combined spectral features with DFA features of raw EEG. Table 5 illustrates the resulting accuracies for the sleep EEG classification based on the various features combination. It can be seen that the combined spectral and DFA features of the EEG filtered waves resulted in the highest accuracy compared to the other feature sets.
Table 1. The confusion matrix of the decision tree validation.
Table 3. Confusion vectors arranged descendingly.
Table 5. Classification accuracies for various features combination.
The system was tested in two steps. The first step incorporated using selected records from the training group (12 subject’s data) for the tuning of the classification engine. The second step incorporated testing the system using the complete records of 22 subjects (including the previous 12 records). Testing the algorithm with complete records considered to be more difficult than testing with the selected epochs as the number of complete records exceeds the number of selected epoch (including epochs that were not used in the training of the algorithm) which would reveal how the algorithm will perform in reality practice.
The high confusion between S1 and WK sleep stages could be justified due to the well-known sleep onset problem that appears in the transition from WK to S1 sleep in the early night. NREMS1 close to sleep onset shows significant alpha rhythm which is characteristic for wake epochs. To overcome this problem, sleep scorers often use EOG and EMG in conjunction with EEG to aid in specifying the exact sleep onset, which is relatively difficult to be specified accurately using EEG alone as done in this approach.
The highest confusion vector element of the system was computed for REM/NREM-S1 as shown in Table 3, emphasized in bold font. Also, the lowest sensitivities of the system were found to be for REM and NREMS1 as illustrated in Table 1 in bold font. This confusion makes a lot of sense because of the dominant theta rhythms inherent in NREMS1 and REM sleep stages. For this reason, the EOG signal could be essential for the separation between NREMS1 and REM sleep stages [2] .
The sensitivity of the proposed system for NREMS3 is 70.7% which is considered relatively-low as compared to the other sleep stages. NREMS2/NREMS3 confusion vector element is the second after the highest as illustrated in Table 3 in bold font. This confusion can be justified due to the similar frequency content (Delta waves) of the EEG signal in these two sleep stages. In addition, the EEG signal loses the long range autocorrelation similarly in these two stages.
4. Conclusions
This study presented a novel algorithm for automated sleep scoring using a single EEG channel. The proposed system implemented sleep scoring by combining spectral and DFA features on a decision tree classifier engine. A clinical dataset was used for initial evaluation of the system. Two MLP sub-classifiers were included in system aiming to reduce the main confusion error of the decision tree classifier. The testing results of the proposed system revealed an overall sleep stages classification accuracy of 87.62%. A good performance was also shown in terms of both sensitivity and specificity.
The proposed system validation results indicate that it is a reliable single EEG lead automated sleep scoring system that could be employed in practical settings to reduce the number of electrodes mounted on patients and consequently the cost of such system. It also makes it more suitable for home use and ambulatory settings. It can also be used as an initial screening tool for sleep specialists to avoid long waiting lists in sleep labs, and unnecessary full polysomnography nights for subjects who may suffer from simple sleep hygiene problems.
The limited number of subjects is considered a limitation of our study. Evaluation using a larger clinical data set is recommended for a more thorough evaluation for the proposed system. Other potential uses of the proposed system could include monitoring the depth of anesthesia in operating rooms.
References
- Rechtschaffen, A. and Kales, A. (1968) A Manual of Standardized Terminology, Techniques and Scoring System for Sleep Stages of Human Subjects. Public Health Service, US Government Printing Office, Washington DC.
- Hopfe, H., Anderer, P., Zeitlohfer, J., Boeck, M., Dorn, H., Gruber, G., Heller, E., Loretz, E., Moser, D., Paraptics, S., Saletu, B., Schmidt, A. and Dorffner, G. (2009) Interraterreliablity for Sleep Scoring According to the Rechtschaffen & Kales and the New AASM Standard. Journal of Sleep Research, 18, 74-84. http://dx.doi.org/10.1111/j.1365-2869.2008.00700.x
- Danker-Hopfe, H., Kunz, D., Gruber, G., Klösch, G., Lorenzo, J.L. and Himanen, S.L. (2004) Interrater Reliability between Scorers from Eight European Sleep Laboratories in Subjects with Different Sleep Disorders. Journal of Sleep Research, 13, 63-69. http://dx.doi.org/10.1046/j.1365-2869.2003.00375.x
- Penzel, T. (2003) Problems in Automatic Sleep Scoring Applied to Sleep Apnea. Engineering in Medicine and Biology Society, Proceedings of the 25th Annual International Conference of the IEEE, Cancun, 17-21 September 2003, 358-361.
- Liang, S.F., Kuo, C.E., Huo, Y.H. and Cheng, Y.C. (2012) A Rule-Based Automatic Sleep Staging Method. Journal of Neuroscience Methods, 205, 169-176.
- Vivaldi, E.A. and Bassi, A. (2006) Frequency Domain Analysis of Sleep EEG for Visualization and Automated State Detection. Proceedings of the 28th IEEE EMBS Annual International Conference, 1, 3740-3743.
- Charbonnier, S., Zoubek, L., Lesecq, S. and Chapotot, F. (2011) Self-Evaluating Automatic Classifier as a Decision. Computers and Biology in Medicine, 41, 380-389. http://dx.doi.org/10.1016/j.compbiomed.2011.04.001
- Estrada, E., Nazeran, H., Nava, P., Behbehani, K., Burk, J. and Lucas, E. (2004) EEG Feature Extraction for Classification of Sleep Stages. Proceedings of the 26th Annual International Conference of the IEEE EMBS, 1, 196-199.
- Pardey, J., Roberts, S. and Tarassenko, L. (1994) Application of Artificial Neural Networks to Medical Signal Processing. IEEE Savoy Place, London.
- Takajyol, A., Katayama, M., Inoue, K., Kumamaru, K. and Matsuoka, S. (2006) Time-Frequency Analysis of Human Sleep EEG. SICEICASE International Joint Conference, Busan, 18-21 October 2006, 3303-3307.
- Li, J., Du, Y. and Zhao, L. (2005) Sleep Stage Study with Wavelet Time-Frequency Analysis. International Conference Neural Networks and Brain, Beijing, 13-15 October 2005, 872-875.
- Glavinovitch, A., Swamy, M.N.S. and Plotkin, E.I. (2007) Wavelet-Based Segmentation Techniques in the Detection of Microarousals in the Sleep EEG. 50th Midwest Symposium on Circuits and Systems, 2, 1302-1305.
- Hjorth, B (1970) EEG Analysis Based on Time Domain Properties. Electroencephalogr. Clinical Neurophysiology, 29, 306-310. http://dx.doi.org/10.1016/0013-4694(70)90143-4
- Gunes, S., Polat, K. and Yosunkaya, S. (2010) Efficient Sleep Stage Recognition System Based on EEG Signal Using k-Means Clustering Based Feature Weighting. Expert Systems with Applications, 37, 7922-7928. http://dx.doi.org/10.1016/j.eswa.2010.04.043
- Koley, B. and Dey, D. (2012) An Ensemble System for Automatic Sleep Stage Classification Using Single Channel EEG Signal. Computers in Biology and Medicine, 42, 1186-1195. http://dx.doi.org/10.1016/j.eswa.2010.04.043
- Adanen, M., Jiang, Z. and Yan, Z. (2012) Sleep-Wake Stages Classification and Sleep Efficiency Estimation Using Single-Lead Electrocardiogram. Expert Systems with Applications, 39, 1401-1413. http://dx.doi.org/10.1016/j.eswa.2011.08.022
- Ping, C.K., Havlin, S., Stanley, H.E. and Goldberger, A.L. (1995) Quantification of Scaling Exponents and Cross over Phenomena in Non-Stationary Heartbeat Time Series. Chaos, 5, 82-87.
- Lee, J.M., Kim, D.J., Kim, I.Y., Park, K.S. and Kim, S.I. (2002) Detrended Fluctuation Analysis of EEG in Sleep Apnea Using MIT/BIH Polysomnography Data. Computers in Biology and Medicine, 32, 37-47. http://dx.doi.org/10.1016/S0010-4825(01)00031-2
- Farag, A.F. and EL-Metwally, S.M. (2012) Detreneded Fluctuation Analysis Features for Automated Sleep Staging of Sleep EEG. International Journal of Biology and Biomedical Technology, 4, 48-60.
- Sun, M., Ryan, N.D., Dahl, R.E., Hsin, H.C., lyengar, S. and Sclabassi, R.J. (1993) A Neural Network System for Automatic Classification of Sleep Stages. Proceedings of the 12th Southern Biomedical Engineering Conference, 137-139.
- Jo, H.G., Park, J.Y., Lee, C.K., An, S.K. and Yoo, S.K. (2010) Genetic Fuzzy Classifier for Sleep Stage Identification. Computers in Biology and Medicine, 40, 629-634. http://dx.doi.org/10.1016/j.compbiomed.2010.04.007
- Hanaoka, M., Ashi, M.K. and Yamazaki, Y. (2001) Automated Sleep Scoring by Decision Tree Learning. Proceedings of the 23rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2, 1751-1754.
- Fraiwan, L., Lweesy, K., Khasawneh, N., Wenz, H. and Dickhaus, H. (2012) Automated Sleep Stage Identification System Based on Time-Frequency Analysis of a Single EEG Channel and Random Forest Classifier. Computer Methods and Programs in Biomedicine, 108, 10-19. http://dx.doi.org/10.1016/j.cmpb.2011.11.005
- Alpaydin, E. (2010) Introduction to Machine Learning. 2nd Edition, The MIT Press, Cambridge, 187-200.
- Kantelhardt, J.W., Bunde, E.K., Rego, H.H.A., Havlin, S. and Bunde, A. (2001) Detecting Long-Range Correlations with Detrended Fluctuation Analysis. Physica A, 295, 441-454. http://dx.doi.org/10.1016/S0378-4371(01)00144-3
- Quinlan, J.R. (1992) C4.5 Programs for Machine Learning. Morgan Koufmann, San Mateo.
- Quinlan, J.R. (1986) Induction of Decision Trees. Machine Learning, 1, 81-106. http://dx.doi.org/10.1007/BF00116251
- Rumelhart, D.E., Hinton, G.E. and Williams, R.J. (1986) Learning Representations by Back-Propagating Errors. Nature, 323, 533-536. http://dx.doi.org/10.1038/323533a0
NOTES

*Corresponding author.


