Engineering
Vol.4 No.11(2012), Article ID:24705,4 pages DOI:10.4236/eng.2012.411104
Experimental Design in Solvent Extraction: A Study for Divalent Metals Separation in D2EHPA/Isoparaffin System
1IFRJ—Federal Institute of Educacion, Science and Technology of Rio de Janeiro, Rio de Janeiro, Brazil
3UFRJ—Chemistry College, Federal University of Rio de Janeiro, Rio de Janeiro, Brazil
2Coordination of Metallurgical and Environmental Processes, Centre for Mineral Technology, Rio de Janeiro, Brazil
Email: *clenilsonjunior@gmail.com
Received August 1, 2011; revised September 22, 2011; accepted October 12, 2011
Keywords: Experimental Design; D2EHPA; Solvent Extraction; Divalent Metals
ABSTRACT
The solvent extraction process combined with tools of experimental design assists in developing procedures for separation and purification of elements or mineral compounds with high purity. In this work the technique was used to replace the traditional methods for the collection of basic information required for the development of a circuit of solvent extraction. According to the literature, several factors may influence the extraction of divalent metals by D2EHPA in sulfate media, among which the concentration of metals in solution. The objective was to study the variables affecting the separation process Mn/Ni/Co/Cu, such as the aqueous/organic (A/O), contact time, concentrations of the divalent metals in sulfuric medium, pH and solvent concentration. An investigation into the variables that control the process was done using a “cube + star” experimental design, with central point. The results demonstrate it is possible to obtain of a satisfactory mathematical model that describes the process.
1. Introduction
Since the 1950s, the solvent extraction (SX) has been increasingly used in the minerals processing industry. Today, solvent extraction has become an important economical, practical and clean hydrometallurgical process and the technique is one of the most versatile methods used for the extraction, separation and recovery of metallic species from aqueous media [1,2].
Various solvent extraction reagents and processes have been proposed for the recovery and separation of metal ions in aqueous solution. Di-(2-ethylhexyl) phosphoric acid (abbreviated as D2EHPA or simply HA) has been used successfully to extract many divalent metal ions from sulphate media as has been reported elsewhere, with varying studies focused, determination of parameters such as rate constant, pH, distribution coefficients, equilibrium constant and composition of extracted species in different conditions. These parameters can be determined via graphical or numerical analysis of experimental data. Nathasarma and Devi (2006) reported the order of extraction of eight metal ions from a sulphate solution using D2EHPA, which is reported as Fe3+ > Zn2+ > Cu2+ > Co2+ > Ni2+ > Mn2+ > Mg2+ > Ca2+ [3-7].
On account of the dimerization of acid phosphoorganic extractants, it is reported that in the formation of complexes with divalent metals ions, these extractants take part as a monomer rather than dimmer, in isoparaffin [8,9]. The reaction of a divalent metal extraction with D2EHPA can be written as Equation (1), when M to be the divalent metal [5]:
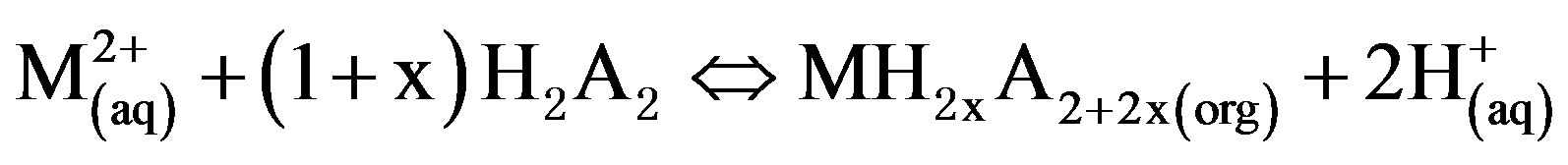 (1)
(1)
Solutions of sulfuric acid have been frequently used as a leaching agent for manganese, cobalt, nickel and copper ore. However, the dissociation of bisulfate ion into hydrogen and sulfate ion is incomplete and a thermodynamic analysis of the acid solution is not trivial [10-20]. Thus, within the process of divalent metals extraction by D2EHPA the aim was to evaluate the influence of four variables as: concentrations of metals (Mn, Co, Ni, and Cu) in the synthetic leach liquor, concentration of extractant D2EHPA, the A/O ratio and the final equilibrium pH upon the percentage of extraction of the metals studied, leading to defining the optimum ranges for operation of the process of solvent extraction systems as studied. The metal concentrations in the synthetic leach liquor were based on the composition of a liquor generated from the leaching of the manganese ore from Mina AzulPará state, Brazil [20].
2. Theoretical
The class of experimental design most often used to adjust models to investigate interaction effects of first order (linear) and second order (quadratic) is the central composite design. This experimental design has a configuration “star + cube”, which consists of a factorial classic experiment of three levels (–1, 0 and +1) a distance of ±1 of the central point, plus 2k axial points (star) at a distance ±1 α of the center point and nc point central [21].
To assess the influence of independent variables on the dependent variable, we conducted a factorial design experimental plan with three levels (–1, 0 and +1) plus a star configuration, third order model, in a total of 40 laboratory experiments, using a factorial design matrix shown in Table 1 [22].

Table 1. Experimental design, ratio A/O and pH equilibrium.
The proposed model for the nonlinear regression is that of Equation (2) where βi’s are the estimated parameters obtained in this model with the second order with central point. It is typically used when one is interested in detecting curvature in a response function, since the regression model is given by:
 (2)
(2)
According to the F test and their calculated probabilities, if p calculated is less than 0.05 (95% confidence) the effect of that variable or interaction is considered significant. Then, parameters can be ruled out where p values were larger than 0.05 (see Table 2). Statistical analysis will be performed later using the software STATISTICA® for comparison also for the developed model.
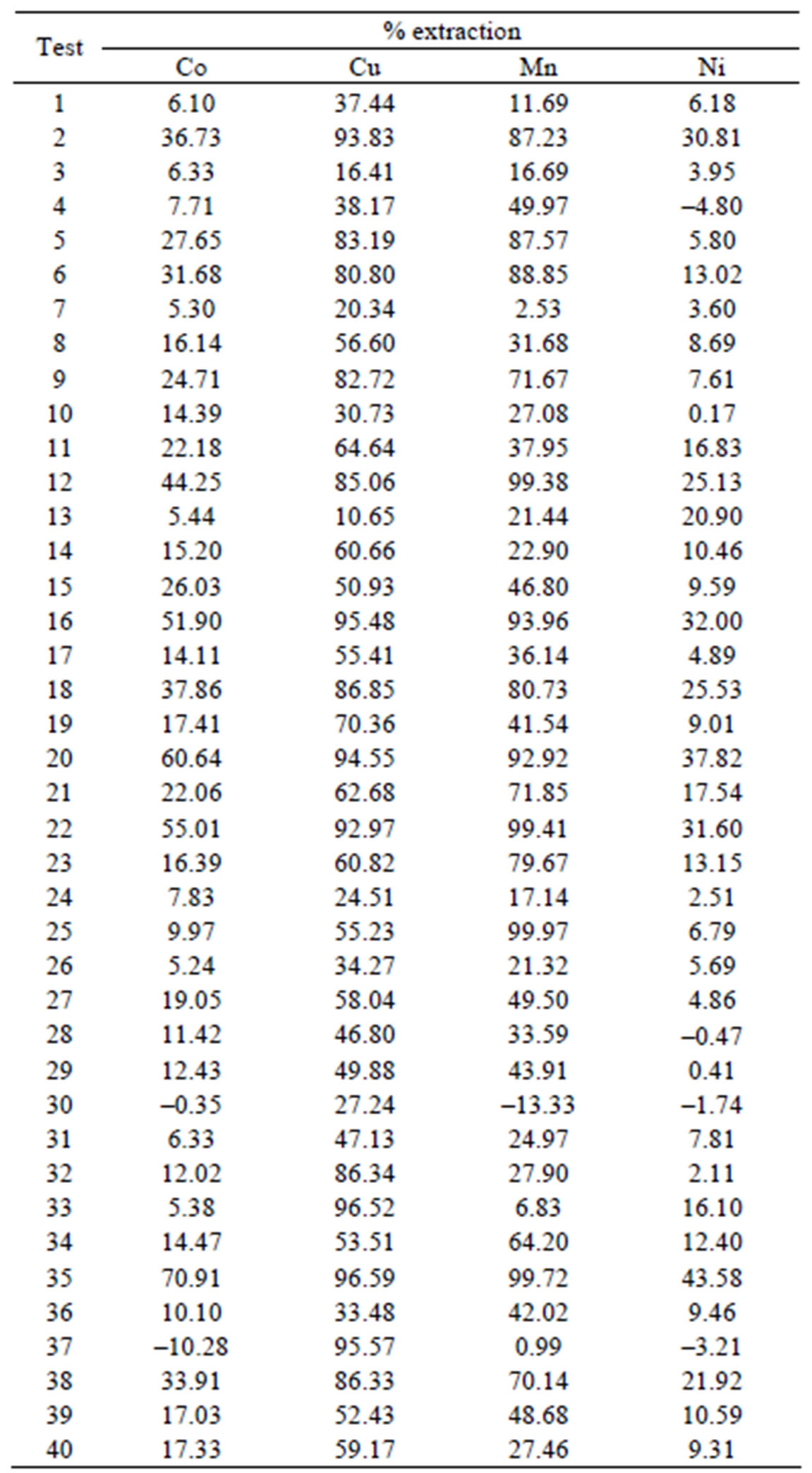
Table 2. Percentage of extraction in the design experimental.
3. Experimental
The similar solutions of synthetic leach liquor were prepared by dissolution of MnSO4 CoSO4·7H2O, NiSO4·6H2O and CuSO4·5H2O (VETEC) in deionised water. The initial pH of the aqueous solutions was controlled by the addition of diluted H2SO4. The solution of Di-(2-ethylhexyl) phosphoric acid (Sigma Aldrich) was prepared by dissolution in Isoparaffin 17/21 (UNIPAR) without any prior purification.
Equal aliquots (25 mL) of aqueous (Vaq) and organic (Vorg) solutions were contacted in a 100 mL glass reactor by a magnetic stirrer (IKA) for 10 min at 298.15 K. After assessment of the balance of the solution was added with the aid of a burette, a solution NaOH 0.5 M, with constant stirring, until reaching the pH determined by experimental design.
Upon reaching a steady pH (unchanging for a period of 5 minutes) the aqueous and organic solutions were decanted into a separating funnel, and the aqueous phase taken for analysis, after the set time of contact, the aqueous and organic phases (Sousa Junior et al., 2010).
The variables considered with the potential to influence the divalent metal extraction (dependent variable) was the concentration of the metals themselves, the volume ratio A/O, the concentration of organic extractant and pH balance (independent variables).
Concentrations of divalent metal in the aqueous phases  were determined by atomic absorption spectrophotometer (Varian, model 50B), and the concentrations
were determined by atomic absorption spectrophotometer (Varian, model 50B), and the concentrations  in the were organic phase determined using the mass balance for manganese. The pH was measured by a pH meter (DIGIMED).
in the were organic phase determined using the mass balance for manganese. The pH was measured by a pH meter (DIGIMED).
4. Results
The results observed in the dependent variable the percentage extraction of Co, Mn, Cu and Ni were representative. The model was based on linear and quadratic effects of all independent variables, according to Table 2 and Figure 1 at 8.
Table 3 lists all the values of effects of the variables and coefficients regression for iterations linear and quadratic in model extraction of divalent metals present in the synthetic bleach.
According to the Pareto chart, shown in Figure 1, considering the linear and quadratic interactions of extraction of cobalt present in a synthetic leach liquor is observed that in addition to the A/O (linear) and pH equilibrium (linear), the relationship A/O quadratic and the concentration of manganese (linear) are important variables in the extraction of the metal that present in synthetic leach liquor.
Figure 2 shows the residual values observed versus
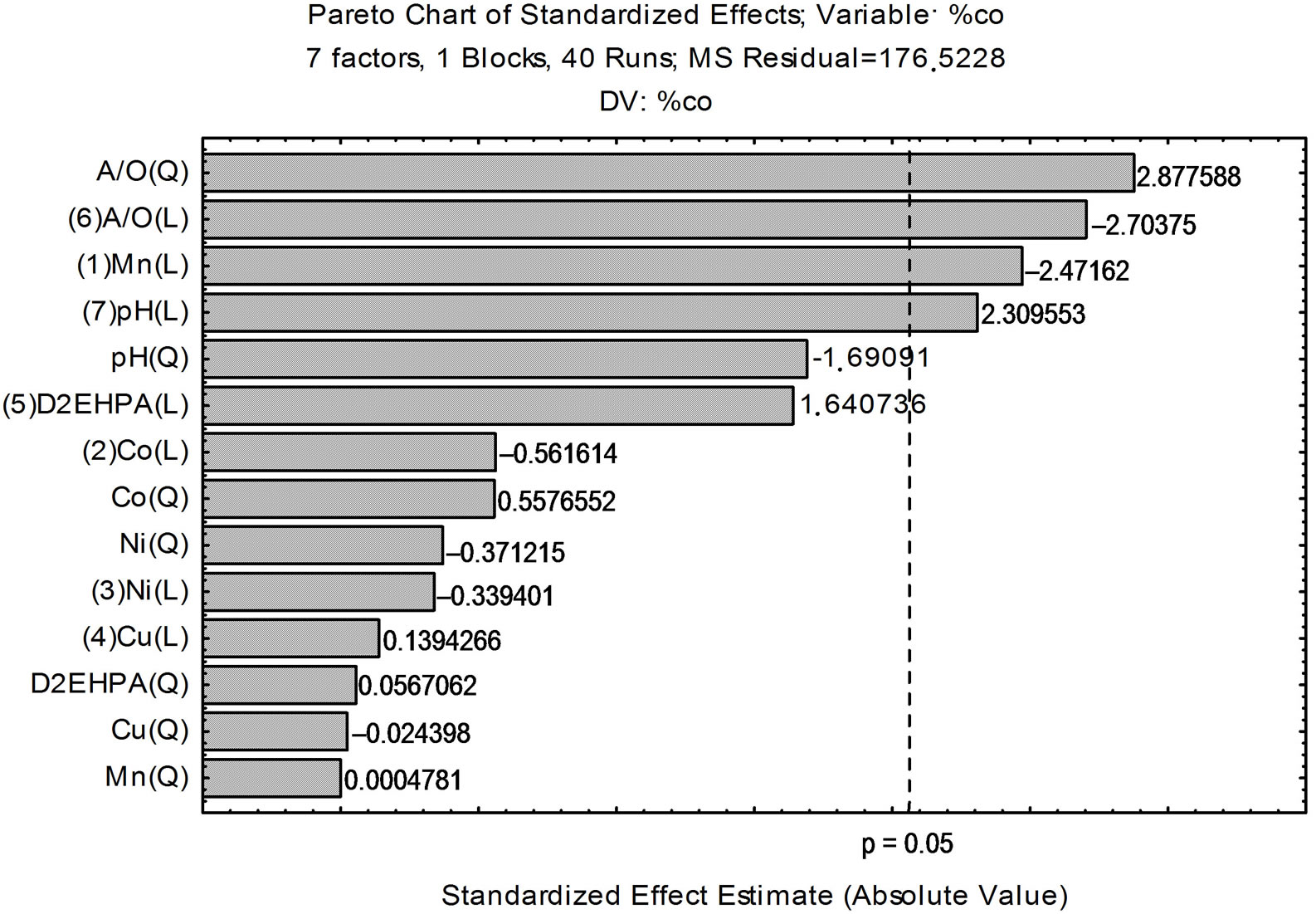
Figure 1. Linear and quadratic effects of the variables tested for Cobalt.

Table 3. Results of the effects of the variables and coefficients regression model.
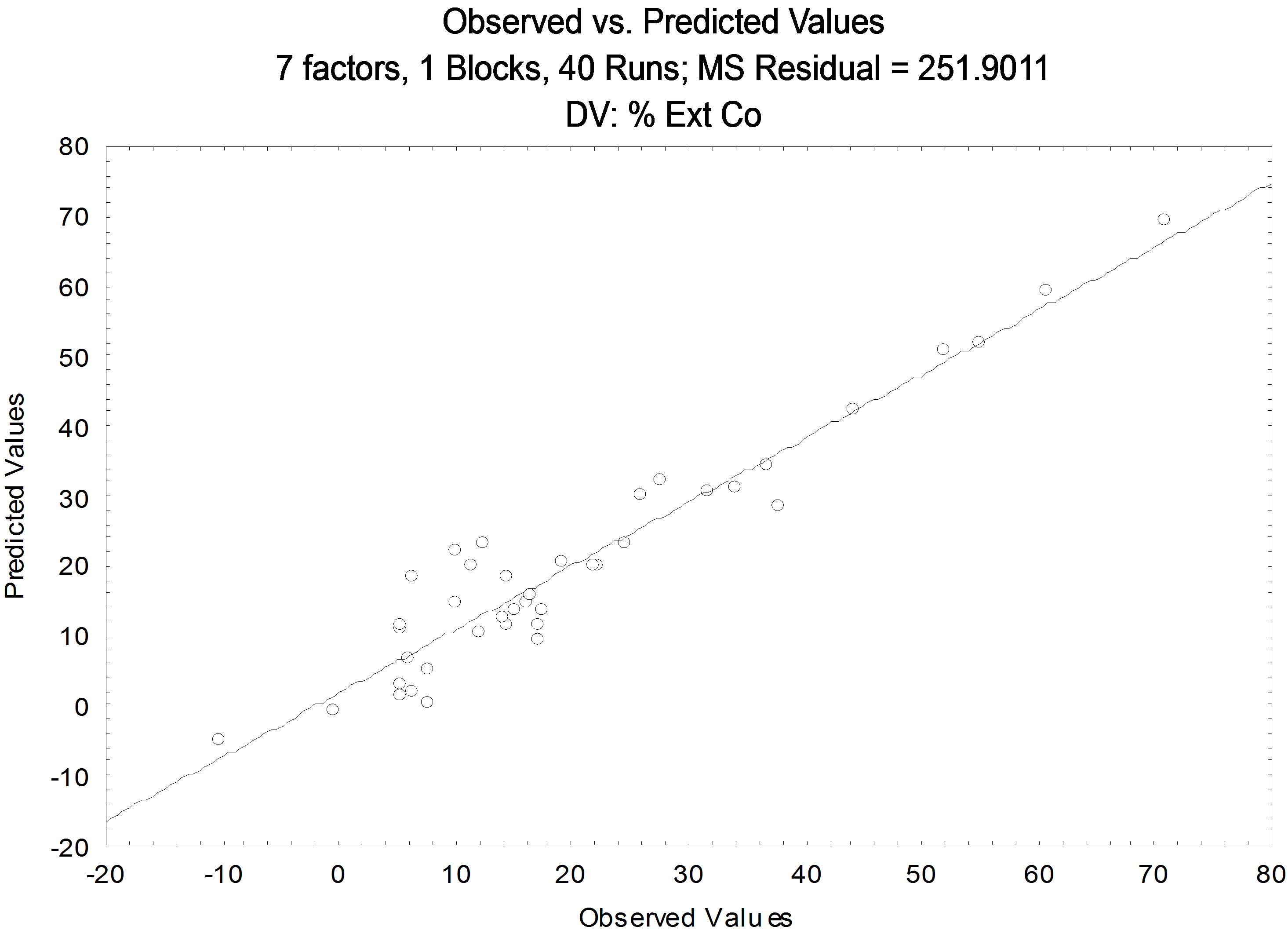
Figure 2. Comparative results between the values predicted by the model and experimental for Cobalt.
residual calculated values. Note that the points are mostly on the baseline and the 95% confidence level. From the values generated, it can get the value of the correlation coefficient (R2) significant, with a value of 0.9145.
Using the model generated for the extraction of cobalt, considering the interactions with linear and quadratic, it is possible to obtain Equation (3), which represents the extraction of divalent metal, present in synthetic leach liquor.
In examining Figure 3, with the interactions linear and quadratic, the variables that are directly related to the extraction of manganese present in the synthetic leach liquor are: the concentrations of D2EHPA and manganese, pH balance, and A/O (linear and quadratic). The other variables do not interfere directly and the model showed a correlation coefficient (R2) with a significant value of 0.9477, in Figure 4.
From the model generated it is possible to obtain the general equation for the percentage of extraction of manganese present in synthetic bleach. The suggested equation (Equation (4)) takes into consideration the model generated with the linear and quadratic interactions, as there are more significant variables for extraction in this model.
 (3)
(3)
 (4)
(4)

Figure 3. Linear and quadratic effects of the variables tested for Manganese.
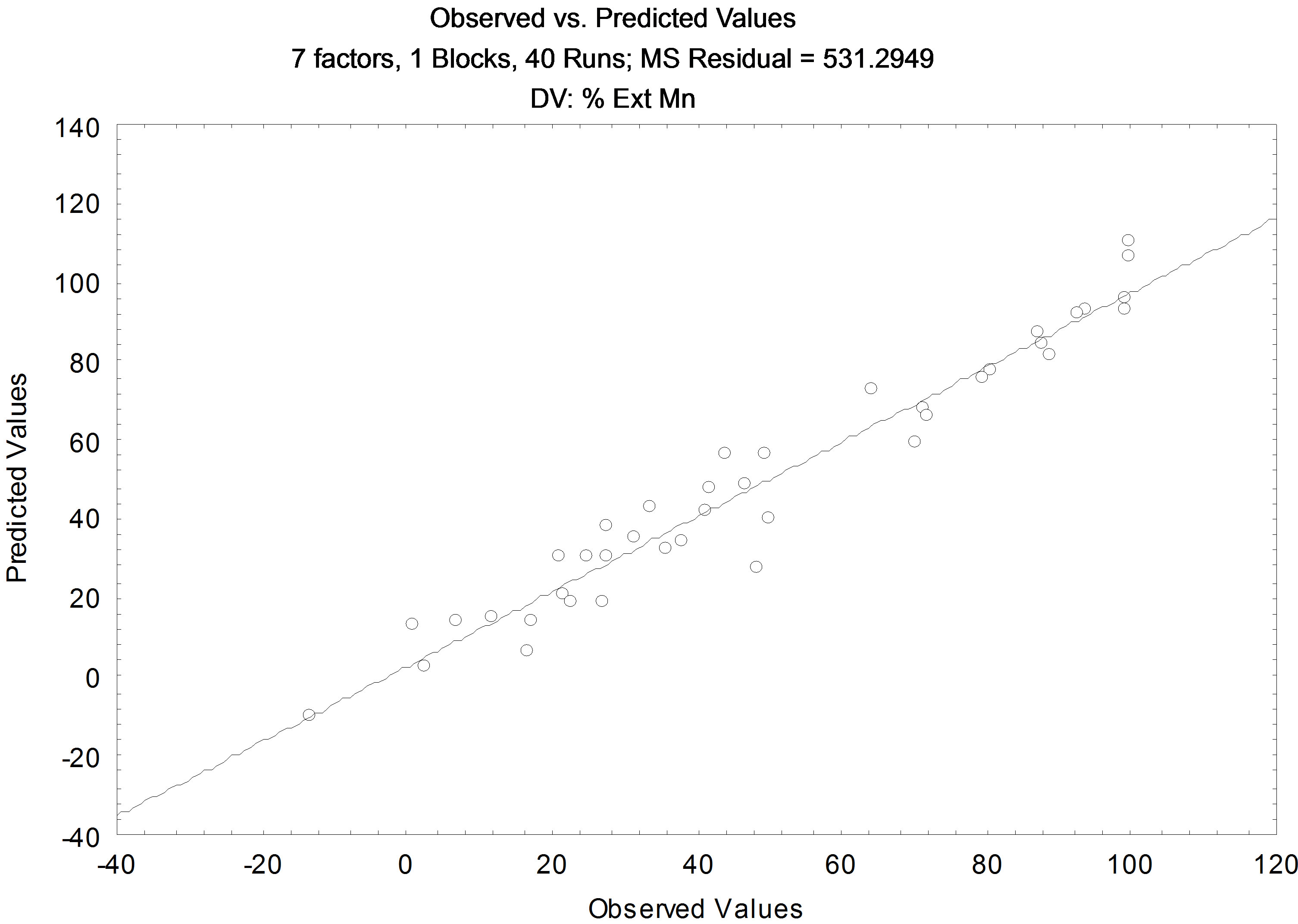
Figure 4. Comparative results between the values predicted by the model and experimental for Manganese.
The Pareto chart for the model considering the linear and quadratic interactions (Figure 5) shows the variables that influence the extraction of copper, only the ratio A/ O and the pH balance, with the confidence level of 95%. The residual values observed versus residual value calculated, is shown in Figure 6, with a coefficient of correlation (R2) of 0.9701.
Using the model generated for the extraction of copper, considering the interactions with linear and quadratic, it is possible to obtain Equation (5), which represents the extraction of divalent metal, present in synthetic leach liquor.
 (5)
(5)

Figure 5. Linear and quadratic effects of the variables tested for Copper.
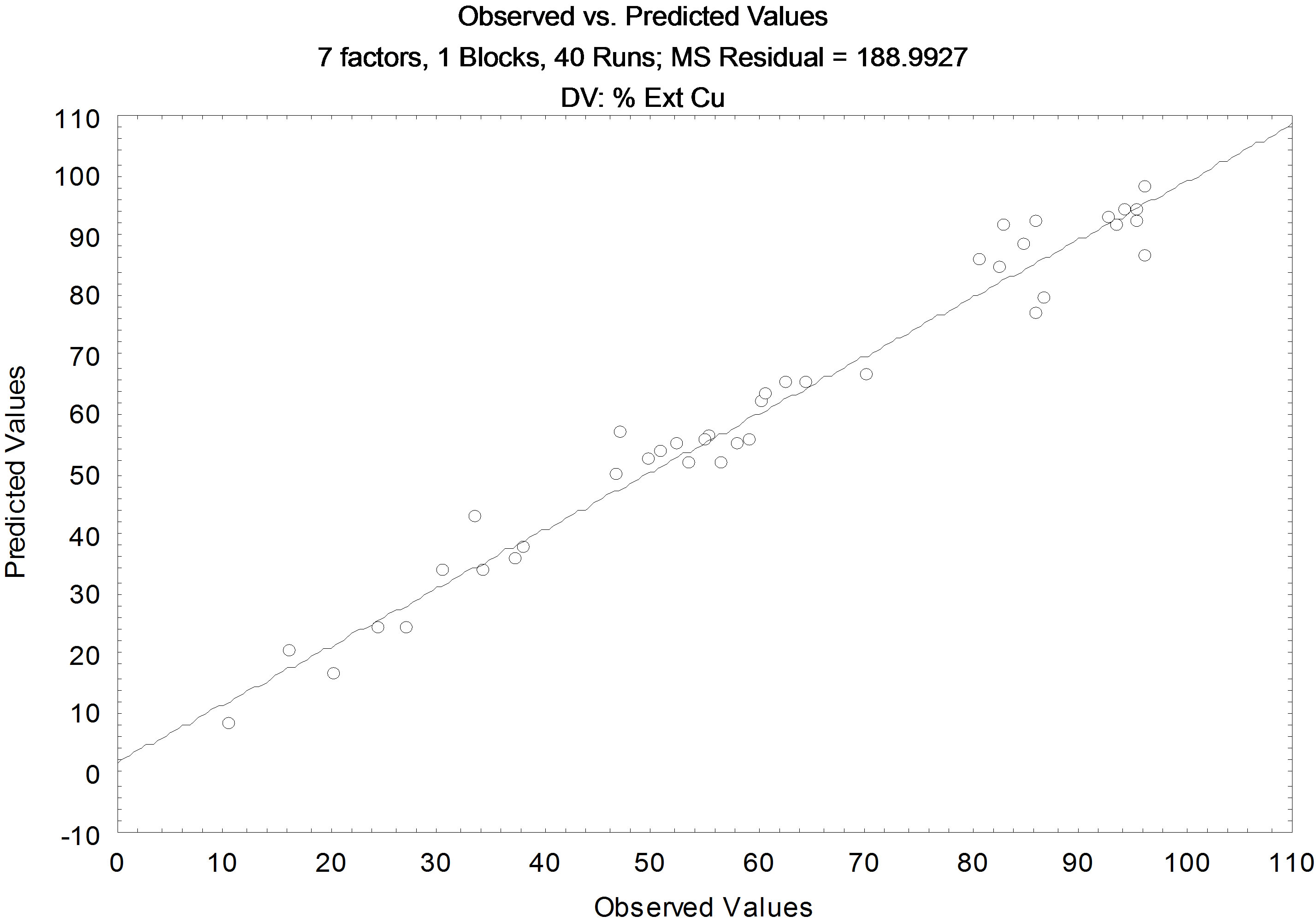
Figure 6. Comparative results between the values predicted by the model and experimental for Copper.
In Figure 7, Pareto chart is shown for extraction of nickel assuming linear and quadratic interactions, and it showed that only the ratio A/O (quadratic), is the variable that influences positively on the extraction of nickel, with the 95% confidence, this means that if the ratio A/O is increased, there will be a greater extraction of nickel present in synthetic leach liquor. The residual values observed versus residual values calculated, is shown in Figure 8, and the correlation coefficient (R2), to present a significant value is 0.9266.
Using the model generated for the extraction of nickel, whereas with linear and quadratic interactions, it is possible to obtain Equation 6, which represents the extraction of divalent metal present in synthetic leach liquor.
 (6)
(6)

Figure 7. Linear and quadratic effects of the variables tested for Nickel.
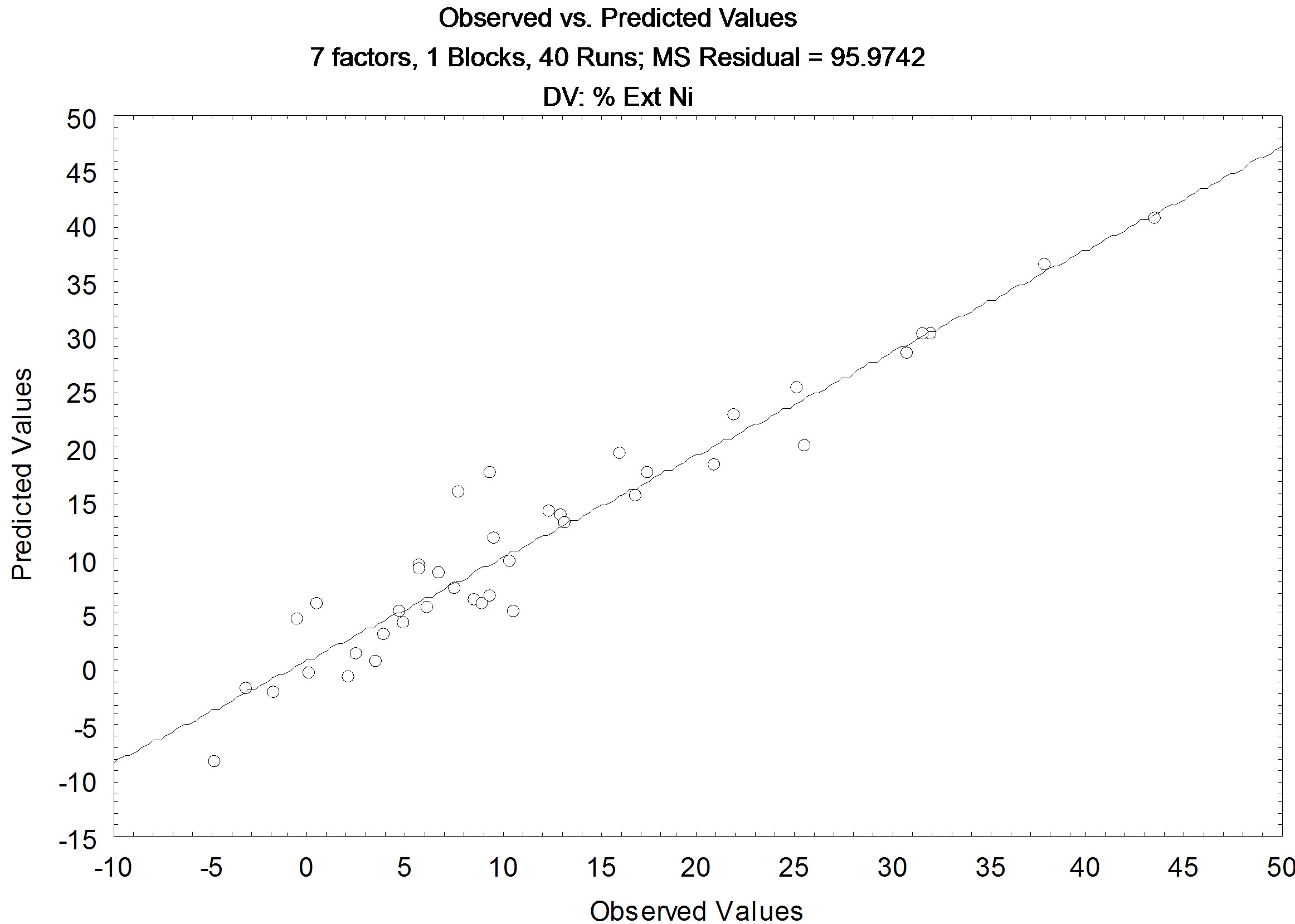
Figure 8. Comparative results between the values predicted by the model and experimental for Nickel.
5. Conclusion
The design of the experiment proved to be an effective technique for modeling systems for solvent extraction. The mathematical models presented for the four metals were good fits as shown by the R2 values (0.9145 for cobalt; 0.9477 for manganese; 0.9701 for copper and 0.9266 for nickel) and the graphs of residual values observed versus calculated residual, in all cases had proper values. Through Pareto chart generated from the model, it can be seen that the ratio A/O (linear or quadratic), followed by pH equilibrium (linear) are the variables that have most influence on the extraction of divalent metals, using D2EHPA in isoparaffins in sulfate media.
REFERENCES
- G. Owusu, “Selective Extractions of Zn and Cd from Zn-Cd-Co-Ni Sulfate Solution Using Di-2-ethylhexyl Phosphoric Acid Extractant,” Hydrometallurgy, Vol. 47, No. 2, 1998, pp. 205-215. doi:10.1016/S0304-386X(97)00044-3
- P. E. Tsakiridis and S. L. Agatzini, “Simultaneous Solvent Extraction of Cobalt and Nickel in the Presence of Manganese and Magnesium from Sulfate Solutions by Cyanex 301,” Hydrometallurgy, Vol. 72, No. 3, 2004, pp. 269-278. doi:10.1016/S0304-386X(03)00180-4
- M. G. Ritcey and A. W. Ashbrook, “Solvent Extraction, Principles and Applications to Process Metallurgy,” Elsevier Scientific Publishing Company, Amsterdam, 1979.
- K. C. Nathsarma and N. Devi, “Separation of Zn(II) and Mn(II) from Sulphate Solutions Using Sodium Salts of D2EHPA, PC 88A and Cyanex 272,” Hydrometallurgy, Vol. 84, No. 3, 2006, pp. 149-154. doi:10.1016/j.hydromet.2006.05.004
- R. K. Biswas and D. A. Begum, “Kinetics of Extraction and Stripping of Ti(IV) in HCl-D2EHPA-Kerosene System Using the Single Drop Technique,” Hydrometallurgy, Vol. 55, No. 1, 2000, pp. 57-77. doi:10.1016/S0304-386X(99)00074-2
- R. K. Biswas, M. A. Habib and M. F. Bari, “Kinetics of Backward Extraction of Mn(II) from Mn-D2EHPA Complex in Kerosene to Hydrochloric Acid Médium Using Single Drop Technique,” Hydrometallurgy, Vol. 46, No. 3, 1997, pp. 349-362. doi:10.1016/S0304-386X(97)00030-3
- R. K. Biswas, M. A. Habib and M. G. K. Mondal, “Kinetics and Mechanism of Stripping of Mn(II)-D2EHPA Complex by Sulphuric Acid Solution,” Hydrometallurgy, Vol. 80, No. 3, 2005, pp. 186-195. doi:10.1016/j.hydromet.2005.06.013
- B. Swain, J. Jeong, J. Lee and G. H. Lee, “Separation of Cobalt and Lithium from Mixed Sulphate Solution Using Na-CYANEX 272,” Hydrometallurgy, Vol. 84, No. 3, 2006, pp. 130-138. doi:10.1016/j.hydromet.2006.03.061
- X. Fu and J. A. Golding, “Solvent Extraction of Cobalt and Nickel in Bis(2,4,4-tri-methylpentyl) Phosphinic Acid, ‘CYANEX 272’,” Solvent Extraction and Ion Exchange, Vol. 5, No. 2, 1987, pp. 205-226. doi:10.1080/07366298708918562
- D. Georgiou and V. G. Papangelakis, “Behaviour of Cobalt during Sulphuric Acid Pressure Leaching of a Limonitic Laterite,” Hydrometallurgy, Vol. 100, No. 1, 2009, pp. 35-40. doi:10.1016/j.hydromet.2009.09.011
- R. G. McDonald and B. I. Whittington, “Atmospheric Acid Leaching of Nickel Laterites Review Part I. Sulphuric Acid Technologies,” Hydrometallurgy, Vol. 91, No. 1, 2008, pp. 35-55. doi:10.1016/j.hydromet.2007.11.009
- M. Niinae, N. Komatsu, Y. Nakahiro, T. Wakamatsua and J. Shibatab, “Preferential Leaching of Cobalt, Nickel and Copper from Cobalt-Rich Ferromanganese Crusts with Ammoniacal Solutions Using Ammonium Thiosulfate and Ammonium Sulfite as Reducing Agents,” Hydrometallurgy, Vol. 40, No. 1, 1996, pp. 111-121. doi:10.1016/0304-386X(94)00085-H
- Y.-F. Shen, W.-Y. Xue, W. Li, S.-D. Li and X.-H. Liu, “Recovery of Mn2+, Co2+ and Ni2+ from Manganese Nodules by Redox Leanching and Solvent Extraction,” Transactions of Nonferrous Metals Society of China, Vol. 17, No. 4, 2007, pp. 1105-1111. doi:10.1016/S1003-6326(07)60233-7
- M. S. Bafghi, A. Zakeri, Z. Ghasemi and M. Adeli, “Reductive Dissolution of Manganese Ore in Sulfuric Acid in the Presence of Iron Metal,” Hydrometallurgy, Vol. 90, No. 2, 2008, pp. 207-212. doi:10.1016/j.hydromet.2007.07.003
- J. M. M. Paixão, J. C. Amaral, L. E. Memória and L. R. Freitas, “Sulphation of Carajás Manganese Ore,” Hydrometallurgy, Vol. 39, No. 1, 1995, pp. 215-222. doi:10.1016/0304-386X(95)00031-B
- C. A. Carvalhido, M. F. Pedrosa and A. H. Martins, “Extração por Solventes Aplicada à Remoção de Metais Pesados Presentes no Licor de Lixiviação do Minério de Manganês da Mina do Azul (PA),” Revista Escola de Minas, Vol. 54, No. 3, 2001, pp. 227-231. doi:10.1590/S0370-44672001000300011
- Y. Shen, W. Xue, W. Li, S. Li and X. Liu, “Recovery of Mn2+, Co2+ and Ni2+ from Manganese Nodules by Redox Leaching and Solvent Extraction,” Transactions of Nonferrous Metals Society of China, Vol. 17, No. 4, 2007, pp. 1105-1111. doi:10.1016/S1003-6326(07)60233-7
- F Pagnanelli, M. Garavini, F. Vegliò and L. Toro, “Preliminary Screening of Purification Processes of Liquor Leach Solutions Obtained from Reductive Leaching of Low-Grade Manganese Ores,” Hydrometallurgy, Vol. 71, No. 3, 2004, pp. 319-327. doi:10.1016/S0304-386X(02)00156-1
- H. Vu, J. Jandová, K. Lisá and F. Vranka, “Leaching of Manganese Deep Ocean Nodules in FeSO4-H2SO4-H2O Solutions,” Hydrometallurgy, Vol. 77, No. 1, 2005, pp. 147-153. doi:10.1016/j.hydromet.2004.09.012
- P. C. Resende, F. S. Barrado and A. H. Martins, “Sulfuric Activation of a Brazilian Manganese Ore for Heavy Metals Removal,” Hydrometallurgy, Vol. 51, No. 3, 1999, pp. 325-333. doi:10.1016/S0304-386X(98)00087-5
- G. E. P. Box and K. B. Wilson, “On the Experimental Attainment of Optimum Conditions,” Journal of the Royal Statistical Society, Vol. 13, No. 1, 1951, pp. 1-45.
- D. C. Montgomery, “Design and Analysis of Experiments,” John Wiley and Sons, Inc., New York, 1997.
NOTES
*Corresponding author.

