Journal of Information Security
Vol. 3 No. 2 (2012) , Article ID: 18833 , 7 pages DOI:10.4236/jis.2012.32021
A Fair Electronic Cash System with Identity-Based Group Signature Scheme
1Department of Statistic and Computer Science, Faculty of Applied Sciences, Red Sea University, Port Sudan, Sudan
2School of Computer Science and Technology, University of Science and Technology of China, Hefei, China
Email: Osman64@mail.ustc.edu.cn, syang@ustc.edu.cn
Received November 10, 2011; revised February 15, 2012; accepted March 24, 2012
Keywords: Elliptic Curve; Bilinear Pairings; Group Signature; Electronic Cash; Trusted Third Party; Tracing Protocol
ABSTRACT
A fair electronic cash system is a system that allows customers to make payments anonymously. Furthermore the trusted third party can revoke the anonymity when the customers did illegal transactions. In this paper, a new fair electronic cash system based on group signature scheme by using elliptic curve cryptography is proposed, which satisfies properties of secure group signature scheme (correctness, unforgeability, etc.). Moreover, our electronic cash contains group members (users, merchants and banks) and trusted third party which is acted by central bank as group manager.
1. Introduction
The first group signature scheme was proposed by David Chaum and van-Heyst in 1991 [1]. Group signature schemes allow a group member to sign messages on behalf of the group. Such signatures must be anonymous and unlinkable but, whenever needed, a designated group manager can reveal the identity of the signer [1-3]. Shamir proposed an identity based signature to simplify key management procedures of certificate-based public key infrastructures (PKI) [4]. A lot of identity based group signatures have been proposed after Shamir [5-8]. Many group signatures scheme have been proposed recently, but several of them were suggested application electronic cash. [9-11] introduced group signatures into electronic cash schemes which are anonymous and unlinkability.
Main Contribution
In this paper, identity based group signature scheme is proposed, which satisfies the electronic cash based on group signatures. Furthermore it provides to keep group member anonymous and unlinkability if he does not cheat. In this scheme we use trusted third party, which acts the group manager. The user is a group member who should register at TTP before start any interaction with the bank.
The rest of this paper is as follows: in the next section, we introduce some preliminaries work. Our identity based group signature is presented in Section 3. In Section 4, we propose a new electronic cash system. We explain security analysis of our scheme in Section 5. Final section concludes.
2. Preliminaries
In this section, we will describe the definition and properties of elliptic curve cryptography, bilinear pairings, Gap Diffie-Hellman Group and Group signature models.
2.1. Elliptic Curve Cryptography
2.1.1. Definition1: Addition Rules of Elliptic Curve [12]
It is possible to define an addition rule to add points on E. The addition rule is specified as follows:
Identity: 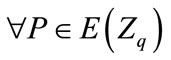
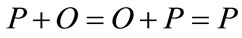
Negation: if 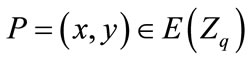 then
then 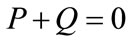 where
where 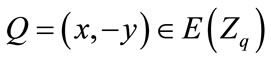 and denoted by
and denoted by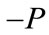 .
.
Note: 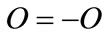
Add two points with different x-coordinates:
Let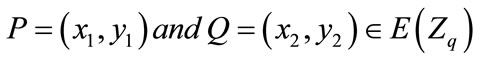 be two points such that
be two points such that  then
then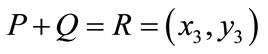 as shown in Figure 1, where
as shown in Figure 1, where
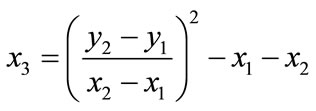
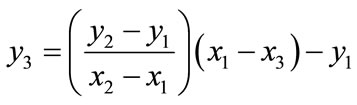
Add a point to itself (double a point) with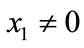 :
:
Let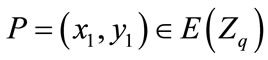 , then
, then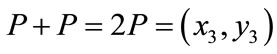 , where:
, where:
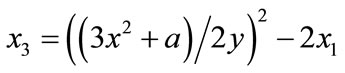
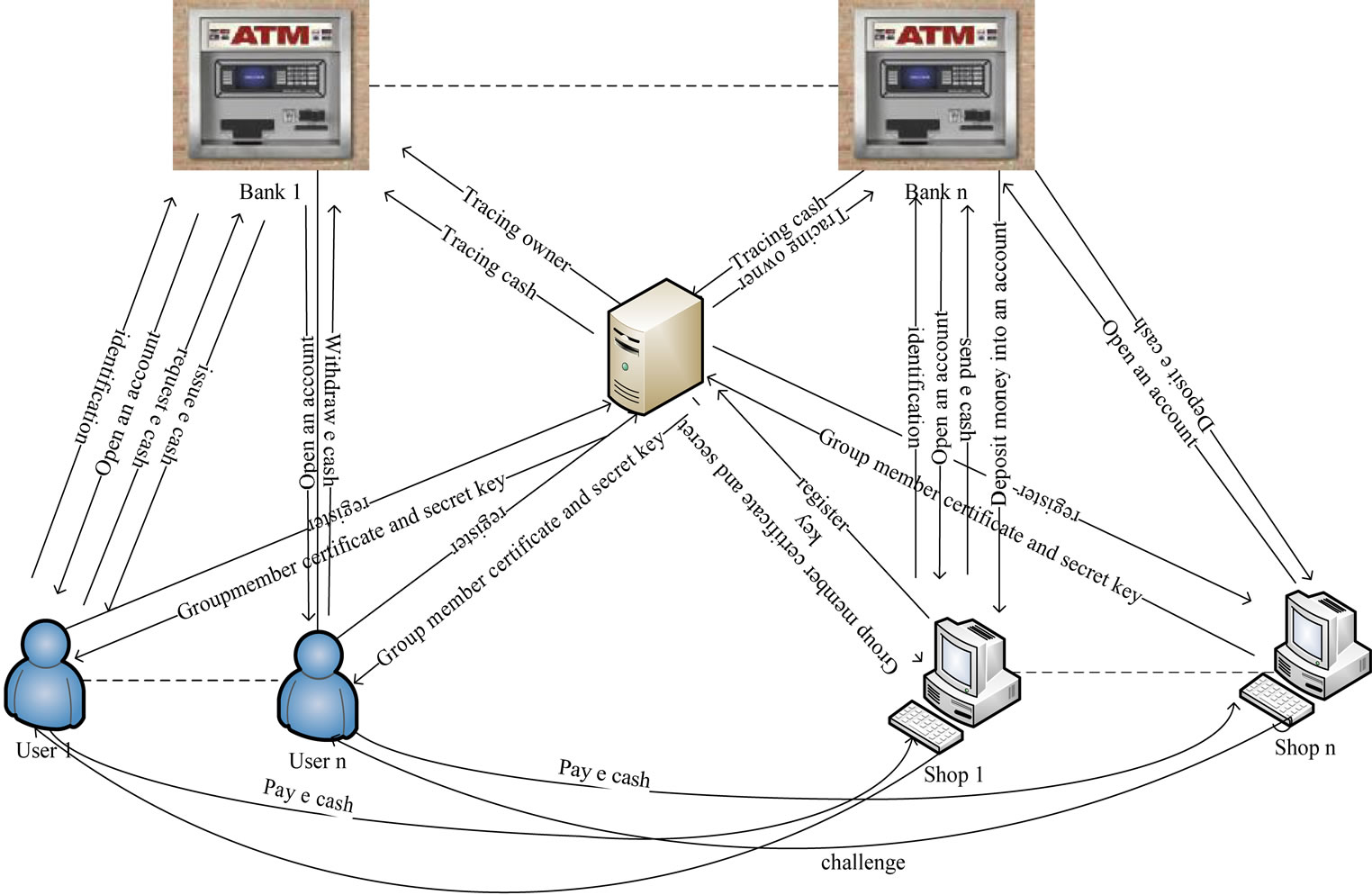
Figure 1. Architecture of our electronic cash scheme.
2.1.2. Definition 2 Elliptic Curve Discrete Logarithm Problem (ECDLP)
Given an elliptic curve E defined over a finite field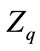 , a point
, a point 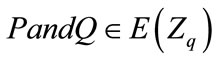 of order n, find the integer
of order n, find the integer 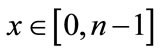 such that
such that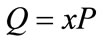 . The integer x is called the discrete logarithm of Q to the base P denoted as
. The integer x is called the discrete logarithm of Q to the base P denoted as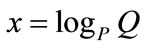 . If x is sufficient large, then it is infeasible to compute it [13].
. If x is sufficient large, then it is infeasible to compute it [13].
2.2. Bilinear Pairings
Let 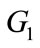 and
and 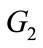 be two cyclic groups generates by P, whose order is a prime q, where
be two cyclic groups generates by P, whose order is a prime q, where 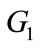 is additive groups and
is additive groups and 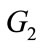 is multiplicative group. A pairing is a function:
is multiplicative group. A pairing is a function:
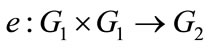
All pairing will satisfy the following properties:
1) Bilinear: For all 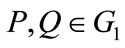 and
and 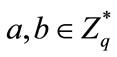 then
then 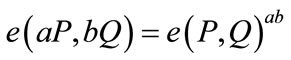
2) Non-degenerate: There exists 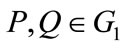 such that
such that 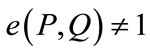
3) Computable: There is an efficient algorithm to compute 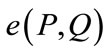 for all
for all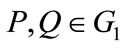 .
.
2.3. Gap Diffie-Hellman Group
We first introduce the following problems in G [14].
1) Discrete Logarithm Problem (DLP): if given P and Q, to find 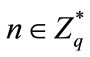 from
from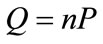 .
.
2) Computation Diffie-Hellman Problem (CDHP). Given 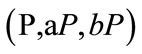 for
for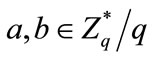 , to compute
, to compute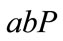 .
.
3) Decisional Diffie-Hellman Problem (DDHP).
Given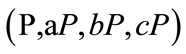 , or
, or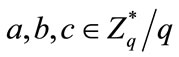 , to decide whether
, to decide whether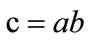 .
.
We call 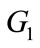 a GDH group if DDHP can be solved in polynomial time but no polynomial times an algorithm can solve CDHP or DLP with non-negligible advantage within polynomial time.
a GDH group if DDHP can be solved in polynomial time but no polynomial times an algorithm can solve CDHP or DLP with non-negligible advantage within polynomial time.
2.4. Group Signature Model
A group signature scheme is comprised of the following procedures [5]:
1) Setup: An algorithm that generates the group public key and a group master key for the group manager.
2) Extract: A protocol between the group manager and a group member that generates the user’s secret key and public key.
3) Sign: A probabilistic algorithm (with inputs as a group public key, a membership secret and a message m) outputs a group signature of m.
4) Verify: An algorithm for establishing the validity of an alleged group signature of a message with respect to the group public key.
5) Reveal: An algorithm that, given a message, a valid group signature on it, a group public key and a group manager’s master key, determines the identity of the actual signer.
A secure group signature scheme should satisfy all or part of the properties:
1) Correctness: Group signatures produced by a group member must be valid.
2) Unforgeability: Only group members are able to sign messages on behalf of the group.
3) Anonymity: It is infeasible to find out the group member who signed a message without the group manager’s secret key.
4) Unlinkability: Deciding whether two different valid signatures were computed by the same group member is computationally hard.
5) Exculpability: Neither a group member nor the group manager can sign on behalf of other group members.
6) Traceability: The group manager is always able to identify the actual signer for a valid signature in case of disputes.
7) Coalition-resistance: No coalition of members can prevent a group signature from being opened.
3. Our Identity Based Group Signature
In this section we consider ID-based group signature scheme from bilinear pairings, which can be implemented as follows:
3.1. Setup
Setup is a system generation. The group manager executes the following:
Choose as defined in 2.2 and choose
as defined in 2.2 and choose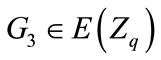 .Select three hash function cryptography
.Select three hash function cryptography 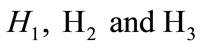 which satisfy
which satisfy 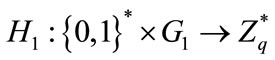
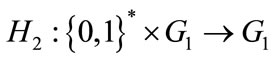 and
and 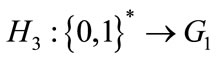 Select
Select 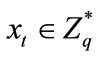 as secret key.
as secret key.
Compute 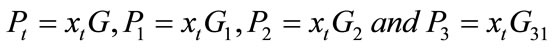 and publish
and publish 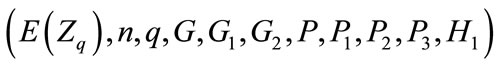 as public key.
as public key.
3.2. Extract
Before the user joins the group, manager should execute this step:
1) Select random number 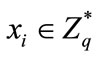 as private key.
as private key.
2) Compute 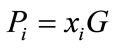 as public key.
as public key.
When the user wants to become the member of group then the user i and the group manager can cooperates as follows:
1) The user sends his public key with ID (identification) to the group manager.
2) Group manager select random numbers 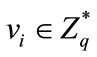 for every member who want become group member.
for every member who want become group member.
3) Group manager calculate 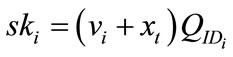 where
where 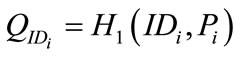 and then sends
and then sends 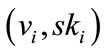 to the user as the membership certificate.
to the user as the membership certificate.
3.3. Sign
When the user wants to sign message m, the user can do the followings:
The user selects random elements 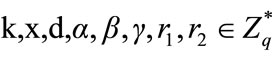 and
and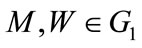 , and then calculates the followings:
, and then calculates the followings:
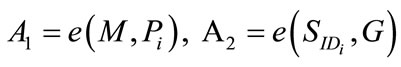
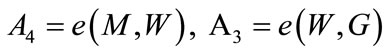
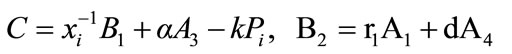
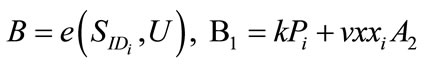
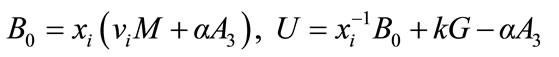
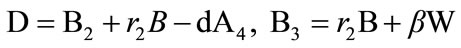
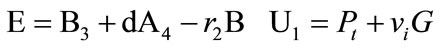
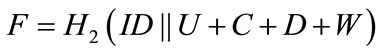
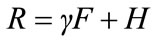
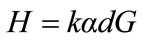
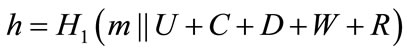
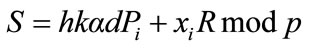
The resulting signature on the message m is (U, C, D, W, R, S).
3.4. Verify
When the receiver wants to verify the group signature (U, C, D, W, R, S) of the message m which is signed by the signer, the receiver first computes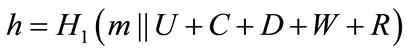 and then verifies
and then verifies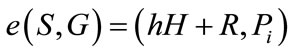 .
.
3.5. Open
This algorithm is only executed by the group manager. Given valid group signatures the group manager can easily find the identity of the signer. The signer cannot deny his group signatures after group manager presents the followings:
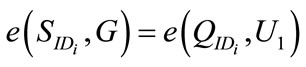
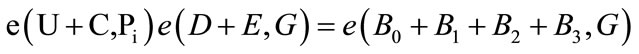
4. Our Electronic Cash System
4.1. Electronic Cash Architecture
In this section, we describe our system architecture and how each protocol of e-cash works. Figure 1 shows configuration of group signatures, which involves three protocols: withdraw protocol, payment protocol and deposit protocol. Thus group signatures architecture consists four main parties: Trust Third Party (TTP) acts the group manager; banks, users and shops acts the group member. Their relation between each part with other as follows:
1) Trusted Third Party (TTP) is acting as group manager and the users act group membership. The user should be registering at TTP before start any interaction with the bank. After registration, the user will get a valid membership certificate and a secret key from TTP.
2) The bank issues the valid electronic cash. The bank protects the privacy of the customers, and also uses the blind signature technique to sign the electronic cash.
3) The customer spends electronic cash in a payment protocol with a shop over an anonymous channel.
4) The shop deposits electronic cash that he gets from the user in the payment protocol into his bank account.
4.2. Setup
TTP (Central Bank (CB)) generates and publishes the same system parameters that proposed in Section 3.1.
When the bank i 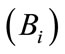 registers in CB, they should perform the following steps:
registers in CB, they should perform the following steps:
1) 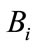 selects random number
selects random number 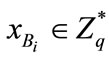 as private key and computes
as private key and computes 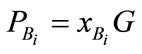 as public key.
as public key.
2) 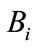 sends public key with his identification
sends public key with his identification 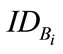 to the CB.
to the CB.
3) The CB does the same in Section 3.2 and sends 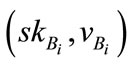 to
to 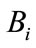 as membership certificate.
as membership certificate.
And also the user i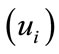 and merchant i
and merchant i 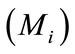 should do the same steps that
should do the same steps that 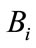 does when they want to register in CB.
does when they want to register in CB.
Then the central bank will send the group member ship 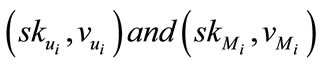 to
to 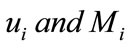 respectively.
respectively.
4.3. Open an Account
Every group member should open an account in any bank he needs it. They need to do as follows:
1) The group member sends 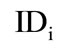 to the bank
to the bank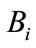 .
.
2) 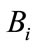 opens an account and sends it to the group member.
opens an account and sends it to the group member.
4.4. Withdraw Protocol
The withdrawal protocol involves 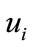 and
and 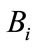 which the user opens an account in. When legal
which the user opens an account in. When legal 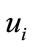 wants to withdraw electronic cash from his account in the bank, the user must prove himself to the bank. The withdraw protocol request contains the amount of electronic cash, which is less than or equal the balance. If the amount is greater than balance then the withdraw protocol should be stopped, otherwise, the user and the bank execute the following steps:
wants to withdraw electronic cash from his account in the bank, the user must prove himself to the bank. The withdraw protocol request contains the amount of electronic cash, which is less than or equal the balance. If the amount is greater than balance then the withdraw protocol should be stopped, otherwise, the user and the bank execute the following steps:
1) the user chooses random number 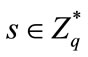 and computes
and computes 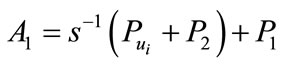
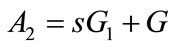 sends A1 and A2 to the bank i.
sends A1 and A2 to the bank i.
2) the bank selects random number 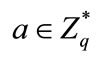 and
and  and computes
and computes
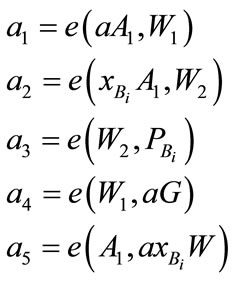
sends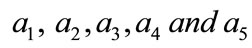 to
to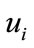 .
.
3) the 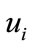 calculates
calculates 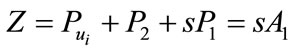
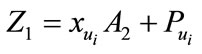 selects random numbers
selects random numbers 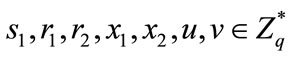 and computes
and computes
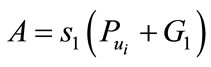 ,
, 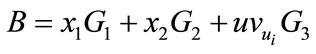 ,
,
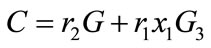 ,
, 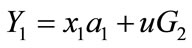
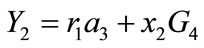 ,
, 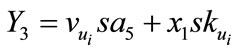
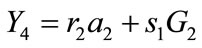 ,
, 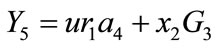
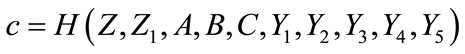
 sends
sends 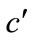 to
to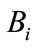 .
.
4) the Bi computes 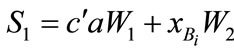 sends
sends  to
to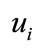 .
.
5) the 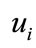 checks
checks
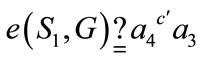 (1)
(1)
and
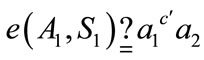 (2)
(2)
If (1) and (2) holds, then the user accepts and computes 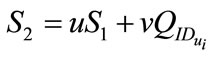
We can proof (1) and (2) as follows:
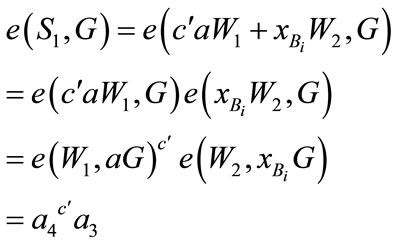
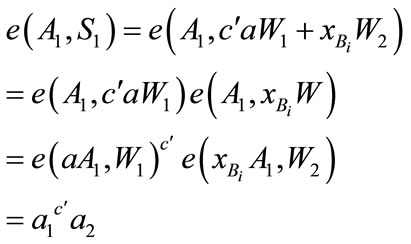
4.5. Payment Protocol
The payment protocol involves the customer and the merchant. If the customer wants to buy some goods from the merchant, they should execute the follows:
1) The customer chooses a random 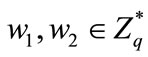 and computes
and computes 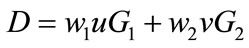
User sends 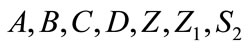 to merchant.
to merchant.
2) The merchant generates a transaction message of payment for the customer d as challenge and sends to user d = H0(A, B, C, D, Z, Z1, S2, 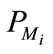 ,amount, amount type, date/time)
,amount, amount type, date/time)
3) User calculates responses
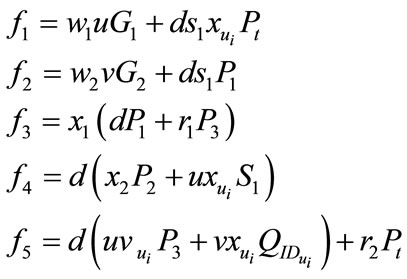
User sends  to merchant.
to merchant.
4) The signature of electronic cash is 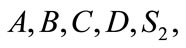
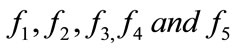 .
.
5) Merchant accepts if and only if
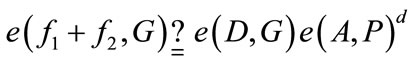 (3)
(3)
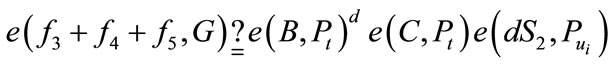 (4)
(4)
Now we can proof (3) and (4) as followings:
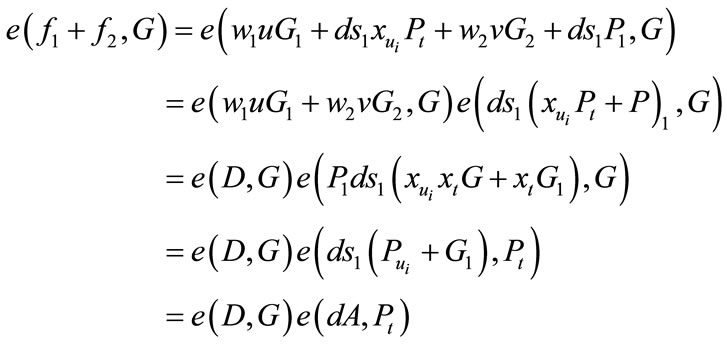
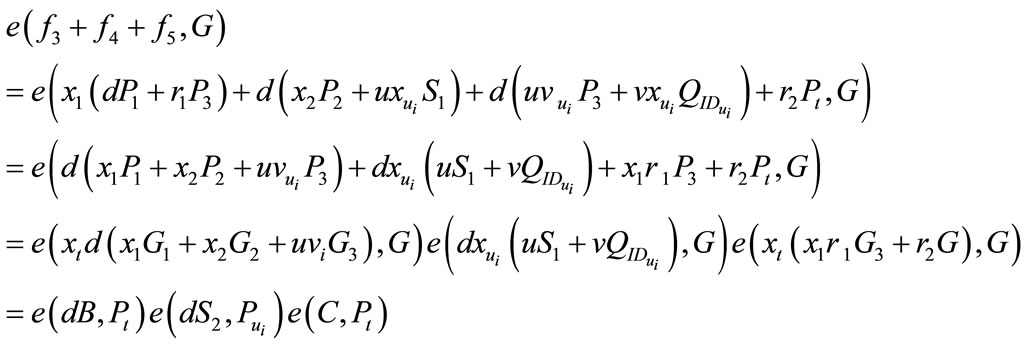
4.6. Deposit Protocol
In this protocol the merchant i sends electronic cash to his bank i. There are two cases we will discuss as follows:
First case: if the shop i and user i have accounts in the same bank. Since the deposit protocol involves merchant and bank, they will execute the following steps:
1) The merchant sends signatures of electronic cash 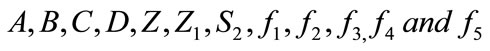 to the bank.
to the bank.
2) The bank verifies the validity of signature of e cash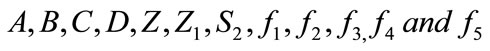 .
.
3) If the signature of e cash 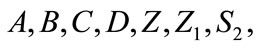
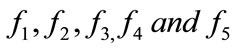 is hold, then the bank searches the deposit database to find out the same electronic cash has been deposited before or not. If it has not been in its deposit database, the bank accepts the electronic cash and credits the amount to the shop account, otherwise the bank i rejects transaction.
is hold, then the bank searches the deposit database to find out the same electronic cash has been deposited before or not. If it has not been in its deposit database, the bank accepts the electronic cash and credits the amount to the shop account, otherwise the bank i rejects transaction.
Second case: if the user i and merchant i have accounts in different banks such as user i has an account in the bank i and shop i has an account in bank j.
Assume merchant i wants to deposit the received electronic cash from user i to his bank j, they will do the following steps:
1) The merchant sends signature of electronic cash 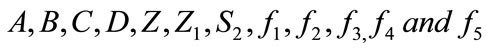 to bank j.
to bank j.
2) Bank j verifies the validity of signature of e cash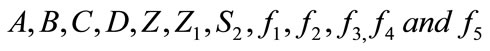 with bank i’s public key.
with bank i’s public key.
3) If it succeeds then bank j sends the electronic cash to bank i.
4) Bank i searches the deposit database to find out whether electronic cash has been deposited before, if it is not has been stored in deposit database then bank i debits the amount from user i account and sends it to the merchant i account in his bank j, otherwise bank i can detect double depositing or double spending.
4.7. The Tracing Protocol
Customer Tracing Protocol
The customer tracing protocol involves the bank and the trusted third party. This protocol is used to determine the identity of the customer in a specific payment transaction. Money laundering is big problem of electronic cash; here it can be protected by detecting the identity of the illegal customers.
1) The customer tracing protocol is as follows:
The bank sends to the CB the signatures of electronic cash 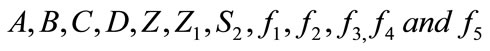 that received from the merchant in the deposit protocol.
that received from the merchant in the deposit protocol.
2) The CB verifies the validity of the signature of electronic cash as the merchant does in the deposit protocol.
3) The CB can calculate 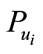 from
from 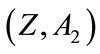 as follows:
as follows:
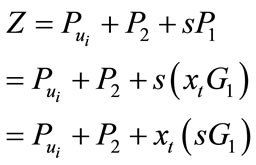 (5)
(5)
From 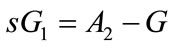 then put it into (5)
then put it into (5)
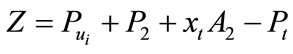
Finally we get
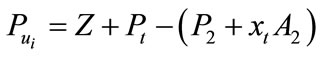
The CB sends 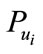 to the bank.
to the bank.
Then the bank can find the actual identity corresponding to 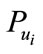 in his database.
in his database.
5. Analysis of Security
Theorem 1
A group member and the group manager cannot sign electronic cash on behalf of the other group members with non-negligible probability.
Proof:
Assume there is a group member who has 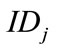 wants to sign electronic cash on behalf of the group member who has
wants to sign electronic cash on behalf of the group member who has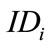 .
.
He chooses random number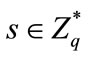 , computes and sends
, computes and sends 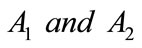 to bank i.
to bank i.
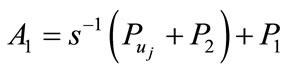
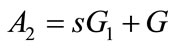
The bank calculates and sends back to him as withdraw protocol.
back to him as withdraw protocol.
He selects random numbers 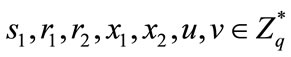 and computes
and computes 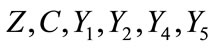 as withdraw protocol, computes
as withdraw protocol, computes 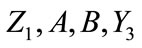 as follows:
as follows:
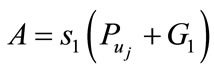 ,
, 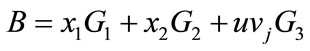 ,
,
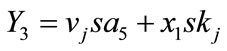 ,
,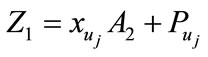
Finally he calculates c as
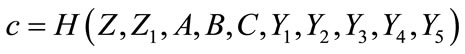
This equation can be equal to that equation in withdraw protocol, if and only if
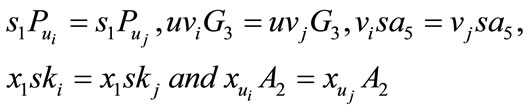
The probability of 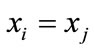 is
is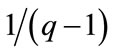 ,
,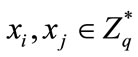 . If he wants to choose exactly
. If he wants to choose exactly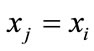 , he needs to solve discrete logarithm problem
, he needs to solve discrete logarithm problem 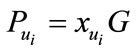 as
as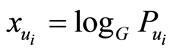 .
.
Theorem 2
The proposed fair electronic cash system can protect the customer’s privacy and keep the system anonymous.
Proof:
Deciding whether a payment signature from a customer requires knowing 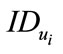 of the user. However, to know
of the user. However, to know 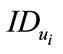 of the user in our scheme requires solving discrete logarithm problem
of the user in our scheme requires solving discrete logarithm problem 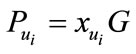 to find out the user secret key. Since solving discrete logarithm problem is very difficult, then no one can know
to find out the user secret key. Since solving discrete logarithm problem is very difficult, then no one can know 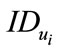 except CB.
except CB.
Theorem 3
In the payment protocol, only users that register in the CB are able to sign a payment message with his membership key.
Proof:
It is difficult to find 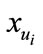 from
from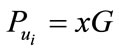 . The forger cannot find the same
. The forger cannot find the same 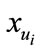 then it is impossible to get certificate membership
then it is impossible to get certificate membership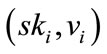 to sign a payment message.
to sign a payment message.
Theorem 4
Our proposed scheme keeps the system unlinkability.
Proof: To decide whether two signatures of electronic cash 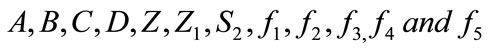 and
and 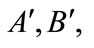
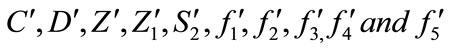 are from the same customer requires deciding whether
are from the same customer requires deciding whether
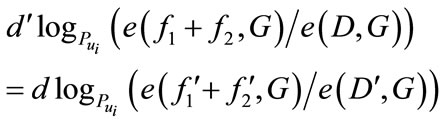 it is not easy to compute it.
it is not easy to compute it.
From the four theorems and traceable protocol above, it is easy to deduce that our scheme satisfies the security properties of group signatures and provides electronic cash against double spending, blackmailing and money laundering.
6. Conclusion
We have presented new fair electronic cash system with identity based group signature scheme. It satisfies all basic requirements to protect electronic cash. Furthermore, we show how our group signature scheme could construct fair electronic cash, which satisfy properties of secure group signature scheme.
REFERENCES
- D. Chaum and E. van Heyst, “Group Signatures,” In: J. Feigenbaum, Ed., Advances in Cryptology: EUROCRYPT ’91—Workshop on the Theory and Application of Cryptographic Techniques, Springer-Verlag & GmbH & Co. K, Berlin and Heidelberg, 1991, pp. 257-265.
- S. Canard and M. Girault, “Implementing Group Signature Schemes with Smart Cards,” Proceedings of the 5th Conference on Smart Card Research and Advanced Application, San Jose, 21-22 November 2002, pp. 1-10.
- L. Chen and T. Pedersen, “New Group Signatures Schemes,” In: A. D. Santis, Ed., Advances in Cryptology— EUROCRYPT 94: Workshop on the Theory and Application of Cryptographic Techniques, Springer-Verlag, Berlin, 1995, pp. 171-181.
- A. Shamir, “Identity-Based Cryptosystems and Signature Schemes,” Proceedings of CRYPTO 84 on Advances in Cryptology, Santa Barbara, 19-22 August 1984, pp. 47- 53.
- X. Chen, F. Zhang and K. Kim, “A New ID-Based Group Signature Scheme from Bilinear Pairings,” 2003. http://eprint.iacr.org/2003/116.2003
- S. Han, J. Wang and W. Liu1, “An Efficient IdentityBased Group Signature Scheme over Elliptic Curves,” Proceedings of the ECUMN 2004, Porto, 25-27 October 2004, pp. 417-429.
- Z. Tan and Z. Liu, “A Novel Identity-Based Group Signature Scheme from Bilinear Maps,” MM Research Preprints, 2003, pp. 250-255.
- J. Cha and J. Cheon, “An Identity-Based Signature from Gap Diffie-Hellman Groups,” Proceedings of the PKC 2003, Miami, 6-8 January 2003, pp. 18-30.
- A. Lysyanskaya and Z. Ramzan, “Group Blind Digital Signatures: A Scalable Solutionto Electronic Cash,” Proceedings of the Financial Cryptography: Second International Conference, FC’98, Anguilla, 23-25 February 1998, pp. 184-197.
- T. Nakanishi, N. Haruna and Y. Sugiyama, “Unlinkable Electronic Couponprotocol with Anonymity Control,” Proceedings of the International Workshop on Information Security (ISW 99), Kuala Lumpur, 6-7 November 1999, pp. 37-46.
- J. Traor´e, “Group Signatures and Their Relevance to Privacy-Protecting Off-Line Electronic Cash Systems,” Proceedings of the Australasian Conference on Information Security and Privacy (ACISP 99), Wollongong, 7-9 April 1999, pp. 228-243.
- D. B. Johnson and A. J. Menezes, “Elliptic Curve DSA (ECDSA): An Enhanced DSA,” 2000. http://www.certicom.com
- D. Hankerson, A. Menezes and S. Vanstone, “Guide to Elliptic Curve Cryptography,” Springer-Verlag, New York, 2004.
- J. Cha and J. Cheon, “An Identity-Based Signature from Gap DiffieHellman Groups,” Proceedings of the PKC 2003, Miami, 6-9 January 2003, pp. 18-30.

