Circuits and Systems
Vol.4 No.2(2013), Article ID:29905,4 pages DOI:10.4236/cs.2013.42031
A Grounded Capacitor Differentiator Using Current Feedback Amplifier
Department of Electronic Engineering, Chung Yuan Christian University, Chung-Li, Taiwan
Email: jwhorng@cycu.edu.tw
Copyright © 2013 Jiun-Wei Horng, Guang-Ting Huang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 14, 2013; revised February 13, 2013; accepted February 20, 2013
Keywords: Active Differentiator; Current-Feedback Amplifier; Current Conveyor; Analog Signal Processing
ABSTRACT
A new non-inverting RC active differentiator network base on a current feedback amplifier and using a grounded capacitor is described. Small time constant can be achieved by adjusting a single grounded resistor. Because the output impedance of the CFA is very low, the output terminal of the proposed circuit can be directly connected to the next stage. Experimental results that confirm theoretical analysis are presented.
1. Introduction
Active RC differentiator networks are useful for a number of applications in the areas of electronic signal processing or signal conditioning [1-10]. Several RC differentiator networks based on conventional operational amplifiers (Op Amps) were proposed [1-5]. However, the finite gain bandwidth product of these Op Amps will limit the accuracy and the operating frequency range. Current feedback amplifiers (CFAs) can provide not only constant bandwidth independent of closed-loop gain but also high slew-rate capability [11]. Thus, it is beneficial to use the current-feedback amplifier as a basic building block to realize analogue signal processing circuits [12- 19]. Note that, the CFA is equivalent to second-generation current conveyor (CCII) with a voltage buffer [11]. On the other hand, circuits that employ only grounded capacitors are beneficial from the point of view of integrated circuit implementation [20].
Patranabis and Ghosh [6] proposed a generic configuration for realizing integrators and differentiators by using one CCII, one grounded capacitor and some resistors. Liu and Hwang [7] proposed five generic configurations for realizing dual-input differentiators using two CCIIs. However, the time constants of the differentiators presented in Figure 1 of [6] cannot be independently adjusted by grounded resistor. Moreover, because the output impedances of these circuits [6,7] are not small, other buffering devices are needed while cascade these circuits to the next stage. Lee and Liu [8] proposed another
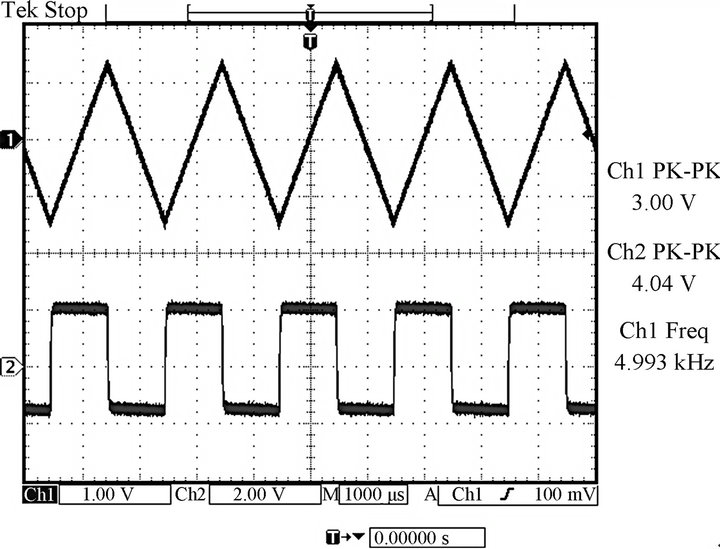
Figure 1. Input and output waveforms of the proposed differentiator.
dual-input differentiator circuit by using one plus-type CFA, one minus-type CFA, five resistors and one floating capacitor. In 2001, Lee and Liu [9] proposed a differentiator circuit by using one minus-type CFA, five resistors and one floating capacitor. In 2003, Nagaria et al. [10] proposed a differentiator circuit by using one plustype CFA, one multiplier, two resistors and one floating capacitor. However, because the differentiator networks in [7-10] employ floating capacitors, these circuits are not ideal for integrated circuit implementation. Furthermore, the differentiators in [8,9] employ minus-type CFAs, since the minus-type CFAs are not comercially available, one minus-type CFA must be implemented by two plus-type CFAs in practical realizations.
In this paper, a new differentiator network by using one plus-type CFA, five resistors and one grounded capacitor is presented. By adjusting the single grounded resistor, small time constant can be achieved. With respect to the CCII based circuits in [6,7], the proposed circuit has the advantage of low output impedance. With respect to the CFA based circuits in [8-10], the proposed circuit uses only grounded capacitor. Moreover, the proposed circuit uses only one plus-type CFA that is simpler than the minus-type CFAs in [8,9].
2. Circuit Description
The circuit symbol of a plus-type CFA is shown in Figure 2. This circuit is equivalent to a plus-type CCII with a voltage buffer [11]. Its characteristic can be modeled as
 (1)
(1)
The proposed differentiator network comprises only one plus-type CFA, five resistors and one grounded capacitor is shown in Figure 3. The use of grounded capacitor is beneficial for integrated circuit implementation [20]. Circuit analysis yields the output voltage as
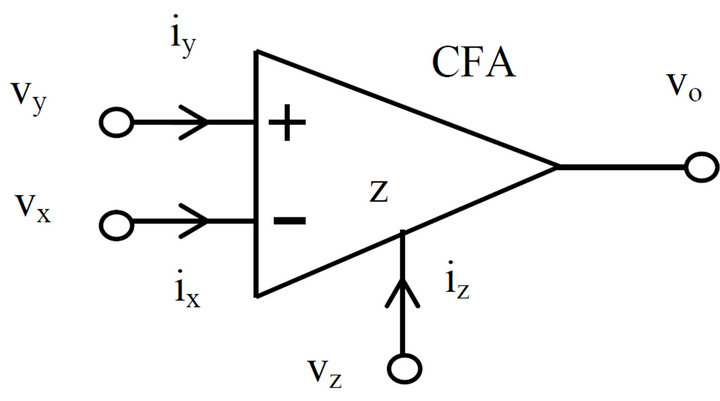
Figure 2. Circuit symbol of current-feedback amplifier.
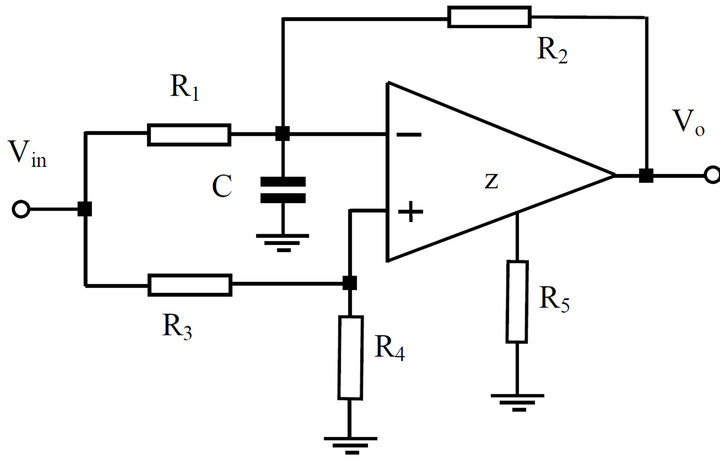
Figure 3. The proposed active RC differentiator circuit.
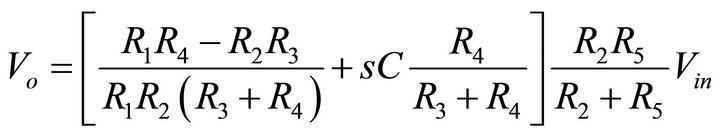 (2)
(2)
Thus, the condition for an ideal non-inverting differentiation function realization is
 (3)
(3)
Under the condition of Equation (3), Equation (2) can be rewritten as
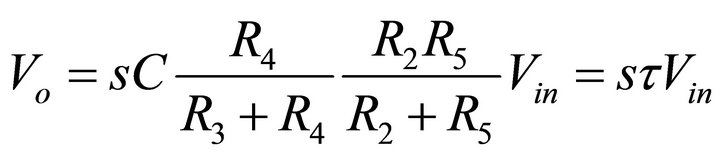 (4)
(4)
where  (5)
(5)
The grounded resistor R5 can independently control the time constant of this differentiator. Small time constant can be achieved by choosing small R5. Because the output impedance of the CFA (terminal vo) is very small, the output terminal of the differentiator can be directly connected to the next stage.
3. Non-Ideal Effects
Taking into account the non-ideal CFA, namely iz = α(s) ix, vx = β(s)vy and vo = γ(s)vz, where α(s) is the current transfers from ix terminal to iz terminal, β(s) is the voltage transfers from vy terminal to vx terminal, and γ(s) is the voltage transfers from vz terminal to vo terminal. The α(s), β(s) and γ(s) can be approximated by first-order lowpass functions, which can be considered to have a unity value for frequency much less than their corner frequencies. By assuming the circuit is working at frequencies much less than the corner frequencies of α(s), β(s) and γ(s), namely, 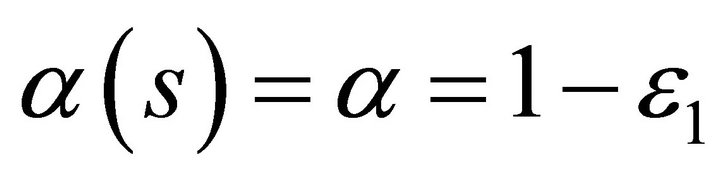 and
and  denotes the current tracking error of a CFA,
denotes the current tracking error of a CFA, 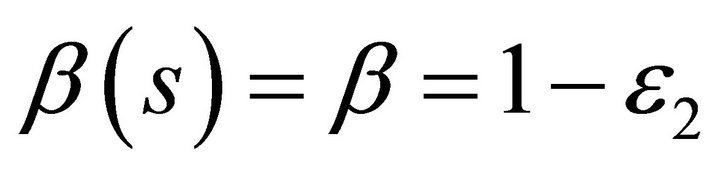 and
and 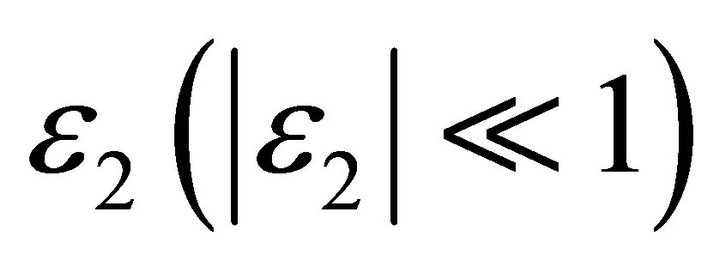 is the input voltage tracking error, and
is the input voltage tracking error, and 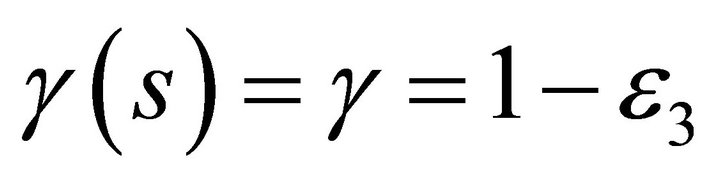 and
and  is the output voltage tracking error. The output voltage Vo becomes
is the output voltage tracking error. The output voltage Vo becomes
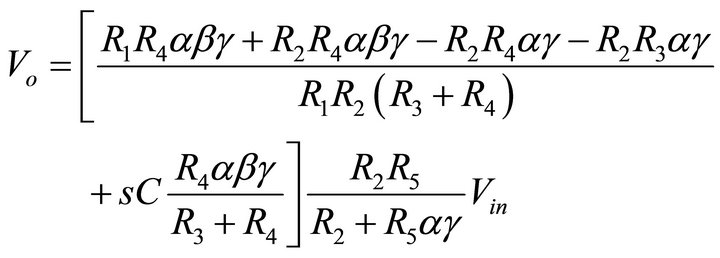 (6)
(6)
Thus, the condition for the non-inverting differentiator can be rewritten as
 (7)
(7)
Under the condition of Equation (7), Equation (6) can be rewritten as
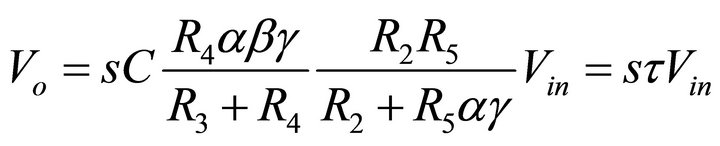 (8)
(8)
where 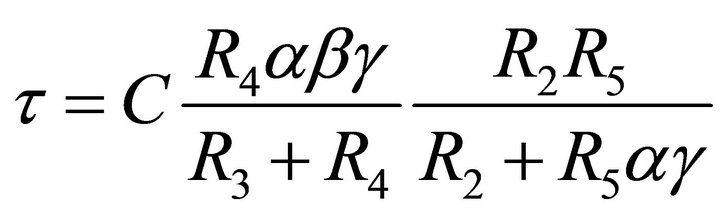 (9)
(9)
From Equations (6)-(9), the tracking errors slightly change the realization condition and time constant of the differentiator. However, the realization condition of the proposed differentiator can still be independently tuned by the resistor R1 and the time constant can also be independently controllable by another resistor R5.
4. Experimental Results
Experiments were made to verify the feasibility of the proposed circuit. The plus-type CFA was implemented using one AD844. The proposed differentiator was built with C = 20 nF, R1 = R2 = R3 = R4 = 19.97 kΩ and R5 = 10.03 kΩ. The triangular waveform with 3 V peak-topeak and 4.993 kHz was applied to Vin (channel 1). The output waveform is shown in Figure 1 (channel 2). Its operating frequency range is from 500 Hz to 35 kHz with a phase error < 10˚. The phase error may be due to the ignored non-idealities of the CFA.
5. Conclusion
An active RC differentiator network with independently tunable small time constant has been presented. The proposed circuit employs only one plus-type CFA, five resistors and one grounded capacitor. The use of only grounded capacitor is ideal for integrated circuit implementation. Because the output impedance of the CFA is very small, the differentiator can be directly connected to the next stage. Experimental results were shown to demonstrate the feasibility of the proposed circuit.
6. Acknowledgements
The authors would like to thank Mr. Guang-Yuan Chen for his assistance in the experiments. The National Science Council, Taiwan supported this work under grant number NSC 101-2221-E-033-070.
REFERENCES
- S. Venkateswaran and K. Radhakrishna Rao, “Multifunction Active RC Circuit with Grounded Capacitors,” Electronics Letters, Vol. 7, No. 24, 1971, pp. 708-710. doi:10.1049/el:19710486
- D. H. Horrocks, “A Non-Inverting Differentiator Using a Single Operational Amplifier,” International Journal of Electronics, Vol. 37, No. 3, 1974, pp. 433-434. doi:10.1080/00207217408900541
- U. C. Sarker, S. K. Sanyal and R. Nandi, “A High-Quality Dual-Input Differentiator,” IEEE Transactions on Instrumentation and Measurement, Vol. 39, No. 5, 1990, pp. 726-729. doi:10.1109/19.58615
- M. A. Al-Alaoui, “A State Variable Approach to Designing a Resistive Input, Low Noise, Noninverting Differentiator,” IEEE Transactions on Instrumentation and Measurement, Vol. 38, 1989, pp. 920-922. doi:10.1109/19.31015
- M. A. Al-Alaoui, “A Novel Differential Differentiator,” IEEE Transactions on Instrumentation and Measurement, Vol. 40, No. 5, 1991, pp. 826-830. doi:10.1109/19.106305
- D. Patranabis and D. K. Ghosh, “Integrators and Differentiators with Current Conveyors,” IEEE Transactions on Circuits and Systems, Vol. 31, No. 6, 1984, pp. 567-569. doi:10.1109/TCS.1984.1085535
- S. I. Liu and Y. S. Hwang, “Dual-Input Differentiators and Integrators with Tunable Time Constants Using Current Conveyors,” IEEE Transactions on Instrumentation and Measurement, Vol. 43, No. 4, 1994, pp. 650-654. doi:10.1109/19.310164
- J. L. Lee and S. I. Liu, “Dual-Input RC Integrator and Differentiator with Tuneable Time Constants Using Current Feedback Amplifiers,” Electronics Letters, Vol. 35, No. 22, 1999, pp. 1910-1911. doi:10.1049/el:19991316
- J. L. Lee and S. I. Liu, “Integrator and Differentiator with Time Constant Multiplication Using Current Feedback Amplifier”, Electronics Letters, Vol. 37, No. 6, 2001, pp. 331-333. doi:10.1049/el:20010252
- R. K. Nagaria, A. Goswami, P. Venkateswaran, S. K. Sanyal and R. Nandi, “Voltage Controlled Integrators/ Differentiators Using Current Feedback Amplifier,” International Symposium on Signals, Circuits and Systems, Vol. 2, 2003, pp. 573-576.
- J. A. Svoboda, L. Mcgory and S. Webb, “Applications of a Commercially Available Current Conveyor,” International Journal of Electronics, Vol. 70, No. 1, 1991, pp. 159-164. doi:10.1080/00207219108921266
- A. M. Soliman, “Applications of Current Feedback Operational Amplifiers,” Analog Integrated Circuits and Signal Processing, Vol. 11, No. 3, 1996, pp. 265-302. doi:10.1007/BF00240490
- J. W. Horng, C. K. Chang and J. M. Chu, “Voltage-Mode Universal Biquadratic Filter Using Single Current-Feedback Amplifier,” IEICE Transactions on Fundamentals, Vol. E85-A, No. 8, 2002, pp. 1970-1973.
- V. K. Singh, A. K. Singh, D. R. Bhaskar and R. Senani, “New Universal Biquads Employing CFOAs,” IEEE Transactions on Circuits and Systems-II: Express Briefs, Vol. 53, No. 11, 2006, pp. 1299-1303.
- D. R. Bhaskar and R. Senani, “New CFOA-Based Single- Element-Controlled Sinusoidal Oscillators,” IEEE Transactions on Instrumentation and Measurement, Vol. 55, No. 6, 2006, pp. 2014-2021. doi:10.1109/TIM.2006.884139
- F. Kacar and H. Kuntman, “CFOA-Based Lossless and Lossy Inductance Simulators,” Radioengineering, Vol. 20, No. 3, 2011, pp. 627-631.
- H. Y. Wang, S. H. Chang, T. Y. Yang and P. Y. Tsai, “A Novel Multifunction CFOA-Based Inverse Filter,” Circuits and Systems, Vol. 2, No. 1, 2011, pp. 14-17. doi:10.4236/cs.2011.21003
- J. W. Horng, C. L. Hou, W. S. Huang and D. Y. Yang, “Voltage/Current-Mode Multifunction Filters Using One Current Feedback Amplifier and Grounded Capacitors,” Circuits and Systems, Vol. 2, No. 2, 2011, pp. 60-64. doi:10.4236/cs.2011.22010
- A. Lahiri, W. Jaikla and M. Siripruchyanun, “First CFOABased Explicit-Current-Output Quadrature Sinusoidal Oscillators Using Grounded Capacitors,” International Journal of Electronics, Vol. 100, No. 2, 2013, pp. 259-273. doi:10.1080/00207217.2012.692632
- M. Bhushan and R. W. Newcomb, “Grounding of Capacitors in Integrated Circuits,” Electronic Letters, Vol. 3, No. 4, 1967, pp. 148-149. doi:10.1049/el:19670114

