Received 14 October 2015; accepted 24 November 2015; published 27 November 2015

ABSTRACT

Using the divergence theorem and the coordinate transformation theory for the general Fickian second law, fundamental diffusion problems are investigated. As a result, the new findings are obtained as follows. The unified diffusion theory is reasonably established, including a self-diffusion theory and an N (N ³ 2) elements system interdiffusion one. The Fickian first law is incomplete without a constant diffusion flux corresponding to the Brown motion in the localized space. The cause of Kirkendall effect and the nonexistence of intrinsic diffusion concept are theoretically revealed. In the parabolic space, an elegant analytical method of the diffusion equation is mathematically established, including a nonlinear diffusion equation. From the Schrödinger equation and the diffusion equation, the universal expression of diffusivity proportional to the Planck constant is reasonably obtained. The material wave equation proposed by de Broglie is also derived in relation to the Brown motion. The fundamental diffusion theories discussed here will be highly useful as a standard theory for the basic study of actual interdiffusion problems such as an alloy, a compound semiconductor, a multilayer thin film, and a microstructure material.

Keywords:

Brown Particle, Boltzmann Factor, Markov Process, Parabolic Law, Error Function

1. Introduction

First of all, we state that the basic diffusion equation of the general nonlinear Fickian second law is discussed in accordance with the fundamental mathematical physics in the present work. The extended diffusion equations in detail are not thus discussed. Nevertheless, the new findings, which are extremely dominant in the diffusion study, are reasonably obtained. In the diffusion history, the problems relevant to the coordinate transformation of diffusion equation had not been discussed in accordance with the Gauss divergence theorem until recently. That is just a reason why the new diffusion theories are discussed in the present study. It will be gradually clarified in the text that the coordinate transformation theory is essentially indispensable for the diffusion study. It is obvious that analyzing the extended diffusion equation must be based on the fundamental diffusion theory. The new fundamental findings different from the existing diffusion theories obtained here will thus exert a great influence on the actual diffusion problems in detail, just because of fundamental ones.

A great many phenomena in various science fields are expressed by using the well-known evolution equations. The diffusion equation is one of them and mathematically corresponds to the Markov process in relation to the normal distribution rule [1] . In other words, the motion of diffusion particles corresponds to the well-known Brown movement satisfying the parabolic law [2] [3] . It is widely accepted that the Brown problem is a general term of investigating subjects in various science fields relevant to the Markov process, such as material science, information science, life science, and social science [4] - [9] .

In physics, we can also understand the diffusion equation in accordance with the Gauss divergence theorem [10] . If we apply the divergence theorem to the diffusion problem for a material under the condition of no sink and source of the material, it is found that the material conservation law is valid for the diffusion particles, regardless of a thermodynamic state of material. The diffusion equation is also called “the continuous equation” and is extremely fundamental one in physics. In history, the heat conduction equation, which is mathematically equivalent to the diffusion equation, was proposed by Fourier, regardless of the Markov process and the divergence theorem [11] .

In accordance with the industrial requirement, the solid materials, such as alloys, semiconductors, and multilayer materials, have been widely fabricated. The heat treatment is indispensable for their fabrication processes then. The migration of particles in a material is caused by the heat treatment. In relation to the migration of their particles, the diffusion problems of various solid materials have been thus widely investigated [12] . Therefore, the diffusion problem is a fundamental study subject in the materials science including the cases of liquid and gas states.

In the present work, the fundamental problems of the general Fickian second law where a driving force affects the diffusion system are discussed in accordance with the mathematical theory. The present analytical method is applicable to interdiffusion problems of an N elements system of every material in an arbitrary thermodynamic state. Although the physical validity of the present method is investigated by using the diffusion data concerning the solid metals, the mathematical generality discussed here is still kept.

The heat conduction equation proposed by Fourier in 1822 has been applied to investigating the temperature distribution in materials [11] . In 1827, the so-called Brown motion was found, where the self-diffusion of water was visualized by pollen micro particle motions [2] [3] . In 1855, Fick applied the heat conduction equation to diffusion phenomena as it had been [13] . Nevertheless, the Brown motion had not been recognized as a diffusion problem until the Einstein theory of Brown motion in 1905, although it was a typical diffusion problem [3] .

Although the concentration of diffusion particles is a real quantity in physics, the temperature is a thermodynamic state quantity. As far as the shape of heat conduction material is unchangeable during a thermal treatment, the coordinate system of heat conduction equation set in a material is a fixed one, since the coordinate system is not influenced by variations of the material internal structure. On the other hand, strictly speaking, the coordinate system of diffusion equation set in the diffusion field (solvent) is a moving one, since it is generally influenced by such variations.

When the Fickian first and second laws (F1 law and F2 law) were proposed, the Gauss divergence theorem had been already reported in 1840 [10] . Nevertheless, the problem of coordinate system of diffusion equation was not mathematically investigated in accordance with the divergence theorem.

In general, it is indispensable for understanding the diffusion problems to discuss their coordinate systems, since it is, strictly speaking, considered that the diffusion particles, solvent particles and also the diffusion region space simultaneously move against the experimentation system in the diffusion region outside.

Although the Fickian laws were still widely applied to various diffusion phenomena as essential equations in physics, the problem between coordinate systems was not discussed. Recently, the diffusion equation was thus mathematically investigated in accordance with the divergence theorem and the coordinate transformation theory [14] - [16] . It is revealed in the text that the diffusion flux should be determined by taking account of the concerned coordinate system of diffusion equation.

Using the corresponding diffusion flux to the coordinate system of diffusion equation for interdiffusion, one way diffusion, impurity diffusion and self-diffusion, they are uniformly discussed in the text. As a result, we found that the foundation of diffusion problems is included in interdiffusion problems. The interdiffusion theory of an 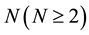elements system applicable to every material was thus reasonably established [16] . In the analysis of interdiffusion problems, the only difference between a binary system and an N elements system is whether the solvent material is one element or 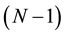elements.

The coordinate transformation theory reveals that the corresponding F1 law to the F2 law is incomplete without a constant diffusion flux relevant to the Brown motion in the localized space. Further, it was also found that the Kirkendall effect (K effect) is caused by a shift between the coordinate systems of the diffusion equation like the Doppler effect relevant to a wave equation is caused by a shift between the fixed coordinate system and the moving one for the wave equation [14] - [17] . At the same time, this means that the concept of intrinsic diffusion is unnecessary for understanding the K effect.

As far as the sink and source of a material is nonexistent in the diffusion system, the Gauss divergence theory shows that the general F2 law satisfies the material conservation law even if a driving force affects the diffusion system. The driving force affects entropy and jump frequencies of diffusion particles in the material. The influence of a driving force is thus all incorporated into the diffusivity of diffusion equation then. In the existing diffusion theory, the diffusion fluxes influenced by a driving force are discussed incorporating not influence of both entropy and jump frequencies but only that of jump frequencies on the diffusivity into them, for example such as a drift velocity. However, such concept as a drift velocity is not necessary for analyzing the diffusion equation, since we can solve a nonlinear diffusion equation in accordance with the fundamental theory in the mathematical physics, regardless of the discussion about diffusion fluxes.

The diffusivity is obtained from the Taylor expansion of a probability density function, satisfying the parabolic law [3] . This indicates that the analysis of diffusion equation is essentially possible in the parabolic space. The diffusivity is defined by an interaction between a diffusion particle and the diffusion field near the diffusion particle itself. This indicates that the diffusivity should be essentially investigated in the quantum mechanics, since the behavior of a micro particle should be investigated by analyzing the Schrödinger Equation (S equation) [18] .

Based on the suggestions mentioned above, the elegant analytical method in the parabolic space is reasonably established in the text [19] [20] . As a result, the solutions of the Boltzmann transformation equation for nonlinear interdiffusion phenomena were, for the first time, obtained as analytical expressions in the parabolic space [21] .

From applying the diffusion equation to a problem of diffusion elementary process, we derived the S equation [22] . It is revealed in the text that the diffusivity corresponds to the angular momentum operator in the quantum mechanics. As a result, the universal expression of diffusivity, which is applicable to every material in an arbitrary thermodynamic state, was obtained in proportional to the Planck constant.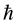

It was also found that the well-known material wave relation proposed by de Broglie in 1923, which is the most fundamental one in materials science, is obtained from a relation between diffusivity expressions [23] . This gives evidence for the theory discussed in the present study.

In the present work, we review the fundamental diffusion theories relevant to the general F2 law, where they are systematically reframed in points of view different from the previous works, adding some new discussions to them. The new findings obtained here will be widely applicable to fundamental problems as a standard theory in various actual diffusion phenomena.

2. Fundamental Theory of Diffusion Equation

As far as a material is conserved in the given region, the divergence theory shows that the diffusion equation is applicable to diffusion phenomena of every material in an arbitrary thermodynamic state. The diffusion information of a material, such as crystal material or amorphous material, and/or solid, liquid and gas states, is all incorporated into the diffusivity in the given diffusion equation. The diffusion equation with such an arbitrary diffusivity is thus investigated in the following.

In the present study, an abbreviate differential notation for an arbitrary independent variable and the well- known Dirac’s bracket notation for an arbitrary vector are used as follows [24] ;

If an operator Q is Hermite one, 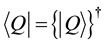is valid in the Hermite conjugate. Here, the notation 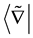is thus defined as because of.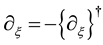

2.1. Diffusion Equation

The function is defined as a normalized concentration where a diffusion particle in the initial state 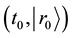exists in the time and space state 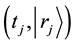after j times jumps. A diffusion particle moves at random. It is, therefore, considered that the jump frequency and jump displacement 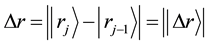are equivalent in probability to their mean values of all diffusion particles in the collective system.

Since it is also considered that the probability of diffusion-jump from the state of to is equivalent to one from the same state to in the isotropic space, the relation of

(2-1)

is thus valid. The Taylor expansion of both sides of Equation (2-1) yields

(2-2)

(2-3)

The substitution of Equations (2-2) and (2-3) into Equation (2-1) gives

(2-4)

Since the averaged and are physically finite, it is considered that becomes a constant value given by

(2-5)

satisfying the well-known parabolic law [3] . Substituting Equations (2-5) into Equations (2-4), the diffusion equation is obtained as

(2-6)

where is rewritten as D when the diffusion-jump direction is not isotropic resulting from the existence of a driving force in the diffusion system.

The existence of a driving force affects diffusivity and the diffusivity D becomes a function of the independent variables t and. In that case, Equation (2-6) gives the diffusion flux yielding

(2-7)

where is a diffusivity caused by a driving force.

On the other hand, using a drift velocity caused by a driving force F, the approximate diffusion flux is expressed as

(2-8)

in the usual textbooks (see Appendix A) [25] . However, the diffusion flux discussed here is different from one given by

(2-9)

In the present study, the discussion about diffusion fluxes is not necessary for analyzing the diffusion equation, since we can solve the nonlinear diffusion equation in accordance with the fundamental theory in the mathematical physics, regardless of diffusion fluxes.

In the following, therefore, Equation (2-6) is directly solved in accordance with the mathematical physics. It is in the nature of things that its analytical method is applicable to the diffusion problems relevant to a driving force then.

For a collective system composed of N elements in the region within the closed surface, the divergence theorem yields

(2-10)

where and are a concentration and a diffusivity for an element j under the condition of no sink and source of the element. The integral calculation of in Equation (2-10) means an inflow flux from the surface outside through the surface element, and y and z are then accepted as constant values because of the multiple integral calculation. Therefore, Equation (2-10) yields the diffusion equation of

(2-11)

in the diffusion field. Defining the outflow flux as a plus value, the diffusion flux is

(2-12)

In mathematics, Equation (2-12) yields

for (2-13)

where is the F1 law and is an integral constant against x. In physics, means a movement of a diffusion region space caused by a movement of the diffusion field. In the coordinate system of diffusion region inside, it should be thus physically accepted as. However, must be taken into account in the coordinate system of diffusion region outside. The intrinsic diffusion flux independent of the time and space is relevant to the Brown motion in the localized space. It plays an important role for understanding a self-diffusion mechanism.

2.2. Coordinate System of Diffusion Equation

As discussed later, the unified theory of diffusion problems shows that the foundation of diffusion is in the interdiffusion problems. In the interdiffusion problems, solvent particles as well as diffusion particles move in the diffusion region space. When a micro particle in a material jumps from a site M to an interstice space N, if we call such an interstice space “micro hole” including a vacancy in case of a crystal material, the micro hole of site N is annihilated and a new micro hole is generated at the site M after jumping.

The diffusion region space interacts with the space of diffusion system outside in accordance with the annihilation and/or generation of micro holes like the diffusion system becomes a thermal equilibrium state resulting from an antinomy between the principle of increase of entropy and that of minimum of free energy.

The coordinate system of the basic diffusion equation must be set in the diffusion field, since the diffusivity depends on an interaction between a diffusion particle and the diffusion field near the diffusion particle itself. In general, therefore, the diffusion problem should be investigated among three coordinate systems, where the origins of two coordinate systems are a point P of the coordinate system set in the diffusion field (solvent) and a point Q of the coordinate system set in the diffusion region space composed of micro holes and the third origin is a point R of the coordinate system set in the diffusion region outside.

In the present work, we investigate an interdiffusion problem applicable to every material in an arbitrary thermodynamic state. It is thus investigated using the original diffusion equation (2-11) of the coordinate system and the diffusion equations transformed into the coordinate systems of and under the condition of.

The origins P and Q are set at a point of solvent material and at a point of micro holes on the initial interface of a diffusion couple. The origin R is set at a point of the diffusion system outside. The x axis is perpendicular to the interface then. The axis and also axis are parallel to the x axis under the condition of at.

It is generally considered that P and Q move with a velocity and with a velocity against R, respectively and also that P moves with a velocity against Q, including a possibility of. The relation among these velocities of

(2-14)

must be physically valid.

Hereafter, we use the suffix P, Q and R for a physical quantity relevant to, and. Equation (2-13) is thus rewritten as

for . (2-13)

When the coordinate origin of moves from that of with a velocity, the relations of

, for (2-15)

are valid under the condition of at. The relations of

, (2-16)

between differential operators are obtained then.

Using Equation (2-16) for Equation (2-11), the diffusion equations of is obtained as

(2-17)

where and. Equation (2-17) leads to the diffusion flux of

, (2-18)

since is in the diffusion region inside.

In the same manner of the above, the diffusion equation of is obtained as

(2-19)

Since is in the diffusion region outside, the diffusion flux becomes

, , (2-20)

where is the diffusion flux of micro holes caused by the movement of the diffusion field against.

3. Interdiffusion Problems

The interdiffusion problems of an N elements system in a diffusion couple composed of arbitrary materials A and B are discussed as follows.

In an amorphous material, we then estimate a specimen cross section perpendicular to the x axis where each cross section interval l corresponds to the averaged jump distance in the solid state or to the averaged collision distance in the gas or liquid state. In a crystal material, we estimate the jump distance l between the nearest neighbor crystal cross sections perpendicular to the x axis.

When materials A and B are in the solid state during a thermal diffusion, we conceive that the cross section S of the material A is uniform and equal to that of the material B. If materials A and B are in the fluid state, we conceive that they are in the receptacle corresponding to the case of solid materials. The interface of diffusion couple between materials A and B is smoothly joined. In that case, the origin of coordinate system is set at a point on the initial interface in the diffusion field and the orientation of x axis is defined as.

The material A is composed of N elements and we define the normalized concentration for in the initial state, also including a possibility of for. The normalized concentration in the material B is similarly defined as.

The concentration and diffusivity of an element j are and at a diffusion time t in the diffusion region. The boundary values of concentration are and.

The remained elements are considered to be a solvent, also including a possibility where becomes a solvent itself in accordance with a given diffusion system.

The cross section of diffusion system is uniform and the shape variation of diffusion couple is usually negligible during the thermal diffusion. In that case, the relation of normalized concentrations yielding

(3-1)

is usually accepted on each cross section between. Here, Equation (3-1) is physically valid regardless of a coordinate system.

3.1. Correlation of Diffusion Fluxes with Coordinate Systems

Equations (2-17) and (3-1) yield

(3-2)

because of. In mathematics, the partial differential equation (3-2) of and is rewritten as

using an arbitrary function of because of. Here, means a diffusion flux dependent on and. On the other hand, means a diffusion flux only dependent only on. Therefore, Equation (3-2) means for an arbitrary. The interdiffusion coefficient is thus defined as

(3-3)

in the diffusion region. We can easily confirm that Equation (3-3) does not depend on a coordinate system. Their boundary values are thus obtained as

and (3-4)

Using Equation (3-3) for the F1 law, the following relation of

(3-5)

is valid regardless of a coordinate system. The relation of

(3-6)

is also valid as discussed later in the self-diffusion theory.

Using Equations (3-5) and (3-6) for Equation (2-20), the relation of

for (3-7)

is obtained. Here, means the total diffusion flux of micro holes against the origin of. In that situation, is valid in the present coordinate system because of, using a velocity of the origin of against the origin of. Equation (3-7) is thus rewritten as

(3-7)

In the same manner, the following relations

(3-8)

(3-9)

are also obtained from Equations (2-13) and (2-18). Equations (3-7)-(3-9) show that the diffusion flux independent of the space coordinate corresponds to the velocity between the coordinate systems. The relation of

(3-10)

must be physically valid because of. Equation (3-10) then yields the previous equation of

(2-14)

because of Equations (3-7)-(3-10).

In the following, is investigated by using the concentration difference and the diffusion junction depth between and. Taking account of their concentration gradients, the flux of diffusion field for an element k () is obtained as

(3-11)

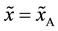
where the suffix means if or if and is tentatively adopted. Here, is adopted instead of as an approximate equation because of.

Equation (3-11) yields

(3-12)

Equation (3-12) shows the movement of against. Substituting Equation (3-12) into Equation (2-14) yields

(3-13)

because of.

3.2. Kirkendall Effect in Interdiffusion Problems

In the metallurgy field, the interface of is the so-called Matano interface (M interface) and that of is the Kirkendall interface (K interface) [17] [26] . In 1947, Kirkendall found in the binary system interdiffusion experimentation that the inert marker set on the K interface in the initial state moves from the M interface during a thermal diffusion and also that the M interface does not move during thermal diffusion, i.e.,. Since then, the displacement between the M interface and the K interface has been called the Kirkendall effect (K effect). Using an experimental value m, the K effect is obtained as

(3-14)

regardless of the space coordinate and it satisfies the parabolic law.

As far as the material shape of a diffusion couple is unchangeable, the K effect also reveals that the total quantity of element I diffusing across the K interface is different from that of element II. In other words, for the micro hole concentration and its thermal equilibrium value between, the relation of

is valid between if is valid between during thermal diffusion, and vice versa. The value of becomes gradually zero in accordance with the thermodynamic principle.

In the binary system interdiffusion problems, the F1 law shows that the relation of

is valid because of, and is valid then for an interdiffusion coefficient. On the other hand, it was also considered that the K effect is caused by a difference between the diffusion flux of element I and that of element II across the K interface. In other words, the so-called intrinsic diffusion coefficient satisfying the relation of was newly conceived to understand the K effect then.

However, the definition of diffusivity shows that the diffusivity is proportional to a statistical jump frequency of a diffusion particle at a point occupied by the diffusion particle itself. It is, therefore, physically difficult to accept what a diffusion particle of the element I or II has two diffusivities and or and at the same point in the concerned diffusion field under the condition of, since the statistical jump frequency value of a diffusion particle should be physically only one in the concerned diffusion field.

In the present diffusion theory, the behavior of micro holes is visualized by the movement of an inert marker in the diffusion region because of the inert characteristic. Therefore, the K effect means a shift between the coordinate systems and after the thermal diffusion. In other words, Equation (3-12) yields the displacement between the K interface and the M interface because of in accordance with the experimental results. The K effect is thus obtained as

(3-15)

satisfying the parabolic law.

The concept of intrinsic diffusion is thus unnecessary for understanding the K effect. Further, the K effect occurs in the interdiffusion not only of metal crystal but also of every material, since it is caused by a shift between the coordinate systems.

Equation (3-15) gives evidence that the K effect is caused by a shift between the coordinate systems, since it does not depend on the space coordinate. Substituting into Equation (3-15) and comparing it with Equation (3-14) give

(3-16)

Here, we must notice that is tentatively adopted in the diffusion junction depth in the present case. Therefore, the value in the relation of

must be concretely investigated so as to be suitable for the concerned interdiffusion problems, since the m value is experimentally obtained.

3.3. Unified Theory of Diffusion Problems

The experimental results show that the relation of is valid in the metallurgy field. This means that the shape of diffusion system is unchangeable before and after diffusion treatment. In that case, Equation (2-19) is thus rewritten as

(3-17)

Equation (3-17) of is thus equivalent to Equation (2-11) of. However, the diffusion flux of Equation (2-20) is rewritten as

,

In the following, various diffusion problems are systematically investigated by applying the diffusion flux of Equation (2-18) to them for, under the condition of

.

Equation (2-18) is then expressed as

(3-18)

(a) Interdiffusion:

Under the condition of, Equation (3-18) becomes

(i)

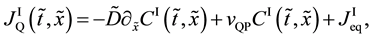
(ii).

(b) One-way diffusion:

Under the condition of, Equation (3-18) becomes

(i),

(ii).

(c) Impurity diffusion:

Under the condition of and, Equation (3-18) becomes

(i), (ii).

(d) Self-diffusion:

Under the condition of and, Equation (3-18) becomes

(i), (ii).

If we rewrite and as

and for

the above theory is still valid in the N elements system. In the diffusion problems, it was thus found that the behavior of diffusion region space plays an important role for understanding diffusion mechanisms.

3.4. Self-Diffusion Theory

The diffusivity expression of Equation (2-5) is valid regardless of pure materials [3] . The Einstein theory of Brown motion shows that the self-diffusion of water is visualized by diffusion phenomena of pollen micro particles. It is thus obvious that the self-diffusion occurs in a pure material. However, even if we apply the F2 law to the self-diffusion problems in a pure material, we cannot understand whether the self-diffusion occurs or not, since the concentration is unchangeable in the self-diffusion system.

Langevin theoretically investigated not the diffusion equation of collective motion but the motion equation of a diffusion particle with a viscosity resistance in a pure liquid material [27] . It was thus revealed that the diffusion particle moves in accordance with the normal distribution rule.

The theories of Langevin as well as Einstein are relevant to diffusion particles with a driving force in a pure material. In other words, the diffusion phenomena of a pure material itself are not directly investigated. However, Equation (2-5) shows that the self-diffusion occurs in a pure material even if there is no driving force in the diffusion system.

The self-diffusion problems have been also experimentally investigated as an impurity diffusion problem by using small quantities of the isotope material. Strictly speaking, however, the self-diffusion problems are obviously different from the impurity ones, as can be seen from the difference of (i) between (c) and (d) in Section 3.3.

As discussed in Section 2.1, the corresponding F 1 law to the F2 law is incomplete without the intrinsic diffusion flux. In the following, therefore, the self-diffusion problems of a pure material are directly investigated in accordance with the intrinsic diffusion flux, regardless of a driving force.

(1) Application of intrinsic diffusion flux to self-diffusion problem

We cannot experimentally confirm in Equation (2-13). The theory of Brown motion reveals that the diffusion phenomena occur in a material even if the macro concentration gradient is zero. The concept of intrinsic diffusion flux should be thus valid in a localized region space. The coordinate notation is, for convenience, used instead of and/or in the following.

Using the coordinate notation for the equation of relevant to the self-diffusion, the relation of

(3-19)

is obtained. If the concentration difference between and is defined as, Equation (3-19) is rewritten as

. (3-20)

Taking account of in Equation (3-19) and using Equation (2-5) for Equation (3-20), we have the relation of

(3-21)

Equation (3-21) shows an instantaneous concentration gradient in the localized time and space in the cause of the thermal fluctuation, even if the macro concentration gradient is zero. In other words, although the concentration gradient of a pure material is zero in macro behavior, it is nonzero in the minute region.

The behavior of concentration distribution in the local space is thus obtained as

(3-22)

In a pure material or a material in the thermal equilibrium state, Brownian particles move in accordance with Equation (3-22). If, the Brownian particles get a standstill state inconsistent with the Einstein theory of Brown motion. The intrinsic diffusion flux is thus an important concept in the fundamental diffusion theory. At the same time, the F1 law is incomplete without.

If we apply Equation (3-22) to the interdiffusion problems, the relation of

(3-23)

is valid in accordance with Equation (3-3). Equation (3-23) reveals that Equation (3-6) is valid because of

.

Using the notation for Equation (3-22), the concentration behavior of an element j in the thermal equilibrium state is expressed as

(3-24)

under the condition of in the localized space.

The diffusion region of self-diffusion problem of a pure material is, for convenience, divided into 2 regions as a binary system interdiffusion problem composed of a pure material I of and the pure material II of at. The diffusion region is between at a time then. The boundary values are for and for under the condition of.

Using Equation (3-24) for, the relations of

and (3-25)

are obtained, where. Equation (3-25) shows that and depend on and that is valid if. If we pay attention only to one side of or, it is obvious that the particle migration occurs via the random movement in the pure material. In other words, the diffusion occurs in a pure material, even if the macro concentration gradient is zero.

On the other hand, if we pay attention to both sides of and in Equation (3-25), seems to be valid, since we cannot actually distinguish their diffusion particles between whether they were ones of or in the initial state at.

(2) Physical meaning of intrinsic diffusion flux

Here, we estimate the value in the following. When the averaged jump distance or the averaged collision distance is written as l in a pure material, the substitution of and into Equation (3-25) yields

(3-26)

where is rewritten as and corresponds to the concentration gradient. It is considered that the order of l is several angstroms and the diffusion junction depth in a usual experiment is several micrometers. Therefore, the absolute value of is considerably small, compared with that of.

We cannot actually observe in the macro state because of Equation (3-6). However, we can approximately estimate it by using the relation of

where is a self-diffusion coefficient obtained from the tracer diffusion experiment for the concerned material, and l corresponds to the averaged jump distance or the averaged collision distance of the diffusion particle.

Equation (3-25) independent of means the time-averaged concentration profile caused by the Brown motion in the localized region space. The diffusion occurs even in a pure material, resulting from the chain reaction of instantaneous jumping of diffusion particle into micro holes caused by a thermal fluctuation in a material minute region. Equation (3-26) thus gives evidence that the Brown motion occurs in a pure material, even if an external force does not exist in the diffusion system.

From the historical point of view, if the F1 law were investigated at an early stage in accordance with the Gauss divergence theory, we might understand the Brown motion behavior before the Einstein theory [2] [3] [14] .

3.5. Diffusion Equation of Micro Holes

The space coordinate dependence of micro holes has been neglected in the diffusion theory mentioned above. In the metallurgy field, however, the experimental results of multiple markers show that their movements depend on the space coordinate in accordance with a marker position set in the initial diffusion couple [28] - [30] . This indicates that we must investigate the space coordinate dependence of micro holes in the diffusion study in detail, since the behavior of micro holes is visualized by the characteristic of inert markers.

In that case, Equation (3-1) is rewritten as

(3-27)

where is the normalized concentration of micro holes between. In general, there is a difference between the thermal equilibrium concentration of micro holes in the

material A and that of in the material B. When the difference is not negligible, the diffusion of micro holes occurs between.

For the thermal equilibrium concentration of micro holes in the diffusion region, the generation/annihilation term of the diffusion equation is expressed as

(3-28)

where is a chemical reaction constant. Taking account of Equation (3-28), the diffusion equation of micro holes is expressed as

(3-29)

where is a diffusivity of micro holes between.

The K-effect shows that the concentration of micro holes yields a supersaturated section and an unsaturated one in the diffusion region. Therefore, the averaged value of diffusion flux yielding

(3-30)

is considered to be negligible. We thus assume that the averaged contribution of the generation/annihilation term to the total diffusion flux in the diffusion system is negligible.

Here, if we integrate Equation (3-29) with respect to x, the diffusion flux relation of

(3-31)

is obtained by neglecting the contribution of Equation (3-30). In that case, Equations (3-27), (2-11) and (3-31) yield

under the condition of. Equation (3-3) is thus rewritten as

(3-32)

Equation (3-32) shows that we can accept a micro hole as a virtual diffusion particle.

The diffusion equation of in the N elements system interdiffusion becomes

(3-33)

using a common interdiffusion coefficient. It seems that Equation (3-33) is an independent equation of. However, it is not independent because of Equation (3-27). When we must investigate the influence of on the interdiffusion problems in detail, the diffusion equation of micro holes yielding

(3-34)

should be investigated. Equation (3-34) shows that the behavior of multiple markers depends on the time and space, since the obtained dependent on the time and space is visualized by the inert markers.

3.6. Application of Present Theory to Actual Diffusion Problems

Hereinbefore, we discussed some fundamental problems in the bulk diffusion of an ideal diffusion couple. The interdiffusion problems for a many elements system, such as an alloy, a compound semiconductor, a multilayer thin film, a microstructure material and so on, have been widely investigated [4] [31] - [34] . It is then fundamentally indispensable for the material science investigation to understand the N () elements system interdiffusion theory, since the migration of each element in a material occurs during the thermal treatment in the material fabrication process.

In the diffusion study history, the concept of intrinsic diffusion has been accepted in order to understand the K effect. In the existing theory of interdiffusion problems, the Darken equation derived from the intrinsic diffusion concept has been widely used for analyzing them [35] . The application of the Darken theory to a many elements system interdiffusion was extremely complicated even if it was a ternary elements system [36] . On the other hand, the simple relation among interdiffusion coefficients obtained here will be extremely useful for analyzing various interdiffusion problems.

As can be seen from the Appendix [B], we revealed that the Darken equation is not mathematically valid. It is also reported that the analytical results obtained by using the Darken equation are not consistent with the experimental results [37] . This fact is consistent with the present theory where there is no such concept of intrinsic diffusion in the diffusion phenomena.

Under the condition of Equation (3-27), therefore, it is necessary for analyzing a many elements system interdiffusion problem to solve the diffusion equations (3-33) and (3-34) of each element in accordance with their initial and boundary conditions. Here, it seems that these diffusion equations are independent of each other since they have a common interdiffusion coefficient. However, it is not independent because of Equation (3-27).

In the parabolic space discussed later, the analytical method of a nonlinear diffusion equation is established. The analytical solutions of Equations (4-48) and (4-49) are thus obtained then. Using them for analyzing each of the above equations, we can fundamentally solve an N () elements system interdiffusion problems. The theory discussed here is thus widely applicable to analyzing the fundamental problems of N elements system interdiffusion.

Since the present analytical theory is fundamental, it will be necessary for actual diffusion problems to modify it partly in accordance with the concerned problems like the Boyle Charles law for an ideal gas state is modified into the van der Waals equation in the actual case by incorporating an interaction between gas particles into it.

4. Analysis of Diffusion Equation in Parabolic Space

Einstein theoretically revealed that the Brownian particles randomly move in accordance with the parabolic law [3] . After that, it was experimentally confirmed by Perrin [38] . The parabolic law is universally shown in phenomena relevant to the normal distribution in a probability problem. The Brown problem is a study subject not only in the material science but also in the complex-system sciences relevant to the Markov process. Therefore, the analytical method of the Brown problem is mathematically common in various science fields.

The diffusion junction depth is directly relevant to the parabolic law. The diffusion problem is justifiably one of the Brown problems. This indicates that the solutions of diffusion problems are possible in the parabolic space. In other words, the analytical method discussed here is widely applicable to various Brown problems.

The F2 law is a continuous equation in the conservation system under the condition of no sink and source of diffusion particles, and it is one of the basic equations in physics. When the existence of a driving force or the sink and/or source of diffusion particles is negligible in a given diffusion system, Equation (2-6) is a parabolic type linear partial differential equation in the evolution equations. A lot of diffusion problems have been investigated by solving the diffusion equation of the time and space since 1855.

When the diffusivity depends on the concentration, the diffusivity becomes a function of the independent variables via the concentration. Even if the diffusion equation depends only on, the mathematical solutions of the nonlinear partial differential equation are almost impossible. A new analytical method in the parabolic space, which is extremely superior in analyzing to the existing ones, is discussed in the following.

4.1. Definition of Parabolic Space

For convenience, hereafter we use the coordinate notation transformed from the time and space into the parabolic space and they are correlated to and under the condition of. The relations of differential operators are obtained as

and

From the similar calculation, the differential operators in the parabolic space are obtained as

, (4-1)

where and because of the Hermite characteristic.

4.2. Diffusion Equation in Parabolic Space

If we directly apply Equation (4-1) to homogeneous partial differential Equation (2-6), the ellipse type differential equation is obtained as

(4-2)

where is physically valid in accordance with initial conditions [21] .

If for, Equation (4-2) becomes

(4-3)

which is the well-known Boltzmann transformation equation [21] . Further, it is rewritten as

(4-4)

The integral calculation of Equation (4-4) yields the integro-differential equation given by

(4-5)

where.

Here, if we define

(4-6)

the expression of

(4-7)

is obtained from using Equation (4-6) for Equation (4-5). Boltzmann transformation equation (4-3) is essentially equivalent to Equation (4-7).

We can accept Equation (4-7) as a diffusion flux in the parabolic space. The F1 law in the time and space cannot be used directly for analyzing a diffusion problem. However, the diffusion flux of Equation (4-7) is possible for analyzing a diffusion problem under the initial condition of Equation (4-6).

Further, as described later, the solutions of three dimensions problems in the parabolic space are obtained as a linear combination among the solutions of each one dimension diffusion problem. Therefore, Equation (4-7) is the most important essential equation relevant to the diffusion problems in the parabolic space.

In the parabolic space, the diffusion flux is defined as

(4-8)

where the component of is expressed as

for (4-9)

using for. Here, note that the initial and/or boundary condition is taken into account in the diffusion flux of Equation (4-6) or (4-8), although it is not taken into account in the F1 law.

Equation (4-8) in the parabolic space is equivalent to Equation (2-6) in the time and space. In mathematics, the following relation of

(4-10)

is generally valid, if the diffusivity D depends on independent variables. Equation (4-10) is extremely useful for analyzing a nonlinear diffusion equation.

4.3. Analytical Solutions of Linear Diffusion Equation

The utility of the present method is confirmed through solving some typical diffusion problems by concrete calculations. The mathematical method used here is also widely applicable to the Brown problems in various science fields.

(1) One dimension parabolic space

We first solve the linear diffusion equation given by

(4-11)

under the initial and boundary conditions of

(4-12)

The initial condition of Equation (4-12) is rewritten as

, (4-13)

in the parabolic space.

Substituting and into Equation (4-5), the initial value of

for (4-14)

is obtained. Using Equation (4-14) for Equation (4-5), the ordinary differential equation of

(4-15)

is obtained.

From the definition of the well-known error function, the general solution of Equation (4-15) is obtained as

(4-16)

where is an integral constant. Using the initial condition of Equation (4-13) for the general solution, the well-known solution is obtained as

(4-17)

In the analytical method in the parabolic space, the solution is thus easily obtained only by the elementary integral. It is, therefore, obvious that the present analytical method is extremely superior in analyzing diffusion equations to the existing methods.

(2) Parabolic space of n dimensions

In case of, Equation (4-9) is rewritten as

for

Using this equation for, the relation of

(4-18)

is obtained from Equation (4-8).

The operation of on both sides of Equation (4-18) yields the Poisson equation given by

(4-19)

We solve the ellipse type differential equation (4-19) corresponding to Equation (2-6) under the initial and boundary conditions in the following.

The initial and boundary values of Equation (2-6) given by

(4-20)

correspond to

(4-21)

in the parabolic space.

In the analysis of Equation (4-19), it is easily found that the equation of

(4-22)

satisfies Equation (4-19). In other words, Equation (4-22) is the particular solution of Equation (4-19). When the general solution of Laplace equation of

(4-23)

is obtained as, the general solution of Equation (4-19) is expressed as

(4-24)

in accordance with the mathematical theory.

Assuming the equation of

(4-25)

and using the variable separation method, the solution of Equation (4-23) is possible. Substituting Equation (4-25) into Equation (4-23), the relation of

is valid. In order to satisfy this equation for an arbitrary, the equation of

(4-26)

must be valid under the condition of

. (4-27)

Equation (4-27) yields for and solution of Equation (4-26) is expressed as

,

where are arbitrary constants. are determined by the initial condition. The well-known solution of Equation (4-19) is thus obtained as

. (4-28)

In case of and, substituting the solution of Equation (4-26) given by

into Equation (4-25), the general solution of Equation (4-23) is obtained as

(4-29)

where are arbitrary constants. However, there is no solution satisfying the initial and boundary conditions because of Equation (4-27). As a result, the general solution of Equation (4-23) is obtained as

(4-30)

under the condition of. Since the initial and boundary conditions yield, the present solution of Equation (4-23) is thus obtained as

where in accordance with the initial and boundary conditions.

The solution of Equation (4-19) is thus obtained as

(4-31)

If we use for, the solution is also presented as

(4-32)

The present study reveals that the particular solution is easily possible and the complementary function of Equation (4-19) is a constant value to satisfy the given initial and boundary conditions because of the singular characteristic of initial conditions. In other words, the diffusion behavior is incorporated into the inhomogeneous term of the Poisson equation. As a result, the solution is obtained as a linear combination of the error functions.

Although the diffusion problems have not ever been investigated in the parabolic space, it is obvious that the present solution is thus exceedingly simple and elegant, compared with the usual solution of

(4-33)

for, where.

(3) Analysis of inhomogeneous diffusion equation

The research subjects of linear diffusion phenomena in detail are often expressed by an inhomogeneous partial differential equation. Therefore, the application of the present method to those problems is investigated. Generally, such linear diffusion equations are expressed as

(4-34)

where L is the linear operator of

(4-35)

From the mathematical theory, the solution of inhomogeneous Equation (4-34) is obtained as

(4-36)

where is the complementary function, i.e., the general solution of homogeneous equation given by

(4-37)

and is a particular solution of

(4-38)

Equation (4-1) shows that the differential operators in the parabolic space are not able to apply to Equation (4-34). However, the linear operator in the parabolic space given by

(4-39)

is possible for analyzing the homogeneous Equation (4-37). In other words, we can obtain the complementary function by the present method. In order to obtain a solution of an inhomogeneous diffusion equation, therefore, we must obtain a particular solution by the existing methods.

4.4. Analytical Solutions of Nonlinear Diffusion Equation

Using the experimental profile for Equation (4-3), Matano obtained the profile in the interdiffusion problems between solid metals in 1933 [26] . The empirical Boltzmann Matano method has been widely applied to the analysis of the interdiffusion experiments between solid metals. However, the mathematical solutions of Equation (4-3) had not yet been obtained since 1894 for such a long time until the recent work [19] . If the analytical solutions of Equation (4-2) or (4-8) obtained, we can understand the effect of a driving force on the diffusivity. In other words, of Equation (2-7) will be analytically obtained.

(1) Analytical method in parabolic space

When the diffusivity is affected by a driving force, the mathematical solutions of the nonlinear equations (2-11) and (4-3) or (4-7) are impossible if no other relation between diffusivity and concentration is given. In that case, the diffusivity depends on the independent variables and Equation (4-10) is generally valid in mathematics then. Equations (4-7) and (4-10) are thus simultaneously solved in the following.

The integro-differential equation (4-5) is superior in the approximate calculation to the second order differential equation (4-3). For example, using an effective diffusivity for the exponential part in Equation (4-5), the relation of

is valid because of the characteristic of the integral calculation, where D is rewritten as an interdiffusion coefficient.

In order to clarify the validity of the present method, we applied the present method to the typical problems of a binary system interdiffusion where the complete solid solution is formed in the interdiffusion region between solid metals. The reason for that is as follows. The Boltzmann Matano method has been widely used for the analysis of various interdiffusion problems. Uncountable papers have been reported and useful findings have been thus accumulated. Even if the present results are thus evaluated by comparing them with the Boltzmann Matano results, the generality of present method is still kept from the viewpoints of mathematical physics.

In the following analysis, the relations of

(4-40)

are adopted as an initial condition in the parabolic space. The coordinate origin is set at a point on the initial interface of a diffusion couple between materials A and B similar to the one under the condition of in Section 3. The interdiffusion region of corresponds to in the parabolic space

because of. Here, the suffix I or II of C and is deleted since the diffusion equation of I is equal to that of II because of.

The countless experimental results always reveal that the profile becomes an S-letter curve or a reverse one similar to the profile of Equation (4-17) [39] . In the typical interdiffusion problems, the Boltzmann Matano method shows that the profile is also an S-letter curve or a reverse one. These indicate that and are expressed as a superposition of the error functions with various inflection points.

The relation of is conveniently adopted in this section. In such a case, the exponential part of Equation (4-5) satisfies

.

Using a constant value between, it is thus defined as

(4-41)

where is a function to correct the error caused by using instead of.

Substituting Equations (4-5) and (4-41) into Equation (4-10) yields the diffusion flux relation of

(4-42)

For the diffusion flux, the physical speculation produces the relation yielding

(4-43)

where is a function of satisfying. Equations (4-42) and (4-43) yield

(4-44)

In relation to a behavior of the error function, Equation (4-44) is divided into following two equations. One is

(4-45)

and the other is

(4-46)

where is a shift parameter caused by the dependence of on and

and

There is evidence for the validity of the above division as shown in the following. When the relation of

is valid, Equation (4-46) is approximately rewritten as and its integral calculation yields

(4-47)

under the condition of Equation (4-40). In the typical interdiffusion problems between solid metals, Equation (4-47) has been widely accepted [40] - [43] . The derivation of Equation (4-47) gives evidence for the validity of division of Equation (4-44) into Equations (4-45) and (4-46).

Since it is thus confirmed that the division of Equation (4-44) into Equations (4-45) and (4-46) is reasonable, Equation (4-45) is analyzed in accordance with mathematical theory. As can be seen from the analyzing process in Ref. [19] , the calculations are considerably complex. As a result, the general solution of

(4-48)

was obtained as an analytical expression using initial values, where

for and for

Here, the relation of for is valid in the present diffusion system. Therefore, the effect of a driving force and/ or a concentration dependence on the diffusivity, which is discussed in Section 2.1, is obtained as

(4-49)

Subsequently, using the obtained solution of Equation (4-48) for Equation (4-46), Equation (4-46) was analyzed also through considerably complex calculations. The general solution of

(4-50)

was thus obtained also as an analytical expression.

Here, the notations used for Equations (4-48) and (4-40) are as follows:

The validity of the present analytical method is numerically investigated by comparing Equations (4-48) and (4-50) with the results of the Boltzmann Matano method. As a result, we found that the present solutions agree well with those of the Boltzmann Matano method [19] .

When the diffusivity does not depend on independent variables, the relation of is valid. In that case, the above relations become

, , and

Equations (4-48) and (4-50) agree with and Equation (4-17) then, respectively. The obtained solution of Equations (4-48) and (4-50) are thus accepted as a generalized ones.

The K effect in the parabolic space is easily obtained as

by transforming Equation (3-15) into the parabolic space under the condition of. The K effect in the parabolic space is thus determined only by the initial values.

(2) Meaning of general solutions obtained as analytical expressions

Since the general solutions are obtained as Equations (4-48) and (4-50), the interdiffusion problems are fundamentally solved as follows:

We denote an impurity diffusivity of a diffusion element I in a pure material B composed of an element II and also denote an impurity diffusivity of the diffusion element II in the pure material A com-

posed of the element I. We first investigate an interdiffusion problem of the diffusion couple between pure materials A and B. It is then well-known that the relations of

and (4-51)

are physically valid.

The solution is determined by using and the values of Equation (4-51) for Equation (4-50). It gives two independent variable values satisfying at and at as follows:

(4-52)

(4-53)

Substituting these and and the values of Equation (4-51) into Equation (4-48), we can determine and for and.

Subsequently, using and for Equations (4-48) and (4-50) as boundary values of interdiffusion coefficients in the binary system, we can obtain the solutions of the interdiffusion problems for the diffusion couple between the material A composed of, and the material B composed of,.

The solutions of an arbitrary binary system interdiffusion problem are thus possible by using impurity diffusivities in the concerned diffusion system. In the N elements system interdiffusion problems, using an impurity diffusivity of an element in the concerned diffusion couple, their solutions are also possible.

In the diffusion history, the nonlinear F2 equation had not been analytically solved until recently, although the numerical solutions were possible. In order to understand the diffusion problems, the corresponding diffusion fluxes to the F2 equation had been thus widely discussed in the existing theories, since it was considered that the mathematical solutions of nonlinear diffusion equation are impossible. For example, such a diffusion flux in the Appendix A has been discussed.

However, the discussion about such a diffusion flux is now unnecessary for understanding the diffusion problems, since the analytical solutions of Equations (4-48) and (4-50) relevant to the nonlinear F2 equation are obtained, regardless of the diffusion fluxes. In other words, as can be seem from Equation (4-49), we can understand the influence of a driving force on the diffusion flux from the obtained solutions.

Based on the above discussions, it is extremely meaningful that the solutions of the nonlinear F2 equation are obtained as analytical expressions.

(3) Nonlinear problems of three dimensions in parabolic space

The analytical solutions of linear diffusion equations were obtained in the parabolic space. Further, we could also obtain the physically meaningful solutions of nonlinear diffusion equation as analytical expressions in the one dimension parabolic space.

In mathematics, it is almost impossible to solve two or three dimensional nonlinear diffusion equation. However, we investigate two or three dimensional problems in the parabolic space in the following.

We rewrite Equation (4-2) into

(4-54)

where

(4-55)

It is impossible to analyze Equation (4-54) exactly since exists in. By reference to the one dimensional case, if we use the effective diffusivity independent of instead of for Equation (4-55) as an approximation, Equation (4-54) becomes

(4-56)

because of.

By reference to Equation (4-19), the solution of Equation (4-56) is obtained as

(4-57)

where are integral constants.

5. Universal Expression of Diffusivity

From applying the diffusion equation to a collision problem between two micro particles in the diffusion elementary process, the S equation is reasonably derived. It is revealed that the diffusivity corresponds to the angular momentum operator in the quantum theory. The universal diffusivity expression, which is applicable to every material in an arbitrary thermodynamic state, is obtained using an essential diffusion constant then. Further, the correlation between the well-known material wave relation and the diffusivity expression is discussed in a minute time and space region.

5.1. Derivation of Schrödinger Equation

If the movement of a material particle is not the Markov process but the continuous process, Equation (2-1) is rewritten as

(5-1)

where.

From the Taylor expansion of both sides of Equation (5-1), the well-known wave equation is obtained as

(5-2)

where is a phase velocity under the condition of. The general solution of Equation (5-2) is given by

(5-3)

where A and are a wave amplitude and an initial phase, and and mean a component of the wave number vector relevant to a wavelength component and an angular velocity relevant to a period T.

The collective behavior of micro particles relevant to the Markov process is expressed by Equation (2-6) derived from their random movements. However, it is revealed in the quantum mechanics that a micro particle has a wave characteristic. The relation of material wave yielding

(5-4)

was thus proposed by de Broglie in 1923, where and are the momentum of a material particle and the Planck constant [23] . The motion of a micro particle relevant to Equation (5-4) should be thus essentially investigated by using the S equation of

(5-5)

where is the wave function and the Hamiltonian meaning the total energy in the given physical system [18] . In case of a free particle, the Hamiltonian H is given by

(5-6)

where m is the particle mass and the momentum or its operator.

When Equation (5-4) is applied to a micro particle behavior, the left-hand side of Equation (5-4) means the particle motion in accordance with the Markov process. On the other hand, the right-hand side means the continuous process resulting from the wave characteristic of the micro particle during a free motion because of the wave factor. This suggests that the S equation correlates with the diffusion elementary process resulting from a random movement caused by a collision between a micro particle and a force field near the micro particle itself.

An activation energy caused by a local thermal fluctuation generates micro holes in a material and at the same time micro particles are possible to jump instantaneously to the nearest neighbor micro holes through each energy barrier. The macro behavior of their collective motion is investigated by using the diffusion equation (2-6).

On the other hand, behavior of a micro particle of mass m in the diffusion field is investigated by the well-known Langevin equation of

(5-7)

where and are the velocity and the viscosity resistance using a resistance factor [27] . Here, is a force caused by a collision and the time-averaged value is considered to be.

The Langevin equation shows that the behavior of a Brown particle in the minute time and space region is incorporated into the force. Therefore, we cannot discuss the Brown motion in the minute region by using the Langevin equation because of. Hereafter, we do not discuss but the acceleration of

(5-8)

caused by a collision between two micro particles in the minute time and space region.

Since the physical essence is still kept even if we consider the simplest collision problem of one dimensional case, we thus investigate a perfect elastic collision problem between micro particles A and B of the same kind. We consider that the particle A moves with a velocity for a direction and collides at time with the particle B in the standstill state.

If we can then clarify the distinction between A and B after the collision, the particle A decelerates from the velocity to the velocity zero and the particle B accelerates from the velocity zero to the velocity between.

On the other hand, if we cannot clarify the distinction between the particles A and B after the collision, it seems that the particle A decelerates from the velocity to the velocity zero between and subsequently accelerates again from the velocity zero to the velocity between. In other words, it seems as if there is no collision process in the particle motion.

If we accept the above latter case, the relation of () must be valid in Equation (5-8) between and in the collision process. This indicates that the impossibility of discrimination between the particles A and B yields between, as can be seen from the expression of Equation (5-8).

It is considered that the above former case corresponds to the Markov process caused by a collision and the latter case corresponds to a continuous process caused by the impossibility of identification between the micro particles. It is thus mathematically necessary for the transformation from the Markov process into the continuous process to introduce the imaginary time into a collision problem between micro particles.

In physics, it is difficult to accept the imaginary time in accordance with the continuity of time. In mathematics, however, the product of a physical quantity Q and an imaginary time is equal to and also that of a physical operator and a real time t is equal to the same result. It is thus considered that the latter case is physically reasonable. However, it is possible that we mathematically analyze the diffusion equation using the imaginary time in accordance with the mathematical equivalence relation. The diffusion equation is thus applied to an elementary diffusion problem using the imaginary time in the following.

Rewriting the concentration of diffusion particles into a quantity of state expressed by a complex function, Equation (2-6) yields

(5-9)

Assuming, Equation (5-9) can be solved by the separation method of variables. Using complex numbers, and determined by the initial and boundary conditions, the general solution of Equation (5-9) is obtained as

(5-10)

where. Substituting into Equation (5-10) yields

Here, using the real functions and, we rewrite the complex function into the complex-value function yielding

(5-11)

Further, substituting Equation (5-11) into Equation (5-9) and multiplying both sides by, we have

(5-12)

because of.

From the partial differential equation of probability, the diffusivity of

(2-5)

is obtained. When a micro particle randomly jumps from a position to another one, the jump orientation becomes the spherical symmetry in probability. Using the relation of relevant to the angular momentum defined by a position vector and a momentum, Equation (2-5) is rewritten as

where, , , is valid in the spherical symmetry space.

The relation of leads to an operator relation of

(5-13)

Substituting Equation (5-13) into Equation (5-12) gives

(5-14)

Here, if we define the imaginary differential operator given by

, (5-15)

Equation (5-14) is rewritten as

(5-16)

Further, the substitution of Equation (5-6) into Equation (5-16) yields the S Equation (5-5). The defined Equation (5-15) is one of the essential operators in the quantum mechanics.

It is considered that the relation of and is valid for a wave packet existing in the minute time and space. In that case, the de Broglie equation

(5-4)

is thus easily obtained because of

, and

At the same time, this gives evidence for the validity of Equation (5-13) derived from the correlation between the diffusion equation and the S equation. It is, therefore, considered that the diffusivity is fundamentally relevant to the Planck constant and it should be determined from the quantum mechanics.

5.2. New Universal Diffusivity

The definition of diffusivity shows that the diffusivity should be essentially determined by analyzing the S equation, since the diffusion particle such as an atom and/or a molecule moves as a material wave packet in the minute space. However, the existing diffusivity has been defined by the classical mechanics. In the following, therefore, a new diffusivity is investigated.

The existence probability P of a micro particle in the collective system of a heat quantity Q and an absolute temperature T is given by the well-known Boltzmann factor of

(5-17)

where is the Boltzmann constant [44] . It is necessary for a jumping of diffusion particle to obtain an activation energy Q caused by a thermal fluctuation. In a collective system composed of micro particles, the diffusivity is thus directly proportional to the probability factor of Equation (5-17).

The jump frequency of a diffusion particle is relevant to a factor derived from an atomic configuration in the diffusion field near the diffusion particle itself, and also it depends on entropy S relevant to a state change of diffusion field. If we define these effect on a diffusivity as, the diffusivity expression of Equation (2-5) or (5-13) is rewritten as

(5-18)

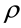
where the molecular or the atomic weight n is expressed as using the particle mass m and the Avogadro constant. Here, is an essential constant in the diffusion phenomena and it is

(5-19)

Equation (3-32) shows that diffusion particles move randomly with a common diffusivity in the concerned diffusion field. On the other hand, Equation (5-18) shows that the diffusivity depends on the mass of diffusion particle. For the diffusion experimentation in a super gravity field, therefore, it is considered that an individuality of a micro particle resulting from the mass effect will be shown in the diffusivity, compared with one in a usual laboratory.

Hereafter, the investigation of will become a dominant subject in the diffusion study as a problem of a few many bodies system in the quantum mechanics, since the essential diffusion constant of Equation (5-19) is thus reasonably obtained.

5.3. Influence of a Driving Force on Diffusivity

The new diffusivity of Equation (5-18) is derived regardless of the bulk diffusion problems. However, it is considerably difficult to determine of Equation (5-18) from the quantum theory in a physical system with an interaction between micro particles [45] [46] . Further, if we consider Equation (5-18) in accordance with the existing diffusivity theory, it seems that there is no room to incorporate a driving force effect into the diffusivity expression of Equation (5-18), since the essential constant has already the diffusivity dimension. On the other hand, the diffusivity expression of Equation (4-48) is derived from analyzing the nonlinear interdiffusion equation with a driving force.

If we incorporate the potential energy caused by a driving force into the activation energy Q in the expression of Equation (5-18), the relation is obtained as

(5-20)

for a material composed of micro particles in the state of an absolute temperature and a heat quantity, since Equation (5-18) corresponds to Equation (4-48) then. In the actual interdiffusion problems, obtained here is useful for fundamental knowledge relevant to a microstructure of material.

Equation (5-18) is thus valid when a driving force is nonexistent in the diffusion system. In other words, the relation of

(5-21)

is considered to be valid between Equations (2-6) and (5-18) for the common and.

As can be seem from Appendix A in the existing theory, the effect of a driving force on the diffusivity is incorporated into the difference of a jump frequency between nearest neighbor crystal plane 1 and plane 2. In relation to the situation, we discuss the difference between the present diffusivity expression and the existing one as follows.

The existence probability of a micro particle in a material depends on the Boltzmann factor of Equation (5-17). The potential energy as well as the activation energy Q gives motive energy and vibrational one to each micro particle in a material. In that case, the potential energy causes that the vibrational energy of micro particle on the crystal plane 1 is different from that of one on the plane 2, since the potential energy depends on the space coordinate. In other words, the existence probability of a micro particle on the plane 1 is different from that of one on the plane 2.

The difference of existence probabilities between a micro particle on the plane 1 and one on plane 2 corresponds to that of the frequencies between them. The effect of a driving force on diffusivity should be thus incorporated into the Boltzmann factor as a potential energy in the present case.

When the potential energy is not so much large, i.e., , the diffusivity D of Equation (2-7) corresponds to

(5-22)

incorporating a driving force effect into the Boltzmann factor for and. Equations (2-7) and (5-22) show that the relation of

(5-23)

is valid. Although the diffusivity gradient of

(5-24)

has the velocity dimension, it is directly relevant to a driving force F because of the definition of mechanics. The left-hand side of Equation (5-24) is thus called the drift velocity in the existing diffusion field (See Appendix A). However, the diffusivity gradient relevant to a driving force is obviously not the velocity concept but the force one.

Substituting Equations (5-22)-(5-24) into the one dimension diffusion equation of the general nonlinear Fickian second law given by

(5-25)

the diffusion equation is obtained as

(5-26)

where is entropy caused by a driving force. It is considered that the second term and third term in the right-hand side of Equation (5-26) mean entropy effect and a frequency effect caused by a driving force F, respectively. The general diffusivity expression is thus obtained by rewriting Equation (5-18) into

(5-27)

In view of the derivation process, the diffusivity expression of Equation (5-27) is applicable to every material in an arbitrary thermodynamic state.

5.4. Operators in Quantum Mechanics

In the quantum mechanics, energy E, momentum and angular momentum are expressed as operators yielding

, ,.

We cannot observe imaginary physical quantities. Therefore, the eigenvalues of their operators are meaningful in the quantum theory.

In a collision problem mentioned above, the concept of acceleration disappears in the quantum theory because of. However, Equation (5-4) shows that the velocity is still a real physical quantity in the minute time and space region, since the momentum conservation law is valid in the collision process.

It is physically considered that the wave image of a micro particle disappears in the quantum theory when the corresponding wave packet exists in the minute space region. Substituting and into Equation (5-3) yields the relation of

(5-28)

and it converges at zero in a minute time. For the wave image, the relations of and mathematically correspond to the relations of and then, compared with and for the particle image.

In mathematics, except for physical constant quantities, physical variables with odd time or space dimensions should be thus accepted as physical operators in the minute time and space region.

The kinetic energy of Hamiltonian is acceptable as a physical quantity and/or a usual differential operator since it is a real variable for the sake of even time or space dimensions. On the other hand, the photon energy expressed by using a frequency should be accepted as an operator, since h is the Planck constant and is an imaginary variable because of in accordance with the wave image of. Therefore, the relation of yields the operator described above.

Using relations of, and for the wave packet in the time and space region, the relation of

(5-29)

yields the operator described above. Further, using for the definition of an angular moment, the above angular moment operator is also obtained.

We investigate a characteristic of diffusivity in the minute time and space regions in the following. Equation (2-5) is rewritten as

(5-30)

for a particle image. Equation (5-4) is also rewritten as

(5-31)

because of and. Substituting Equation (5-31) into Equation (5-30), the diffusivity expression of

(5-32)

is obtained as an operator.

Substituting Equation (5-32) into Equation (2-6), we have

(5-33)

Multiplying both sides of Equation (5-33) by and rewriting C into, the S Equation (5-14) is thus obtained again. In mathematics, the diffusion equation and the S equation are thus correlated only to the replacement of between their equations in the real time and space.

6. Results

In 1855, Fick applied the heat conduction equation proposed by Fourier in 1822 to diffusion phenomena as it had been. In general, however, the discussion of coordinate transformation of the general nonlinear F2 law is indispensable for understanding the diffusion phenomena. Nevertheless, the coordinate transformation of a diffusion equation had not been discussed for a long time until the recent works [14] - [16] [19] [20] [22] .

Applying the divergence theorem to a diffusion equation, therefore, we investigated the problems of coordinate transformation in the diffusion systems. In relation to the investigation, a new diffusion flux of Equation (2-13) was defined in accordance with the mathematical physics. The new diffusion flux revealed that the F1 law is incomplete without the intrinsic diffusion flux.

The coordinate transformation theory shows also that the K effect is caused by a shift between the coordinate systems like the Doppler effect of the wave equation is caused by a shift between them. The theoretical Equation (3-15) relevant to the K effect was reasonably obtained in accordance with the empirical Equation (3-14) then. At the same time, it was also revealed that the concept of intrinsic diffusion is nonexistent in the diffusion theory, although we had accepted as an indispensable concept for understanding the K effect for a long time until recently.

In relation to the coordinate transformation theory, further, using the new diffusion flux applicable to various diffusion problems, the unified diffusion theory relevant to every material in an arbitrary thermodynamic state was established, including a self-diffusion theory and also an N elements system interdiffusion theory.

The self-diffusion theory has been indirectly discussed in the existing one, where the self-diffusion behavior of a pure material is visualized by any other diffusion particles in the pure material. In the present theory, the self-diffusion mechanism of a pure material itself is discussed using the intrinsic diffusion flux. In an N elements system interdiffusion, it was found that each of diffusion particles moves randomly with a common diffusivity of Equation (3-32) in the diffusion field, as if the gas molecules in a given space move randomly, regardless of their species in accordance with the Boyle Charles law.

The essence of diffusion phenomena is shown in the parabolic law. Based on the concept, a new diffusion flux applicable to analyzing diffusion problems was derived as Equation (4-7) and/or (4-8) in the parabolic space. The analytical method in the parabolic space was thus established. It was then revealed that the analysis in the parabolic space is exceedingly superior in calculation to the existing analytical methods. For example, the solutions of nonlinear diffusion equation were, for the first time, obtained as the analytical expressions of Equations (4-48) and (4-50). The effect of a driving force on the diffusivity was then obtained as Equation (4-49) from the solution of Equation (4-48).

The definition of diffusivity indicates that the diffusivity should be essentially investigated as a few many bodies problem in the quantum mechanics. Based on the concept, the S equation was derived from applying the diffusion equation to a diffusion elementary process. In the analytical process, we found that the diffusivity corresponds to an angular momentum operator in the quantum mechanics. The new universal diffusivity expression was thus obtained as Equation (5-27) using an essential diffusion constant of Equation (5-19). It is essentially applicable to every material in an arbitrary thermodynamic state.

It was also found that the material wave equation proposed by de Broglie, which is the most fundamental relation in the materials science, was derived from the relation between diffusivity expressions of Equations (2-5) and (5-13) in the diffusion elementary process. This gives evidence for the validity for the present diffusion theory.

7. Discussion

Even if a driving force exists in the diffusion system under the condition of no sink and source, the divergence theorem shows that a collective behavior of micro particles depends only on a diffusivity of the general nonlinear F2 law. Whenever the diffusivity of a micro particle in a material is given, the collective behavior of micro particles is thus determined only by solving the diffusion equation. The diffusivity depends on a material internal structure composed of micro particles. Therefore, the investigation of diffusivity is the most important subject in the diffusion study. Based on the concept discussed here, the present study was performed.

In relation to the Darken equation, even if a concentration profile is reasonably reproduced by using intrinsic diffusion coefficients as parameters, we cannot directly evaluate its validity of the used diffusivity values, since the diffusivity profile is not obtained by a direct observation. In other words, we can usually perform the numerical simulation to a high precision only by using fitting parameters for the given equation, regardless of a physical validity. As far as the Darken equation is not mathematically correct as shown in the Appendix B, it is thus necessary for us to reexamine a great many results of interdiffusion problems obtained by using the unsuitable Darken equation.

As revealed in the text and Appendix B, we believe that the F1 law and the intrinsic diffusion concept as well as the Darken equation are misunderstanding matters in the diffusion history. Nevertheless, they have been accepted as reasonable ones for such a long time in the concerned field.

If we consider serious influences of their misunderstanding matters on student education and young researcher training in the concerned field, they should be solved as soon as possible, since they have been still described as plausible ones in a lot of existing textbooks. One of the present work aims is thus to make them universally known in the concerned field.

Since the general solutions of nonlinear diffusion equation are analytically obtained in the parabolic space, the diffusion problems under the condition of no sink and source are essentially solved. The influence of a driving force on the diffusivity is thus reasonably obtained as Equation (4-49) from the analytical solutions of Equations (4-48) and (4-50). The discussions about diffusion fluxes are thus now essentially unnecessary for fundamental diffusion problems.

In the actual diffusion problems in detail, further investigation will be required for various difficult problems, for example, such a problem where the sink and source exists in the concerned diffusion system. Even in that case, however, it is no doubt that the fundamental theories discussed here are still useful for their fundamental investigations, just because of fundamental ones.

The investigations relevant to the many elements system interdiffusion problems, such as an alloy, a compound semiconductor, a multilayer thin film, and a microstructure material, are extremely important as an actual problem. Under the condition of Equation (3-27), corresponding Equations (4-48) and (4-50) to solutions of Equation (3-33) and using solutions of Equation (3-34) obtained numerically for a many elements system interdiffusion problems, their solutions are possible.

As mentioned at the beginning of this section, the foundation of diffusion problem is relevant to not the diffusion flux but the diffusion equation for the concerned diffusion system. The influence of a driving force on a diffusion system should be thus incorporated into the diffusivity of the concerned diffusion equation, e.g., Equation (5-25), although the problem relevant to a driving force is discussed in the existing theory using a drift velocity in the diffusion flux representation (see Appendix A).

In the present study, the fundamental diffusion problems are surveyed in accordance with the mathematical physics. As a result, the new useful findings for the diffusion study are reasonably derived from the essential discussions about the general nonlinear Fickian diffusion equation. In particular, the analytical method established in the parabolic space will be applicable not only to diffusion problems but also to Brown problems in various science fields as a useful method.

Finally, we hope that the new findings are useful for the material science researches and also that the present aims are accomplished.

Cite this paper

TakahisaOkino, (2015) Mathematical Physics in Diffusion Problems. Journal of Modern Physics,06,2109-2144. doi: 10.4236/jmp.2015.614217

References

Appendix A

In Ref. [25] , the influence caused by a driving force in the planar diffusion phenomena is investigated in relation to jump frequencies of diffusion particles between the nearest neighbor crystal planes.

The net diffusion flux J of diffusing particles across a plane between two nearest neighbor crystal planes 1 and 2 is expressed as

, (A-1)

where and are the atom concentrations per unit area on each plane, and and are the jump frequencies for an atom to jump from plane 1 to plane 2 and from plane 2 to plane 1. The coordinate axis x is perpendicular to each plane and equal to the diffusion direction.

The relation between concentration per unit volume and concentration per unit area is expressed as

(A-2)

where a is a lattice constant and in the present case.

Here, the following relations are considered as;

, (A-3)

where.

Substituting Equations (A-2), (A-3) into Equation (A-1), the relation of

(A-4)

is obtained. Using the notations given by

and (A-5)

the diffusion flux of

(A-6)

is derived. Here, is defined as a diffusivity of tracer diffusion. If, means the diffusivity when a driving force is nonexistent in the diffusion system.

On the other hand, if we use the Taylor expansion in the above calculations, the relation of

(A-7)

and

(A-8)

are valid. Using Equations (A-7), (A-8) for Equation (A-1), the relation similar to Equation (A-6) is obtained as

, (A-9)

where. Equations (A-6) and (A-9) show that corresponds to the diffusivity gradient given by

. (A-10)

Equation (A-9) should be essentially equivalent to Equation (2-7) as shown by

(A-11)

However, it seems that Equation (A-11) is not generally valid. The reason is as follows.

When a driving force exists in the diffusion system, it affects entropy and jump frequencies of diffusion particles. As a result, the diffusivity is affected by a driving force, since the diffusivity depends directly on entropy and a frequency. The problem of entropy is extremely important for the diffusion phenomena. However, the effect of entropy is not taken into account in the derivation process of Equation (A-6) or (A-9). Therefore, the diffusion flux discussed here is not generally applicable to the diffusion problems relevant to a driving force.

Equations (4-48) and (4-50) reveal that we can solve a nonlinear diffusion equation even if a driving force exists in the diffusion system. Further, the effect of a driving force on the diffusivity is obtained as Equation (4-49). The diffusion flux discussed here is thus unnecessary for solving a nonlinear diffusion equation.

Further, the divergence theorem shows that the diffusion equation is obtained from the diffusion flux of Equation (A-9) as

. (A-12)

As discussed in Section 2.1, even if a driving force exists in the diffusion system, the diffusion equation (2-6) of

(A-13)

must be valid for the diffusion particles, except such an external force as Coulomb force for an ion particle.

Equation (A-12) is obviously inconsistent with Equation (A-13). This is evidence that Equation (A-6) neglecting an influence of entropy caused by a driving force is incorrect. In relation to the Equation (5-24), the diffusivity gradient is directly relevant to a driving force. Although the last term in the right-hand side of Equation (A-12) is the derivation term of a driving force because of Equation (5-24), we cannot understand such an effect of relevant to the random movement of diffusion particles in the diffusion system inside. If the force F is an external one where it is deliberately introduced into the diffusion system from the diffusion system outside, such phenomena may be possible. In other words, such diffusion flux of Equation (A-6) is not suitable in the present discussion, since the influence of a driving force should be incorporated into the Boltzmann factor as a potential energy caused by a driving force, as discussed in Section 5.3.

For example, one can easily notice that a force moment of vector quantity is not relevant to a kinetic energy of scalar quantity, although they have the same dimension of each other. Even if the drift velocity has the dimension of in the present case, it is thus not relevant to a velocity itself, since it is relevant to a driving force F as can be seem from Equation (5-24).

In general, the diffusion problems should be discussed using not the diffusion flux but the original diffusion equation, since the mathematical theory shows that the diffusion flux should be originally understood after the diffusion equation has been solved.

Appendix B

In the text, the K-effect was reasonably understood as a shift between the coordinate systems. This indicates that the intrinsic diffusion concept is not only needless but also nonexistent in the diffusion phenomena.

Based on the intrinsic diffusion concept, Darken derived a relation between the interdiffusion coefficient and intrinsic diffusion coefficient [35] . However, he repeated misunderstandings inconsistent with the fundamental mathematics theory in the analyzing process. Nevertheless, the so-called Darken Equation (D equation) has been widely applied to interdiffusion problems for such a long time since 1948. In the following, we reveal that the D equation is incorrect in mathematics.

When a driving force exists in the diffusion system, the diffusion phenomena are expressed as

(2-6)

In that case, using the Equation (2-17) transformed from Equation (2-6) for, the relation of

(B-1)

is valid, where the coordinate notation and the velocity are, for convenience, rewritten as and v. Here, the velocity used in Equation (2-15) means the velocity of diffusion region space caused by the diffusion of solvent particles. At the same time, it is visualized by an inert marker set on the initial interface because of the inert characteristic of markers.

Equation (B-1) yields

(B-2)

because of. Here, note that Equation (B-2) is obviously a partial differential equation of and. Therefore, the mathematical theory shows that Equation (B-2) corresponds to

(B-3)

where is an arbitrary function of.

Nevertheless, Darken solved Equation (B-2) as an ordinary differential equation with respect to. In other words, using k as an integral constant value instead of the, he thought that the relation of

(B-4)

is valid. Using an unsuitable initial value for Equation (B-4), it was rewritten as

(B-5)

Here, the functional equation (B-5) is not valid, since the left-hand side depends only on and the right- hand side depends on and. Thus, he failed again to notice the mistake in the fundamental mathematics.

Under the condition of in Equation (2-18) in accordance with the existing theory, the diffusion flux becomes

. (B-6)

In any case, if we substitute Equation (B-5) into Equation (B-6), the relation of

(B-7)

is obtained. By comparing Equation (B-7) with the F1 law of, the D equation is perfunctorily derived as

(B-8)

He also failed to notice the mistake relevant to the basic theory of physics, since we cannot directly compare with expressed in the different coordinate system, as can be seen from the derivation of Equation (2-17).

It seems that and are independent of each other in the above analytical process. In other words, he thought that the K effect is caused by the difference between and. They are symbolically rewritten as and in Equation (B-8) and are named “intrinsic diffusion coefficients” then.

In addition, even if we accept Equation (A-6) in Appendix A, it is not suitable to use it for the movement of K interface in the present case, since the drift velocity depends on a time and a space coordinate, while the experimental result of Equation (3-14) shows that the K effect depends on only a time. It is obvious that the problem of K effect is a one to be discussed using not the diffusion flux Equation (A-6) but the diffusion Equation (2-6) taking account of a driving force. Further, the present interdiffusion problem should be expressed by Equation (2-6). If it is so, the corresponding diffusion flux must be not Equation (A-6) but Equation (B-6) obtained from Equation (2-6).

Hereinbefore, it was revealed that the D equation is obviously inconsistent with the theory in mathematical physics. Equation (B-8) is thus entirely meaningless and at the same time the concept of intrinsic diffusion is an illusion in the diffusion history. That the D equation has been highly applied to various interdiffusion problems by a lot of researchers for a long time since 1948 is one of the extremely few cases of misunderstanding problems in the science history.