Journal of Modern Physics
Vol.06 No.09(2015), Article ID:59021,9 pages
10.4236/jmp.2015.69135
Cold Electron Quantum Mechanical Model for Superconductivity
Zhenhua Mei1, Qingxian Yu1, Shuyu Mei2*
1Qingdao University of Science and Technology, Qingdao, China
2School of Medicine, Shandong University, Jinan, China
Email: mzh62@qust.edu.cn, yqx67@qust.edu.cn, *mzh62@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 June 2015; accepted 21 August 2015; published 24 August 2015
ABSTRACT
To explain superconductivities and make up for the lack of current theory, a new quantum theory of cold electron was proposed. The key point is that we accepted the concept of electron orbital rotation instead of traditional electron spin. It leads to an important conclusion that the electron at low temperature is running in a flat orbital. The physical mechanism of superconductivities is so explained preferably. Under the assumption that the electrons have their motion tracks and the tracks can be described in atoms, the situations of electron will be changed a lot. The new concept of cold electron is then established. It means that the electrons can feel temperature. The Schrödinger function is the function of ideal electron indeed. Hot electron looks like the electron of the ideal electron. As temperature goes much lower, the electron orbits will obviously departure to what Schrödinger function described, and run in a flat one. The orbital shape of paired electron depends on temperature, transitioning from three- to two-dimension. Comparing the orbital shape to that of common electron, the paired cold electron saved quite some space in atomic crystal lattice. It created the preconditions for the phase transition at low critical temperature.
Keywords:
Superconductivity, Cold Electron, Quantum Mechanics, Theory

1. Introduction
Superconductivity means that no electrical resistance appears when a special material was under low critical temperature, Tc. As we know that, the best conductive metal silver has its general resistivity of 1.58 × 10−8 Ω∙m, while the superconductor has less resistivity than the detection limit of 1 × 10−28 Ω∙m. The great applications of super24conductor encourage people to continue looking for new superconductive materials at higher temperature. Up to now, the development of superconduction has undergone more than one hundred years since 1911. Many events have arisen to be landmarks of great significance in science [1] , namely Tc as 4.2 K in mercury (Kamerlingh Onnes, 1911), 23.2 K in Nb-Ge alloy (Gavaler, 1973), 35 K in La-Ba cuprate (Miiller & Bednorz, 1986), 93 K in Y-Ba cuprate (C.W. Chu, 1987; Z.X. Zhao, 1987), 125 K in Tl-Ba-Ca cuprate (Z.Z. Sheng, 1988), 135 K in Hg-Ba-Ca cuprate (A. Schilling, 1993), 164 K in high pressure Hg-Ba-Ca cuprate (C.W. Chu, 1994), 39 K in MgB2 (J. Nagamatsu, 2001), and 52 K in Nd-As-F iron oxide (Z.X. Zhao, 2008) etc.
Meanwhile, the theoretical researches were accompanied continually for explaining and directing the superconduction [1] . The main theories were London model (F. London, 1935) [2] , G-L theory (Ginzburg-Landan, 1950) [3] , and BCS theory (J. Bardeen, L.N. Cooper, J.R. Schrieffer, 1957) [4] . Eliashberg & Nambu (1960) improved the BCS theory and found the Eliashberg equation [5] [6] . McMillan (1968), Allen and Dynes (1975) afterwards introduced experimental data to carry on curve fitting for simply solving Eliashberg equation [7] [8] . Based on this, the Wine2k and Quantum Espressso etc. calculation software packages were produced; so their results are not exactly the ab-initio quantum calculation; however many of us misunderstand this.
The London model and G-L theory are good macroscopic quantum theory, but they explain the superconductivity with the lack of mechanism. The BCS theory as a microscopic theory explained the formation of Cooper pair of electron, but failed in its mechanism of electron-phonon interaction when Tc is higher than 40 K. So far, there is no coherent and uniform theory being widely accepted in the field of superconduction [9] - [12] . Here, we proposed a new concept of “cold electron” in order to reveal the nature of superconductivity.
2. Theoretical Thinking before Modeling
2.1. Further Understanding of Quantum Mechanics I
Quantum mechanical theory was established in 1926s by scientists namely Schrödinger, Planck, De Broglie, Dirac, and Pauli et al. Considering relativistic effect, the quantum mechanics could calculate the properties and structural information of atom and molecules accurately, almost without any exceptions; the rest of thing is how to solve the Schrödinger equation as exactly as possible. The huge success of quantum mechanics has drawn high admirations and prestige from all of world.
Band theory is derived by the quantum mechanics. It is considered to be the most efficient theory for explaining the electroconductivity of common materials. Different matter has different band gap between its bottom conduction and top valence energy band, and different band gap means different conductivities. It could be an insulator, a semiconductor or conductor according to its gap size. The superconductivity should also be included in band theory. However, the present problem is that, at the critical temperature a non-negligible gap size remains according to the calculation of quantum mechanics. The gap size can’t cause a zero electrical resistance.
To speak frankly, traditional quantum mechanics can’t explain the superconductivity well; say nothing of the perfect diamagnetism of superconductor. Then, how to judge and treat the traditional quantum mechanics? Our opinion in this paper insist on that the great achievements of quantum mechanics and its theoretical system is beyond doubt; abandon this for other attempting theory is lifeless and inadvisable in field of superconductivity. We must inherit the theoretical system of quantum mechanics firmly. Find out the crux of the problem, and explain superconductivity in a compatible new theory after modifying the errors wherein.
2.2. Further Understanding of Quantum Mechanics II
The Schrödinger wave equation in quantum mechanics is derived from normal one-dimensional wave equation. After several mathematical transformations processing such as double derivative, substituting the momentum for wavelength, substituting the total and potential energy for momentum, and extrapolating the dimension from one to three, the Schrödinger wave equation was finally obtained. If the mass and mathematical expressions of potential energy of electron were substituted into the equation, then the obtained Schrödinger wave function, Ψ, would be considered to be the description of the form of motion of electron in an atom. Furthermore, if we substituted the mass and mathematical expressions of potential energy of the earth into the equation, then the result, Ψ, would be the description of the earth moving around the sun, because of the limitless of substitution of the wave equation. As the earth has far less wave nature, the shape of Ψ must be a sphere at least to s orbital. It is quite different from the circular motion in a plane as is well known.
Although a circular and spherical ones are quite different, but closely related. The two-dimensional circular motion could change its orbit under perturbation, and abundant plenty of the changed orbits formed the sphere-like orbital. Up to the theoretical level, the universal representation is that two-dimensional circular motion could become the three-dimensional orbital under perturbation. The ratio of three to two dimensional depends upon the intensity of perturbation. As to the electron in an atom or molecule, the perturbations mainly come from the thermal motion; it is the thermal motion that changed the two-dimensional motion into a three-dimensional orbital.
The wave function, Ψ, is continuous and differentiable. Wave function is originally suitable for describing the wave, rather than the particulate nature of electron. As it always did, the electron has played the role. That’s why the occurrence of famous interpretation of Bonn probability density afterward. The role that particle electron successfully played as wave is all attributed to its wave nature, the high speed and high thermal motion of electron. Otherwise, the results of quantum mechanics would be quite different from the facts.
2.3. Electron’s Cold and Hot Issues
The temperature of object is essentially a measure of the average energy of thermal motion of molecules and atoms. Heat transformation between molecules and atoms is realized through the interaction of electrons outside the nucleus. In traditional theory, the electrons are regarded as the heat conduction and heat radiation messenger or carrier, however, any hot meanings has not been given in itself, in other words, the concept of temperature of electron were regarded meaningless. Was that reasonable? Have any proof of electron that should have no temperature meaning? In statistical view, the temperature relates to a degree of confusion. Electrons are all in doing their own business in order. It doesn’t seem to make sense that the degree of confusion of electrons is almost unchanged after heat effect.
The running tracks of electron should be different in yes or no interfering circumstance. At the interference of heat, electron must change its orbit, the higher the temperature, the bigger it was and vice versa. The irregular thermal motion lead to the irregular variation of orbit, changing dimension from two to three, i.e., the three dimensional orbital is the heat performance of electron, the higher the temperature, the bigger it contains. In above mechanism, we could say that the electron can feel temperature; the orbital shape of electron depends on temperature. Taking orbital as an example, it takes a spherical shape at a higher temperature, and an ellipsoid one at a lower; at absolute zero of temperature it would be the orbital in a plane.
2.4. Issues of Electronic Spin
The conception of electronic spin was first proposed by Ralph Kronig, George Uhlenbeck and Samuel Goudsmit in 1925. In 1928, Dirac established relativistic equation of quantum mechanics, and a screw factor was showed in its solution. In 1945, the spin of electron was successfully applied in quantum mechanical orbitals by Pauli, expressed as exclusion principle, which plays an important part in the quantum mechanics.
Whenever people talk about the electronic spin currently, an awkward saying which must attached is that the spin is the intrinsic attributes of electron, and it does not correspond to any of real physical meaning. We have to do so in demand for the taking value of angular momentum, because the real physical meaning of the spin of electron would lead to a paradox that the electronic boundary would even run faster than light. The most basic reason which fallen into this embarrassed situation is that many of us believed that Dirac had proved the existence of the spin of electron, and the quantum mechanics happened to need a magnetic rotation for electron, furthermore, all the previous conclusions are proved to be right with almost no exceptions at that time.
In fundamental physics, the appearance of puzzled saying is not that of the true essence of nature and physics style. As to the problem of electron spin, Z.H. Mei et al. (2013) have given very strong arguments in their paper [13] ; they revealed that the screw factor resulted in Dirac equation is a relativistic effect, rather than the real spin of electron; as a matter of fact, the real acting factor is the rotation of electron in an orbit, simplified here as just “orbital rotation”.
2.5. About the Uncertainty Principle
The intuitive concept, orbital rotation, is not easily been recognized and accepted by scientific communities. It is due to the uncertainty principle.
In 1927, starting from the non-commutability between the position and momentum, Heisenberg found and named the uncertainty relation, and explained the characters to be dependent from measure. Soon afterwards, Earl Kennard (1927) and Howard Robertson (1929) improved the work and resulted in the modern uncertainty relation inequality; regarded it as a natural disposition of micro particles, and to be independent from measure, and renamed it as the uncertainty principle. The third attitude was that they consider these two completely different expressions to be equivalent.
No matter what kinds of things they were, an important thing is that, all of them implied or acquiesced in an arbitrary deduction (not put forward formally) that, “the electron cannot exists in its trajectory movement”, as a part of principle of quantum mechanics as everyone knows.
Then, under the guidance of quantum mechanics, people have become more cautious, taboo any impression of electronic particle nature, say nothing of understanding and accepting the concept of “orbital rotation”. Anyway, the uncertainty principle implied a sort of deep meaning; it shocked the strict causality and the world view that people long-term believe and adhere to. The relation of uncertainty is right, but the understanding of its meaning is significant. All in all the problems have been focused on the deduction. How can we face it?
It has proved that the uncertainty relation is a consequence of the wave nature of electron. The uncertainty relation is not an independent character of nature. Since the wave nature of electron has hold in hand, it isn’t necessary to attend to what the uncertainty relation means.
On the other hand, recall that particular favor has paid on wave quantum mechanics; we have been intoxicated and paralyzed by the aura of quantum mechanics. Is the superconducting that make us wake up, let us see clearly the limitation of the traditional quantum mechanics. It make us to rethink why can the Bohr atomic model explain the hydrogen spectral series accurately to be regarded as a wrong thing at starting point, complain why we have to temporarily abandon the description of pure wave quantum mechanics for explaining the general dispersion force between all of molecules, worry the unsolved physical mechanism of the formation of light polarizability and the elliptic polarization, and look back the embarrassed issue we faced in electron spin. So, if a direct answer must be given, it seems that, as to the explanation of uncertainty relation, Heisenberg was right, and Earl Kennard would be wrong.
3. Theoretical Modeling
Hypothesis: Earl Kennard’s arbitrary deduction of uncertainty principle is wrong, and the electron has its trajectory motion and can be described because of the conservation law of momentum that any micro particle must comply with.
This is the only hypothesis the theory requires. If there is no influence of the deduction of the uncertainty principle, it is the hypothesis that does not required originally. After the assumption, we can establish some new concepts.
3.1. Introducing Concept of Orbital Rotation
Accept the concept that the electron exists in the state of rotation in an orbit, simplified as “orbital rotation”. It is the orbital rotation that generates the vectorial magnetism of electron [13] .
3.2. Establishing Concept of Cold Electron
Traditional Schrödinger wave function is a description of the state function of ideal electron. The actual new Schrödinger wave function should be related to temperature. In the absence of outside interference or at absolute temperature of zero, the orbital of electron takes the shape of two-dimension. It converts to three-dimension as temperature increases; the higher the temperature is, the greater the proportion it converts, i.e., the electron orbital shape is temperature dependent. Electron may be different in cold or hot state as the temperature can be low or high. The electron in atoms at low temperature is called the “cold electron”. As temperature goes much lower, the electron orbits will obviously departure to what Schrödinger function described. The cold electron’s orbital would present in an obvious flat character.
3.3. Formation of Cooper Pair of Electron
Cold electron runs in a flat orbital. It seems as a current carrying coil and possesses strong magnetism. In case of two electrons running in the same orbital, acting as two coils which occupy the same space, they have no way but to overlapped with each other. Only if the possession of opposite direction of orbital rotation, will the two electrons can be attracted, coupled and paired to each other by magnetism, and the Cooper pair (we still so call it) is then formed. The shape of the orbital is flat and directional. The coupling (or pairing) means the overlapping of trajectory of the two electrons, instead of the direct proximity in distance. In fact, the position of the two electron is at both ends of the orbit; the between electrons is still in a far distance. On the other hand, the coupling degree between the electron orbits is temperature gradient. So the formation of Cooper pair of electron has no absolute criterion. The magnetism of perfect coupling Cooper pair would be completely offset within its orbital.
3.4. Mathematical Description
Following Bohr’s atomic model theory, we attempt to describe a running electron in atom in s orbit state. Some parameters used here are presented at first. The Avogadro constant, N0 = 6.022 × 1023; the permittivity of free space, ε0 = 8.85419 × 10−
For convenience, the typical element copper (Cu) was chosen for study.
The orbital radius for valance electron of Cu atom, 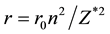 = 1.17 × 10−10 m, then,
= 1.17 × 10−10 m, then, 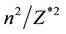 = 1.17 × 10−10/(0.529 × 10−10) = 2.2117.
= 1.17 × 10−10/(0.529 × 10−10) = 2.2117.
As to the valance electron of copper, n = 4,
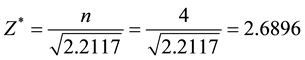
The shield coefficient, 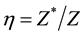 = 2.6896/29 = 0.092745;
= 2.6896/29 = 0.092745;
The kinetic energy of electron, 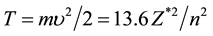 eV = 13.6/2.2117 = 6.1491 eV = 9.851 × 10−19 J, then;
eV = 13.6/2.2117 = 6.1491 eV = 9.851 × 10−19 J, then;
The velocity of electron, υ = 1.4706 ×
The frequency of circuit electron,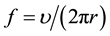 ;
;
The current of circular electron;
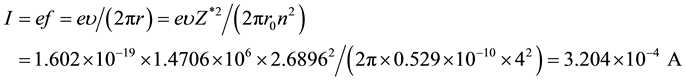
The paired electrons in same orbit have opposite magnetic moment direction. They may magnetically attract each other only if they were overlapped in a definite thickness of space, as shown in Figure 1(a).
The magnetic flux density,  (where, n0 is the number of turns of the coil in a unit length, μ0 the permeability of vacuum).
(where, n0 is the number of turns of the coil in a unit length, μ0 the permeability of vacuum).
So, the magnetic attractive force,

For two electrons in same orbit, the distance would be as large as possible, thus the distance, R ≈ 2r. And the shield coefficient come from the nuclear has the same value as η, so we have the charge repelling force,
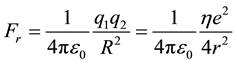
As the attractive force must equal to the repelling force we have, Fa = Fr, solve the equation we have,
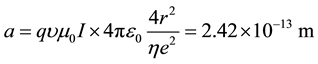
Such we obtained the self-inductance coefficient,

Figure 1. Description of paired cold electron with opposite direction in s orbital. (a) Overlapped electron orbit with the thick of a at 0 K; (b) Two flat electron orbit with the cross angle of φ at certain temperature; (c) The ellipsoid orbital shape of paired cold electron at certain temperature.
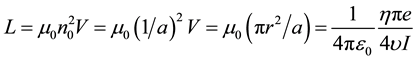
For a single paired magnetic energy we have,
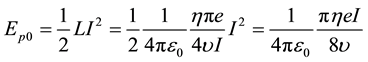
Express it in unit of molar, we obtained,
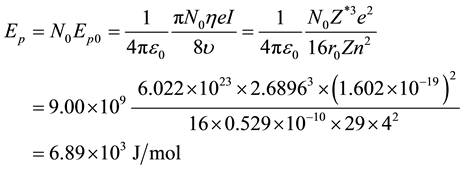 (1)
(1)
So, the heat against the paired magnetic energy cause a deviation in angle (φ) cross each other at the center, as expressed in Figure 1(b), and then the deviation of paired magnetic energy,
 (2)
(2)
We know that, the work for two charges (qa and qb) separation in one-dimensional range (r1 → r2) can express as
In case of lattice here, r1 is the distance between irons. Increasing temperature cause the increasing short radius of ellipsoid orbit (as expressed in Figure 1(b)), and the increasing short radius of ellipsoid orbit cause the distance increasing from r1 to r2. So, we have relation,
where r express the valence orbital radius as has used above in this paper. It is clear that, 
Then, we obtained the work (caused by temperature),

where, the coefficient ξ is the ratio of orbital diameter to lattice distance,
For heat energy in thermodynamics,
It is the heat energy that caused the deviation of paired magnetic energy (W1) and the lattice work (W2). So, we have relation,
Finally we obtained,

It must be noticed that, the lattice energy, U, has quite different value whether it is in normal or super condensed state, and the U also depend upon the kinds of matter.
The ratio (f) of short to long axis radius of ellipsoid equals to sinφ, its shape varies with temperature as shown in Figure 1(c). Some corresponding data are listed in Table 1 according to Equation (4) if roughly choice the parameters ξ and U as the values of 1 and 3000 × 103 J/mol respectively. As to the lack of data of U in super condensed state, we temporarily treat it as the same as normal.
As to the inner electron of copper atom, according to Equations (1) and (4) at same temperature, with the decrease of number n, the effective nuclear charge number, Z*, increase; the two vary parameters will result in the large decrease of f. In other words, the shape of inner electron pairs is much flat than the outer ones.
4. Results and Discussion
4.1. Theoretical Explanation of Superconductivity by Cold Electron
4.1.1. Perfect Diamagnetism
Under ordinary temperature, the magnetic attraction was weaken for their coiled trajectory merely partial overlapping by a cross angle (φ) of two electrons. In this case, the repulsion is dominant between the two electrons; they tend to occupy different orbitals possessing same (or nearly same) energy level and adjust to same rotating direction (parallel magnetic direction) to keep attraction and obtain low energy state. But the situations changed at a proper low temperature; the cross angle (φ) was small; the magnetic attraction of coiled trajectory of two electrons became the dominant factor; the single electrons tended to pair in same orbital to obtain low energy
Table 1. Corresponding radios (f) of short to long axis radius of ellipsoid with temperature accordingly, where the parameters ξ and U was assumed to be 1 and 3000 × 103 J/mol respectively.
state. The Cooper pair of electron was then formed. The magnetism is offset in every single orbital, and the magnetic character in atoms disappeared, not to mention the magnetism of a bulk material. That’s just the fundamental reasons of the phenomenon of perfect diamagnetism, taking place after the phase transition at critical temperature.
At extreme low critical temperature, the electron in atoms in bulk material was changed from hot to cold, and formed the flat Cooper pair. It offers a great space for lattice compression, i.e., at 135 K compared to normal temperature, the lattice compressible space can be calculated as
That is a quite considerable compression in space for a solid matter. As the flat orbital directions of Cooper pair are inharmonious, the rest room can’t be used by lattice atoms easily. The volume of the object does not change at first. The lattice of the object is in a metastable state. However, under an external stimulus or lower temperature, the atomic lattice can be destroyed, and the lattice compression takes place. The object was transformed into super condensed state.
Any material will be transited into super condensed state at a certain critical temperature. In super condensed state, the interactions between orbitals will suddenly strengthen due to the shorter distance between atoms.
The orbitals of conduction band have higher energy level than valence band, and occupy the outer space. On the basis of molecular orbital theory of quantum mechanics, the interaction and energy splitting of the conduction band are stronger than the valence band. The energy levels of the bottom of conduction band decrease greatly than the valence band, resulting in a sharp decreased band gap and great enhancement of conductivity. As to superconducting materials, the band gap decrease to a particular value of almost zero. Thus electrons in valence band were excited into the conduction band by energy of thermal radiation in normal environment, and the characteristic of superconduction occurred with the resistance of zero.
Electron in the conduction band was regarded as free between total atoms because of its delocalization, but it’s not absolute the case. According to the calculations of quantum mechanics, any electronic orbital is boundless, and can be seem as delocalization; the only difference is the probability of delocalization. Electron in the conduction band just has more probabilities than that of valence band, and more times the electron would run around its own nucleus. For a superconductor, the current intensity is limited, depending upon the delocalized probability. Based on this reason, any material may be seemed as superconductivity, the only difference was the size of the critical current intensity. When the current intensity exceeds a critical value, the resistance would appear. Reducing the temperature into super condensed state is for the increasing of critical current intensity of superconductors.
4.1.4. Advantages of the Proposed Theory
The proposed model of cold electron quantum mechanics can explain superconductivities at both low and high Tc. Cold electron offers a great space for lattice compression. It offers a new microscopic mechanism of the formation of Cooper pair, not the using of phonon. The introduction of phonon in BCS theory is isolated in theoretical system and not compatible with quantum mechanical system; it threw away the quantum mechanics perfectly. The proposed model in this paper explained the necessity of the possession of opposite direction of orbital rotation of paired electron. Especially it explains the perfect diamagnetism smoothly.
The model is the inheritance and development of traditional quantum mechanics; its advantage is promising to become a uniform and global theory. It could be expected that the perfect real ab-initio quantum (temperature included) calculation and the dispersion force between all of molecules and the physical mechanism of light polarizability can be achieved and explained by the developed new quantum mechanics in future.
4.2. Theoretical Prediction of Superconductivity
In the critical temperature, the superconductor is in the metastable state before phase transition at first. Though it was in the phase transition temperature, the metastable structure also has certain stability; the phase transition will not take place unless it was stimulated after ultrasonic wave, electric pulse, mechanical vibration, static pressure and supercooling temperature etc. It is to say that, there are no superconducting properties before phase transition takes place. Therefore, it is necessary to distinguish between the critical temperature and critical temperature of supercooling when measuring. The real critical temperature is naturally higher than that of supercooling.
A non-zero energy band gap exists inevitably between the conduction and valence bands of superconductor. The gap size is comparable to heat radiation of environment at normal temperature. The band gap should be as small as possible, preferably without. So there is no need to design and manufacture a band gap in superconductor artificially.
Superconductor and superconducting state are different concept. The superconductor is the materials with the resistance of zero, and there exists no superconducting current. When electrical voltage was applied to the superconductor, the superconducting current would form and entered the state of superconducting. The process of voltage applied to or current changing is the process of resistance generating, and also to be the process of energy transformation, storage and release. At superconducting state, the resistance would be zero if the current does not change.
Superconductivity and perfect diamagnetism are two independent superconducting properties; meanwhile there is some association between them. Because of the character of perfect diamagnetism, the Cooper pair of electrons which would travel with no reluctance from other electrons is beneficial to conduction and is promoting and accelerating the approach between the band levels of conduction and valence. Perfect diamagnetism plays a supportive role for superconductivity.
Superconductivity has a critical temperature, and the perfect diamagnetism has the same. The two properties are appeared after the phase transformation, since the character of diamagnetism is temperature gradient. It is to say that the electrons already have coupled well before the phase transition. However, after the phase transition, the electrons would couple further because of the sudden increased lattice energy. Hence, the perfect diamagnetism has no other different critical temperature. This suggests that the material would happen to a phase transition of super condensed state at same temperature if a material was found with perfect diamagnetism at a certain critical temperature.
The perfect diamagnetism is different from superconductivity in their extents. The superconductivity can reach to its extreme (with resistance of zero), while the perfect diamagnetism can’t.
Any material can happen to a phase transition of super condensed state at a certain temperature, and the diamagnetism and conductivity would be all abrupt enhanced afterwards. The most common materials can mutate into perfect diamagnetism, only a spot of them―the special materials―possessing superconductivities.
4.2.5. Advantages of Compression
In the condition of pressure applied, superconductor would enter super condensed state earlier. It is beneficial to raise the critical temperature, the greater the pressure, the higher the critical temperature. This pressure can both come from external and the internal stress.
4.2.6. Advantages of Layered Structure
In the super condensed state, the electron orbital is flat arranged orderly, the chemical bond has more advantages in layered direction. It enhanced the joint of material, and the conductivity in layered direction would be better than that of other direction. So, the choice of originally layered or acicular structural materials would be relatively beneficial in raising the critical temperature of superconductor.
4.2.7. Advantages of Strength of Chemical Bond
In normal conditions, the stronger the chemical bond between atoms in materials is, the higher the critical temperature would be.
4.2.8. Advantages of Conduction
In normal conditions, a material with preferable conductivity has small band gap. It created a favorable condition for conduction band can finally close to valence band after entered super condensed state at low temperature. Unilateral speaking, a normal good conducting material would be advantageous in superconducting at high temperature.
4.2.9. Advantages of Doping
The doped material can make an original insulator to a semiconductor, an original semiconductor to a conductor. Similarly, doping will make a conductor to a good conductor and then a superconductor. The essence of doping is the change of energy level of conduction or valence band. The N type doping is the ascension of valence band, resulting in reduced band gap; the P type doping is the reduction of conduction band, also resulting in the purpose of reducing the band gap. For the study of superconducting materials, doping (including PN type composite doping) is beneficial to improve the critical temperature of superconductor.
4.2.10. Avoiding Elements of Paramagnetism
The existence of paramagnetic elements such as Nd, Fe, Mn, Co, Ni and Cr and so on would need a proper low temperature for pairing the single electron orbital to form the Cooper pair. So the magnetic elements would hinder the achievement of perfect diamagnetism of a studied superconductive material. For researching high temperature superconductor, the paramagnetic elements must be avoided; the existence of iron Cu2+ is not considered to be a good factor either.
5. Conclusions
The proposed cold electron quantum mechanical model is compatible with traditional quantum mechanical system and explained superconductivities well. It needs to be further tested and perfected in practice in future.
At low critical temperature the paired cold electrons save quite some space in atomic crystal lattice. It creates the preconditions for the phase transition. Chemical bond is so changed sharply, and some special materials become superconductor. The highest critical temperature of superconductor must be below the limitation of about 553 K.
Cite this paper
ZhenhuaMei,QingxianYu,ShuyuMei, (2015) Cold Electron Quantum Mechanical Model for Superconductivity. Journal of Modern Physics,06,1298-1307. doi: 10.4236/jmp.2015.69135
References
- 1. Jin, J.X. (2008) Journal of Electronic Science and Technology of China, 6, 225-236.
- 2. Shen, L.N. (1985) Cryogenics and Superconductivity (in Chinese), 40, 64-70.
- 3. Qu, H. and Zhou, S.P. (1999) Acta Physica Sinica (in Chinese), 48, 352-362.
- 4. Wang, W.G. (1990) College Physics (in Chinese), 4, 1-3.
- 5. Nambu, Y. (1960) Physical Review, 117, 648.
http://dx.doi.org/10.1103/PhysRev.117.648 - 6. Eliashberg, G.M. (1960) Soviet Physics—JETP, 11, 696.
- 7. Mcmillan, W. (1968) Physical Review, 167, 331.
http://dx.doi.org/10.1103/PhysRev.167.331 - 8. Allen, P. and Dynes, R. (1975) Physical Review B, 12, 905.
http://dx.doi.org/10.1103/PhysRevB.12.905 - 9. Zhao, Z.X. (2011) Physics (in Chinese), 40, 351-352.
- 10. He, Q. (1993) Physics and Engineering (in Chinese), 4, 1-6.
- 11. Chen, C.X., Chen, S.G. and Huo, Y.P. (1961) Acta Physica Sinica (in Chinese), 17, 31-40.
- 12. Lin, D.H., Tong, C.Z., Zhang, J. and Wu, Z.M. (2002) Journal of Chongqing University (in Chinese), 25, 142-144.
- 13. Mei, Z.H., Mei, S.Y. and Yu, Q.X. (2013) Discovery Science, 5, 20-23.
NOTES
*Corresponding author.










