Received 4 February 2015; accepted 27 June 2015; published 30 June 2015

ABSTRACT

This article gives the potential energy function of quark in the gluon field, derives the wave function of quark in stationary state and the quark confinement and asymptotic freedom, shows that a quark is composed of two different color gluons, expounds the formation mechanism of the quark confinement and asymptotic freedom and the physical substance of “colors” of quark, and discusses the stability of hadrons in the end.

Keywords:

Gluon Field, Potential Energy and Wave Function of Quark, Confinement and Asymptotic Freedom, Composition of Quark, Substance of “Colors” of Quark

1. Introduction

According to the analysis of experiments, quantum chromodynamics tends to think that quarks inside hadron have two important features―the quark confinement and asymptotic freedom [1] -[7] . The reason the two important features have not been proved in theory for a long time is that the previous literature of QCD did not give specific potential energy function of quark from which the two features can be derived [8] - [16] . Most of the literature focuses on the general properties of the quantum gauge field and the application of the perturbation method in QCD, but the quark confinement and asymptotic freedom is just a problem of the bound state that cannot be solved by the perturbation method. For this reason, this article will give the potential energy function of quark in gluon field on the basis of the parton model of hadron and the quantum gauge theory, derive the wave function of quark in stationary state and the quark confinement and asymptotic freedom from that potential energy function, show that a quark is composed of two different color gluons, expound the formation mechanism of the quark confinement and asymptotic freedom and the physical substance of “color” of quark, and discuss the stability of hadrons in the end. We will see that the potential energy function of quark and the assumption of that a quark is composed of two different color gluons put forward in this article are in accordance with a lot of experiments, and so are reasonable and credible.

2. The Potential Energy Function of Quark

Without missing generality, we discuss the proton as an example since the proton is the only stable hadron. Assume that there is a spherical symmetrical gluon field of the radius R in the proton where the gluons are point particles. In order to have the confinement and asymptotic freedom for the valence quarks 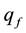(the subscript f is a flavor index) we construct a spherical symmetrical potential energy function of quark in the following:

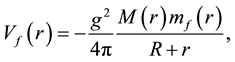(1)

where r is the distance from the center to the quark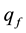, , 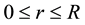and

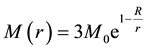(2)

is the interactional mass of proton within the range of radius r, where the factor 3 is from that the quark has three kinds of “colors” in the proton whose mass is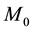; and

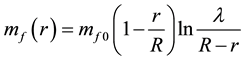(3)

is the interaction mass of quark and running, the constant 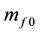is the mass of constituent quark whose mass is

usually taken approximately as one third of nuclear mass; 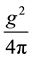is the strong interaction constant, 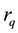is the ra-

dius of quark, and the constant,.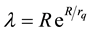

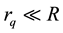It is not difficult to see that from Equations (2) and (3) since

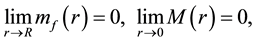(4)

there are

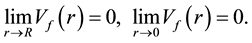(5)

The above two equations show the gluon field is within the proton and limited.

3. The Probability Density of Quark

It is interesting that the mass distribution in the proton can tell us intuitively why there is the quark confinement and asymptotic freedom. From equation (2) we obtain the mass density in the proton

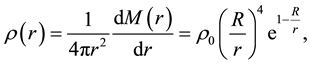(6)

where 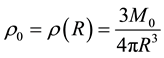is both the mass density at the boundary and the average mass density in the proton, and shows that the introduction of factor of 3 is necessary in Equation (2). Write

(7)

where is the wave function of quark with flavor f and color c in stationary state. As said previously, the mass of constituent quark is one third of the nuclear mass, if assume the probability density is independent of flavor f and color c, then

(8)

and it satisfies the normalization condition:

(9)

So the wave function of quark with flavor f and color c in stationary state is

(10)

where, the energy, T_fc is the free energy of quark and its potential energy

， as shown in the Equation (1).

Thus the probability density of quark distribution

(11)

where is the volume of proton. The above equation shows that the distribution of quarks or the con-

struction of proton is independent of energy of quarks, and this is commonly referred to as the scaling. From the

above equation we can know that the probability density has the maximum at,

at the boundary and zero at the center, as shown in the Figure 1. This implies that the distribution probability of quarks in the region of is greater far than that near the center. This is obviously because that the quarks are fermions. From Figure 1 we could see that the formation of the quark confinement and asymptotic freedom is very natural, and we prove it directly in the following.

4. The Quark Confinement and Asymptotic Freedom

Substitute Equations (2) and (3) into Equation (1) which could be written as

(12)

where the constant. And the net force on the quark is

(13)

Take we have

Note and, the second term in the brackets on the left side in above equation could be neglected, and

so the position of that the net force is zero

(14)

The function curve of the potential energy is shown as the Figure 2, where is at, the net force on the quark is the gravitation; and at, the net force is the repulsion.

It is not difficult to see that from Equation (13)

(15)

this is the quark confinement; and

(16)

this is the asymptotic freedom. Thus, we have derived both the quark confinement and the asymptotic freedom from Equation (1). In order to find out the physical mining of the quark confinement and asymptotic freedom, let us discuss the coupling coefficient of quark with the gluon field.

5. The Running Coefficient of Coupling

Rewrite the net force on quark (see the Equation (13)) into Coulomb type:

(17)

where

(18)

is the coupling coefficient of quark with the mass. It is just the running coefficient of coupling to change with the movement of quark. Obviously, there is

(19)

this is identical with equation (15) in physical meaning and denotes the quark confinement, too. And

(20)

this shows that the net force on quark in the depths of gluon field is repulsion. The above equation is coincident

with Equation (16) in physical meaning, and the reason the Equation (16) equals zero is that, but

for the coupling coefficient. What is the physical picture hidden behind the quark confinement and asymptotic freedom, then?

6. The Composition of Quark

As shown in Equation (4) there is

(21)

this shows that the mass of quark turns out to be zero near the boundary of the proton. What does that imply? Since Equation (1), from which the quark confinement and asymptotic freedom have been derived, is credible and is one of important factors in it, so, we have to give a reasonable explanation about what is the physical meaning of the above equation.

We know the gluons have no mass according to the quantum gauge theory. Thereby, the logical explanation of the above equation is that when a quark enters the region of, it gets closer and closer to the boundary of the proton, the gravitation on it is greater and greater, and it resolves into the gluons eventually. But this implies that a quark is composed of gluons. How do gluons constitute a quark, then?

Firstly, if we believe that quark consists of gluons, the gluons should be charged because quarks are charged. Otherwise, the conservation law of charge will be violated. In fact, quantum gauge theory did not conclude that gluons are not charged. It is inappropriate to equate the gluon and photon. However, a quark cannot be composed of two gluons with equal and opposite electric charges. If so, quark is electrically neutral.

Secondly, the gluons as quanta of non-Abelian gauge field should be fermions rather than bosons. In fact, because the quarks are fermions of spin 1/2, the gluons to constitute a quark should be fermions, too. Therefore, two gluons of the same color are repulsive to each other and cannot constitute a quark according to Pauli exclusion principle. The gluons to constitute a quark can only be different gluons in color.

From the above analysis we could put eight kinds of gluons into two groups according to the electric charge of gluons. The gluon group consists of four kinds of gluons, their electric charges are

(22)

the anti-gluon group consists of four kinds of anti-gluons, their electric charges are

(23)

where the color index. The spin of every gluon or anti-gluon is one fourth.

Assuming that only the two different color gluons or anti-gluons can constitute a quark or anti-quark, the two groups constitute justly 6 kinds of quarks or anti-quarks shown in the following, respectively.

Quarks:

(24)

Anti-quarks:

(25)

If the electric charge or spin of a quark equals the sum of that of its two constituent gluons, the charge of 6 kinds of quarks is

(26)

where. Similarly, the charge of 6 kinds of anti-quarks is

(27)

and the spin of every quark or anti-quark is.

The gluons and anti-gluons could annihilate into different particles in different interactional courses when they met. For example, the meson composed of the anti-quark and quark, or the two gluons and two anti-gluons, could annihilate into or [3] .

7. The Formation of Quark Confinement and Asymptotic Freedom

According to the above composition rules of quarks, the formation mechanism of the quark confinement and asymptotic freedom could be explained clearly.

A quark composed of two different color gluons is repulsed by same quarks (or gluons) according to Pauli exclusion principle, and at the same time attracted due to the exchange of gluons with the rest quarks (or gluons). Since the number of the same gluons in color is only one eighth of the total gluons and anti-gluons, the probability of a quark to be attracted is greater than its probability to be repulsed in the general case. But when a quark is in the region of, especially, in the depths of gluon field, the gravitation from all directions is weaker and roughly balanced out due to the infrequent exchange of gluons with the rest quarks or gluons, the net force on the quark is repulsion, as shown in Equation (20), and the quark is in a state of approximate free motion, this is the asymptotic freedom. When a quark is in the region of, especially, in the fringe region, the stronger gravitation toward the inner region keeps the quark in bound state, or even disintegration into gluons due to the frequent exchange of gluons with the rest quarks or gluons, this is the quark (gluons) confinement. In short, the reason the quarks and gluons are in the stable bound state is that there is the internal repulsion and surface tension in the proton.

8. The Physical Substance of “Color” of Quark

As said previously, gluons are fermions. So a quark composed of two different color gluons has three kinds of wave functions, or three kinds of “colors”. If the probability of the quark in each “color” state is equal, the hadron observed is in the singlet color state, or colorless state. This could be proved in the following.

Since a quark is composed of two different color gluons and, its free energy could be written as

(28)

where are the respective energy of two gluons, and is their binding energy. According to the Ising model [14] , the binding energy of two gluons as point particles with spin (neglect their electromagnetic binding energy) could be written as

(29)

where is the quantum of binding energy of two gluons and different for different quarks in flavor, so the mass is different for different quark. Substituting which is the number of gluons in the quark,

which is the number of states of that two spins equal and which is the number of states of that one spin equal into the above equation, we obtain

(30)

Substituting the above equation into Equation (28) and then into Equation (10), we see that the wave function of quark has three different components, or the three kinds of “colors”:

(31)

Notice the probability density is independent of the binding energy or “colors”, there is

(32)

This is Equation (11) used previously, it shows that the valence quark is in the singlet color state. Therefore the hadron observed is in the singlet color state, or colorless state.

9. The Stability of Hadrons

A lot of experiments show that the pseudoscalar mesons and baryons are unstable besides proton. According to the above composition rules of quarks, it is not difficult to see that from the equations (33) and (34) [15] -[17] the reason the pseudoscalar mesons

(33)

are unstable is that they contain gluons and anti-gluons annihilated each other in meeting, and the reason the baryons are unstable besides proton is that they contain the same gluons repulsive to each other. The reason the proton is stable is that it is a lightest baryon in octet.

(34)

As for the so-called particles in decuplet shown in Equation (35) [15] -[17] , the reason they are unstable is that they are in resonance or excited state unlike general particles, and transit naturally towards the ground state. Therefore, we cannot consider that the repulsion between same gluons makes the particles to be unstable only according to the form of Equation (35). The repulsion between same gluons should not be one of important factors in the transition.

(35)

10. Conclusion

The above analysis shows that the potential energy function of quark and the assumption of that a quark which is composed of two different color gluons put forward in this article are in accordance with a lot of experiments, and so are reasonable and credible.

References