Journal of Modern Physics
Vol.06 No.05(2015), Article ID:55833,5 pages
10.4236/jmp.2015.65069
Critical Theory of Two-Dimensional Mott Transition: Integrability and Hilbert Space Mapping
Federico L. Bottesi1, Guillermo R. Zemba1,2
1Facultad de Ingeniería, Pontificia Universidad Católica Argentina, Buenos Aires, Argentina
2Physics Department, Comisión Nacional de Energía Atómica, Buenos Aires, Argentina
Email: fbottesi@gmail.com, zemba@tandar.cnea.gov.ar
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 February 2015; accepted 17 April 2015; published 21 April 2015
ABSTRACT
We reconsider the Mott transition in the context of a two-dimensional fermion model with density-density coupling. We exhibit a Hilbert space mapping between the original model and the Double Lattice Chern-Simons theory at the critical point by use of the representation theory of the q-oscillator and Weyl algebras. The transition is further characterized by the ground state modification. The explicit mapping provides a new tool to further probe and test the detailed physical properties of the fermionic lattice model considered here and to enhance our understanding of the Mott transition(s).
Keywords:
Mott Transition, Conformal Field Theory, Chern-Simons Theory, Effective Field Theory, Quantum Groups, Integrable Models, Strongly Correlated Electrons

1. Introduction
The physical properties of strongly correlated electron systems are difficult to predict or even to describe, mainly because of the lack of suitable reliable tools to study them. Among these systems, the Mott Insulators (i.e., electronic systems which undergo a metal-insulator transition driven by correlations) have a prominent place. Most of the studies of the Mott transition are based on the microscopic dynamics of the electron system. The models are defined by an electron Hamiltonian that is then solved either by some approximation or by numerical methods. Both methods have their limitations, which have been discussed, e.g., in [1] . As of today, there are two basic tools to study the Mott transition that complement themselves. One is the Dynamical Mean Field Theory (DMFT) method, valid in the limit of infinite space dimensions [2] . The other tool is the use of integrability properties such as the Bethe Ansatz or bosonization techniques in some specific models, mostly in one spatial dimension. Different, non-perturbative approaches to models that display some form of Mott transition are therefore desirable. One such approach is that of the EFTs [3] , which has been shown to be a powerful tool for dealing with strongly correlated systems (in particle, condensed matter physics and statistical mechanics, among other areas of knowledge). The EFT in condensed matter physics has its roots in Landau’s ideas of effective degrees of freedom and their characterization throughout symmetry. It has been further developed after the introduction of the Renormalization Group ideas following Wilson’s approach. The main idea is to first identify the characteristic effective degrees of freedom of a given system at a given energy scale (usually arising from the phenomenology), identifying their symmetries and then writing down the most general Hamiltonian (or Lagrangian) compatible with those symmetries.
For the case of the Mott transition, we have applied the EFT method to a fermion model on the lattice with density-density coupling in a previous paper [4] . In that article, we have provided an extension of the method of integrability to a (2 + 1)-dimensional spinless fermion model with nearest neighbors Coulomb interactions, having written down an Effective Field Theory (EFT) to further study the properties of the model at the Mott transition critical point. The goal of the present article is to reformulate this approach in a different, perhaps more straightforward fashion which could be useful for future developments and generalizations, and to shown that the EFT previously obtained is actually the corresponding (equivalent) field theory at the level of the Hilbert space at the critical point. Moreover, under this approach, we will show that, the Mott transition is characterized as a change in the ground state.
2. Fermionic Model and Its Integrability
We start by considering the following Hamiltonian model:
 (1)
(1)
where 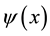 is the fermion field, x labels the lattice sites and
is the fermion field, x labels the lattice sites and 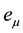 are the unit lattice vectors pointing to the nearest neighbors of a given site, a is the lattice spacing, t is the hopping parameter,
are the unit lattice vectors pointing to the nearest neighbors of a given site, a is the lattice spacing, t is the hopping parameter, 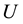 is the (constant) Coulomb potential,
is the (constant) Coulomb potential, 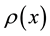 is the charge density (normal-ordered with respect to the half-filling ground state),
is the charge density (normal-ordered with respect to the half-filling ground state), 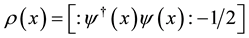 and
and 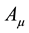 is an Abelian statistical gauge field defined on the links of the lattice.
is an Abelian statistical gauge field defined on the links of the lattice.
This model can be mapped into the two-dimensional anisotropic Heisenberg ( spin) model by means of a two-dimensional Jordan-Wigner transformation [5] :
spin) model by means of a two-dimensional Jordan-Wigner transformation [5] :
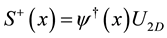 (2)
(2)
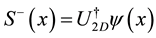 (3)
(3)
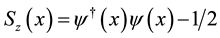 (4)
(4)
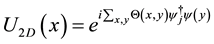 (5)
(5)
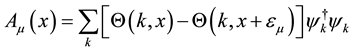 (6)
(6)
where 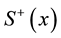 and
and 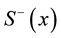 are the rising and lowering spin operators for spin one-half particles, and
are the rising and lowering spin operators for spin one-half particles, and 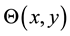 is the lattice angle between two points in a two-dimensional square lattice.
is the lattice angle between two points in a two-dimensional square lattice.
The partition function of the two-dimensional Heisenberg model, in the Hamiltonian framework, can be written as:

where 





where

where, we have made some abuse of notation since now 
As it is known, the 


where the 


which codifies the zero-curvature condition of a “quantum scattering problem”. Here 



where 





where q is the deformation parameter. The corresponding L operators are:

where we have used 




This means that the original model is mapped onto the q-oscillator model. It then becomes possible to study the states of the lattice fermion model (1) by analyzing the representations of the q-oscillator algebra.
For 


for 


To achieve a deeper understanding of the solution that we have just discussed, we may use a crucial property of the ZTE. Namely, the ZTE can be projected (or reduced) onto the Yang-Baxter equation after tracing out over one (temporal or spatial) direction. Tracing out over the y-column we obtain a one-dimensional Heisenberg 
In order to identify the critical point with the values of the parameters in the fermion model (1) let us remind that the reduced one-dimensional model (which has a long history) have been solved in [7] , and it is known to undergo a metal-insulator (Mott transition), and a charge density wave ordering (CDW) with a breakdown of the parity symmetry above the Mott gap. This Mott transition appears when

We will now study the representations of the q-Oscillattor algebra at the Mott transition point


which have cyclic representations for


Now we claim that the “corresponding” field theory at the level of the Hilbert space is a Double-Lattice-Chern Simons theory with abelian gauge group. To show this, first we shall impose periodic boundary conditions in the original fermion model, and compactify the manifold onto a torus such that the original square lattice matches with the lattice made by the homology cycles of this torus, and consider the Abelian C-S action [11]

this a topological gauge field theory with natural observables provided by Wilson Loops:

In holomorphic coordinates, the gauge field may be decomposed as:

where 




The local Gauge transformations on the CS theory are defined by:


where 




which satisfy a Weyl-algebra:

On the basis

the operators (29) act as:


where
Then, taken 




Secondly, we note that the projection property of the ZTE implies that each row (or column) is a 



Taking into account that the degrees of freedom of the Fermion Model (1) must be restricted to a square lattice, using the fact that the q-oscillator algebra splits into two Weyl algebras and using the parity of the original model, we deduce that the corresponding (equivalent) Field Theory at the Mott critical point of the fermion model (1) is a Double Lattice Chern-Simons theory:

with coupling constant


right), and where



the lattice-parameter) [14] . This theory has quantum group symmetry 
tion parameter 
3. Conclusion
In this article, we have reconsidered the integrability of the two-dimensional density-density coupled fermion moldel (1), which follows from the solution of the Zamolodchikov’s Tetrahedron equation associated with the 


Acknowledgements
G. R. Zemba is a member of CONICET (Argentina).
References
- Bottesi, F.L. and Zemba, G.R. (2011) Annals of Physics, 326, 1916-1940. http://dx.doi.org/10.1016/j.aop.2011.04.010
- Georges, A., Kotliar, G., Krauth, W. and Rosenberg, M. (1996) Reviews of Modern Physics, 68, 13.
- Polchinski, J. (1992) Effective Field Theory and the Fermi Surface. Lectures TASI, arXiv: hep-th/9210046.
- Sergeev, S.M. (2006) International Journal of Mathematics and Mathematical Sciences, 2006, Article ID: 92064. http://dx.doi.org/10.1155/IJMMS/2006/92064
- Fradkin, E. (1989) Physical Review Letters, 63, 322. http://dx.doi.org/10.1103/PhysRevLett.63.322
- Zamolodchikov, A. (1981) Communications in Mathematical Physics, 79, 489. http://dx.doi.org/10.1007/BF01209309
- Shankar, R. (1990) International Journal of Modern Physics, B4, 2371. http://dx.doi.org/10.1142/S0217979290001121
- Sergeev, S. (2006) Physics Letters, A357, 417-419. http://dx.doi.org/10.1016/j.physleta.2006.04.089
- Bazhanov, V.V. and Sergeev, S.M. (2006) Journal of Physics, A39, 3295. http://dx.doi.org/10.1088/0305-4470/39/13/009
- Kuniba, A., Okado, M. and Sergeev, S. (2015) Tetrahedron Equation and Generalized Quantum Groups. arXiv: 1503.08536 [math.QA]. Bazhanov, V.V. and Sergeev, S.M. (2015) Yang-Baxter Maps, Discrete Integrable Equations and Quantum Groups. arXiv: 1501.06984 [math-ph]. Kuniba, A., Okado, M. and Sergeev, S. (2015) Letters in Mathematical Physics, 105, 447-461. Mangazeev, V.V., Bazhanov, V.V. and Sergeev, S.M. (2013) Journal of Physics, A46, 465206.
- Korepanov, I.G. (1995) Algebraic Integrable Dynamical Systems, 2+1-Dimensional Models in Wholly Discrete Space- Time, and Inhomogeneous Models in 2-Dimensional Statistical Physics. arXiv: solv-int/9506003.
- Grensing, G. (1998) Physics Letters, B419, 258. http://dx.doi.org/10.1016/S0370-2693(97)01459-7
- Bos, M. and Nair, V.P. (1990) International Journal of Modern Physics, A5, 959. http://dx.doi.org/10.1142/S0217751X90000453
- Trugengerber, C.A. (1994-1995) Topics in Planar Gauge Theories. Lausanne U.
- Witten, E. (1989) Communications in Mathematical Physics, 121, 351. http://dx.doi.org/10.1007/BF01217730



