Received 22 September 2014; revised 21 October 2014; accepted 16 November 2014

ABSTRACT

Prevailing and conventional wisdom as drawn from both Professor Albert Einstein’s Special Theory of Relativity (STR) and our palatable experience, holds that photons are massless particles and that, every particle that travels at the speed of light must―accordingly, be massless. Amongst other important but now resolved problems in physics, this assumption led to the Neutrino Mass Problem―namely, “Do neutrinos have mass?” Neutrinos appear very strongly to travel at the speed of light and according to the afore-stated, they must be massless. Massless neutrinos have a problem in that one is unable to explain the phenomenon of neutrino oscillations because this requires massive neutrinos. Experiments appear to strongly suggest that indeed, neutrinos most certainly are massive particles. While this solves the problem of neutrino oscillation, it directly leads to another problem, namely that of “How can a massive particle travel at the speed of light? Is not this speed a preserve and prerogative of only massless particles?” We argue herein that in principle, it is possible for massive particles to travel at the speed of light. In presenting the present letter, our hope is that this may aid or contribute significantly in solving the said problem of “How can massive particles travel at the speed of light?”

Keywords:

Curved Spacetime Dirac Equation, General Spin Dirac Equation, Massive Photon, Unified Field Theory

“It counsels us to carry alternative hypotheses in our heads and see which ones best match the facts. It urges on us a fine balance between no-holds-barred openness to new ideas, however heretical, and the most rigorous skeptical scrutiny of everything―new ideas and established wisdom. ”

Carl Sagan (1934-1996)

1. Introduction

Despite the death and lack of solid experimental proof [1] -[4] , it is generally agreed (perhaps believed) that photons have no mass. Though this notion of a zero-mass photon has been questioned over the years [5] - [9] , this deeply entrenched notion has been deduced from the logical fusion of two (seemingly) immutable facts of experience so well supported by experimental evidence. The first is Professor Albert Einstein [10] ’s energy- momentum dispersion relation, namely:

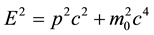(1)

where 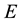is the total energy of the particle, 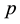is this particle’s momentum, 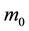is this same particle’s rest mass and is the speed of light in vacuum. The second fact is that the energy of the photon has been found from experience to be given by:

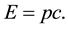(2)

If (1) and (2) are both applicable to the photon with all the identical symbols holding the same meaning, then, it follows directly that; that is, the rest mass of the photon must be zero. In the parlance of physics, this is generalised and stated by saying “a photon has no mass”. It is thus accepted forthwith that if a particle has zero rest mass, it will (must) travel at the speed of light. Conversely, if a particle travels at the speed of light, its rest mass must vanish identically.

Beginning in Section 2, we herein, place the two dispersion relations (1) and (2) into the dock for some cross- examination, whereafter we come to the interesting and startling conclusion that it must in principle be possible to have massive photons (i.e. non-zero rest mass photons) obeying these two relations simultaneously and concurrently i.e., massive particles that travel at the speed of light.

2. Silent Assumption

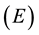As a first step, we would like to consider what we consider a hidden assumption in our proclamations on the photon mass. This hidden assumption in all the reasoning leading to the fact that for photons, is that the energies in the formulae 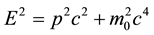and are identical. On a more fundamental level, there is no priori nor posteriori justification for this clandestine assumption. 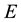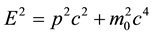If these two energies are different, that is, say the in is the total gravitational energy 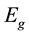of the photon so that 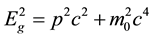; and the E in is say total kinetic energy of the photon so that, then, it is possible for. Combining these (i.e., and) would lead to where generally.

3. Small Mass Photon

Above, we have argued that if the in, , is not identical to the in the photon energy formula, , then, is not necessarily identical to zero. The afore-stated reasoning―while plausible, it may be considered weak because it is difficult to justify that the in, , is not identical to the in the photon energy formula,. Here, we drop this argument and take a more robust path. We give an argument that we believe is much stronger, plausible and better believable than the previous argument. For example, from the formula, , if, , then, we can write, , as,

, so that to first order approximation, we will have:

(3)

In the above Formula (3), the term, , is easily recognised from Newtonian mechanics as the kinetic energy of a particle. This fact that the Einstein energy-momentum relationship, , is able to reproduce the Newtonian kinetic energy term, , has been taken as a good sign on Einstein’s STR as it is required of any succeeding theory to reproduce results from its predecessor under certain first order approxi- mation.

The condition, , is not the only possibility. On a different but very relevant note, this condition, , can be considered to be applicable to matter. Logically, the other possibility is that,. Assuming that, , is applicable to photons, then, as before, we can write, , as, so that for the photon―to first order approximation, we will have:

(4)

The term, , is easily recognised from experience as the energy of a photon. The second extra term, , is a new term. If the Formula (2) is accepted¹ (as the first order approximation) formula for the energy of a photon, then, what (4) essentially means is that the new extra energy in (4), i.e., is so small that it is immeasurable―it is beyond the detection of our experimental capabilities, leading only to the component, , being detected as the photon energy. For this to be so, there is need for the rest mass, , to be extremely small.

Rightly, according to Dr. Sviratcheva (1999)², an experiment or observational measurement that fails to conclusively find or positively detect a mass for the photon, such a measurement does not prove that the photon mass is zero as is widely believed (without the direct proof); it merely shows that this mass is less than the limit or accuracy of the experiment in question. From this, we conclude that if the photon has mass as we believe, then, this mass must be very small so much that our measuring precession and accuracy may not have reached those levels where this photon mass can safely be pinned down. However, small it may be, this mass plays an important and pivotal role in the physics of the photon and the very foundations of physics. The currently accepted upper bound on the photon mass, , is impressively small, i.e., , which is times the mass of the electron (cf. [11] ).

Clearly, the latter argument―that the mass of the photon maybe small, so small that it most certainly has escaped detection of our finest experiments; this argument is much stronger than the former argument. If the energy, , was within detection, then, we would have had, , for the photon. With, , certainly, one can not trivially combine this formula with Einstein’s energy-momentum relation, , to obtain,. Perhaps, we³ where too quick to conclude from experiments that the formula, E = pc, is binding. By this (binding) we mean that the formula, , is accurate to any decimal place of the photon energy. The component, , will pop-up at higher decimal places which are not accessible to us in our current experimental capabilities and endeavours.

Before we depart in the present section, it is important that we take note of what the relation (4) implies or means insofar as the group velocity of massive photons is concerned. We know that, hence, from (4), it follows directly from, that:

(5)

that is to say, the speed of of light for massive photons now depends on the photon’s momentum (or wave- length, k). This has serious implications, especially on the phenomenon of Gamma Ray Bursts (GRBs) where it has been observed that photons of different energies originating from the same position in space where a GRB event has occurred, these (photons of different wave-lengths) arrive at the Earth’s detectors seconds or minutes apart. Amongst others, this phenomenon points to the fact that the speed of light may very well have a wave- length dependence as is implied in (5). In Section 9, we will look at this issue of GRBs.

4. Inertial and Gravitational

In continuing in the building of our thesis, we shall in this section demonstrate a simple and yet important point, namely that, the rest mass of a particle as defined in Professor Einstein’s Special Theory of Relativity (STR) can be identified with the inertial mass (as defined fundamentally in Newtonian mechanics) of a particle. This is not a new idea, it is as old as the STR itself. What is new perhaps is that this idea can be used to identify and distinguish gravitational mass from inertial mass. As is well known, there is at least two distinct and important kinds of mass that enter Newtonian mechanics, these are the gravitational and inertial mass. Most notably, due to Professor Einstein (in 1907 cf. [12] ), these two kinds of masses are considered to be identical.

4.1. Inertial Mass

The first fundamental mass is the inertial mass which enters in Newton’s second law of motion. As it was first stated by the great Sir Isaac Newton, this law states that the resultant of all the forces acting on a body is equal to the rate of change of motion of that body, i.e.:

(6)

By motion, Newton meant the momentum of the body in question. Momentum is the product of inertial mass and the velocity of the body in question. In most cases considered in natural systems, the inertial mass of the particle is a constant of motion, so this law is often stated as:

(7)

The vector quantity is the acceleration of the body in question. The inertial mass gives matter its inertial properties.

4.2. Gravitational Mass

The second kind of fundamental mass enters Newtonian mechanics in Newton’s law of universal gravitation is the gravitational mass (and). This mass is some sort of charge as is the case with electric charge between to electric charges. Newton’s law of universal gravitation states that the gravitational force drawing together two objects of gravitational mass and that are separated by a distance is:

(8)

where is Newton’s constant of universal gravitation and is the unit vector along the line joining the centres of mass of these objects and the negative sign is there to denote the fact that the gravitational force is a force of attraction.

Pertaining the gravitational and inertial mass, we have the Weak Equivalence Principle (WEP) due to Galileo which states that test bodies fall with the same acceleration independent of their internal structure or com- position: in other words, the gravitational mass appearing in (8) and inertial mass appearing (7) are the same i.e.. Throughout this reading, in order to distinguish between gravitational and inertial mass, we shall use the subscripts “” and “g” respectively i.e. and.

As has been done in [13] , we are going to denote the ratio between the gravitational and inertial mass as:

(9)

Now, taking a step further toward our desired end, we know from Einstein’s STR that the total energy of a particle is such that:

(10)

where is its speed and and. In the non-relativistic limit where, to first order approximation (10) is given by:

(11)

The term is the usual classical kinetic energy of the particle where the particle’s

inertial mass as defined in Newton second law, namely. It is generally agreed that in the non- relativistic limit, the equations of Einstein’s STR must reduce to the well known Newtonian equations. Accept- ing this bare thesis―invariably, this means that the rest mass as it appears in (11) can or must be identified with the classical inertial mass of a particle, i.e.:

(12)

From the forgoing, it means we can write (11) as:

(13)

Now, the energy E is equal to i.e.. The question is what is this in the formula; is it the gravitational or inertial mass? If as stated in the introduction of this section, we have only two kinds of masses, the gravitational or inertial mass, can only be one of these two. If this mass is the inertial mass, it would mean that the kinetic energy of any particle must be zero for all times and all situations in life since:

. This is obviously nonsense and must be rejected forthwith without any

further deliberations. This leaves us with no choice but to identify the in with the gravitational mass, i.e.:

(14)

In this case where, the kinetic energy emerges as nothing but the difference between the gra- vitational and inertial energy of a particle i.e.. Therefore, written with all the masses well labelled i.e. in-terms of the gravitational and inertial mass, (13) must sure be written as:

(15)

At this point, we have attained our desired objective i.e., we have shown that in principle, one can define or identify the rest mass as the inertial mass. Further, we have defined the gravitational mass as-well.

5. Massive Photon

Having somewhat defined the gravitational and inertial mass, let us revisit the idea presented in Section 2 where we stated that there is a hitherto hidden assumption in all the reasoning leading to the fact that for photons. This clandestine assumption lies in that the energies in the formulae and are assumed to be identical i.e. they represent the same energy. Are they really the same energy? Strangely, as far as our survey of the available literature that we have had the fortune to set our eyes and mind, we have come not across anyone that has wondered whether or not these energies are one and the same energies.

Is not the energy “” the kinetic energy of the photon since this energy is wholly associated with the motion of the photon? For example, in the photoelectric effect that led the great Einstein to make the hypothesis that light comprises a stream of tiny billiard-ball-like particles called photons, this kinetic energy “pc” of the photon is transformed not into another form of energy, but into the kinetic energy of the electron that gets ejected from the metal surface. This strongly suggests that “pc” is actually the kinetic of the photon and nothing more. The energy E in is not only the kinetic energy as this energy includes the potent locked-up energy. Perhaps we have not been all correct in assuming that the energy in is the kinetic energy of the photon. Actually, on a most pristine and fundamental level of reasoning, there really is no priori nor posteriori justification for this hitherto clandestine assumption.

If these two energies are different, that is, say the energy in is the total gravitational energy as argued in Section 2 and the in is say total kinetic energy of the photon so that, then, it is possible for because if we combine these two formulae (i.e., and), one is led to:

(16)

where generally. More convincing here is the idea presented in Section 3, that is to say, the photon mass is small, so small that we have failed to directly detect it with our present technology.

6. Speed of Massive Photons

In the present section, we shall―accordingly; derive an exact expression for the group velocity of massive photons of spin-. Thus far, we have used the equation, , whenever dealing with the energy-momentum of matter and radiation. From here-on, we now are going to abandon this equation in favour of the recently proposed general spin energy-momentum equation, [14] [15] . The energy- momentum equation, , is that of a particle whose spin is, , which in the parlance of quantum physics, we say the particle has spin-.

This equation i.e. [14] [15] , has not been explored since it is new―the scientific community is still to evaluate the worthy of its salt. Be that it may―as the author of the equation, we strongly believe it will stand the test of time―surely, we can not wait for the evaluation of it, but push for its relevance insofar as correspondence with physical and natural reality is concerned. So, as we apply it here, we do so on this faith that this equation is a sure advancement and a step forward from Professor Albert Einstein [10] ’s energy-momentum relationship,.

Since the photon is a spin-1 particle, according to this new equation, , it follows that, , for the photon. In Section 10, it will become clear when we analysis the motion of star light (electro- magnetic waves) that this fact that for a photon we must have, , if Newtonian gravitation is to stand-up to the eclipse measurements of the Solar gravitational bending of star light. This fact on its it own―i.e., the fact that for a photon we must have,; explains the missing factor “2” in the gravitational bending of light angle in Newtonian gravitation. We take this as a notable achievement of the theory of the Curved Spacetime Dirac Equations presented in the readings [14] - [16] , in that this theory has been able to furnish a missing piece of a great puzzle. It is an achievement in much the same way that Professor Paul Dirac [17] [18] ’s equation furnished the puzzle of the gyromagnetic ratio of the electron (see e.g. [16] on how the Dirac equation solved the gyromagnetic ratio of the electron).

Now, we come to the main issue of the present section―that of calculating the speed massive photons. The dispersion relation corresponding to the equation, , is:

(17)

where is Planck’s normalised constant, and are the angular frequency and the wave-number of a photon whose mass is,. If we set, , then, the above Equation (17) can be written as:

(18)

Setting, , implies that, if, , is the wavelength of a particle of energy, , then, is the wavelength of a spin- particle of the same energy,.

Now, if the mass, , of the photon is―say, dependent on the wave-number (and spin as-well) i.e. [consequently], then, the magnitude of the group velocity, , of such photons is according to (18) given by:

(19)

where is some constant wave-number that we shall define clearly latter and is the magnitude of the phase velocity of the photon whose spin is s/2. Since and are constants, let us set and as-well:

(20)

so that (19) becomes:

(21)

From (20), we have:

(22)

Solving this equation, i.e. (22), gives:

(23)

Writing (23) in-terms of the momentum, that is, with and, we will have:

(24)

It is interesting to note that. The state is the spin state. For the avoi- dance of digression, we will not say anything about this observation in the present reading. We we will leave this in the mind of the reader to ponder about its possible meaning. All we can say is that―there hidden in this state, there seems to be some exciting physics that can be be harnessed, very rich physics to do with cosmogony―the very origins of matter, its creation.

Now, we have to find a way to deduce the value for and the expression. To do this, we shall make use of (5). The expression (5) is a first order approximation for massive spin- photons. The ex- pression (21) is not an approximation but an exact expression. Naturally, we would expect (21) to give us (5) when evaluated to first order approximation. In-order for this to be so, we find that we must have be such that, which intrun implies that:

(25)

and for, we must have. From these settings, (21) will be such that:

(26)

As one can verify for themselves, the expression (26) does reduce to (5) when evaluated to first order approxi- mation. We take (26) is the exact expression giving the group velocity of spin- massive photons. For spin-1 photons which are such that, we will have as is the case in reality.

7. Distinction between Matter and Radiation

In this section, we shall ask and subsequently make the endeavour to answer the question “What distinguishes matter from radiation or radiation from matter?” We find that the answer to this question is within reach of the present ideas. One distinguishing feature of radiation (photons) is it appears to always propagate at the constant speed, while matter travels at varied speed from a zero up to nearly the speed of light. By seeking a relationship between the group and phase velocity using the idea that, we find that the question “What distinguishes matter from radiation or radiation from matter?” can be answered decisively.

If one where to go by the thesis presented in Section 6, then, they may very well draw the following conclusion:

1) For matter, we must have,.

2) For radiation, we must have,.

While the above define the energy-momentum regimes satisfied by both matter and energy respectively, we believe these conditions do not in general define matter and radiation. For example, it would mean that if a material particle were accelerated to high enough energy-momentum regimes where, that material particle must now become a photon. What this means is that the above conditions, while satisfied by both matter and radiation, these are not sufficient to define the distinction between matter and or radiation.

Let us consider the scenario where is not a function of (or) i.e. a scenario where the rest mass is constant. For such a scenario, the group velocity will be such that:

(27)

If the momentum of the particle is defined as it is defined in the STR i.e., as, , then,

substituting this into (27), one can show that. Since can take non-relativistic values and can be equal to zero, we must conclude that this setting must represent and define matter. Since we have already shown in Section 6 that the setting leads to a particle that is such that, it follows from the foregoing that we can define matter and radiation as follows:

1) For matter to be distinctly defined as matter, we must have, , i.e., is not a function of (or).

2) For radiation to be be distinctly defined as radiation, we must have,. For such systems, i.e., such system are never found in a state of relative rest (just as appears to be the case for photons).

We shall take the above as distinctly defining matter and radiation.

8. γ-Factor

We here calculate or deduce the -factor for matter and radiation.

8.1. Matter

From the equation and from the arguments presented above, it follows that we have to conclude that for matter, we must have:

(28)

In [13] , we have presented a way to measure the -factor for matter. Additionally, we have also presented (in Ref. [13] ) a way out of the problem that may arise from the violation of the WEP by showing that a conformal theory of gravitation will be needed to preserve Einstein’s all-embellished Principle of Equivalence which stands as the rock-solid foundational basis of his much celebrated General Theory of Relativity (GTR).

We put forward a proposal to test the hypothesis here set-forth that may vary depending on the particle’s position in a gravitational field of a massive central gravitating body. Our proposal is to use the very same experiment that the great Sir Isaac Newton used to measure this quantity i.e., the simple pendulum experiment. The period of a simple pendulum of length under and a variable is given by:

(29)

where is the gravitational field strength at the Earth’s surface. From the above, we can write , where:

(30)

In the above, is the average value of the period of the pendulum as measured in the laboratory. Likewise, the value is the average value of as measured in the laboratory. Now given that where is the eccentricity of the Earth’s orbit and is the semi-luctus rectum of this orbit: is the minimum radial distance of closest approach of the Earth to the Sun. From the given information, it follows that:

(31)

If a seasonal variation in is found as shown in Figure 1, it would be a clear indicator of the correctness of the present ideas. The greatest difficulty would be in the accuracy of the measurements, one would require a clock that can measure time to an accuracy of 12 significant figures. To see this, lets make a crude but accurate calculation. We know that, and that on average l = 1.49 × 10¹¹ m, and taking, so that. It follows that in-order to measure the period of the pendulum in a way that will yield results, one has to be able to measure this period to the significant figure.

For example, let us take a simple pendulum of length and further, let us assume that gravitational field strength at the Earth’s surface, such a pendulum will have a period of:

(32)

In this time interval, the most important figures are the last three numbers in bold and with an over-bar. These are the figures that will determine the correctness of our assertion because over the course of a year (preferably from January to December), these three figures are expected to vary in a way conforming to our assertion set- forth here-above. So, the proposed experiment must have the capacity to measure time durations to an accuracy of at least. This sensitivity is well within the capabilities of current technology and thus it should be possible to conduct this experiment.

8.2. Radiation

From (4), i.e., it follows that for radiation, we must have:

(33)

What the above means is that deflection of light by the Sun should take at least the Newtonian deflection of

0.87". This means that deflections in the range 0.87" - 1.75" are permitted: this deepens of the value of. Not only that, deflections exceeding Einstein’s 1.75" prediction are also permitted. We have made the endeav- our to address these and other issues arising from the present findings in the letter [13] .

9. Time Delay in GRBs

Without shying away from the truth, theories without any grounds on which to test them are worthless. They stand there with their miniature beauty only to be marvelled at for their shear beauty and nothing more and beyond. A true scientist needs to find solid ground on which their theories may be falsified―only this way will our science take great forward leaps into new territory. As such, we propose grounds on which the idea of photon mass as proposed herein can be investigated.

For this effort to test the proposed theory, we make an appeal to the measurement of time-delays in the arrival times of gamma-rays. These gamma rays of different energies which exhibit an arrival time-delay are supposedly emanating from the same event, that is to say, these flashes of gamma-rays where produced at the same time and left the same place at the same time. If the speed of light is to be dependent on the wavelength of light (energy), then, it is expected that there must be an observed time delay in the arrival times of these energy bundles.

If correct, then, in no uncertain terms, Equation (19) spells it out clearly that if the mass of a photon is a function of its wavelength (energy), then, photons of different energies will travel at different speeds. Clearly, an energy dependent speed of light has the potential to explain the puzzling time delays observed in Gamma-ray Bursts (GRBs) which where first reported by in 1973 by Klebesadel et al. [19] .

GRBs are the most intense gamma-ray events in the known Universe, originating from any random directions from the sky in a manner that is without precedent in all history of astronomy. When GRBs are observed, the more energetic emission arrives well after the low energetic emission. If these gamma-rays are emanating from the same event (source), they must leave this event at the same time and the observed delay must be due to a difference in speed of the low and high energy electromagnetic waves.

To demonstrate this, let be the distance from Earth where with GRB has occurred and let be the time taken for this flush to travel from the moment of emission to when it is observed on Earth. Further, let be the group velocity of these electromagnetic waves. From the information given, we know that, from which it follows that. If is the measure of the change of the speed of light from its vacuum speed, then, the meaning of which is that. The distance is measured by means of the redshift, , of the after-glow i.e. for galaxies and star moving at non- relativistic velocities where; this means:

(34)

From this equation, it is clear that if, there is going to be a time delay in the arrival of photons of varying speeds. Therefore, it follows from (26) that, to first order approximation, we will have for two photons of energy and that:

(35)

where is a differential change in the group velocity of electromagnetic waves which corresponds to a differential change, of the square of the two photons. Inserting as given in (35) into (34), leads us to:

(36)

Therefore, from (36), if for the data for which, we make the setting and, then upon a plot of vs, one would―if (36) where correct, expect these data to produce a straight line graph whose slope is. What the above little exercise is telling us is that a well calculated and carefully planned study of the GRBs data may reveal a relationship for the variation of the the rest mass of the photons with energy if-and-only-if this time delay in the arrival of GRBs is due to the energy dependence of the speed of electromagnetic waves with energy.

10. Bending of Light

As already said―in the reading [13] , it is argued that the pivotal, all-important, critical, crucial and supposedly watershed factor “2” emerging from Professor Einstein’s GTR and used in Solar eclipse measurements by Sir Professor Dr. Arthur S. Eddington as the clearest indicator yet that Einstein’s GTR is indeed a superior theory to Newton’s theory of gravitation may not be adequate as an arbiter to decide the fate of Newtonian gravitational theory. Therein in [13] , it is demonstrated or argued that the gravitational deflection of electromagnetic waves barely passing the limb of a massive object with mass and radius is given by:

(37)

What this essentially means for the Solar gravitational bending of starlight where the deflection angle has been measured to be very close to that predicted by the GTR i.e. δ = 1.75"; is that for such photons, we must have.

Now, given that for photons of spin- is given by (33), it follows that substituting this into (37), we will have:

(38)

Since, , it follows that the deflection is quantised as a result of the spin of the photon. This issue of the quantized gravitational deflection will be dealt with in a future reading.

What is interesting here about the Formula (38) is that is naturally fits the gravitational deflection of star light whose spin in 1 because for spin-1 photons, the value of is 2. Inserting this into (38), we obtain the same formula as that obtained from Einstein’s GTR. A value of implies that, thus, photons must have equal portions of gravitational and inertial mass.

11. General Discussion

If what we have presented herein is proven or shown to hold, then, the implications thereof have serious foresee- able repercussions and ramifications across the broad spectrum of physics as contemporary physics hitherto assumes that the mass of a photon is identically equal to zero, especially the embellished Standard Model of Particle Physics (SMPP). We have argued that this assumption may not be correct as it is based on a hitherto hidden and clandestine assumption that is not necessary; this assumption can be gotten reed off. It appears highly likely that is photons have mass, this mass must be extremely small behold the direct.

More than this, we have argued that, in principle, physics (i.e. Einstein’s STR and the theory of waves) has no problem with a massive photon that travels at the speed of light. If the ideas herein are accepted or acceptable, then, this places physics on a sure pedestal to consider massive photons as plausible physical objects of the Universe.

For example, in Quantum Electrodynamics (QED) and Quantum Field Theory (QFT) which are one of the two critical foundational pillars of the SMPP, a massive photon is not consistent with gauge invariance or renormalizability. However, via Proca Electrodynamics, one can devise a theory of massive photons [6] . Besides, one can also accommodate massive photons in Podolsky Electrodynamics. From the foregoing, it is clear that physics has never ruled out massive photons [5] [6] . Perhaps the reason they have been neglected in main- stream science is the shear difficulty that may be brought about by trying to renormalize the resulting theory. Renormalisation of QFT with a massless photon is already a nightmare, what more with a massive photon? However, from a theoretical perspective, if the rest mass of the photon where non-zero, classical electromagne- tism, QED and QFT would remain untroubled in spite of the undesired loss of gauge invariance [6] . On the beautiful side of things, loss of gauge invariance is too high a price to pay―few physicist would be prepared to pay this price. However, despite the desideratum of the physicist, if observations are to point in that direction, the only choice we have is to submit and move on.

On the more realistic side of things, if one can obtain results which are in satisfactory agreement with experience using a massless photon, why bother with an additional unessential? Simple let the sleeping dogs lay. In any case, Occam’s “all-powerful and very sharp” Razor forbids the unnecessary addition of non-essentials, so, there are very many good reasons to ignore massive photons. Perhaps physicist will consider them when they can longer avoid them at all. For now, there strongly appears to be no real need for them.

However, the notion that every particle that travels at the speed of light must―accordingly, be massless leads to an important but now solved problem in physics, this assumption has led to the Neutrino Mass Problem― namely, “Do neutrinos have mass?” According to Einstein’s STR, if neutrinos are massless, they must travel at the speed of light and conversely, if neutrinos travel at the speed of light, they must be massless. According of a recent CERN press release⁴ refuting the claim of faster-than light speed for neutrinos supposedly detected by the OPERA Collaboration in September of 2011, neutrinos strongly appear to travel at the speed of light.

Further, in order to explain neutrino oscillation, that is, the change of neutrinos from one state to the other⁵, neutrinos must have mass. Endowing neutrinos with mass helped solve one of the outstanding problems in Solar physics known as the Solar neutrino problem. The Standard Solar Model (SSM) which is a theory detailing how the Sun produces its energy predicted that the Sun must produce a specific amount of neutrinos. Prior to the 1988 Sudbury Neutrino Observatory (SNO) Experiment, all neutrino detectors that had ever attempted to measure the rate at which the Sun made neutrinos were getting values between 1/3 and 2/3 of what was expected from theory. This meant that there was a dearth in neutrinos produced by the Sun if the SSM was right―this deficiency came to be known as the Solar Neutrino Problem (SNP). Neutrino oscillations resolved the SNP: the electron neutrinos produced in the Sun partly change into other flavors which prior experiments could not detect. Other than this, measurements indicate that neutrinos most certainly have mass. Additionally―as alreadly stated above, neutrinos most certainly travel at the speed of light. We seem to have a apparent contradiction here!

Ceteris paribus: in the light of popular contemporary physics, how can a massive particle travel at the speed of light? Is not this speed a preserve and prerogative of only massless particles? If observations are to take their rightful place in Science, which is that they take precedence over all our theories, then, we have but no choice except to accept that massive particles most certainly can travel at the speed of light as strongly appears to be the case with neutrinos.

The only way is to amend our theories to conform with observations and experiments. To that end, we have demonstrated herein that in principle, it is possible for massive particles to travel at the speed of light. In our supposition that only massless particles must travel at the speed of light and conversely, that, if a particle does happen to travel at the speed of light, it must accordingly be massless, we have argued that this assumption may not be correct as it hinges on a hitherto hidden and clandestine assumption that is surely not necessary; this assumption can swiftly be gotten reed off. Further, a small mass photon has here been shown to be a possible explanation as to the failure by both observations and experiments to pin-down the photon mass.

If they exist as we propose herein, massive photons pause a problem namely that they are according to Maxwell-Proca Electrodynamics supposed be a short range phenomenon. As far as observations and experi- ments reveal and can tell, the electromagnetic phenomenon is a long range phenomenon. This raises the question: “If photons are massive, how do they come to be a long range phenomenon?. This question is desively dealt with in [20] .

12. Conclusions

Assuming the correctness (or acceptability) of the ideas presented herein, we hereby make the following conclusions:

1) As is typically assumed, massive photons do not necessarily lead to a violation of gauge invariance as we have shown that an appropriate choice of the gauge leads to a gauge invariant electrodynamics of massive photons.

2) The current belief or position that for a particle to travel at the speed of light it must be massless may not entirely be correct as this is based on a hitherto hidden and clandestine assumption that the energies in the formulae and E = pc are identical i.e. they represent the same form of energy. This hitherto priori and posteriori unjustified assumption is not really necessary. Dropping this assumption leads to the plau- sibility of massive photons and massive particles that travel at the speed of light.

3) Neutrinos may very well be good candidates to be described by the present ideas of massive particles travelling at the speed of light. These neutrinos must have a non-zero -factor, the meaning of which is that they must suffer gravitational deflection as happens with normal electromagnetic waves when they graze the limb of massive gravitating objects like the Sun.

4) Gravitational deflection of monochromatic electromagnetic waves (such as gamma and radio waves) by the Sun presents the best way to measure the mass of photons by measuring⁶.

5) It has been shown herein that it is possible for a photon to be massive. What is left to be answered is how massive photons come about to mediate as a long range phenomenon. This question is decisively dealt with in [20] .

Acknowledgements

We are heftily grateful to the National University of Science & Technology (NUST)’s Research & Innovation Department and Research Board for their unremitting support rendered toward our research endeavours; of particular mention, Prof. Dr. P. Mundy, Dr. P. Makoni, Dr. D. J. Hlatywayo and Prof. Dr. Y. S. Naik’s unwavering support. We are grateful to the insights of Dr. William Straub―his insights have helped refine some portions of the present theory. This reading is dedicated to my mother Setmore Nyambuya and to the memory of my dearly missed departed father Nicholas Nyambuya (27.10.1947-23.09.1999).

References