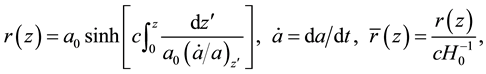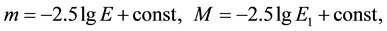Journal of Modern Physics
Vol.05 No.15(2014), Article ID:50151,12 pages
10.4236/jmp.2014.515153
Gravitationally-Neutral Universe
Alexey V. Klimenko, Vladimir A. Klimenko
Physics Department, Chelyabinsk State University, Chelyabinsk, Russia
Email: alklimenko@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 June 2014; revised 18 July 2014; accepted 14 August 2014
ABSTRACT
In the present article, we give a variant of the theory of gravity, which distinguishes between par- ticles and antiparticles. In this theory that called two-signed gravity, in contrast to Einstein’s gravity, contributions from particles and antiparticles in the tensor, which are the source of the gravitational field are taken with different signs. In two-sign gravity, antiattraction exists between particles and antiparticles. In the framework of two-signed gravitation, it is naturally assume that Universe is not only electroneutral, but also gravitationally neutral too. In present paper, we suggest model of homogeneous, isotropic, uniformly expanding Universe. It is shown, what within framework of that model, which does not contain any free parameters, well explained observed dynamics of the Universe.
Keywords:
Vacuum, Particles, Antiparticles, Einstein’s Gravitation, Two-Signed Gravitation, Antiattraction

1. Introduction
In the present paper, some doubts as to the correctness of the following hypotheses of modern physics are expressed.
1a) Gravity does not differentiate between particles and antiparticles.
2a) A decisive role in the dynamics of the modern Universe is played by dark energy.
The first of these is at the basis of Einstein’s theory of gravity [1] -[6] , and the second is the most important in modern cosmology [2] [6] .
Instead of these hypotheses are some alternative approaches are assumed:
1b) Gravity distinguishes between particles and antiparticles.
2b) The dynamics of the Universe is determined by gravitationally-neutral matter, which does not create its accelerated expansion.
The paper presents a theory of gravity, based on these approaches. In this theory, the basic idea of Einstein regarding the relationship of gravity and space-time geometry is preserved. It is shown that the proposed theory does not contradict the observations, and they are very easily explained within the framework these theory.
A brief description of the content of the work is given below.
Section 2 of the work shows that it follows from the equations of the General Relativity Theory (GRT) for Vacuum, the latter can be filled by two kinds of vacuum forms of matter. In case of flat space-time, Vacuum is filled with ideal gravitationally-neutral vacuum form of matter. The idea of determining role of gravitationally-neutral vacuum form of matter on the evolution of Universe is one of fundamental idea in the present work.
If four-dimensional space-time is curved, then vacuum contains dark energy besides gravity-neutral matter and is described by an Λ-term of Einstein’s equations.
The description of the theory of gravity, which distinguishes particles and antiparticles and which is called two-signed gravity is given in Section 3. In contrast to Einstein gravity, contributions of particles and antiparticles in the tensor which is a source of the gravitational field in two-signed gravity are taken with different signs. In this gravity, there exists antiattraction between the particles and antiparticles. The present paper describes a version of two-signed gravity, in which there exists an antiparticle for any particle including the photon, different from it. Theoretically, is possible a version of the theory, in which some of the particles coincide with their antiparticles, please see [7] . The choice between these alternatives can be made on the basis of observations and experiments.
In two-signed gravitation, a gravitational field by particles and antiparticles is perceived differently. In Section 4, written some equations for geodesics in the views of particles and antiparticles. Under the same initial conditions, particles and antiparticles move differently.
In Section 5, within the framework of two-signed gravity, the dynamics of the gravity-neutral homogeneous isotropic Universe is investigated. The hypothesis of gravitational neutrality of the Universe is based on the idea of Dirac regarding the charge symmetry of the Universe. It was expressed by him in his Nobel lecture. Also it is based on the idea that not only ordinary matter is gravity-neutral in general, but the vacuum form of matter has this property as well.
An explanation of some important astronomical observations, for which cosmological effects are significant within a framework of gravity-neutral Universe, is given in Section 6. It is shown that within of framework of this very simple model, are well explained by these observations.
In conclusion, we present the main results of the work.
In Section 8, we show that there is reason to believe that Λ-term is zero.
2. Vacuum Form of Matter
2.1. Vacuum and Gravity
According to the General Relativity Theory (GRT), the geometric properties of four-dimensional space-time are described by the following metric:
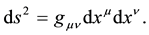 (1)
(1)
Metric coefficients
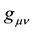 are functions of space-time coordinates
are functions of space-time coordinates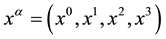 . At the core of GRT is a hypothesis of the relationship of the gravitational field and the geometric properties of space-time. Functions give
. At the core of GRT is a hypothesis of the relationship of the gravitational field and the geometric properties of space-time. Functions give
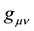 a description of this field (please see, for example, [1] -[6] ).
a description of this field (please see, for example, [1] -[6] ).
In the pioneering work of “Principles of General Theory of Relativity” (1916) [5] , Einstein showed that equations describing the gravitational field in a vacuum (in regions of space, which are free from usual forms of matter) can be written as
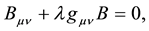 (2)
(2)
where
 is a constant;
is a constant;
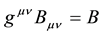 is a trace of the Einstein tensor
is a trace of the Einstein tensor ;
;
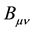 is a symmetric tensor obtained by an convolution of Riemann curvature tensor
is a symmetric tensor obtained by an convolution of Riemann curvature tensor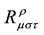 :
:
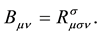 (3)
(3)
Tensor
 can be written as
can be written as
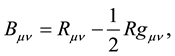 (4)
(4)
where
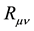 is a Ricci tensor, and R is its trace. The Ricci tensor
is a Ricci tensor, and R is its trace. The Ricci tensor
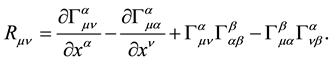 (5)
(5)
Christoffel symbols
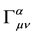

Einstein believed that the choice of gravitational field equations in the form of (2) is associated with minimum arbitrariness, since beside
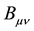
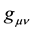
Usually, they believe (please see [1] [5] ) that Equations (2) for the gravitational field in a vacuum is reduced to the following equations:
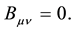
In a general case, this is not so. All the solutions of Equations (7) are contained in (2). At the same time, not all solutions of Equations (2) are the solutions of (7). A full set of solutions of Equations (2) for vacuum is given in [8] .
Einstein believed that Equations (2) describes the gravitational field in empty spaces. It is now believed that Einstein’s vacuum is not empty and is filled with vacuum forms of matter (please see [6] [9] ). Let us show that Equation (2) contains a description of at least two kinds of such matter.
2.2. Dark Energy
Using relation (4), we find that the trace of the Einstein tensor
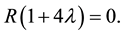
Hence follows that for all

At the same time, as seen from (8), when

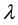
We will show that in a vacuum scalar curvature can not be a variable quantity. Taking the covariant derivative of the left-hand side of Equation (2) and taking into account the Bianchi identity
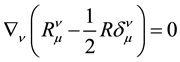
please see ([1] [6] ), we find that
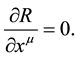
This means that when
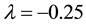
In case when scalar curvature R is different from zero, using the following notation

we will write Equations (2) as
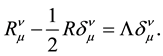
Usually, this equation is referred to as the Einstein equation with an Λ-term for the gravitational field in a vacuum [10] . Constant Λ is called a cosmological constant (please see [2] [6] )
In case matter is present, Einstein's equations are written as [1] -[6]
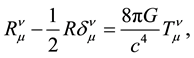
where
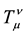
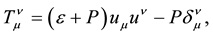
where
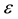

Taking into account (13), (14) and (15), often (please see [6] [9] [11] ) the Λ-term in the equations of Einstein is considered as describing the vacuum form of matter, called dark energy. It is thought that this matter is ideal, and its thermodynamic properties are determined by the following formulas:
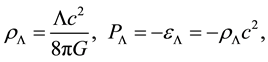
where
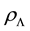
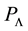
Einstein interpreted the Λ-term as describing the nonremovable curvature of space-time [10] .
Often it is believed hypothetically and in the presence of other types of matter that
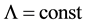
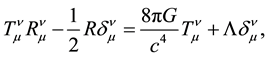
where
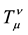
In modern physics, it is suggested that the value of cosmological constant
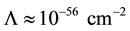
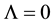
2.3. Gravitationally-Neutral Matter
We will show that Equations (2) for a gravitational field in a vacuum except for the dark energy, also contains a description of some other vacuum form of matter. To show this, let us consider the problem of the dynamics of the Universe from which all usual forms of matter are removed, in the framework of Equations (2).
We assume that three-dimensional space of an idealized universe, filled only with vacuum forms of matter is homogeneous and isotropic. To describe the geometry of the space it is convenient to proceed from the geometric analogy, seeing the space as a homogeneous and isotropic three-dimensional hypersurface in four-dimen- sional fictitious space (please see, for example, [11] ). The geometry of this three-dimensional hypersurface defined by parameter k, and as well as scale factor a which is often called the radius of a curvature.
Parameter k may assume three possible values: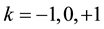
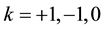
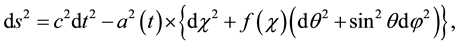
where
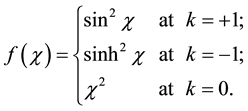
Using metric (18) Equations (2) can be converted (please see, for example, [2] [6] ) to the cosmological Friedmann equation in a standard way:
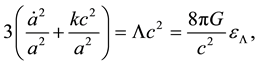
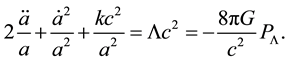
Considering the left side of these equations as “geometric” and right side as the “material”, we conclude that they contain a description of some substance. As is shown in Section 2.2 and as may be seen from Equations (20), (21), in the considered problem this substance is dark energy. Its parameters are defined by (16), and it fills space, if scalar curvature R of four-dimensional space-time is non-zero.
In case when

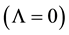
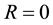
If


where
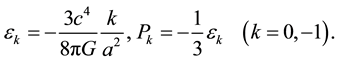
From (22)-(24) it is obvious that when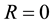
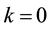
Fundamentally, a different situation is when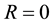

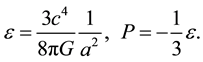
This matter is ideal, and its energy-momentum tensorcan be written in the form of (18). As can be seen from (22), (23), the dynamics of an idealized universe filled with matter of form (25), is determined by very simple equations

In a general case, according to the standard GRT (please see, for example, [2] [6] ), cosmological acceleration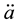
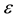
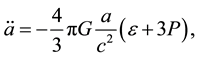
where a is the scale factor of the Universe. From (27) it is seen that the medium for which the equation of state
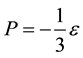
therefore, we believe, is gravity-neutral. A particular case of this matter is a vacuum form of matter (25).
If the summands describing gravitational-neutral matter (25) in flat three-dimensional space are shifted from the right side of Friedmann equations to the left side, then they describe the curvature there. Matter disappears but there appears a curvature. We believe that matter does not disappear, and the curvature of three-dimensional space can be interpreted as gravitationally-neutral matter. This is similar to how an Λ-term, according to Einstein, describes the unrecoverable curvature of four-dimensional space-time, and in modern cosmology it is interpreted as describing the dark energy.
3. Particles, Antiparticles and Gravity. Antiattraction
3.1. Two-Signed Gravity
In Einstein’s theory of gravity (GRT), an energy-momentum tensor of space environment, is a source of the gravitational field and all forms of matter contribute to this tensor. The contributions of all components of space environment, including particles and antiparticles are taken with the same sign. Einstein's gravity does not distinguish between particles and antiparticles [1] -[6] .
GRT has been reliably verified experimentally for macroscopic bodies. Regarding the description of the motion of elementary particles and antiparticles in a gravitational field, proposed in GRT it should be regarded as hypothetical. Gravity is too weak to study its impact on the individual elementary particles using direct experiments [12] . Either, there is no possibility of the experimental study of motions in gravitational fields of macroscopic bodies consisting of antimatter, because of their absence in the part of the Universe, observer by us.
Only recently it has been attempted to hold a laboratory investigation of gravitational interaction of matter with antimatter. ALPHA’s collaboration at CERN, in conjunction with the American National Laboratory in Berkeley, is conducting an experiment that will perhaps permit one to understand whether there is antiattraction between particles and antiparticles [13] .
In the absence of experimental restrictions, it is possible to assume hypothetically that gravity distinguish between particles and antiparticles, and the converse assertion is contained in the standard GRT, is not correct.
In the present paper, a hypothesis is expressed that a gravitational field distinguishes between particles and antiparticles. With regard to this assumption, an option of gravity, in which a tensor is a source of a gravitational field is proposed in which some-type contributions of particles and antiparticles are taken with different signs, in contrast to a tensor of energy-momentum.
In [7] an option of the theory of gravitation distinguishing between particles and antiparticles with a contribution of modern concepts was considered, which it is assumed that there are particles that are identical to their antiparticles and which are not sources of a gravitational field. A photon was attributed to these particles. The observed deviation of photons in a gravitational field possibly testifies to the fact that in two-sign gravity the idea that there are no antiphotons, is not a correct.
In the present paper, in order to harmonise the idea of gravity distinguishing between particles and antiparticles with current ideas that all components of space environment are sources of a gravitational field, the following hypothesis is put forward.
Any particle including a photon has an antiparticle. With regards this hypothesis, a theoretical model describing gravity, termed two-signed gravity is formulated in the present paper.
According to Einstein’s theory, under the same initial conditions any particles and antiparticles acquire accelerations of the same magnitude and sign and move along the same trajectories. Different is the situation in two-signed gravity which distinguishes between particles and antiparticles. Under the same initial conditions, particles and antiparticles acquire accelerations of the same magnitude but different of sign and move along different trajectories. In this regard, under the same conditions all particles move in the same manner. The same holds true for antiparticles.
As in Einstein’s gravity, it is considered in two-signed gravity that a gravitational field is what is determined by a deviation space-time metric from a pseudo-euclidian metric inertial reference frames of the Special Theory of Relativity [1] -[6] .
In idealised inertial reference systems, while using Cartesian coordinates
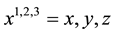
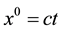
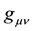

A true gravitational field is described by metric tensor
In the present paper, we show that in two-signed gravity its properties further depend on what a frame of reference consists of particles or antiparticles. In this gravity, readings of constructively identical clocks, some of which are composed of matter and while other of antimatter, will diverge in a gravitational field when placed side by side. A duration between two events occurring in one and the same point of a gravitational field depends on whether it is measured by “clocks” or “anticlocks”. The wavelengths of photons and antiphotonsare measured differently in a gravitational field. The fact of the dependence of spatial-temporal relations on a choice of the material measurement standards will be marked by us as a description of a gravitational field either in terms of particles, or in terms of antiparticles.
In two-signed gravity concepts defined by the terms “worlds” and “antiworlds” are useful. They define regions of the Universe, containing either particles or antiparticles alone, respectively. These idealizations are convenient in a theory. We believe that in ultimate cases of worlds and antiworlds equations of two-signed gravity should turn into equations of Einstein’s gravity.
In the framework of the theory of the gravitational field which distinguishes between particles and antiparticles, it is shown that even in the Early Universe its disintegration occurred into areas consisting of baryons (worlds), and areas consisting of antibaryons (antiworlds) [14] .
3.2. The Equations of Two-Signed Gravitation
Ideologically two-signed gravity is close to the GRT. As in Einstein’s gravity in two-signed gravity components of a metric tensor are values that describe the gravitational field. As in Einstein’s gravity, energy-momentum tensors of particles and antiparticles are sources of a gravitational field. A fundamental difference of two-signed gravity from that of Einstein consists in that same-type contributions of particles and antiparticles in the right- hand parts of these equations are taken with different signs.
It may seem that such a definition of sources of a gravitational field runs contrary to the law of conservation of energy. However, this is not true. In two-signed gravity it is believed that the total energy of the Universe is divided into two equal parts: the energy of matter and that of antimatter, and these parts do not change during of Universe’s evolution.
“Gravitational charges” corresponding to these energies have opposite signs for particles and antiparticles. The Universe is gravitationally-neutral.
In two-signed gravity, 4-acceleration of particles and antiparticles are equal in magnitude but differ by sign under the same conditions. With this in mind, we believe that particles and antiparticles experience deviations of a space-time metric from a pseudo-euclidian metric (a gravitational field) as having different signs. A space- time metric in representations of particles and antiparticles is not same thing. Metric tensors in representations of particles
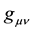
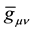
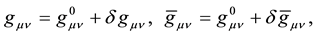
where
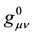
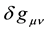

In two-signed gravity, space environment is considered by us as a two-fluid entity. One of the fluids consists of particles, another of antiparticles. It is assumed that in addition to usual forms of matter, space environment contains a gravity-neutral vacuum form of matter. We believe, that Vacuum is gravitationally-neutral.
Two-signed gravity equations in the representation of particles are written by us in the following form
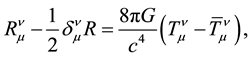
where
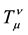
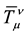
In the presentation of antiparticles, two-signed gravity equations are written in a form symmetric to (30):

In the worlds and antiworlds, equations (30) and (31) are reduced to Einstein’s Equations (14).
Equations (30), (31) are fundamentally different from Einstein’s equations in those cases when it is not possible to use an idealized approximation of worlds and antiworlds. This take place when processes of birth/ annihilation of particles/antiparticles proceed with high speed in the space environment and when there are comparable quantities of particles and antiparticles present in it. These cases are typical of the Early Universe, as well as of relativistic stages of the evolution of cosmic objects.
The left parts of Einstein’s equations, and Equations (30), (31) of two-signed gravity are satisfy Bianchi’s identities (please see [1] -[6] ):

Considering Bianchi’s identities, in (30) and (31), we conclude that in equations of two-signed gravitation contain the conservation law of “gravitational charge”:
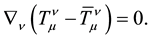
We believe that apart from the law of conservation of “gravitational charge” there exists a law of conservation of total energy of space environment, equal to a sum of energies of particles and antiparticles. It can be written as

In two-signed gravity, these equations are complementary. In this sense, the proposed theory is ordinary, if compared with other theories that describe non-gravitational interactions.
Equations (33), (34) may be simultaneously valid only if they are split into two independent equations
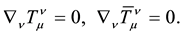
It follows from these equations that two-signed gravity is associated a significant change in our understanding of energy. Energy becomes “two-signed”. Not only conservation of energy, but also conservation of energies associated with particles and antiparticles taken separately taken place.
We will write equations of two-signed gravitation for a case of weak gravitational fields in the presentation of particles.
We assume the smallness of macroscopic velocities of the particles/antiparticles, and we also believe that a gravitational field itself is weak. If a gravitational field is weak and velocities of the particles/antiparticles are much lower than speed of light, then only component
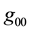
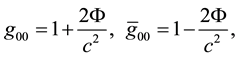
where
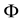

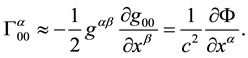
In non-relativistic limit
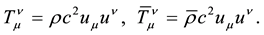
In this limit,
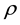

A macroscopic motion of matter/antimatter is considered to be slow. Because of this, we neglect all the spatial components of 4-velocity:
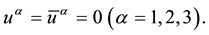
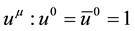
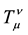
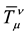
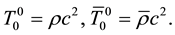
Considering (39), Equations (30) are written by us in the following form:
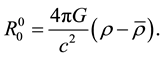
In the calculation of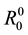

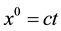
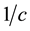

Substituting (37) in (41), we obtain
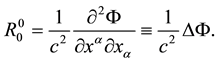
Taking into account (40), (42) we write equations of two-signed gravitation in the limit of weak gravitational fields in the presentation of particles in the following form:
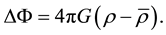
For the practical use of this equation, the equations describing the creation/destruction of particles/antipar- ticles, as well as equations describing their motion should be also written. A non-relativistic approximation in two-signed gravity in [14] was used in solving the problem of the disintegration of the Universe into worlds and antiworlds.
4. Geodesic for Particles and Antiparticles
A particle exsisting in a gravitational field is not only exposed to an action from a field, but it also affects itself the field, changing it. However, if a “gravity charge” of a particle is not great then its effect on the field may be neglected. In this case, considering the motion of a particle in a given field, we can assume that the field itself is independent either on the coordinates or speed of the particle. Similar reasoning is also valid for antiparticles.
An equation of the motion of a particle in a gravitational field is obtained by the appropriate generalisation of a differential equation of the free motion of a particle in the Special Theory of Relativity. This equation states that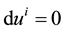
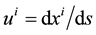
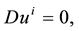
where
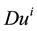
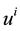
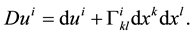
Considering (44), (45), we find that
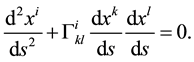
These are the sought equations of the motion of a particle in a gravitational field. It is obvious that the motion of a particle in a gravitational field is determined by values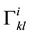
Particles and antiparticles enter two-signed gravity in an equal manner. Considering this, equations describing the motion of antiparticles in a gravitational field in their presentation, are written in the following form:
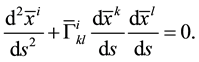
where
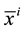
In their own presentation, particles and antiparticles move along the geodesics in the gravitational field. But the presentation of particles and antiparticles regarding a metric of space-time differs. At any point of a gravitational field, 4-accelerations of particles and antiparticles are equal in magnitude but opposite in sign. One and the same gravitational field by particles and antiparticles perceive in a different way. The concept of a geodesic is not absolute. Geodesics for particles and antiparticles are not the same.
If a gravitational field is weak and velocities of particles/antiparticles are much lower than the speed of light, then only component
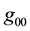
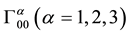
Taking into account Equations (36) and (37), as well as (46) and (47), describing the motion of particles and antiparticles can be written as
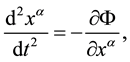
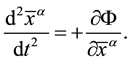
From Equations (48) and (49), it follows that particles and antiparticles in a given gravitational field move along different trajectories. Accelerations, which they acquire at any point of a gravitational field, are equal in magnitude but opposite in sign. Equations of motion for all particles are the same and do not depend on their mass and composition. The same is true for antiparticles.
5. Gravitationally-Neutral Universe
We will investigate the dynamics of the Universe in the framework of two-signed gravity. We believe that the latter is homogeneous and isotropic. We assume that there are equal quantities of particles and antiparticles contained in it. In two-signed gravity, this means that ordinary matter, in general, is gravitationally-neutral.
Assuming the existence the gravitational neutrality of ordinary matter, we believe that a vacuum form of matter is gravitationally neutral too, and therefore, there is no dark energy, see Appendix. Given the above assumptions, consider that the Universe is homogeneous, isotropic and gravitationally-neutral.
The space-time metric of the considered Universe, in the co-moving frame of reference, can be written in the form of Equation (18). Using this metric, the equations of two-signed gravitation (30) can transformed to cosmological Friedmann equations for a homogeneous isotropic gravitationally-neutral Universe in a standard way:
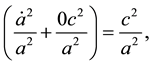
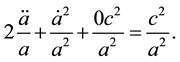
We also take into account the fact that apart from particles and antiparticles the gravitationally-neutral matter fills the Universe and its parameters are defined by Formulas (25).
We will write Friedmann’s Equations (50), (51) as
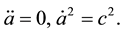
The solution of Equations (52) with boundary conditions
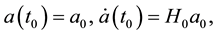
where t0 is the age of the Universe, H0 is the Hubble constant has the following form:
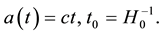
Icon “0” here and further in the text refers to values defining the state of the modern Universe. In the gravitationally-neutral Universe there is an equilibrium of forces of attraction and repulsion. Consequently, the Universe expands uniformly.
We term a cosmological model described by Equation (54) as an S1-model (S-Simple). According to the S1- model, four-dimensional space-time of gravitationally-neutral Universe is pseudo-Euclidean, while the corresponding three-dimensional space is flat.
In the next section, the S1-model is applicable for the explanation of certain important astronomical observations.
6. Explanation of Observations
6.1. Lifetime of the Universe
In an S1-model, the lifetime of the Universe
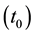
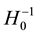
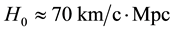
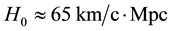
6.2. “Magnitude―Redshift” Relation
One of effective ways of verifying the correctness of a cosmological model is using a method based on a comparison of relatio theoretically calculated within the framework of a model an observable relation “magnitude―redshift” for objects that have a certain absolute luminosity [2] [6] [15] -[18] .
A formula describing this relationship has the following form
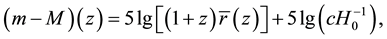
where
L is an absolute luminosity of an observed object that has redshift z;
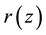
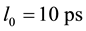
A formula that determines photometric distance
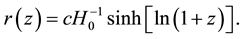
Using Equations (55), (56), we calculate dependence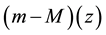

Figure 1. Dependence
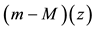

As can be seen, the model describes well the observational data for supernovae of type Ia.
7. Conclusions
・ A variant of the theory of gravity is proposed, distinguishing between particles and antiparticles. It is assumed that any particle, also a photon, has an antipaticle that is different to it. This theory has been termed as that of two-signed gravity.
・ Some equations describing two-signed gravity has been written. It preserved the idea of Einstein’s gravitation regarding the interrelation between gravity and geometrical properties of space-time. It is believed that a source of a gravitational field (curvatures of space-time) is a tensor in which contributions of particles and antiparticles are taken with different signs. In such a description of sources of a gravitational field, there exists antiattraction between particles and antiparticles.
・ In two-signed gravitation, particles and antiparticles perceptions the same gravitational field differently and
move under the equal initial conditions―according to different trajectories. Geodesics for particles and antiparticles do not coincide.
・ A hypothesis has been proposed regarding the gravitational neutrality of the Universe. Some arguments in the support of the neutrality have been furnished. Within the framework of two-signed gravity, such a model is the simplest and the most beautiful among a multitude of other theoretically permissible models.
・ A cosmological model of a uniformly homogeneous gravitationally-neutral Universe (S1-model) has been proposed. In the gravitationally-neutral Universe, there exists an equilibrium of gravity and antigravity and therefore the Universe expands evenly. An S-model not includes any parameters and has a clear physical meaning.
・ It has been shown that in the framework of an uniformly expanding Universe the observed dynamics of Universe are well explained. We believe that this is an important argument in favour of the correctness of the ideas presented in the present paper.
Currently, there are no observations that could be interpreted as a direct proof of the existence of antiattraction between particles and antiparticles. Just recently some attempts have been made in order to fulfill this fundamental task experimentally.
If the presence of antiattraction between particles and antiparticles is proved, then it would entail not only a revision of the existing ideas about the dynamics of the Universe, which is shown in this paper, but also of many others. For example, the existing ideas of baryon asymmetry, regarding of the mechanism of the origin of structures in the Universe and of the problem of singularities in gravity may change. Physics of gravity may become more beautiful, richer and more ideologically closer to the quantum theory.
8. Appendix
Concerning the Problem of the Cosmological Constant
In the standard theory of gravitation (GRT), there exists a problem of the cosmological constant. It consists in the following. The value of the density energy of physical vacuum,
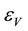
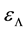
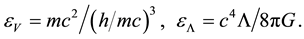
Taking into account only the electron and positron contribution to the energy density of vacuum, and believing that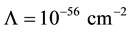
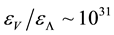
In the modern physical theory, it is considered that, owing to a huge distinction in energy densities
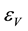
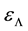
In two-sign gravitation, this problem is solved in a natural way. Considering that physical vacuum consists of virtual particles and antiparticles, and their contributions to the tensor which is a source of a gravitational field are taken with an opposite sign. If one assumes that vacuum is symmetrical as to particles and antiparticles, their huge contributions to what is called Einstein’s Λ-term are being reduced, and the cosmological constant appears to be equal to zero.
In two-sign gravitation, an assumption that
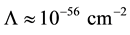
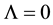
References
- Landau L.D. and Lifshitz, E.M. (1971) The Classical Theory of Fields. Pergamon Press, Oxford.
- Zel’dovich, Y.B. and Novikov, I.D. (1975) The Structure and Evolution of the Universe [in Russian]. Nauka, Moscow:
- Weinberg, S. (1972) Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. John Wiley & Sons, Hoboken.
- Misner, C.W., Thorne, K.S. and Whiller, J.A. (1973) Gravitation. Vol. 1, 2, 3. W. H. Freeman and Company, New York.
- Einstein, A. and Minkowski, H. (1920) The Principle of Relativity. University of Calcutta, Calcutta, 89-163.
- Gorbunov, D.S. and Rubakov, V.A. (2008) Introduction to the Theory of the Early Universe. Hot Big Bang Theory [in Russian]. LKI, Moscow.
- Klimenko, A.V. and Klimenko, V.A. (2013) Particles, Antiparticles and Gravity. Gravity-Neutral Universe [in Russian]. Herald of the Chel. State. Un., 17.
- Klimenko, A.V. and Klimenko, V.A. (2013) Geometric Properties of the Homogeneous Isotropic Vacuum [in Russian]. Herald of the Chel. State. Un., 17.
- Chernin, A.D. (2008) Physics-Uspekhi, 178, 267-300.
- Einstein, A. (1965) Cosmology Question and General Theory of Relativity [in Russian]. In: Collection of Sci. Works, Vol. 1. Nauka, Moscow,
- Gliner, E.B. (2002) Physics-Uspekhi, 172, 221-228.
- Okun, L.B. (1988) Elementary Particle Physics [in Russian]. Nauka, Moscow.
- The ALPHA Collaboration and Charman, A.E. (2013) Description and First Application of a New Technique to Measure the Gravitational Mass of Antihydrogen. Nature Communications 4, art. num. 1785.
- Klimenko, A.V. and Klimenko, V.A. Worlds and Antiworlds [Appendix for the Present Article: “Gravitationally-Neutral Universe”].
- Perlmutter, S., Aldering, G., Goldhaber, G., Knop, R.A., Nugent, P., Castro, P.G., et al. (1999) The Astrophysical Jour- nal, 517, 565-586.
- Riess, A.G., Filippenko, A.V., Challis, P., Clocchiatti, A., Diercks, A., Garnavich, P.M., et al. (1998) The Astrophysical Journal, 116, 1009. http://dx.doi.org/10.1086/300499
- Astier, P., Guy, J., Regnault, N., Pain, R., Aubourg, E., Balam, D., et al. (2006) Astronomy and Astrophysics, 447, 31- 48. http://dx.doi.org/10.1051/0004-6361:20054185
- Riess, A.G., Strolger, L.G., Casertano, S., Ferguson, H.C., Mobasher, B., Gold, B., et al. (2007) The Astrophysical Journal, 659, 98. http://dx.doi.org/10.1086/510378