ABSTRACT

Based on two versions of Maxwell’s Equations we investigate the Poynting vector, the energy transport and the dispersion relation both for rightand left-handed systems. Furthermore, it is shown that the latter systems are necessarily dispersive in contrast to the former ones. In the end we discuss a published example where the mixing of expressions of both versions of Maxwell’s Equations leads to unphysical conclusions. The presentation demonstrates for students how flexible can be the work with different versions of electrodynamics but also how carefully one has to be thereby.

Keywords:Leftand Right-Handed Systems, Negative Refractive iNdex, Poynting Vector, Maxwell’s Equations, Metamaterials, Dispersion Relation

1. Introduction

Feynman [1] has named the discovery of the laws of electrodynamics by Maxwell “the most significant event of the 19^th century”. Indeed, these laws were and are fundamental for the development of modern industry. For example, no electronic devise would exist without the knowledge of Maxwell’s famous Equations. However, today, more than 150 years after the finding, we are still hampered by a lot of different versions of Maxwell’s Equations. There are two distinct basic systems namely the SIand the cgs-system where the latter is still used in many textbooks (e.g. [2] ). Furthermore, in every basic system Maxwell’s Equations can be written in several forms with different definitions especially for the magnetic part. This situation was called by [1] a “horrible thing”. Nevertheless, we could forget this trouble for the investigations of materials in the optical range because in this case the relative magnetic permeability is simple unity. Therefore, a distinction between the magnetic field 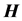and the magnetic induction 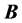would be captious as pointed out by Landau and Lifschitz [3] . The situation has been changed, however, with the rediscovery of the interest on materials with a negative refractive index in a theoretical paper by [4] . The first experiment showing negative refraction of a metamaterial was performed by [5] .

A survey of the history of negative refractive index going back as far as to 1905 is presented online by [6] . To possess a negative refractive index the material must have both a negative dielectric permittivity and a negative magnetic permeability. By this way 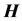and become different and we are faced with the problems mentioned above. This turns out to be not only a potential but a real source of confusions and possible errors. An illustrating example is discussed below.

2. Maxwell’s Equations, Poynting Vector, Dispersion Relations

In the following we investigate two different versions of Maxwell’s Equations in the SI-system. For this purpose we determine the electromagnetic field energy density, the Poynting vector, and the dispersion relations and discuss the distinctions. The two versions are taken from [7] . The first version reads

(1)

where 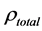is the sum of the free and the bound charges, 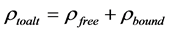, is the free (or, in other terminologies, the “external” or “true”) current, 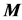is the magnetization and is the polarization. We have to complement these Equations by the constitutive relations or material Equations

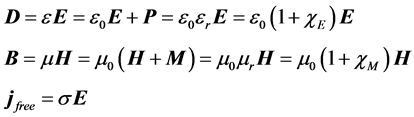(2)

where e is the dielectric permittivity, m is the magnetic permeability, χ_E and χ_M are the dielectric and magnetic susceptibility, and σ is the electrical conductivity. For homogeneous and isotropic materials all three quantities are frequency dependent complex functions. In the following unless stated otherwise we neglect the dispersion and treat the quantities as complex numbers. By calculating the divergence of the cross product of and 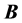we find for the divergence of the Poynting vector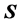

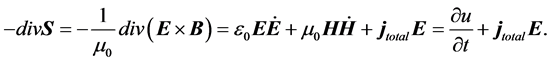(3)

Equation (3) expresses the energy conservation saying that the sum of the divergence of the Poynting vector plus the change of the electromagnetic field energy plus the production of Joule’s heat has to be zero. Note the material properties are completely contained in this first version in the total current.

The Poynting vector and the electromagnetic field energy density u and are given by

(4)

Since the fields are quadratic in the expressions in (4) we have to write them in real form. Taking the derivative of u with respect of time we obtain for monochromatic fields

(5)

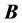This result indicates that u only consists of the vacuum fields, pointed out by the use of instead of in (4), and that the divergence of the Poynting vector is described completely by the last term in (3). Since the vacuum has no sinks or sources u has to be a constant. Once more, the complete material properties are included in the total current. In version 2 below, we will get exactly the opposite situation. The products and 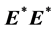in (5) vanish due to the temporal averaging. The same is valid, of course, also for the magnetic terms.

If we calculate the curl of Equation (3) in (1) and insert Equation (4) we get the dispersion relation of the electric field. By changing the order of the calculation we obtain the relation of the magnetic induction. Both Equations read

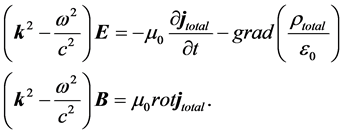(6)

These dispersion relations look rather unfamiliar for the first representation of Maxwell’s Equations and they are not very useful. With the aim to get more manageable expressions, we substitute the currents now in (1)

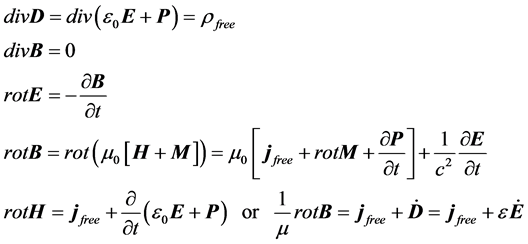(7)

where we used (2) and the relation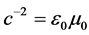. By this way we have find a second representation of Maxwell’s Equations.

In this case the Poynting vector, the field energy density, and the dispersion relations read completely different

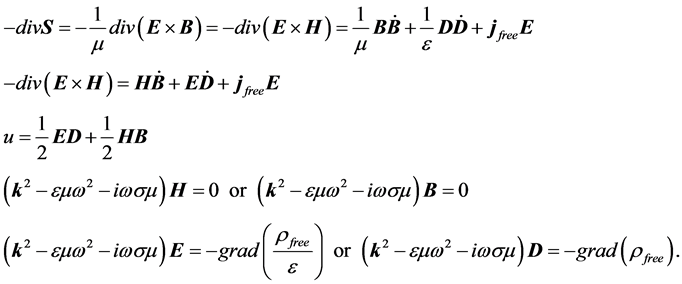(8)

For vanishing external charges the dispersion relations will convert into the standard formula.

Assuming that the external current vanishes in the first Equation of (8), we see that the material properties are included now in the fields 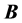and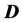. The two field terms read in case of monochromatic wave

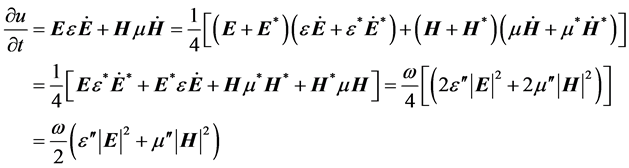(9)

where two primes are representing the imaginary part of the dielectric function and of the magnetic permeability, respectively. This formula shows that the energy loss (dissipation) is determined by the imaginary parts of e and m. Note that we used the property Im(e^*) = −Im(e). Furthermore, we conclude from (9) that 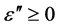and 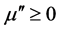since the energy density must be positive.

Let us summarize and compare the most important Equations of both versions.

(10)

Both versions are, of course, correct and can be used but one has strictly to note not to mix Equations of different versions. This hint is not redundant because this happens even in peer reviewed papers. Below we will discuss an example where this restriction is not taken into account.

There is still a long-standing discussion on the right notation of Poynting’s vector in the literature. For example, Obukhov and Hehl (2003) derived for it

(11)

This expression corresponds to the first Equation of (4). Although this confirms our notation of Poynting’s vector in version 1 this does not imply that the other notation in version 2 is wrong. To approve this we transform the Poynting vector from the first version in the second one in the following

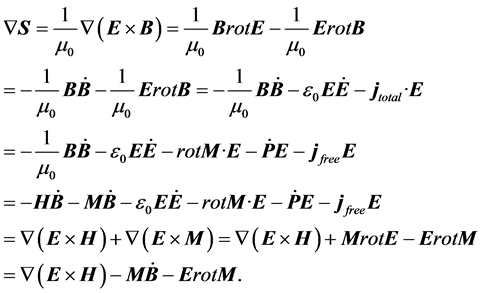(12)

Comparing the 4^th with the last row of Equation (12) shows that the two terms, and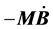, drop out and we obtain finally

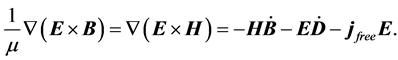(13)

By this way we can claim that both Poynting vectors are a correct notation in the frame of its respective version of Maxwell’s Equations. Although we can define a lot of different expressions for the Poynting vector we have to assure that the divergence of has the correct unit (W/m³ in the SI-system). In fact, there is no unique definition of Poynting’s vector and this seems to be a weak point of electrodynamics. Moreover, one can define an arbitrarily large number of different expressions and no experimental way exists to tell which the correct version is (Feynman, 1989). We will come back to this point by the discussion of the left-handed materials. It should be noted here, however, that the vector potential related to the magnetic field is the more relevant quantity because one can measure effects in regions where 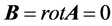but not. This was already mentioned by Feynman. He writes that “We have introduced because it does have an important physical significance... In any region where 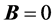even if is not zero, such as outside a solenoid, there is no discernible effect of. Therefore, for a long time it was believed that was not a “real” field. It turns out, however, that there are phenomena involving quantum mechanics [Aharonov-Bohm effect] which show that the field is in fact a ‘real’ field in the sense we have defined it” [1] . Very recently, Refs. [8] [9] has presented experimental (Maxwell-Lodge effect) and theoretical evidence that this is not restricted to quantum mechanics but also valid in classical electrodynamics.

3. Phase, Group and Energy Transport Velocity

For dispersionless media the group velocity, the phase velocity and the velocity of energy propagation are identical. The latter is defined by the ratio of the time-averaged Poynting vector over the time-averaged energy density

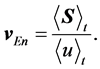(14)

Without restriction of generality let the plane wave propagate along the x direction with E = E_y and B = B_z

(15)

where E₀ and B₀ are complex amplitudes. It is in every case possible to rotate the coordinate system in the wanted direction. From (8) we get for the field energy density

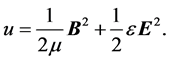(16)

Carrying out the time average yields

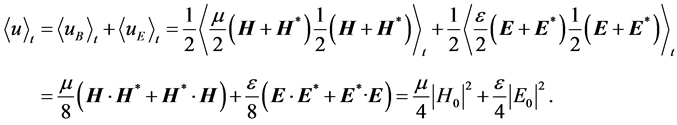(17)

The magnetic part can be recast by means of the dispersion relation of Equation (8) and with the third Equation of Equation (7). For a system without external current, σ = 0, we find

(18)

In analogue manner we calculate the time averaged Poynting vector

(19)

Finally, we get for the energy transport velocity from Equation (18) and Equation (19)

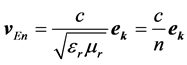(20)

with n as the refractive index and the unit vector in k-direction. For the phase and group velocity we obtain from Equation (8) immediately

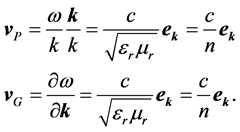(21)

As expected, all three velocities are identical far away of any resonance.

Up to now, only normal right-handed systems were investigated. For left-handed systems we have to make some changes because the real parts of e, m and n are smaller than zero. As a consequence, the dispersion relation of Equation (8) may be written now as

(22)

where Σ is defined by

(23)

Furthermore, LHS must be dispersive as can be seen immediately from the Equation for the field energy density. For weak absorption in the so called transparent regime this Equation is given by (Landau and Lifschitz 1980).

(24)

Equation (24) has to be regarded as an approximation since the necessary absorbing part is suppressed. The fact that LHS must be absorbing is based on the Kramers-Kronig relation

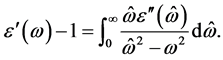(25)

For the integral has no solution besides of 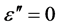but this corresponds to the trivial vacuum case.

Since the field energy density must be positive we conclude that the terms in (24) containing the dielectric permittivity and the magnetic permeability have to fulfil

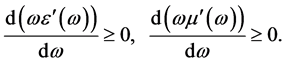(26)

For LHS the Poynting vector is changed to

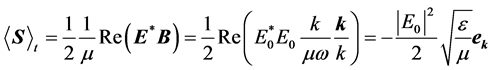(27)

under use of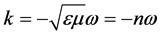. We see that the Poynting vector and the wave vector are oppositely directed in case of LHS. For the energy transport velocity we get from Equations (24) and (27)

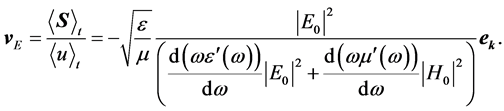(28)

This can be rewritten as

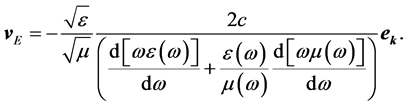(29)

The denominator of Equation (29) is positive as discussed above and therefore the group velocity is parallel to the Poynting vector and antiparallel to the wave vector. This is in contrast to the behaviour in RHS. In regions of normal dispersion v_E is reduced to the group velocity v_g if the system is nearly lossless. In the case of dispersion the group velocity is defined by

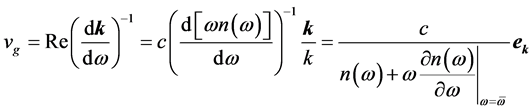(30)

where we made use of

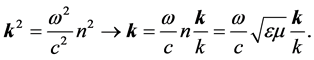(31)

Calculating the differentiation in the denominator of (30) and few manipulations leads to

(32)

It is easy to show that the evaluation of Equation (29) comes to the same result. The denominators of Equation (29) and Equation (32) are positive as discussed above. Therefore the group and energy transport velocity are parallel to the Poynting vector and antiparallel to the wave vector.

For the modelling of LHS the dielectric permittivity and the magnetic permeability are often described by the Drude or Lorentz model ([10] [11] ). Taking Drude’s model for e and omitting the constant ε₀ we get

(33)

where w_p is again the plasma frequency and u is the scattering rate. The real part is negative for frequencies well below the plasma frequency and the imaginary one is always positive. For the derivative in Equation (28) follows

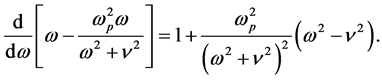(34)

Obviously, Equation (34) is only positive as demanded if w > u. This is, however, in agreement with the condition of weak absorption (transparency regime) assumed by the derivation of Equation (24). In the case of Lorentz’s model we obtain

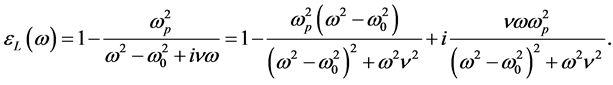(35)

Insertion of the real part in Equation (26) yields

(36)

Equation (36) takes positive values between zero and close to the resonance. It has, however, large negative values around w₀. The dominant contribution comes from the third term and is proportional to. This is per definition a large number.

4. An Example of Misleading Use of Electrodynamics

Because there is no change for the Poynting vector due to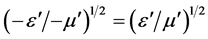, see Equation (19) or Equation (27), the velocity of energy transport is again parallel to. The phase velocity, however, is antiparallel to the Poynting vector as immediately follows from Equation (21). From this fact a condition can be derived for the appearance of a negative refraction index ([12] )

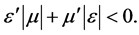(37)

This condition is equivalent to

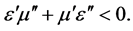(38)

Let us now calculate Joule’s heat, the energy loss due to the resistance. In an isotropic system Joule’s heat is given by

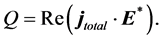(39)

For the total current we make the ansatz 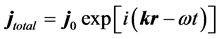and for the the electric field we use a similar expression. Assuming we get from Equation (10) for

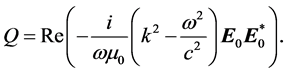(40)

If one now replace the square of the wave vector by

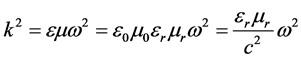(41)

then follows for

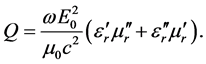(42)

Although this expression has the correct unit (W/m³) it is wrong. The reason therefore is that the total current in Equation (39) belongs to version 1 and contains all the material properties. In this case, however, the fields are simple the vacuum fields and consequently the relative terms in Equation (41) are unity. In reality Equation (41) results from version 2 but there is no current, Equation (39) is zero, if one neglects the free current. Exactly this is implicit assumed in Equation (41). We know, however, that the loss in the dispersion less materials is correct described by the expression (9) in version 2 which is depending only on the imaginary parts. Although it is not quite accurate we can sometimes ignore for RHSs the dispersion but this is not longer possible for LHSs. For LHSs a dispersion is required otherwise we would get a negative energy density (see Equation (24)). Therefore, even when Equation (42) would be right, it is not suited for LHSs. The dielectric permittivity and the magnetic permeability in Equation (42) cannot be simple complex numbers. For materials with dispersion the right side of Equation (13) reads

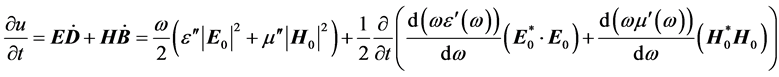(43)

where the field amplitudes are changing with time much slower than the exponential part. Obviously, a direct conclusion about the sign of the right hand side of Equation (43) is not possible. We know, however, that the derivates in the bracket of Equation (43) are positive for the Drude and Lorentz model in the extent of validity of the theory (weak absorption). Therefore it is physically not justified to switch simple the sign for the real parts in Equation (42), as done by [13] and then conclude that a negative refractive index is impossible because Q has to be positive.

5. Summary

In this paper we have derived and compared some electromagnetic properties of leftand right-handed systems. Especially the phase, group and energy transport velocity are considered. Furthermore, we discussed the opportunities presented by the accurate utilization of different versions of Maxwell’s Equations but also the possible pitfalls. An explicit example of the latter case was considered and the published claim that a negative refraction index is impossible due to a negative loss is physically falsified. Additionally it was shown that LHS has to be dispersive.

References