Journal of Modern Physics
Vol.4 No.11(2013), Article ID:40191,6 pages DOI:10.4236/jmp.2013.411189
Generation of Exactly Solvable Potentials of Position-Dependent Mass Schrödinger Equation from Hulthen Potential
1Physics Department, Nalbari College, Nalbari, India
2Physics Department, Gauhati University, Guwahati, India
Email: hansrajb12345@gmail.com
Copyright © 2013 Hangshadhar Rajbongshi, Ngangkham Nimai Singh. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 14, 2013; revised October 12, 2013; accepted November 11, 2013
Keywords: Position-Dependent Mass; Hulthen Potential; Co-Ordinate Transformation; Extended Transformation; Exact Analytic Solution
ABSTRACT
Exactly Solvable Potentials (ESPs) of Position-Dependent Mass (PDM) Schrödinger equation are generated from Hulthen Potential (parent system) by using Extended Transformation (ET) method. The method includes a Co-ordinate Transformation (CT) followed by Functional Transformation (FT) of wave function. Mass function of parent system gets transformed to that of generated system. Two new ESPs are generated. The explicit expressions of mass functions, energy eigenvalues and corresponding wave functions for newly generated potentials (systems) are derived. System specific regrouping method is also discussed.
1. Introduction
There are many physical examples of quantum mechanical problems in which Position-Dependent Mass (PDM) makes its appearance and leads to effective interactions giving interesting results. Application of PDM Schrö- dinger equations is found in different branches of Physics like Condensed Matter Physics, Material Science, Nuclear Physics etc. Special application of principal concept of PDM is found in the investigation of electronic properties of semiconductors [1], quantum dots and quantum wells [2, 3], quantum liquids [4], Nuclear many body problems[5] etc. In these cases, Exact Analytic Solution (EAS) of PDM Schrödinger equation for a physical potential provides maximum information of the system. Therefore, there has been a sustained effort in calculating EAS of PDM Schrödinger equation providing us with energy eigenvalues and corresponding eigenfunctions for physical potentials. Such studies use different methods known for solving constant mass Schrödinger equations or an extension of them. Point Canonical Transformation (PCT) [6-10], Nikiforov-Uvarov (NU) method [11-13], Supersymmetry (SUSY) quantum mechanics approach [14,15], Quadratic Algebra [16], Darboux Transformation (DT) [17,18] etc. are different approaches used in the study of PDM Schrödinger equations.
In this paper, we are trying to generate Exactly Solvable Potentials (ESP)s of PDM Schrödinger equation by using Extended Transformation (ET) method [19]. Ethics of the method is not to solve PDM Schrödinger equation to obtain wave functions, energy eigenvalues and mass function for a particular physical potential, but to generate exactly solvable potentials of PDM Schrödinger equation from an already solved potential. The method provides us with direct way of calculating the wave functions, energy eigenvalues and mass function for the generated system from the already solved potential. The spirit of ET method is similar to that of SUSY quantum mechanics approach, but in ET method, one needs no concern about the concept of supersymmetry and shape invariance which is essential in SUSY quantum mechanics approach. We start with a known exactly solved Quantum System (QS). Then we invoke a Co-ordinate Transformation (CT) followed by Functional Transformation (FT) of wave function and a set of plausible ansätze to mould the transformed equation to standard form of PDM Schrödinger equation. In addition, we introduce transformation of mass function which transforms the mass function of known system to that of generated system. Most of the potentials generated by this method are Sturmian, and some of them can be made normal as well as physical by system specific regrouping method. In transformation method, the normalization of the wave functions of the generated QS can easily be verified in most cases.
The paper is organized as follows: the method is discussed in Section 2, implementation of the method in practical QS with Hulthen potential is shown in Section 3 and finally, conclusions and findings of results are discussed in Section 4.
2. Formalism
We start with Hermitian effective Hamiltonian for a Position-Dependent Mass (PDM) system in one dimension (2m0 = ħ = 1) [20]
 (1)
(1)
where Veff(x) is the effective potential given by
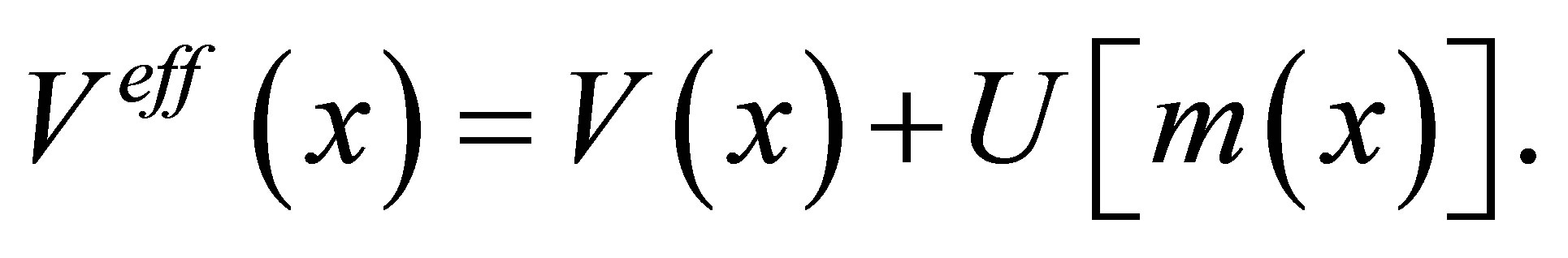 (2)
(2)
Here V(x) is the real potential profile and 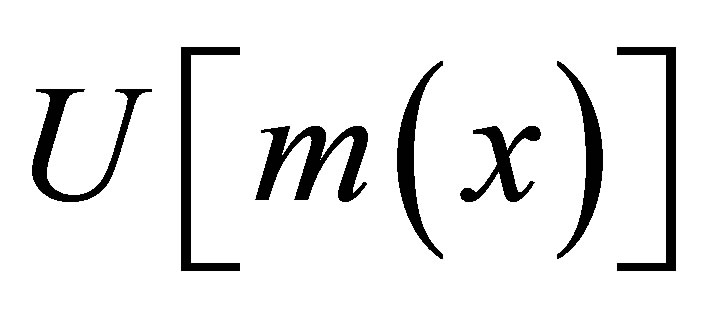 is the modification emerging from position-dependent mass given by
is the modification emerging from position-dependent mass given by
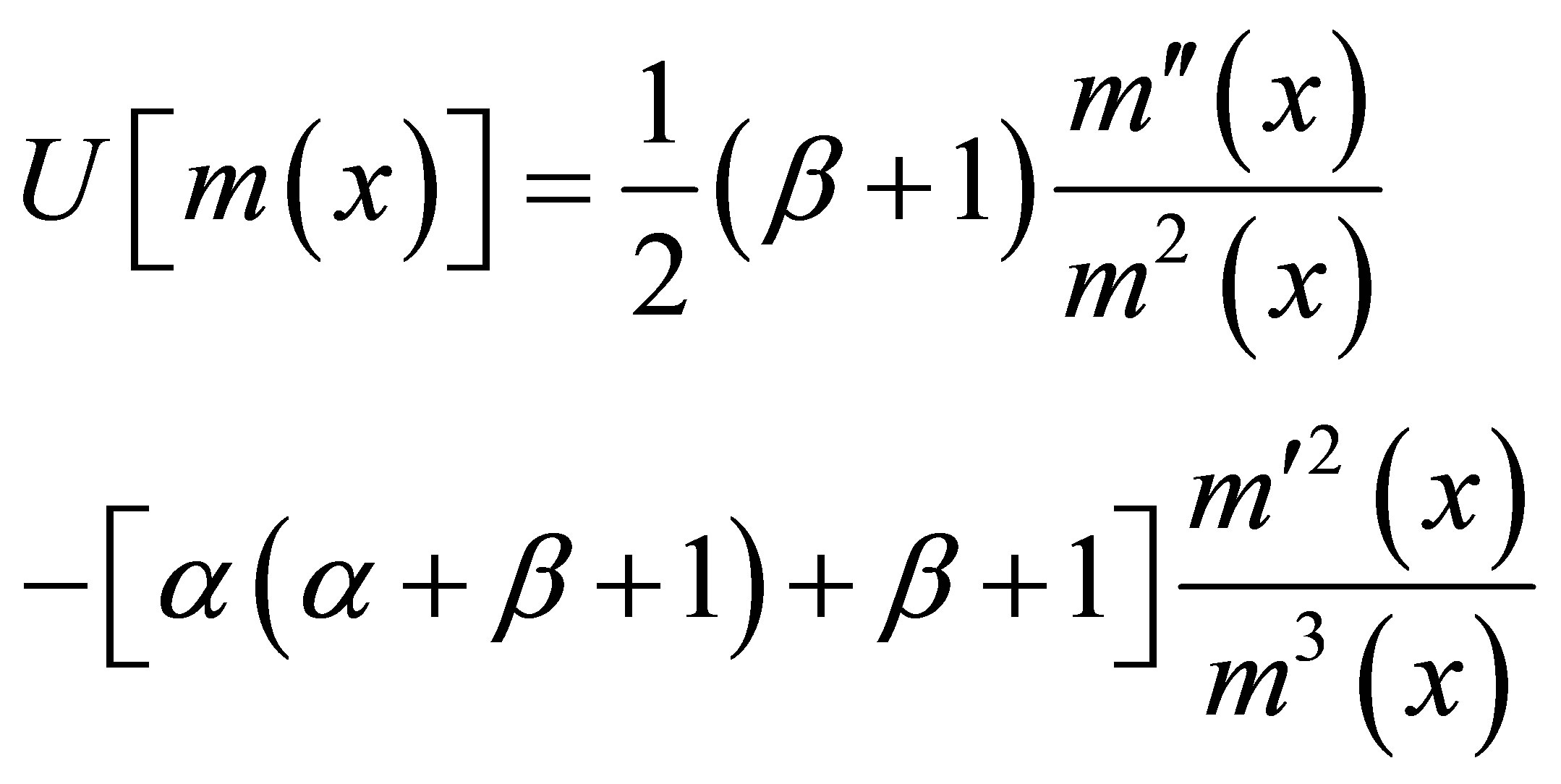 (3)
(3)
where α, β, γ are ambiguity parameters satisfying the constraint relation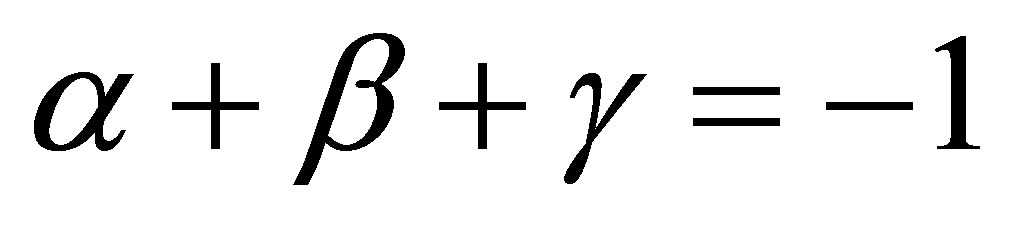 , and m(x) is the dimensionless mass function related to constant mass m0 and PDM M(x) by
, and m(x) is the dimensionless mass function related to constant mass m0 and PDM M(x) by 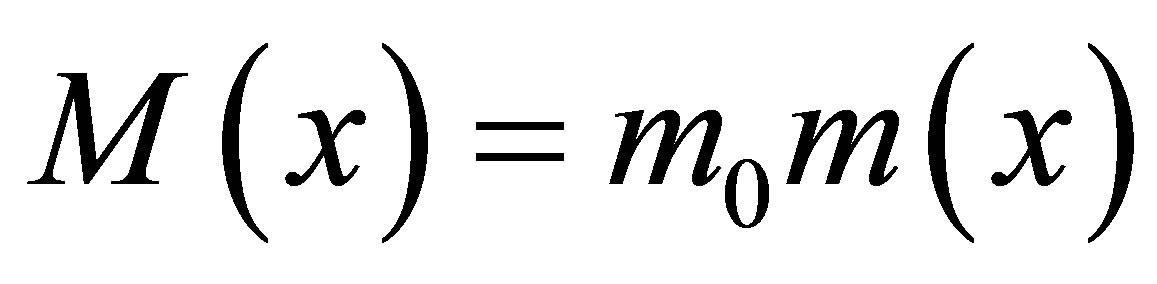 [21]. The prime stands for derivative of the function with respect to its argument.
[21]. The prime stands for derivative of the function with respect to its argument.
Thus one dimensional position-dependent mass (1DPDM) Schrödinger equation is written as
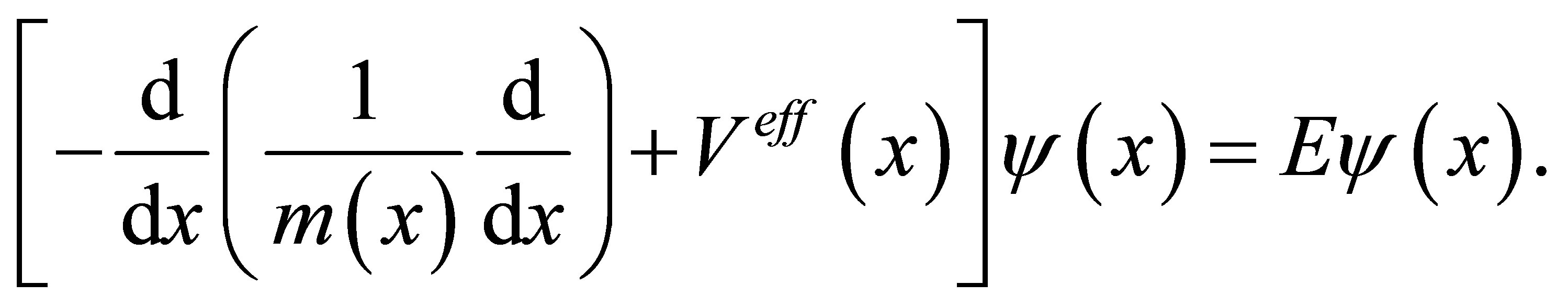
The above equation finally takes the form
 (4)
(4)
We have considered a real quantum mechanical potential VA(x), which is termed as A-quantum system (A-QS). 1D-PDM Schrodinger equation for A-QS is
 (5)
(5)
Equation (5) is exactly solvable for VA(x), i.e. the normalized eigenfunctions ψA(x), energy eigenvalues 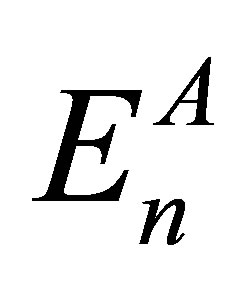 and mass function mA(x) are known for given VA(x).
and mass function mA(x) are known for given VA(x).
We now invoke a Co-ordinate Transformation (CT)
 (6)
(6)
followed by a Functional Transformation (FT) of the wave function
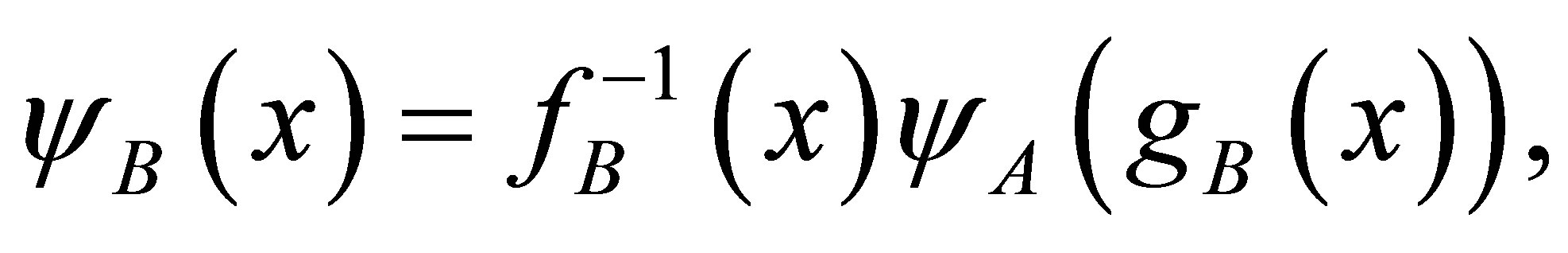 (7)
(7)
where ψB(x) stands for wave function of transformed quantum system, hereafter called the B-QS. The transformation function gB(x) must be a differentiable function of at least class C3. The gB(x) and the modulated amplitude 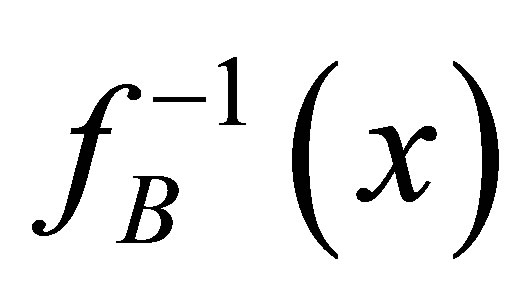 have to be specified within the framework of ET.
have to be specified within the framework of ET.
Application of ET to Equation (5) of the A-QS, gives
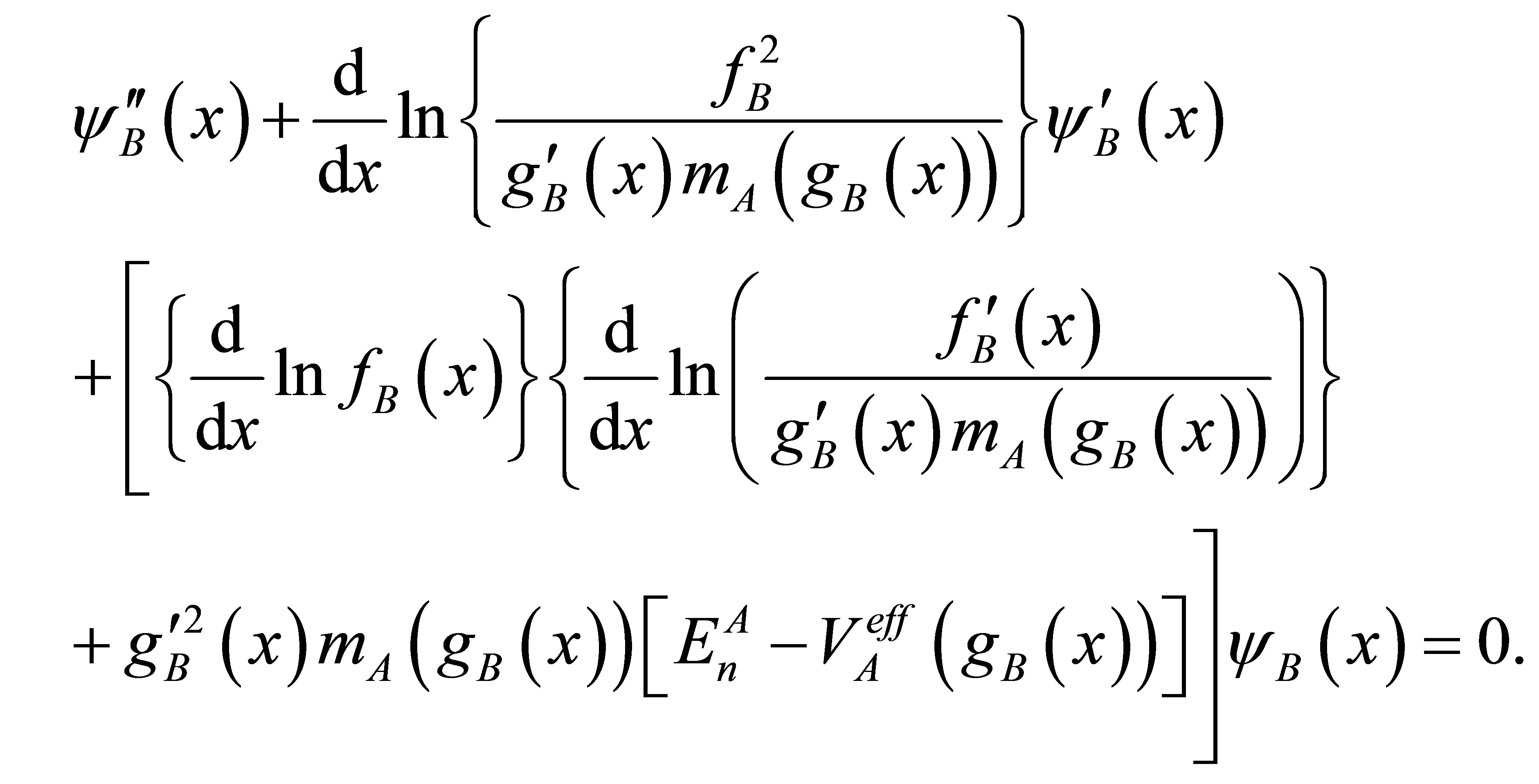 (8)
(8)
Since mass depends on position, we introduce transformation of mass i.e. mA(x) of A-QS transforms to new mass function mB(x) of B-QS, as given below
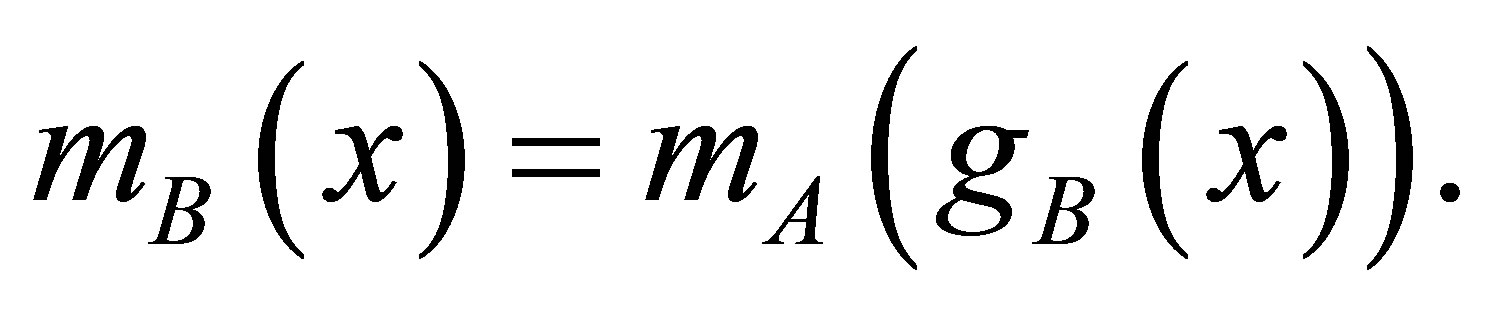 (9)
(9)
Therefore Equation (8) for B-QS, takes the intermediate form
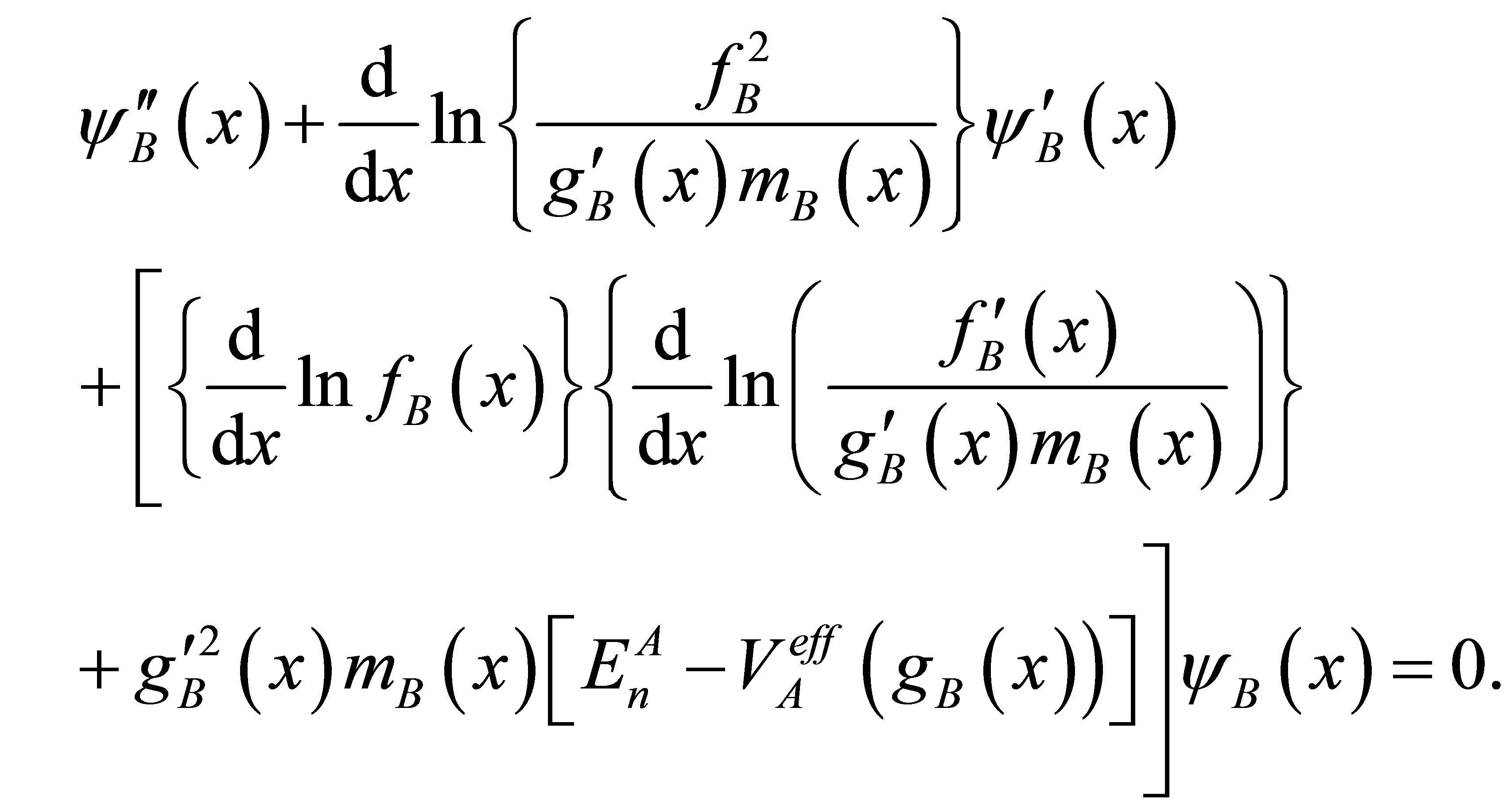 (10)
(10)
Consistency demands that the co-efficient of 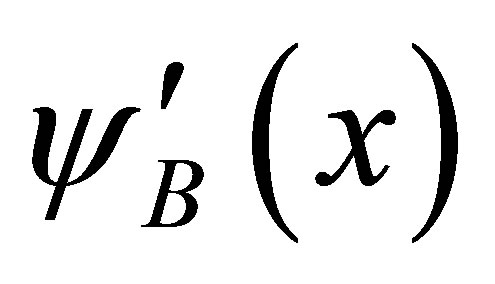 in Equation (10) must be identical to
in Equation (10) must be identical to  which gives
which gives
 (11)
(11)
and changes Equation (10) to
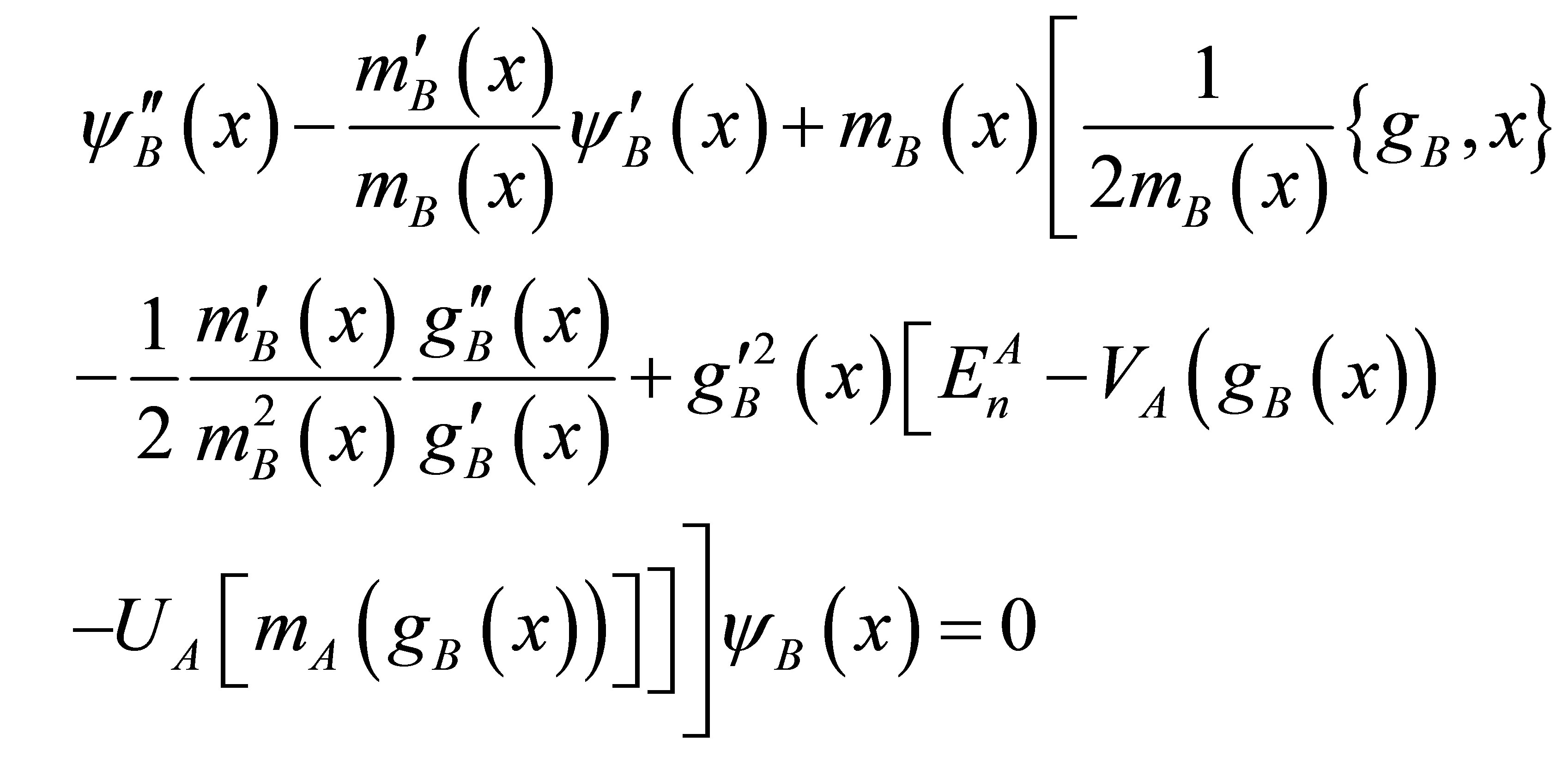 (12)
(12)
where
 (13)
(13)
is the Schwartzian derivative symbol and NB is the integration constant which plays the role of normalization constant of the energy eigenfunctions.
In order to mould Equation (12) to the standard form of 1D-PDM Schrödinger equation, the following plausible ansätze have to be made, which are an integral part of the ET method.
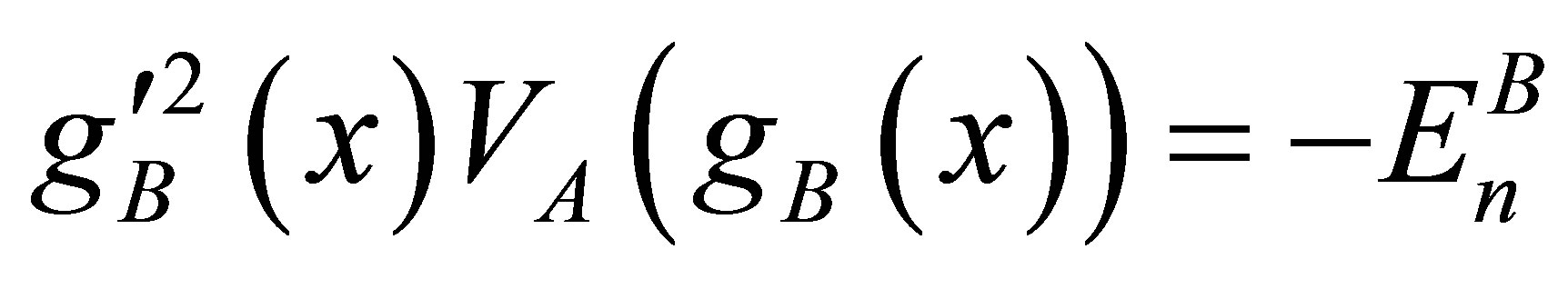 (14)
(14)
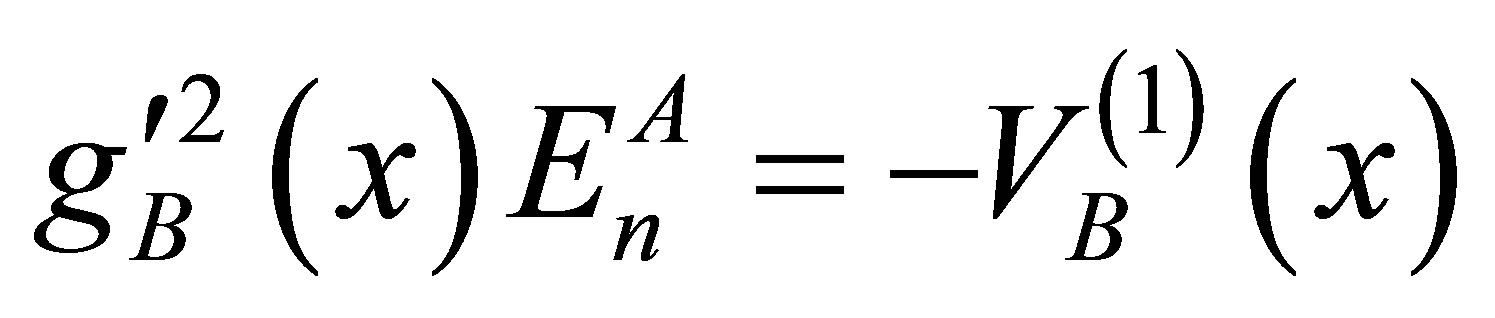 (15)
(15)
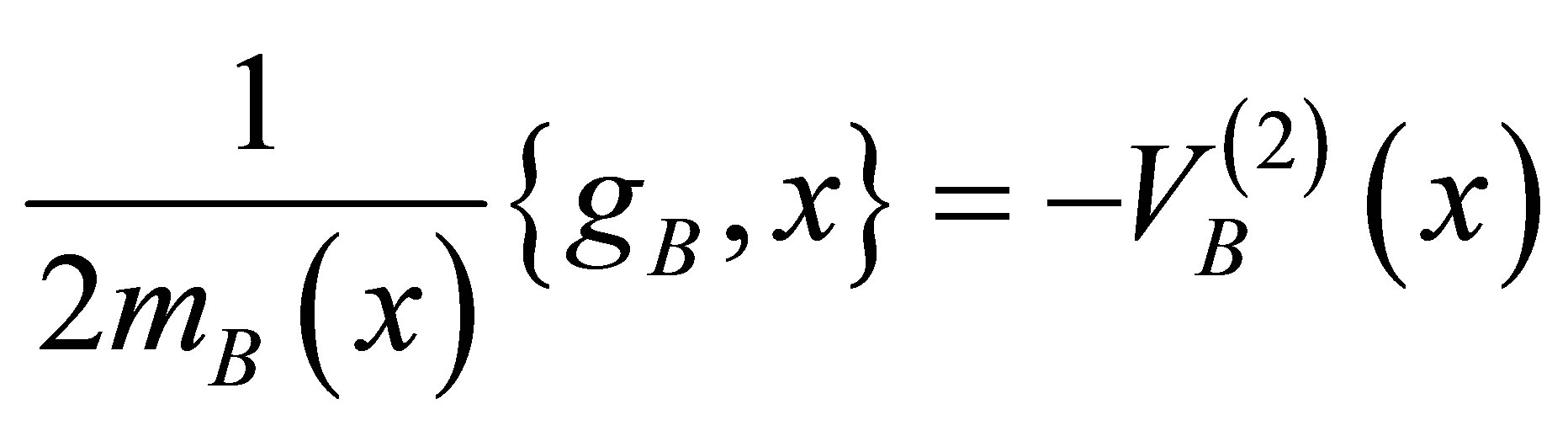 (16)
(16)
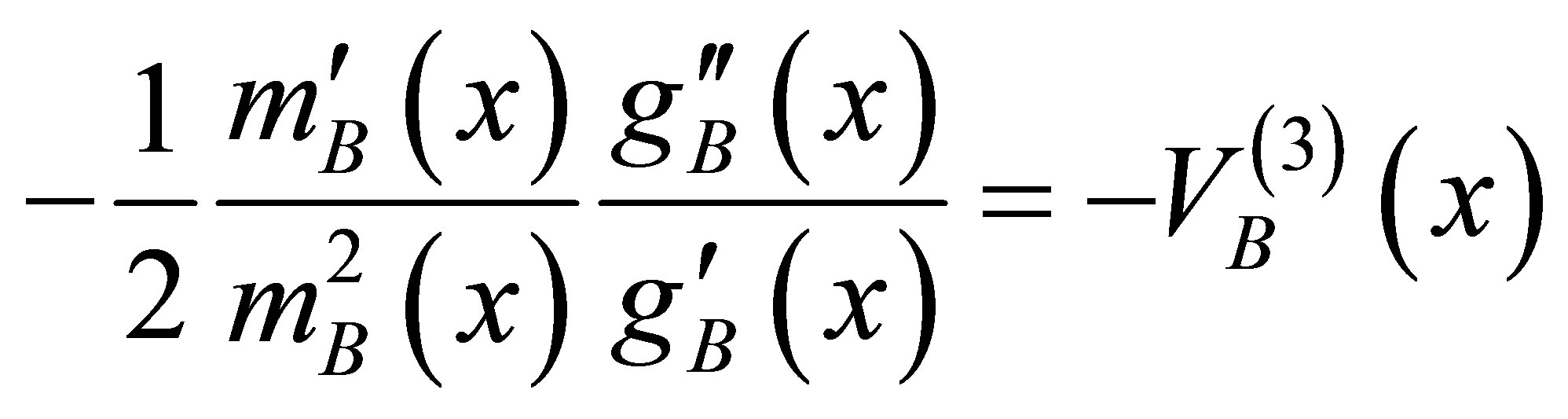 (17)
(17)
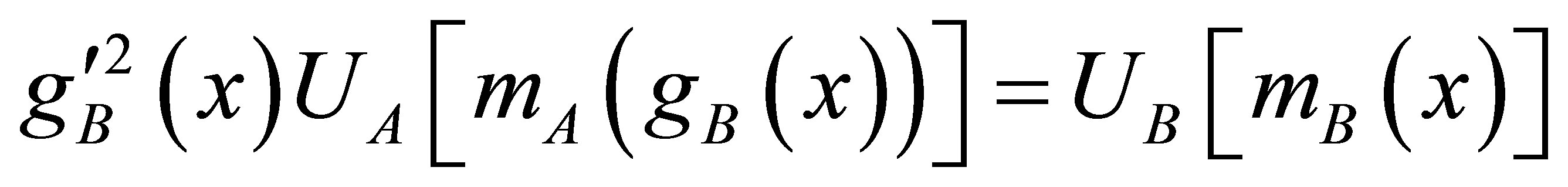 (18)
(18)
Among these ansätze Equation (14) specifies the functional form of gB(x). Equations (15) to (18) give the BQS potential VB(x) as
 (19)
(19)
and effective potential as
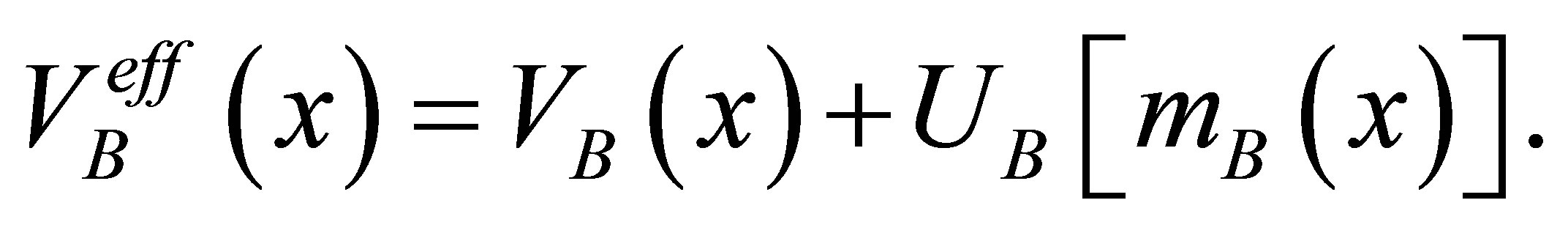 (20)
(20)
Finally 1D-PDM Schrödinger equation for B-QS takes the form
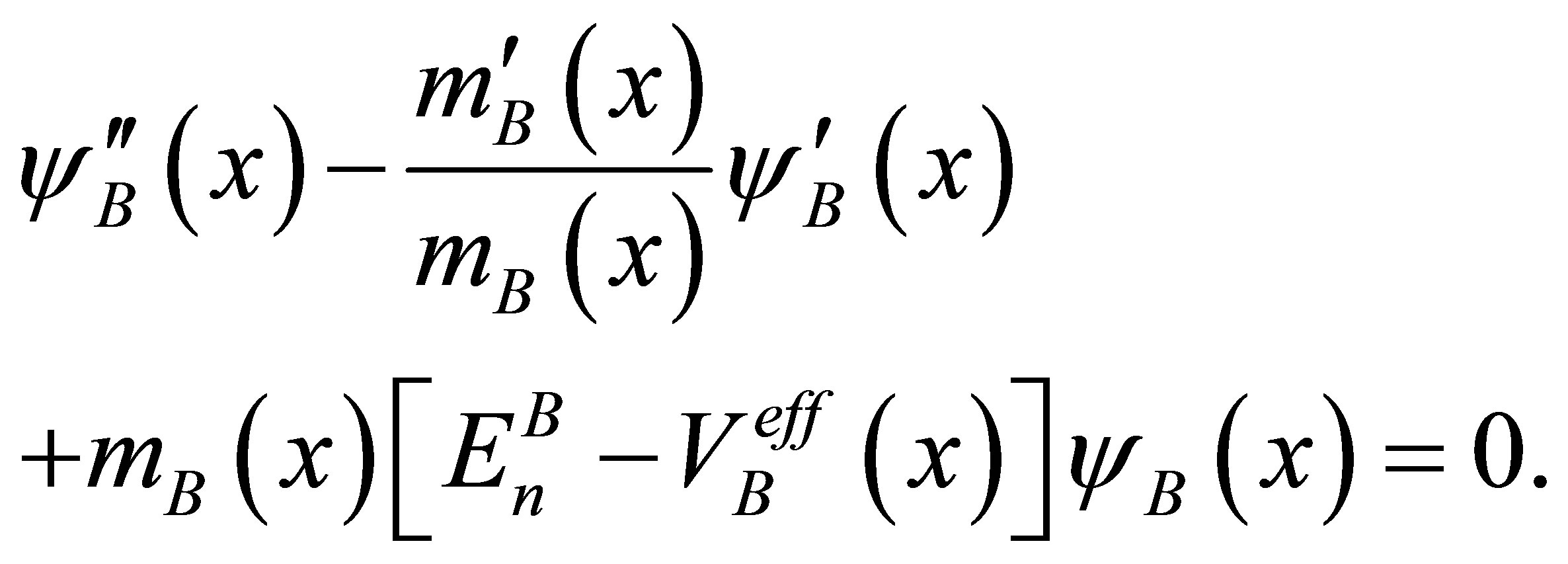 (21)
(21)
3. Generation of ESPs from Hulthen Potential
We have considered Hulthen potential as a typical representative of an exactly solved quantum system whose exact solution of 1D-PDM Schrödinger equation is available/possible [12].
The deformed Hulthen potential, denoted as VA(x) is given by
 (22)
(22)
where V0 is the compact form of the three parameters which are atomic number (in atomic system), deformed parameter q and screening parameter. The Hulthen potential is a short range potential which behaves like a Coulomb potential for small values of x and decreases exponentially for large values of x. The deformed Hulthen potential reduces to the Hulthen form for q = 1, to standard Wood-Saxon potential for q = −1 and to the exponential potential for q = 0. It is a special case of the Eckart potential which has been used in many different areas like Nuclear, Atomic, Condensed matter and Chemical Physics.
V0 is the compact form of the three parameters which are atomic number (in atomic system), deformed parameter q and screening parameter. The Hulthen potential is a short range potential which behaves like a Coulomb potential for small values of x and decreases exponentially for large values of x. The deformed Hulthen potential reduces to the Hulthen form for q = 1, to standard Wood-Saxon potential for q = −1 and to the exponential potential for q = 0. It is a special case of the Eckart potential which has been used in many different areas like Nuclear, Atomic, Condensed matter and Chemical Physics.
For
 (23)
(23)
the discrete energy eigenvalues are
 (24)
(24)
and the corresponding eigenfunctions are
 (25)
(25)
where
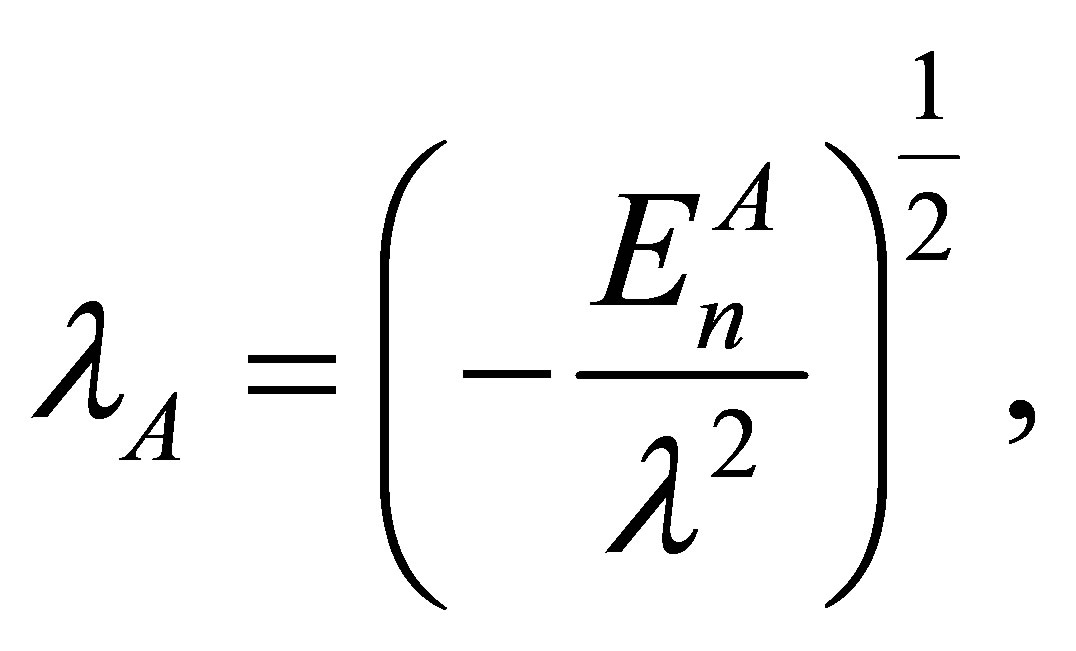
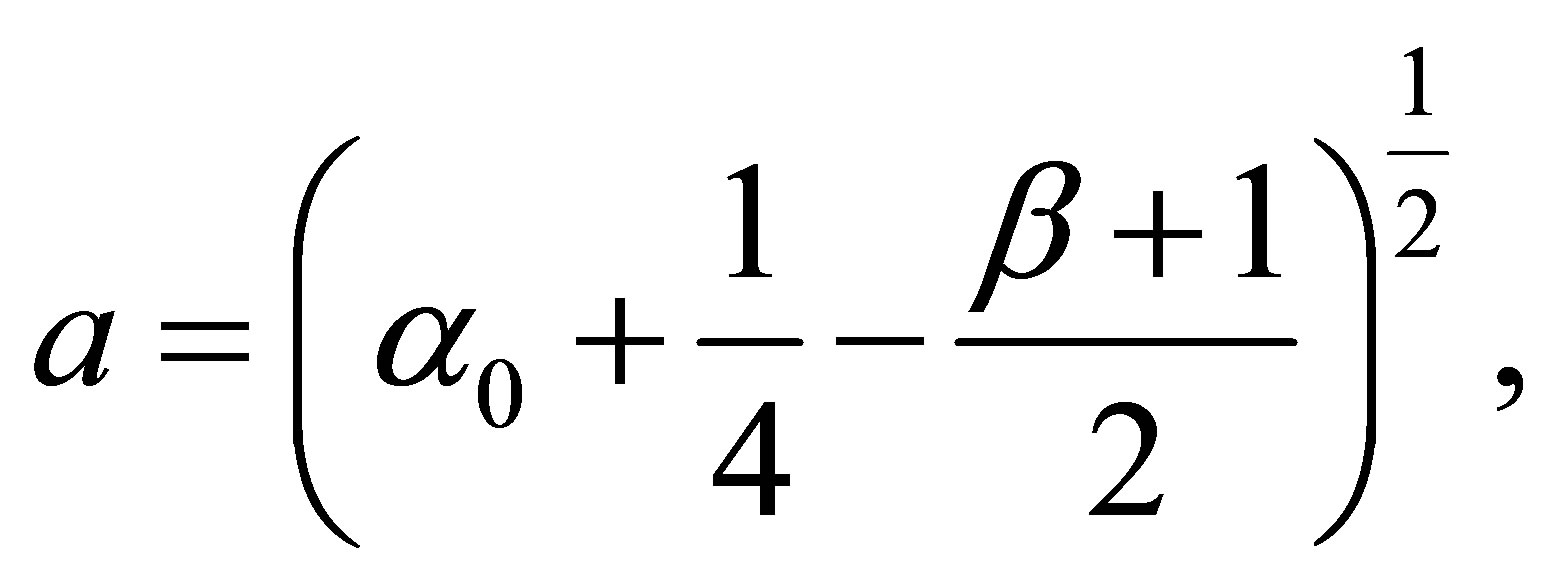
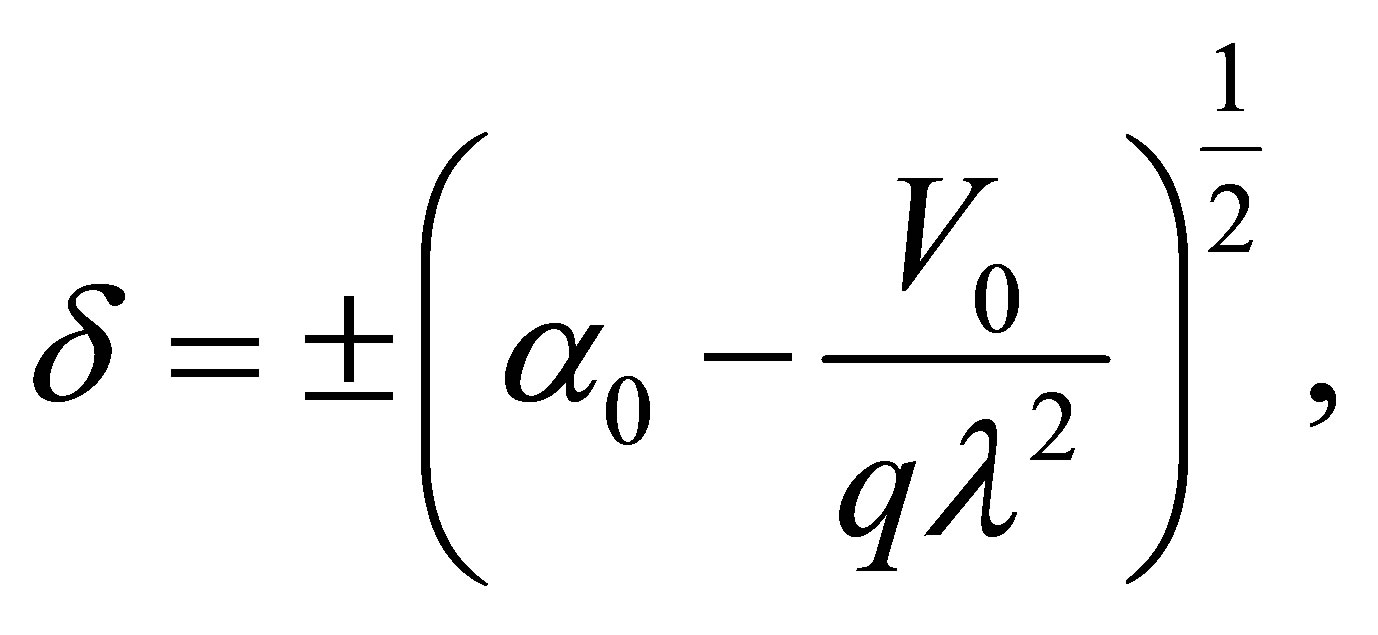

and
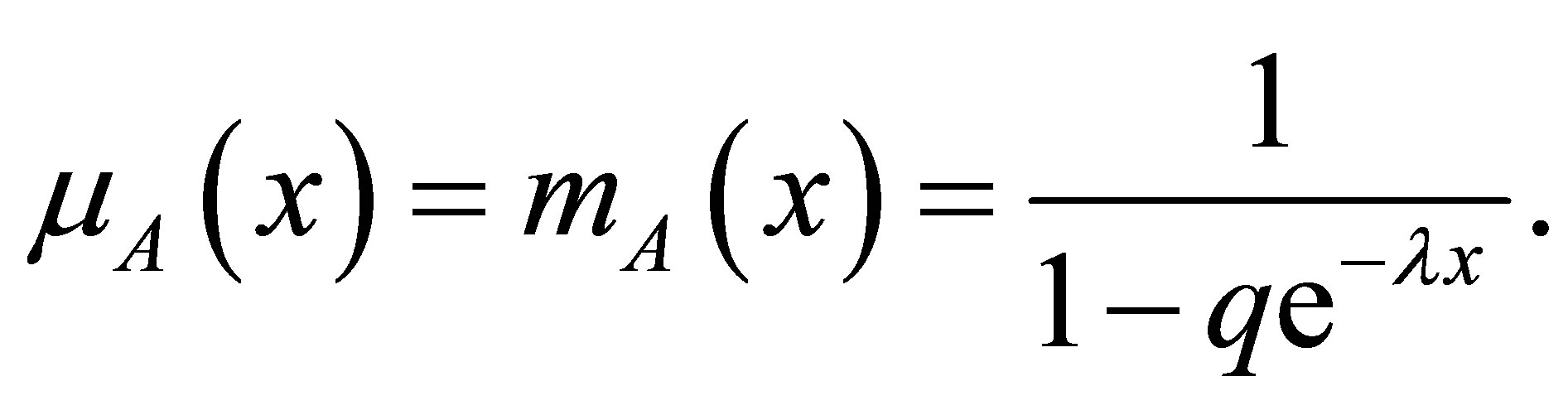
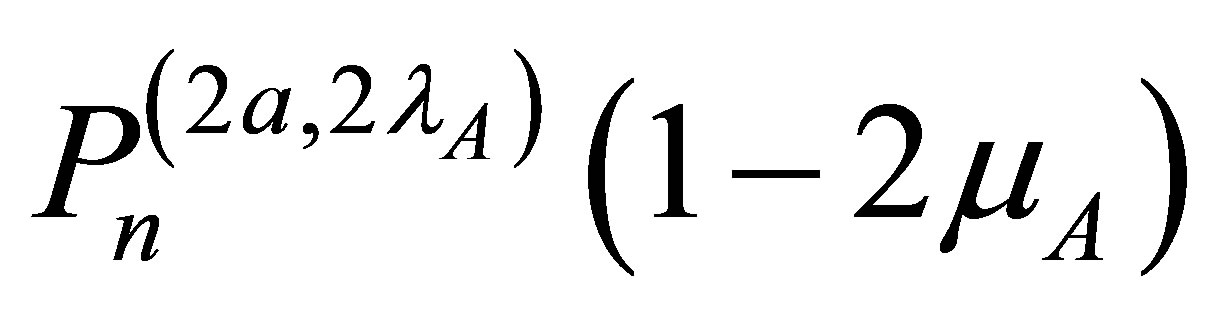 are well known Jacobi Polynomials and NA is normalization constant.
are well known Jacobi Polynomials and NA is normalization constant.
The parameters  and
and 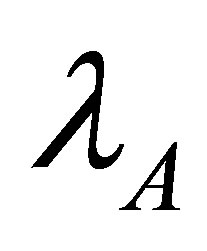 satisfy the relation
satisfy the relation
 (26)
(26)
3.1. Generation of B-Quantum System: First Order Transformation
Using Equations (22) and (14), the transformation function gB(x) is found as
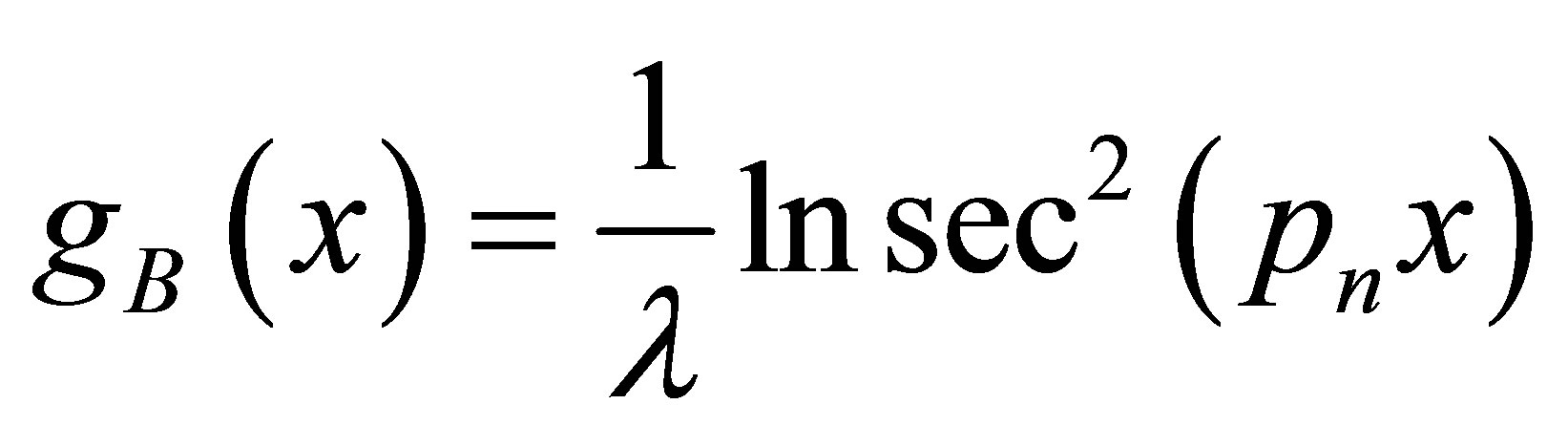 (27)
(27)
where
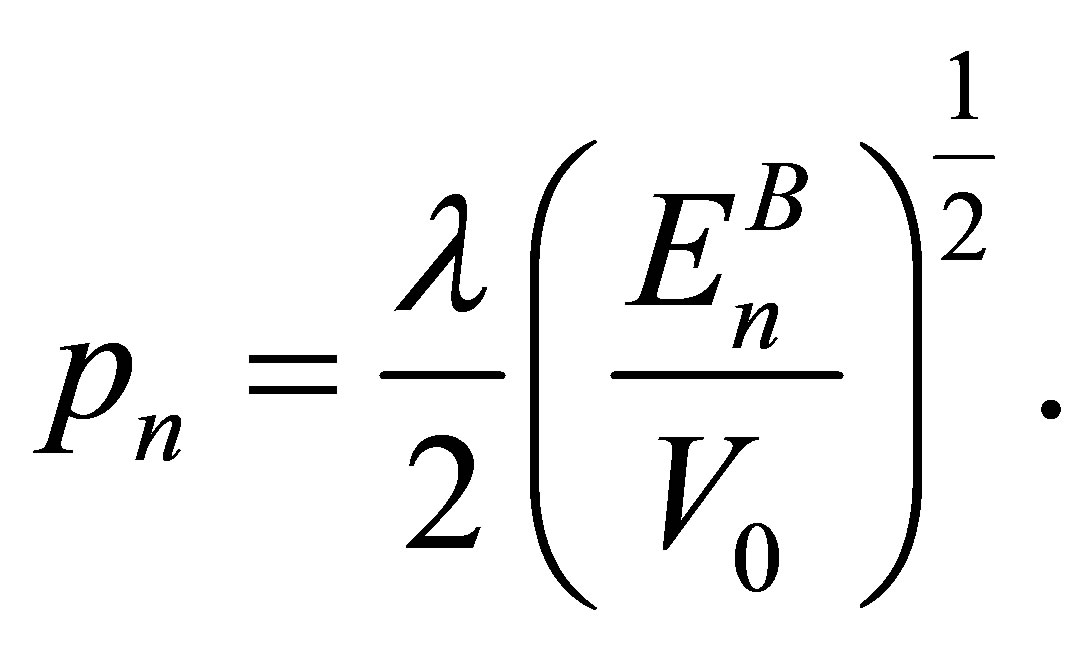 (28)
(28)
We have put q = 1 which gives local property gB(0) = 0.
Equations (27) and (9) yield the mass function of B-QS as
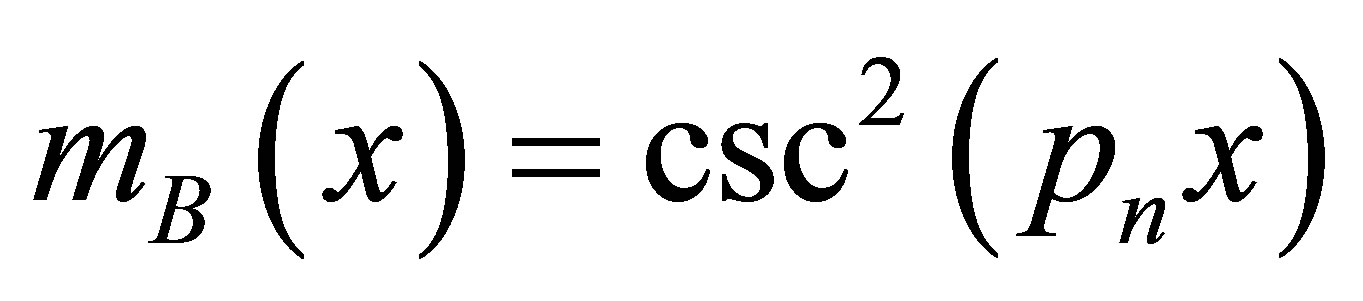 (29)
(29)
Using Equation (27) in Equations (15)-(18), we have found
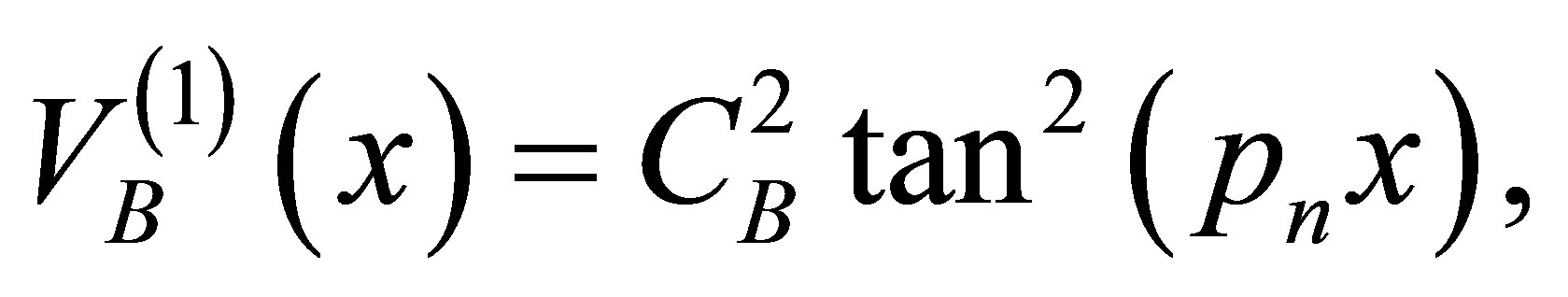 (30)
(30)
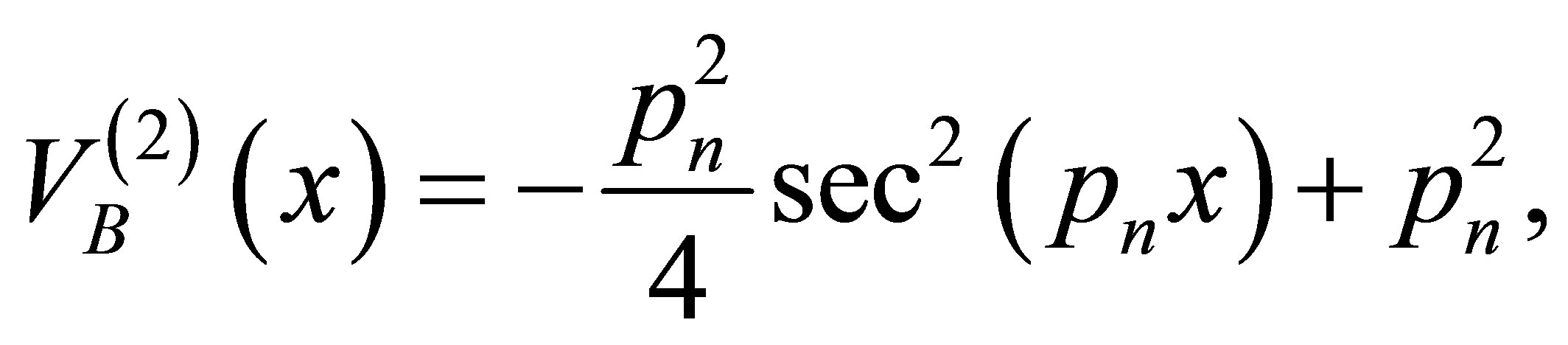 (31)
(31)
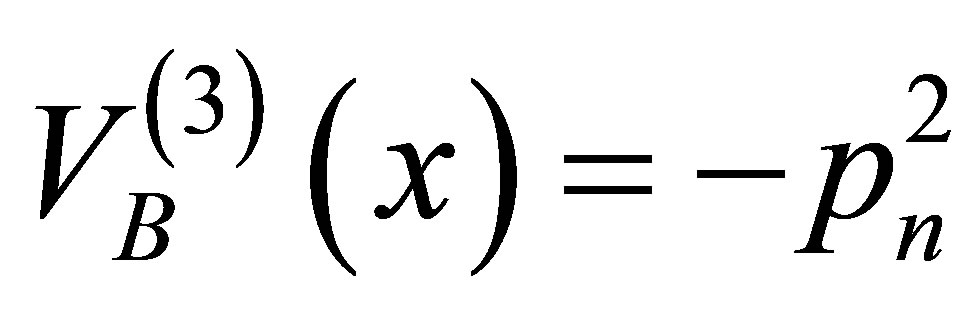 (32)
(32)
and
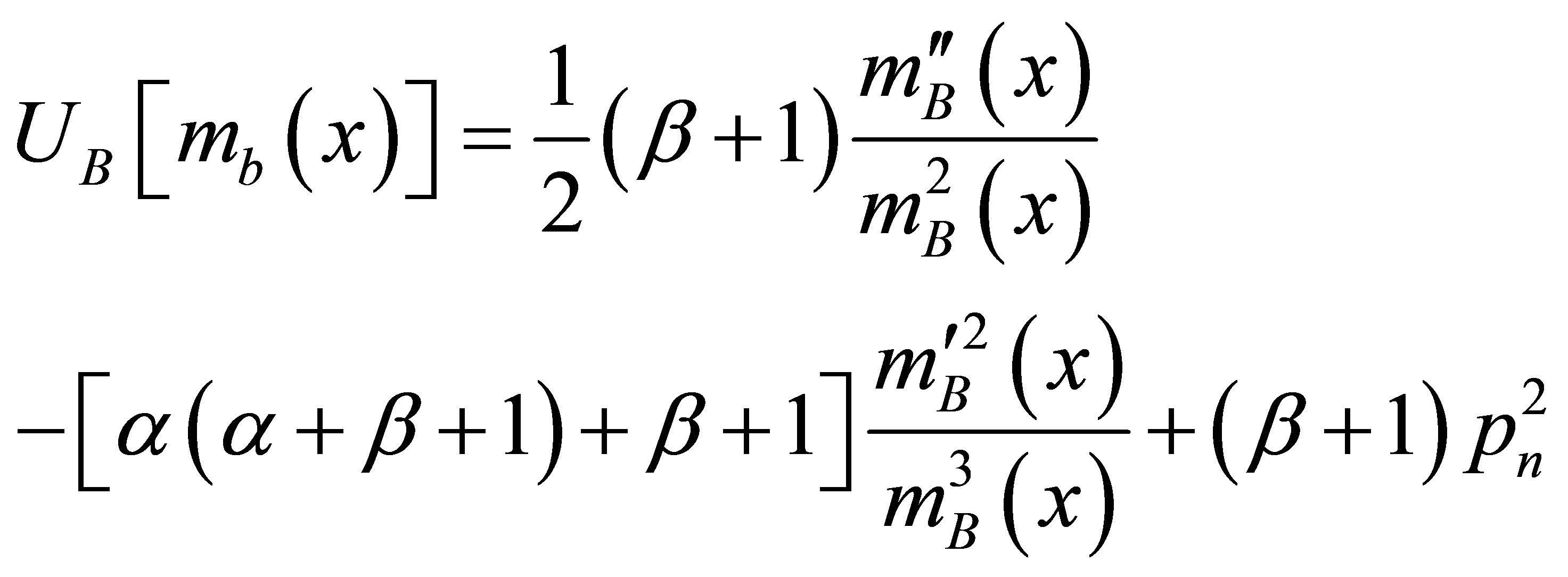 (33)
(33)
respectively, where
 (34)
(34)
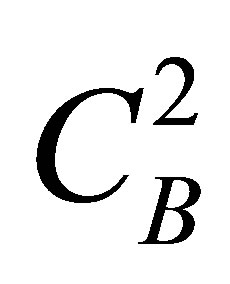 is the characteristic constant of B-QS obtained from the transformation of A-QS. Equation (34) subsequently provides us with the energy eigenvalues of B-QS.
is the characteristic constant of B-QS obtained from the transformation of A-QS. Equation (34) subsequently provides us with the energy eigenvalues of B-QS.
The potential of B-QS, VB(x) is found from Equation (19) as
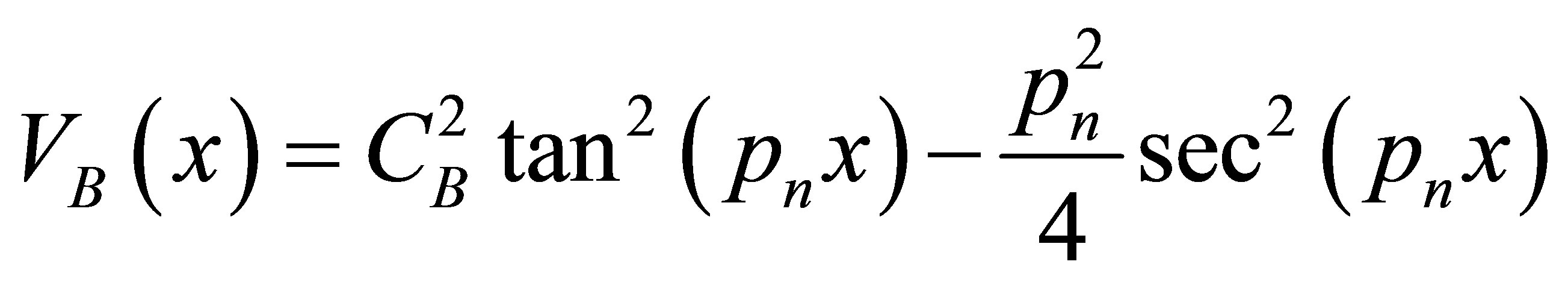 (35)
(35)
which specifies a sturmian QS.
The characteristic constant 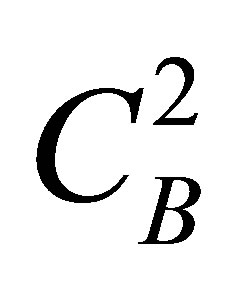 of B-QS can also be written as
of B-QS can also be written as
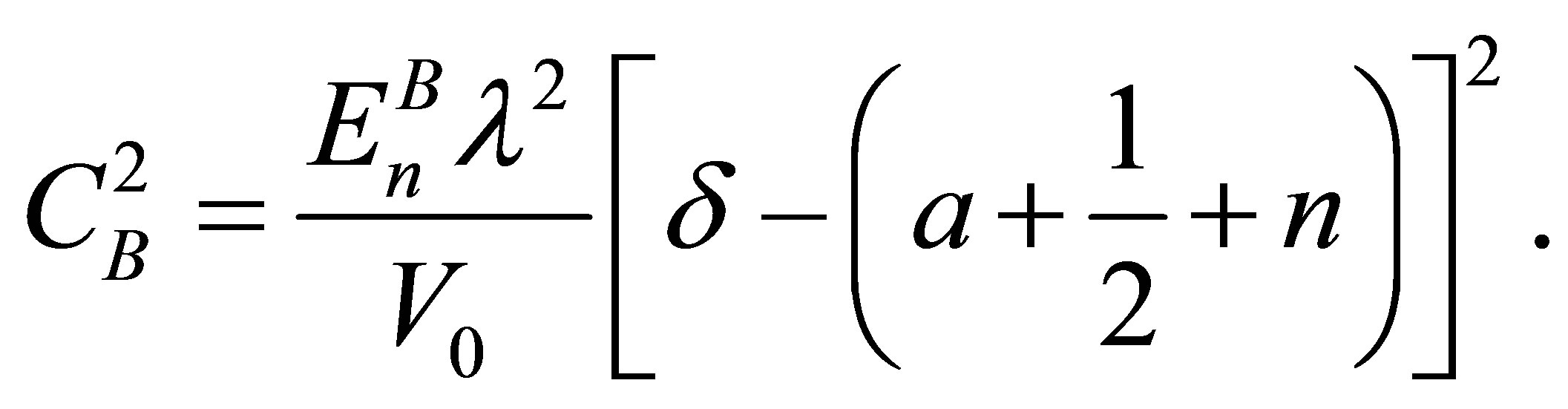 (36)
(36)
Using Equation (36), we have found the energy eigenvalues of B-QS as
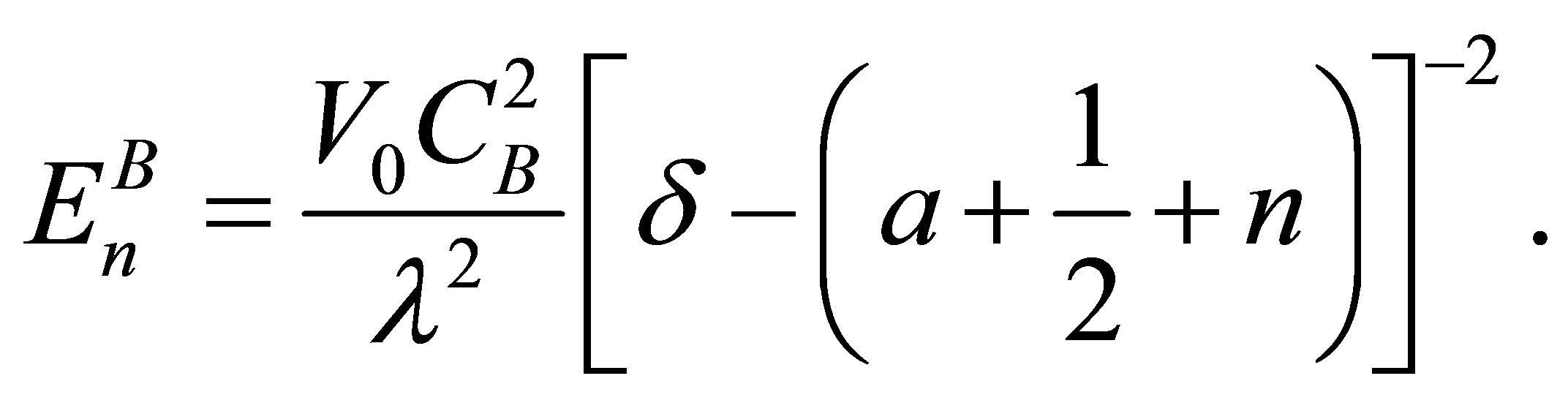 (37)
(37)
The exact eigenfunctions of the generated B-QS come out from Equation (7) as
 (38)
(38)
where
 (39)
(39)
and NB is normalization constant.
The potential VB(x) is n-dependent through n-dependence of pn. This special type of energy dependent potential is equipped with only a single normalized eigenstate. The Sturmian form of B-QS comprises a finite set of QSs. This Sturmian form of B-QS can be converted to a normal QS by a system specific regrouping method, where we have to redefine the parameters of A-QS preserving the type of constraint equations.
To make 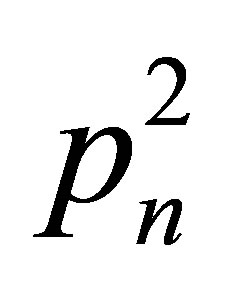 n-independent we make V0 → Vn by setting
n-independent we make V0 → Vn by setting 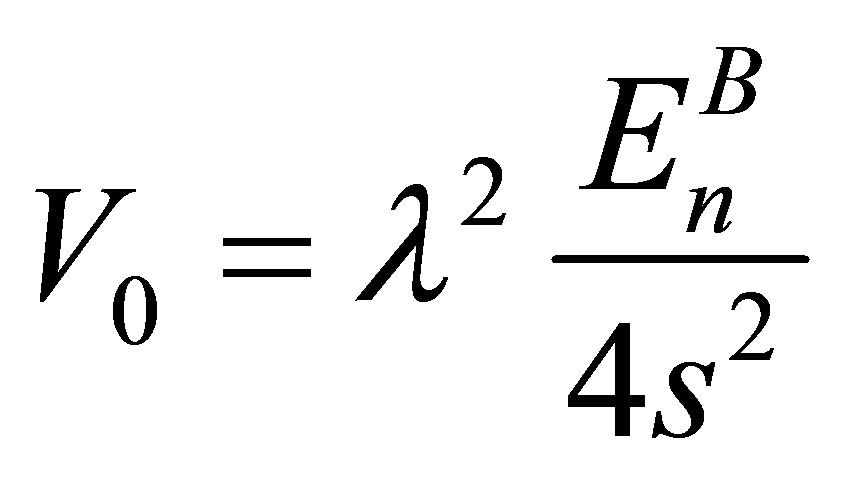 where a scale factor s is introduced.
where a scale factor s is introduced.
This leads to pn → p = s, a constant.
As a result, the normal form of the newly generated BQS potential, VB(x) comes out to be
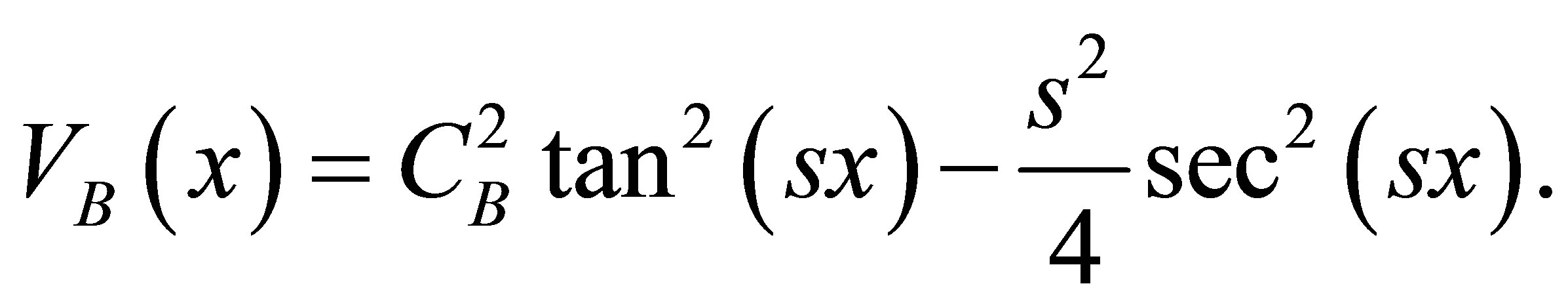 (40)
(40)
And the expression for energy eigenvalues of the generated B-QS is found to be
 (41)
(41)
where
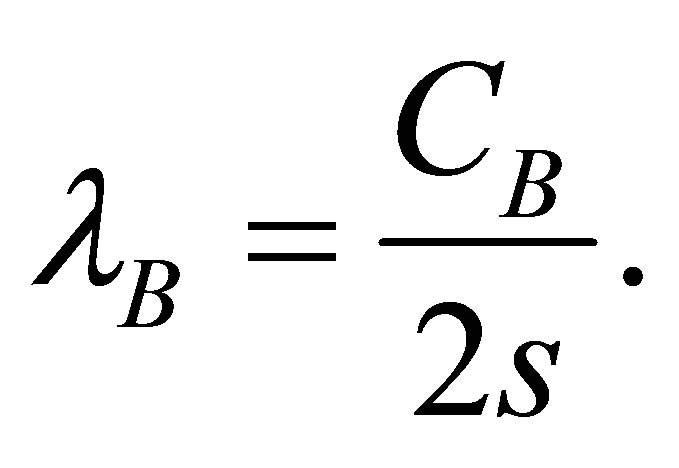
Now we introduce a parameter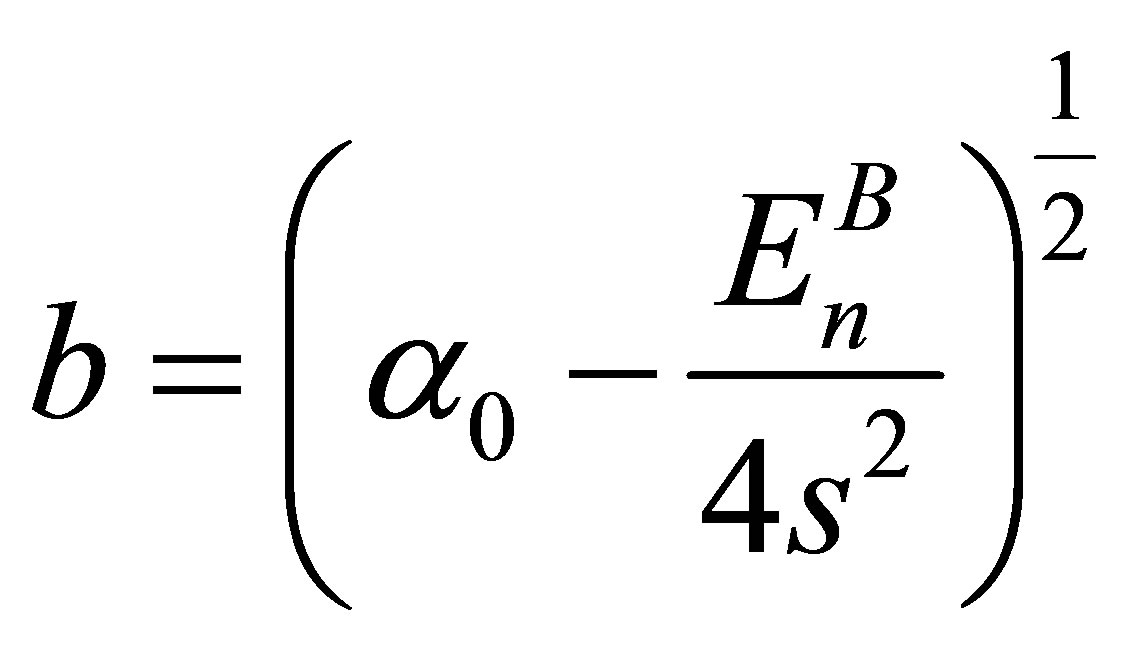 . Parameters
. Parameters  and b satisfy the relation
and b satisfy the relation
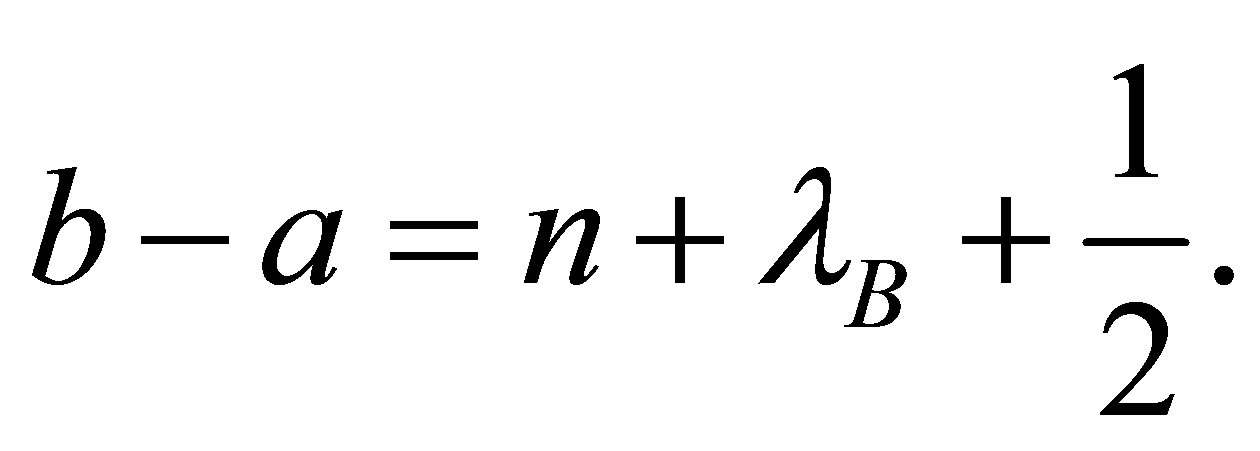 (42)
(42)
The corresponding exact energy eigenfunctions of the newly generated B-QS come out to be
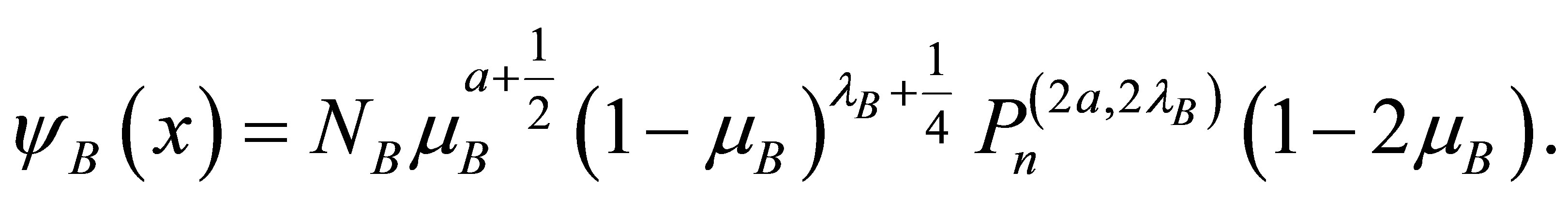 (43)
(43)
3.2. Generation of C-Quantum System: Second Order Transformation
From the potential of B-QS as obtained from Equation (40), we may choose one of the terms as working potential and applying ET we can generate another new QS, which is designated as C-QS, by the above procedure. The B-QS potential consists of two terms, from which the working potential can be chosen in 22-1 i.e. 3 different ways. But we consider the single term working potential only for simplicity. It appears that the choice of 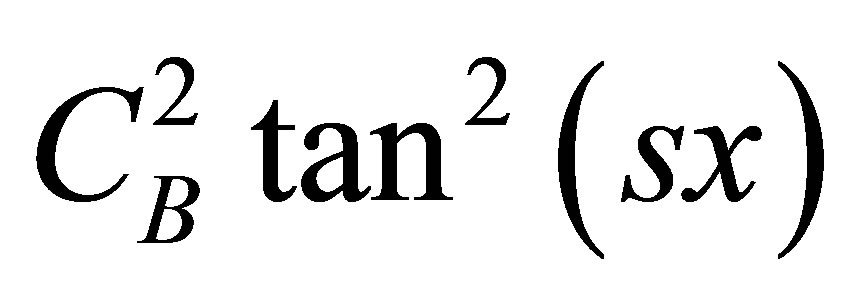 as the working potential reverts it back to the parent QS. We have chosen
as the working potential reverts it back to the parent QS. We have chosen  as the working potential from VB(x). The transformation of mass function and the set of ansätze required to write Equation (12) in standard form of 1D-PDM Schrödinger equation for C-QS are written as
as the working potential from VB(x). The transformation of mass function and the set of ansätze required to write Equation (12) in standard form of 1D-PDM Schrödinger equation for C-QS are written as
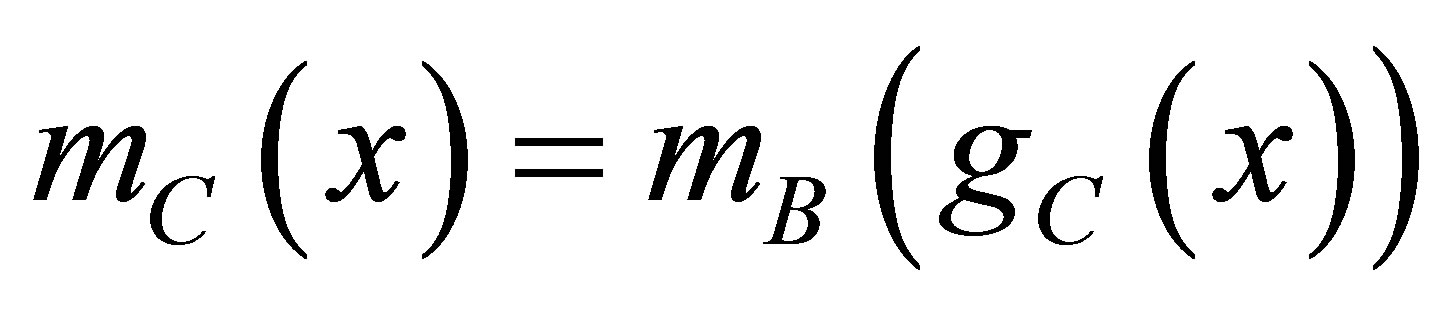 (44)
(44)
and
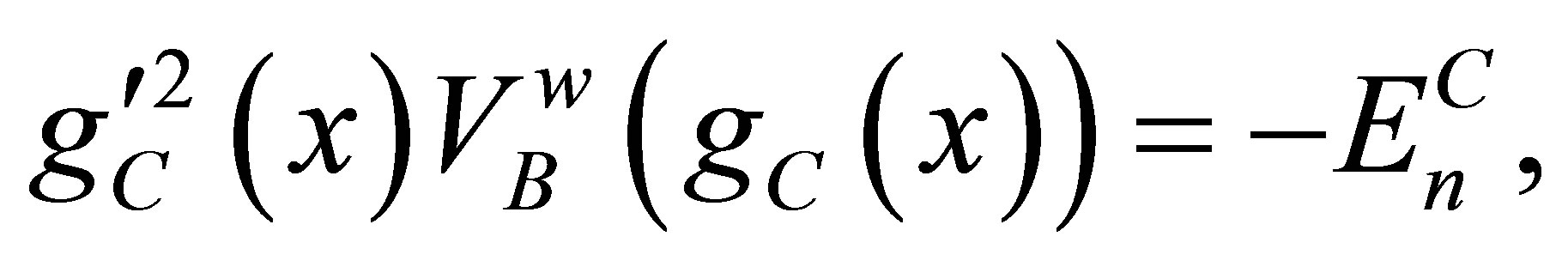 (45)
(45)
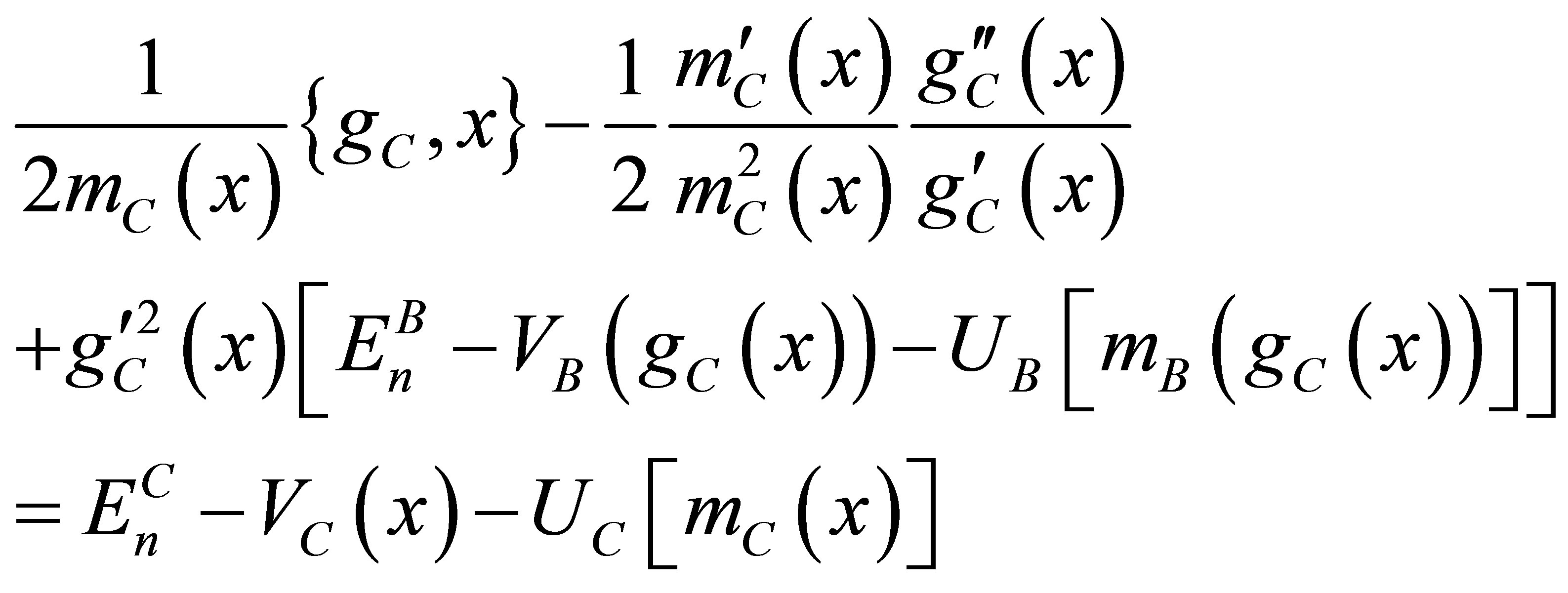 (46)
(46)
respectively. From Equation (45) we have got the transformation function gC(x) as
 (47)
(47)
where
 (48)
(48)
From Equations (44) and (47), we have found the mass function of C-QS as
 (49)
(49)
The Sturmian form of C-QS potential VC(x) and modification 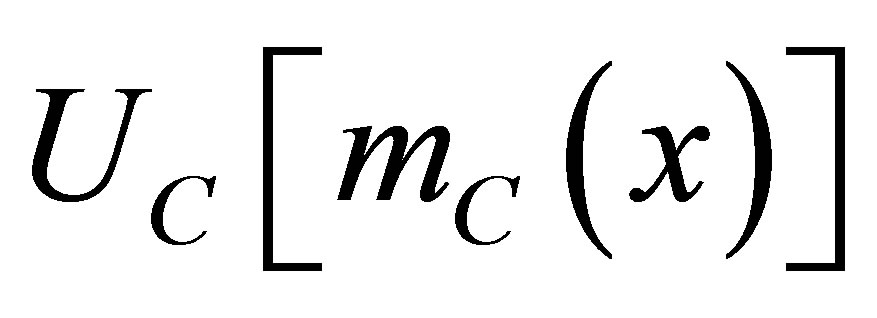 comes out as
comes out as
 (50)
(50)
and
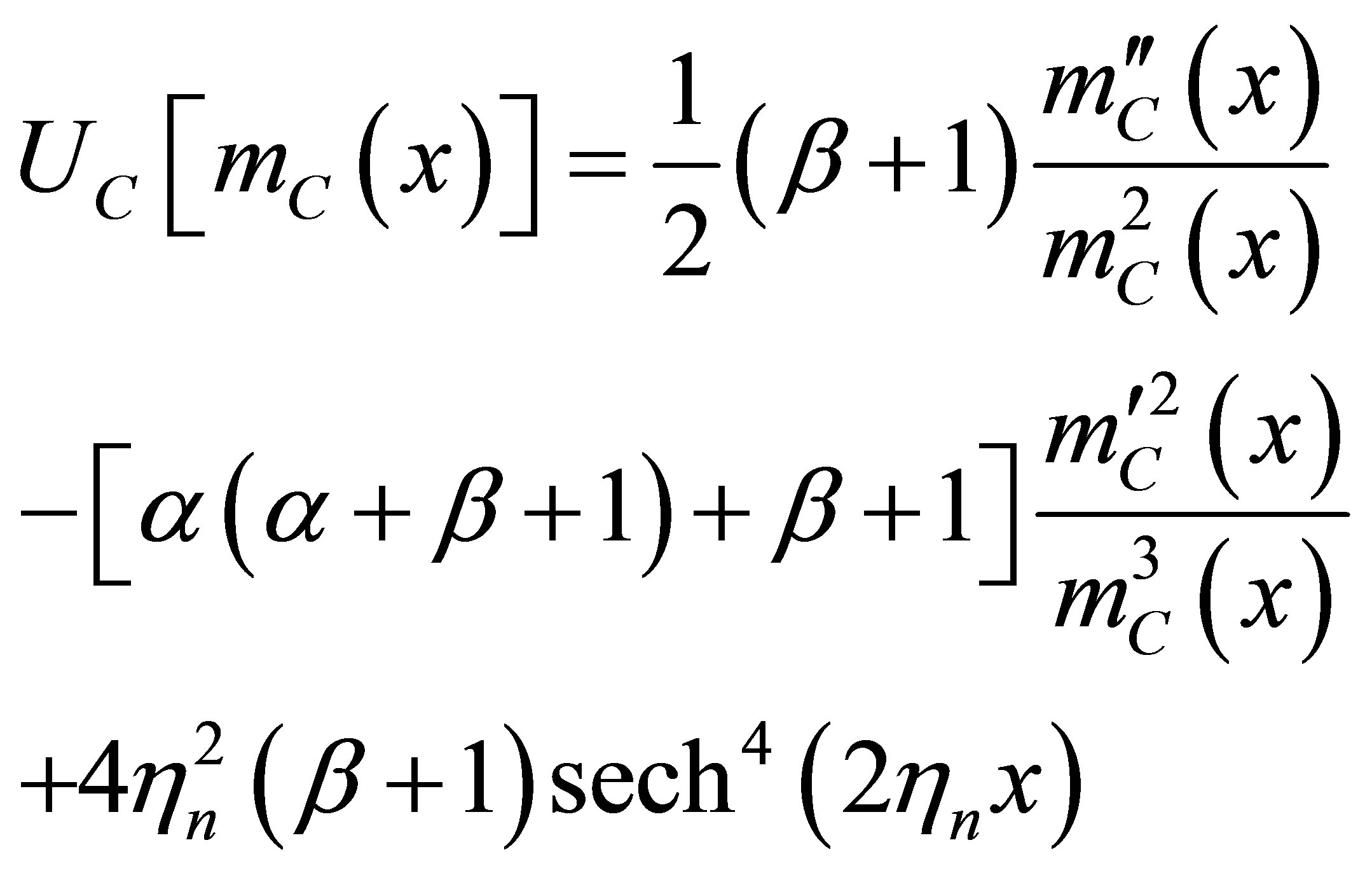 (51)
(51)
respectively. Where 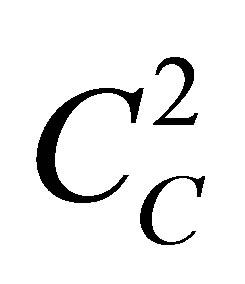 is the characteristic constant of C-QS obtained from the transformation of B-QS and is given by
is the characteristic constant of C-QS obtained from the transformation of B-QS and is given by
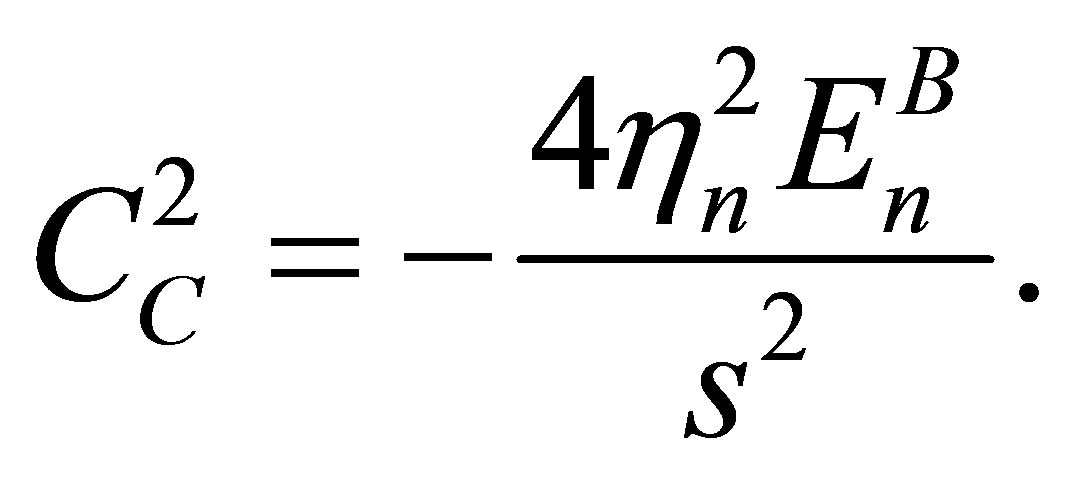 (52)
(52)
The effective potential of C-QS is
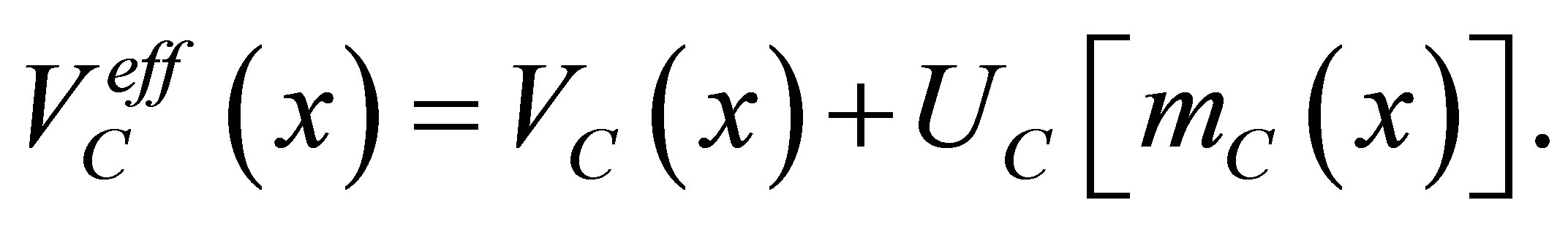 (53)
(53)
However, it is not possible to make the Sturmian C-QS potential VC(x) normal as in the case of B-QS. From Equations (48) and (52) we have found the energy eigenvalues of C-QS as
 (54)
(54)
The energy eigenfunctions of C-QS is obtained as
 (55)
(55)
where NC is normalization constant and
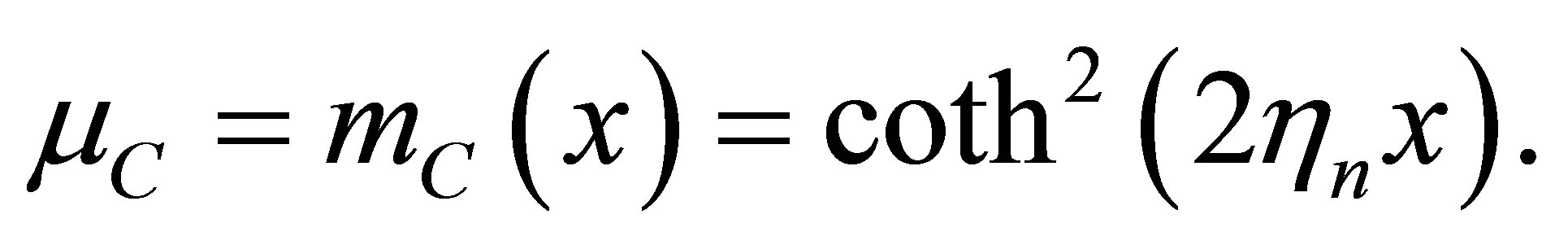 (56)
(56)
Our choice of
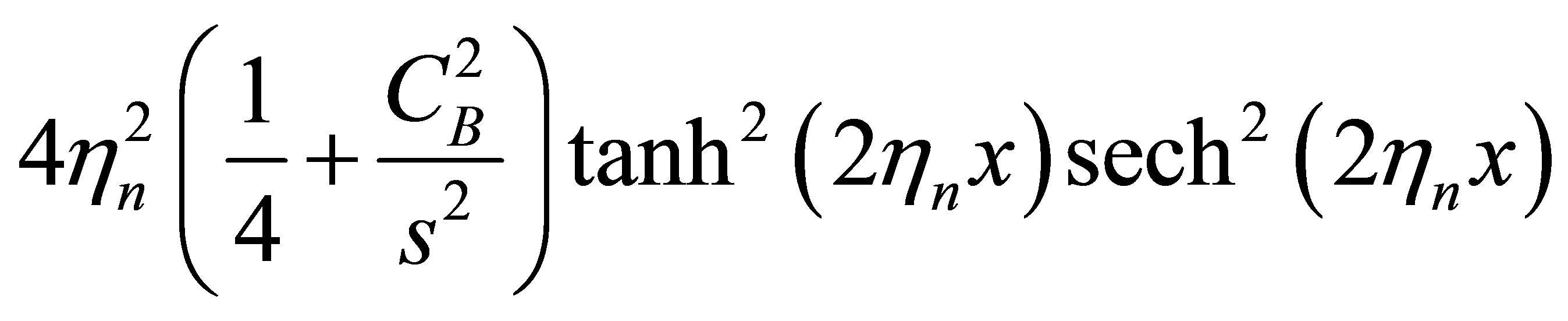
from multiterm potential VC(x) as working potential will also lead to a new form of Sturmian potential which can not be made normal as well as physical by any specific regrouping method.
4. Conclusion
We have presented a method of generating ESPs of PDM Schrödinger equation from a known potential. Two ESPs are generated by successive application of ET on Hulthen potential. The generated potentials are non-power law potential. New mass functions for newly generated systems are also obtained. In constant, mass problems, mass of the generated system and that of parent system remain same, but in case of PDM problems, mass function of parent system gets transformed to new mass function of the generated system. This is a unique feature of this method. Wave functions of generated systems are analytically verified. In case of non-power law potentials, the generated potentials are found to be generally Sturmian. We have converted the Sturmian form of the B-QS potential to normal form by system specific regrouping method. It is evident that the ET may be applied successively any number of times to generate new QSs when we are considering a non power law potential. The present formalism can be generalized to N-dimensional PDM Schrödinger equation.
5. Acknowledgements
We are thankful to (Late) Prof. S. A. S. Ahmed, Gauhati University, Guwahati, India, who had initiated the problem and also extended valuable help in the initial stage of the work.
REFERENCES
- G. Bastard, “Wave Mechanics Applied to Semiconductor Heterostructure,” Editions de Physique, Les Ulis, France, 1988.
- P. Harrison, “Quantum Wells, Wires and Dots,” Wiley, New York, 2000.
- L. Serra and E. Lipparini, EuroPhysics Letter, Vol. 40, 1997, pp. 667-672. http://dx.doi.org/10.1209/epl/i1997-00520-y
- F. Arias de Saavedra, J. Boronat, A. Polls and A. Fabrocini, Physical Review B, Vol. 50, 1994, pp. 4248-4251. http://dx.doi.org/10.1103/PhysRevB.50.4248
- P. Ring and P. Schuck, “The Nuclear Many Body Problem,” Springer, New York, 1980. http://dx.doi.org/10.1007/978-3-642-61852-9
- A. D. Alhaidari, Physical Review A, Vol. 66, 2002, Article ID: 042116. http://dx.doi.org/10.1103/PhysRevA.66.042116
- C. Tazcan and R. Sever, Journal of Mathematical Chemistry, Vol. 42, 2007, pp. 387-395.
- M. Jafarpour and B. Ashtari, Advanced Studies in Theoretical Physics, Vol. 5, 2011, pp. 131-142.
- B. Gönül, O. Özer, B. Gönül and F. Üzgün, Modern Physics Letters A, Vol. 17, 2002, p. 2453.
- A.-P. Zang, P. Shi, Y.-W. Ling and Z.-W. Hua, Acta Physica Polonica A, Vol. 120, 2011, pp. 987-991.
- C. Tezcan, R. Sever and Ö. Yeşiltas, International Journal of Theoretical Physics, Vol. 47, 2008, p. 1713.
- R. Sever, C. Tezcan, Ö. Yesiltas and M. Bucurgat, International Journal of Theoretical Physics, Vol. 47, 2008, pp. 2243-2248.
- S. Meyur, Bulgarian Journal of Physics, Vol. 38, 2011, pp. 357-363.
- R. Koç and H. Tütüncüler, Annalen der Physik, Vol. 12, 2003, pp. 684-691.
- C. Quesne, B. Bagchi, A. Banergee and V. M. Tkachuk, Bulgarian Journal of Physics, Vol. 33, 2006, pp. 308- 318.
- C. Quesne, Sigma, Vol. 3, 2007, 14 p. http://dx.doi.org/10.3842/SIGMA.2007.067
- A. Schulze-Halberg, International Journal of Modern Physics A, Vol. 22, 2007, pp. 1735-1769.
- A. Schulze-Halberg, International Journal of Modern Physics A, Vol. 23, 2008, pp. 537-546. http://dx.doi.org/10.1142/S0217751X0803807X
- S. A. S. Ahmed, International Journal of Theoretical Physics, Vol. 36, 1997, pp. 1893-1905. http://dx.doi.org/10.1007/BF02435851
- B. Gönül and M. Koçak, Chinese Physics Letters, Vol. 22, 2005, p. 2742.
- O. Von Roos, Physical Review B, Vol. 27, 1983, pp. 7547-7552. http://dx.doi.org/10.1103/PhysRevB.27.7547

