Journal of Modern Physics
Vol.4 No.12(2013), Article ID:41482,9 pages DOI:10.4236/jmp.2013.412204
Damping-Antidamping Effect on Comets Motion
Departamento de Fsica, Universidad de Guadalajara, Guadalajara, México
Email: gulopez@cencar.udg.mx
Copyright © 2013 G. V. López, E. M. Juárez. This is an open access article distributed under the Creative Commons Attribu- tion License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 12, 2013; revised October 15, 2013; accepted November 11, 2013
Keywords: Quantum Computer; Controlled-Not Gate; Diamond
ABSTRACT
We make an observation about Galilean transformation on a 1-D mass variable system which leads us to the right way to deal with mass variable systems. Then using this observation, we study two-body gravitational problem where the mass of one of the bodies varies and suffers a damping-antidamping effect due to star wind during its motion. For this system, a constant of motion, a Lagrangian and a Hamiltonian are given for the radial motion, and the period of the body is studied using the constant of motion of the system. Our theoretical results are applied to Halley’s Comet.
1. Introduction
There is not doubt that mass variable systems have been relevant since the foundation of the classical mechanics and modern physics [1]. These type of systems have been known as Gylden-Meshcherskii problems [2-9], and among these type of systems one could mention: the motion of rockets [10], the kinetic theory of dusty plasma [11], propagation of electromagnetic waves in a dispersive nonlinear media [12], neutrinos mass oscillations [13] and [14], black holes formation [15], and comets interacting with solar wind [16]. This last system belongs to the so called “gravitational two-body problem” which is one of the most studied and well known system in classical mechanics [17]. In this type of system, one assumes normally that the masses of the bodies are fixed and unchanged during the dynamical motion. However, when one is dealing with comets, beside to consider its mass variation due to the interaction with the solar wind, one would like to have an estimation of the the effect of the solar wind pressure on the comet motion. This pressure may produce a dissipative-antidissipative effect on its motion. The dissipation effect must be felt by the comet when this one is approaching to the sun (or star), and the antidissipation effect must be felt by the comet when this one is moving away from the sun. To deal with these type of mass variation problem, it has been proposed that the Newton equation must be modified [10] and [18] since the system becomes noninvariant under change of inertial systems (Galileo transformation).
In this paper, we will make a first observation about this statement which indicates that the such a proposed modification of Newton’s equation has some problems and rather the use of the original Newton equation is the right approach to deal with mass variation systems, which it was used in previous paper [19] to study two-bodies gravitational problem with mass variation in one of them, where we were interested in the difference of the trajectories in the spaces  and
and . As a consequence, there is an indication that mass variation problems must be dealt as noninvariant under Galilean transformation. Second, we study the two-body gravitational problem taking into consideration the mass variation of one of them and its damping-antidamping effect due to the solar wind. The mass of the other body is assumed big and fixed , and the reference system of motion is chosen just in this body. In addition, we will assume that the mass lost is expelled from the body radially to its motion. Doing this, the three-dimensional two-body problem is reduced to a one-dimensional problem. Then, a constant of motion, the Lagrangian, and the Hamiltonian are deduced for this one-dimensional problem, where a radial dissipative antidissipative force proportional to the velocity square is chosen. A model for the mass variation is given, and the dampingantidamping effect is studied on the period of the trajectories, the trajectories themselves, and the aphelion distance of a comet. We use the parameters associated to comet Halley to illustrate the application of our results.
. As a consequence, there is an indication that mass variation problems must be dealt as noninvariant under Galilean transformation. Second, we study the two-body gravitational problem taking into consideration the mass variation of one of them and its damping-antidamping effect due to the solar wind. The mass of the other body is assumed big and fixed , and the reference system of motion is chosen just in this body. In addition, we will assume that the mass lost is expelled from the body radially to its motion. Doing this, the three-dimensional two-body problem is reduced to a one-dimensional problem. Then, a constant of motion, the Lagrangian, and the Hamiltonian are deduced for this one-dimensional problem, where a radial dissipative antidissipative force proportional to the velocity square is chosen. A model for the mass variation is given, and the dampingantidamping effect is studied on the period of the trajectories, the trajectories themselves, and the aphelion distance of a comet. We use the parameters associated to comet Halley to illustrate the application of our results.
2. Mass Variation Problem and Galileo Transformation
To simplify our discussion and without losing generality, we will restrict myself to one degree of freedom. Newton equation of motion is given by
 (1)
(1)
where  is the quantity of movement,
is the quantity of movement,  is the total external force acting on the object,
is the total external force acting on the object,  and
and  are its time depending mass and velocity of the body (motion of the mass lost is not considered). Galileo transformations to another inertial frame
are its time depending mass and velocity of the body (motion of the mass lost is not considered). Galileo transformations to another inertial frame ![]() which is moving with a constant velocity
which is moving with a constant velocity ![]() respect our original frame
respect our original frame ![]() are defined as
are defined as
 (2)
(2)
 (3)
(3)
which implies the following relation between the velocity seen in the reference system![]() ,
, ![]() , and the velocity seen in the reference system
, and the velocity seen in the reference system ,
,  ,
,
 (4)
(4)
Multiplying the last term by  and making the differentiation with respect to
and making the differentiation with respect to , one gets
, one gets
 (5)
(5)
where  is given by
is given by
 (6)
(6)
Therefore, Equations (1) and (5) have the same form but the force is different since in addition to the transformed force term , one has the term
, one has the term . This noninvariant form of the force under Galilean transformation has lead to propose [10] and [18] that Newton Equation (1) to modify Newton’s equation of motion for mass variation objects, to keep the principle of invariance of equation under Galilean transformations, of the form
. This noninvariant form of the force under Galilean transformation has lead to propose [10] and [18] that Newton Equation (1) to modify Newton’s equation of motion for mass variation objects, to keep the principle of invariance of equation under Galilean transformations, of the form
 (7)
(7)
where ![]() is the relative velocity of the escaping mass with respect the center of mass of the object. When one does a Galilean transformation on this equation, one gets
is the relative velocity of the escaping mass with respect the center of mass of the object. When one does a Galilean transformation on this equation, one gets
 (8)
(8)
where  is given by
is given by
 (9)
(9)
which has the same form as Equation (7). However, assume for the moment that  and
and . So, from Equation (7), it follows that
. So, from Equation (7), it follows that
 (10)
(10)
where . In this way, if we have a mass variation of the for
. In this way, if we have a mass variation of the for  (for example), one would have a velocity behavior like
(for example), one would have a velocity behavior like
 (11)
(11)
which is not acceptable since one can have ,
,  and
and  depending on the value
depending on the value![]() . Even more, since for
. Even more, since for , the equation resulting in the reference system
, the equation resulting in the reference system  is the same, i.e. in
is the same, i.e. in  one gets the same type of solution,
one gets the same type of solution,
 (12)
(12)
which is independent on the relative motion of the reference frames, and this must not be possible due to relation (4).
In addition, it worths to mention that special theory of relativity can be seen as the motion of mass variation problem, where the mass depends on the velocity of the particle of the form , with
, with ![]()
being the speed of light. This system is obviously not invariant under Galilean transformation, and given the force, Newton’s equation motion is always kept in the same form to solve a relativistic problem,  , [20] and [1].
, [20] and [1].
3. Mass Variation and Equations of Motion
Having explained and clarify the problem of mass variation [21], Newton’s equations of motion for two bodies interacting gravitationally, seen from arbitrary inertial reference system, and with radial dissipativeantidissipative force acting in one of them are given by
 (13)
(13)
and
 (14)
(14)
where  and
and  are the masses of the two bodies,
are the masses of the two bodies,  and
and  are their vectors positions from the reference system,
are their vectors positions from the reference system,  is the gravitational constant
is the gravitational constant ,
, is the nonnegative constant parameter of the dissipativeantidissipative force, and
is the nonnegative constant parameter of the dissipativeantidissipative force, and
 is the Euclidean distance between the two bodies. Note that if
is the Euclidean distance between the two bodies. Note that if  and
and  one has dissipation since the force acts against the motion of the body, and for
one has dissipation since the force acts against the motion of the body, and for 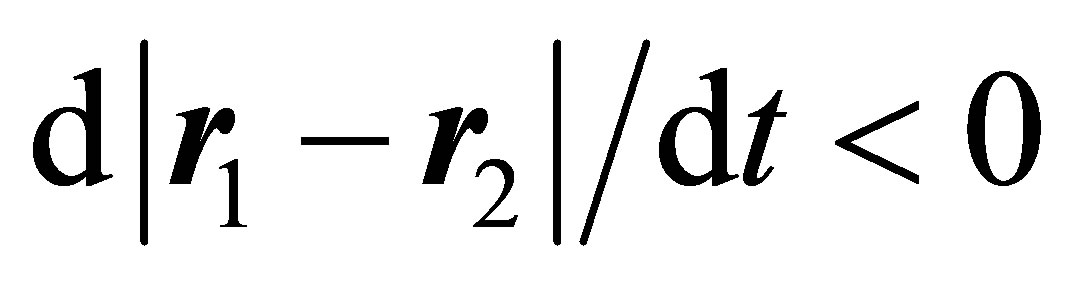 one has anti-dissipation since the force pushes the body. If
one has anti-dissipation since the force pushes the body. If  this scheme is reversed and corresponds to our actual situation with the comet mass lost.
this scheme is reversed and corresponds to our actual situation with the comet mass lost.
It will be assumed the mass  of the first body is constant and that the mass
of the first body is constant and that the mass  of the second body varies. Now, It is clear that the usual relative,
of the second body varies. Now, It is clear that the usual relative,  , and center of mass,
, and center of mass,  , coordinates defined as
, coordinates defined as  and
and  are not so good to describe the dynamics of this system. However, one can consider the case for
are not so good to describe the dynamics of this system. However, one can consider the case for  (which is the case star-comet), and consider to put our reference system just on the first body
(which is the case star-comet), and consider to put our reference system just on the first body . In this case, Equation (13) and Equation (14) are reduced to the equation
. In this case, Equation (13) and Equation (14) are reduced to the equation
 (15)
(15)
where one has made the definition ,
, 
is its magnitude,  and
and  is the unitary radial vector. Using spherical coordinates
is the unitary radial vector. Using spherical coordinates ,
,
 (16)
(16)
one obtains the following coupled equations
 (17)
(17)
 (18)
(18)
and
 (19)
(19)
Taking  as solution of this last equation, the resulting equations are
as solution of this last equation, the resulting equations are
 (20)
(20)
and
 (21)
(21)
From this last expression, one gets the following constant of motion (usual angular momentum of the system)
 (22)
(22)
and with this constant of motion substituted in Equation (20), one obtains the following one-dimensional equation of motion for the radial part
 (23)
(23)
Now, let us assume that  is a function of the distance between the first and the second body,
is a function of the distance between the first and the second body, . Therefore, it follows that
. Therefore, it follows that
 (24)
(24)
where  is defined as
is defined as . Thus, Equation (23) is written as
. Thus, Equation (23) is written as
 (25)
(25)
which, in turns, can be written as the following autonomous dynamical system
 (26)
(26)
Note from this equation that  is always a nonpositive function of
is always a nonpositive function of  since it represents the mass lost rate. On the other hand,
since it represents the mass lost rate. On the other hand,  is a negative parameter in our case.
is a negative parameter in our case.
4. Constant of Motion, Lagrangian and Hamiltonian
A constant of motion for the dynamical system (26) is a function  which satisfies the partial differential equation [22]
which satisfies the partial differential equation [22]
 (27)
(27)
The general solution of this equation is given by [23]
 (28)
(28)
where  is an arbitrary function of the characteristic curve
is an arbitrary function of the characteristic curve  which has the following expression
which has the following expression
 (29)
(29)
and the function  has been defined as
has been defined as
 (30)
(30)
During a cycle of oscillation, the function 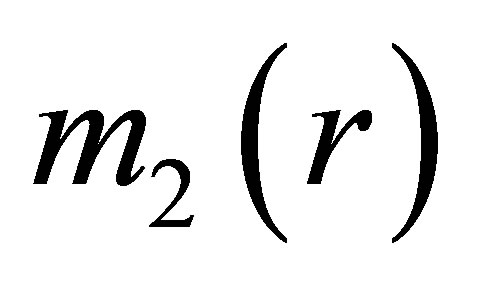 can be different for the comet approaching the sun and for the comet moving away from the sun. Let us denote
can be different for the comet approaching the sun and for the comet moving away from the sun. Let us denote  for the first case and
for the first case and  for the second case. Therefore, one has two cases to consider in Equation (28) which will denoted by
for the second case. Therefore, one has two cases to consider in Equation (28) which will denoted by . Now, if
. Now, if  denotes the mass at aphelium (+) or perielium (−) of the comet,
denotes the mass at aphelium (+) or perielium (−) of the comet,  represents the functionality in Equation (28) such that for
represents the functionality in Equation (28) such that for  constant and
constant and  equal zero, this constant of motion is the usual gravitational energy. Thus, the constant of motion can be chosen as
equal zero, this constant of motion is the usual gravitational energy. Thus, the constant of motion can be chosen as , that is,
, that is,
 (31)
(31)
where the effective potential  has been defined as
has been defined as
 (32)
(32)
This effective potential has an extreme at the point  defined by the relation
defined by the relation
 (33)
(33)
which is independent on the parameter  and depends on the behavior of
and depends on the behavior of . This extreme point is a minimum of the effective potential since one has
. This extreme point is a minimum of the effective potential since one has
 (34)
(34)
Using the known expression [24-26] for the Lagrangian in terms of the constant of motion,
 (35)
(35)
the Lagrangian, generalized linear momentum and the Hamiltonian are given by
 (36)
(36)
 (37)
(37)
and
 (38)
(38)
The trajectories in the space  are determined by the constant of motion (31). Given the initial condition
are determined by the constant of motion (31). Given the initial condition , the constant of motion has the specific value
, the constant of motion has the specific value
 (39)
(39)
and the trajectory in the space  is given by
is given by
 (40)
(40)
Note that one needs to specify  also to determine Equation (22). In addition, one normally wants to know the trajectory in the real space, that is, the acknowledgment of
also to determine Equation (22). In addition, one normally wants to know the trajectory in the real space, that is, the acknowledgment of . Since one has that
. Since one has that  and Equations (22) and (40), it follows that
and Equations (22) and (40), it follows that
 (41)
(41)
The half-time period (going from aphelion to perihelion (+), or backward (−)) can be deduced from Equation (40) as
 (42)
(42)
where  and
and ![]() are the two return points resulting from the solution of the following equation
are the two return points resulting from the solution of the following equation
 (43)
(43)
On the other hand, the trajectory in the space  is determine by the Hamiltonian (38), and given the same initial conditions, the initial
is determine by the Hamiltonian (38), and given the same initial conditions, the initial  and
and  are obtained from Equations (38) and (37). Thus, this trajectory is given by
are obtained from Equations (38) and (37). Thus, this trajectory is given by
 (44)
(44)
It is clear just by looking the expressions (40) and (44) that the trajectories in the spaces  and
and  must be different due to complicated relation (37) between
must be different due to complicated relation (37) between ![]() and
and ![]() [19].
[19].
5. Mass-Variable Model and Results
As a possible application, consider that a comet looses material as a result of the interaction with star wind in the following way (for one cycle of oscillation)
 (45)
(45)
where the parameters  and
and  can be chosen to math the mass loss rate in the incoming and outgoing cases. The index “i” represent the ith-semi-cycle, being
can be chosen to math the mass loss rate in the incoming and outgoing cases. The index “i” represent the ith-semi-cycle, being  and
and  the aphelion
the aphelion  and perihelion
and perihelion ![]() points (
points (![]() is given by the initial conditions, and one has that
is given by the initial conditions, and one has that ). For this case, the functions
). For this case, the functions  and
and  are given by
are given by
 (46)
(46)
and
 (47)
(47)
where we have defined  and
and . Using the Taylor expansion, one gets
. Using the Taylor expansion, one gets
 (48)
(48)
and
 (49)
(49)
The effective potential for the incoming comet can be written as
 (50)
(50)
and for the outgoing comet as
 (51)
(51)
where  and
and  are given in the Appendix. We will use the data corresponding to the sun mass
are given in the Appendix. We will use the data corresponding to the sun mass  and the Halley comet [27] and [28]
and the Halley comet [27] and [28]

 (52)
(52)
with a mass lost of about  per cycle of oscillation. Although, the behavior of Halley comet seem to be chaotic [29], but we will neglect this fine detail here. Now, the parameters
per cycle of oscillation. Although, the behavior of Halley comet seem to be chaotic [29], but we will neglect this fine detail here. Now, the parameters ![]() and
and  appearing on the mass lost model, Equation (45), are determined by the chosen mass lost of the comet during the approaching to the sun and during the moving away from the sun (we have assumed the same mass lost in each half of the cycle of oscillation of the comet around the sun). Using Equation (50) and Equation (51) in the expression (40), the trajectories can be calculated in the spaces (
appearing on the mass lost model, Equation (45), are determined by the chosen mass lost of the comet during the approaching to the sun and during the moving away from the sun (we have assumed the same mass lost in each half of the cycle of oscillation of the comet around the sun). Using Equation (50) and Equation (51) in the expression (40), the trajectories can be calculated in the spaces ( ). Figure 1 shows these trajectories using
). Figure 1 shows these trajectories using
 (or
(or ) for
) for  and (continuos line), and for
and (continuos line), and for  (dashed line), starting both cases from the same aphelion distance. As one can see on the minimum, dissipation causes to reduce a little bit the velocity of the comet, and the antidissipation increases the comet velocity, reaching a further away aphelion point. Also, when only mass lost is considered
(dashed line), starting both cases from the same aphelion distance. As one can see on the minimum, dissipation causes to reduce a little bit the velocity of the comet, and the antidissipation increases the comet velocity, reaching a further away aphelion point. Also, when only mass lost is considered  the comet returns to aphelion point a little further away from the initial one during the cycle of oscillation. Something related with this effect is the change of period as a function of mass lost
the comet returns to aphelion point a little further away from the initial one during the cycle of oscillation. Something related with this effect is the change of period as a function of mass lost . This can be see on Figure 2, where the period is calculated starting always from the same aphelion point
. This can be see on Figure 2, where the period is calculated starting always from the same aphelion point . Note that with a mass lost of the order
. Note that with a mass lost of the order  (Halley comet), which correspond to
(Halley comet), which correspond to , the comet is well within 75 years period. The variation of the ratio of the change of aphelion distance as a function of mass lost
, the comet is well within 75 years period. The variation of the ratio of the change of aphelion distance as a function of mass lost  is shown on Figure 3. On Figure 4, the mass lost rate is kept fixed to
is shown on Figure 3. On Figure 4, the mass lost rate is kept fixed to , and the variation of the period of the comet is calculated as a function of the dissipative-antidissipative parameter
, and the variation of the period of the comet is calculated as a function of the dissipative-antidissipative parameter  (using
(using  for convenience). As one can see, antidissipation always wins to dissipation, bringing about the increasing of the period as a function of this parameter. The reason seems to be that the antidissipation acts on the comet when this ones is lighter than when dissipation was acting (dissipation acts when the comet approaches to the sun, meanwhile antidissipation acts when the comet goes away from the sun). Since the period of Halley comets has not changed much during many turns, we can assume that the parameter
for convenience). As one can see, antidissipation always wins to dissipation, bringing about the increasing of the period as a function of this parameter. The reason seems to be that the antidissipation acts on the comet when this ones is lighter than when dissipation was acting (dissipation acts when the comet approaches to the sun, meanwhile antidissipation acts when the comet goes away from the sun). Since the period of Halley comets has not changed much during many turns, we can assume that the parameter  must vary in the interval
must vary in the interval . Finally, Figure 5
. Finally, Figure 5

Figure 1. Trajectories in the  space with
space with  .
.

Figure 2. Period of the comet as a function of the mass lost ratio.

Figure 3. Ratio of aphelion distance change as a function of the mass lost rate.

Figure 4. Period of the comet as a function of the parameter .
.
shows the variation, during a cycle of oscillation, of the ratio of the new aphelion  to old aphelion
to old aphelion  as a function of the parameter
as a function of the parameter .
.

Figure 5. Ratio of the aphelion increasing as a function of the parameter .
.
6. Conclusion and Comments
We have shown that the proposed modified Newton equation for mass variation systems has some problems. Therefore, we have considered that it is better to keep Newton’s equations of motion for mass variable systems to have a consistent approach to these problems. Having this in mind, the Lagrangian, Hamiltonian and a constant of motion of the gravitational attraction of two bodies were given when one of the bodies has variable mass and the dissipative antidissipative effect of the solar wind is considered. By choosing the reference system in the massive body, the system of equations is reduce to 1-D problem. Then, the constant of motion, Lagrangian and Hamiltonian were obtained consistently. A model for comet-mass-variation was given, and with this model, a study was made of the variation of the period of one cycle of oscillation of the comet when there are mass variation and dissipation-antidissipation. When mass variation is only considered, the comet trajectory is moving away from the sun, the mass lost is reduced as the comet is farther away (according to our model), and the period of oscillations becomes bigger. When dissipation antidissipation is added, this former effect becomes higher as the parameter 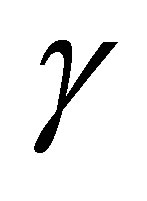 becomes higher.
becomes higher.
REFERENCES
- G. López, L. A. Barrera, Y. Garibo, H. Hernández and J. C. Salazar, International Journal of Theoretical Physics, Vol. 43, 2004, p. 1.
- H. Gylden, Astronomische Nachrichten, Vol. 109, 1884, pp. 1-6. http://dx.doi.org/10.1002/asna.18841090102
- I. V. Meshcherskii, Astronomische Nachrichten, Vol. 132, 1893, p. 93.
- I. V. Meshcherskii, Astronomische Nachrichten, Vol. 159, 1902, p. 229.
- E. O. Lovett, Astronomische Nachrichten, Vol. 158, 1902, pp. 337-344. http://dx.doi.org/10.1002/asna.19021582202
- J. H. Jeans, MNRAS, Vol. 85, 1924, p. 2.
- L. M. Berkovich, Celestial Mechanics, Vol. 24, 1981, pp. 407-429. http://dx.doi.org/10.1007/BF01230399
- A. A. Bekov, Astron. Zh., Vol. 66, 1989, p. 135.
- C. Prieto and J. A. Docobo, Astronomy & Astrophysics, Vol. 318, 1997, p. 657.
- A. Sommerfeld, “Lectures on Theoretical Physics,” Vol. 1, Academic Press, 1964.
- A. G. Zagorodny, P. P. J. M. Schram and S. A. Trigger, Physical Review Letters, Vol. 84, 2000, pp. 3594-3597. http://dx.doi.org/10.1103/PhysRevLett.84.3594
- O. T. Serimaa, J. Javanainen and S. Varró, Physical Review A, Vol. 33, 1986, pp. 2913-2927. http://dx.doi.org/10.1103/PhysRevA.33.2913
- H. A. Bethe, Physical Review Letters, Vol. 56, 1986, pp. 1305-1308. http://dx.doi.org/10.1103/PhysRevLett.56.1305
- E. D. Commins and P. H. Bucksbaum, “Weak Interactions of Leptons and Quarks,” Cambridge University Press, Cambridge, 1983.
- F. W. Helhl, C. Kiefer and R. J. K. Metzler, “Black Holes: Theory and Observation,” Springer-Verlag, 1998. http://dx.doi.org/10.1007/b13593
- P. W. Daly, Astronomy & Astrophysics, Vol. 226, 1989, p. 318.
- H. Goldstein, “Classical Mechanics,” Addison-Wesley, 1950.
- A. R. Plastino and J. C. Muzzio, Celestial Mechanics and Dynamical Astronomy, Vol. 53, 1992, pp. 227-232. http://dx.doi.org/10.1007/BF00052611
- G. López, International Journal of Theoretical Physics, Vol. 46, 2007, pp. 806-816. http://dx.doi.org/10.1007/s10773-006-9085-4
- C. Møller, “Theory of Relativity,” Oxford University Press, Oxford, 1952.
- M. Spivak, “Physics for Mathematicians, Mechanics I,” Publish or Perish Inc., 2010.
- G. López, “Partial Differential Equations of First Order and Their Applications to Physics,” World Scientific, 1999. http://dx.doi.org/10.1142/4006
- F. John, “Partial Differential Equations,” Springer-Verlag, New York, 1974.
- J. A. Kobussen, Acta Phys. Austr., Vol. 51, 1979, p. 193.
- C. Leubner, Physics Letters A, Vol. 86, 1981, pp. 68-70. http://dx.doi.org/10.1016/0375-9601(81)90166-3
- G. López, Annals of Physics, Vol. 251, 1996, pp. 372-383. http://dx.doi.org/10.1006/aphy.1996.0118
- G. Cevolani, G. Bortolotti and A. Hajduk, Il Nuovo Cimento C, Vol. 10, 1987, pp. 587-591. http://dx.doi.org/10.1007/BF02507255
- J. L. Brandy, Journal of the British Astronomical Association, Vol. 92, 1982, p. 209.
- B. V. Chirikov and V. V. Vecheslavov, Astronomy & Astrophysics, Vol. 221, 1989, p. 146.
Appendix
Expression for  and
and :
:
 (A1)
(A1)
where  is the mass of the body at the aphelion, and we have made the definitions
is the mass of the body at the aphelion, and we have made the definitions
 (A2)
(A2)
 (A3)
(A3)
where  is the mass of the body at the perihelion, and we have made the definition
is the mass of the body at the perihelion, and we have made the definition
 (A4)
(A4)
and the function  is the exponential integral,
is the exponential integral,
 (A5)
(A5)

