Journal of Modern Physics
Vol.4 No.2(2013), Article ID:28326,6 pages DOI:10.4236/jmp.2013.42034
High Intensity Focused Ultrasound Optimal Device Design for Targeted Prostate Cancer Treatment: A Numerical Study
1Lakehead University, Thunder Bay Regional Research Institute, Ontario, Canada
2National Institute of Health and Medical Research (INSERM), Lyon, France
Email: lcuriel@lakeheadu.ca
Received November 27, 2012; revised December 28, 2012; accepted January 7, 2013
Keywords: Focused Ultrasound; Prostate Cancer; Thermal Ablation; Non-Invasive Treatment; BHTE; HIFU
ABSTRACT
A parametric study was performed to design a device capable of treating small targeted regions within the prostate using high intensity focused ultrasound, while sparing the surrounding organs and minimizing the number of elements. The optimal focal length (L), operating frequency (f), element size (a) and central opening radius for lodging an imaging probe (r) of a device that would safely treat tissue within the prostate were obtained. Images from the Visible Human Project were used to determine simulated organ sizes and treatment locations. Elliptical tumors were placed throughout the simulated prostate and their lateral and axial limits were selected as test locations. Using graphics processors, the acoustic field and Bio-Heat Transfer Equation were solved to calculate the heating produced during a simulated treatment. L, f, a and r were varied from 45 to 75 mm, 2.25 to 3 MHz, 1.5 to 8 times the wavelength and 9 to 12.5 mm, respectively. The resulting optimal device was a 761-element concentric-ring transducer with L = 68 mm, f = 2.75 MHz, a = 2.05λ and r = 9 mm. Simulated thermal lesions showed that it was possible to treat target tumors consistent with reported locations and sizes for prostate cancer.
1. Introduction
Trans-rectal high intensity focused ultrasound (HIFU) is currently used in clinic as a minimally-invasive approach for prostate cancer treatment [1]. Two trans-rectal HIFU clinical commercial systems are currently available: AblathermTM (EDAP-TMS, Vaux-en-Velin, France) and Sonablate® (Focus Surgery, Inc., IN, USA). The standard treatments performed using these systems ablate the entire prostate. This causes some associated morbidity resulting on partial or total loss of potency (43.2% of patients), stress incontinence (5.7%), urinary tract infections (7.1%), pelvic pain (5.7%) and rarely rectourethral fistula (2.2%) [2-6]. This morbidity is usually attributed to the ablation of nerves and structures within the prostate, and it could be significantly reduced by treating only the affected areas and therefore reducing the amount of ablated tissue. This can be achieved by using a phasearray device capable of dynamically focusing the energy to limit the treatment to target tumor masses within the prostate.
The design of such an array can be done by using numerical tools. This kind of design usually starts with the proposal of geometry and simulations are run to predict the behavior and analyze the feasibility of treating the desired regions [7-10]. The process is then iterated until a satisfactory compromise is obtained. This process can be time consuming and is not guaranteed to give the optimal result since it requires analyzing multiple configurations and parameters. An alternative to this process is presented in this paper. A numerical method that allowed us to obtain an optimal geometry for a multi-element device with specific ergonomic constraints was used. By combining analytical and numerical platforms with parallel processing using graphic processing units we were able to perform a large number of simulations on manageable execution times allowing for optimization studies in order to obtain a successful configuration. Thermal lesions were finally simulated for the optimal configuration and confirmed that the targets could be reached. This method and platform can shorten device development time and cost, and it can be used as a treatment planning tool.
2. Materials and Methods
2.1. Virtual Device and Simulation Environment
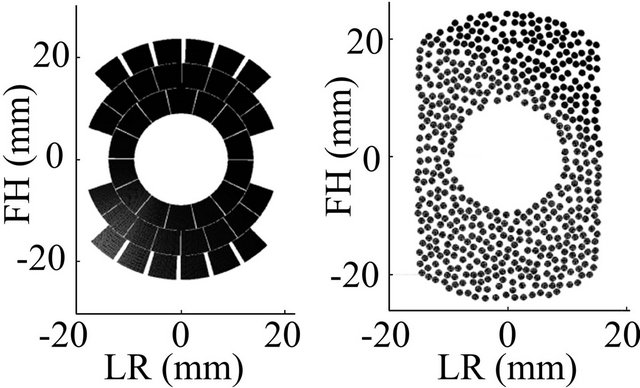
An initial geometry was chosen to be close to the current treatment probe in use for the AblathermTM machine [7] (50-mm spherical cap truncated at 31 mm with a central opening for lodging an imaging transducer). The array configurations were then constructed as described in [11]. Two array configurations were analyzed: a concentric ring array with independent sectional elements and a circular-element array with a pseudorandom pattern (Figure 1).
A simulation environment was created from full body histological images taken from the Visible Human Male Server Project (VHSMP, Ecole Polytechnique Federale de Lausanne, Switzerland) [12]. One hundred transverse images with a resolution of 0.2 × 0.2 × 1 mm were analyzed using an in-house developed interface in order to obtain a 3D structure of the prostate and neighboring structures (bladder, rectum, muscular tissue, ductus deferens, seminal vesicles, rectal wall, rectal muscle and nerve bundle).
2.2. Parametric Study
A parametric study was performed to determine the optimal focal length (L), operating frequency (f), element size (a) and central opening (r) for a device capable of treating different locations within the prostate without secondary lesions while minimizing the number of elements.
Using an in-house interface and the images from the VHSMP, the device was positioned at the center of the rectum and the maximum and minimum distances necessary to achieve a treatment throughout the organ were defined. Figure 2 shows the closest and farthest distances from the centre of the device needed to treat the prostate at different anatomical locations. This determined the minimal and maximal focusing locations as 31 and 65 mm.
The acoustic field was simulated in a model of the pelvic region. The propagation media considered for the simulation was: coolant liquid (water) between the transducer ant the tissues, rectum and then soft tissue. The geometry of the coolant was modeled as an elliptical cylinder with a major diameter of 39 mm and a minor
 (a) (b)
(a) (b)
Figure 1. Schematic for the simulated arrays: (a) concentric ring and (b) random. FH: foot head; LR: left right direction for treatment.
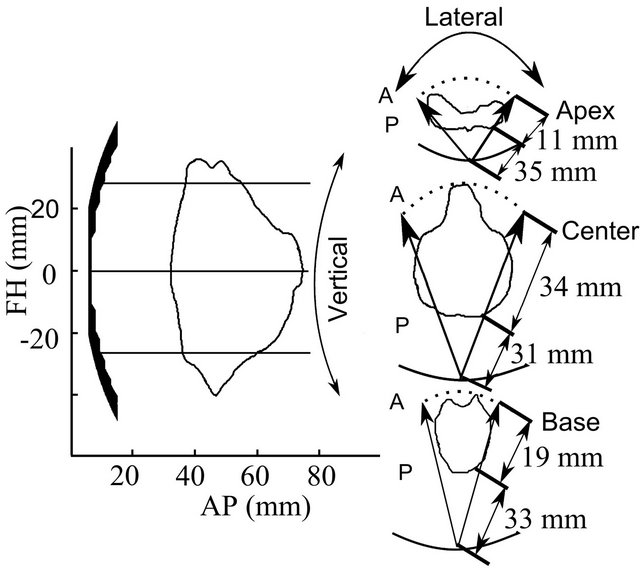
Figure 2. Transducer positioning to treat the prostate and limits for treatment at different anatomical locations. FH: foot head; AP: anterior posterior.
diameter of 26 mm [7]. The rectal wall was modeled as an elliptical cylinder with a major diameter of 45 mm and a minor diameter of 32 mm [7] and a thickness of 6 mm (obtained from the VHSMP images).
The acoustic field simulation was performed using the Rayleigh-Sommerfeld diffraction integral given by [13]
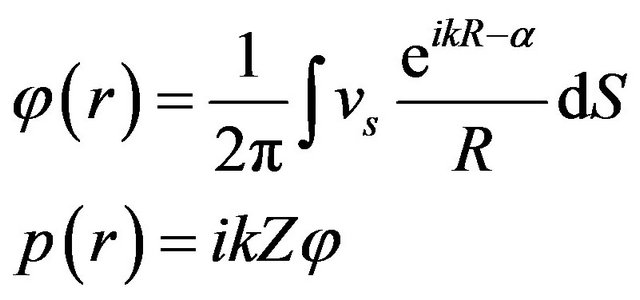 (1)
(1)
where νs is the particle velocity at surface dS, R = R1 + R2 + R3, R is the distance sound propagates with R1 through the coolant liquid, R2 through the rectal wall, and R3 through the prostatic tissue, α is the attenuation factor obtained as R1α1 + R2α2 + R3α3, dS is the surface area, k = 2π/λ, λ is the wavelength and Z is the acoustic impedance of water.
The focal length was ranged from 45 to 60 mm by with 1-mm steps and the element size from 1λ to 8λ by steps of 0.05λ. The operating frequency was varied from 2.25 to 3 MHz by steps of 0.25 MHz. The size of the central opening was varied from a radius of 1 to 11 mm by steps of 2 mm. For each combination of parameters we evaluated the degree of focusing by the ratio [14].
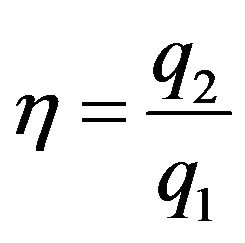 (2)
(2)
where q2 and q1 are the acoustic pressure at the secondary and primary lobe, respectively. The goal was set for a configuration with the fewest elements and value of η ≤ 0.5. The acoustic attenuation was 2.9 × 10−4 Np/m/MHz for the coolant, 4.1 Np/m/MHz for the rectal wall and 9 Np/m/MHz for the prostate [7]. Simulations were performed using in-house developed and optimized code using two Tesla C1060 (NVIDIA, Santa Clara, CA, USA) graphics processors.
2.3. Steering Capabilities
For the optimal configuration obtained from the parametric study, the steering capabilities were evaluated to ensure that tumors at different locations within the prostate could be treated. We first determined the maximum lateral steering possible at the anterior and posterior of the prostate with the device located in front of the apex, center and base of the prostate (Figure 2). Then the maximum vertical steering obtained at the center of the prostate was evaluated. The value of η (Equation (2)) was used to evaluate the degree of focusing. Focusing was tested at off-axis distances from 1 mm to 16 mm by steps of 0.25 mm.
2.4. Thermal Simulation
The temperature increase obtained with the optimal configuration was estimated using the Bio-Heat Transfer Equation (BHTE) [15] and the thermal dose concept [16] at different relevant treatment locations. These locations were chosen using clinical MR images and pathology from 37 patients reported by Coakley et al. [17]. Virtual tumors with a size equivalent to the minimum (0.02 cc), average (0.79 cc) and maximum (3.7 cc) volumes reported in [17] were modeled as ellipsoids and located close the prostatic capsule. The BHTE was then used to calculate the temperature obtained with the optimal configuration focused at the centre and edges of the target virtual tumor [15] by
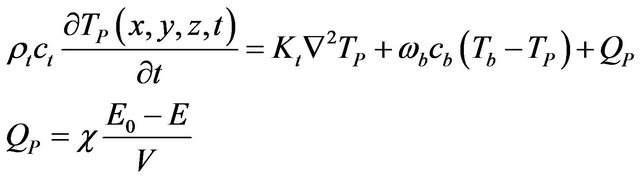 (4)
(4)
where ρt, ct, and Kt are the density, specific heat and thermal conductivity of the tissue, respectively, TP is the temperature a point P(x, y, z) and time t, ωb, cb and Tb are the perfusion rate, specific heat and temperature of blood, respectively, E0 and E are the acoustic energy entering and exiting a volume V and χ is the acoustic absorption coefficient.
The BHTE was implemented using the numerical Finite Difference Time Difference technique [18] with boundary conditions at the borders of the tissue volume set to body temperature (37˚C) and thermo-mechanical properties of tissues were defined in [8]. The effect of this cooling was simulated as a boundary condition using a Newtonian flux convention [19] and a temperature of 13˚C. Tissues that reached a thermal dose of 240 minutes or greater were considered as ablated tissues [20]. If any of the tested sites within each virtual tumor formed a secondary lesion (outside of the target tumor), it was considered a failed treatment.
3. Results
3.1. Parametric Study
The optimal configuration was a concentric ring array with a focal length of 68 mm, an operating frequency of 2.75 MHz, a diameter of 50 mm, a truncated width of 31 mm, a 9-mm in radium central opening and an element width of 2.05λ for a total of 761 elements.
3.2. Steering Capabilities
Table 1 shows the steering capabilities reached by the optimal concentric ring and random arrays. The random array was capable of steering farther in the lateral direction when focusing close to the transducer but this deteriorated when the focusing was done at deeper locations. Overall, the deeper the focal region the more difficult it was to achieve steering and the random array was unable to steer at the deeper locations.
3.3. Thermal Simulations
Adequate focusing and lesion formation was possible at all limits of the virtual tumors using the concentric ring device, except for the two largest located at the prostate peripheral zone (located closest to the device).
Figure 3 shows the simulated lesions (thermal dose above 14,400 s) obtained when electronically steering the optimal configuration to reach the edges of the largest tumor that was virtually defined.
When treating tumors in the peripheral zone, secondary lesions were observed when targeting the posterior limit of the tumors (closest to the device). These secondary lesions appeared deeper than the targeted focus at approximately twice the focal length (towards the anterior region of the prostate). They were caused by grating lobes produced when the dynamic focus was located out of the steering range of the elements on the outer rings of
Table 1. Steering capabilities for optimal devices.
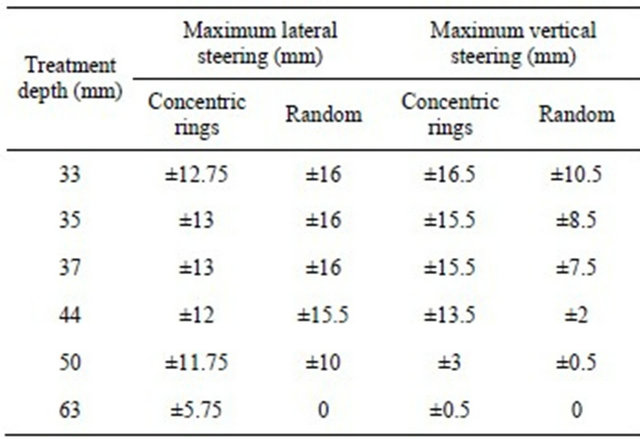
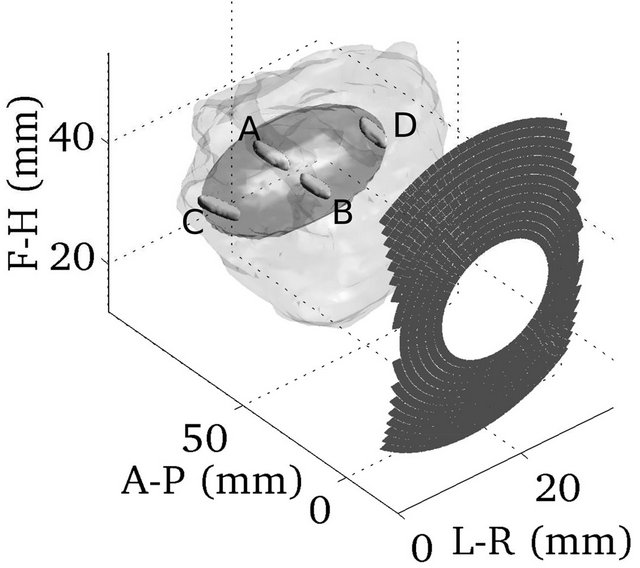
Figure 3. Simulated thermal lesions at four extremes of the larger virtual target tumor.
the device (Table 1) [14].
Table 2 shows the results for thermal simulations at all the defined targets. The size of the target tumors at peripheral and transitional prostate zones were defined based on MR images [17]. The size of the calculated thermal lesion when targeting the tumors varied depending on the location and the size of the target tumor since the maximum steering required was different in order to cover the entire tumor. Lesions were generally smaller for medium-sized tumors since to reach these tumors the device does not require as much steering and we are closer to the natural focus of the device. The lesions were generally larger for targets in the transitional region. The acoustic power required to obtain a lesion also increases with target lesions that require steering (larger tumors located outside of the central axis of the device).
For the peripheral zone targets where the secondary lesions appeared two solutions were proposed to avoid them: partial excitation of the elements and mechanical device rotation. By exciting only the elements closest to the center of the device we could decrease the phase difference between elements and eliminate the secondary lesion while minimizing the acoustic intensity at the surface. A series of simulations was performed with 50% to 75% of the elements excited and it was found that secondary lesions were eliminated with 56% of active elements when targeting a large peripheral tumor (3700 mm3) and with 71% when targeting the medium peripheral tumor (790 mm3). The device could also be rotated on the left-right direction by ±π/8 in order to eliminate the secondary lesions.
The overall maximum acoustic intensity at the surface of the transducer for treatment was 22.74 W/cm2. This maximum occurred when focusing at the location the lateral edge of large tumors in the peripheral zone with only 56% of the elements active. This intensity was high as a result of the reduced surface area caused by elements being off.
4. Discussion and Conclusion
On this study we used an extensive parametric study us-
Table 2. Thermal simulations for different target tumor sizes and locations.

ing computational tools to obtain an optimal configuration for a trans-rectal HIFU device for localized prostate cancer treatment. We found an optimal device with a concentric ring array configuration, a focal length of 68 mm, an operating frequency of 2.75 MHz, a diameter of 50 mm truncated at 31 mm, an element width of 2.05λ and an 18-mm diameter central opening.
The simulation environment accurately depicted the male pelvis using histological images of tissue. The limitation of this simulated anatomical environment was the fact that only one subject is available and that images come from a 38-year-old man, whereas prostate cancer patients treated with HIFU have a mean age of 69 [5]. As a result, the volume of the prostate used for simulations was approximately 20 cc whereas typical patients have a prostate volume up to 40 cc [3]. Nevertheless, the targets used for this treatment are similar to those performed in HIFU transrectal therapy [7] and are compatible with the reported anatomical findings from tumors [17].
The rectum distention due to the transducer and the circulation of coolant liquid was accurately incorporated into the simulation environment. This consideration was important for the validity of the study because the transducer causes the rectal wall to be closer to the prostate increasing the risk of rectal wall damage causing rectourethral fistula [4]. All observed thermal doses at the rectal wall remained below the lesion threshold and as a result no rectal wall damage was predicted by the simulations.
The focal length of the optimal device is located deeper than the target depth (33 to 63 mm). Similar results have been reported for HIFU prostate treatment devices [7] and when simulating the treatment of a trial fibrillation in the heart [19].
The random circular element array configuration was tested on this study to determine if secondary lobes could be reduced with this approach. However, this type of device did not perform as well as the concentric ring array since the active surface area was too low and the acoustic field could not be successfully steered. This is an important consideration to make for HIFU devices that need to fit constrained spaces such as transrectal approaches.
The thermal simulation showed that even though the device was able to treat all locations in the target tumors, different strategies are needed during the treatment: partial excitation or rotating the device. The proposed simulation can be used to determine these strategies as a tool for treatment planning. The ability of conducting fast calculations is then an important asset of this tool.
The size of individual simulated lesions varied as a function of the distance to the center of the device, with lesions farther from the transducer being larger. This effect is in direct relationship to the elliptical focus of the device. The platform can also be used for accurate treatment planning that takes into account these variations.
Finally, the numerical approach used in the study involved the use of algorithms and techniques that utilize graphic processing units (GPUs). This allowed for reduced the computation times and allowed exploring large variations of the parameters. Also, the cost of a GPU system is considerably lower than other alternatives for fast calculation, making this methodology an attractive fast and low cost tool for device design and treatment planning [21].
5. Acknowledgements
This work was funded by NSERC Discovery Canada granted to LC and an ORF grant from the Ministry of Research and Innovation, Ontario.
REFERENCES
- S. Crouzet, X. Rebillard, D. Chevallier, et al., “Multicentric Oncologic Outcomes of High-Intensity Focused Ultrasound for Localized Prostate Cancer in 803 Patients,” European Urology, Vol. 58, No. 4, 2010, pp. 559-566. doi:10.1016/j.eururo.2010.06.037
- T. Uchida, H. Ohkusa, H. Yamashita, et al., “Five Years Experience of Transrectal High-Intensity Focused Ultrasound Using the Sonablate Device in the Treatment of Localized Prostate Cancer,” International Journal of Urology, Vol. 13, No. 3, 2006, pp. 228-233. doi:10.1111/j.1442-2042.2006.01272.x
- L. Poissonnier, J. Y. Chapelon, O. Rouviere, et al., “Control of Prostate Cancer by Transrectal HIFU in 227 Patients,” European Urology, Vol. 51, No. 2, 2007, pp. 381- 387. doi:10.1016/j.eururo.2006.04.012
- C. Netsch, T. Bach, E. Gross and A. J. Gross, “Rectourethral Fistula after High-Intensity Focused Ultrasound Therapy for Prostate Cancer and Its Surgical Management,” Urology, Vol. 77, No. 4, 2011, pp. 999-1004. doi:10.1016/j.urology.2010.10.028
- A. Blana, S. Rogenhofer, R. Ganzer, et al., “Eight Years’ Experience with High-Intensity Focused Ultrasonography for Treatment of Localized Prostate Cancer,” Urology, Vol. 72, No. 6, 2008, pp. 1329-1333. doi:10.1016/j.urology.2008.06.062
- F. J. Murat, L. Poissonnier, M. Rabilloud, et al., “Midterm Results Demonstrate Salvage High-Intensity Focused Ultrasound (HIFU) as an Effective and Acceptably Morbid Salvage Treatment Option for Locally Radiorecurrent Prostate Cancer,” European Urology, Vol. 55, No. 3, 2008, pp. 640-649. doi:10.1016/j.eururo.2008.04.091
- S. Pichardo, A. Gelet, L. Curiel, S. Chesnais and J. Y. Chapelon, “New Integrated Imaging High Intensity Focused Ultrasound Probe for Transrectal Prostate Cancer Treatment,” Ultrasound in Medicine and Biology, Vol. 34, No. 7, 2008, pp. 1105-1116. doi:10.1016/j.ultrasmedbio.2007.12.005
- L. Curiel, F. Chavrier, B. Gignoux, S. Pichardo, S. Chesnais and J. Y. Chapelon, “Experimental Evaluation of Lesion Prediction Modelling in the Presence of Cavitation Bubbles: Intended for High-Intensity Focused Ultrasound Prostate Treatment,” Medical and Biological Engineering and Computing, Vol. 42, No. 1, 2004, pp. 44-54. doi:10.1007/BF02351010
- G. S. Chen, C. Y. Lin, J. S. Jeong, et al., “Design and Characterization of Dual-Curvature 1.5-Dimensional High-Intensity Focused Ultrasound Phased-Array Transducer,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 59, No. 1, 2012, pp. 150-155. doi:10.1109/TUFFC.2012.2166
- D. Pajek and K. Hynynen, “The Design of a Focused Ultrasound Transducer Array for the Treatment of Stroke: A Simulation Study,” Physics in Medicine and Biology, Vol. 57, No. 15, 2012, pp. 4951-4968. doi:10.1088/0031-9155/57/15/4951
- S. Pichardo and K. Hynynen, “New Design for an Endoesophageal Sector-Based Array for the Treatment of Atrial Fibrillation: A Parametric Simulation Study,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 56, No. 3, 2009, pp. 600-612. doi:10.1109/TUFFC.2009.1076
- E. P. F. de Lausanne, “Visible Human Server,” 2012. http://visiblehuman.epfl.ch/
- X. Fan and K. Hynynen, “The Effect of Wave Reflection and Refraction at Soft Tissue Interfaces during Ultrasound Hyperthermia Treatments,” Journal of the Acoustical Society of America, Vol. 91, No. 3, 1992, pp. 1727- 1736. doi:10.1121/1.402452
- R. Cobbold, “Foundations of Biomedical Ultrasound,” Oxford University Press, Oxford, 2007.
- H. H. Pennes, “Analysis of Tissue and Arterial Blood Temperatures in the Resting Human Forearm,” Journal of Applied Physiology, Vol. 85, No. 1, 1998, pp. 5-34.
- S. A. Sapareto and W. C. Dewey, “Thermal Dose Determination in Cancer Therapy,” International Journal of Radiation Oncology, Vol. 10, No. 6, 1984, pp. 787-800. doi:10.1016/0360-3016(84)90379-1
- F. V. Coakley, J. Kurhanewicz, Y. Lu, et al., “Prostate Cancer Tumor Volume: Measurement with Endorectal MR and MR Spectroscopic Imaging,” Radiology, Vol. 223, No. 1, 2002, pp. 91-97. doi:10.1148/radiol.2231010575
- X. Yin, L. M. Epstein and K. Hynynen, “Noninvasive TransEsophageal Cardiac Thermal Ablation Using a 2-D Focused, Ultrasound Phased Array: A Simulation Study,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 53, No. 6, 2006, pp. 1138-1149. doi:10.1109/TUFFC.2006.1642512
- S. Pichardo and K. Hynynen, “Circumferential Lesion Formation around the Pulmonary Veins in the Left Atrium with Focused Ultrasound Using a 2D-Array Endoesophageal Device: A Numerical Study,” Physics in Medicine and Biology, Vol. 52, No. 16, 2007, pp. 4923- 4942. doi:10.1088/0031-9155/52/16/014
- C. Damianou and K. Hynynen, “The Effect of Various Physical Parameters on the Size and Shape of Necrosed Tissue Volume during Ultrasound Surgery,” Journal of the Acoustical Society of America, Vol. 95, No. 3, 1994, pp. 1641-1649. doi:10.1121/1.408550
- S. D. C. Walsh, M. O. Saar, P. Bailey and D. J. Lilja, “Accelerating Geoscience and Engineering System Simulations on Graphics Hardware,” Computers and Geosciences, Vol. 35, No. 12, 2009, pp. 2353-2364. doi:10.1016/j.cageo.2009.05.001

