Journal of Modern Physics
Vol.4 No.1(2013), Article ID:27228,12 pages DOI:10.4236/jmp.2013.41014
Theoretical Study with Rovibrational and Dipole Moment Calculation of the SiO Molecule
1Faculty of Science, Beirut Arab University, Beirut, Lebanon
2Khalifa University, Sharjah, UAE
Email: *fkorek@yahoo.com
Received October 20, 2012; revised November 21, 2012; accepted November 30, 2012
Keywords: Ab Initio Calculation; SiO Molecule; Potential Energy Curves; Spectroscopic Constants; Dipole Moment; Rovibrational Calculation
ABSTRACT
Via CASSCF/MRCI and RSPT2 calculations (single and double excitation with Davidson correction) the potential energy curves of 20 electronic states in the representation 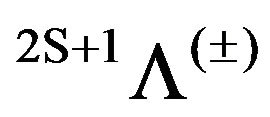 of the molecule SiO have been calculated. By fitting these potential energy curves to a polynomial around the equilibrium internuclear distance re, the harmonic frequency ωe, the rotational constant Be, and the electronic energy with respect to the ground state Te have been calculated. For the considered electronic states the permanent dipole moment μ have been plotted versus the internuclear distance r. Based on the canonical functions approach, the eigenvalues Ev, the rotational constant Bv and the abscissas of the turning points rmin and rmax have been calculated. The comparison of these values to the experimental and theoretical results available in the literature is presented. In the present work 8 higher electronic states have been studied theoretically for the first time.
of the molecule SiO have been calculated. By fitting these potential energy curves to a polynomial around the equilibrium internuclear distance re, the harmonic frequency ωe, the rotational constant Be, and the electronic energy with respect to the ground state Te have been calculated. For the considered electronic states the permanent dipole moment μ have been plotted versus the internuclear distance r. Based on the canonical functions approach, the eigenvalues Ev, the rotational constant Bv and the abscissas of the turning points rmin and rmax have been calculated. The comparison of these values to the experimental and theoretical results available in the literature is presented. In the present work 8 higher electronic states have been studied theoretically for the first time.
1. Introduction
The silicon monoxide SiO molecule is of considerable astrophysical interest, it is detected in the interstellar medium and in a variety of astrophysical objects which are mostly associated with warm, dense, and shocked gas [1]. Because of the interaction between high velocities jets emerging from a young star and the surrounding molecular environment a large fraction of the silicon monoxide relative to hydrogen molecule are found in the high velocity gas components of molecular outflows [2]. This abundance of SiO comes from the sputtering of dust grains in shocked regions and the subsequent release of Si-bearing material into the gas phase [3-7].
In recent years silica nanoparticles has attracted considerable attention due to their potential applications in many fields including ceramics, chromatography, catalysis and chemical mechanical polishing [8], nanodevices and mesoscopic research [9]. Altman et al. [9] probed the behavior of light absorption of silica nanoparticles at high temperatures in the Urbach region, and compare it with that in bulk materials. They assumed that, the SiO vapor emission does not contribute significantly to the flame radiation in visible. This can be easily justified by considering that the lower state of a SiO molecule involved in transitions in visible light is not a ground state of the SiO molecule, but a highly excited one [10].
By studying the published data in literature on the molecule SiO, one can notice the large discrepancy between these values either theoretical or experimental. The values of the electronic transition energy Te with respect to the ground state X1Σ+ vary as
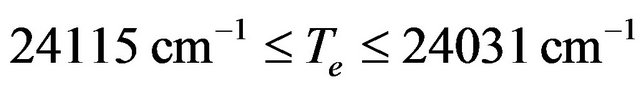 ,
,
 [12]and
[12]and  [12] respectively for the electronic states (1)3Σ+, (1)3Σ+, (2)3Σ. Similar data can be found for different spectroscopic constants of different electronic states. Stimulated by these discrepancies, the important connection between energy relations of solids and molecules [13], and based on our previous theoretical calculation [14-23], we performed an ab initio study of the low-lying electronic states of the molecule SiO below 132,500 cm–1. In this work, we investigate the potential energy curves (PECs), the electric dipole moment and spectroscopic constants for the 20 2S+1Λ± lowlying electronic states of this molecule obtained by MRCI and RSPT2 calculations. Taking advantage of the electronic structure of the investigated electronic states of the SiO molecule and by using the canonical functions approach [24-26], the eigenvalues Ev, the rotational constant Bv and the abscissas of the turning points rmin and rmax have been calculated up to the vibrational level v = 52.
[12] respectively for the electronic states (1)3Σ+, (1)3Σ+, (2)3Σ. Similar data can be found for different spectroscopic constants of different electronic states. Stimulated by these discrepancies, the important connection between energy relations of solids and molecules [13], and based on our previous theoretical calculation [14-23], we performed an ab initio study of the low-lying electronic states of the molecule SiO below 132,500 cm–1. In this work, we investigate the potential energy curves (PECs), the electric dipole moment and spectroscopic constants for the 20 2S+1Λ± lowlying electronic states of this molecule obtained by MRCI and RSPT2 calculations. Taking advantage of the electronic structure of the investigated electronic states of the SiO molecule and by using the canonical functions approach [24-26], the eigenvalues Ev, the rotational constant Bv and the abscissas of the turning points rmin and rmax have been calculated up to the vibrational level v = 52.
2. Computational Approach
2.1. Ab Initio Calculation
The PECs of the lowest-lying electronic states of SiO molecule have been investigated via CASSCF method. MRCI and RSPT2 calculations (single and double excitations with Davidson corrections) were performed. Silicon atom is treated in all electron schemes where the 14 electrons of the silicon atom are considered using the cc-PVTZ basis set including s, p, d and f functions [27]. The oxygen atom is treated in all electron schemes where the 8 electrons of the oxygen atom are considered using the DGauss-a2-Xfit basis set including s, p and d functions [28]. Among the 22 electrons explicitly considered for the SiO molecule (14 electrons for Si and 8 for O), 18 inner electrons were frozen in subsequent calculations so that 4 valence electrons were explicitly treated. This calculation has been performed via the computational chemistry program MOLPRO [29] taking advantage of the graphical user interface GABEDIT [30].
The PECs for the 20 electronic states in the representation 2S+1Λ(±) obtained from MRCI calculation have been obtained for 222 internuclear distances in the range 1.06 Å ≤ r ≤ 4.00 Å. These potential energy curves for the singlet, triplet and quintet electronic states in the different symmetries are given, respectively in Figures 1-3.
The spectroscopic constants such as the vibration harmonic constants ωe and ωexe, the internuclear distance at equilibrium re, the rotational constant Be, and the electronic transition energy with respect to the ground state Te have been calculated by fitting the energy values around the equilibrium position to a polynomial in terms of the internuclear distance. These values are given in Table 1 together with the available values in the literature either theoretical or experimental. The comparison of our MRCI calculated values of reωe, and Be for the ground state X1Σ+ with those given in literature, either theoretical or experimental, shows an excellent agreement with the relative differences
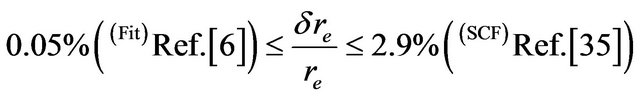 ,
,
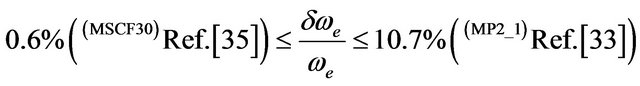 ,
,

Figure 1. Potential energy curves of the lowest singlet and triplet Σ and ∆-states of the molecule SiO.

Figure 2. Potential energy curves of the lowest singlet and triplet Σ and ∆-states of the molecule SiO.
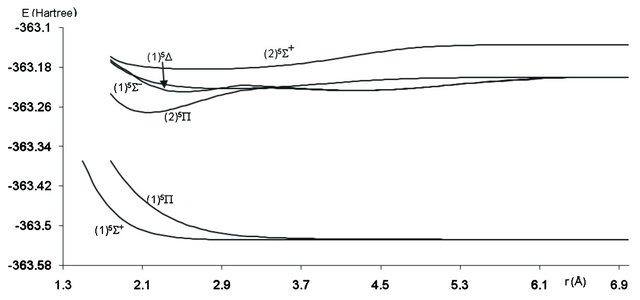
Figure 3. Potential energy curves of the lowest quintet states of the molecule SiO.
Table 1. Spectroscopic constants for the electronic states of the molecule SiO.

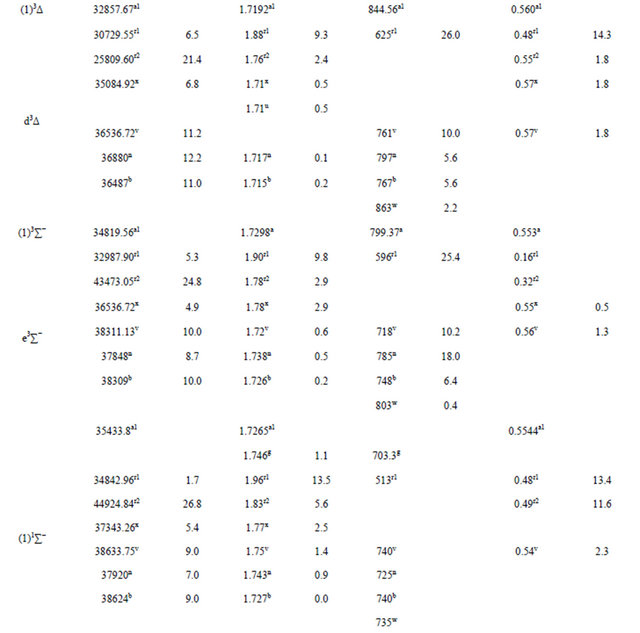
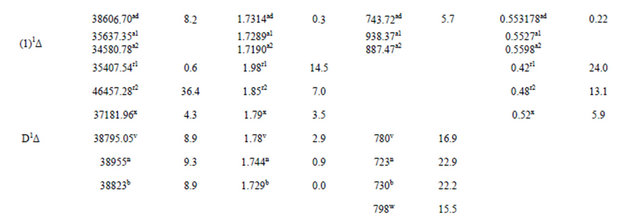
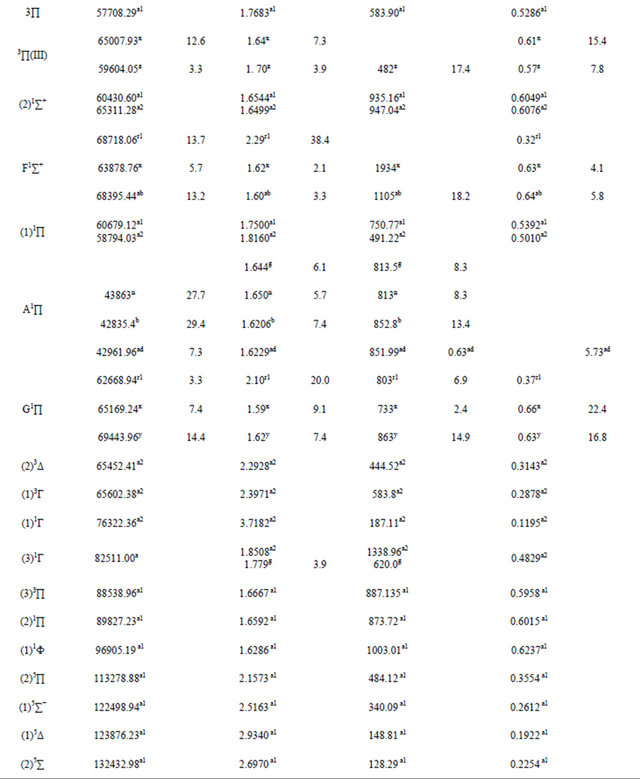
a1For present work with MRCI calculation; a2For present work with RSPT2 calculation; bRef.[10]; c1(experimental)Ref. [31]; c2(B3-LYP1)Ref.[31]; c3(B3-LYP2)Ref.[31]; c4(BP86)Ref.[31]; c5(MP2_1)Ref.[31]; c6(MP2_2)Ref.[31]; dRef.[32]; e1(MRCI+Q)Ref.[6]; e2(Fit)Ref.[6]; f1(SCF)Ref.[33]; f2(CI-SD)Ref.[33]; f3CEPA-1)Ref.[33]; g(SCF+CI)Ref.[34]; h1(SCF)Ref.[35]; h2(MCSCF30)Ref.[35]; h3(MCSCF-CI)Ref.[35]SCF; i(exp)Ref.[36]; j(exp)Ref.[37]; k(exp)Ref.[38]; mRef.[39]; nRef.[40]; pRef.[44]; r1Ref.[11]; r2Ref.[11]; s1Ref.[45]; s2Ref.[45]; tRef.[46]; uRef.[47]; vRef.[48]; wRef.[49]; xRef.[50]; yRef.[51]; zRef.[52]; qRef.[53]; abRef.[54]; acRef.[55]; adRef.[56]; N.B experimental value c1 (Ref.[ 31]) is in solid methane.
 .
.
The agreement becomes less by comparing our calculated value of ωexe with the experimental values of literature [10,32,36-38,44,55] where the relative difference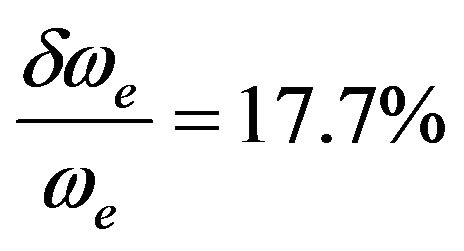 . One can notice that, the theoretical value of ωexe published in literature varies between 5.0 cm–1 and 8.0 cm–1 for the ground state [6,33-35]. The comparison of our calculated values by using the RSPT2 and MRCI techniques with those available in literature for the spectroscopic constants re, ωe and Be shows the average values
. One can notice that, the theoretical value of ωexe published in literature varies between 5.0 cm–1 and 8.0 cm–1 for the ground state [6,33-35]. The comparison of our calculated values by using the RSPT2 and MRCI techniques with those available in literature for the spectroscopic constants re, ωe and Be shows the average values
 ,
,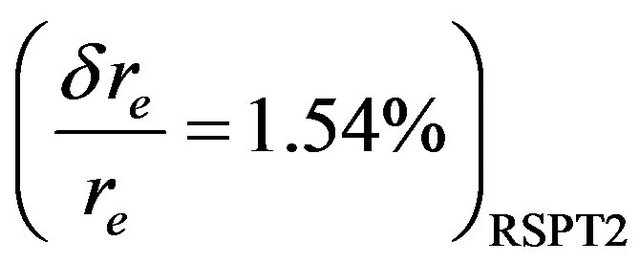 ,
,
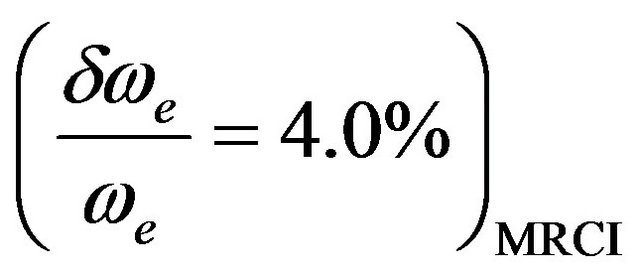 ,
, ,
,
 ,
, .
.
From theseresults one can find that, the RSPT2 technique may gives better value for ωe while MRCI technique gives better values for re and Be for the ground state of the molecule SiO.
By comparing our calculated values of Te for the states (1)3Σ+, (1)3Σ, (1)3Σ–, (1)1Σ–, (1)1Σ, (2)1Σ with those obtained experimentally in literature one can find an overall acceptable agreement with relative difference
 in Refs.[10,36] and larger relative difference for the states (1)3Σ+, (2)1Σgiven in Refs.[3339,43] with relative difference
in Refs.[10,36] and larger relative difference for the states (1)3Σ+, (2)1Σgiven in Refs.[3339,43] with relative difference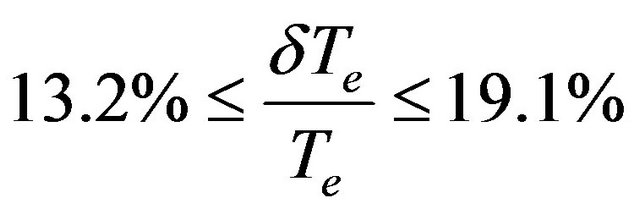 .
.
One can notice that, the comparison of our calculated value of Te, for the considered electronic states, with those calculated in literature shows an excellent agreement by using one technique of calculation with
 (Ref.[11]) and disagreement by using another technique with
(Ref.[11]) and disagreement by using another technique with 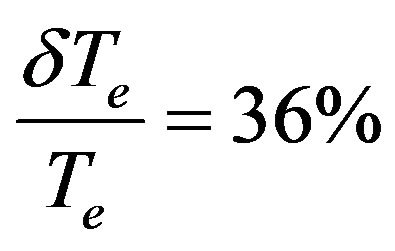 (Ref.[11]) for the same state (1)1Σ. Concerning the assignment of our calculated value of the 1Σ state, it is in good agreement with the calculated values of G1Σ state [32,38] and acceptable agreement with the experimental value given in Ref.[39]. The comparison of our values of Te with the newly published theoretical work by using the MRCI approach [56] shows an acceptable agreement for the 2 excited electronic states (1)3Σ+ and (1)1Σ– with relative differences 11.9% and 8.2% respectively.
(Ref.[11]) for the same state (1)1Σ. Concerning the assignment of our calculated value of the 1Σ state, it is in good agreement with the calculated values of G1Σ state [32,38] and acceptable agreement with the experimental value given in Ref.[39]. The comparison of our values of Te with the newly published theoretical work by using the MRCI approach [56] shows an acceptable agreement for the 2 excited electronic states (1)3Σ+ and (1)1Σ– with relative differences 11.9% and 8.2% respectively.
The comparison of our calculated values of re, ωe, and Be, for the excited states, with those given in literature experimentally [10,48,51,54] shows that, our values of re and Be are in very good agreement for all the investigated states with
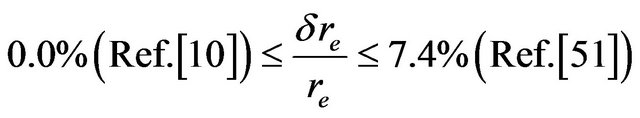 and
and
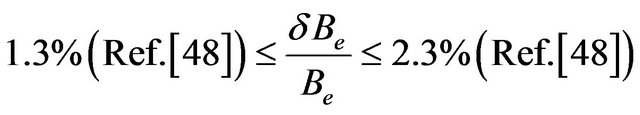 except the value of Be for the state G1 where
except the value of Be for the state G1 where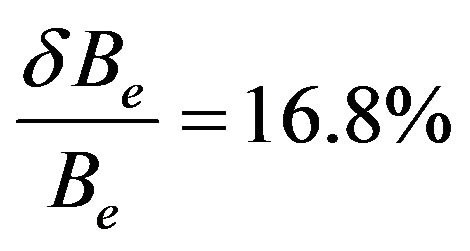 . Our values of ωe are also in very good agreement with the experimental values for the electronic states with
. Our values of ωe are also in very good agreement with the experimental values for the electronic states with  and becomes larger for the other investigated electronic states with
and becomes larger for the other investigated electronic states with
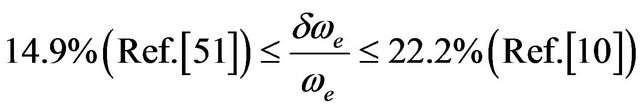 .
.
Similarly, by comparing our calculated values of reωe, and Be with those calculated in literature, one can notice that an excellent agreement by using one technique of calculation with relative differences 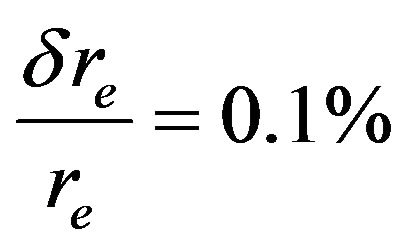 for the state (1)3Σ+ (Ref.[40]),
for the state (1)3Σ+ (Ref.[40]), 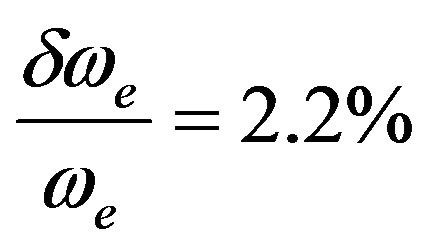 for the state (1)3Σ
for the state (1)3Σ
(Ref.[49]), and 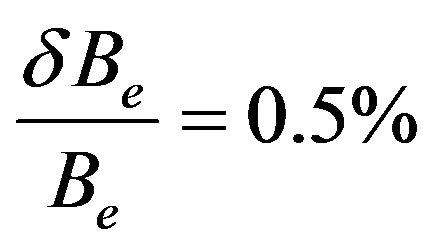 for the state (1)3Σ– (Ref.
for the state (1)3Σ– (Ref.
[50]) and disagreement by using another technique with
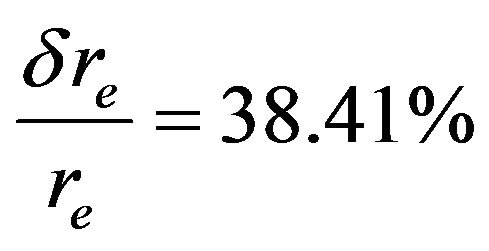 for the state (2)1Σ+ (Ref.[11]),
for the state (2)1Σ+ (Ref.[11]),
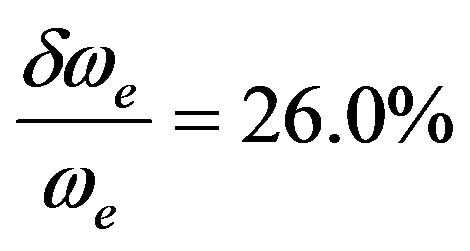 for the state (1)3Σ (Ref.[11]), and
for the state (1)3Σ (Ref.[11]), and
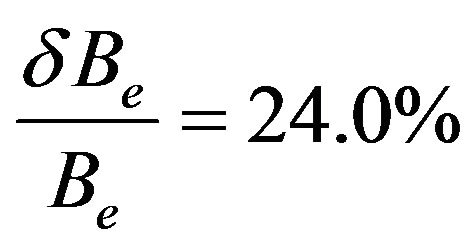 for the state (1)1Σ (Ref.[11]). These discrepancies in the theoretical results can be referred to the basis used in this calculation, the number of valence electron, the software used, the bad assignment of a state ….etc. While the comparison with the recent results of Ref.[56] for the 2 states (1)3Σ+ and (1)1Σ– by using an approach similar to that we used in the present work shows an excellent agreement for the values of re and Be and good agreement for ωe. For the state 1Σ, there is an excellent agreement with the value of ωe and good agreement with the values of re and Be. The SiO molecule possesses sizable dipole moments of 3.0982 D [41]. Such magnitudes of the dipole moment should be sufficient for sustaining dipole-bound states (DBSs). Extensive experimental and computational studies [42,43] of an extra-electron attachment to a number of polar molecules have shown the critical value of the dipole moment required to support a DBS to be 2.5 D. The electric dipole moment is also of great utility in the construction of molecular orbital based models of bonding and helping in the search for an understanding of the macroscopic properties of imperfect gases, liquids and solids. The expectation value of this operator is sensitive to the valence electrons and the general predictive quality of the computational methodology.
for the state (1)1Σ (Ref.[11]). These discrepancies in the theoretical results can be referred to the basis used in this calculation, the number of valence electron, the software used, the bad assignment of a state ….etc. While the comparison with the recent results of Ref.[56] for the 2 states (1)3Σ+ and (1)1Σ– by using an approach similar to that we used in the present work shows an excellent agreement for the values of re and Be and good agreement for ωe. For the state 1Σ, there is an excellent agreement with the value of ωe and good agreement with the values of re and Be. The SiO molecule possesses sizable dipole moments of 3.0982 D [41]. Such magnitudes of the dipole moment should be sufficient for sustaining dipole-bound states (DBSs). Extensive experimental and computational studies [42,43] of an extra-electron attachment to a number of polar molecules have shown the critical value of the dipole moment required to support a DBS to be 2.5 D. The electric dipole moment is also of great utility in the construction of molecular orbital based models of bonding and helping in the search for an understanding of the macroscopic properties of imperfect gases, liquids and solids. The expectation value of this operator is sensitive to the valence electrons and the general predictive quality of the computational methodology.
For the investigated electronic states, we calculated in the present work the permanent dipole μ(r) for 1.2 Å ≤ r ≤ 4 Å (Figures 4 and 5). Each time an adiabatic state loses its ionic character, it becomes again neutral and the corresponding dipole moment tends towards zero.
2.2. The Vibration-Rotation Calculation
Within the Born-Oppenheimer approximation, the vibration rotation motion of a diatomic molecule in a given electronic state is governed by the radial Schrödinger equation
 (1)
(1)
where r is the internuclear distance, v and J are respectively the vibrational and rotational quantum numbers, 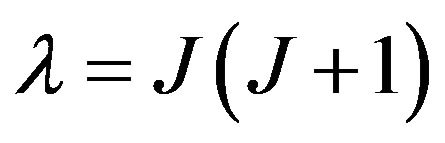 ,
, 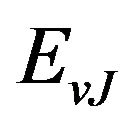 and
and 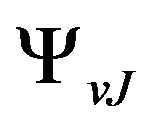 are respectively the eigenvalue and the eigenfunction of this equation. In the perturbation theory these functions can be expanded as
are respectively the eigenvalue and the eigenfunction of this equation. In the perturbation theory these functions can be expanded as
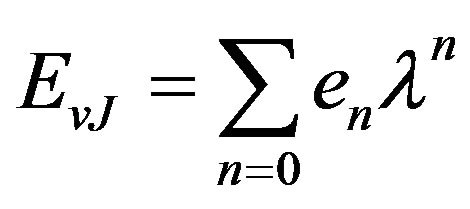 (2)
(2)
 (3)
(3)
with e0 = Ev, e1 = Bv, e2 = –Dv···, f0 is the pure vibration
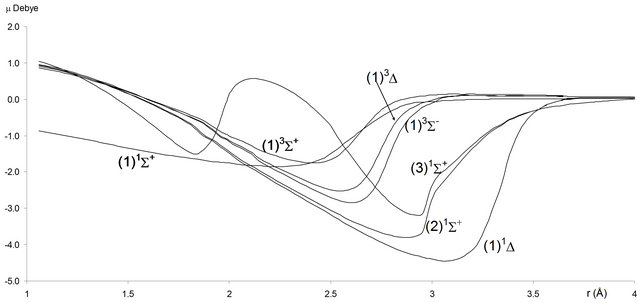
Figure 4. Permanent dipole moment curves of the lowest singlet and triplet and ∆-states of the molecule SiO.
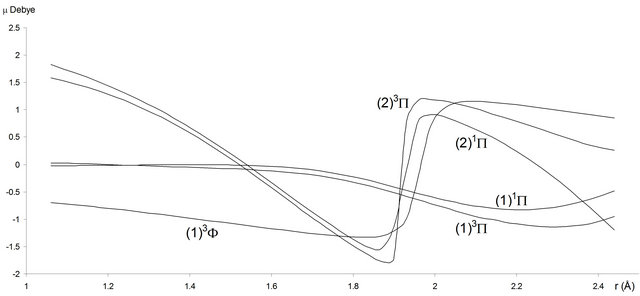
Figure 5. Permanent dipole moment curves of the lowest singlet and triplet Σ and ∆-states of the molecule SiO.
wave function and fn its rotational corrections. By replacing Equations (2) and (3) into Equation (1) and since this equation is satisfied for any value of l, one can write [24-26]
 (4)
(4)
 (5-1)
(5-1)
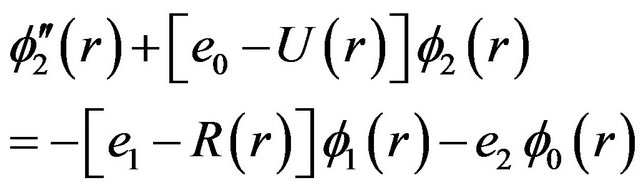 (5-2)
(5-2)
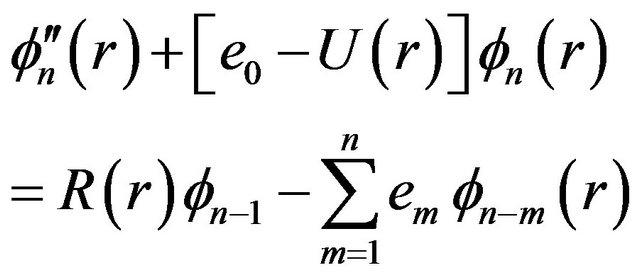 (5-n)
(5-n)
where , the first equation is the pure vibrational Schrödinger equation and the remaining equations are called the rotational Schrödinger equations. One may project Equations (7) onto f0 and find
, the first equation is the pure vibrational Schrödinger equation and the remaining equations are called the rotational Schrödinger equations. One may project Equations (7) onto f0 and find
 (6-1)
(6-1)
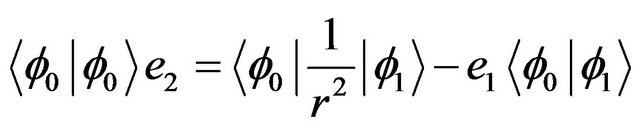 (6-2)
(6-2)
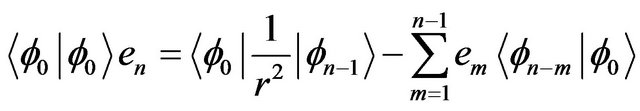 (6-n)
(6-n)
Once e0 is calculated from Equation (4),  can be obtained by using alternatively Equations (5) and (6). By using the canonical functions approach [24-26] and the cubic spline interpolation between each two consecutive points of the PECs obtained from the ab initio calculation of the SiO molecule, the eigenvalue Ev, the rotational constant Bv, the distortion constant Dv, and the abscissas of the turning point rmin and rmax have been calculated up to the vibration level v = 52. These values for the state X1Σ+, (1)1∆, (1)3Σ, (1)3Π, (2)3Π and (2)1Π (as illustration) are given in Table 2. The comparison of our calculated values of Ev, Bv, rmin and rmax with the experimental data of Ref.[55] for the ground state X1Σ+ shows an excellent agreement for the 35 considered vibrational levels. Similar results are obtained by comparing our calculated values of Bv with the calculated Shi et al. [56] for the considered states.
can be obtained by using alternatively Equations (5) and (6). By using the canonical functions approach [24-26] and the cubic spline interpolation between each two consecutive points of the PECs obtained from the ab initio calculation of the SiO molecule, the eigenvalue Ev, the rotational constant Bv, the distortion constant Dv, and the abscissas of the turning point rmin and rmax have been calculated up to the vibration level v = 52. These values for the state X1Σ+, (1)1∆, (1)3Σ, (1)3Π, (2)3Π and (2)1Π (as illustration) are given in Table 2. The comparison of our calculated values of Ev, Bv, rmin and rmax with the experimental data of Ref.[55] for the ground state X1Σ+ shows an excellent agreement for the 35 considered vibrational levels. Similar results are obtained by comparing our calculated values of Bv with the calculated Shi et al. [56] for the considered states.
Table 2. Values of Ev, Bv, Dv and rmin and rmax of the SiO molecule.


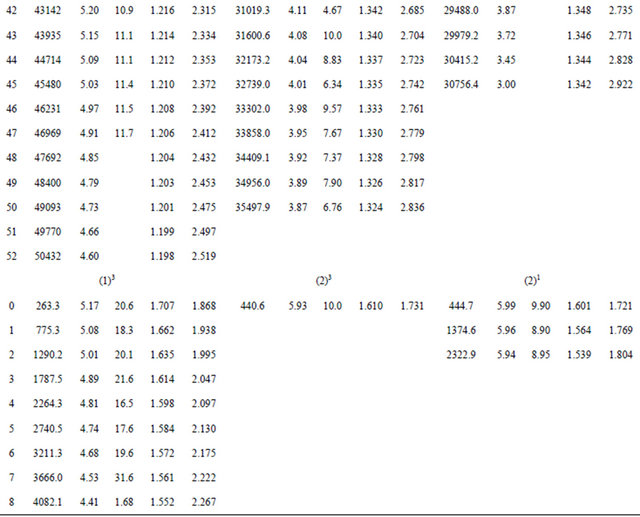
*First entry for the present work; **Second entry Refs. [51,54].
3. Conclusion
In the present work, the ab initio investigation for the 20 low-lying singlet and triplet electronic states of the SiO molecule has been performed via CAS-SCF/MRCI method. The potential energy and the dipole moment curves have been determined along with the spectroscopic constants Te, re, ωe, ωexe and the rotational constant Be for the lowest-lying electronic states. The comparison of our results, for the ground and excited states, with those obtained experimentally in literature shows an overall very good agreement, while the agreement with the theoretical data depends on the technique of calculation. By using the canonical functions approach [24-26], the eigenvalue Ev, the rotational constant Bv, and the abscissas of the turning points rmin and rmax have been calculated up to the vibrational level v = 52 with an excellent agreement by comparing with the available results in literature. Eight electronic states have been investigated in the present work for the first time. These newly obtained results maybe confirmed by the investigation of new experimental works on this molecule.
REFERENCES
- R. W. Wilson, A. A. Penzias, K. B. Jefferts, M. Kutner and P. Thaddeus, “Discovery of Interstellar Silicon Monoxide,” The Astrophysical Journal, Vol. 167, 1971, pp. L97-L100. HUdoi:10.1086/180769U
- J. Martin-Pintado, R. Bachiller and A. Fuente, “SiO Emission as a Tracer of Shocked Gas in Molecular Outflows,” Astronomy and Astrophysics, Vol. 254, No. FEB (I), 1992, pp. 315-326.
- D. R. Flower and G. P. des Forêt, “Non-Thermal Sputtering of Interstellar Grains in Magnetohydrodynamic Shocks,” Monthly Notices of the Royal Astronomical Society, Vol. 275, No. 4, 1995, pp. 1049-1056.
- P. Schilke, C. M. Walmsley, G. P. des Forêts and D. R. Flower, “SiO Production in Interstellar Shocks,” Astronomy and Astrophysics, Vol. 321, No. FEB (I), 1997, pp. 293-304.
- S. D. Le Picard, A. Canosa, G. P. des Forêts, C. Rebrion-Rowe and B. R. Rowe, “The Si(3PJ)+O2 Reaction: A Fast Source of SiO at Very Low Temperature; CRESU Measurements and Interstellar Consequences,” Astronomy and Astrophysics, Vol. 372, No. 3, 2001, pp. 1064- 1070.
- F. Dayou and A. Spielfiedel, “Ab Initio Calculation of the Ground (1A’) Potential Energy Surface and Theoretical Rate Constant for the Si+O2\SiO+O Reaction,” Journal of Chemical Physics, Vol. 119, No. 8, 2003, pp. 4237-4250. HUdoi:10.1063/1.1594172U
- I. Jiménez-Serra, J. Martin-Pintado, A. Rodriguez-Franco and S. Martin, “Grain Evolution across the Shocks in the L1448-mm Outflow,” The Astrophysical Journal Letters, Vol. 627, No. 2, 2005, 2005, pp. L121-L124.
- N. T. X. Huynh, V.V. Hoang and H. Zung, “Evolution of Structure of SiO2 Nanoparticles upon Cooling from the Melt,” PMC Physics B, 2008, Article ID: 16. HUdoi:10.1186/1754-0429-1-16U
- I. S. Altman, D. Lee, J. D. Chung, J. Song and M. Choi1, “Light Absorption of Silica Nanoparticles,” Physical Review B, Vol. 63, No. 16, 2001, pp. 161402(R)-161402(R).
- K. P. Huber and G. Herzberg, “Constants of Diatomic Molecules,” Van Nostrand, Reinhold, 1979.
- T. G. Heil and S. H. Schaefer, “Potential Curves for the Valence—Excited States of Silicon Monoxide. A Theoretical Study,” Journal of Chemical Physics, Vol. 56, No. 2, 1972, pp. 958-969. HUdoi:10.1063/1.1677254U
- H. Varambhia, M. Gupta, A. Faure, K. L. Baluja and J. Tennyson, “Electron Collision with the Silicon Monoxide (SiO) Molecule Using the R-Matrix Method,” Journal of Physics B: Atomic, Molecular and Optical Physics, Vol. 42, No. 9, 2009, Article ID: 095204. HUdoi:10.1088/0953-4075/42/9/095204U
- J. R. Smith, H. Schlosser, W. Leaf, J. Ferrante, J. H. Rose, “Connection between Energy Relations of Solids and Molecules,” Physical Review A, Vol. 39, No. 2, 1989, pp. 514-517. HUdoi:10.1103/PhysRevA.39.514U
- S. Abdul-Al, M. Korek and A. R. Allouche, “HTheoretical Electronic Structure of the Lowest-Lying States of the YI MoleculeH,” Chemical Physics, Vol. 308, No. 1-2, 2005, pp. 1-6. HUdoi:10.1016/j.chemphys.2004.07.032U
- M. Korek, Y. A. Moghrabi and A. R. Allouche, “Theoretical Calculation of the Excited States of the KCs Molecule Including the Spin-Orbit Interaction,” Journal of Chemical Physics, Vol. 124, No. 9, 2006, Article ID: 094309. HUdoi:10.1063/1.2173239U
- M. Korek, S. Bleik and A. R. Allouche, “Theoretical Calculation of the Low Laying Electronic States of the Molecule NaCs with Spin-Orbit Effect,” Journal of Chemical Physics, Vol. 126, No. 12, 2007, Article ID: 124313. HUdoi:10.1063/1.2710257U
- F. Taher-Mansour, A. R. Allouche, M. Korek, “HTheoretical Electronic Structure of the Lowest-Lying States of ScCl Molecule below 22,500 cm−1H,” Journal of Molecular Spectroscopy, Vol. 248, No. 1, 2008, pp. 61-65. HUdoi:10.1016/j.jms.2007.11.012U
- M. Korek, S. Kontar, F. Taher-Mansour and A. R. Allouche, “Theoretical Electronic Structure of the Molecule ScI,” International Journal of Quantum Chemistry, Vol. 109, No. 2, 2009, pp. 236-242. HUdoi:10.1002/qua.21779U
- M. Korek, S. Al-Shawa and G. Younes, “HTheoretical Calculation of the Electronic Structure of the Molecule LiRb Including the Spin-Orbit InteractionH,” Journal of Molecular Structure: THEOCHEM, Vol. 899, No. 1-3, 2009, pp. 25-31. HUdoi:10.1016/j.theochem.2008.12.006U
- M. Korek and S. N. Abdul-Al, “HRovibrational Study and Dipole Moment Calculation of the Molecule YF with Spin-Orbit InteractionH,” Chemical Physics, Vol. 355, No. 2-3, 2009, pp. 130-134. HUdoi:10.1016/j.chemphys.2008.11.022U
- A. Hamdan and M. Korek, “HTheoretical Calculation of the Low-Lying Sextet Electronic States of CrF MoleculeH,” Chemical Physics, Vol. 369, No. 1, 2010, pp. 13-18. HUdoi:10.1016/j.chemphys.2010.01.023U
- A. Hamdan and M. Korek, “Theoretical Calculation of the Low-Lying Quartet States of the CrF Molecule,” Canadian Journal of Chemistry, Vol. 89, No. 10, 2011, pp. 1304-1311. HUdoi:10.1139/v11-082U
- A. Hamdan and M. Korek, “Theoretical Study with Vibration-Rotation and Dipole Moment Calculations of Quartet States of the CrCl Molecule,” International Journal of Quantum Chemistry, Vol. 111, No. 12, 2011, pp. 2960-2965. HUdoi:10.1002/qua.22602U
- H. Kobeissi, M. Korek and M. Dagher, “HOn the Computation of Diatomic Centrifugal Distortion Constants: Exact Solutions for Initial Value ProblemsH,” Journal of Molecular Spectroscopy, Vol. 138, No. 1, 1989, pp. 1-12. HUdoi:10.1016/0022-2852(89)90092-1U
- M. Korek and H. Kobeissi, “Highly Accurate Diatomic Centrifugal Distortion Constants for High Orders and High Levels,” Journal of Computational Chemistry, Vol. 13, No. 9, 1992, pp. 1103-1108. HUdoi:10.1002/jcc.540130909U
- M. Korek, “A One Directional Shooting Method for the Computation of Diatomic Centrifugal Distortion Constants,” Computer Physics Communications, Vol. 119, No. 2-3, 1999, pp. 169-178. HUdoi:10.1016/S0010-4655(98)00180-5U
- T. H. Dunning, “Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen,” Journal of Chemical Physics, Vol. 90, No. 2, 1989, pp. 1007-1024. HUdoi:10.1063/1.456153U
- N. Godbout, D. R. Salahub, J. Andzelm and E. Wimmer, “Optimization of Gaussian-Type Basis Sets for Local Spin Density Functional Calculations. Part I. Boron through Neon, Optimization Technique and Validation,” Canadian Journal of Chemistry, Vol. 70, No. 2, 1992, pp. 560-571. HUdoi:10.1139/v92-079U
- H. J. HWernerH, P. J. Knowles, R. HLindhH,H F. R. ManbyH, M. HSchützH, P. Celani, T. HKoronaH, G. HRauhutH, R. D. Amos, A. Bernhardsson, A. Berning, D. L. HCooperH, M. J. O. HDeeganH, A. J. Dobbyn, F. Eckert, C. Hampel, G. Hetzer, A. W. Lloyd,H S. J. McNicholasH,H W. MeyerH, M. E. Mura, A. Nicklaß, P. Palmieri,H R. PitzerH, U. Schumann,H H. StollH,H A. J. StoneH, R. Tarroni and T. Thorsteinsson, “MOLPRO Is a Package of Ab Initio Programs,” 2008. http://www.molpro.net/info/molpro2006.1/molpro_manual
- A. R. Allouche, “Gabedit—A Graphical User Interface for Computational Chemistry Softwares,” Journal of Computational Chemistry, Vol. 32, No. 1, 2011, pp. 174-182. HUdoi:10.1002/jcc.21600U
- M. Friesen, M. Junker, A. Zumbusch and H. Schnöckel, “Raman-Spectroscopy of Oligomeric SiO Species Isolated in Solid Methane,” Journal of Chemical Physics, Vol. 111, No. 17, 1999, pp. 7881-7888. HUdoi:10.1063/1.480123U
- C. E. Moore, “Atomic Energy Levels,” National Bureau of Standards Circular, Washington DC, 1949.
- P. Botschwina and P. Rosmus, “An Ab Initio Calculation of Spectroscopic Properties of SiO and HOSi+,” Journal of Chemical Physics, Vol. 82, No. 3, 1985, pp. 1420-1427. HUdoi:10.1063/1.448465U
- S. R. Langhoff and J. O. Arnold, “Theoretical Study of the X1+, A1, C1−, and E1+ States of the SiO Molecule,” Journal of Chemical Physics, Vol. 70, No. 2, 1979, pp. 852-863. HUdoi:10.1063/1.437491U
- H. J. Werner, P. Rosmus and M. Grimm, “HAb Initio Calculations of Radiative Transition Probabilities in the X1σ+ State of SiO and the X2σ+ and A2 Π states of SiO+H,” Chemical Physics, Vol. 73, No. 1-2, 1982, pp. 169-178. HUdoi:10.1016/0301-0104(82)85158-6U
- T. Törring, Zeitschrift für Naturforschung, Vol. 23A, 1968, pp. 777-778.
- E. L. Manson Jr., W. W. Clark, F. C. Delucia and W. Gordy, “Millimeter Spectrum and Molecular Constants of Silicon Monoxide,” Physical Review A, Vol. 15, No. 1, 1977, pp. 223-226. HUdoi:10.1103/PhysRevA.15.223U
- F. J. Lovas, A. G. Maki and W. B. Olson, “HThe Infrared Spectrum of SiO near 1240 cm−1 and Its Relation to the Circumstellar SiO MaserH,” Journal of Molecular Spectroscopy, Vol. 87, No. 2, 1981, pp. 449-458. HUdoi:10.1016/0022-2852(81)90416-1U
- G. L. Gutsev, P. Jena and R. J. Bartlett, “Two ThermoDynamically Stable States in SiO− and PN−,” Physical Review A, Vol. 58, No. 6, 1998, pp. 4972-4974. HUdoi:10.1103/PhysRevA.58.4972U
- S. Chattopadhyaya, A. Chattopadhyaya and K. Kummar Das, “Configuration Interaction Study of the Low-Lying Electronic States of Silicon Monoxide,” The Journal of Physical Chemistry A, Vol. 107, No. 1, 2003, pp. 148-158. HUdoi:10.1021/jp021845vU
- J. W. Raymonda, J. S. Muenter and W. A. Klemperer, “Electric Dipole Moment of SiO and GeO,” Journal of Chemical Physics, Vol. 52, No. 7, 1970, pp. 3458-3462. HUdoi:10.1063/1.1673510U
- G. L. Gutsev and L. Adamowicz, “Electronic and Geometrical Structure of Dipole-Bound Anions Formed by Polar Molecules,” Journal of Chemical Physics, Vol. 99, No. 36, 1995, pp. 13412-13421. HUdoi:10.1021/j100036a015U
- C. Desfrançois, H. Abdoul-Carime and J. P. Schermann, “Ground-State Dipole-Bound Anions,” International Journal of Modern Physics B, Vol. 10, No. 12, 1996, pp. 1339- 1395. HUdoi:10.1142/S0217979296000520U
- M. E. Sanz, M. C. McCarthy and P. Thaddeus, “Rotational Transitions of SO, SiO, and SiS Excited by a Discharge in a Supersonic Molecular Beam: Vibrational Temperatures, Dunham Coefficients, Born-Oppenheimer Breakdown, and Hyperfine Structure,” Journal of Chemical Physics, Vol. 119, No. 22, 2003, pp. 11715-11727. HUdoi:10.1063/1.1612481U
- G. Hager, R. Harris and S. G. Hadley, “The a3Σ+→X1Σ+ and b3Π→X1Σ+ Band Systems of SiO and the a3Σ+→X1Σ+ Band System of GeO Observed in Chemiluminescence,” Journal of Chemical Physics, Vol. 63, No. 7, 1975, pp. 2810-2821. HUdoi:10.1063/1.431713U
- H. Bredohl, R. Cornet, I. Dubois and F. Remy, “The a3Πj-X1B+ transition of SiO,” Journal of Physics B: Atomic and Molecular Physics, Vol. 7, No. 3, 1974, pp. L66- L69. HUdoi:10.1088/0022-3700/7/3/019U
- S. Nagaraj and R. D. Verma, “A3Σ-3Π Transition of the SiO Molecule,” Canadian Journal of Physics, Vol. 48, No. 12, 1970, pp. 1436-1440. HUdoi:10.1139/p70-181U
- R. Field, A. Lagerqvist and I. Renhorn, “HThe Spectrum of Si18O in the Vacuum Ultraviolet RegionH,” Journal of Molecular Spectroscopy, Vol. 49, No. 1, 1974, pp. 157- 166. HUdoi:10.1016/0022-2852(74)90104-0U
- D. L. Hildenbrand, “The Gaseous Equilibrium Ge + SiO = GeO + Si and the Dissociation Energy of SiO,” High Temperature Science, Vol. 4, 1972, pp. 244-245.
- J. Oddershede and N. Elander, “Spectroscopic Constants and Radiative Lifetimes for Valence Excited Bound States in SiO,” Journal of Chemical Physics, Vol. 65, No. 9, 1976, pp. 3495-3505. HUdoi:10.1063/1.433577U
- A. Lagerqvist, I. Renhorn and N. Elander, “The Spectrum of SiO in the Vacuum Ultraviolet Region,” Journal of Molecular Spectroscopy, Vol. 46, No. 2, 1973, pp. 285- 315. HUdoi:10.1016/0022-2852(73)90043-XU
- N. Elander and A. Lagerqvist, “On the E1Σ+-X1Σ+ System of SiO in the Vacuum Ultraviolet Region,” Physica Scripta, Vol. 3, No. 6, 1971, pp. 267-271. HUdoi:10.1088/0031-8949/3/6/005U
- J. Klache, “Trends in Ground and Excited State Electron Affinities of Group 14, 15, and 16 Mixed Diatomic Anions: A Computational Study,” Physical Chemistry Chemical Physics, Vol. 4, No. 14, 2002, pp. 3311-3317. HUdoi:10.1039/b201498jU
- A. Lagerqvist, I. Renhorn and N. Elander, “HThe Spectrum of Si18O in the Vacuum Ultraviolet RegionH,” Journal of Molecular Spectroscopy, Vol. 49, No. 1, 1974, pp. 157- 166. HUdoi:10.1016/0022-2852(74)90104-0U
- R. Tipping and C. Chakerian Jr., “Vibration-Rotation Intensities of SiO,” Journal of Molecular Spectroscopy, Vol. 88, No. 2, 1981, pp. 352-363. HUdoi:10.1016/0022-2852(81)90185-5U
[57] NOTES
[58]
[59] *Corresponding author.
[60]

