Journal of Modern Physics
Vol.3 No.7(2012), Article ID:21102,5 pages DOI:10.4236/jmp.2012.37083
Temperature Dependent Motion of a Massive Quantum Particle
Department of Physics, Shanghai Jiao Tong University, Shanghai, China
Email: jppeng@sjtu.edu.cn
Received April 23, 2012; revised May 24, 2012; accepted June 17, 2012
Keywords: Thermodynamics; Internal energy; Entropy generation
ABSTRACT
We report model calculations of the time-dependent internal energy and entropy for a single quasi-free massive quantum particle at a constant temperature. We show that the whole process started from a fully coherent quantum state to thermodynamic equilibrium can be understood, based on statistics of diffracted matter waves. As a result of thermal interaction between the particle and its surroundings, the motion of the particle shows new feature.
1. Introduction
Recent experiments of absorption of a single photon by a single atom [1], nondestructive cooling of a single ion using an ultracold atomic bath [2], and the imaging of spin direction of a single atom [3] have demonstrated intriguing possibilities of controlling and measuring of quantum processes on the atomic scale. Among couplings of such a system with its surrounding, keeping it at adequate low temperature is believed to be essential to maintaining the quantum coherence. The question appears to be important and interesting: To what extent can temperature affect the behavior of a quantum system containing a single or a few quantum particles? It is well-known that statistical mechanics deals with macroscopic systems consisting of large number of microscopic particles [4]. For a system of N particles at a finite temperature, it is generally true that the relative fluctuations of an extensive quantity vary as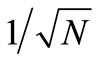 , which gets larger and larger as N decreases. If we wish to keep the statistical error below one percent then a system would have to contain more than about ten thousand particles. The obstacle arises if one tries to apply the standard procedure of statistical physics in a present-day textbook directly to study the temperature dependent behavior of a quantum system containing a few quantum particles. For an atom confined in a harmonic potential, it could be overcome by considering a single particle Hamiltonian coupled to a multi-mode quantum thermal bath, where relaxation of the particle depends on the coupling modes with acceptable fluctuations [5,6]. Another approach is to perform statistics directly on the matter wave of a quantum particle by taking into account the detailed configuration of diffraction in real space, where the bath acts as the heat reservoir at a constant temperature and is large enough to cause unacceptable errors [7]. Here we improve the latter approach and study the thermodynamic process of a quasi-free massive quantum particle from a coherent single quantum state to thermodynamic equilibrium. We show analytical expressions of the time-dependent internal energy and entropy. Due to thermal interaction between the particle and its surroundings, the process of decoherence is temperature dependent and its translational motion shows new feature.
, which gets larger and larger as N decreases. If we wish to keep the statistical error below one percent then a system would have to contain more than about ten thousand particles. The obstacle arises if one tries to apply the standard procedure of statistical physics in a present-day textbook directly to study the temperature dependent behavior of a quantum system containing a few quantum particles. For an atom confined in a harmonic potential, it could be overcome by considering a single particle Hamiltonian coupled to a multi-mode quantum thermal bath, where relaxation of the particle depends on the coupling modes with acceptable fluctuations [5,6]. Another approach is to perform statistics directly on the matter wave of a quantum particle by taking into account the detailed configuration of diffraction in real space, where the bath acts as the heat reservoir at a constant temperature and is large enough to cause unacceptable errors [7]. Here we improve the latter approach and study the thermodynamic process of a quasi-free massive quantum particle from a coherent single quantum state to thermodynamic equilibrium. We show analytical expressions of the time-dependent internal energy and entropy. Due to thermal interaction between the particle and its surroundings, the process of decoherence is temperature dependent and its translational motion shows new feature.
2. Model Calculations
We consider a structureless massive quantum particle moving in a space at constant temperature T as shown in figure 1. Although there is no interaction with other particles, the particle is quasi-free because a circular aperture of radius a0 for its matter wave is considered. The quantum particle is assumed to be of kinetic energy E0 initially at the origin and is described by a wave-packet sharply peaked at the de Broglie wavelength 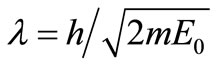 , with m being its mass and h the Plank’s constant. The wave front propagates along x-axis at group velocity Vg = h/(mλ). For simplicity, we assume that the radius a0 of the matter wave aperture is large compared with the wavelength λ so that the shape and linear dimension of the forward-going wave-front remains unchanged as the wave propagates. It is important that every point at the edge of the wave-front generates out-going fully spherical waves and the kinetic energy associated with the forward-going wave-front follows the form [7].
, with m being its mass and h the Plank’s constant. The wave front propagates along x-axis at group velocity Vg = h/(mλ). For simplicity, we assume that the radius a0 of the matter wave aperture is large compared with the wavelength λ so that the shape and linear dimension of the forward-going wave-front remains unchanged as the wave propagates. It is important that every point at the edge of the wave-front generates out-going fully spherical waves and the kinetic energy associated with the forward-going wave-front follows the form [7].

Figure 1. Cross section schematic of a free quantum particle passing through a matter wave aperture of radius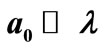 . The whole space is assumed to be at constant temperature T. Arrows in line indicate the wave-front of the mater wave pulse. Circles indicate out-going spherical waves diffracted at the edge of the wave-front. The expectation value
. The whole space is assumed to be at constant temperature T. Arrows in line indicate the wave-front of the mater wave pulse. Circles indicate out-going spherical waves diffracted at the edge of the wave-front. The expectation value 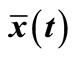 for the position of the particle is temperature dependent.
for the position of the particle is temperature dependent.
 , (1)
, (1)
where L is a temperature dependent parameter of dimension length and is expected to be infinitely large as the temperature tends to zero. This is just the energy for the source to generate out-going fully spherical waves. We define a probability density function for the particle
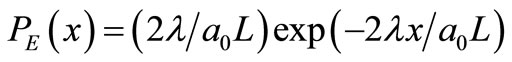 . (2)
. (2)
There exists a step length d0, so that the energy for fully spherical waves generated in d0 is E0PE(nd0)d0 when the forward-going plane-wave front is at the position nd0, where n is an integer. In principle, the particle may be in any of these diffracted states besides the forward-going plane-wave state, i.e., the particle itself constitutes automatically a thermodynamic system as a result of diffraction at the edge of its matter-wave front. The probability for different energy states is known here and, in general, all energy states are not equally likely. If one can distinguish energy states in more detail, a smaller step Δx should be used and the degeneracy replaced by d0/Δx. Thermal interaction between the particle’s system and the surrounding space becomes possible and the space here acts as the heat reservoir at constant temperature T.
The partition function of the particle should take into account contributions from forward-going wave-front and all spherical waves diffracted at the edge. The partition function at a given time is then
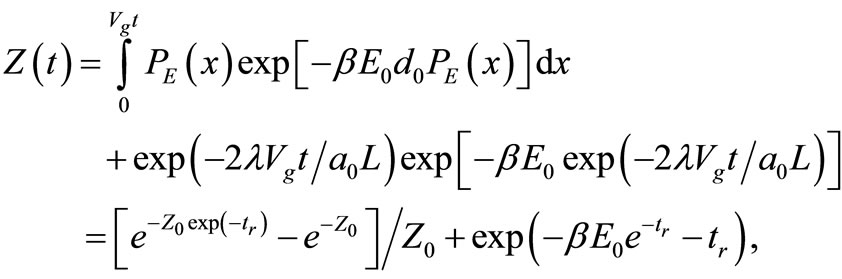 (3)
(3)
where the notation β = 1/kBT is used as usual with kB being the Boltzmann constant. The constant Z0 is defined as the non-zero real solution of the transcend equation
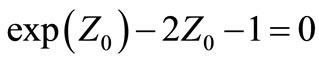 . (4)
. (4)
With the help of the Lambert W function [8], we obtain Z0 = −W−1(1/2e1/2) − 1/2 and we use an approximate value Z0 = 1.25643 in our numerical calculations. Here we have used the correct form of the step length 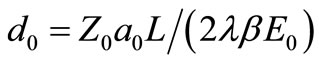 instead of the wavelength, and tr = t/tc is the time scaled with a temperature dependent characteristic time defined by
instead of the wavelength, and tr = t/tc is the time scaled with a temperature dependent characteristic time defined by
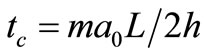 . (5)
. (5)
The expectation value for the energy of the particle or its internal energy is
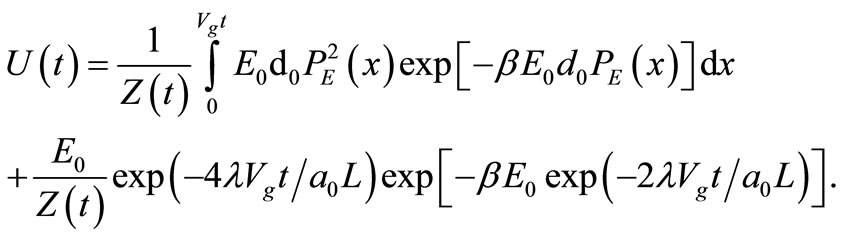 (6)
(6)
The first term comes from all those out-going spherical waves diffracted at the edge, and the second term from the forward-going wave-front itself as a whole. The internal energy of the particle is written as
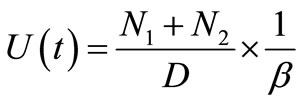 , (7)
, (7)
with
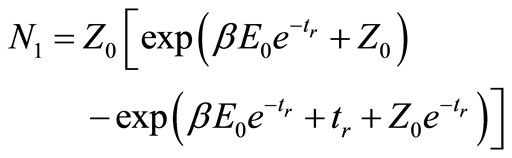 ,
,

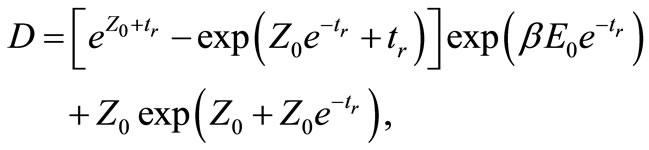
depending on the temperature and the particle’s initial energy in a complicated form.
In Figure 2 we plot the numerical results of the internal energy for various initial energies and temperatures. In general, a quantum particle absorbs or gives out heat continuously when its initial energy E0 is less or more than kBT/2. At the special point E0 = kBT/2, our numerical calculations show that the curve moves downward initially and then upward continuously, indicating exchange of energy taking place between the particle and its surrounding space in the whole process. The limiting value
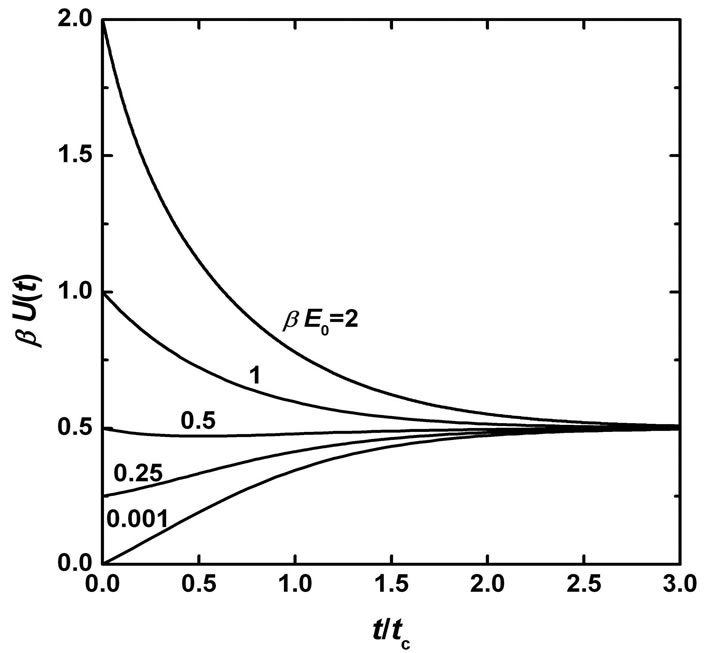
Figure 2. Scaled internal energy βU(t) as a function of the scaled time t/tc. Values of βE0 are labeled on the curves.
of the internal energy for the freedom in the x-direction is kBT/2, regardless of its initial energy. The limit is already reached for t/tc > 3 in our numerical calculations and the overall decay or increase in internal energy does not follow the simple exponential form. Physically, the process describes the evolution of the particle starting from a fully coherent initial state with well defined energy in quantum mechanics to a series of possible states. Although states representing the forward-going wavefront remain coherent, those states diffracted at the edge at different time are no longer coherent at finite temperatures as a result of heat exchange. The process breaks down if a collision occurs in a gas.
After a sufficient long time, the probability for the particle in the coherent state disappears and the internal energy reaches the universal thermodynamic energy in equilibrium with the surrounding environment. The time needed to reach the limit of internal energy could in some sense be viewed as the coherence decay time of a quantum particle in a space at a finite temperature. Therefore, the present work might be utilized in understanding the temperature dependence for the coherence decay time observed recently for individual molecules at room temperature [9].
We now calculate the average value of the particle’s position to obtain information of where it is at a given time. Although out-going spherical waves diffracted at the edge are no longer coherent at finite temperatures, the overall probability projected on x-axis in the range –Vgt < x < Vgt can be calculated without mathematical difficulties. The thermodynamic expectation of the particle’s position in the x-direction is written as
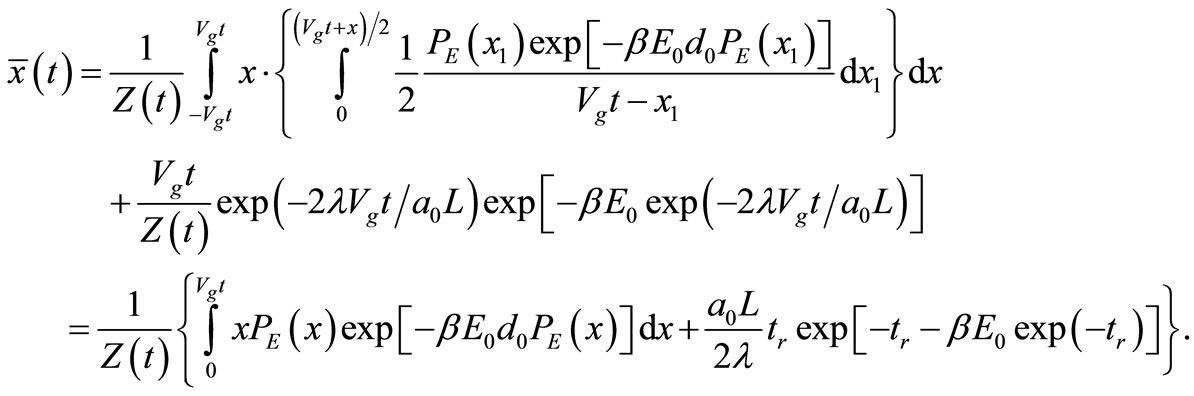 (8)
(8)
The first term represents contributions from all those out-going spherical waves and the second term from the forward-going wave-front. The explicit result is
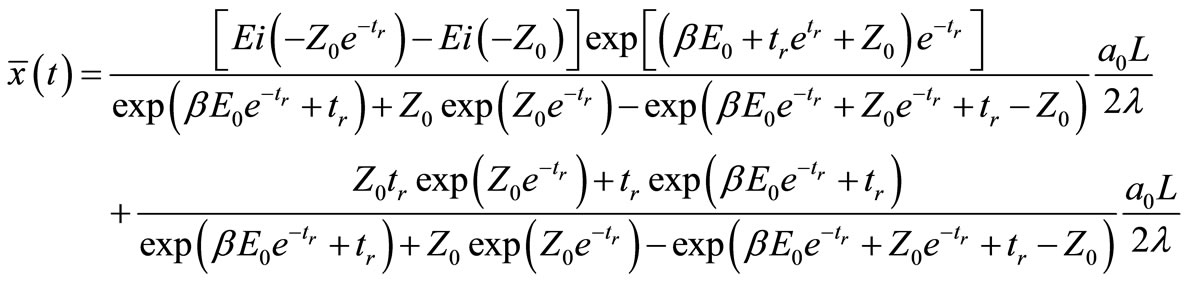 (9)
(9)
with 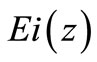 being the exponential integral function of argument z [10]. Note that the particle, in principle, may be found anywhere in the range
being the exponential integral function of argument z [10]. Note that the particle, in principle, may be found anywhere in the range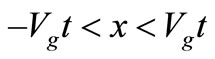 . It is interesting that
. It is interesting that 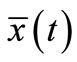 shows dependences not only on the initial energy of the particle, but also on the temperature and the spatial confinement for its matter wave.
shows dependences not only on the initial energy of the particle, but also on the temperature and the spatial confinement for its matter wave.
Figure 3 shows the numerical results of Equation (9) for the scaled average position 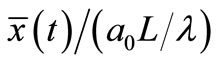 versus the scaled time t/tc for various combinations of temperature and initial energy. It increases continuously with increasing time, approaching a limit within a time of several tc. It is true that a particle with higher initial energy reaches the limit at a later time. The limit is
versus the scaled time t/tc for various combinations of temperature and initial energy. It increases continuously with increasing time, approaching a limit within a time of several tc. It is true that a particle with higher initial energy reaches the limit at a later time. The limit is
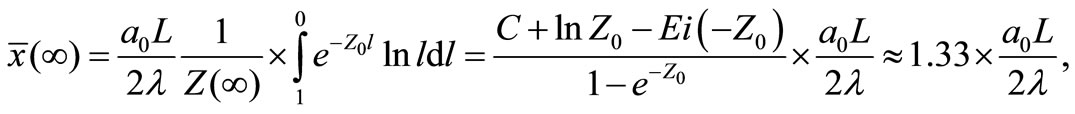 (10)
(10)
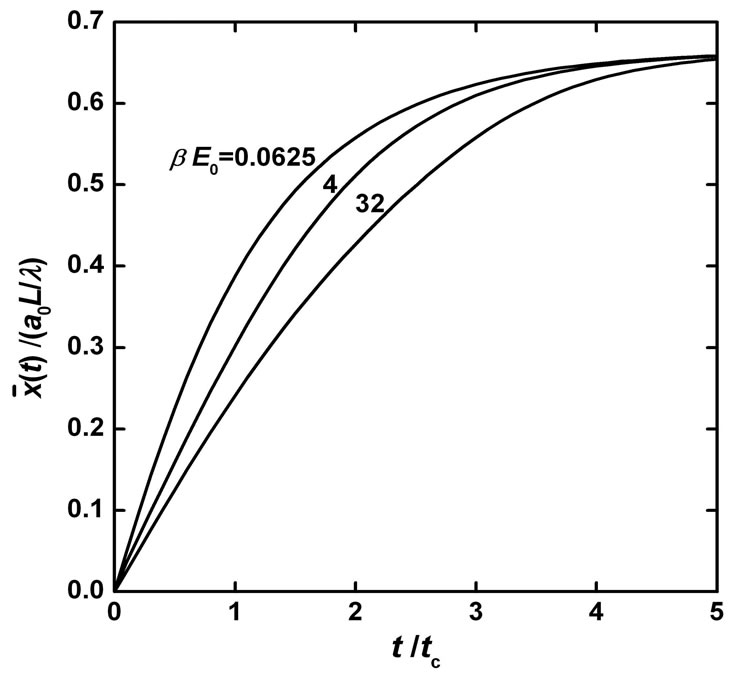
Figure 3. Scaled average position 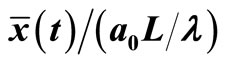 versus the scaled time t/tc for various values of βE0.
versus the scaled time t/tc for various values of βE0.
where C = 0.577216 is the Euler’s constant [10]. If the particle could not feel the temperature of the space, we would have the relation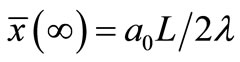 .
.
The entropy, measuring the amount of uncertainty of the particle, can also be calculated because the probability distribution is known. The uncertainty relation 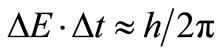 in quantum mechanics tells us that waves diffracted at the edge should be indistinguishable when the wave-front moves forward within about one wavelength. We choose λ as the step length and rewrite the probability in discrete form
in quantum mechanics tells us that waves diffracted at the edge should be indistinguishable when the wave-front moves forward within about one wavelength. We choose λ as the step length and rewrite the probability in discrete form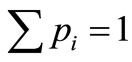 . The entropy is calculated using the definition
. The entropy is calculated using the definition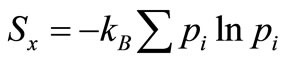 , which is perfectly unambiguous for time-dependent system of any size. Under the condition
, which is perfectly unambiguous for time-dependent system of any size. Under the condition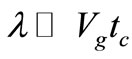 , we find the timedependent entropy of the particle for the coordinate is
, we find the timedependent entropy of the particle for the coordinate is
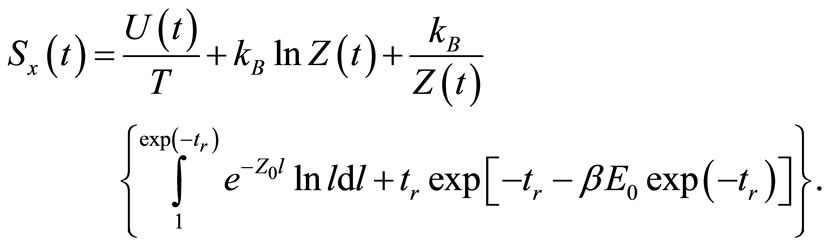 (11)
(11)
Here the constant term 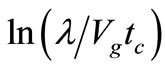 has been neglected. The last term can be understood as the result of expansion of the particle’s matter-wave. The entropy starts from zero and then increase monotonically with increaseing time. As
has been neglected. The last term can be understood as the result of expansion of the particle’s matter-wave. The entropy starts from zero and then increase monotonically with increaseing time. As 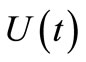 and
and 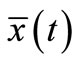 reach their limits, the entropy for each freedom converges to a universal value
reach their limits, the entropy for each freedom converges to a universal value
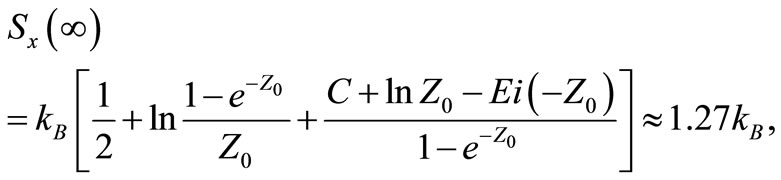 (12)
(12)
with no regards to the temperature and the initial state of the particle. The result holds also for a free quantum particle. As a consequence of the wavelike nature of the particle, the feature is purely quantum mechanical without classical counterpart.
The possibility of experimental observation depends on developing single quantum particle experiment in which there is very little chance for two wave packets to overlap. It seems to have been demonstrated by past experiments on the diffractions of neutrons [11], electrons [12] and atoms [13]. For electrons, the length of a single electron wave packet could be as short as 1 μm [12]. It is difficult at present to observe directly the instantaneous position of a single quantum particle, since an unavoidable quantum coupling with the apparatus must be invoked in the measurement [14,15]. However, it is possible to experiment with a beam of incident particles at a single wave-length. If the final positions of the incident particles are recorded by a row of detectors on x-axis, the average value of position predicted in Equation (10) may be observable.
3. Conclusion
The motion of a quasi-free massive quantum particle in a space at a finite temperature shows interesting phenomena arising from thermal interaction. The important point is that a nonzero temperature of the environment inherently destroys the coherence of a quantum particle and the whole process can be modeled.
REFERENCES
- N. Piro, et al., “Heralded Single-Photon Absorption by a Single Atom,” Nature Physics, Vol. 7, 2011, pp. 17-20. doi:10.1038/nphys1805
- C. Zipkes, S. Palzer, C. Sias and M. Koehl, “A Trapped Single Ion inside a Bose-Einstein Condensate,” Nature, Vol. 464, No. 18, 2010, pp. 388-391. doi:10.1038/nature08865
- D. Serrate, et al., “Imaging and Manipulating the Spin Direction of Individual Atoms,” Nature Nanotechnology, Vol. 5, 2010, pp. 350-353. doi:10.1038/nnano.2010.64
- L. D. Landau and E. M. Lifshitz, “Statistical Physics,” 3rd Edition, Pergamon Press Ltd, Oxford, 1980.
- A. E. Allahverdyan and Th. M. Nieuwenhuizen, “Extraction of Work from a Single Thermal Bath in the Quantum Regime,” Physical Review Letters, Vol. 85, No. 9, 2000, pp. 1799-1802. doi:10.1103/PhysRevLett.85.1799
- G. W. Ford and R. F. O’Connell R, “A Quantum Violation of the Second Law,” Physical Review Letters, Vol. 96, No. 2, 2006, p. 020402. doi:10.1103/PhysRevLett.96.020402
- J. P. Peng, “Statistics of a Free Single Quantum Particle at a Finite Temperature,” Modern Physics Letters B, Vol. 24, No. 25, 2010, pp. 2541-2547. doi:10.1142/S0217984910024912
- R. M. Corless, G. H. Gonnet, D. E. G. Hare, D. J. Jeffrey and D. E. Knuth, “On the Lambert W Function,” Advances in Computational Mathematics, Vol. 5, No. 1, 1992, pp. 329-361. doi:10.1007/BF02124750
- R. Hildner, D. Brinks and N. F. van Hulst, “Femtosecond Coherence and Quantum Control of Single Molecules at Room Temperature,” Nature Physics, Vol. 7, 2011, pp. V 172-177. doi:10.1038/nphys1858
- I. S. Gradshteyn and I. M. Rizhik, “Tables of Integrals, Series, and Products,” 7th Edition, Elservier Inc., London, 2007.
- A. Zeilinger, R. Gaehler, C. G. Shull, W. Treimer and W. Mampe, “Singleand Double-Slit Diffraction of Neutrons,” Reviews of Modern Physics, Vol. 60, No. 4, 1988, pp. 1067-1073. doi:10.1103/RevModPhys.60.1067
- A. Tonomura, J. Endo, T. Matsuda and T. Kawasaki, “Demonstration of Single-Electron Buildup of an Interference Pattern,” American Journal of Physics, Vol. 57, No. 2, 1989, pp. 117-120. doi:10.1119/1.16104
- D. W. Keith, C. R. Ekstrom, Q. A. Turchtte and D. E. Pritchard, “An Interferometer for Atoms,” Physical Review Letters, Vol. 66, No. 21, 1991, pp. 2693-2696. doi:10.1103/PhysRevLett.66.2693
- C. Presilla, R. Onofrio and M. Patriarca, “Classical and Quantum Measurements of Position,” Journal of Physics A: Mathematical and General, Vol. 30, No. 21, 1997, pp. 7385-7411. doi:10.1088/0305-4470/30/21/014
- J. Mauritsson, et al., “Coherent Electron Scattering Captured by an Attosecond Quantum Stroboscope,” Physical Review Letters, Vol. 100, No. 7, 2008, p. 073003. doi:10.1103/PhysRevLett.100.073003

