Journal of Modern Physics
Vol.3 No.9(2012), Article ID:22610,8 pages DOI:10.4236/jmp.2012.39129
Influence of the Magnetic Field on the Graphene Conductivity
1Volgograd State Socio-Pedagogical University, Volgograd, Russia
2Volgograd State Technical University, Volgograd, Russia
Email: svkruchkov@yandex.ru, eikuhar@yandex.ru
Received June 23, 2012; revised July 30, 2012; accepted August 7, 2012
Keywords: Graphene; Magnetoconductivity; Magnetic Oscillations; Shubnikov-de Haaz Effect; Graphene Superlattice
ABSTRACT
The transversal conductivity of the gap-modification of the graphene was studied in the cases of weak nonquatizing and quantizing magnetic field. In the case of nonquantizing magnetic field the expression of the current density was derived from the Boltzmann equation. The dependence of conductivity and Hall conductivity on the magnetic field intensity was investigated. In the case of quantizing magnetic field the expression for the graphene transversal magnetoconductivity taking into account the scattering on the acoustic phonons was derived in the Born approximation. The graphene conductivity dependence on the magnetic field intensity was investigated. The graphene conductivity was shown to have the oscillations when the magnetic field intensity changes. The features of the Shubnikov-de Haas oscillations in graphene superlattice are discussed.
1. Introduction
The development of the microand nanoelectronics requires the search of new materials and structures. Presently the investigators are attracted by the electron features of the graphene (monolayer carbon) which is obtained in the laboratory recently [1]. The heightened interest in the electronic properties of the graphene is related with the following. Firstly experimentally the electron mean free path is shown to have the order of a micrometer in graphene [1]. This fact allows the graphene using for creation of the micrometer devices working in the ballistic regime. The high electrical conductivity of the graphene makes it the prospective material for using in the nanoelectronics along with carbon nanotubes [2]. The samples of the field-effect transistors and number of other electronic devices based on it have already worked out [3,4].
Secondly this material has a number of unusual properties due to it band structure peculiarities [5-7]. Nonparabolicity and non-additivity of the graphene electronic spectrum enable the appearance of a number of the nonlinear kinetic effects in this material [8-11]. Besides near the so-called Dirac points of the Brillouin zone for the gapless modification of the graphene the dispersion law is linear in the absolute value of the quasimomentum which is corresponding to the massless particles [7]. Furthermore this fact allows the graphene using for the verifying of the relativistic effects.
More recently, the electric properties of the graphene superlattice (GSL) are under investigations [12-16].
The theoretical and experimental studies of the influence of the external fields of different configuration on the graphene transport features are held recently [17-25]. The conductivity oscillations in the graphene under the spatially modulated magnetic field are investigated theoretically in [17]. The theory of the electron transport of the charge carriers with Dirac spectrum in the weak magnetic field taking into account the scattering on the charge impurity is built in [18]. In [16-22] the magnetic oscillation effects in the structures based on the graphene are studied. The magnetic field influences on the high frequency conductivity and on the electromagnetic waves absorption of the graphene are investigated in [22-25]. The quantum theory of the transverse magnetoconductivity oscillations (Shubnikov-de Haaz effect) in the twodimentional system with Dirac spectrum are studied in [21].
When the graphene is put on the substrate (SiC for example) then the gap arises (so-called the gap modification of the graphene [26,27]). The electron spectrum of the gap modification of the graphene can be written in the view [10]:
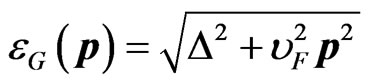 , (1)
, (1)
where  is the quasimomentum,
is the quasimomentum,  is the gap semiwidth,
is the gap semiwidth,  is the velocity on the Fermi surface.
is the velocity on the Fermi surface.
When the graphene sheet is applied upon a periodic substrate, a superlattice (SL) is formed on the graphene surface [28]. The dispersion low of GSL was studied in [28] where the energy of electron motion near the Dirac point along the SL axis was shown to be periodically dependent on the electron quasimomentum in this direction. The electron spectrum of the graphene superlattice was written in the following model view [29]:
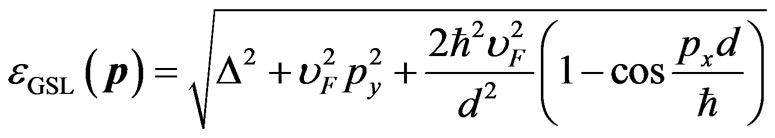 , (2)
, (2)
which is in good agree with dispersion low [28] if the following condition is performed: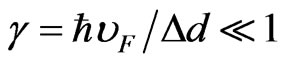 .
.
In this paper the dependence of the graphene gap modification conductivity on the magnetic field intensity was investigated. Moreover the peculiarities of Shubnikov-de Haaz effect in the graphene superlattice were discussed.
Consider the graphene lying in the plane  under the crossed magnetic and electric fields so that the magnetic field intensity
under the crossed magnetic and electric fields so that the magnetic field intensity 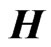 is directed perpendicularly to the graphene plane and the electric field intensity
is directed perpendicularly to the graphene plane and the electric field intensity 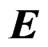 is directed along the axis
is directed along the axis .
.
2. The Nonquantizing Magnetic Field Influence on the Conductivity of the Gap Modification of the Graphene
Consider the case of the nonquantizing magnetic field: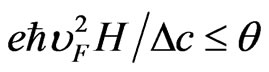 , where
, where 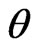 is the electron gas temperature in energy units. Current density arising in graphene under the condition described above is calculated with the following formula:
is the electron gas temperature in energy units. Current density arising in graphene under the condition described above is calculated with the following formula:
 , (3)
, (3)
where 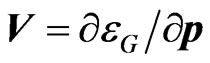 is the electron velocity,
is the electron velocity,  is the nonequilibrium state function which is determined from the Boltzmann equation written in the approximation of the constant relaxation time
is the nonequilibrium state function which is determined from the Boltzmann equation written in the approximation of the constant relaxation time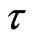 :
:
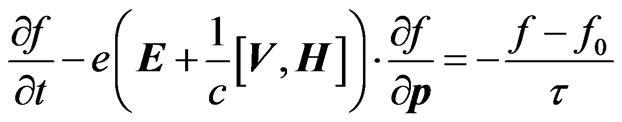 . (4)
. (4)
The solution of the kinetic Equation (4) is the following function:
 , (5)
, (5)
where  is the equilibrium state function. The electron momentum
is the equilibrium state function. The electron momentum 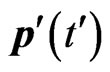 is the solution of the classical equation of motion:
is the solution of the classical equation of motion:
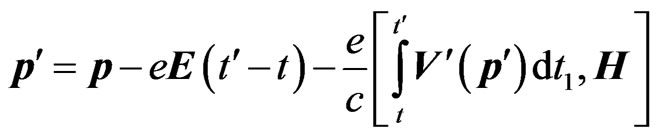 . (6)
. (6)
where 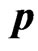 is initial momentum. Solving (6) by the iterations of the small parameter
is initial momentum. Solving (6) by the iterations of the small parameter  we obtain the following expression in linear approximation of the electric field intensity:
we obtain the following expression in linear approximation of the electric field intensity:
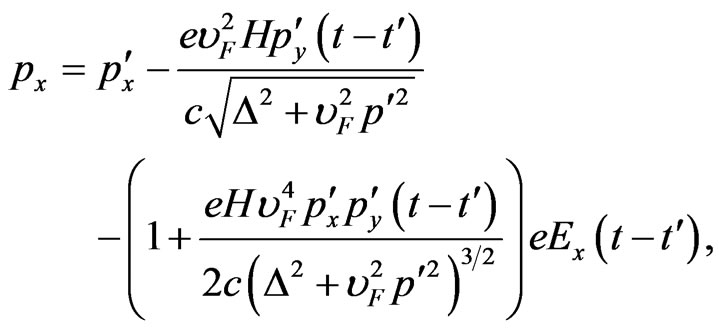 (7)
(7)
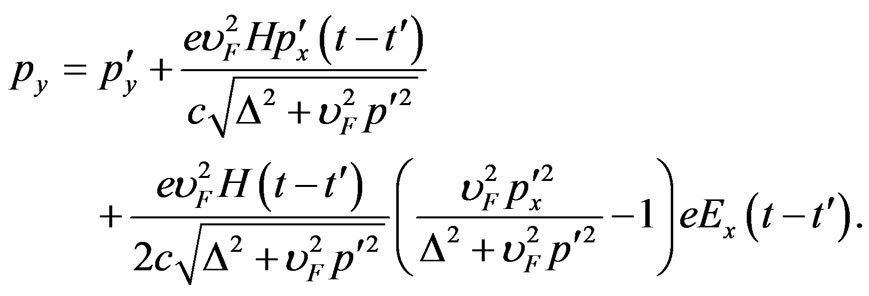 (8)
(8)
Introduce the following denotations:
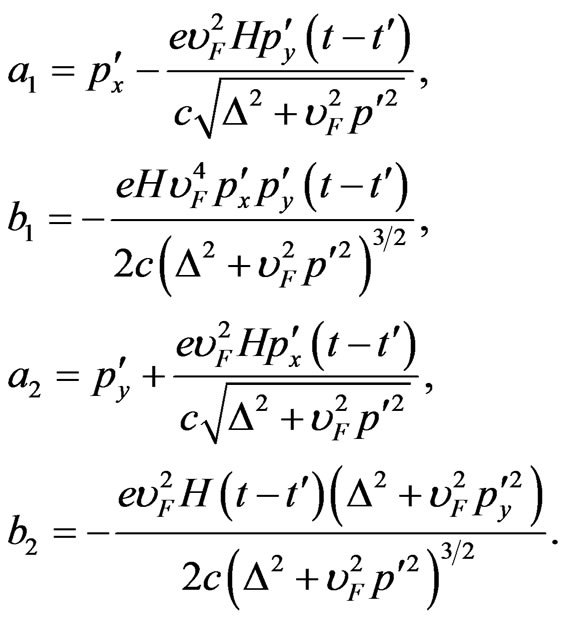 (9)
(9)
Replacing (5) - (8) to (3) and considering that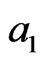 ,
,  ,
,  are the odd functions of
are the odd functions of 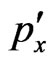 and
and 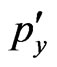 we define the projections of current density in the linear approximation of
we define the projections of current density in the linear approximation of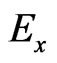 :
:
 (10)
(10)
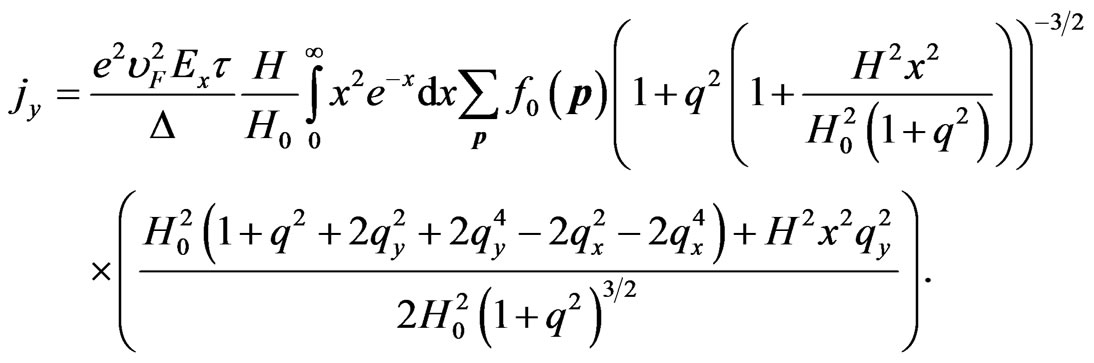 (11)
(11)
In (10) and (11) we introduced dimensionless variables: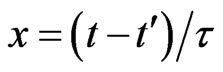 ,
,  and denote
and denote . Choose the equilibrium state function in the view of Boltzmann function:
. Choose the equilibrium state function in the view of Boltzmann function:
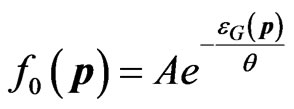 , (12)
, (12)
where  is the constant determined from the normalization condition:
is the constant determined from the normalization condition:
 , (13)
, (13)
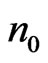 is the surface concentration of the charge carriers. Replace in (10), (11) and (13) the summation by the momentum
is the surface concentration of the charge carriers. Replace in (10), (11) and (13) the summation by the momentum  to the integration in the polar coordinates:
to the integration in the polar coordinates:
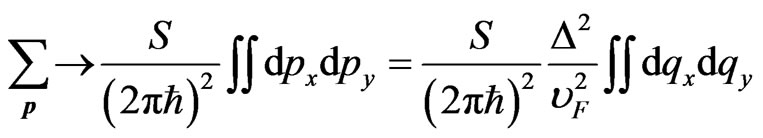 .
.
As a result we obtain the following expressions for the projections of the current density:
 , (14)
, (14)
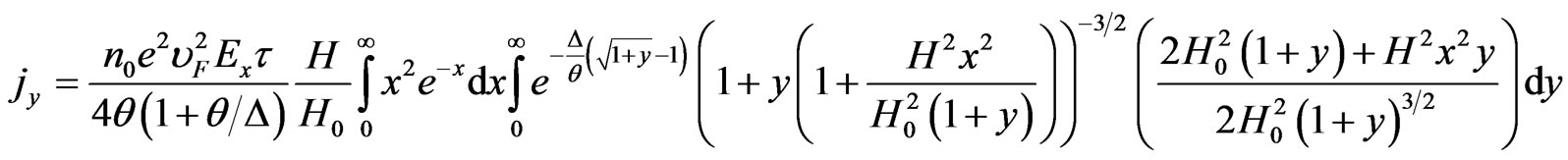 . (15)
. (15)
The components of the conductivity tensor are determined from the formulas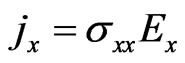 ,
,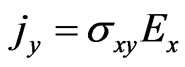 . Therefore the magnitoconductivity of the graphene is equal to:
. Therefore the magnitoconductivity of the graphene is equal to:
 (16)
(16)
Hall conductivity has the view:
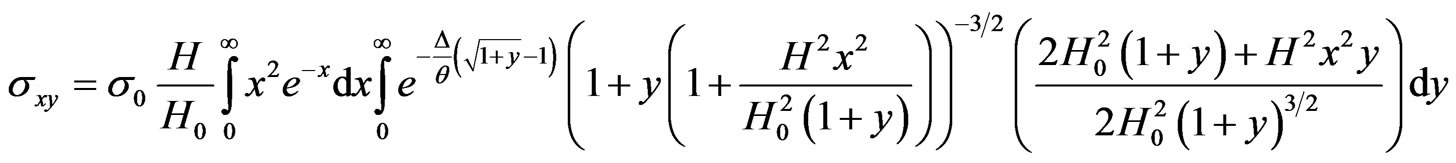 . (17)
. (17)
where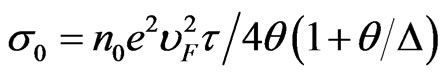 .
.
The conductivity tensor dependence on the magnetic field intensity is investigated numerically. The plots of the conductivity dependence on the magnetic field intensity built with the formulas (16) and (17) for the following values of parameters: 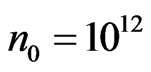 cm–2,
cm–2, 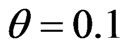 eV,
eV,  s,
s,  cm/s, are shown on the Figure 1. At low temperatures
cm/s, are shown on the Figure 1. At low temperatures  and weak magnetic fields
and weak magnetic fields 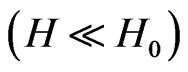 the formulas (16) and (17) can be written approximately in the view:
the formulas (16) and (17) can be written approximately in the view:
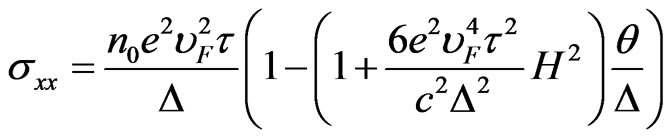 , (18)
, (18)
 . (19)
. (19)

Figure 1. The conductivity tensor dependence on the magnetic field intensity at θ = 0.1 eV and at several values of ∆.
3. The Oscillations of the Transversal Conductivity of the Gap Modification of the Graphene under the Quantizing Magnetic Field
Define the graphen magnetoconductivity in the case of the quantizing magnetic field at law temperatures:  . In [21] where Shubnicov-de Haas effect was studied Landau levels were supposed to have a finite width due to the charge scattering on the lattice inhomogeneity. Herewith the particular scattering mechanism was not considered and broadening of the Landau levels was introduced as a phenomenological parameter. Calculate the transverse manetoconductivity of the gap modification of the graphene taking into account the elastic scattering of the electrons on the acoustic phonons. The wave function envelope
. In [21] where Shubnicov-de Haas effect was studied Landau levels were supposed to have a finite width due to the charge scattering on the lattice inhomogeneity. Herewith the particular scattering mechanism was not considered and broadening of the Landau levels was introduced as a phenomenological parameter. Calculate the transverse manetoconductivity of the gap modification of the graphene taking into account the elastic scattering of the electrons on the acoustic phonons. The wave function envelope  of the electron is determined from the Schrödinger equation with the Hamiltonian
of the electron is determined from the Schrödinger equation with the Hamiltonian 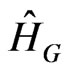 obtained from (1) by replacing
obtained from (1) by replacing 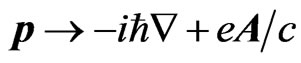 , where vector potential is equal
, where vector potential is equal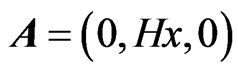 . Acting twice with
. Acting twice with  to the function
to the function  we obtain the following:
we obtain the following:
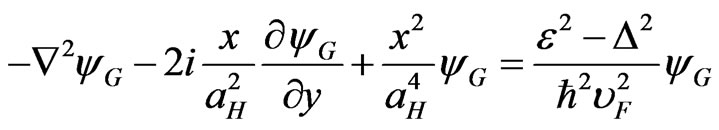 . (20)
. (20)
where 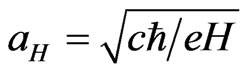 is Larmor radius. The next function is the solution of the Equation (20):
is Larmor radius. The next function is the solution of the Equation (20):
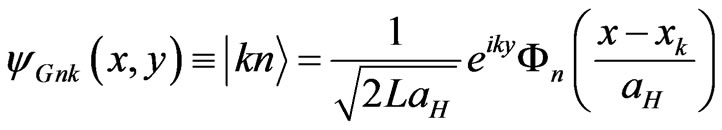 , (21)
, (21)
where  is the oscillator function,
is the oscillator function,  is the projection of the wave vector of the electron on the axis
is the projection of the wave vector of the electron on the axis ,
, 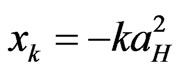 ,
, 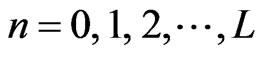 is the linear size of the graphene. Eigen values of the electron energy are as follows:
is the linear size of the graphene. Eigen values of the electron energy are as follows:
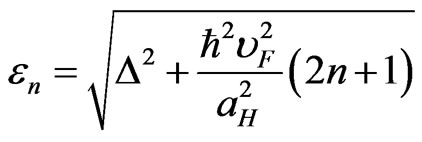 . (22)
. (22)
From the cyclic conditions along the axis :
:  number
number  is followed to take the values:
is followed to take the values:
 ,
,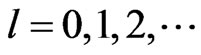 (23)
(23)
To calculate the current density in the graphene under the quantizing magnetic field we use the method developed in [30]. Consider the weak electric field  is applied along the axis
is applied along the axis . Then the components of the current density for the particles ensemble described by a density matrix
. Then the components of the current density for the particles ensemble described by a density matrix  is determined by the formula:
is determined by the formula:
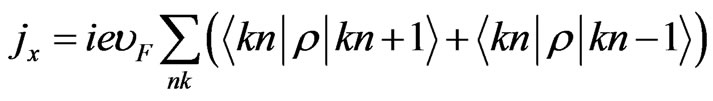 . (24)
. (24)
The total density matrix 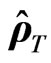 taking into account the transition processes is determined from the equation:
taking into account the transition processes is determined from the equation:
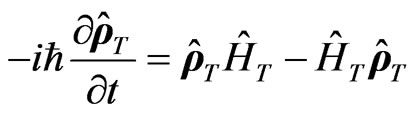 where
where 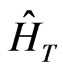 is Hamiltonian taking into account the magnetic field, the electric field and the scattering potential
is Hamiltonian taking into account the magnetic field, the electric field and the scattering potential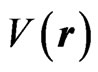 :
:
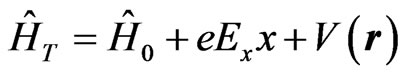 .
.
The stationary density matrix  is the total density matrix after such a long period of time during which all transition processes disappear. In Born approximation in scattering potential
is the total density matrix after such a long period of time during which all transition processes disappear. In Born approximation in scattering potential 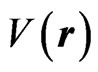 and in linear approximation in the electric field intensity we obtain:
and in linear approximation in the electric field intensity we obtain:
 . (25)
. (25)
After substitution of (25) in (24) and after the some transformations we obtain the following expression for the transversal magnetoconductivity of graphene which coincides with the Titeica formula [30]:
 . (26)
. (26)
Consider the electrons dissipate on the acoustic phonons in graphene. Then the scattering potential can be written in the following view [31]:
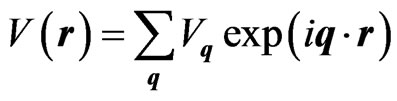 , (27)
, (27)
where ,
, 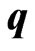 is the wave vector of the acoustic phonons,
is the wave vector of the acoustic phonons,  is the deformation potential,
is the deformation potential, 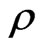 is the surface density of graphene,
is the surface density of graphene,  is the sound velocity in graphene,
is the sound velocity in graphene, 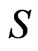 is the sample area. After substitution of (27) in (26) we obtain:
is the sample area. After substitution of (27) in (26) we obtain:
 . (28)
. (28)
From (28) the conductivity is shown to be different from zero in the case when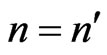 . The absolute value of the matrix element included in the formula (28) is equal:
. The absolute value of the matrix element included in the formula (28) is equal:
 , (29)
, (29)
where 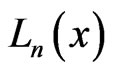 is the Laguerre polynomial. After substitution of (29) in (28) and after calculation of the sum by
is the Laguerre polynomial. After substitution of (29) in (28) and after calculation of the sum by 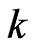 and
and 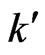 we obtain:
we obtain:
 , (30)
, (30)
where
 . (31)
. (31)
If the conductivity oscillations are small in compared with the non-oscillatory part then it can be taken into account in one of the sum (30) only. At low temperatures electron gas is degenerate. Hence Fermi-Dirac state function is needed to use as the function 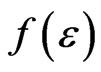 in the formula (30). Using the Poisson formula [32] we transform (30) to the following view:
in the formula (30). Using the Poisson formula [32] we transform (30) to the following view:
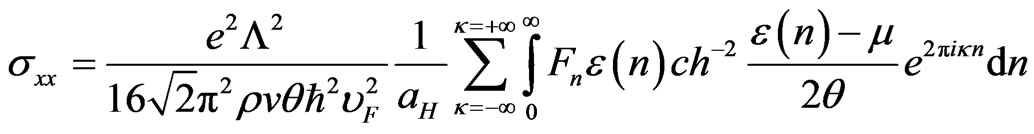 , (32)
, (32)
where  is the chemical potential,
is the chemical potential,  is the electron gas temperature. The factor
is the electron gas temperature. The factor 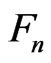 represents a slowly varying function of
represents a slowly varying function of  in compared with the oscillatory part in the integrand of (32) and its numerical value has the order of unity. When
in compared with the oscillatory part in the integrand of (32) and its numerical value has the order of unity. When  the expression (32) can be written approximately:
the expression (32) can be written approximately:
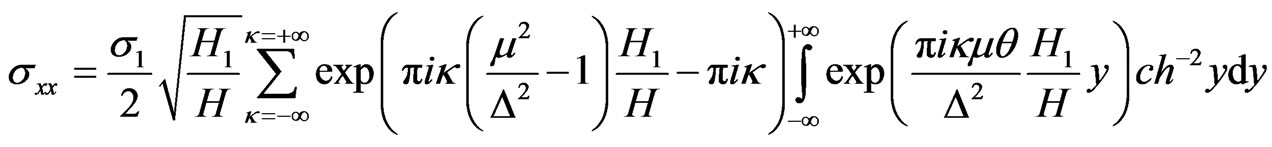 , (33)
, (33)
where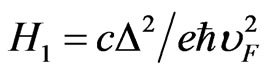 ,
,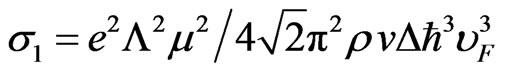 . Since
. Since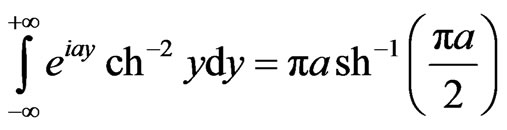 , so the formula (33) can be rewritten as:
, so the formula (33) can be rewritten as:
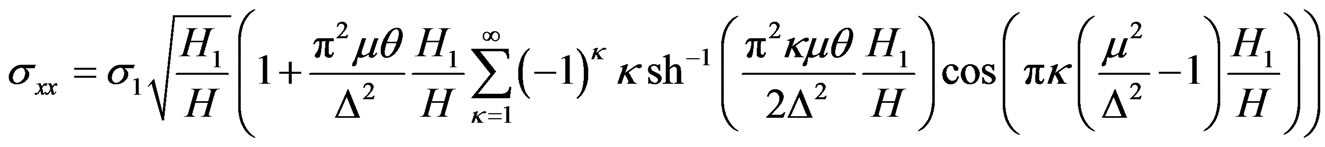 , (34)
, (34)
On the Figure 2 the graphene conductivity dependences on the magnetic field intensity constructed by the formula (34) are shown.
4. The Shubnikov-de Haaz Effect in the Superlattice Based on the Graphene
To calculate conductivity of GSL we have to define the energy of electron in the GSL under the quantizing magnetic field. The wave function envelope  of the electron is determined from the Schrödinger equation with the Hamiltonian
of the electron is determined from the Schrödinger equation with the Hamiltonian 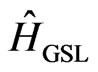 obtained from (2) by replacing
obtained from (2) by replacing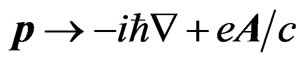 , where vector potential is chosen in form
, where vector potential is chosen in form . Acting twice with
. Acting twice with 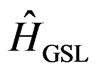 to the wave function
to the wave function 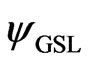 we obtain the following equation:
we obtain the following equation:
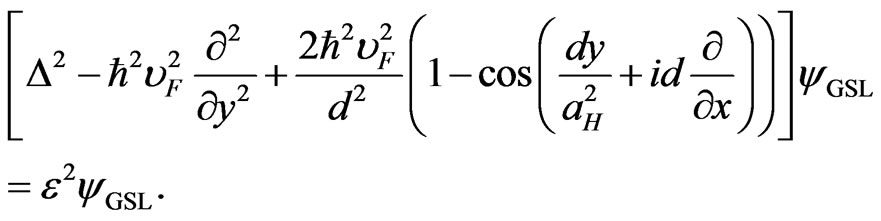 (35)
(35)
The solution of (35) is found in the view [33]:
 . (36)
. (36)
Replacing (36) in (35) we have Mathieu equation:
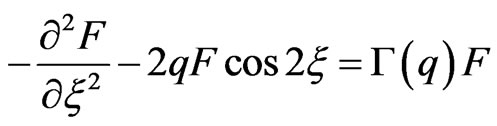 , (37)
, (37)
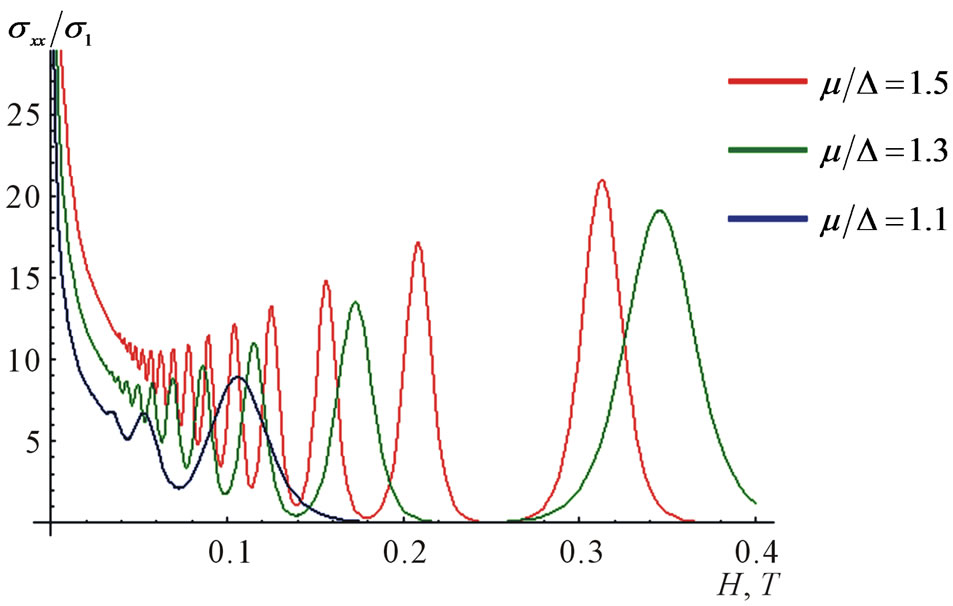
Figure 2. Graphene transversal conductivity dependence on the magnetic field intensity at μ/∆ = 1.1, θ/∆ = 0.01 and at several values of μ/θ.
where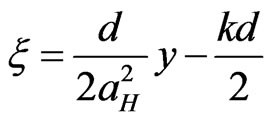 ,
, 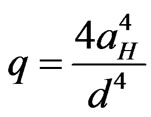 ,
,
 . If
. If  then following expression for the energy is obtained [33]:
then following expression for the energy is obtained [33]:
 , (38)
, (38)
where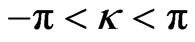 ,
,  functions
functions 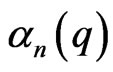 and
and  have the view:
have the view:
 , (39)
, (39)
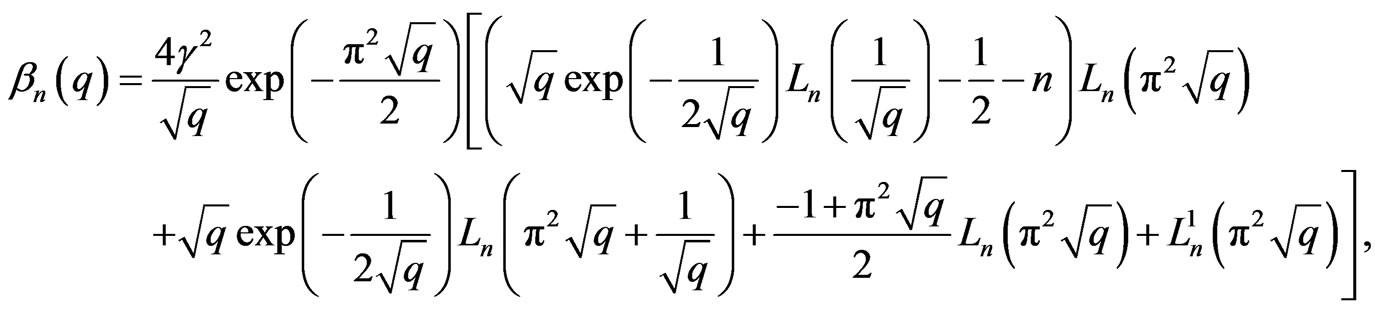 (40)
(40)
where 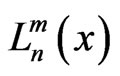 is adjoint Laguerre polynomial.
is adjoint Laguerre polynomial.
The magnetoconductivity of GSL can be estimated using formula (30) and making there the following changes:
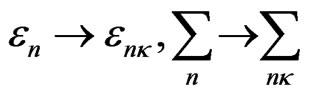
Thus we have:
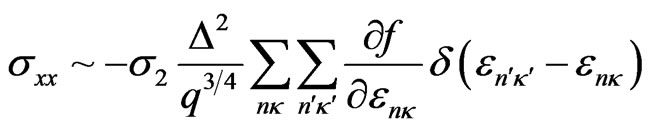 , (41)
, (41)
where ,
,  is Fermi-Dirac state function. After some transformations we have:
is Fermi-Dirac state function. After some transformations we have:
 . (42)
. (42)
If temperature is equal to zero then:
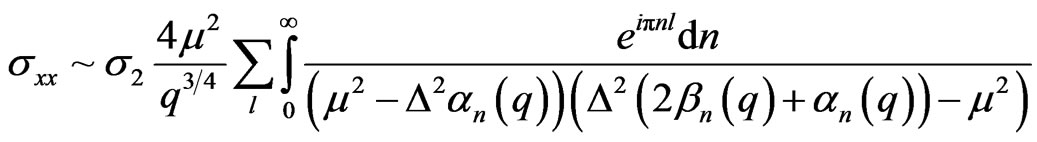 . (43)
. (43)
5. Conclusions
In the case of weak magnetic fields when the quantizing is not manifested the graphene magnetoconductivity 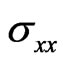 is seen from the Figure 1 and from the formula (18) to decrease when the magnetic field intensity increases. It is related with the Larmour radius decreases and as a consequence with the electron localization increases. The formulas (14) and (15) should be noted to cease to be valid for intense magnetic fields because it was derived from the motion Equation (6) which is solved by the iterations with the parameter
is seen from the Figure 1 and from the formula (18) to decrease when the magnetic field intensity increases. It is related with the Larmour radius decreases and as a consequence with the electron localization increases. The formulas (14) and (15) should be noted to cease to be valid for intense magnetic fields because it was derived from the motion Equation (6) which is solved by the iterations with the parameter  in turn. Such method is justified for small
in turn. Such method is justified for small .
.
In strong quantizing magnetic fields for graphene as well as for degenerate bulk semiconductors there are oscillations of the transverse magnetoconductivity due to the nonmonotonic dependence of the density of states on the energy and are periodic in the inverse magnetic field. However the oscillation period is not proportional to  than that of materials with a quadratic dispersion law and has a more complicated dependence on
than that of materials with a quadratic dispersion law and has a more complicated dependence on . For the gap modification of graphene in the case when
. For the gap modification of graphene in the case when 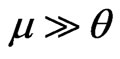 the oscillation period is seen from the formulas (34) to be proportional to the difference
the oscillation period is seen from the formulas (34) to be proportional to the difference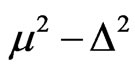 . Thus the values
. Thus the values  changing enable to control the magnetoconductivity oscillation period. The same result was obtained in [21]. However, it should be mentioned the expression (34) for the conductivity does not include the phenomenological Landau level width [21].
changing enable to control the magnetoconductivity oscillation period. The same result was obtained in [21]. However, it should be mentioned the expression (34) for the conductivity does not include the phenomenological Landau level width [21].
In GSL the dependence of the magnetic oscillations on 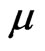 is seen from the formula (43) to be more difficult than that of graphene and bulk semiconductor. Obtaining an explicit view of such dependence is the subject of further research.
is seen from the formula (43) to be more difficult than that of graphene and bulk semiconductor. Obtaining an explicit view of such dependence is the subject of further research.
For strong magnetic field  the nonoscillatory part is seen from the formula (34) to decrease when the magnetic field intensity decreases as
the nonoscillatory part is seen from the formula (34) to decrease when the magnetic field intensity decreases as 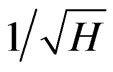 unlike the materials with a quadratic dispersion law where
unlike the materials with a quadratic dispersion law where  in strong magnetic fields [30]. The same result
in strong magnetic fields [30]. The same result  is obtained at absolute zero of temperature whereas formula (16) gives the dependence
is obtained at absolute zero of temperature whereas formula (16) gives the dependence  the intense magnetic fields. Such difference is explained by the formula (16) ceases to be true when intensity H increases.
the intense magnetic fields. Such difference is explained by the formula (16) ceases to be true when intensity H increases.
6. Acknowledgements
The work was supported by the RFBR grant No. 10-02- 97001-р_povolgie_а and was performed within the program “The development of science potential of the High Education”.
REFERENCES
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, “Electric Field Effect in Atomically Thin Carbon Films,” Science, Vol. 306, No. 5696, 2004, pp. 666-669. doi:10.1126/science.1102896
- J. Milton Pereira Jr., P. Vasilopoulos and F. M. Peeters, “Graphene-Based Resonant-Tunneling Structures,” Applied Physics Letters, Vol. 90, No. 13, 2007, pp. 132122- 132125. doi:10.1063/1.2717092
- Z. Chen, Y.-M. Lin, M. J. Rooks and P. Avouris, “Graphene Nano-Ribbon Electronics,” Physica E, Vol. 40, No. 2, 2007, pp. 228-234. doi:10.1016/j.physe.2007.06.020
- Y. Q. Wu, P. D. Ye, M. A. Capano, Y. Xuan, Y. Sui, M. Qi, J. A. Cooper, T. Shen, D. Pandey, G. Prakash and R. Reifenberger, “Top-Gated Graphene Field-Effect-Transistors Formed by Decomposition of SiC,” Applied Physics Letters, Vol. 92, No. 9, 2008, Article ID: 092102. doi:10.1063/1.2889959
- A. H. C. Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, “The Electronic Properties of Graphene,” Reviews of Modern Physics, Vol. 81, No. 1, 2009, pp. 109-162. doi:10.1103/RevModPhys.81.109
- S. Reich, J. Maultzsch, C. Thomsen and P. Ordejon, “Tight-Binding Description of Graphene,” Physical Review B, Vol. 66, No. 3, 2002, pp. 035412-035417.
- P. R. Wallace, “The Band Theory of Graphite,” Physical Review, Vol. 71, No. 9, 1947, pp. 622-634. doi:10.1103/PhysRev.71.622
- S. A. Mikhailov, “Nonlinear Cyclotron Resonance of a Massless Quasiparticle in Graphene,” Physical Review B, Vol. 79, No. 24, 2009, pp. 241309-241313. doi:10.1103/PhysRevB.79.241309
- D. V. Zav’yalov, S. V. Kryuchkov and E. V. Marchuk, “On the Possibility of Transverse Current Rectification in Graphene,” Technical Physics Letters, Vol. 34, No. 11, 2008, pp. 915-917. doi:10.1134/S1063785008110047 D. V. Zav’yalov, V. I. Konchenkov and S. V. Kryuchkov, “Mutual Rectification of Alternating Currents Induced by Electromagnetic Waves in Graphene,” Physics of the Solid State, Vol. 51, No. 10, 2009, pp. 2157-2160. doi:10.1134/S1063783409100278 D. V. Zav’yalov, V. I. Konchenkov and S. V. Kryuchkov, “Influence of a Magnetic Field on the Mutual Rectification of Alternating Currents Induced by Electromagnetic Waves in Graphene,” Physics of the Solid State, Vol. 52, No. 4, 2010, pp. 800-804. doi:10.1134/S1063783410040219 L. A. Chernozatonskii, P. B. Sorokin, E. E. Belova, I. Bryuning and A. S. Fedorov, “Metal-Semiconductor (Semimetal) Superlattices on a Graphite Sheet with Vacancies,” JETP Letters, Vol. 84, No. 3, 2006, pp. 115-118. doi:10.1134/S0021364006150033 L. A. Chernozatonskii, P. B. Sorokin, E. E. Belova, I. Bryuning and A. S. Fedorov, “Superlattices Consisting of ‘Lines’ of Adsorbed Hydrogen Atom Pairs on Graphene,” JETP Letters, Vol. 85, No. 1, 2007, pp. 77-81. doi:10.1134/S002136400701016X
- F. Guinea, M. I. Katsnelson and M. A. H. Vozmediano, “Midgap States and Charge Inhomogeneities in Corrugated Graphene,” Physical Review, Vol. 77, No. 7, 2008, pp. 075422-075429. doi:10.1103/PhysRevB.77.075422
- H. Sevincli, M. Topsakal and S. Ciraci, “Superlattice Structures of Graphene-Based Armchair Nanoribbons,” Physical Review, Vol. 78, No. 24, 2008, pp. 245402-245409. doi:10.1103/PhysRevB.78.245402
- M. R. Masir, P. Vasilopulos and F. M. Peeters, “Tunneling, Conductance, and Wavevector Filtering through Magnetic Barriers in Bilayer Graphene,” Physical Review, Vol. 79, No. 3, 2009, Article ID: 035409. doi:10.1103/PhysRevB.79.035409
- M. Tahir and K. Sabeeh, “Quantum Transport of Dirac Electrons in Graphene in the Presence of a Spatially Modulated Magnetic Field,” Physical Review B, Vol. 77, No. 19, 2008, pp. 195421-195426. doi:10.1103/PhysRevB.77.195421
- X.-Z. Yan and C. S. Ting, “Magnetoconductivity of Dirac Fermions in Graphene under Charged Impurity Scatterings,” New Journal of Physics, Vol. 11, No. 9, 2009, Article ID: 093026. doi:10.1088/1367-2630/11/9/093026
- T. Shen, Y. Q. Wu, M. A. Capano, L. P. Rokhinson, L. W. Engel and P. D. Ye, “Magnetoconductance Oscillations in Graphene Antidot Arrays,” Applied Physics Letters, Vol. 93, No. 12, 2008, pp. 122102-122110. doi:10.1063/1.2988725
- J. Jobst, D. Waldmann, F. Speck, R. Hirner, D. K. Maude, T. Seyller and H. B. Weber, “Quantum Oscillations and Quantum Hall Effect in Epitaxial Graphene,” Physical Review B, Vol. 81, 2010, pp. 195434-195440. doi:10.1103/PhysRevB.81.195434
- S. G. Sharapov and V. P. Gusynin, “Magnetic Oscillations in Planar Systems with the Dirac-Like Spectrum of Quasiparticle Excitations II: Transport Properties,” Physical Review B, Vol. 71, No. 12, 2005, pp. 125124-125132.
- K. Y. Bliokh, “Weak Antilocalization of Ultrarelativistic Fermions,” Physics Letters A, Vol. 344, No. 2-4, 2005, pp. 127-130. doi:10.1016/j.physleta.2005.06.062
- V. P. Gusynin, S. G. Sharapov and J. P. Carbotte, “Dirac Quasiparticles in the Magneto-Optical Response of Graphene,” Journal of Physics: Condensed Matter, Vol. 19, 2007, Article ID: 026222. doi:10.1088/0953-8984/19/2/026222
- N. M. R. Peres, F. Guinea and A. H. C. Neto, “Electronic Properties of Disordered Two-Dimensional Carbon,” Physical Review B, Vol. 73, 2006, pp. 125411-125434.
- V. P. Gusynin and S. G. Sharapov, “Transport of Dirac Quasiparticles in Graphene: Hall and Optical Conductivities,” Physical Review B, Vol. 73, No. 24, 2006, pp. 245411- 245429. doi:10.1103/PhysRevB.73.245411
- S. Y. Zhou, G.-H. Gweon, A. V. Fedorov, P. N. First, W. A. de Heer, D.-H. Lee, F. Guinea, A. H. C. Neto and A. Lanzara, “Substrate-Induced Band Gap Opening in Epitaxial Graphene,” Nature Materials, Vol. 6, No. 10, 2007, pp. 770-775. doi:10.1038/nmat2003
- A. Mattausch and O. Pankratov, “Ab Initio Study of Graphene on SiC,” Physical Review Letters, Vol. 99, No. 7, 2007, Article ID: 076802. doi:10.1103/PhysRevLett.99.076802 P. V. Ratnikov, “Superlattice Based on Graphene on a Strip Substrate,” JETP Letters, Vol. 90, No. 6, 2009, pp. 469-474. doi:10.1134/S0021364009180143
- S. V. Kryuchkov, E. I. Kuhar and V. A. Yakovenko, “Effect of the Mutual Rectification of Two Electromagnetic Waves with Perpendicular Polarization Planes in a Superlattice Based on Graphene,” Bulletin of the Russian Academy of Sciences: Physics, Vol. 74, No. 12, 2010, pp. 1679-1681. doi:10.3103/S1062873810120129
- E. Adams and T. Holstein, “Quantum Theory of Transversal Galvanic-Magnetic Phenomena,” Journal of Physics and Chemistry of Solids, Vol. 10, No. 4, 1959, pp. 254-297. doi:10.1016/0022-3697(59)90002-2
- E. H. Hwang and S. D. Sarma, “Dielectric Function, Screening, and Plasmons in Two-Dimensional Graphene,” Physical Review B, Vol. 75, No. 20, 2007, pp. 205418-205424.
- L. D. Landau and E. M. Lifshits, “Physical Kinetics,” Physical and Mathematical Literature, Moscow, 2001, pp. 462-466.
- A. G. Zhylich, “The Energy Spectrum of Electrons and Optical Properties of the Superlattice in a Magnetic Field,” Physics of the Solid State, Vol. 36, No. 3, 1994, pp. 792- 804.

