Applied Mathematics
Vol.07 No.09(2016), Article ID:66857,14 pages
10.4236/am.2016.79085
Idempotent Elements of the Semigroups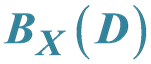 
Defined by Semilattices of the Class 
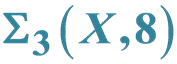When 
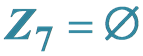
G. Tavdgiridze, Ya. Diasamidze, O. Givradze
Department of Mathematics, Faculty of Physics, Mathematics and Computer Sciences, Shota Rustaveli Batumi State University, Batumi, Georgia
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
Received 18 March 2016; accepted 24 May 2016; published 27 May 2016
ABSTRACT
In this paper, complete semigroup binary relation is defined by semilattices of the class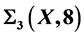
. We give a full description of idempotent elements of given semigroup. For the case where X is a finite set and
, we derive formulas by calculating the numbers of idempotent elements of the respective semigroup.
Keywords:
Semilattice, Semigroup, Binary Relation, Idempotent Element
1. Introduction
Definition 1.1. Let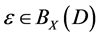
. If 
or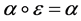 
for any
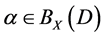, then 
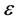is called an idempotent element or called right unit of the semigroup 
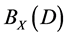respectively.
Definition 1.2. We say that a complete X-semilattice of unions D is an XI-semilattice of unions if it satisfies the following two conditions:
a) 
for any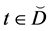
;
b) 
for any nonempty element Z of D (see [1] , Definition 1.14.2 or see [2] , Definition 1.14.2).
Definition 1.3. Let D be an arbitrary complete X-semilattice of unions,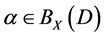
. If
then it is obvious that any binary relation 
of a semigroup 
can always be written in the form
the sequel, such a representation of a binary relation 
will be called quasinormal.
Note that for a quasinormal representation of a binary relation
, not all sets 
can be different from an empty set. But for this representation the following conditions are always fulfilled:
a)
, for any 
and
;
b) 
(see [1] , Definition 1.11 or see [2] , Definition 1.11).
Theorem 1.1. Let D, 
, 
and I denote respectively the complete X-semilattice of unions D, the set of all XI-subsemilattices of the semilattice D, the set of all right units of the semigroup 
and the set of all idempotents of the semigroup
. Then for the sets 
and I the following statements are true:
a) if 
and
, then
1) 
for any elements 
and 
of the set 
that satisfy the condition
;
2)
;
3) the equality 
is fulfilled for the finite set X.
b) if
, then
1) 
for any elements 
and 
of the set 
that satisfy the condition
;
2)
;
3) the equality 
is fulfilled for the finite set X (see [1] [2] Theorem 6.2.3).
2. Results
Lemma 2.1. Let 
and
. Then the following sets are all XI-subsemilattices of the given semilattice D:
1) 
(see diagram 1 of the Figure 1);
2) 
(see diagram 2 of the Figure 1);
3) 
(see di-
agram 3 of the Figure 1);
4) 
(see diagram
4 of the Figure 1);
5) 
(see diagram
5 of the Figure 1);
6) 
(see diagram 6 of the Figure 1);
7) 
(see diagram 7 of the Figure 1);
8) 
(see diagram 8 of the Figure 1);
9) 
(see diagram 9 of the Figure 1);
10) 
(see diagram 10 of the Figure 1);
11) 
(see diagram 11 of the Figure 1);
12) 
(see diagram 12 of the Figure 1);
13) 
(see diagram 13 of the Figure 1);
14) 
(see diagram 14 of the Figure 1);
15) 
(see diagram 15 of the Figure 1);
16) 
(see diagram 16 of the Figure 1);
Proof: This lemma immediately follows from the ( [3] , lemma 2.4).
Lemma is proved.
We denote the following semitattices 
as follows:
1)
, where
;
2) 
where
;
3) 
where
;
4) 
where
;
5) 
where
;
6) 
where
, 
, 
, 
,
;
7) 
where, 
, 
, 
,
;
8) 
where
;
9) 
10) 
where
, 
, 
, 
,
;
11) 
where
;
12) 
where, 
, 
, 
, 
,
, 
,
;
13) 
14) 
15) 
16) 
Theorem 2.1. Let
, 
and
. Binary relation 
is an idempotent relation of the semigroup 
iff binary relation 
satisfies only one conditions of the following conditions:
1)
;
2)
, where
, 
, and satisfies the conditions:
,
;
3)
, where
, 
, and satisfies the conditions:
, 
, 
,
;
4)
, where
, 
, and satisfies the conditions:
, 
, 
, 
, 
,
;
Figure 1. All Diagrams XI-subsemilattices of the semilattice D.
5)
, where
,
, and satisfies the conditions:
, 
, 
,
, 
, 
, 
,
;
6)
, where
, 
,
and satisfies the conditions:
, 
, 
,
;
7)
, where, 
,
, 
, 
, 
and satisfies the conditions: 
, 
, 
, 
, 
,
;
8)
, where
,
and satisfies the conditions:
, 
, 
, 
, 
, 
, 
, 
, 
;
9)
, where
, 
,
, 
, 
and satisfies the conditions:
, 
,
, 
, 
, 
, 
,
;
10)
, where, 
,
, 
, 
and satisfies the conditions:
, 
,
, 
,
;
11)
, where
,
and satisfies the conditions:, 
, 
, 
, 
, 
,
;
12)
,
where
, 
, 
, 
, 
,
and satisfies the conditions:, 
, 
,
, 
,
;
13)
, where
,
, 
, 
, 
, 
, 
, 
and satisfies the conditions:
, 
, 
, 
, 
, 
, 
, 
,
;
14)
, where, 
,
and satisfies the conditions:
, 
,
, 
, 
, 
,
;
15)
, where
and satisfies the conditions:
, 
,
, 
, 
, 
,
,
;
16)
,
where, 
and satisfies the conditions:
, 
,
, 
, 
, 
, 
,
,
.
Proof. This Theorem immediately follows from the ( [3] , Theorem 2.1]).
Theorem is proved.
Lemma 2.2. If X be a finite set, then the following equalities are true:
a)
;
b)
;
c)
;
d)
;
e)
;
f)
;
g)
;
h) 
i) 
j)
;
k)
;
l)
;
m) 
n) 
o)
;
p)
.
Proof. This lemma immediately follows from the ( [3] , lemma 2.6).
Lemma is proved.
Lemma 2.3. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
.
Proof. By definition of the given semilattice D we have
.
If the following equalities are hold
,
then
.
[See Theorem 1.1] Of this equality we have:
.
[See statement a) of the Lemma 2.2.]
Lemma 2.4. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
if
.
Then
.
[See Theorem 1.1] Of this equality we have:
[See statement b) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.5. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
If
Then
[See Theorem 1.1]. Of this equality we have:
[See statement c) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.6. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
If
Then
[See Theorem 1.1] Of this equality we have:
[See statement d) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.7. Let 
and
.If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
If
Then
[See Theorem 1.1] Of this equality we have:
[See statement e) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.8. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
[See Theorem 1.1] Of this equality we have:
[See statement f) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.9. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
If
[See Theorem 1.1] Of this equality we have:
[See statement g) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.10. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
If
[See Theorem 1.1] Of this equality we have:
[See statement h) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.11. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
.
If the following equality is hold 
then
.
[See Theorem 1.1] Of this equality we have:
[See statement i) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.12. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice 
we have
If
[See Theorem 1.1] Of this equality we have:
[See statement j) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.13. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
If
[See Theorem 1.1] Of this equality we have:
[See statement k) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.14. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
[See Theorem 1.1] Of this equality we have:
[See statement l) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.15. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
. If the following
equality is hold 
then
.
[See Theorem 1.1] Of this equality we have:
[See statement m) of the Lemma 2.2.]
Lemma is proved.
Lemma 2.16. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
. If the following
equality is hold 
then
.
[See Theorem 1.1] Of this equality we have:
[See statement n) of the Lemma 2.2).]
Lemma is proved.
Lemma 2.17. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. By definition of the given semilattice D we have
. If the following
equality is hold 
then
.
[See Theorem 1.1] Of this equality we have:
[See statement o) of the Lemma 2.2).]
Lemma is proved.
Lemma 2.18. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
.
Proof. By definition of the given semilattice D we have
. If the fol-
lowing equality is hold 
then
.
[See Theorem 1.1] Of this equality we have:
.
[See statement p) of the Lemma 2.2).]
Lemma is proved.
Theorem 2.2. Let 
and
. If X is a finite set, then the number 
may be calculated by the formula
Proof. This Theorem immediately follows from the Theorem 2.1.
Theorem is proved.
Example 2.1. Let
, 
, 
, 
, 
, 
, 
, 
, 
, 
Cite this paper
G. Tavdgiridze,Ya. Diasamidze,O. Givradze, (2016) Idempotent Elements of the Semigroups BX(D) Defined by Semilattices of the Class ∑3 (X,8) When Z7=Ø. Applied Mathematics,07,953-966. doi: 10.4236/am.2016.79085
References
- 1. Diasamidze, Ya. and Makharadze, Sh. (2013) Complete Semigroups of Binary Relations. Kriter, Turkey.
- 2. Diasamidze, Ya. and Makharadze, Sh. (2010) Complete Semigroups of Binary Relations. Sputnik+, Moscow. (In Russian)
- 3. Diasamidze, Ya., Givradze, O. and Tavdgiridze, G. (2016) Idempotent Elements of the Semigroups Bx(D) Defined by Semilattices of the Class ∑3(X,8) When Z7≠Ø. Applied Mathematics, 7, 193-218.
http://dx.doi.org/10.4236/am.2016.73019