Received 4 January 2016; accepted 26 February 2016; published 29 February 2016

ABSTRACT

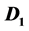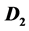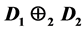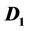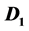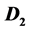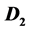The 2-sum of two digraphs and, denoted, is the digraph obtained from the disjoint union of and by identifying an arc in with an arc in. A digraph D is supereulerian if D contains a spanning eulerian subdigraph. It has been noted that the 2-sum of two supereulerian (or even hamiltonian) digraphs may not be supereulerian. We obtain several sufficient conditions on and for to be supereulerian. In particular, we show that if and are symmetrically connected or partially symmetric, then 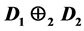is supereulerian.

Keywords:

Supereulerian, Digraph 2-Sums, Arc-Strong-Connectivity, Hamiltonian-Connected Digraphs

1. Introduction

We consider finite graphs and digraphs, and undefined terms and notations will follow [1] for graphs and [2] for digraphs. Throughout this paper, the notation 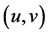denotes an arc oriented from u to v. A digraph D is strict if it contains no parallel arcs nor loops; and is symmetric if for any vertices u, 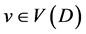, if, then. If two arcs of D have a common vertex, we say that these two arcs are adjacent in D. A directed path in a digraph D from a vertex u to a vertex v is called a -dipath. To emphasize the distinction between graphs and digraphs, a directed cycle or path in a digraph is often referred as a dicycle or dipath. A dipath P is a hamiltonian dipath if. A digraph D is hamiltonian if D contains a hamiltonian dicycle. An -hamiltonian dipath is a hamiltonian dipath from x to y. A digraph D is hamiltonian-connected if D has an -hamiltonian dipath for every choice of distinct vertices.

As in [2] , denotes the arc-strong-connectivity of D. A digraph D is strong if and only if. For, we define

For a subset, the subdigraph arc-induced by is the digraph, where is the set of vertices in V which are incident with at least one arc in.

Let

When, we write and. Let and denote the out-neighbourhood and in-neighbourhood of v in D, respectively. Vertices in, are called the out-neighbours, in-neighbours of v. Thus for a digraph D and an integer,

(1)

Boesch, Suffel, and Tindell [3] in 1977 proposed the supereulerian problem, which seeks to characterize graphs that have spanning eulerian subgraphs. They indicated that this problem would be very difficult. Pulleyblank [4] later in 1979 proved that determining whether a graph is supereulerian, even within planar graphs, is NP- complete. Catlin [5] in 1992 presented the first survey on supereulerian graphs. Chen et al. [6] surveyed the reduction method associated with the supereulerian problem and their applications. An updated survey presenting the more recent developments can be found in [7] .

It is natural to consider the supereulerian problem in digraphs. A digraph D is eulerian if it contains a closed ditrail W such that, or, equivalently, if D is strong and for any,. A digraph D is supereulerian if D contains a closed ditrail W such that, or, equivalently, if D contains a spanning eulerian subdigraph. Some recent developments on supereulerian digraphs are given in [8] -[12] .

A central problem is to determine or characterize supereulerian digraphs. In Section 2, the 2-sum of two digraphs and is defined, and some basic properties of 2-sums are discussed. We will observe that a 2-sum of two supereulerian (or even hamiltonian) digraphs may not be supereulerian. Thus it is natural to seek sufficient conditions on and for the 2-sum of and to be supereulerian. In the last section, we will present several sufficient conditions for supereulerian 2-sums of digraphs. In particular, we show that if and are either symmetrically connected or partially symmetric (to be defined in Section 3), then is supereulerian.

2. The 2-Sums of Digraphs

The definition and some elementary properties of the 2-sums of digraphs are presented in this section. A digraph is nontrivial if it contains at least one arc. Throughout this section, all digraphs are assumed to be nontrivial.

Definition 2.1 Let and be two vertex disjoint digraphs, and let and be two distinguished arcs. The 2-sum of and with base arcs and is obtained from the union of and by identifying with and with, respectively. When the arcs and are not emphasized or is understood from the context, we often use for.

Lemma 1 Let and be two vertex disjoint strong digraphs. Then

Proof. Let be an integer such that, and let. We shall show that. By (1), there exists a proper nonempty vertex subset such that. Let. We argue by contradiction and assume that.

By Definition 2.1, we have and in. If and, we obtain that and, then and. It follows by (1) that, contrary to the assumption that. Similarly, if and, then and, hence a contradiction to the assumption that is obtained from.

Thus, we may assume that and. Let. Then is a proper nonempty subset of, and. It follows by (1) that contrary to the assumption that.

Example 2.1 The converse of Lemma 1 may not always stand, as indicated by the example below, depicted in Figure 1. Let and. Let

and

. Let and.

Then, it is routine to verify that. While is strong, the digraph contains a vertex

with, and so.

Lemma 2 A digraph D is not supereulerian if for some integer, has vertex disjoint subsets satisfying both of the following:

i)

ii).

Proof. By contradiction, we assume that both i) and ii) hold and D is supereulerian. Let S be a spanning eulerian subdigraph of D, then and. Since S is eulerian, for any subset, it follows that. Thus, by ii), we conclude that

(2)

By i) and by (2), there must be a with such that, contrary to the assumption that.

Lemma 2 can be applied to find examples of hamiltonian digraphs whose 2-sum is not supereulerian, as shown in Example 2.2 below.

Example 2.2 Let be integers and and be two vertex disjoint dicycles with length and, respectively. We claim that is not supereulerian. To justify this claim, we denote, and. Without loss of generality, we assume that and, and. Let and be subdigraphs of with, and, respectively. By Lemma 2, we conclude that is not supereulerian (see Figure 2).

3. Sufficient Conditions for Supereulerian 2-Sums of Digraphs

In this section, we will show several sufficient conditions on and to assure that the 2-sum

is supereulerian.

Proposition 1 Let and be two vertex disjoint supereulerian digraphs with and, and let denote. Each of the following holds.

i) For some, if has a spanning eulerian subdigraph such that, then is supereulerian.

ii) If for some, is hamiltonian-connected, then is supereulerian.

Proof. i) Since and are supereulerian digraphs, and are strongly connected, and so by Lemma 1, is also strongly connected. Without loss of generality, we assume that and has a spanning eulerian subdigraph such that. Since is supereulerian, we can pick a spanning eulerian subdigraph in. Then and. It follows that is a spanning eulerian subdigraph in.

ii) Without loss of generality, we assume that and is hamiltonian-connected, and so has a -hamiltonian dipath and a -hamiltonian dipath. Since is supereulerian, contains a spanning eulerian subdigraph. Define

As in any case, S is strongly connected and every vertex satisfies, and so S is eulerian. Since, for, we conclude that S is a spanning eulerian subdigraph of, and so is supereulerian.

Theorem 2 [13] If a strict digraph on vertices has or more arcs, then it is hamiltonian- connected.

Corollary 1 Let be a strict digraph on vertices and with. If is a supereulerian digraph, then is supereulerian.

Proof. By Theorem 2, is hamiltonian-connected. Then by Proposition 1 (ii), is supereulerian.

Two classes of supereulerian digraphs seem to be of particular interests in studying supereulerian digraph 2- sums. We first present their definitions.

Definition 3.2 Let D be a digraph such that either or. If for any, D contains a symmetric dipath from u to v, then D is called a symmetrically connected digraph.

Given a digraph D, define a relation ~ on such that if and only if or D has a symmetrically connected subdigraph H with. By definition, one can routinely verify that ~ is an equivalence relation. Each equivalence class induces a symmetrically connected component of D. Hence D is symmetrically connected if and only if D has only one symmetrically connected component. A symmetrically connected component of D is also called a maximal symmetrically connected subdigraph of D. When D has more than one symmetrically connected components, we have the following definition.

Definition 3.3 Let D be a weakly connected digraph and be the set of maximal symmetrically connected subdigraphs of D with. If for any proper nonempty subset,

(3)

then D is partially symmetric.

It is known that both symmetrically connected digraphs and partially symmetric digraphs are supereulerian.

Theorem 3 ( [14] and [15] ) Each of the following holds.

i) Every symmetrically connected digraph is supereulerian.

ii) Every partially symmetric digraph is supereulerian.

A main result of this section is to show that the digraph 2-sums of symmetrically connected or partially symmetric digraphs are supereulerian.

Lemma 3 Let and be two vertex disjoint digraphs with and , and let denote. Each of the following holds.

i) If and are symmetrically connected, then is symmetrically connected.

ii) If and are partially symmetric, then is partially symmetric.

iii) If is symmetric and is partially symmetric, then is partially symmetric.

Proof. i) For any vertices, we shall show that always has a symmetric dipath. If for some, we have, then as is symmetrically connected, contains a symmetric -dipath P. Since is a subdigraph of, P is also a symmetric -dipath of. Hence we may assume that and. Since and are symmetrically connected, contains a symmetric -dipath and contains a symmetric -dipath. By Definition 2.1, and represent the same vertex in, and so is a symmetric -dipath in.

ii) Fix. Since is partially symmetric, for some integer, let be the set of all maximal symmetrically connected subdigraphs of. Without loss of generality, we assume that and; and for some with and, and. (We allow the possibility that and/or). Define, for and,

Then, is the set of all maximal symmetrically connected sub- digraphs of. Note that and. We shall show by definition that is partially symmetric. To do that, let be a nonempty proper subset of. We shall show that (3) holds.

Since, we either have or . By symmetry, we may assume that.

Suppose first that. Let. Then

. Since is partially symmetric, there exist an, a vertex,

and an such that

This implies that the vertex, , and such that

Thus (3) holds in this case.

Hence we may assume that. Since is a proper subset, we must have. Since, we also have. With a similar argument, we conclude that (3) must also hold in this case.

iii) Let and let be the set of all maximal symmetrically connected subdigraphs of with and for some,. (We allow the possibility that). Define

Then is the set of all maximal symmetrically connected subdigraphs of. Note that with this notation. Let be a nonempty proper subset of. We shall show that (3) holds.

Let. Since is proper, is a nonempty proper subset of. Since is partially symmetric, by Definition 3.2, there exist an, a vertex, and an such that

This implies that vertex, and such that

Thus (3) holds, and so by definition, is partially symmetric.

Theorem 4 Let and be two digraphs. Each of the following holds.

i) If and are symmetrically connected, then is supereulerian.

ii) If and are partially symmetric, then is supereulerian.

iii) If is symmetric and is partially symmetric, then is supereulerian.

Proof. This follows from Theorem 3 and Lemma 3.

It is also natural to consider sufficient conditions on and for to be hamiltonian.

Theorem 5 If is hamiltonian and is hamiltonian-connected digraphs, then is hamiltonian.

Proof. Let with be a hamiltonian dicycle of and. Let and, and. Since is hamiltonian-connected, contains a -hamiltonian dipath P. Thus is a hamiltonian dicycle in.

Theorem 6 (Thomassen [16] ) If a semicomplete digraph D is 4-strong, then D is hamiltonian-connected.

By Theorem 5 and 6, we have the following corollary.

Corollary 2 Let and be two 4-strong semicomplete digraphs, then is hamiltonian.

Acknowledgements

The research of Juan Liu was partially supported by grants NSFC (No. 61363020, 11301450) and China Scholarship Council, and the research of Xindong Zhang was supported in part by grants NSFC (No. 11461072) and the Youth Science and Technology Education Project of Xinjiang (No. 2014731003).

Cite this paper

Khalid A.Alsatami,XindongZhang,JuanLiu,Hong-JianLai, (2016) On a Class of Supereulerian Digraphs. Applied Mathematics,07,320-326. doi: 10.4236/am.2016.73029

References