Applied Mathematics
Vol.06 No.12(2015), Article ID:61549,7 pages
10.4236/am.2015.612186
Multicriteria Partial Cooperative Games
Graziano Pieri1, Lucia Pusillo2*
1Department of Science for Architecture (DSA), University of Genoa, Genoa, Italy
2Department of Mathematics (DIMA), University of Genoa, Genoa, Italy

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 10 October 2015; accepted 27 November 2015; published 30 November 2015

ABSTRACT
In this paper, we study an approach to environmental topics, through multicriteria partial cooperative games. In general, not all players wish to cooperate to solve a common problem, so we consider a model where only some decision-makers cooperate. Starting from the transformation of a coalition game into a strategic one, we give a new concept of solution for partial cooperative models proving an existence theorem.
Keywords:
Non Cooperative Games, TU-Games, Strong Nash Equilibrium, Pareto Equilibrium, Environmental Models

1. Introduction
Environmental pollution and the consequent climate change have induced many game theorists to study these topics through mathematical games. When players (countries, regions, etc.) cooperate, each player pollutes less than under a non cooperative behavior and the more the cooperating countries, the greater the total benefit. An example is the pollution of shallow lakes, an interesting question studied in [1] . If all decision-makers cooperated, shallow lakes could remain clean, but in fact only a part of players cooperate so they (and we) do not reach the optimum.
In our models, we consider n players where some work together, so we speak of partial cooperative games. These models arise from the observation of real life.
This is the ancient problem named “The tragedy of Commons” [2] , and deeply studied by many authors, such as in [3] and [4] . The overexploitation of commons, the selfish pursuit of one’s own benefit can lead to the worst social outcome.
Is it possible for individuals to cooperate without being compelled by a law? (see [3] ). Since there are no institutions which can enforce international environmental agreements (IEAs), international cooperation is very difficult.
In order to contain the emissions of pollutants, in 1997 the Kyoto Protocol to the “Framework Convention on Climate Change” limited emissions of carbon dioxide, methane, nitrous oxide, halocarbons, perfluorocarbons and sulfur hexafluoride, but the pollution problem is far from being solved satisfactorily.
Many environmental problems are studied in [5] -[9] .
An interesting approach was made in [10] , where the author makes a model through a cooperative game with non-empty core.
Over the past few years, many game theorists were interested in the problem of coalition formation (see [11] - [16] and references in these).
It seems to us that the mathematical game theory offers a natural medium to the study of environmental models. Our approach to such a problem is to study a cooperative situation modeled by a coalitional game
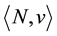 and to define, based on it, a new game which shows the process of making coalitions in the initial model.
and to define, based on it, a new game which shows the process of making coalitions in the initial model.
In the applications to real life, it is natural to consider multicriteria situations, because a player wishes to “optimize” multiple criteria. For example, one problem is to reduce pollution and to increase production, two objectives which are often opposed or not compatible. In the classic approach to TU-games, an allocation rule is defined to predict how rational players distribute among them the gain from cooperation. In our model, we study a game where players have multiple criteria “to optimize” and propose a new concept of solution (coalitional Pareto equilibrium), using an allocation rule to define the players’ payoff.
About multicriteria or vector games, see [16] -[20] .
In the text, we will use equally the words “multicriteria” or “multiobjective” or “vector” games. We will use “multicriteria partial cooperative games” or “multiobjective environmental games” when only a proper subset of N is formed by cooperating players.
This paper is organized as follows: in Section 2, we set up notations and known results which will be useful for our model, in Section 3, we describe a non-cooperative model called participation game inspired by Monderer and Shapley’s model [13] , and then we provide a new solution for a partial cooperative game (or environmental game) and an existence result. Section 4 contains conclusions and some ideas for further research. Many examples illustrate the paper.
2. Notations and Preliminary Results
In this section we consider multiobjective problems that are models where the decision makers have many objectives “to optimize”.
Let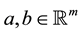 ,
,
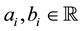 , we consider the following preferences:
, we consider the following preferences:
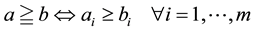 ;
;
 and
and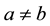 ;
;
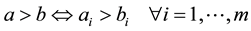 .
.
Analogously we define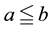 ,
,
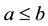 ,
,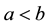 .
.
Let us consider a multiobjective (or multicriteria) TU-game
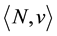 where N is the set of n players and
where N is the set of n players and
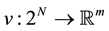 is the characteristic function of the game, with
is the characteristic function of the game, with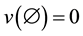 . It assigns to each coalition
. It assigns to each coalition
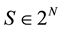 a m-vector, m being the number of objectives, equal for each player:
a m-vector, m being the number of objectives, equal for each player:
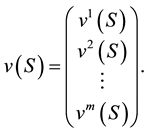
In an environmental game, if all players cooperate, the grand coalition forms and obtains the best (we will specify the meaning in the next pages).
Let us write
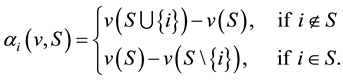
Definition 2.1 A multicriteria game



Definition 2.2 We call i a dummy player if

Now let us define one solution for a cooperative game: the Shapley value. It was introduced by Shapley in the fifties. It is one of the most interesting solution concepts in the cooperative game theory. Intuitively it has a link with the average of the marginal contributions of each player joing (see [14] [19] for more details).
Definition 2.3 The Shapley value of



where s and n denote the cardinality of the coalitions S and N respectively.
Keep in mind that an allocation rule



A “good” allocation rule verifies the following axioms:
1) Efficiency property (EFF for short):
2) Weak Monotonicity property (WMON for short): given two games





3) Dummy Out property (DUMOUT for short): for all






The Shapley value verifies the three axioms written.
To explain better the notations, let us consider the following:
Example 2.1 Let

where we mean


The first objective is the reduction of pollution percentage and the second is the increase of industrial production. If player (industry) 1 decides to act alone, its production increases by 15% but it can reduce its pollution only by 10%. If player 1 cooperates with player 2 (a second industry), their production increases by 50% and they can reduce their pollution combined by 40%... If all players cooperate, they increase their production by 80% and reduce their pollution of 90%. The Shapley value for this bi-criteria game is:
Let us consider a multicriteria non cooperative game



For




To define environmental games and a solution for them, we need one for cooperative games (for example the aforementioned Shapley value) as well as one for non cooperative games. To this end, we remember the definition of Pareto equilibrium (PE for short), which is the commonly used solution for (non-cooperative) multiobjective games.
Definition 2.4 Let G be a multicriteria non-cooperative game.
A strategy profile

1) weak Pareto equilibrium if

2) strong Pareto equilibrium if

The set of weak and strong Pareto equilibria will be denoted by wPE and sPE respectively.
Intuitively


Example 2.2 Let G be the bicriteria non cooperative game in the table below
Two countries (players) have two strategies: to reduce their sulphur dioxide emissions (C) or not to reduce (nC).
They have two objectives to pursue: to save the cost of the national health institute and to increase the people health.
In pure strategies the equilibria are:

In this paper we are not interested in mixed strategies.
3. From a Coalition Game to a Strategic One
There are no doubts that we must reduce the pollution following carbon dioxide emissions. One of the most serious problems is the contribution of each country. In this paper we suggest such models and a solution (the coalitional Pareto equilibrium) as will enable all countries to obtain the best through cooperation.
In many practical situations, the interaction among decision-makers may be a mix of cooperative and non- cooperative behavior.
Although the players in the same coalition cooperate, there are also coalitions made up of only one player. Furthermore different coalitions do not cooperate with each other.
In such models we speak of partial cooperative games or environmental games (about partial cooperation, see [6] [21] [22] ).
Let us consider


By





We can define the non cooperative participation game in normal form


The utility function for player i is defined as follows:
where
Intuitively, we start with a TU-game and an allocation rule


In the following definition we generalize the concept of strong Nash equilibrium (sNE for short) to a notion of equilibrium profile for vector games. We call it coalitional Pareto equilibrium.
Definition 3.1 We say that






We note that if

Definition 3.2 We say that a multicriteria partial cooperative game has a partial equilibrium if there is a cPE for the corresponding participation game.
Example 3.1 Let us consider the following bicriteria game.
There are three industries (players) which work near a great shallow lake. They have pursue two objectives: the first is the reduction of toxic substances spilt into the lake, the second is the gain of having a lake with clean water, many fishes and green plants. The total cooperation give a real benefit to all.
In this table we write for example:


Let the Shapley value be the allocation rule agreed upon by all players. We can use the following table to take a quick look at the coalitional Pareto equilibria (Table 1).
The first two columns represent the game in example 3.1, the others represent the Shapley value relative to the game vS where S is the coalition written in the first column.
There are two cPE:
and
From Vector Optimization problems we can learn that, the m scalar games generated from breaking down the vector game, do not necessarily inherit its structure.
In fact if we break down the considered bicriteria game of the example 3.1 into two games (the first one pertaining to the first criterion, the second one pertaining the second criterion), we can remark that


We will now provide the following existence theorem for a coalitional Pareto equilibrium.
In the authors’ opinion this is an interesting result, because there is an incentive to cooperate: in the hypotheses of the theorem (which are often verified in the models of real life), if all players cooperate (read: if all countries cooperate), the grand coalition forms and there is an efficient solution for all members.
Table 1. A bicriteria partial cooperative game.
Theorem 3.1 Let


Proof. From definition of Shapley value and

Let us suppose, by contradiction, that




This leads us to state that there is at least a component




This is a contradiction with the properties of
Corollary 3.1 Let G be a multicriteria partial cooperative game. If

Remark 3.1 The result of theorem 3.1 is valid considering an allocation rule verifying the three axioms: EFF, WMON and DUMOUT.
4. Conclusions and Open Problems
Game theorists apply with success the Game Theory to environmental models and emission problems. In this paper, we consider a game where some players cooperate and others do not. We call this game “partial cooperative”. To give a new notion of solution for these games, we start trasforming the structure of a cooperative game into a strategic one. This new game is defined considering as strategies the coalitions to which player i wish to belong and the utility function assigns the Shapley value to each player who wants cooperate and

We provide a new concept of equilibrium for multiobjective environmental games, the coalitional Pareto equilibrium which generalizes the idea of strong Nash. This concept, differently from the Nash equilibrium, captures the idea of efficient equilibrium.
An existence theorem and many examples complete the paper.
As concerns possible further research, it would be interesting to study the partial cooperative problem where the allocation rule is different from the Shapley value or to consider games with utility functions in uncertainty intervals, (see [18] ). Some of these issues are work in progress.
Acknowledgements
The second author has been supported by the Gruppo Nazionale per l’Analisi Matematica, la Probabilitá e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM).
Cite this paper
GrazianoPieri,LuciaPusillo, (2015) Multicriteria Partial Cooperative Games. Applied Mathematics,06,2125-2131. doi: 10.4236/am.2015.612186
References
- 1. Göran-Maler, K., Xepapadeas, A. and De Zeeuw, A. (2003) The Economics of Shallow Lakes. Environmental and Resource Economics, 26, 603-624.
- 2. Hardin, G. (1968) The Tragedy of Commons. Science, 162.
- 3. Axelrod, R. and Dion, D. (1988) The Further Evolution of Cooperation. Science, 1242, 1385-1390.
- 4. Ostrom, E. (1990) Governing the Commons. The Evolution of Institution for Collective Action. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511807763 - 5. Carraro, C. and Siniscalco, D. (1993) Strategies for the Protection of the Environment. Journal of Public Economic, 52, 309-328.
http://dx.doi.org/10.1016/0047-2727(93)90037-T - 6. Finus, M. (2001) Game Theory and International Environmental Cooperation. Edward Elgar Ed.
- 7. Hanley, N., Shogren, J.F. and White, B. (1997) Environmental Economics in Theory and Practice. MacMillan, London.
- 8. Morgan, J. and Prieur, F. (2013) Global Emission Ceiling versus International Cap and Trade: What Is the Most Efficient System When Countries Act Non-Cooperatively? Environmental Modeling and Assessment.
http://dx.doi.org/10.1007/s10666-013-9361-7 - 9. Tidball, M. and Zaccour, G. (2005) An Environmental Game with Coupling Constraints. Environmental Modeling and Assessment, 10, 153-158.
- 10. Fläm, S.D. (2006) Balanced Environmental Games. Computers and Operations Research, 33, 401-408.
- 11. Aumann, R.J. and Dréze, J. (1974) Cooperative Games with Coalition Structures. International Journal of Game Theory, 3, 217-237.
http://dx.doi.org/10.1007/BF01766876 - 12. Borm, P.E.M. and Tijs, S.H. (1992) Strategic Claim Games Corresponding to an NTU-Game. Games and Economic Behavior, 4, 58-71.
http://dx.doi.org/10.1016/0899-8256(92)90005-D - 13. Monderer, D. and Shapley, L.S. (1996) Potential Games. Games and Economic Behavior, 14, 124-143.
http://dx.doi.org/10.1006/game.1996.0044 - 14. Myerson, R. (1997) Game Theory. Analysis of Conflict. Harvard University Press.
- 15. Owen, G. (1977) Values of Games with a Priori Unions. In: Boehan, V. and Nachthanp, H., Eds., Mathematical Economics and Game Theory, Springer-Verlag, Berlin, 76-88.
http://dx.doi.org/10.1007/978-3-642-45494-3_7 - 16. Pusillo, L. and Tijs, S. (2012) E-Equilibria for Multicriteria Games. In: Cardaliaguet, P. and Cressman, R., Eds., Advances in Dynamic Games, Annals of the International Society of Dynamic Games, Vol. 12, Birkhäuser, Boston, 217- 228.
- 17. Patrone, F., Pusillo, L. and Tijs, S. (2007) Multicriteria Games and Potentials. TOP, 15, 138-145.
http://dx.doi.org/10.1007/s11750-007-0008-1 - 18. Pieri, G. and Pusillo, L. (2010) Interval Values for Multicriteria Cooperative Games. AUCO Czech Economic Review, 4, 144-155.
- 19. Puerto Albandoz, J. and Fernandez Garcia, F.R. (2006) Teoria de Juegos Multiobjetivo. Imagraf Impresores, Sevilla.
- 20. Shapley, L.S. (1959) Equilibrium Points in Games with Vector Payoffs. Naval Research Logistic Quarterly, 6, 57-61.
http://dx.doi.org/10.1002/nav.3800060107 - 21. Ayoshim, D.A. and Tanaka, T. (2000) On the Partial Cooperative Games. Non Linear Analysis and Convex Analysis, Rimskokyuroku, 1136, 9-12.
- 22. Mallozzi, L. and Tijs, S. (2008) Partial Cooperation and Non-Signatories Multiple Decision. AUCO Czech Economic Review, 2, 21-27.
- 23. Meca-Martínez, A., Sánchez Soriano, J., García-Jurado, I. and Tijs, S. (1998) Strong Equilibria in Claim Games Corresponding to Convex Games. International Journal of Game Theory, 27, 211-217.
http://dx.doi.org/10.1007/s001820050067
NOTES
*Corresponding author, the authors’ names are written only in the alphabetic order.













