ABSTRACT

We consider the estimation of nonparametric regression models with predictors being measured with a mixture of Berkson and classical errors. In practice, the Berkson error arises when the variable X of interest is unobservable and only a proxy of X can be measured while the inaccuracy related to the observation of the proxy causes an error of classical type. In this paper, we propose two nonparametric estimators of the regression function in the presence of either or both types of errors. We prove the asymptotic normality of our estimators and derive their rates of convergence. The finite-sample properties of the estimators are investigated through simulation studies.

Keywords:

Berkson Error, Classical Error, Deconvolution, Kernel Method, Mixed Measurement Errors

1. Introduction

Let 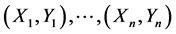denote a sequence of independent and identically distributed random vectors. In traditional non-parametric regression model analysis, one is in- terested in the following model

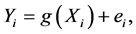(1)

where 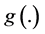is assumed to be a smooth, continuous but unknown function; the random errors are assumed to be normally and independently distributed with mean 0 and constant variance; and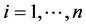. Here, the predictor X is usually assumed to be directly observable without errors. Both the direct observation and error-free assumptions are however seldom true in most epidemiologic studies. For the violation of the error-free assumption, [1] considered an environmental study which studied the relation of mean exposure to lead up to age 10 (denoted as X) with intelligence quotient (IQ) among 10-year-old children (denoted as Y) living in the neighborhood of a lead smelter. Each child had one measurement made of blood lead (denoted as W), at a random time during their life. The blood lead measurement (i.e., W) became an approximate measure of mean blood lead over life (X). However, if we were able to make many replicate measurements (at different random time points), the mean would be a good indicator of lifetime exposure. In other words, the measure- ments of X are subject to errors and W is a perturbation of X. In the measurement error literature, this is known as the classical error model and Model (1) becomes

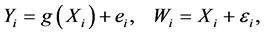(2)

where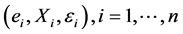, are mutually independent and 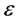represents the classical measurement error variable. Various methods and approaches for analyzing Model (2) such as deconvolution kernel approaches (e.g., [2] [3] [4] ), design-adaptive local poly- nomial estimation method (e.g., [5] ), methods based on simulation and extrapolation (SIMEX) arguments (e.g., [6] [7] [8] [9] ), and Bayesian approach (e.g., [10] ) have been extensively studied in the literature.

In many studies, it is however too costly or impossible to measure the predictor X exactly or directly. Instead, a proxy W of X is measured. For the violation of the direct observation assumption, [1] modified the aforementioned environmental study in which the children’s place of residence at age 10 (assumed known exactly) were classified into three groups by proximity to the smelter―close, medium, far. Random blood lead samples, collected as describe in the aforementioned design, were averaged for each group (denoted as W), and this group mean used as a proxy for lifetime exposure for each child in the group. Here, the same approximate exposure (proxy) is used for all subjects in the same group, and true exposures, although unknown, may be assumed to vary randomly about the proxy. This is the well-known Berkson error model. In other words, the predictor X are not directly observable and measurements on its surrogates W are available instead. The true predictor X is then a perturbation of W. The model of interest now becomes

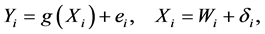(3)

where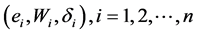, are mutually independent. Model (3) was first con- sidered by [11] and the estimation of the linear Berkson measurement error models was discussed in [12] . Methods based on least squares estimation ( [13] ), minimum distance estimation ( [14] [15] ), regression calibration ( [16] ) and trigonometric functions ( [17] ) have been studied.

The stochastic structure of Model (3) is fundamentally different from Model (2). Here, the measurement error of Model (2) is independent of X, but dependent on W. This distinctive feature leads to completely different procedures in estimation and inference for the models. In particular, nonparametric estimators that are consistent in Model (2) are no longer valid in Model (3), and vice versa. In most of the existing literature, the measurement error is supposed to be only one of the two types. In the Berkson model (3), it is usually assumed that the observable variable W is measured with perfect accuracy. However, this may not be true in some situations. In such cases, W is observed through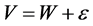, where 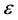is a classical measurement error. [18] presented a good discussion of the origins of mixed Berkson and classical errors in the context of radiation dosimetry. Under this mixture of measurement errors, we observe a random sample of independent pairs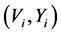, for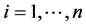, generated by

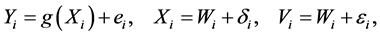(4)

where, , and are mutually independent, and the re- spective error densities and are assumed to be known. Due to its potentially wide applications, statistical procedures for analyzing Model (4) has received more attention recently. For instance, a regression calibration approach was proposed by [19] and [20] in a parametric context of random exposure. [21] considered a bayesian approach for a semi-parametric regression function. [22] developed a nonparametric density estimation approach for contaminated data with a mixture of Berkson and classical errors but without further extending to estimate the regression function. [23] proposed a two-step nonparametric kernel method for estimating the regression function but its calculation is complicated. In this paper, we propose two non- parametric estimators for the regression function curve with the predictor being measured with either classical error, Berkson error, or a combination of both. The difficulty primarily depends on the relative smoothness of the error densities and. When is smooth enough (relative to), we are able to construct a nonparametric estimator that converges to the target curve at the parametric rate. For less smooth density, we propose a kernel estimator that converges at rates ranging from to rates that are close to the deconvolution rates.

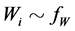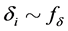This paper is organised as follows. In Section 2, we propose estimators for the regression function curve. We then derive the asymptotic normality of our estimators under some regularity conditions and give the rates of convergence in Section 3. Section 4 presents some numerical results from simulation studies. A brief discussion will be given in Section 5. All technical results and proofs are deferred to the Appendix.

2. Proposed Estimators

Let be a random sample from Models (4), and, , , and be the characteristic functions of, , , and, respectively. We have the following relationships:

Hence, if does not vanish,

Since and are assumed to be known, an estimate of can be computed as

Noticing that, if is absolutely integrable, the characteristic function and its density function have the following relation

under the condition that, the density estimator of is then given by

(5)

where

As a result, we propose the following estimator for

(6)

Example 1 Let the error densities and in Model (4) be normal densities with mean zero and variances and, respectively. It follows that

with. If we assume, then the

ratio is the characteristic function of another normal random variable. By (6), the estimator of can be written as

where is the density of the variable. If, the ratio is not integrable, and the estimators (5) and (6) can not be calculated. To overcome this issue, we propose an alternative approach for estimating.

Using a kernel function with a bandwidth h, we consider the following kernel estimator for

and an estimator for is then given by

where is the characteristic function of the kernel function.

Proceeding as above, we get an alternative estimator of by

(7)

where

(8)

Therefore, when (6) is no longer valid, we propose the following estimator for

(9)

Remark 1 To ensure that the proposed estimator (9) is well-behaved, we need to make the following assumption.

Condition A:

1. for all t; and

2. and.

Example 2 We use the same model as in Example 1 with. In this case, to ensure (A2) to be valid, it is rather common to choose kernels that have a compactly supported characteristic function. For example, we choose the sinc kernel, which has characteristic function, the indicator function of the interval. From (8), we have

Remark 2

1. The above two nonparametric estimators of were given by [22] ;

2. When the variance of in Models (4) is equal to 0, which is the Berkson error model, the estimator (6) becomes

(10)

where is the density function of; and;

3. When the variance of in Models (4) is equal to 0, which is the classical error model, given in (9) reduces to the estimator of [2] .

3. Theoretical Properties

In this section, we study asymptotic properties of the estimators proposed in Section 2. In particular, the properties of the estimator at (6) are clear. It is easy to check that the numerator and the denominator are both unbiased estimators of and, respectively and that, converges at the fast parametric rate. Properties of the estimator at (9) need to further explore and, in what follows, we derive them.

3.1. Asymptotic Results for

In this section, we investigate the large-sample properties of the estimator at (9). For this purpose, we present the following regular conditions which are mild and can be found in [2] .

Condition B:

1. have zero means and uniformly bounded variances;

2., and are bounded, and and g have bounded kth derivatives;

3. is a real and symmetric kernel and has finite moment of order k. Namely, for and; and

4. The conditional moment is bounded for all u and some.

Let. The mean squared error (MSE) of the estimator is described in the next Theorem.

Theorem 1 ((MSCE)) Suppose that Conditions A and B hold. Then, for each x such that,

(11)

where.

Explicit rates of convergence of the estimator can be found by examination of the asymptotic behaviour of the MSE. For the bias, using the Taylor expansion of the first term on the right-hand side of Equation (11), we have

where.

The second term on the right-hand side of Equation (11) describes the variance of. The asymptotic behaviour of this term is more difficult to evaluate since it depends on the tail behaviour of the ratio, as [14] discussed, which can be classified into the following:

1. An exponential ratio of order is

(12)

with, , , and,.

2. A polynomial ratio of order is

(13)

with, and.

3.1.1. Asymptotic Mean Squared Error (AMSE)

In this section, we study the asymptotic behaviour of the MSE where behaves like an exponential or a polynomial.

Theorem 2 Suppose that Conditions A and B hold and that the first half inequality of (12) is satisfied. Assume that is supported on. Then, for each x such that, we have

with being some positive constant and.

When is exponentially smoother than, we obtain a slower logarith- mic rate which is similar to the deconvolution rate for supersmooth error given in [2] . More precisely, the optimal bandwidth is of order with, and the estimator then converges at the rate of.

Theorem 3 Suppose Conditions A and B hold, and that. Then,

under the polynomial ratio (13), for each x such that, we have

with being some positive constant, and.

We obtain that, when behaves like a polynomial ratio of order in the tail, the convergence rates range from to deconvolution rate of ordinary smooth error of [2] . More precisely, the optimal bandwidth is of order when, and the estimator then converges at the rate of. When, the optimal bandwidth is of order and the estimator converges at the rate of.

3.1.2. Asymptotic Normality

The theorem below establishes asymptotic normality in the exponential ratio case.

Theorem 4 Under the conditions of Theorem (2), and for bandwidth with,

where and.

The next theorem establishes asymptotic normality in the polynomial ratio case.

Theorem 5 Suppose that Conditions A and B hold and that the inequality of (13) is satisfied. Assume that and. Then, under

and as, for each x such that, we have

where is the same as given in Theorem (4) and is equal to the second term on the right-hand side of Equation (11).

The proofs of all theorems are postponed to the Appendix.

3.2. Unknown Measurement Error Distribution

When the error densities are unknown, they can be readily estimated from additional observations (e.g., a sample from the error densities, replicated data or external data) and these estimates can be substituted into (6) and (9) to produce the estimate of. For sufficiently large sample size, the rates of convergence of the estimates remain unchanged when and are replaced by their consistent estimators (e.g., [4] [17] [24] ).

4. Simulation Studies

We study numerical properties of the estimators proposed in Section 2. Note that we have defined two estimators, at (6) and (9). The first exists when is inte- grable, and the estimator (9) otherwise. We use the notations and for the esti- mators (6) and (9) respectively. We use the notation for the estimator that ignores the errors, that is, the estimator is the classical Nadaraya-Watson estimator of based on direct data from,. Note that is exactly equal to when. In addition, we use for the estimator of [23] .

We apply the various estimators introduced above to some simulated examples (see, [23] ):

1. (sinusoidal),

2. (sharp unimodal), and

3. (asymmetric);

where is the density of an variable. For each of the above regression functions, we generate 200 data sets of randomly sampled vectors, as follows. We generate a random sample from, a random sample from and a random sample from, and put and, , where is the density of an variable, and we take and to be either normal or Laplace with zero mean. Then we generate a random sample as, where the errors are normally distributed with zero mean and variance, where with denoting the mean-squared deviation of g from its average value. We simply denoted and by, and other similar.

In our simulations we consider sample sizes, and in each case we generate 200 samples from the distribution of the random vector. Except if stated otherwise, we adopt the second order kernel K corresponding to , which is necessary to calculate and. For the band- width h, it is necessary to calculate, and, we select the value h that mini- mises the cross-validation (CV) criterion, , where the sub- script meant that the estimator was constructed without using the jth observation. We report the Integrated Squared Error, , where is the estimator considered. In all graphs, to illustrate the performance of an estimator, we show the estimated curves corresponding to the first (Q1), second (Q2) and third (Q3) quartiles of the ordered ISEs. The target curve is always represented by a solid curve. In the tables we provide the average values, denoted by MISE, of the 200 cal- culated ISEs.

Figure 1 and Table 1 illustrate the way in which the estimator improves as sample size increases. We compare, for various sample sizes, the results obtained for estimating curve (a) when, and with the pair of variance ratios equals (0.1, 0.4), and for estimating curve (b) when and ~ (N, L), (N, N), (L, L) or (L, N) with . We see clearly that, as the sample size increases, the quality of the estimators improves significantly in all cases.

For any nonparametric method for regression problem, the quality of the estimator also depends on the discrepancy of the observed sample. That is, for any given family of densities, and, and any given the noise-to-signal ratios, the performance of the estimator depends on the variances of, and. Here, we compare the results obtained from estimating curve (c) for different values of

. As expected, Figure 2 shows that the best performance usually occur for smaller error variance (e.g.,). It is noteworthy that the effect of the variances on the estimator performance is obvious in model (4).

Finally, we compare (or), and. Figure 3 shows the boxplots of the quantities of and for estimating curve (a) when and, where is the ISE of our proposed estimator, is the ISE of the estimator that ignores the errors, and is the ISE of the estimator of [23] . Here, each boxplot is constructed from 200 samples. Here, in panel (a)-(L-L) (or (a)-(N-N)), the mixed errors are both Laplace (or both normal). Here, and also in panel (a)-(N-L) (or (a)-(L-N)), the errors are and (or and). In each panel, for X-axis = 1 to 7, = (0.1, 0.4), (0.1, 0.3), (0.2, 0.3), (0.2, 0.2), (0.3, 0.2), (0.3, 0.1) or (0.4, 0.1). The more a boxplot is located below the zero horizontal line, the better our method compared with the other two estimators. In the same situation, Table 2 and Table 3 report the average integrated square error (MISE) for estimating curves (b) and (c) respectively. As expected, our proposed estimator substantially outperformed the estimator that completely ignores any measurement errors. Our results show that our proposed estimator usually works better than the estimator proposed by [23] for estimating curves (a) and (b). It is noteworthy that the estimator proposed by [23] may perform better than our proposed estimator when curve (c) with is esti- mated.

5. Discussion

In this paper, we propose a new method for estimating non-parametric regression models with the predictors being measured with a mixture of Berkson and classical errors. The method is based on the relative smoothness of and. When is

smooth enough (relative to), we propose a nonparametric estimator (6) that converges to the target curve at the parametric rate. For less smooth function, we propose a kernel estimator (9) that converges at rates ranging from to rates that are close to the deconvolution rates. Numerical results show that the new esti- mators are promising in terms of correcting the bias arising from the errors-in- variables. It generally preforms better than the approach proposed by [23] . The metho- dology can be readily extended to the prediction problem of nonparametric errors-in- variables regression (see, e.g., [16] ). Extension of our method to the problems con- sidered in [5] is of future research interest.

Acknowledgements

This work was supported by Natural Science Foundation of Jiangxi Province of China under grant number 20142BAB211018.

Cite this paper

Yin, Z.H., Liu, F. and Xie, Y.F. (2016) Nonparametric Regression Estimation with Mixed Measurement Errors. Applied Mathematics, 7, 2269-2284. http://dx.doi.org/10.4236/am.2016.717179

References

Appendix

Proof of Theorem 1

Let, where

, we have

(14)

and

(15)

where. The result follows immediately from 14 and 15.

Proofs of the Results of Section 3.1.1.

Lemma 1 Suppose that is supported on, and for all t. Then, for

, we have

where, here, and below, C denotes a generic positive and finite constant.

Proof. It follows from (A2) of Condition A that for some large enough constant. Since, we have

The conclusion follows from

The proof for the other result is similar and requires Parseval's Theorem.

From (14) and Lemma 1, we have

The proof of Theorem 2 follows from the expressions of and.

The proof of Theorem 3 is the same as the proof of Theorem 2, but in this case we need the following lemma.

Lemma 2 Suppose that for all t, and

. Then, we have

with.

The proof of Lemma 2 is similar to the proof of Lemma 1 and is omitted.

Proofs of the Results of Section 3.1.2.

A standard decomposition gives, goes in pro- bability to and thus we only need to prove the asymptotic normality for. As given in [25] , a sufficient condition for the following asymptotical normality

is that the Lyapounov's condition holds, i.e., for some,

Letting, we have

Under the conditions given in the theorem 4, we can prove that

Under the conditions given in the theorem 5, we can prove that

The rest is standard and is omitted.