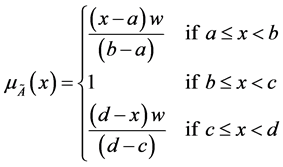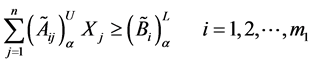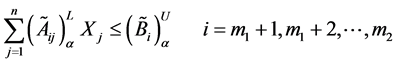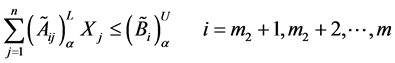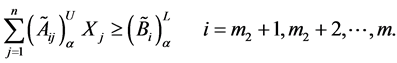Applied Mathematics
Vol.06 No.14(2015), Article ID:62503,15 pages
10.4236/am.2015.614208
Goal Programming for Solving Fractional Programming Problem in Fuzzy Environment
Anil Kumar Nishad, Shiva Raj Singh*
Department of Mathematics, Banaras Hindu University, Varanasi, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 October 2015; accepted 28 December 2015; published 31 December 2015
ABSTRACT
This paper is comprised of the modeling and optimization of a multi objective linear programming problem in fuzzy environment in which some goals are fractional and some are linear. Here, we present a new approach for its solution by using α-cut of fuzzy numbers. In this proposed method, we first define membership function for goals by introducing non-deviational variables for each of objective functions with effective use of α-cut intervals to deal with uncertain parameters being represented by fuzzy numbers. In the optimization process the under deviational variables are minimized for finding a most satisfactory solution. The developed method has also been implemented on a problem for illustration and comparison.
Keywords:
Fuzzy Sets, Trapezoidal Fuzzy Number (TFN), Multi-Objective Linear Programming Problem (MOLPP), Multi-Objective Linear Fractional Programming Problem (MOLFPP)

1. Introduction
The modeling of a real life optimization problem in general needs to address several objective functions and hence become a multiobjective programming problem in a natural way. The goal programming developed by Charnes and Cooper [1] emerged a powerful tool to solve such multiobjective programming problems. Since commencement of the goal programming technique, it has been enriched by many research workers such as Lee [2] , Ignizio [3] [4] and many more. It undoubtedly established that goal programming has been one of the major breakthroughs in dealing with multi objective linear programming problems but still it fails to deal with situations when parameters are imprecise or vague. On the other hand, the development of fuzzy set by Zadeh [5] motivated Zimmermann [6] to give another approach of solving multi objective programming as fuzzy program- ming. Thus a new dimension of goal programming was introduced as fuzzy goal programming by Narsimhan [7] [8] and Ignigio [4] . However, one of the major problems which are faced by decision makers is the modeling of ill conditioned optimization problems or the problems where the coefficients are imprecise and vague. Thus the classical mathematical programming methods of optimization failed to model such problems. Bellman and Zadeh [9] gave a concept that the constraints and goals in such situations may be viewed as fuzzy sets.
Further, in many practical optimization problems the decision making becomes further complicated in situations when multiple objectives are conflicting and non commensurate or imprecise in nature. Thus such method based on goal programming needs the additional information from decision makers for priority structure of various goals and their respective aspiration levels. In view of resolving this difficulty of setting appropriate priority and aspiration levels to various objective functions, Mohanty and Vijayraghavan [10] gave a fuzzy approach to multiobjective linear programming problem to get an equivalent goal programming problem by developing a method to compute appropriate priority levels. Kuwano [11] gave a α-optimal solution to fuzzy multiobjective linear programming problem using goal programming approach. At the same time, Chanas and Kuchta [12] also considered the imprecision problem in multi objective optimization by considering interval valued objective functions. The theory of fuzzy goal programming was further enriched by Chen and Tsai [13] , Stancinlesu et al. [14] in view of providing more satisfying solutions. Thus a popular min-max approach in goal programming was studied by Lin [15] , Yaghoobi and Tamiz [16] and Cheng et al. [17] . However, on application side Soliman et al. [18] , Mishra and Singh [19] and Bharati et al. [20] used fuzzy goal programming model in agricultural sector. Recently fuzzy goal programming problems with interval coefficients and interval weights have been studied by Sen and Pal [21] and Hossein Hajiagha [22] . The readers may get a review of linear programming in works of Lotfi et al. [23] and Marbini and Tavana [24] . Recently Cheng [25] used a deviation degree measure of fuzzy numbers and applied a weighted max-min method to solve a fuzzy multi objective linear programming problem.
In problem of production planning, financial engineering and in several other areas, there are situations where one has to optimize the efficiency of the system, and thus the objective functions become ratio of two objective functions and give rise to fractional programming problem. Further there may be more such fractional objectives and thus may become a multi objective fractional programming problem. Luhandjula [26] gave a fuzzy approach to multi objective linear fractional programming problem in fuzzy environment which has been further developed by Chakraborty and Gupta [27] , Pal et al. [28] , Pop and Minasian [29] and Cui et al. [30] . The subject has been vastly envisaged by several workers and thus various approaches have been developed to solve fractional programming problems by fuzzy goal programming method given by Mehrjerdi [31] , Singh and Kumar [32] , Biswas and Dewan [33] and Ohta and Yamaguchi [34] . The solution of a fractional programming problem with interval valued coefficients has been studied by Pal and Sen [35] and Effati and Pakdaman [36] . Singh et al. [32] considered the solution of a combination of fuzzy multi objective linear programming problem and linear fractional programming problem using a goal programming approach. Thus motivated with above studies, we have extended the work of Ohta and Yamaguchi [34] to solve the fractional goal programming problem with imprecise parameters by computing the appropriate priority and weight to each goals to find optimal solution. The work done has been organized in various sections as follows. Section 2 provides the preliminaries of the subject to make the study self sufficient. Section 3 deals with the a cut presentation of multi objective linear programming problem followed by a cut presentation of linear fractional programming problem with its solution procedure. The methods developed in Sections 3 and 4 have been implemented on a numerical problem given in Section 5 followed by result and discussion placed in Section 6.
2. Preliminaries
Definition 1. Fuzzy Set
Let X is a collection of objects denoted by x, then a fuzzy set
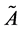 in X is a set of ordered pairs:
in X is a set of ordered pairs:
 , where
, where
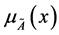 is called the membership function or grade of membership of x in
is called the membership function or grade of membership of x in
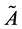 that maps X to the membership space
that maps X to the membership space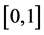 .
.
Definition 2. Fuzzy Number
A Fuzzy set
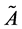 of real line ℝ with membership function
of real line ℝ with membership function
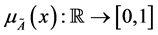 is called a fuzzy number, if it holds following axioms.
is called a fuzzy number, if it holds following axioms.
1)
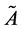 is normal set.
is normal set.
2)
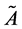 is convex fuzzy set.
is convex fuzzy set.
3)
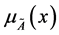 is upper semicontinuous.
is upper semicontinuous.
4)
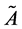 is bounded.
is bounded.
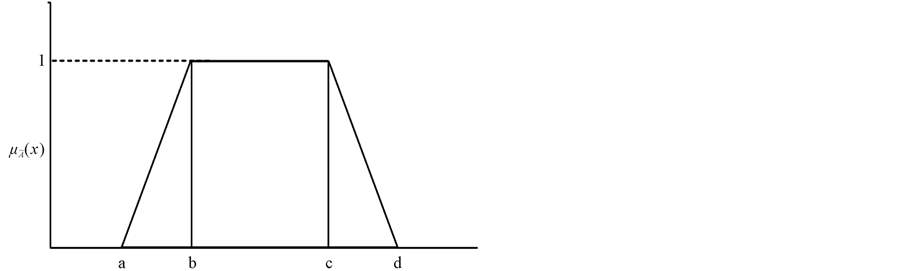
Definition 3. Trapezoidal Fuzzy Number (TFN)
A trapezoidal fuzzy number with parameters
 denoted by
denoted by
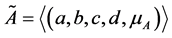 as given in Figure 1 is a FS on real line ℝ whose membership function is defined as follows:
as given in Figure 1 is a FS on real line ℝ whose membership function is defined as follows:
If in a trapezoidal FN we take
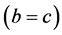 then it becomes a triangular fuzzy number (TFN) with the parameters
then it becomes a triangular fuzzy number (TFN) with the parameters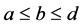
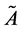
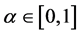
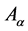
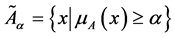
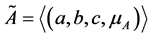
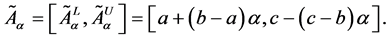
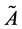
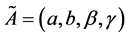
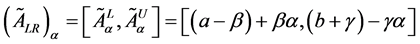
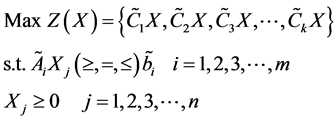
Figure 1. Membership function of TFN.
where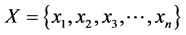
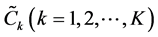
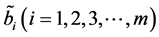
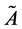
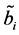
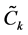
Let
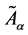
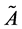
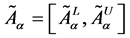
Where
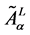
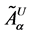
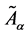
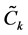
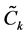
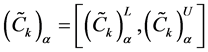
where
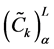
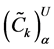
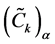
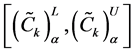
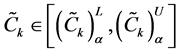
Now the lower and upper bound for the respective α-cut intervals of the objective function are defined as
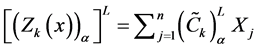
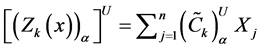
In the next step, we to construct a membership function for the maximization type objective function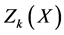
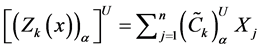
Similarly to construct a membership function for minimization type objective function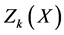
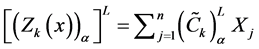
And the constraint inequalities
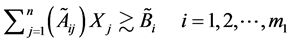
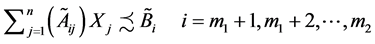
can be written in terms of α-cut values as
and the fuzzy equality constraint
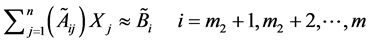
can be transformed into two inequalities as
Thus the undertaken maximization problem is transformed in to the following multi objective linear programming problem (MOLPP) as
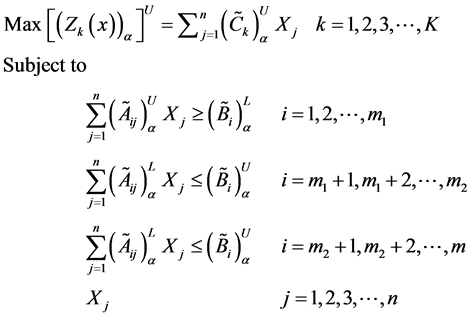
Now consider the transformation of objectives to fuzzy goals by means of assigning an aspiration level to each of them. Thus applying the goal programming approach, the problem (9) can be transformed in to fuzzy goals by taking certain aspiration levels and introducing under deviational variables to each of the objective functions. In proposed method the above maximization type objective function, is transformed as
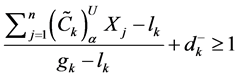
where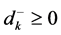
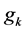
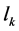
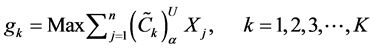
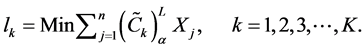
Now using min-sum goal programming method, the above fuzzy goal programming problem is converted in to single objective linear programming problem as follows.
Find
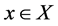
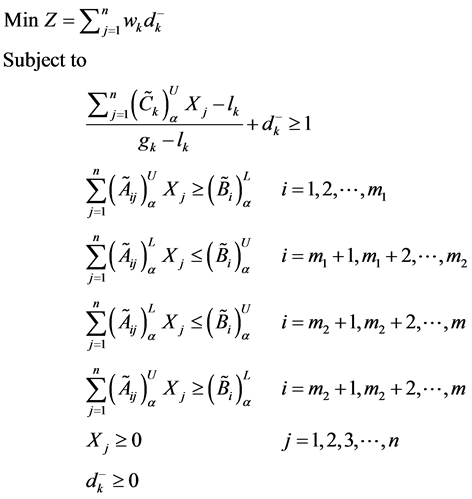
Here, Z represents the achievement function and the weights wk attached to the under deviational variables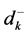
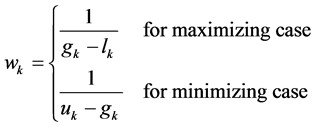
4. Fractional Goal Programming Formulation with α-Cut of the Fuzzy Parameters
Let us consider a fractional optimization problem with n decision variables, m constraints and
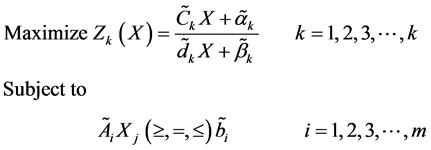
where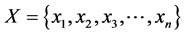
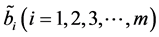
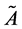
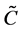
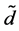
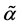
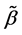
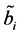
It is also to assume that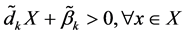
Since, above problem (15) have fuzzy coefficients which have possibilistic distribution in an uncertain intervals and hence the problem can be written in terms of its α-cut intervals.
Now the lower and upper bound for the respective α-cut intervals of the objective function are defined as
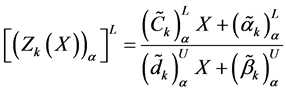
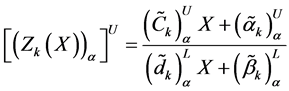
In the next step, we to construct a membership function for the maximization type objective function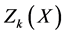
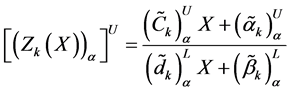
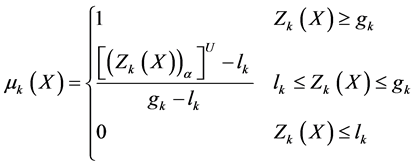
Similarly we construct a membership function for minimization type objective function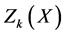
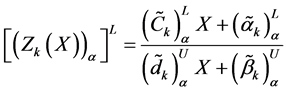
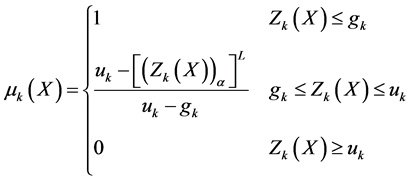
And the constraint inequalities and equalities are transformed as defined in the Equation (6), (7) and (8).
Now the undertaken maximization problem is transformed in to the following linear programming problem (LPP) as
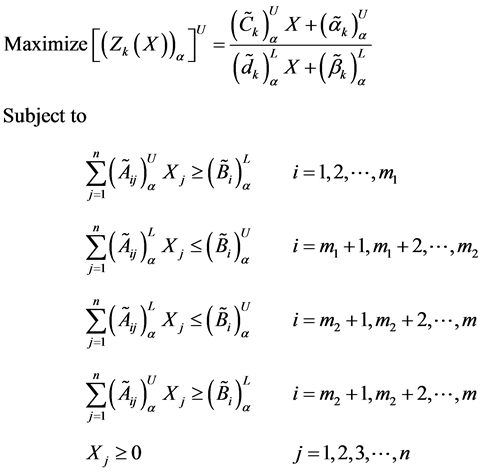
Further consider the conversion of objectives to fuzzy goals by means of assigning an aspiration level to the objective function. Thus applying the goal programming method, the problem (22) can be transformed in to fuzzy goal by taking certain aspiration levels and introducing under deviational variables to the objective function. In proposed method the above maximization type objective function, is transformed as
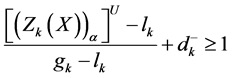
where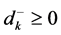
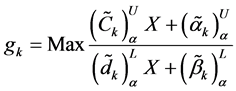
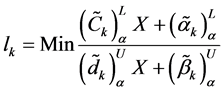
Now using min-sum goal programming method, the above fuzzy goal programming problem is converted in to single objective linear programming problem as follows.
Find
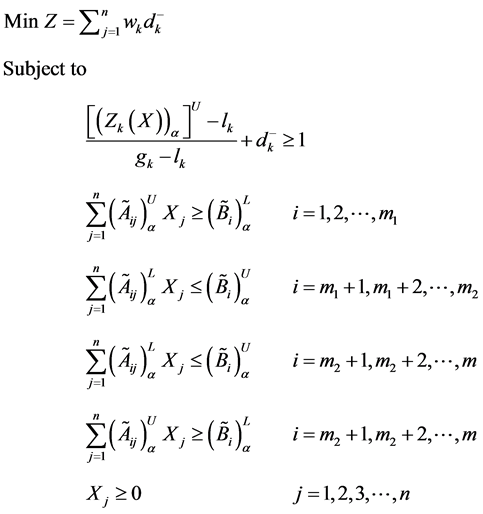
Here Z represents the achievement function and the weights
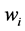
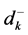
Linearization of Membership Goal
For simplicity to solve the problem (27) we linearize the membership goal which is non-linear in nature and can be write in the following form
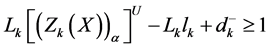
where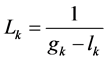
Introducing the expression of
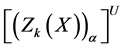
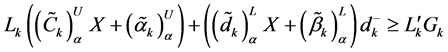
where
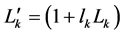
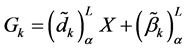
Now by using the method of variable change given by Kornbluth and Steuer [36] the goal in the expression (28) can be linearized as follows.
Let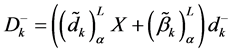
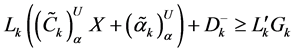
with
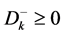
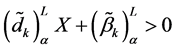
Now in decision making, to minimize the negative deviational variable
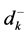
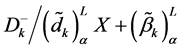
It may be noted that when membership goal is fully achieved, the value of negative deviational variable becomes zero (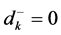
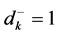
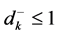
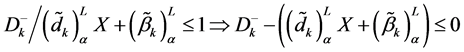
Now for a given value of α, under the framework of Goal Programming, (min-sum Goal programming) [10] , the problem under consideration can be presented as.
Find X so as to
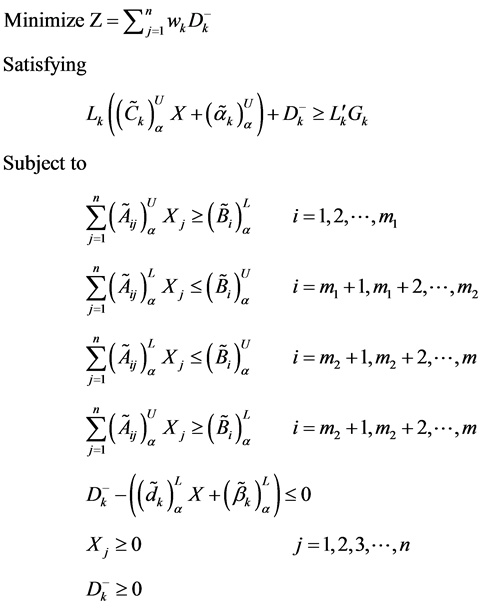
Here Z represents the achievement function and the weights wi attached to the under deviational variable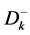
5. Numerical Illustration
In view of illustrating the developed method in previous section, we consider the modelling and optimization of a problem of electronic component maker dealing in domestic and overseas markets as undertaken by Ohta and Yamaguchi [18] . The company wishes to make a mid-term production plan for three months. The company has two types of products, A and B, estimated and anticipated prices and expected gross margins products are shown in Table 1. The time required for individual products in the process and amount used of the principle materials are shown in Table 2 with amount of the expected demand shown in Table 3.
The company cherishes the idea of determine the Amount of production which satisfies the following goals and other fuzzy number with good balance as shown in Table 4.
Supposing that the amount of domestic production is x1 and the amount of overseas production is x2 for product A and the amount of domestic production is x3 and the amount of overseas production is x4 for product B. Now using data from Table 1 to Table 4, the mathematical formulation for all the fuzzy goals of the under taken problem of production system are as follows.
Table 1. Price and grass margin of each product ($).
Table 2. The time required in the process (hours) and principle materials (units).
Table 3. Expected demand.
Table 4. Aspiration levels of goals and other fuzzy numbers.

Solving the above problem by proposed method as described in section 2, first we replace the fuzzy numbers in coefficients by their α-cuts and thus above multi-objective linear fractional programming problem (32) is transformed into the following problem

Now to consider the solution of above problem (33), we apply the developed fuzzy fractional goal programming method developed in section 4 and 5 and consider its solution for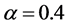
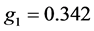
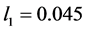
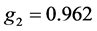
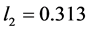
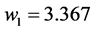
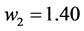
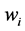
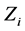

where
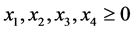
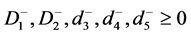
The above linear programming problem (34) has been solved by the MATLAB®, and optimal solution for decision variables are obtained as
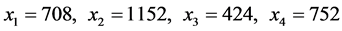
And the values of objective functions are Z1 = 0.149 or 14.9%, Z2 = 0.713 or 71.3%, Z3 = 15885.52, Z4 = 604.04, Z5 = 18447.96.
6. Results and Discussion
The developed method uses the a-cut representation of fuzzy numbers which deals with imprecision in optimization problem. We compare the results obtained by the proposed method with the results of Ohta and Yamaguchi [33] in terms of satisfaction of various goals. The achievements of various goals by method of Ohta and Yamaguchi are Z1 = 13.53%, Z2 = 64.99%, Z3 = (14504.9, 15003.7), Z4 = (580.8, 586.8), Z5 = (18082.21, 18383.8), whereas by the proposed method the achievements of goal are Z1 = 14.9%, Z2 = 71.3%, Z3 = 15885.52, Z4 = 604.04, Z5 = 18447.96. Clearly the level of satisfaction of each goal by the proposed method is higher than the previous results. The proposed method has a further advantage that in general it is a difficult task to set priority weight for various goals in multi-objective programming problem. The situation becomes more tedious when the goals are conflicting in nature. It is hard to set a definite weight for a fractional goal obtained in modeling by taking the ratio of two objective functions. The proposed method also computes the appropriate weight to each goal and hence provides a better solution.
Thus for modeling the optimization problems having vagueness and imprecision in information with fuzzy optimization approach various methods are available in literature for various situations. The fuzzy optimization problems are classified in various categories, such as problems with fuzzy coefficients in constraints, fuzzy coefficients in objective functions and problems with fuzzy inequalities. The proposed method is more suitable to find the optimal solutions of the problems having L-R number fuzzy coefficients to various field of production planning problem, transportation problem, and other real world multi-objective programming problems.
Cite this paper
Anil KumarNishad,Shiva RajSingh, (2015) Goal Programming for Solving Fractional Programming Problem in Fuzzy Environment. Applied Mathematics,06,2360-2374. doi: 10.4236/am.2015.614208
References
- 1. Charnes, A. and Cooper, W.W. (1968) Management Models of Industrial Applications of Linear Program. Vol. 1-2, Wiley, New York.
- 2. Lee, S.M. (1972) Goal Programming for Decision Analysis. Auerbach Publishers, Philadelphia.
- 3. Ignizio, J.P. (1976) Goal Programming and Extensions. D.C. Heath, Lexington.
- 4. Ignizio, J.P. (1982) Notes and Communications on the (Re)Discovery of Fuzzy Goal Programming. Decision Sciences, 13, 331-336.
http://dx.doi.org/10.1111/j.1540-5915.1982.tb00152.x - 5. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353.
http://dx.doi.org/10.1016/S0019-9958(65)90241-X - 6. Zimmermann, H.J. (1978) Fuzzy Programming and Linear Programming with Several Objective Functions. Fuzzy Sets and Systems, 1, 45-55.
http://dx.doi.org/10.1016/0165-0114(78)90031-3 - 7. Narasimhan, R. (1980) Goal Programming in a Fuzzy Environment. Decision Science, 11, 325-336.
http://dx.doi.org/10.1111/j.1540-5915.1980.tb01142.x - 8. Narasimhan, R. (1981) On Fuzzy Goal Programming-Some Comments. Decision Science, 12, 532-538.
http://dx.doi.org/10.1111/j.1540-5915.1981.tb00103.x - 9. Bellman, R.E. and Zadeh, L.A. (1970) Decision Making in a Fuzzy Environment. Management Sciences, 17, 141-164.
http://dx.doi.org/10.1287/mnsc.17.4.B141 - 10. Mohanty, B.K. and Vijayaraghawan, T.A.S. (1995) A Multiobjective Programming Problem and Its Equivalent Goal Programming Problem with Approprite Priorities and Aspiration Levels: A Fuzzy Approach. Computers & Operations Research, 22, 771-778.
http://dx.doi.org/10.1016/0305-0548(94)00066-H - 11. Kuwano, H. (1996) On the Fuzzy Multi-Objective Linear Programming Problems: Goal Programming Approach. Fuzzy Sets and Systems, 82, 57-64.
http://dx.doi.org/10.1016/0165-0114(95)00231-6 - 12. Chanas, A. and Kuchta, D. (1996) Multiobjective Programming in Optimization of Interval Objective Functions—A Generalized Approach. European Journal of Operational Research, 94, 594-598.
http://dx.doi.org/10.1016/0377-2217(95)00055-0 - 13. Chen, L.H. and Tsai, F.C. (2001) Fuzzy Goal Programming with Different Importance and Priorties. European Journal of Operational Research, 133, 548-556.
http://dx.doi.org/10.1016/S0377-2217(00)00201-0 - 14. Stanciulescu, C., Fortemps, P., Installe, M. and Wertz, V. (2003) Multi-Objective Fuzzy Linear Programming Problems with Fuzzy Decision Variables. European Journal of Operational Research, 149, 654-675.
http://dx.doi.org/10.1016/S0377-2217(02)00449-6 - 15. Lin, C.C. (2004) A Weighted Max-Min Model Fuzzy Goal Programming. Fuzzy Sets and Systems, 142, 407-420.
http://dx.doi.org/10.1016/S0165-0114(03)00092-7 - 16. Yaghoobi, M.A. and Tamiz, M. (2007) A Method for Solving Fuzzy Goal Programming Problems Based on MINMAX Approach. European Journal of Operational Research, 177, 1580-1590.
- 17. Cheng, H.F., Huang, W.L., Zhon, Q. and Cai, J. (2013) Solving Fuzzy Multiobjective Linear Programming Problems Using Deviation Degree Measures and Max-Min Method. Applied Mathematical Modeling, 73, 6855-6869.
http://dx.doi.org/10.1016/j.apm.2013.01.048 - 18. Soliman, O., Sarker Rahul, A. and Zahir, S. (2008) Fuzzy Goal Programming Model with Parametric Analysis for Regional Sustainability Development under Climate Change: A Case of Agriculture Sector. ASOR Bulletin, 27, 2-15.
- 19. Mishra, B. and Singh, S.R. (2013) Linear Fractional Programming Procedure for Multi Objective Linear Programming Problem in Agriculture System. International Journal of Computer Applications, 61, 45-52.
- 20. Bharati, S.K., Nishad, A.K. and Singh, S.R. (2014) Solution of Multi-Objective Linear Programming under Intuitionistic Fuzzy Environment. In: Babu, B.V., Nagar, A., Deep, K., Pant, M., Bansal, J.C., Ray, K. and Gupta, U., Eds., Proceedings of the Second International Conference on Soft Computing for Problem Solving (SocProS 2012), December 28-30, 2012, Advances in Intelligent Systems and Computing, Vol. 236, Springer India, New Delhi, 161-171.
http://dx.doi.org/10.1007/978-81-322-1602-5_18 - 21. Sen, S. and Pal, B.B. (2013) Interval Goal Programming Approach to Multiobjective Fuzzy Goal Programming Problems with Interval Weights. Procedia Technology, 10, 587-595.
http://dx.doi.org/10.1016/j.protcy.2013.12.399 - 22. Seyed, H. and Razavi, H. (2013) Multi-Objective Linear Programming with Interval Coefficients: A Fuzzy Set Based Approach. Emerald, 42, 482-496.
- 23. Azzabi, L., Dorra, A., Kaddour, B. and Abdessamad, K. (2014) Fuzzy Goal Programming to Optimization the Multi-Objective Problem. Science Journal of Applied Mathematics and Statistics, 2, 14-19.
http://dx.doi.org/10.11648/j.sjams.20140201.12 - 24. Marbini, A.H. and Tavana, M. (2011) An Extension of the Linear Programming Method with Fuzzy Parameters. International Journal of Mathematics in Operational Research, 3, 44-55.
- 25. Luhandjula, M.K. (1984) Fuzzy Approaches for Multiple Objective Linear Fractional Optimization. Fuzzy Sets and Systems, 13, 11-23.
http://dx.doi.org/10.1016/0165-0114(84)90023-X - 26. Chakraborty, M. and Gupta, S. (2002) Fuzzy Mathematical Programming for Multi Objective Linear Fractional Programming Problem. Fuzzy Sets and Systems, 125, 335-342.
http://dx.doi.org/10.1016/S0165-0114(01)00060-4 - 27. Pal, B.B., Moitra, B.N. and Maulik, U. (2003) A Goal Programming Procedure for Fuzzy Multiobjective Linear Fractional Programming Problem. Fuzzy Sets and Systems, 139, 395-405.
http://dx.doi.org/10.1016/S0165-0114(02)00374-3 - 28. Pop, B., Minasian, I. and Stancu, M. (2008) A Method of Solving Fully Fuzzified Linear Fractional Programming Problems. Journal of Applied Mathematics and Computing, 27, 227-242.
http://dx.doi.org/10.1007/s12190-008-0052-5 - 29. Cui, Y.H., Qu, J., Peng, Y., Wang, L. and Li, B. (2010) The Study of the Solution on Multi-Objective Linear Programming Problem under Fuzzy. 2010 Asia-Pacific Conference on Wearable Computing Systems (APWCS), Shenzhen, 17-18 April 2010, 286-290.
http://dx.doi.org/10.1109/APWCS.2010.79 - 30. Mehrjerdi, Y.Z. (2011) Solving Fractional Programming Problem through Fuzzy Goal Setting and Approximation. Applied Soft Computing, 11, 1735-1742.
- 31. Pitam, S., Kumar, S.D. and Singh, R.K. (2011) Fuzzy Multiobjective Linear plus Linear Fractional Programming Problem: Approximation and Goal Programming Approach. International Journal of Mathematics and Computers in Simulation, 5, 395-404.
- 32. Animesh, B. and Dewan, S. (2012) Priority Based Fuzzy Goal Programming Technique to Fractional Fuzzy Goals Using Dynamic Programming. Fuzzy Information and Engineering, 4, 165-180.
- 33. Ohta, H. and Yamaguchi, T. (1996) Linear Fractional Goal Programming in Consideration of Fuzzy Solution. European Journal of Operation Research, 92, 157-165.
http://dx.doi.org/10.1016/0377-2217(95)00052-6 - 34. Pal, B.B. and Sen, S. (2008) A Goal Programming Procedure for Solving Interval Valued Multi-Objective Fractional Programming Problems. 16th International Conference on Advanced Computing and Communications, ADCOM 2008, Chennai, 14-17 December 2008, 297-302.
- 35. Sohrab, E. and Morteza, P. (2012) Solving the Interval Valued Linear Programming Problem. American Journal of Computational Mathematics, 2, 51-55.
http://dx.doi.org/10.4236/ajcm.2012.21006 - 36. Kornbluth, J.S.H. and Steuer, R.E. (1981) Multiple Objective Linear Fractional Programming. Management Science, 27, 1024-1039.
http://dx.doi.org/10.1287/mnsc.27.9.1024
NOTES
*Corresponding author.