Received 27 July 2015; accepted 25 August 2015; published 28 August 2015

ABSTRACT

In this study, the impulsive predator-prey dynamic systems on time scales calculus are studied. When the system has periodic solution is investigated, and three different conditions have been found, which are necessary for the periodic solution of the predator-prey dynamic systems with Beddington-DeAngelis type functional response. For this study the main tools are time scales calculus and coincidence degree theory. Also the findings are beneficial for continuous case, discrete case and the unification of both these cases. Additionally, unification of continuous and discrete case is a good example for the modeling of the life cycle of insects.

Keywords:

Time Scales Calculus, Predator-Prey Dynamic Systems, Periodic Solutions, Coincidence Degree Theory, Beddington-DeAngelis Type Functional Response

1. Introduction

The relationships between species and the outer environment, and the connections between different species are the description of the predator-prey dynamic systems which is the subject of mathematical ecology in biomathematics. Various types of functional responses in predator-prey dynamic system such as Monod-type, semi-ratio- dependent and Holling-type have been studied. [1] is an example for the study about Holling-type functional response. In this paper, we consider the predator-prey system with Beddington DeAngelis type functional response and impulses. This type of functional response first appeared in [2] and [3] . At low densities this type of functional response can avoid some of the singular behavior of ratio-dependent models. Also predator feeding can be described much better over a range of predator-prey abundances by using this functional response.

In a periodic environment, significant problem in population growth model is the global existence and stability of a positive periodic solution. This plays a similar role as a globally stable equilibrium in an autonomous model. Therefore, it is important to consider under which conditions the resulting periodic nonautonomous system would have a positive periodic solution that is globally asymptotically stable. For nonautonomous case there are many studies about the existence of periodic solutions of predator-prey systems in continuous and discrete models based on the coincidence theory such as [4] -[12] .

Impulsive dynamic systems are also important in this study and we try to give some information about this area. Impulsive differential equations are used for describing systems with short-term perturbations. Its theory is explained in [13] -[15] for continuous case and also for discerete case there are some studies such as [16] . Impulsive differential equations are widely used in many different areas such as physics, ecology, and pest control. Most of them use impulses at fixed time such as [17] [18] . By using constant functions, some properties of the solution of predator-prey system with Beddington-DeAnglis type functional response and impulse impact are studied in [19] for continuous case.

In this study unification of continuous and discrete analysis is also significant. To unify the study of differential and difference equations, the theory of Time Scales Calculus is initiated by Stephan Hilger. In [20] [21] , unification of the existence of periodic solutions of population models modelled by ordinary differential equations and their discrete analogues in form of difference equations, and extension of these results to more general time scales are studied.

The unification of continuous and discrete case is a good example for the modeling of the life cycle of insects. Most of the insects have a continuous life cycle during the warm months of the year and die out in the cold months of the year, and in that period their eggs are incubating or dormant. These incubating eggs become new individuals of the new warm season. Since insects have such a continuous and discrete life cycle, we can see the importance of models obtained by the time scales calculus for the species that have unusual life cycle. Therefore, in this paper we try to generalize periodic solutions of predator-prey dynamic systems with Beddington-DeAn- glis type functional response and impulse to general time scales.

2. Preliminaries

Below informations are from [20] . Let X, Z be normed vector spaces, 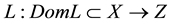be a linear mapping, 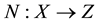be a continuous mapping. The mapping L will be called a Fredholm mapping of index zero if 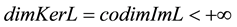and ImL is closed in Z. If L is a Fredholm mapping of index zero and there exist continuous projections and such that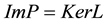, , 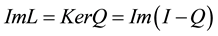then it follows that is invertible. We denote the inverse of that map by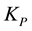. If Ω is an open bounded subset of X, the mapping N will be called L-compact on Ω if 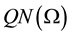is bounded and 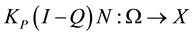is compact. Since ImQ is isomorphic to KerL, there exists an isomorphism.

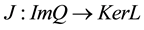The above informations are important for the Continuation Theorem that we give below.

Theorem 1. (Continuation Theorem). Let L be a Fredholm mapping of index zero and N be L-compact on Ω. Suppose

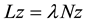(a) For each, every solution z of is such that;

(b) 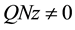for each and the Brouwer degree Then the operator equation has at least one solution lying in.

We will also give the following lemma, which is essential for this paper.

Lemma 1. Let and. If is w-periodic, then

3. Main Result

The equation that we investigate is:

(1)

, , , , , ,

, and Here is periodic, i.e

if then and, ,

, , and

Each functions are from

Lemma 2. If and then all positive solutions are tends to 0 as t tends to infinity.

Proof. If we using the first equation of (1) we obtain,

Since Hence

Similarly

Theorem 2. In addition to conditions on coefficient functions

If

and

then there exist at least a w-periodic solution.

Proof. with the norm:

and

with the norm:

Let us define the mappings and by such that

and such that

Then, and are constants.

is closed in and, therefore is a Fredholm mapping of index zero.

There exist continuous projectors and such that

and

where

The generalized inverse is given,

Let

and

Clearly, and are continuous. Since and are Banach spaces, then by using Arzela-

Ascoli theorem we can find is compact for any open bounded set Addition-

ally, is bounded. Thus, is L-compact on with any open bounded set

To apply the continuation theorem we investigate the below operator equation.

(2)

Let be any solution of system (2). Integrating both sides of system (2) over the interval we obtain,

(3)

From (2) and (3) we get

(4)

where

(5)

where

Note that since and there are q impulses which are constant, then there exist, such that

(6)

(7)

By the second equation of (3) and (6) and the first assumption of Theorem 2, we have

and where

Using the second inequality in Lemma 1 we have

(8)

By the first equation of (3) and (6) we get where

using the first inequality in Lemma 1 and (4), we have

(9)

By (8) and (9) Using (9), second equation of (3) and first equation of (7), we can derive that

Therefore

By the assumption of the theorem we can show that

and

where

Hence, by using the first inequality in Lemma 1 and the second equation of (3),

(10)

We can also derive from the second equation of (3) that

Again using second assumption of Theorem 2 we obtain

and where

By using the second inequality in Lemma 1 and (5), we obtain

(11)

By (10) and (11) we have Obviously, and are both inde-

pendent of. Let. Then Let and verifies the requirement (a) in Theorem 1. When, is a constant with then

where such that

Define the homotopy where

Take as the determinant of the jacobian of G. Since, then jacobian of G is

All the functions in jacobian of G is positive then is always positive. Hence

Thus all the conditions of Theorem 1 are satisfied. Therefore system (1) has at least a positive w-periodic solution.

Theorem 3. If same conditions are valid for the coefficient functions in system (1) and

is satisfied then there exist at least a w-periodic solution.

Proof. First part of the proof is very similar with the proof of Theorem 2. By (2), (3) and (6)

By (3) Also by the assumption of Theorem 3 Then we get .

And using the second inequality in Lemma 1 we have

(12)

By the first equation of (3) and (6)

Then we get where

Using the first inequality in Lemma 1 we have

(13)

By (12) and (13) From the second equation of (3) and the second equation of (7), we can derive that

Therefore

Since then where

Hence, by using the first inequality in Lemma 1 and the second equation of (3),

(14)

By the assumption of Theorem 3 there exists such that

is true. We need to get such that Let us assume there exists such

that Then by using (6) and (7) we obtain

If such t, s does not exists then . Also from the first equation of (3), we have

By using first inequality in Lemma 1, we have, where

Using the second equality in (3) and the assumption of the Theorem 4, we obtain

This implies where

Hence, according to the above discussion we have Using second inequality

in Lemma 1 we have where

Thus Obviously, and are both independent of. Let

. Then Let then Ω verifies the requirement

(a) in Theorem 1. Rest of the proof is similar to Theorem 2.

Let there are two insect populations (one of them the predator, the other one the prey) both continuous while in season (say during the six warm months of the year), die out in (say) winter, while their eggs are incubating or dormant, and then both hatch in a new season, both of them giving rise to nonoverlapping populations. This situation can be modelled using the time scale

Here impulsive effect of the pest population density is after its partial destruction by catching, poisoning with chemicals used in agriculture (can be shown by) and impulsive increase of the predator population density is by artificially breeding the species or releasing some species. In addition to these, if the model assumes a BeddingtonDeAngelis functional response as in (1) and if the assumptions in Theorem 2 or 3 are satisfied then there exists a 1-periodic solution of (1).

Corollary 1. If in the system (1) and

is satisfied then the system (1) has at least one w-periodic solution.

Example 1. k start with 0.

Impulse points:, and.

,

,

Example 1 satisfies all the conditions of Theorem 2, thus it has at least one periodic solution.

Example 2. k start with 0.

Impulse points:, and.

,

,

Example 2 satisfies all the conditions of Theorem 3, thus it has at least one periodic solution.

Theorem 4. If all the coefficient functions in system (1) is positive, w-periodic, from and impulses are 0; also

is satisfied then there exist at least a w-periodic solution.

Proof. First part of the proof is similar to Theorem 2, only difference is the zero impulses. If the assumption of Theorem 4 is true then there exists such that for all

is satisfied. Suppose there exist such that. Then similar to proof of Theorem 4 we can find.

If such s, t does not exist. Using the first equation of (1) and assuming is the minimum of. Then

Thus we get

Then

If is a right dense point then If is right scattered, we interested

with the maximum of the solution. Let be the maximum of x(t).

Then If, then

If, then

Thus

Using (3) and (7) above results we obtain

This implies

Hence, according to the above discussion we have Using second inequality in

Lemma 1 we have Thus Rest of the proof

is similar to Theorem 2.

Corollary 2. In Theorem 4 if we take as then we get Theorem 3 in [21] .

Example 3. k start with 0.

Example 3 satisfies all the conditions of Theorem 4, thus it has at least one periodic solution.

All the graphs that we see in Figures 1-3 are obtained by Mathlab.

4. Discussion

In this paper, the impulsive predator-prey dynamic systems on time scales calculus are studied. We investigate when the system has periodic solution. Furthermore, three different conditions have been found which are necessary for the periodic solution of the predator-prey dynamic systems with Beddington-DeAngelis type functional response. Also by using graphs, we are able to show that the conditions that are found in Theorem 2, 3

and 4 are enough for the periodic solution of the given system. In this work, since our system can model the life cycle of the such species like insects, what we have done new is finding necessary condition for the periodic solution of the given predator-prey system with sudden changes. In addition to these, according to the structure of the given time scale, the conditions that are found in Theorem 2, 3 and 4 become useful.

Cite this paper

Ayşe FezaGüvenilir,BillurKaymakçalan,Neslihan NesliyePelen, (2015) Impulsive Predator-Prey Dynamic Systems with Beddington-DeAngelis Type Functional Response on the Unification of Discrete and Continuous Systems. Applied Mathematics,06,1649-1664. doi: 10.4236/am.2015.69147

References