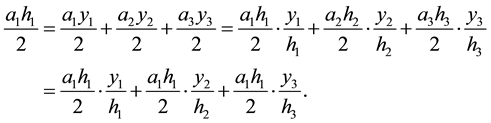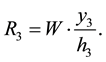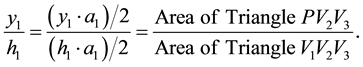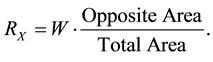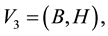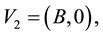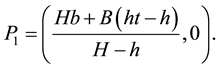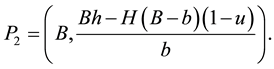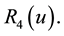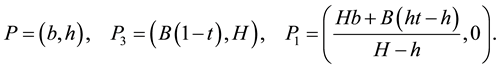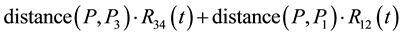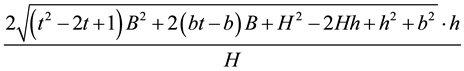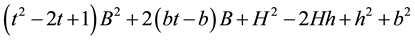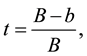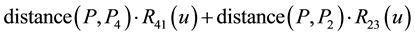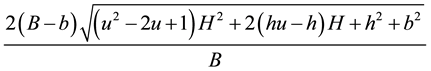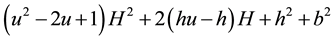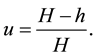Applied Mathematics
Vol.06 No.03(2015), Article ID:54973,17 pages
10.4236/am.2015.63055
Reactions on Rigid Legs of Rectangular Tables
Jorge Garcia1, Greg Wood2, Fernando Barrera-Mora3
1Mathematics Department, CSU Channel Islands, Camarillo, USA
2Physics Department, CSU Channel Islands, Camarillo, USA
3Área Académica de Matemáticas y Física, UAEH, Hidalgo, Mexico
Email: jorge.garcia@csuci.edu, gregory.wood@csuci.edu, fbarrera10147@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 January 2015; accepted 23 March 2015; published 24 March 2015
ABSTRACT
A weight is placed on the top of a rectangular rigid ideal table with four legs, each leg is placed at each vertex of the rectangular table. It is assumed that the legs do not bend when the weight is added. The reactions are computed by assuming the table is supported on a beam, introducing two new beam parameters and minimizing a deflection function of the new parameters. A physical experiment is performed in the lab and the reactions on each leg are provided. The experimental results match the theoretical ones obtained by the proposed model. Geometrical interpretations of the results are given.
Keywords:
Reaction Forces, Rectangular Table, Deflection, Rigid Table, Indeterminate Case, Torque

1. Introduction
Euler [1] set a problem in St. Petersburg Academy of Sciences in 1773 in his dissertation De pressione ponderis in planum cui incumbit. The problem consisted of placing a weight on the surface of a rectangular table supported on four legs and determining the four reaction forces of the legs. Euler claimed that the solution to this problem “is not only much harder but also doubtful and misleading”. He said that the imperfections of the feet might force the body to rest on only three legs and the pressure on the fourth one may be null. In Section 3, we observe that the problem arises because the system of equations given by the mechanics of static equilibrium is a linear system of equations that consists of three equations and four unknowns, being these four unknowns precisely the reaction forces at the legs of the table. This linear system of equations is called an indeterminate system.
Euler then changed the problem: the support is no longer on a rigid plane but on a soil. Euler argued that to understand the problem on a rigid body, one must pose the problem on a soft body, and that once this problem has been understood there, the solution from one body to another can be carried out by a mathematical calculus argument (a limit argument), “in the case of a soft ground where four feet penetrate, one must assume that the pressures brought about by the feet are proportional to those movements”. This is the principle where Euler based his arguments. He stressed that even though here a soft ground is considered, this phenomena is in- dependent of the ground because the movements, that were hypothetically introduced, “happen with the support of our imagination”.
After Euler posed and discussed the problem, many people have studied it in depth, each contributing at some extent towards a richer interpretation of the problem. These people [2] include Jean Baptiste Lerond d’Alambert in 1780 who dedicated to the support problems part of a memoir entitled Sur quelques questions de Méchanique, Abbot Charles Bossut in 1788 who gives an interpretation of a triangular table in terms of two levers, Paolo Delanges of Brescia in 1790 who three times in 1790, 1798 and 1811 made a proposal for an experimental investigation, Pietro Paoli in 1792 who checked the validity of the computations done by others regarding the problem, Anton Maria Lorogna in 1794 who attempted to formulate a “reasonable” principle that can not be obtained from the principle of mechanics, Mariano Fontana [3] in 1798 who provides a formula to obtain the reactions on a parallelogramic table by imagining that the weight is transmitted to the sides of the parallelogram, later Fontana writes “I started to meditate more carefully about this problem and I have found that, the solution to the problem is not determined only by the principles of mechanics”. We will refer to Fontana later in this paper.
Other people that also worked on this problem (see [2] ) were Guiseppe Venturoli in 1806, Gabrio Piola in 1824, Barsotti in 1842 and Ottaviano Fabrizio Mossotti in 1858; Malfatti in 1805 published three memoirs, in one of them he stresses that if the object is placed at the center of a regular polygon, all the reactions at each of the vertices of the polygon will be equal and hence they can not be “assigned arbitrarily”, hence in this case there is no statics indetermination. It was finally Navier [4] in his Résumé des leçons données à l’Ecole royale des ponts et chaussées in 1825 who recognized that the indeterminate system will no longer be indeterminate if one takes into account the “elasticity of the reacting bodies”. Even though the solution to the problem of the rectangular table appears for the first time in Castigliano’s thesis in 1873, Augustin Cournot in 1828 is the one who describes an extrema point in the pressure involved in the problem, he talks about a minimum for the pressure exerted in the body. A derivation of the solution can be appreciated in Du Bois 1902 [5] , he considers that each foot of the table is hence a spring obeying Hooks’ Law and the work expressed in terms of the potential energy is computed. Using The Principle of Least Work, a fourth equation is obtained by obtaining the derivative of the total potential energy and setting it to zero. Therefore we now have a system of four in- dependent equations and four unknowns which can be solved in this case providing a unique solution.
There is a list of people who contributed to the solution of the problem during the 1830-1873 period, the list includes Moseley, Pagani and Menabrea, Massotti and Dorna among others. For a more detailed history of the problem you can read [2] .
The paper by Benvenuto [2] contains not only more details about the history of the problem itself but also gives a geometrical interpretation of the triangular table solution (as the one we have in this paper), it provides a short discussion and a geometrical interpretation of a solution given by Fontana to the general parallelogramic case (hence the rectangular case is included) which we will address in Section 5.
Recently, three NASA engineers Surya N. Patnaik, Dale A. Hopkins and Gary R. Halford published a paper in 2004 [6] where they discussed the problem and introduce a compatibility condition (a fourth equation) that they obtained based on the deformation displacements of the legs, these deformations are written in terms of the angles at which the table tilts. When this compatibility condition is expressed in terms of the forces, it is then concluded that the sum of the reactions of two opposite corners of the table matches the sum of the reactions of the other two opposite corners. After all, the solution to the new system of four equations with four unknowns that Patnaik, Hopkins and Halford obtained agrees with the one described in Du Bois [5] .
One of our main hypotheses (and here we differ from the results obtained by all the previous people) is that the legs of the table are completely rigid, i.e. they do not deflect or deform. The way we approach the problem is by considering the fact that the reactions on the legs are known and given in terms of two parameters. These parameters are obtained by first assuming that the four legs are replaced by a beam with end points at opposite edges of the table, then changing roles with the other two sides of the table. One important and natural assump- tion is a consistency condition on the forces in terms of these two parameters. We finally give a condition (and here is where our main contribution comes in) on the deflection of the table (not of the legs). This process allows us to minimize such deflections obtaining the values of the parameters we started with initially, providing therefore one more equation which, together with the three that one has by considering mechanical assumptions, one is able to find a solution for the table of rigid legs. In a forthcoming paper, we will generalize these results to the quadrilateral table and we are also considering increasing the number of legs on a future paper.
Regarding the structure of the paper, in Section 2, we discuss the Beam and the Triangular case, in each case we solve the system and we provide a geometrical interpretation that matches the ones given in Benvenuto [2] . In Section 3, we carefully analyze and discuss the indeterminate case of a rectangular table. Right after, in Section 4, we establish the main hypotheses under which we will solve the rectangular table case. It is precisely in Section 5 where we give conditions that will help us to solve the problem.
Finally, in Section 6 we provide some lab results that are consistent with the theoretical values obtained by the proposed theoretical model. A discussion on how these lab values are obtained is contained in this section too.
2. Beam and Triangular Tables
In this section we will discuss the beam (one dimensional table) and the triangular table case.
2.1. Beam Case
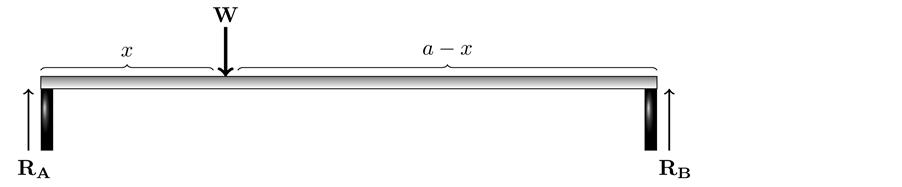
A load
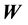 of magnitude
of magnitude
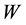 is placed at a point (at a distance x from one of the end points) on the beam of length a. The load is placed perpendicular to the beam. Two reaction forces
is placed at a point (at a distance x from one of the end points) on the beam of length a. The load is placed perpendicular to the beam. Two reaction forces
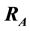 and
and
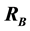 at the end points of the beam occur in the opposite directions of the load
at the end points of the beam occur in the opposite directions of the load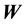 . Figure 1 illustrates the beam and the forces.
. Figure 1 illustrates the beam and the forces.
Here we are interested in finding the magnitudes
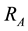 and
and
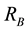 of the reaction forces
of the reaction forces
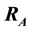 and
and
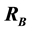 on each leg of the beam. We assume that the beam and the legs are rigid. This problem can be easily solved using torques. The equilibrium equation system
on each leg of the beam. We assume that the beam and the legs are rigid. This problem can be easily solved using torques. The equilibrium equation system
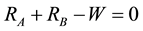
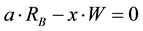
has the following solution
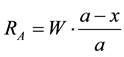

2.2. Geometric Interpretation
Given a leg of the beam, the point where the load is placed divides the beam into two segments, one adjacent to the given leg and one opposite to it, in each case, the solution takes the form
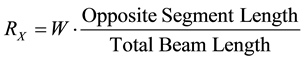
Figure 1. The beam case consists of a two legs table and a load W located at distance x from one of the legs.
2.3. Triangular Table
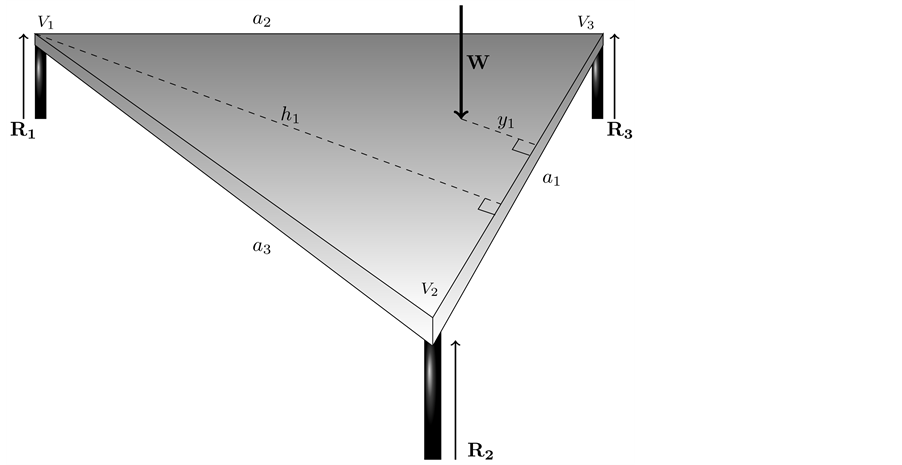
Consider a triangular table of sides
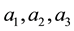 and legs at vertices
and legs at vertices

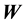
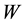
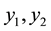
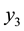
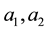
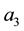
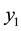

Here we have a rigid surface and we are assuming that the legs do not bend. For


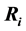
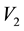

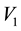
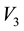
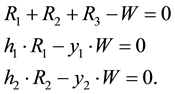
When we solve the system we find that
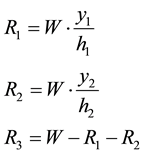
By adding the three small areas of the triangles
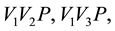
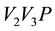
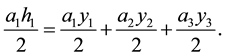
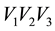
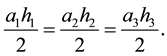
Figure 2. In this triangular table, the point where the load W is placed, determines height y1 with respect to the vertex V1.
Figure 3. The point P divides the triangle in three triangles by drawing lines from P to each vertex.
Hence
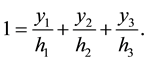
From Equation (2.3) and Equation (2.2) we can also conclude that
2.4. Geometric Interpretation
On the table’s surface, let’s draw three lines from the point where the load is located to the three corners of the table. We obtain three smaller triangles (shaded differently on the figure) inside the big triangle as in Figure 3.
Among these three triangles, the triangle
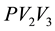

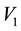
We observe that
From the solution to the triangular case given by Equation (2.2) and the previous observation, we can establish a formula to obtain the magnitude of the reaction forces at any single leg in the triangular table according to
3. Rectangular Table, Indeterminate Case
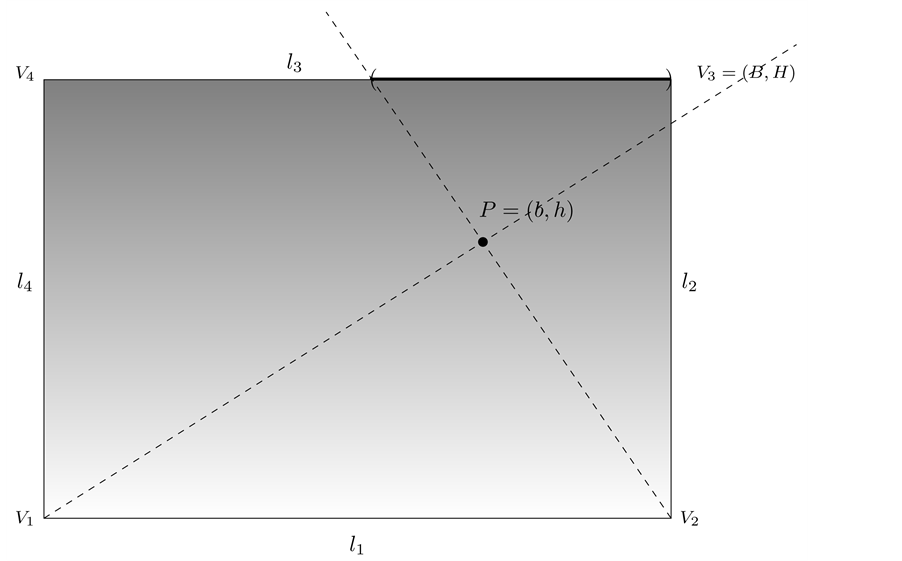
Consider a rectangular table of sides B and H and legs at each of its vertices
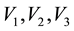

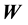
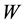
Here once more we have a rigid surface and we are assuming that the legs do not bend. For
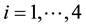

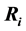
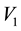
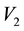

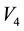
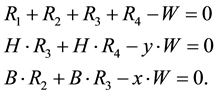
Figure 4. Rectangular table and load W on the table placed at a point with distances x and y to the sides of the table.
This is all the mechanics says about the system. Systems of three equations and four unknowns might have no solutions or have an infinite number of solutions according to the consistency of the system and the existence of non-trivial solutions to the homogeneous system. It is the case that this system is consistent and the homo- geneous system has non-trivial solutions, hence it has an infinite amount of solutions. We call these type of systems indeterminate systems.
Patnaik and Hopkins [6] discussed the problem under different hypotheses. They assume that the legs deform and take in consideration the modulus of elasticity and the cross-sectional areal of the legs. By using the principle of least work, they arrive at a fourth equation which they refer to it as compatibility condition:

Adding this equation to the system 3.4 we obtain solutions where sometimes the reactions magnitudes are negative according to where the load is placed (a negative magnitude of a reaction means that the reaction force is pointing in the same direction as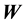
We should note that the problem we are approaching here is different. We will define the problem in the next section.
4. Main Hypotheses
We are considering a rectangular table whose legs bent, shrink or deflect a sufficiently small amount that we are neglecting it, therefore in our case, the legs of this rectangular table deflect zero, i.e., they do not deflect at all. We are also assuming that the table’s surface is rigid, uniform and homogeneous enough to disregard any conditions about the material, hence we are also assuming that our table is an ideal rigid table. Let’s assume for the moment that the table weights 0 (at the end of the problem, to obtain the final reactions magnitudes at each leg, we could add 1/4 of the table weight to each reaction by symmetry).
The fact that in our case the legs do not deflect is the main difference with the work of Patnaik and Hopkins [6] . Whereas in the results of Patnaik and Hopkins, the reactions on some legs might point downwards because their flexible-legs table tilts, in our case, that does not happen, all the reactions point upwards.
Main Hypothesis 4.1. The rectangular table consists of a rigid flat surface and rigid legs, hence neither the legs nor the surface deform or deflect. An ideal object of weight

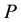
5. Solving the Rectangular Table Case
Consider a view from the top of the rectangular table described on Section 3. We are labeling the vertices with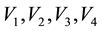
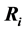
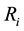
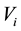
and they have the following coordinates,
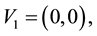
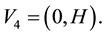
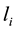
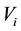
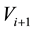
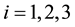
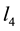

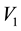
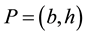
the point where the load

Since the legs are rigid, the table does not tilt, hence each magnitude
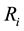
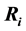
We can imagine for a second that legs 3 and 4 disappear and that we want to equilibrate the table by placing an extra leg, leg 34 at a point
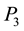
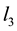
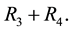

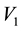
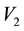
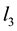

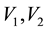

Let’s place such a leg at the point
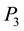
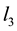
number between 0 and 1 such that
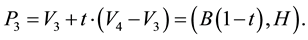
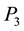
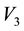

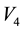
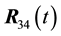
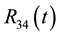
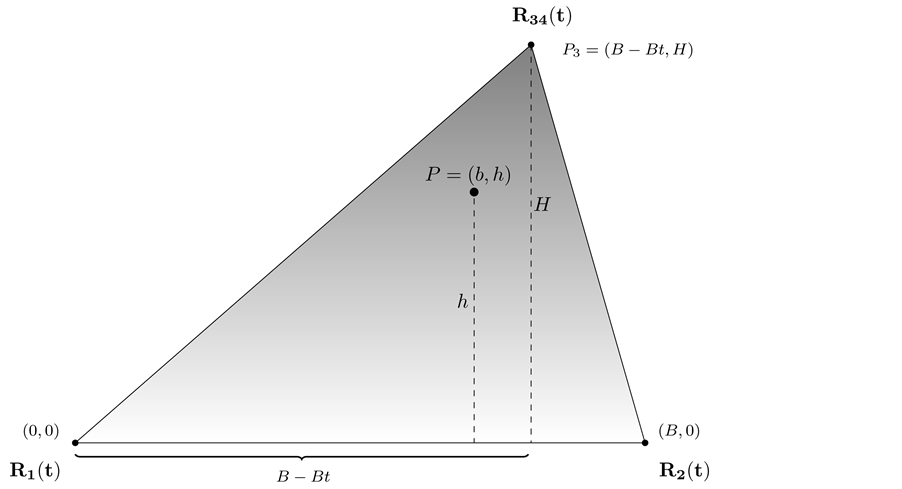
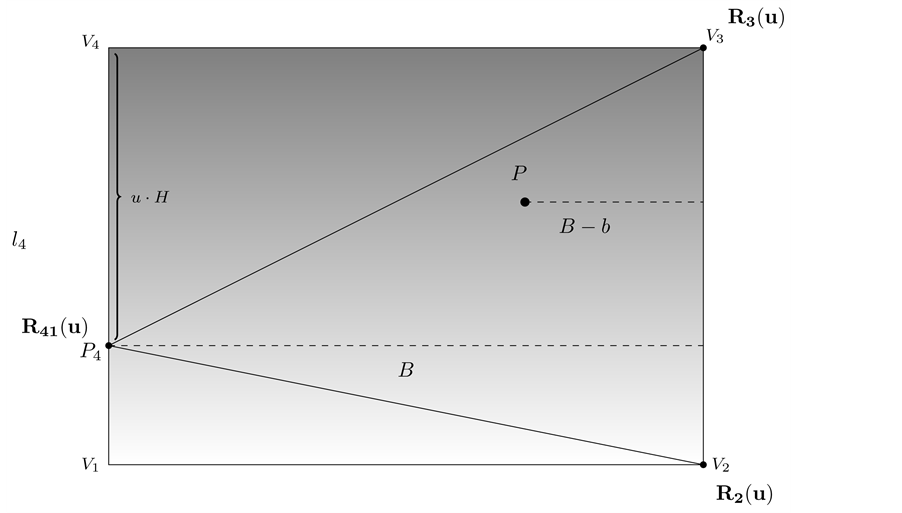
From Figure 6, we can assume that the table we are dealing with is a triangular table, therefore the solved case applies (Figure 7).
If we calculate the resultant torque on the body about the x-axis as well as calculating the torque about the y-axis, we can also obtain an equilibrium equation system (equivalent to System 2.1) for this triangular table
Figure 5. In this view from the top of the rectangular table described before, a load W is placed on the table. On segment l3 is drawn an interval where leg 34 will be placed.
Figure 6. In this view from the top of the rectangular table described before, reaction force R34(t) on segment l3 replaces forces R3 and R4 for some t in the interval [0; 1].
Figure 7. Triangular table supported at V1; V2 and P3 = P3(t) has reaction forces R34(t); R1(t) and R3(t).
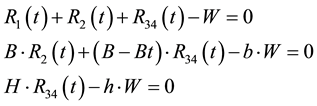
We can easily solve for
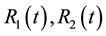
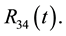

If we now remove leg 34 and place back the leg 3 and leg 4,
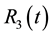
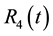
To summarize, the solution to the rectangular case that depends on the parameter t, is given by
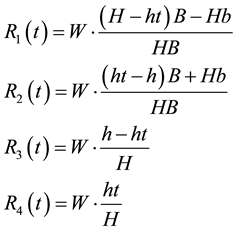
The solution
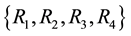
Condition 5.1.
The reactions
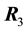
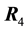
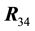
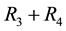

The procedure that follows consists of finding such point
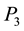
Similar to the description above, the reactions
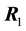
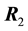
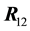
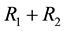
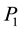
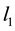

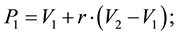
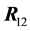
tutes the reactions
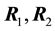
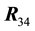
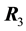
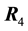
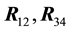
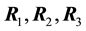
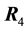
Condition 5.2. The points

Under this condition, the point
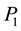
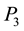
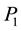
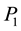
When we do the same analysis as before, but this time using leg 3, leg 4 and leg 12 (at the point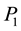

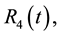
Similarly, we can now think that the reactions

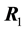

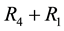
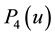
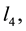
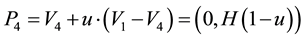
Performing the same analysis as before, we calculate the resultant torque on the body about the axis determined by
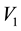
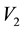
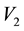
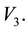
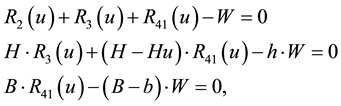
Proceeding as before, we arrive at the solution to the system 5.8
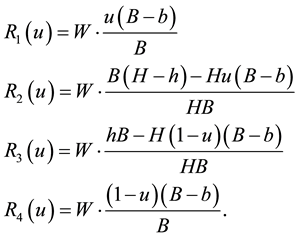
Analogously to Condition 5.2, the point

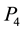
Figure 8. In this view from the top of the rectangular table described before, reaction force R41(u) on segment l4 replaces forces R4 and R1 for some u in the interval [0; 1].
Figure 9. Points P3; P and P1 are collinear as well as points P4; P and P2.
When doing the same analysis, such point also determines the same values
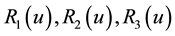
These conditions of collinearity, do not provide any extra information, it only allows us reduce to two para- meters

A natural assumption is that the solution given by considering the point
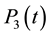

Condition 5.3. The solutions to the system 5.9 agree with the solutions to system 5.7, in other words, the system is self-consistent.
This brings us to the equation
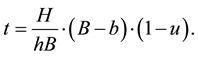
This does not solve the problem; however, whichever the solution is, there are parameters t and u such that the solution can be expressed as in the system 5.7 or 5.9, and those parameters should be related by Equation (5.10).
Since we are considering a rigid surface, we are expecting that the surface strains only a little bit, we really want the surface to strain the least to be in equilibrium, it is then a natural requirement to ask that the
table strains the least in two directions. Let’s consider only the line that goes from
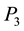
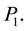
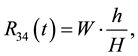

A way of measuring the deflection of the surface along this line is by considering the sum of the magnitudes of the torques at the points
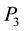
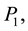
In our case, since

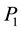
Since we are asking this quantity to be minimum, we need to minimize this as a function of t. The previous expression is minimum when the inside of the square root is minimum, hence to minimize the previous ex- pression, we set to zero the derivative of
with respect to t, which gives

therefore the point
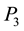

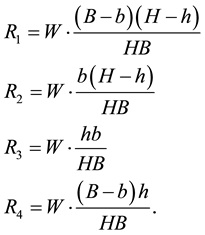
If we now consider the other line that goes from
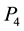
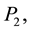
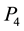
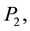
Once more, using collinearity and similar triangles, this quantity becomes
By a similar argument, minimizing the previous expression is equivalent to minimize the expression inside the square root as a function of u. Therefore, we need to set to zero the derivative of
which gives
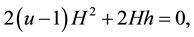
Notice that this value of u agrees with the one obtained by substituting
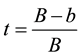
Therefore the point
which also provides, according to System 5.7, the solutions
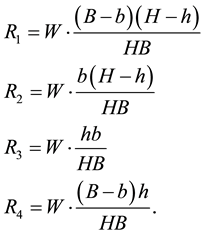
In a forthcoming paper, we will generalize these results.
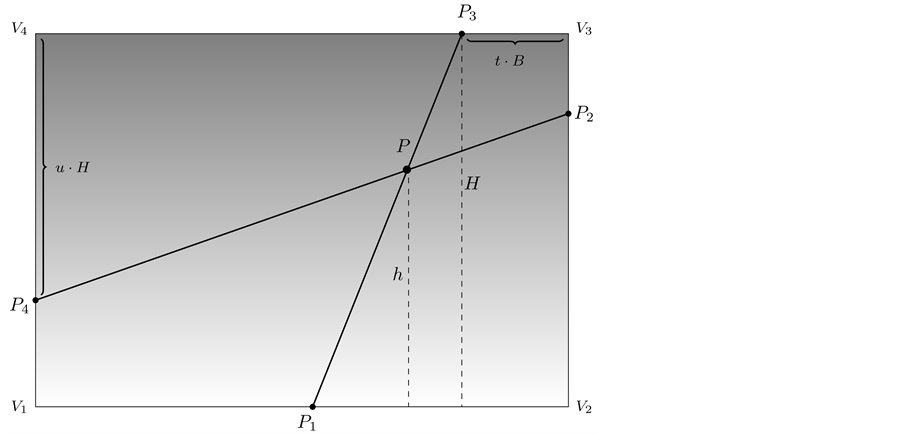
Geometric Interpretation
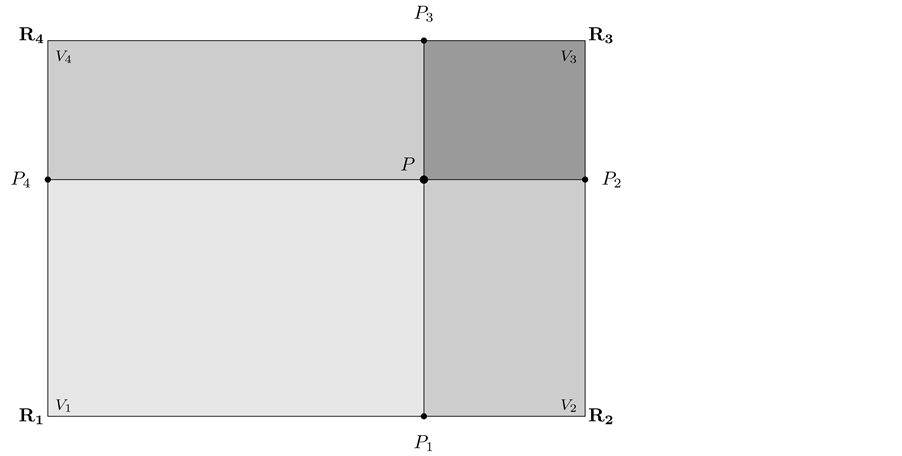
We notice that the solutions achieved here are self consistent, the points
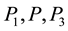
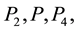
From Figure 10, it can be easily seen, by drawing the corresponding lines, that the points
To each vertex of the table, among the four areas of those rectangles, one area is where the vertex is located, two areas are adjacent to the vertex and one area is opposite to the vertex. The formula obtained in Solution 5.11 or in 5.12 to compute the magnitudes of the reactions at any single leg in the rectangular table is given by
as proposed by Fontana [3] (when the parallelogram becomes a rectangle); however, Fontana imagined that this formula had to be true without any hypothesis and never justified such formula. We, in this paper, stated the conditions under which this formula is true.
6. Experimental Results
6.1. Summary of Experimental Results
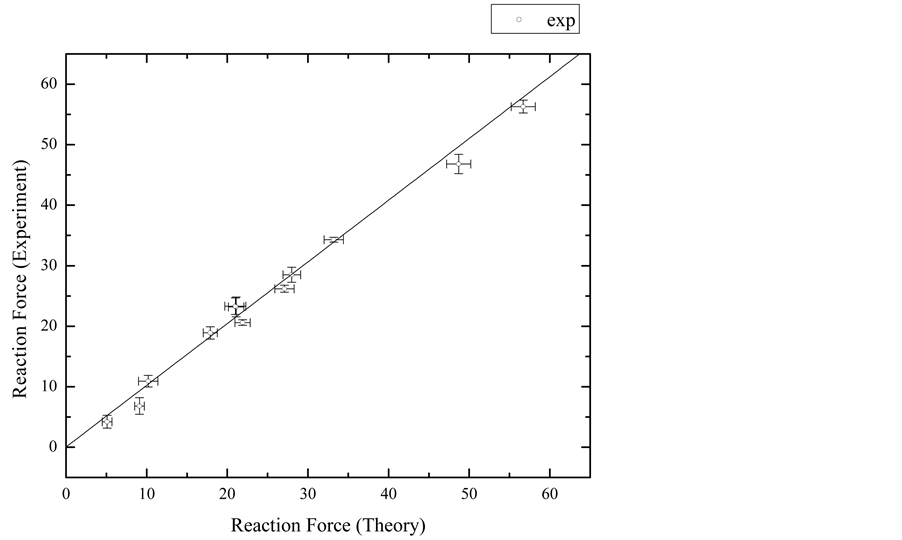
To test the predictions of the Equation (5.11) above, load weights of mass 0.200 kg up to 3.50 kg were sus- pended from a rectangular aluminum plate. Reaction forces were measured by digital scales affixed to the cor- ners of the plate. A detailed procedure is described below. The resulting experimental reaction forces agree well with the theory, as seen in Figure 11. The experimental values versus the theoretical ones are fit by a straight line and the resulting fitting parameters are consistent with agreement. The slope is consistent with one (best fit slope of
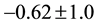
In Figure 11, the solid line is a best fit line to the data and is consistent with agreement between theory and experiment: The slope is consistent with one (best fit slope of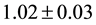
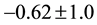
Figure 10. The point P where the load W is placed divides the rectangle into four rectangles. In this gure, rectangle P1PP2V2 is opposite to vertex V4.
Figure 11. Experimental versus theoretical fractions of the load weight found at each reaction force.
mental fraction reaction force is the slope of a linear fit such as those in Figure 12 (reaction forces versus load weights). The y-error bars on the data are uncertainties from the resulting linear fits, such as in Figure 12. The x-error bars are from calculations of the uncertainties of the positions of the load weights, limited by the ap- paratus.
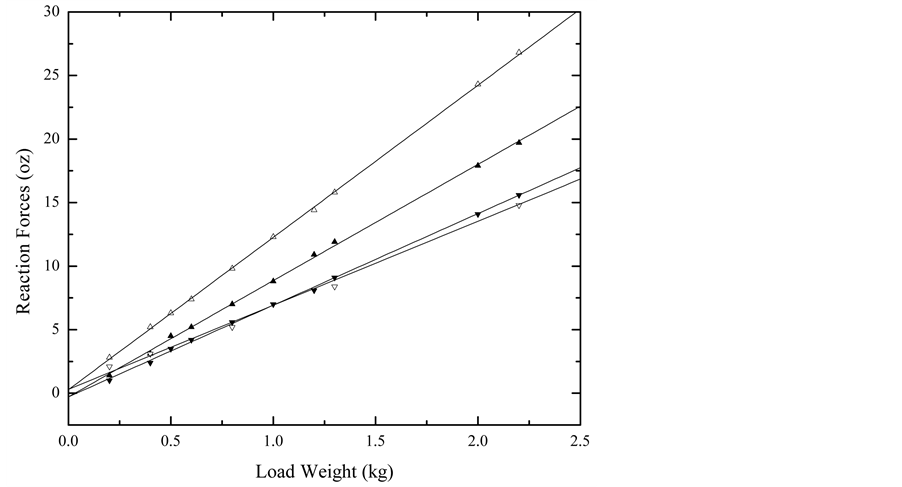
Each reaction force in Figure 11 is derived from a series of data of the measurement of reaction force versus load weight. In Figure 12, the four reaction forces are plotted versus load weight for one of the three locations (called Location 2, details below). The slope of each linear fit is included in Table 1. To form the fraction sup- ported by one reaction force, the slope corresponding to that force is divided by the sum of the four slopes.
In Figure 12, total plate size is (34.35, 22.9) cm. Data are summarized in Table 1.
On Table 1, the slopes and y-intercepts are from the linear regression fits of the experimental reaction forces versus load weight, plotted in Figure 12. The fractions of the load weight supported by each leg (the
On Table 2, the three locations load weights were placed are labeled 2, 3, and 6. Experimental fractions of support of the load weight (labeled f(exp) in this table) are computed as in Table 1: by dividing the slope of the individual reaction force versus load weight graph by the sum of the slopes. Theory is computed by Equation (5.12). The uncertainty is solely from the uncertainty in the experimental slope. Although the agreement is quite good between experiment and theory, there is additional uncertainty beyond only that of the linear regression fits. Possible sources are discussed below.
On Table 3, all values have a measurement uncertainty of 0.1 cm, but the nuts affixing the machine screws to the plate have diameters of 0.8 cm, thus this latter uncertainty is employed to produce the x-error bars on Figure 12.
6.2. Estimation of Uncertainties
The slopes and y-intercept values in the data Table 1 and Table 2 have uncertainties which arise from the linear regression fitting (performed with Originlabs Origin software). Individual reaction force measurements have
Figure 12. Reaction forces for the load weight placed at (20.7, 12.6) cm.
Table 1. The table of reaction forces for weight at location two, given by (20.7, 12.6) cm in the (34.35, 22.9) cm plate.
Table 2. Summary of all three experiments.
Table 3. Coordinates of the three load weights (Loc 2, 6 and 3) and the four corner supports (Labeled AD) in rectangular form.
uncertainties of 10 grams due to the limitations of the accuracy of the scales (this corresponds, roughly, to the size of the symbols in Figure 12). The masses used as load weights are accurate to under 1% which is negligible compared to other sources.
In calculating the theoretical rigid plate reaction forces, from Equation (5.11), above, the dominant source of uncertainty is the location of the load weights. These are constrained by the size of the nuts, which are 8.0 ± 0.2 mm across (from corner to corner, the longest distance across the hexagonal nut) thus the uncertainty of the load weight position is taken to be ±4 mm, which produces the horizontal error bars in Figure 12. The other meas- urements dealing with the dimensions of the plate are, somewhat arbitrarily, assigned zero uncertainty. If the uncertainty due to the nuts (same size as above) at the corners of the plate are included, significantly larger error bars are produced.
6.3. Procedure
The goal of the procedure is to measure the distribution of weight from a single load weight onto supports places at the four corners of the table. To do so, it is important that the table remain level during measurements. Several methods were investigated to reach optimal conditions the most successful of which are detailed below (Figure 13).
Four PASCO SE-9372 laboratory jacks are places close to, but outside, where the four corners of the rec- tangular plate will lie. Height of each jack is set to near the middle of the range of travel, allowing future up or down adjustment. At approximately equal height, a right angle clamp is affixed to each ring stand. Steel cross- bars are connected to pairs of ring stands. A carpenter’s level is used to check for levelness. With meter stick, ensure the crossbars are roughly parallel and separated by the width of the plate.
The longer side of the rectangle is here termed the length; the shorter side the width. The longer sides should be directly under the crossbars. PE scales are clamped to crossbars. Scales are connected to the plate via steel machine hooks with threads which screw into the plate. To avoid stripping the threads, washers are placed below the plate and tightened. The threaded screws give a second method (after the lab jacks) to level the plate. At this point, level the plate adjusting only the screws. Ensure the hooks below the PE scales are vertical. To detect any deviation from levelness, one or more carpenter’s levels can be left on the plate. The four PE scales are tarred at this point.
Now the load weight can be suspended from the plate and the reaction forces can be measured by the four scales. However, if the load weight is not placed near the center of the plate, large load weights cause the plate to rotate out of level. For these larger load weights, re-level the plate using the lab jacks, then remove load weight. Plate will rotate somewhat out of level. Tare scales. Add load weight (which will rotate the plate back very close to level) and record reaction force readings.
6.4. Materials
Plates are fabricated from 6061 aluminum with a thickness of 3.18 mm with threaded holes for the load weights and measuring reaction forces of inner diameter 2.69 mm, outer diameter of 3.51 mm. Steel washers connecting
Figure 13. One of the PE scales supporting the rectangular plate and a dark hanging weight below. The black threaded eye bolt has black washers clamping it to the plate both above and below the plate. However, these can be loosened and the threaded bolt can be adjusted slightly to help level the plate, initially. Later re-leveling of the plate for large masses is done via lab jacks (not pictured) which support the ring stands which in turn support the horizontal crossbars (seen near the top of the gure).
screws to plate have a width from corner to corner of 8.0 mm and a width from flat side to parallel flat side of 7.0 mm and a height of about 2.5 mm.
Weights and scales are affixed to the plate via steel machine screws, clamped to plate via washers. Scales are West-Boao Science & Technology Co., Ltd. brand ETWT001 portable electronic scales, with maximum load of 50 kg and accuracy to 10 grams.
7. Conclusion
Through this paper the well known beam case was provided, the triangular table case was also provided and the geometrical interpretations of the reaction forces at any given leg were given. The indeterminate case of the rectangular table, also well known, was discussed. The hypotheses to our problem in Section 4 clarified the situation of the problem we wanted to solve. By employing the method of introducing two parameters and supporting the table on ideal beams and minimizing a quantity that somehow measures the deflection of the table surface, we were able to solve the problem in Section 5. The main difference of our method and the one provided by Patnaik, Hopkins and Halford [6] is that we have different hypotheses. The results from Patnaik, Hopkins and Halford [6] and our result do not contradict each other, we just approach the same problem but with different conditions. The method that we provide here will be generalized in a forthcoming paper by the same authors. A physical experiment was performed and described in Section 6. In the same section, laboratory results were obtained and these results are consistent with the theoretical values obtained by our proposed theoretical model. Although the solution provided here has not been analyzed before, its novelty might con- tribute to some applications on the mechanics and engineering of solid structures.
Acknowledgements
We thank the Editor and the referee for their comments. The authors acknowledge the assistance of Phil West with the fabrication of several aluminum plates.
References
- Euler, L. (1774) De Pressione ponderis in planum cui incumbit. Novi Commentarii academiae scientiarum Petropolitanae, 18, 289-329.
- Benvenuto, E. (1984) A Brief Outline of the Scientific Debate Which Preceded the Works of Castigliano. Meccanica, 19, 19-32. http://dx.doi.org/10.1007/BF01558450
- Fontana, M. (1792) Della Dinamica, libri tre, 2, Pavia. (See specially pages 34-45, 95, 98.)
- Navier, Claude-Louis-Marie-Henri, Summary of Lessons Taught at the School of Civil Engineering on the Application of Mechanics to the Establishment of Structures and Machines. First Part, 10th Edition, Corrected and Augmented. Carilian-Goeury, Paris, 1833.
- Bois, A.J.D. (1902) The Mechanics of Engineering. John Wiley & Sons, Chapman & Hall, London.
- Patnaik, G.R.H.S.N. and Hopkins, D.A. (2004) Integrated Force Method Solution to Indeterminate Structural Mechanics Problems. National Aeronautics and Space Administration, Cleveland, 104-108.