Applied Mathematics
Vol.06 No.02(2015), Article ID:53896,13 pages
10.4236/am.2015.62034
Availability Importance Measures for Virtualized System with Live Migration
Junjun Zheng, Hiroyuki Okamura, Tadashi Dohi
Department of Information Engineering, Graduate School of Engineering, Hiroshima University, Higashi-Hiroshima, Japan
Email: z1023@s.rel.hiroshima-u.ac.jp, okamu@rel.hiroshima-u.ac.jp, dohi@rel.hiroshima-u.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 January 2015; accepted 6 February 2015; published 10 February 2015
ABSTRACT
This paper presents component importance analysis for virtualized system with live migration. The component importance analysis is significant to determine the system design of virtualized system from availability and cost points of view. This paper discusses the importance of components with respect to system availability. Specifically, we introduce two different component importance analyses for hybrid model (fault trees and continuous-time Markov chains) and continuous-time Markov chains, and show the analysis for existing probabilistic models for virtualized system. In numerical examples, we illustrate the quantitative component importance analysis for virtualized system with live migration.
Keywords:
Virtualized System, Live Migration, System Availability, Component Importance Analysis, Fault Tree, Continuous-Time Markov Chain

1. Introduction
Virtualization is one of the key technologies to deploy cloud computing, which provides a variety of system resources as a service over the Internet [1] . The virtualization is to create software components that emulate behavior of hardware units and platform, and is to control them in a software platform. The virtualization can be classified to several classes. For example, VMware, Xen and KVM can provide virtual machines that emulate physical computers as software. Also Docker offers more lightweight virtual machines than VMware, Xen and KVM as processes. From the reliability point of view, the virtualization is promising to deploy high-availability (HA) system. As is well known, the most popular virtualization is to create virtual machines (VMs) as software components that behave actual computers. However, since VMs are essentially software processes on platform, they can be migrated to another physical server running the virtualization platform. In particular, if two physical servers have the same platform that can drive virtual machines, we exploit the live migration between them [2] . The live migration is a technique that allows a server administrator to move a running virtual machine of application between different physical machines without disconnecting the client or application. The live migration drastically improves the system availability by migrating a failed virtual machine on a platform to another platform.
Although the virtualization is a promising way for HA services, the design of system architecture is not so easy, compared to non-virtual system. For example, the system availability can easily be improved by increasing physical servers which run the virtualization platform. However, from the points of cost and energy consumption, it is not always the best design. That is, towards the best design of virtualized system, we should consider the method to evaluate the system performance beforehand.
On the performance index, Kundu et al. [3] presented statistical models using regression and artificial Neural networks. Also, Okamura et al. [4] proposed a queueing model to evaluate energy efficiency of virtualized system design. On the system index for reliability and availability, Cully et al. [5] and Farr et al. [6] built and evaluated their schemes to enhance the system availability in virtualized system design. Myint and Thein [7] also evaluated a system architecture combining virtualization and rejuvenation. Vishwanath and Nagappan [8] collected operation data of virtualized system and performed statistical analysis to reveal a causal relationship between server failures and hardware repairs. Kim et al. [9] focused on failure modes of virtualized system and presented availability evaluation using fault trees and continuous-time Markov chains (CTMCs). Also Matos et al. [10] developed the CTMC model representing the dynamic behaviors of live migration in the virtualized system. Zheng et al. [11] considered the component importance analysis for non-virtualized and virtualized system based on the model by Kim et al. [9] .
This paper is an extension work of [11] . In [11] , we have developed a method to evaluate the importance (the effect of a component’s availability on the system availability) of components for hybrid models. The hybrid model consists of fault trees (FTs) and CTMCs. The FTs are top level descriptions for the system failure and represent causal relationship between component failures and system failures. The disadvantage of FT is not to describe the dynamic behaviors. To address this problem, dynamic FT is also proposed in [12] . On the other hand, CTMC can well describe the dynamic behaviors of system. In the hybrid model, CTMCs are used for defining the behavior of components. The advantage of hybrid model is to obtain the structure function of system failure with respect to component failures from FT and to be able to define the dynamic behaviors of components. Based on this feature, we have proposed the component importance analysis for hybrid model in [11] . However, the hybrid model had a limitation for the model expression. For example, when two or more components have interactions between them, the structure function cannot always be explicitly expressed. In such cases, we cannot use the hybrid model. Instead of using the hybrid model, we should use a CTMC describing whole the system behavior. In the component analysis of virtualized system, the behavior of live migration is this case. In fact, Matos et al. [10] presented only a CTMC for the live migration. Since the structure function cannot be obtained from the CTMC, we cannot also apply the component importance analysis by [11] to the live migration model. In this paper, we introduce the state-of-art component importance analysis [13] and apply it to the CTMC-based live migration model to reveal the component importance in the context of live migration.
The rest of this paper is organized as follows. Section 2 presents the hybrid model for virtualized system design in [11] , and introduces the component importance analysis for the hybrid model from the availability point of view. In Section 3, we explain the CTMC model for live migration presented in [10] , and show the component importance analysis by using only CTMCs. In Section 4, we illustrate the component importance analysis of hybrid model and live migration model for virtualized system. Section 5 concludes this paper with some remarks.
2. Availability Importance Analysis for Hybrid Model
2.1. Fault Trees
In this section, we introduce the availability model for virtualized system which was presented in [9] . For example, the system under consideration provides two different services such as Web and SQL servers to clients. When one of the servers has been stopped, the system also causes a system failure. In [9] , they assumed that a host equips not only hardware units; CPU, memory (Mem), power subsystem (Pow), network device (Net), cooling subsystem (Cool) but also a software component; virtual machine manager (VMM).
Figure 1 illustrates the fault tree (FT) for virtualized system when there are two physical hosts. In the system design, each host provides a specific service, and is supposed to install the same VMM where the virtual machines (VMs) run and provide the services. One of the important features provided by the VMM is the live migration [2] . The live migration is a technique that can enhance the system availability by migrating the VMs when system failure occurs. More precisely, when a physical host is stopped, all the VMs running on the host can migrate to another physical host without the down time. In fact, most of the VMM products such as Xen, VMware and Hyper-V provide the live migration. However, in order to use the live migration, the two hosts are required to share a common storage area network (SAN) which is a service to provide hard disk drives through a high-speed network using Fiber Channel or iSCSI technologies. In Figure 1, the top event means the system failure and the leaf nodes correspond to the events that respective components are failed. The nodes, H1 (H2) and HW1 (HW2) represent the events that the host 1 (host 2) is failed and the hardware failure occurs in the host 1 (host 2), respectively. The failure of the system is given by an AND gate because of the live migration. In addition, the VM failure (VM1 or VM2) is connected to the failure of another host (H2 or H1) with an AND gate. This is because even if the VM is failed on one VMM, it can be migrated to another VMM. On the other hand, the failure of SAN causes the system failure directly, and therefore the top event is given by an OR gate connected to these events.
2.2. Continuous-Time Markov Chain (CTMC) Models
In [9] , Kim et al. defined the continuous-time Markov chain (CTMC) models to represent behavior of hardware and software components. This section briefly introduces the CTMC models presented in [9] .
In the availability modeling, the state of system can be classified into two sets: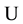 , the set of up (operational) states in which the system is available; and
, the set of up (operational) states in which the system is available; and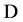 , the set of down (or failure ) states in which the system is unavailable. Figure 2 shows the 3-state CTMC availability models of CPU and Mem components proposed in [9] . In the figure, the states UP, DN and RP mean that the component is available, the component is failed, and the component is under repair, respectively. Hence the states DN and RP are classified into
, the set of down (or failure ) states in which the system is unavailable. Figure 2 shows the 3-state CTMC availability models of CPU and Mem components proposed in [9] . In the figure, the states UP, DN and RP mean that the component is available, the component is failed, and the component is under repair, respectively. Hence the states DN and RP are classified into 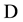 set in the availability model. Moreover,
set in the availability model. Moreover, 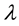 and
and 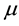 denote failure and repair rates of the component. For example, if the host equips 2-way CPUs, the failure rate is given by
denote failure and repair rates of the component. For example, if the host equips 2-way CPUs, the failure rate is given by 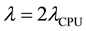 by using the failure rate of a single CPU because both processors are needed for the operation. Also, the transition from DN to RP corresponds to the event that a repair person is summoned and its mean time is given by
by using the failure rate of a single CPU because both processors are needed for the operation. Also, the transition from DN to RP corresponds to the event that a repair person is summoned and its mean time is given by 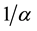 using the rate of summoning inherent in the component.
using the rate of summoning inherent in the component.
Figure 1. The FT diagram of virtualized system.
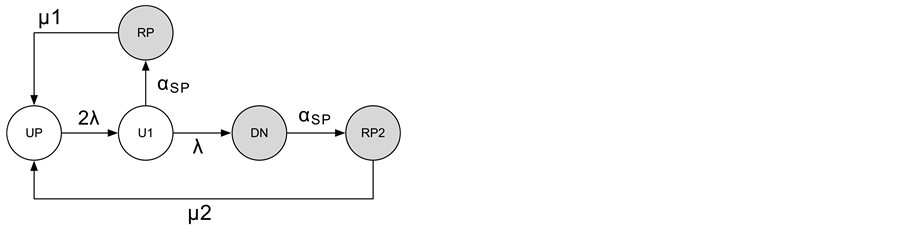
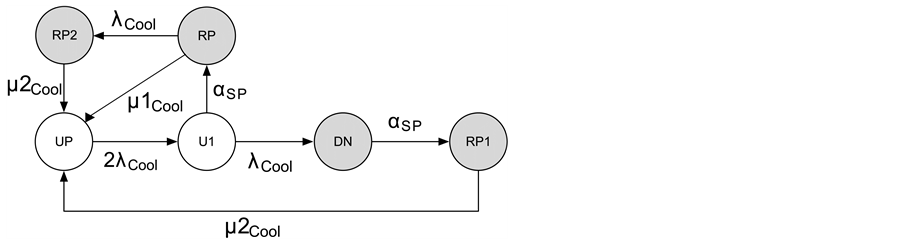
As seen in Figure 3, Kim et al. [9] applied the 5-state availability model to describe the dynamic behaviors of components Pow and Net which are described as 2-unit redundant (parallel) subsystems. In the figure, white and gray nodes represent up and down states respectively. The main difference from the 3-state availability model is to add the state U1 representing that only one unit is failed, since the component failure is caused when both of two units are failed. Moreover, the model adds a repair state RP2 where two units are failed. For the components, Cool and SAN, the CTMC models are extended from the 5-state availability model. Concretely, in the CTMC for Cool as shown in Figure 4, they added a transition from RP to RP2, namely, the Cool availability model allows the event occurrence that one unit fails while another unit is under repair. In the CTMC for SAN as shown in Figure 5, a state CP is put to the transition between the states UP and RP, which means the mirrored data is copied from a working disk unit to the repaired disk unit under RAID1 design. The transition rate from CP to UP is given by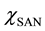 . Additionally, since the working disk unit may fail in the CP state, they added a transition from CP to RP2 with the failure rate of a disk unit
. Additionally, since the working disk unit may fail in the CP state, they added a transition from CP to RP2 with the failure rate of a disk unit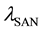 .
.
The CTMC model for VMM is given by Figure 6. As seen in this figure, since the software failure cannot be detected immediately, the state DT is added, which means the failure is detected. In [9] , after the failure detection, the system takes an action to reboot VMM with mean time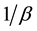 . It is empirically known that most of transient failures in software can be recovered by the system reboot [14] . In this CTMC model, the reboot will be unsuccessful with probability
. It is empirically known that most of transient failures in software can be recovered by the system reboot [14] . In this CTMC model, the reboot will be unsuccessful with probability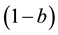 . Hence the state DW indicates that the failure is not recovered by a failed system reboot, and a repair person is summoned.
. Hence the state DW indicates that the failure is not recovered by a failed system reboot, and a repair person is summoned.
In [9] , based on the CTMC model in Figure 6, they built the CTMC model for VM which takes account of the dynamic behaviors of the live migration. Thus the CTMC model for VM was quite complicated so that the
Figure 2. State transition diagram of the CPU and memory availability models.
Figure 3. State transition diagram of the power (or network card) availability model.
Figure 4. State transition diagram of the cooling system availability model.
Figure 5. State transition diagram of the SAN availability model.
Figure 6. State transition diagram of the VMM/VM availability model.
system failure in the virtualized system cannot be represented by the FT. Since this paper describes the correlation between the failures of VM and host by the AND gate in the FT representation, the CTMC model simply becomes the same model as VMM, i.e., the model of Figure 6 can also represent the availability for VM.
Based on these CTMC models, the steady-state availability for component x can be calculated as follows.
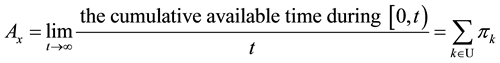
where 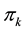


2.3. Importance Measures
Let Ai be the steady-state availability of component i. Then we have the following steady-state availability for a host in the virtualized system according to the FT analysis:

where HW is the set of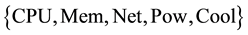

where
In [15] , Cassady et al. proposed the importance measures of components in terms of availability. They assumed the FT model with the events that are described by the 2-state availability model. The 2-state availability model is a CTMC model with only two states: up and down. In such modeling, Cassady et al. [16] defined two importance measures as the derivatives of the system availability:

where 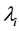

In this paper, since we do not treat the 2-state availability model to represent the component availability, the importance measures proposed in [16] cannot directly be applied to evaluating the virtualized system. This paper proposes a preprocessing based on the aggregation of CTMC-based availability model [18] before applying the availability importance measures.
The aggregation is a technique to transform CTMC-based availability models into a equivalent 2-state, 2-transition availability model which has the same availability as the original model. As mentioned before, the states of CTMC-based availability models can be classified into 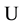



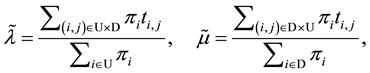
where the set 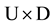


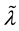
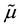
By applying the aggregation to the component availability models as preprocessing, the availability importance measures of the component i can be rewritten by

where 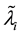

3. Component Importance for Live Migration
In the previous section, we have introduced the component importance for the structure function given by the FT model. The model considered the live migration as a static structure. However, since the live migration is essentially described by a dynamic behavior, the previous method cannot analyze how effect of components on the dynamic behaviors of live migration. Thus in this section, we consider the component importance on live migration from the viewpoint of dynamic behaviors, that is, we apply the component importance analysis for a CTMC representing the dynamic behaviors of live migration presented in [10] .
3.1. Model Description
Matos et al. [10] presented the CTMC for live migration in the virtualized system. This availability model does not consider the detailed behavior of hardware components (e.g., CPU, Mem, Pow) and the VMM, but only the components of VMs (VM1 and VM2), hosts (H1 and H2) and applications (App1 and App2).
Table 1 shows notations for the state of system which are based on the current conditions of components. Concretely, each state is indicated by six characters. The first character means the state of H1. The notations “U”, “F” and “D” correspond to the conditions where H1 is up, H1 fails and the failure is detected, respectively. The second character represents the state of VM1 and its application (App1). When both are up, the character is given by “U”. If VM1 fails, it is “Fv”. When the failure is detected, the character becomes “Dv”. Also, when a manual repair is applied, the character is “Pv”. If App1 fails, it is “Fa”. When the failure of App1 is detected, the
Table 1. The states of system.
state of system is represented by “Da”. If App1 requires an additional repair in the case where the application restart cannot solve the problem, the character is given by “Pa”. Also, when VM1 and App1 are restarting, the state is given by “R”. If VM1 and App1 are not running on the H1, then the character is “X”. The third character represents whether or not VM2 and App2 are running on H1. If VM2 and App2 run on H1, the character is given by “U”. If they are restarting on H1, the character is “R”. Otherwise, if they are not running on H1, the character is “X”. The fourth through sixth characters represent the state of H2 in the same manner as the first through third characters. Figure 7 shows the state transition diagram for live migration in the virtualized system which is described by the CTMC model in [10] . Also, Table 2 presents the parameters of the CTMC model. For example, 
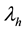
3.2. Importance Analysis
Dissimilar to the case of FT model, we do not know the structure function in the CTMC. We consider the component importance analysis by only using the parameter sensitivity analysis.
Let Q be the infinitesimal generator of CTMC described in Figure 7. Then the steady-state probability vector πs is given by the linear equations;

Figure 7. CTMC availability model for live migration.
Table 2. Model parameters.
where 1 is a column vector whose elements are 1. Also we define the following vectors:
・ 
・ 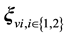
・ 
・ 
Then the component availability is given by a inner product of πs and

On the other hand, the system availability can be obtained by

Similar to the case of FT model, we define the importance measures of component i as follows.

where 


Similarly, the importance measure with respect to repair rate is given by

Thus the problem is to estimate the sensitivity 
To estimate the sensitivities for all the component availabilities, we consider the sensitivities of system and component availabilities with respect to model parameters. Suppose that 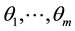

where 
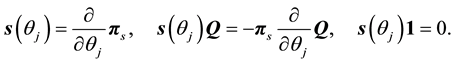
By using the vector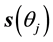

According to [19] , the estimates of 

where T is the transpose operator. By substituting the estimates of the sensitivities into Equations (11) and (12), we have the component importance measures for live migration.
4. Numerical Illustration
4.1. Hybrid Model
In this section, we illustrate the quantitative component importance analysis of hybrid model for virtualized system. Table 3 presents the parameters of the CTMC models for all components. For example, 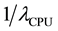

Using the aggregation technique, we first transform the availability models for all components into the equivalent 2-state, 2-transition models, then compute the effective failure and repair rates for components based on the model parameters. We also compute the component availabilities, and these results are shown in Table 5. From this table, we can see the availabilities of hardware units are relatively high by the comparison to the availabilities of software components, especially for SAN, the availability is quite high.
We then compute the system availabilities based on the structure functions and the component availabilities. The availabilities of a hardware unit and a host, and the system availability are presented in Table 6. From this table, the sufficiently high availability of the virtualized system implies that the live migration is considerably effective to enhance the system availability.
Next we derive the importance measures of components in the virtualized system by using Equation (6), and the effective failure and repair rates shown in Table 5. The importance measures of components in terms of the system availability are shown in Table 7. Note that this table presents the importance measures of components only in a host, because the components of the host 1 and 2 are assumed to be the same in the system design, and the importance measures of same components in the host 1 and 2 are identical.
Table 3. MTTF/MTTR of components.
Table 4. Other model parameters.
Table 5. Effective failure and repair rates and component availabilities.
Table 6. Availabilities of hardware units, host and system.
Table 7. Component importance measures in the virtualized system.
Table 7 shows that the importance measure with respect to failure rate is higher than that with respect to repair rate for any component. The importance measure regarding failure rate, 


4.2. Dynamic Model for Live Migration
This section illustrates the quantitative component importance analysis of the CTMC for live migration in the virtualized system. Based on these parameters shown in Table 8, we first compute the availabilities for all components and system which are shown in Table 9. From this table, we find that the availability of VM is the highest among those of the other components because of the live migration.
Next we compute the effective failure and repair rates for all components based on the aggregation of CTMC model, and the results are shown in Table 10. From this table, it is found that the repair rate of VM are much higher than that in Table 5. As mentioned before, the FT model considered the live migration as a static structure which cannot represent the dynamic behaviors of system. However, since the live migration is essentially described by a dynamic behavior, the dynamic behaviors have been taken into account in the CTMC model for live migration. The higher repair rate of VM confirms the effectiveness of live migration in the virtualized system. Table 11 presents the importance measures for components in the virtualized system. As observed in Table 10
Table 8. Model parameters.
Table 9. Availabilities of host, VM, application components and system.
Table 10. Effective failure and repair rates.
Table 11. Component importance measures in the dynamic model for live migration.
and Table 11, we find that, although the failure rate of VM is higher than that of host, the importance measures of VM are much lower than those of host. This is because the repair rate of VM is very high. Also, comparing Table 9 with Table 10, we can see that the availability of host is the lowest among those of others, because the repair rate of host is also the lowest. This indicates that, the component host is important, and any change in its associated parameters will have a large effect on the system availability. And this conclusion also can be confirmed from Table 11.
Table 11 shows that the importance measures of host is the most highest. Moreover, by comparing between the importance measure with respect to failure and repair rates for each component, it is found that the importance measure with respect to failure rate is higher than that with respect to repair rate. Therefore, it indicates that the improvement of failure rate of host is more efficient to enhance the system availability.
5. Conclusions
In this paper, we have dealt with quantitative component importance analysis of virtualized system with live migration in terms of availability. In [11] , we have developed a method to evaluate the importance of components for hybrid model which consists of fault trees (FTs) and CTMCs. However, the hybrid model had a limitation for the model expression in the situation where two or more components have interactions between them. Instead of using the hybrid model, we considered a CTMC model for live migration presented in [10] . This paper introduced the state-of-art component importance analysis [13] and applied it to the CTMC-based live migration model to reveal the component importance in the context of live migration. More precisely, our method is based on the aggregation techniques of CTMC-based availability models [18] and the importance measures with respect to failure and repair rates [16] . Also, we proposed a method to estimate the sensitivities of system availability with respect to component availabilities. In numerical examples, we illustrated the quantitative component importance analysis of hybrid model and live migration model for virtualized system, and compared the importance of components. In future, we intend to improve our method so that it can be applied to more complicated event models. Also, we will focus on the component importance analysis for Markov chain in terms of reliability.
References
- Furht, B. and Escalante, A. (2010) Cloud Computing Fundamentals. In Handbook of Cloud Computing, Springer, 3-19. http://dx.doi.org/10.1007/978-1-4419-6524-0_1
- Clark, C., Fraser, K., Hand, S., Hansen, J.G., Jul, E., Limpach, C., Pratt, I. and Warfield, A. (2005) Live Migration of Virtual Machines. In: Proceedings of the 2nd Conference on Symposium on Networked Systems Design & Implementation―Volume 2, USENIX Association, Berkeley, 273-286.
- Kundu, S., Rangaswami, R., Dutta, K. and Zhao, M. (2010) Application Performance Modeling in a Virtualized Environment. Proceedings of the 16th IEEE International Symposium on High-Performance Computer Architecture, Bangalore, 9-14 January 2010, 1-10.
- Okamura, H., Shigeoka, K., Yamasaki, K., Dohi, T. and Kihara, H. (2012) Performance Evaluation of Cloud Computing in PaaS Environments. Supplemental Proceedings of 42nd Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN2012), 36, 122-127.
- Cully, B., Lefebvre, G., Meyer, D., Feeley, M., Hutchinson, N. and Warfield, A. (2008) Remus: High Availability via Asynchronous Virtual Machine Replication. Proceedings of the 5th USENIX Symposium on Networked Systems Design and Implementation, USENIX Association, Berkeley, 161-174.
- Farr, E., Harper, R., Spainhower, L. and Xenidis, J. (2008) A Case for High Availability in a Virtualized Environment (HAVEN). Proceedings of the 2008 Third International Conference on Availability, Reliability and Security (ARES'08), Barcelona, 4-7 March 2008, 675-682.
- Hla Myint, M.T. and Thein, T. (2010) Availability Improvement in Virtualized Multiple Servers with Software Rejuvenation and Virtualization. Proceedings of 4th International Conference on Secure Software Integration and Reliability Improvement, Singapore, 9-11 June 2010, 156-162.
- Vishwanath, K.V. and Nagappan, N. (2010) Characterizing Cloud Computing Hardware Reliability. Proceedings of the first ACM Symposium on Cloud Computing (SoCC'10), Indianapolis, 10-11 June 2010, 193-204.
- Kim, D.S., Machida, F. and Trivedi, K.S. (2009) Availability Modeling and Analysis of a Virtualized System. Proceedings of the 15th IEEE Pacific Rim International Symposium on Dependable Computing (PRDC-2009), Shanghai, 16-18 November 2009, 365-371.
- Matos, R.D.S., Maciel, P.R.M., Machida, F., Kim, D.S. and Trivedi, K.S. (2012) Sensitivity Analysis of Server Virtualized System Availability. IEEE Transactions on Reliability, 61, 994-1006.
- Zheng, J., Okamura, H. and Dohi, T. (2012) Component Importance Analysis of Virtualized System. Proceedings of the 9th IEEE International Conference on Autonomic & Trusted Computing (ATC2012), Fukuoka, 4-7 September 2012, 462-469.
- Cepin, M. and Mavko, B. (2002) A Dynamic Fault Tree. Reliability Engineering & System Safety, 75, 83-91. http://dx.doi.org/10.1016/S0951-8320(01)00121-1
- Okamura, H., Zheng, J. and Dohi, T. (2015) Sensitivity Estimation for Markov Reward Models and Its Application to Component Importance Analysis. (In Submission)
- Castelli, V., Harper, R.E., Heidelberger, P., Hunter, S.W., Trivedi, K.S., Vaidyanathan, K. and Zeggert, W.P. (2001) Proactive Management of Software Aging. IBM Journal of Research and Development, 45, 311-332. http://dx.doi.org/10.1147/rd.452.0311
- Trivedi, K.S. (2001) Probability and Statistics with Reliability, Queueing, and Computer Sciences Applications. 2nd Edition, John Wiley & Sons, New York.
- Cassady, C.R., Pohl, E.A. and Jin, S. (2004) Managing Availability Improvement Efforts with Importance Measures and Optimization. IMA Journal of Management Mathematics, 15, 161-174. http://dx.doi.org/10.1093/imaman/15.2.161
- Birnbaum, Z.W. (1969) On the Importance of Different Components in a Multicomponent System. In: Krishnaiah, P.R., Ed., Multivariate Analysis―II, Academic Press, New York, 581-592.
- Lanus, M., Yin, L. and Trivedi, K.S. (2003) Hierarchical Composition and Aggregation of State-Based Availability and Performability Models. IEEE Transactions on Reliability, 52, 44-52. http://dx.doi.org/10.1109/TR.2002.805781
- Strang, G. (2009) Introduction to Linear Algebra. 4th Edition, Wellesley Cambridge Press, Wellesley.