Received 20 November 2014; accepted 3 December 2014; published 13 January 2015

ABSTRACT

In this paper, the homotopy perturbation Sumudu transform method (HPSTM) is extended to solve linear and nonlinear fractional Klein-Gordon equations. To illustrate the reliability of the method, some examples are presented. The convergence of the HPSTM solutions to the exact solutions is shown. As a novel application of homotopy perturbation Sumudu transform method, the presented work shows some essential differences with existing similar application, and also four classical examples highlight the significance of this work.

Keywords:

Mittag-Leffler Functions, Caputo Derivative, Sumudu Transform, Homotopy Perturbation Method, Klein-Gordon Equation

1. Introduction

Nonlinear phenomena that appear in many areas of scientific fields such as solid state physics, plasma physics, fluid dynamics, mathematical biology and chemical kinetics are modeled in terms of nonlinear partial differential equations and in many scientific and engineering applications; one of the corner stones of modeling is partial differential equations. For example, the Klein-Gordon equation of the form

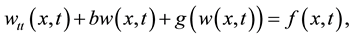(1)

with initial conditions

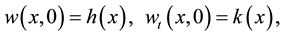(2)

appears in modeling of problems in quantum field theory, relativistic physics, dispersive wave phenomena, plasma physic, nonlinear optics and applied physical sciences. The complexity of the equations though requires the use of numerical and analytical methods in most cases. Numerous analytical and numerical methods have been presented in recent years. Some of these analytical methods are the Fourier transform method [1] , the fractional Green function method [2] , the popular Laplace transform method [3] [4] , the Sumudu transform method [5] , the iteration method [4] , the Mellin transform method and the method of orthogonal polynomials [3] .

Some numerical methods are also popular, such as the homotopy perturbation method (HPM) [6] - [8] , the modified homotopy perturbation method (MHPM) [9] , the differential transform method (DTM) [10] , the variational iteration method (VIM) [11] [12] , the homotopy analysis method (HAM) [13] [14] , the Sumudu decomposition method [15] and the Adomian decomposition method [16] [17] .

Among these methods, the HPM is a universal approach which can be used to solve FODEs and FPDEs; on the other hand, various methods are combined with the homotopy perturbation method, such as the variational homotopy perturbation method, which is a combination of the variational iteration method and the homotopy perturbation method [18] . Another such combination is the homotopy perturbation transformation method which is constructed by combining two powerful methods, namely, the homotopy perturbation method and the Laplace transform method [19] .

The Sumudu transformation method is one of the most important transform methods introduced in the early 1990s by Gamage K. Watugala. It is a powerful tool for solving many kinds of PDEs in various fields of science and engineering [20] [21] . And also various methods are combined with the Sumudu transformation method, such as the homotopy analysis Sumudu transform method (HASTD) [22] , which is a combination of the homotopy analysis method and the Sumudu transformation method. Another example is the Sumudu decomposition method (SDM) [23] , which is a combination of the Sumudu transform method and the Adomian decomposition method.

In this paper, an efficient approach is proposed to use the homotopy perturbation Sumudu transform method (HPSTM) to derive the exact solution of various types, which is a combination of the homotopy perturbation method and the Sumudu transform method. However, Singh [24] used the homotopy perturbation Sumudu transform method to obtain the exact solution of linear and nonlinear equations which are PDEs of integer order. In this paper we consider the fractional Klein-Gordon equation

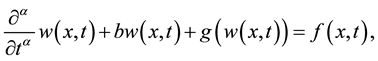(3)

and try to show the convergence of the homotopy perturbation Sumudu transform method in solving this equation.

The paper is structured in six sections. In Section 2, we begin with an introduction to some necessary definitions of fractional calculus theory. In Section 3, we describe the basic ideal of the homotopy perturbation method. In Section 4, we describe the homotopy perturbation Sumudu transform method. In Section 5, we present four examples to show the efficiency of using HPSTM to solve FPDEs and also to compare our results with those obtained by other existing methods. Finally, relevant conclusions are drawn in Section 6.

2. Basic Definitions of Fractional Calculus

In this section, we present the basic definitions and properties of the fractional calculus theory, which are used further in this paper.

Definition 1. A real function is said to be in the space 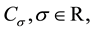if there exists a real number 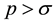such that 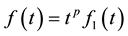where 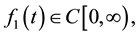and it is said to be in the space 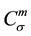if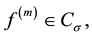

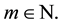
Definition 2. The left sided Riemann-Liouville fractional integral of order 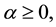of a function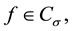 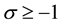is defined as:

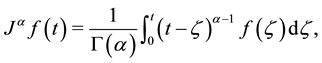(4)

where and is the Gamma function.

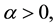
Definition 3. Let The Caputo fractional derivative of is defined in [18] as follows:

(5)

Note that according to [13] , Equations (4) and (5) become

(6)

and

(7)

Definition 4. The single parameter and the two parameters variants of the Mittag-Leffler functions are denoted by and respectively, which are relevant for their connection with fractional calculus, and are defined as:

(8)

(9)

Some special cases of the Mittag-Leffler function are as follows:

1)

2)

3)

Other properties of the Mittag-Leffler functions can be found in [25] . These functions are generalizations of the exponential function, because, most linear differential equations of fractional order have solutions that are expressed in terms of these functions.

Definition 5. Sumudu transform over the following set of functions,

(10)

is defined by

(11)

where

Some special properties of the Sumudu transform are as follows:

1)

2)

3)

4)

Other properties of the Sumudu transform can be found in [26] .

Definition 6. is the Sumudu transform of And according to ref. [26] we have:

1) is a meromorphic function, with singularities having and

2) there exists a circular region with radius and positive constants, and with

then the function is given by

(12)

Definition 7. The Sumudu transform, of the Caputo fractional integral is defined as [5]

(13)

then it can be easily understood that

(14)

3. The Basic Idea of the Homotopy Perturbation Method

In this section, we will briefly present the algorithm of this method. At first, the following nonlinear differential equation is considered:

(15)

with the boundary conditions

(16)

where and are a general differential function operator, a boundary operator, a known an analytical function and the boundary of the domain respectively.

The operator can be decomposed into a linear operator, denoted by, and a nonlinear operator, denoted by. Therefore, Equation (15) can be written as follows

(17)

Now we construct a homotopy with satisfies:

(18)

which is equivalent to

(19)

where is the initial approximation of Equation (15) that satisfies the boundary condition and is an embedding parameter.

When the value of is changed from zero to unity, we can easily see that

(20)

(21)

in topology, this changing process is called deformation, and Equations (20) and (21) are called homotopic.

If the -parameter is considered as small, then the solution of Equations (17) and (18) can be expressed as a power series in as follows

(22)

The best approximation for the solution of Equation (15) is

(23)

4. The Homotopy Perturbation Sumudu Transform Method

In order to elucidate the solution procedure of this method, we consider a general fractional nonlinear partial differential equation of the form:

(24)

with and subject to the initial condition

(25)

where is the Caputo fractional derivative, is the source term, is the linear operator and is the general nonlinear operator.

Taking the Sumudu transform (denoted throughout this paper by) on both sides of Equation (24), we have

(26)

Using the property of the Sumudu transform and the initial conditions in Equation (25), we have

(27)

and

(28)

Operating with the Sumudu inverse on both sides of Equation (28) we get

(29)

Now, pplying the classical perturbation technique. And assuming that the solution of Equation (29) is in the form

(30)

where is the homotopy parameter. The nonlinear term of Equation (29) can be decomposed as

(31)

where are He’s polynomials, which can be calculated with the formula [27]

(32)

Substituting Equation (30) and (31) in Equation (29), we get

(33)

Equating the terms with identical powers of, we can obtain a series of equations as the follows:

(34)

By utilizing the results in Equation (34), and substituting them into Equation (30) then the solution of Equation (24) can be expressed as a power series in. The best approximation for the solution of Equation (24) is:

(35)

5. Applications

In this section, in order to assess the applicability and the accuracy of the fractional homotopy Sumudu transform method the following four examples.

Example 1. Consider the time-fractional partial differential Klein-Gordon equation

(36)

subject to the initial conditions

(37)

Taking the Sumudu transform on both sides of Equation (36), thus we get

and

Using the property of the Sumudu transform and the initial condition in Equation (37), we have

(38)

Operating with the Sumudu inverse on both sides of Equation (38) we get

(39)

By applying the homotopy perturbation method, and substituting Equation (30) in Equation(39) we have

(40)

Equating the terms with identical powers of ,, we get

Thus the solution of Equation (36) is given by

(41)

If we put in Equation (41) or solve Equation (36) and (37) with we obtain the exact solution

which is in full agreement with the result in Ref. [28] .

Example 2. Consider the inhomogeneous linear time-fractional partial differential Klein-Gordon equation

(42)

subject to the initial conditions

(43)

Taking the Sumudu transform on both sides of Equation (42), thus we get

and

Using the property of the Sumudu transform and the initial condition in Equation (43), we have

(44)

Operating with the Sumudu inverse on both sides of Equation (44) we get

(45)

By applying the homotopy perturbation method, and substituting Equation (30) in Equation (45) we have

(46)

Equating the terms with identical powers of we get

Thus the solution of Equation (42) is given by

(47)

If we put in Equation (47) or solve Equation (42) and (43) with we obtain the exact solution

which is in full agreement with the result in Ref. [28] .

Example 3. Consider the non-linear time-fractional partial differential Klein-Gordon equation

(48)

subject to the initial conditions

(49)

Taking the Sumudu transform on both sides of Equation (48), thus we get

and

Using the property of the Sumudu transform and the initial condition in Equation (49), we have

(50)

Operating with the Sumudu inverse on both sides of Equation (50) we get

(51)

By applying the homotopy perturbation method, and substituting Equation (30) in Equation (51) we have

(52)

Equating the terms with identical powers of we get

Thus the solution of Equation (48) is given by

(53)

If we put in Equation (53) or solve Equation (48) and (49) with and so on, we can find that

we obtain the exact solution

which is in full agreement with the result in Ref. [28] .

Example 4. Consider the one-dimensional linear inhomogeneous fractional Klein-Gordon equation

(54)

subject to the initial conditions

(55)

Taking the Sumudu transform on both sides of Equation (54), thus we get

and

Using the property of the Sumudu transform and the initial condition in Equation (55), we have

(56)

Operating with the Sumudu inverse on both sides of Equation (56) we get

(57)

By applying the homotopy perturbation method, and substituting Equation (30) in Equation (57) we have

(58)

Equating the terms with identical powers of we get

Thus the solution of Equation (54) is given by

(59)

If we put in Equation (59) or solve Equation (54) and (55) with we obtain the exact solution

which is in full agreement with the result in Ref. [29] .

As it is presented above in Example 4 we obtained homotopy perturbation Sumudu transform solution of Equation (54) for values of Figures 1-4 show the approximate solutions for Equation (54) obtained for the three different values of using the homotopy perturbation Sumudu transform method

(HPSTM). The values of is the only case for which we know the exact solution and the results of (HPSTM) are in excellent agreement with the exact solution.

6. Conclusion

In this paper, we have introduced a combination of the homotopy perturbation method and the Sumudu transform method for time fractional problems. This combination builds a strong method called the HPSTD. This method has been successfully applied to one-dimensional fractional equations and also for problems of linear and nonlinear partial differential equations. The HPSTD is an analytical method and runs by using the initial conditions only. Thus, it can be used to solve equations with fractional and integer order with respect to time. An important advantage of the new approach is its low computational load.

References