Applied Mathematics
Vol.05 No.13(2014), Article ID:47830,4 pages
10.4236/am.2014.513191
Asymptotic Estimates for Second-Order Parameterized Singularly Perturbed Problem
Mustafa Kudu
Department of Mathematics, Faculty of Art and Science, Erzincan University, Erzincan, Turkey
Email: muskud28@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 April 2014; revised 20 May 2014; accepted 3 June 2014
ABSTRACT
The boundary value problem (BVP) for parameterized singularly perturbed second order nonlinear ordinary differential equation is considered. The boundary layer behavior of the solution and its first and second derivatives have been established. An example supporting the theoretical analysis is presented.
Keywords:
Parameterized Problem, Asymptotic Bounds, Singular Perturbation, Boundary Layer

1. Introduction
In this paper, we are going to obtain the asymptotıc bounds for the following parameterized singularly perturbed boundary value problem (BVP):
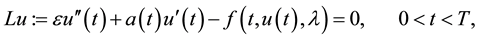 (1)
(1)
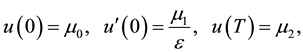 (2)
(2)
where 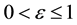 is a perturbation parameter,
is a perturbation parameter,  are given constants and
are given constants and 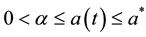 is a sufficiently smooth function in
is a sufficiently smooth function in . Further , the function
. Further , the function 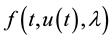 is assumed to be sufficiently continuously differentiable for our purpose function in
is assumed to be sufficiently continuously differentiable for our purpose function in  and
and
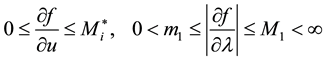 . (3)
. (3)
By a solution of (1), (2) we mean pair 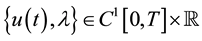 for which problem (1), (2) is satisfied.
for which problem (1), (2) is satisfied.
An overview of some existence and uniqueness results and applications of parameterized equations may be obtained, for example, in [1] -[10] . In [11] - [14] , some approximating aspects of this kind of problems have also been considered. The qualitative analysis of singular perturbation situations have always been far from trivial because of the boundary layer behavior of the solution. In singular perturbation cases, problems depend on a small parameter 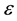 in such a way that the solution exhibits a multiscale character, i.e., there are thin transition layers where the solution varies rapidly while away from layers it behaves regularly and varies slowly [15] [16] . In this note we establish the boundary layer behaviour for
in such a way that the solution exhibits a multiscale character, i.e., there are thin transition layers where the solution varies rapidly while away from layers it behaves regularly and varies slowly [15] [16] . In this note we establish the boundary layer behaviour for  of the solution of (1)-(2) and its first and second derivatives. Example that agree with the analytical results is given.
of the solution of (1)-(2) and its first and second derivatives. Example that agree with the analytical results is given.
Theorem 1.1. For 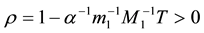 the solution
the solution 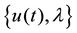 of the problem (1), (2) satisfies,
of the problem (1), (2) satisfies,
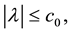 (4)
(4)
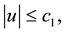 (5)
(5)
where

and

provided 




Proof. We rewrite Equation (1) in the form

where,




From (7) for the first derivate, we have

Integrating this equality over 

from which by setting the boundary condition 

Applying the mean value theorem for integrals, we deduce that,

and

Also, for first and second terms in right side of (10), for 

It then follows from (11)-(13)

Next from (9), we see that
Under the conditions 






Using the maximum principle whith barrier functions 

The inequlities (14), (15) immediately leads to (4), (5). After taking into consideration the uniformly boundnees in 



which proves (6) for 


from which after taking into consideration here 

Next, differentiation (1) gives


with

and due to our assumptions clearly,
Consequently, from (17), (18) we have
which proves (6) for
Example. Consider the particular problem
where, 

with
First and second derivatives have the form
Therefore we observe here the accordance in our theoretical results described above.
References
- Pomentale, T. (1976) A Constructive Theorem of Existence and Uniqueness for the Problem. Zeitschrift für Ange- wandte Mathematik und Mechanik, 56, 387-388. http://dx.doi.org/10.1002/zamm.19760560806
- Goma, I.A. (1977) Method of Successive Approximations in a Two-Point Boundary Problem with Parameter. Ukrainian Mathematical Journal, 29, 594-599. http://dx.doi.org/10.1007/BF01085968
- Jankowski, T. (2001) Monotone İterations for Differential Problems. Miskolc Mathematical Notes, 2, 31-38.
- Jankowski, T. and Lakshmikantham, V. (1997) Monotone Iterations for Differential Equations with a Parameter. Journal of Applied Mathematics and Stochastic Analysis, 10, 273-278. http://dx.doi.org/10.1155/S1048953397000348
- Jankowski, T. (1999) Generalization of the Method of Quasilinearization for Differential Problems with a Parameter, Dynamic Systems an Applications, 8, 53-72.
- Rontó, M. and Csikos-Marinets, T. (2000) On the Investigation of Some Non-Linear Boundary Value Problems with Parameters. Miskolc Mathematical Notes, 1, 157-166.
- Rontó, M. (2000) On Non-Linear Boundary Value Problems Containing Parameters. Archivum Mathematicum, 36, 585-593.
- Staněk, S. (1997) Nonlinear Boundary Value Problem for Second Order Differential Equations Depending on a Parameter. Mathematica Slovaca, 47, 439-449.
- Zhang, P. (2011) Existence of Positive Solutions for Nonlocal Second-Order Boundary Value Problem with Variable Parameter in Banach Spaces. Fixed Point Theory and Applications, 43, 1687-1812. http://dx.doi.org/10.1186/1687-1812-2011-43
- Fěckan, M. (1994) Parametrized Singularly Perturbed Boundary Value Problems. Journal of Mathematical Analysis and Applications, 188, 426-435. http://dx.doi.org/10.1006/jmaa.1994.1436
- Amiraliyev, G.M., Kudu M. and Duru, H. (2004) Fınıte-Difference Method for Parameterızed Sıngularly Pertur Bed Problem. Journal of Applied Mathematics, 3, 191-199. http://dx.doi.org/10.1155/S1110757X0440103X
- Amiraliyev, G.M., Kudu M. and Duru, H. (2006) Uniform Difference Method for a Parameterized Singular Pertur Bation Problem. Applied Mathematics and Computation, 175, 89-100. http://dx.doi.org/10.1016/j.amc.2005.07.068
- Amiraliyeva I.G. and Amiraliyev, G.M. (2009) Uniform Difference Method for Parameterized Singularly Pertur Bed Delay Differential Equations. Numerical Algorithms, 52, 509-552. http://dx.doi.org/10.1007/s11075-009-9295-y
- Turkyilmazoglu, M. (2011) Analytic Approximate Solutions of Parameterized Unperturbed and Singularly Perturbed Boundary Value Problems. Applied Mathematical Modelling, 35, 3879-3886. http://dx.doi.org/10.1016/j.apm.2011.02.011
- Nayfeh, A.H. (1981) Introduction to Perturbation Techniques. JohnWiley & Sons, New York.
- O’Malley Jr., R.E. (1991) Singular Perturbation Methods for Ordinary Differential Equations. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4612-0977-5













