Applied Mathematics
Vol.5 No.10(2014), Article
ID:46525,8
pages
DOI:10.4236/am.2014.510144
New Exact Traveling Wave Solutions for Some Coupled BBM Equations
Ye Zhao1, Qian Xu2
1Department of Mathematics and Physics, Beijing Institute of Petrochemical Technology, Beijing, China
2Department of Basic Courses, Beijing Union University, Beijing, China
Email: wzhaoye2002@tom.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 March 2014; revised 6 April 2014; accepted 13 April 2014
ABSTRACT
The present paper deals with results of explicit traveling wave solutions for some coupled BBM equations. By detailed computation and using the 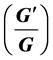 -expansion method, many traveling wave solutions are given. These traveling waves are in the form of hyperbolic functions, the trigonometric functions and the rational functions, which show the reliability and efficiency of the used method.
-expansion method, many traveling wave solutions are given. These traveling waves are in the form of hyperbolic functions, the trigonometric functions and the rational functions, which show the reliability and efficiency of the used method.
Keywords:Traveling Waves, 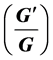 -Expansion Method, Coupled BBM Equation
-Expansion Method, Coupled BBM Equation

1. Introduction
The study of the traveling wave solutions for nonlinear PDEs plays an important role in the study of nonlinear physical phenomena. Therefore, finding explicit solutions of physics equations is an important and interesting subject. In this paper, we discuss the exact traveling wave solutions for the following nonlinear evolution equations which can be used to describe small-amplitude long waves on the surface of water in a channel.
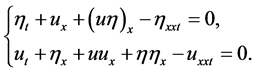 (1)
(1)
Some previous works on the existence and orbital stability of bell-shaped solitary waves with zero and nonzero asymptotic value have been obtained in [1] [2] . Our interest in the present work is to seek many new solutions for the coupled Equations (1). The method we used here is  -expansion method which is proposed by Wang et al. in [3] . This method assumed that the traveling wave solutions can be expressed by a polynomial in
-expansion method which is proposed by Wang et al. in [3] . This method assumed that the traveling wave solutions can be expressed by a polynomial in , where
, where 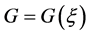 satisfies the second-order ordinary differential equation
satisfies the second-order ordinary differential equation
 . The solutions obtained are expressed by hyperbolic functions, the trigonometric functions and the rational functions. We note that the solutions obtained in this paper extend the existence results in [1] [2] . Until now this method is widely used by many authors [4] -[7] , and exact solutions for a variety of nonlinear equations are obtained. Especially, Akbar, Norhashidah and Zayed [6] proposed the extended
. The solutions obtained are expressed by hyperbolic functions, the trigonometric functions and the rational functions. We note that the solutions obtained in this paper extend the existence results in [1] [2] . Until now this method is widely used by many authors [4] -[7] , and exact solutions for a variety of nonlinear equations are obtained. Especially, Akbar, Norhashidah and Zayed [6] proposed the extended  - expansion method in which the solutions are presented in the form
- expansion method in which the solutions are presented in the form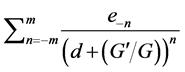 . Recently, TahaNoorani and Hashim [7] apply this method to provide closed-form traveling wave solutions of the generalized thin film equations and stand thin film equation, in which the related balance numbers are not the usual positive integers.
. Recently, TahaNoorani and Hashim [7] apply this method to provide closed-form traveling wave solutions of the generalized thin film equations and stand thin film equation, in which the related balance numbers are not the usual positive integers.
Since every nonlinear equation has its own physically significant rich structure, still much work has to be done. In this paper, we propose some new exact traveling wave solutions for Equations (1), and which stresses its power of  -expansion method in handling nonlinear equations.
-expansion method in handling nonlinear equations.
2. Exact Solutions for Equations (1)
Substituting the solution  into (1), where
into (1), where 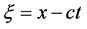 and
and 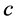 represents the wave speed, we obtain
represents the wave speed, we obtain
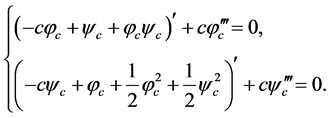 (2)
(2)
Integrating the equations and the integration constants are chosen as zero, it can be converted to the ODEs
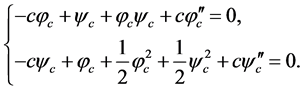 (3)
(3)
Next, we apply the 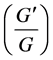 -expansion method to solve Equations (3). Firstly, considering the homogeneous balance between the highest order derivative and the non-linear term, we suppose the solutions of (3) can be written in the form
-expansion method to solve Equations (3). Firstly, considering the homogeneous balance between the highest order derivative and the non-linear term, we suppose the solutions of (3) can be written in the form
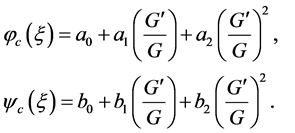 (4)
(4)
where 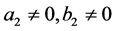 and
and 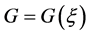 satisfies the second order linear ODE
satisfies the second order linear ODE
 (5)
(5)
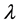 and
and  are real constants. Using the general solutions of ODE (5), it is easy to obtain
are real constants. Using the general solutions of ODE (5), it is easy to obtain
 (6)
(6)
By Euqations (4) and (5) we derive
 (7)
(7)
 (8)
(8)
Substituting (4) (7) and (8) into (3), collecting all terms with the same powers of  and setting each coefficient to zero, we get two sets of algebraic equations for
and setting each coefficient to zero, we get two sets of algebraic equations for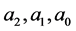 ,
, 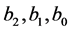 and
and .
.
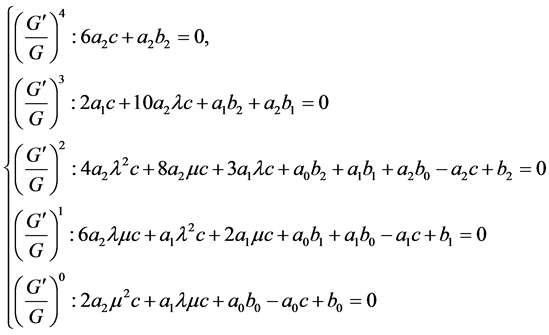
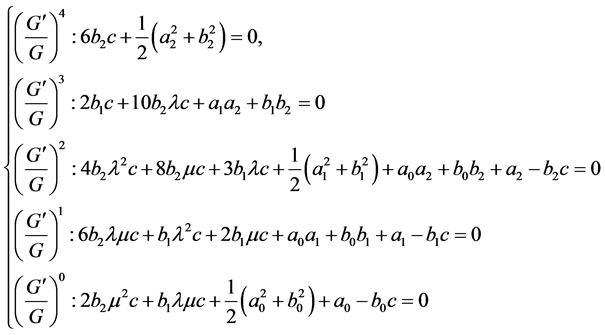
Solving the above algebraic equations yields eight groups of values of unknowns.
1.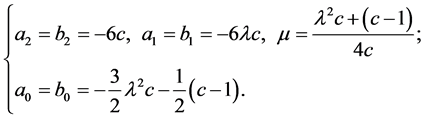 (9)
(9)
2.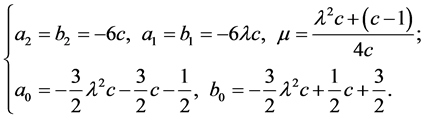 (10)
(10)
3.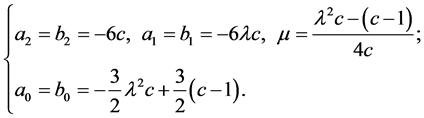 (11)
(11)
4. (12)
(12)
5.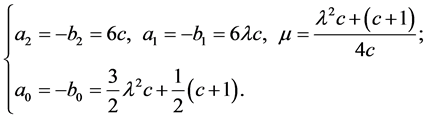 (13)
(13)
6.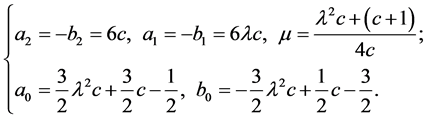 (14)
(14)
7. (15)
(15)
8.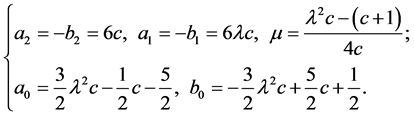 (16)
(16)
Substituting (9)-(16) into (5), using the expression (6), three types of traveling wave solutions of (1) are given as follows.
Case a. When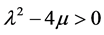 ,
,
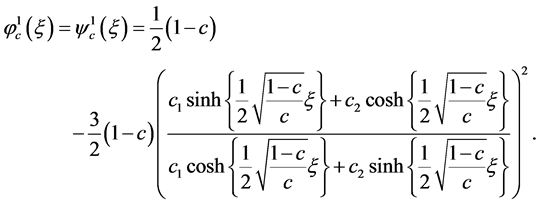 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
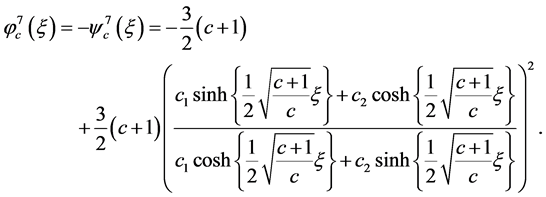 (23)
(23)
 (24)
(24)
Case b. When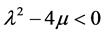 ,
,
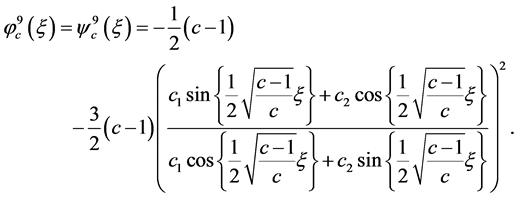 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
 (29)
(29)
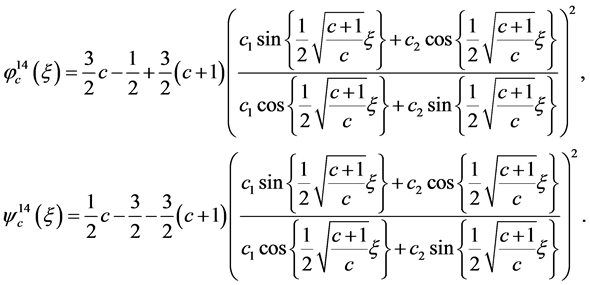 (30)
(30)
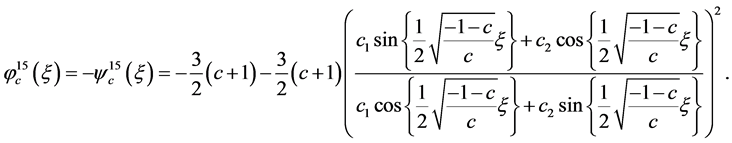 (31)
(31)
 (32)
(32)
Case c. When ,
,
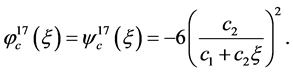 (33)
(33)
 (34)
(34)
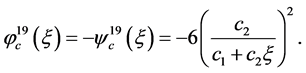 (35)
(35)
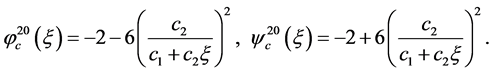 (36)
(36)
Remark If  or
or , the waves obtained in the form of (17)-(24) are just the waves given in [1] [2] .
, the waves obtained in the form of (17)-(24) are just the waves given in [1] [2] .
Acknowledgements
Research is supported by Science Foundation of the Education Commission of Beijing (No. KM201210017008, No. KZ201310028030), NSF of Beijing (1132003) and Youth foundation of Beijing Institute of Petrochemical Technology (No. N10-04).
References
- Cui, L.W. and Zhao, Y. (2012) Orbital Stability of Solitary Waves for Coupled BBM Equations. Advances in Mathematics (Chinese), 41, 341-346.
- Zhao Y. and Xu, Q. (to appear) Existence and Instability of Solitary Waves with Nonzero Asymptotic Value for Some BBM Equations.
- Wang M., Li, X. and Zhang, J. (2008) The
 -Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423. http://dx.doi.org/10.1016/j.physleta.2007.07.051
-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Physics Letters A, 372, 417-423. http://dx.doi.org/10.1016/j.physleta.2007.07.051 - Bekir A. (2008) Application of the
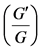 -Expansion Method for Nonlinear Evolution Equations. Physics Letters A, 372, 3400-3406. http://dx.doi.org/10.1016/j.physleta.2008.01.057
-Expansion Method for Nonlinear Evolution Equations. Physics Letters A, 372, 3400-3406. http://dx.doi.org/10.1016/j.physleta.2008.01.057 - Zayed, E.M.E. and Al-Joudi, S. (2010) Application of an Extended
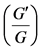 -Expansion Method to Find Exact Solutions of Nonlinear PDEs in Mathematical Physics. Mathematical Problems in Engineering, 2010, Article ID: 768573.
-Expansion Method to Find Exact Solutions of Nonlinear PDEs in Mathematical Physics. Mathematical Problems in Engineering, 2010, Article ID: 768573. - Ali Akbar, M., Ali, N .H.M. and Zayed, E.M.E. (2012) A Generalized and Improved
- Taha, W.M., Noorani, M.S.M. and Hashim, I. (2014) New Exact Solutions of Sixth-Order Thin-Film Equation. Journal of King Saud University—Science, 26, 75-78.
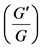 -Expansion Method for Nonlinear Evolution Equations. Mathematical Problems in Engineering, 2012, Article ID: 459879.
-Expansion Method for Nonlinear Evolution Equations. Mathematical Problems in Engineering, 2012, Article ID: 459879. 
