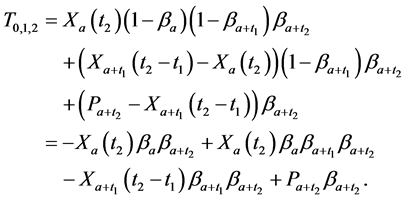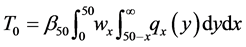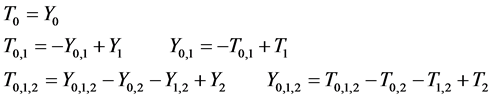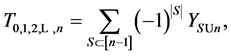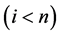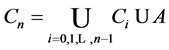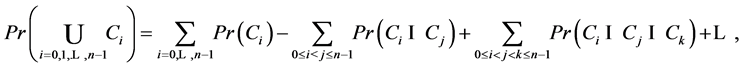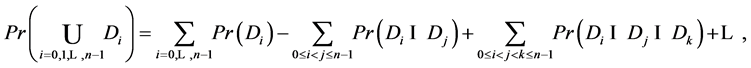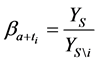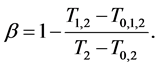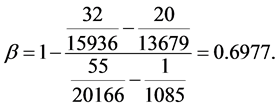Applied Mathematics
Vol.05 No.17(2014), Article ID:50799,7 pages
10.4236/am.2014.517265
An Exact Formula for Estimation of Age-Specific Sensitivity for Screening Tests
Ning Jia, Sandra J. Lee*
Department of Biostatistics and Computational Biology, Dana-Farber Cancer Institute, Boston, USA
Email: ning@jimmy.harvard.edu, *sjlee@jimmy.harvard.edu
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 August 2014; revised 16 September 2014; accepted 23 September 2014
ABSTRACT
There has been a growing interest in screening programs designed to detect chronic progressive cancers in the asymptomatic stage, with the expectation that early detection will result in a better prognosis. One key element of early detection programs is a screening test. An accurate screening test is more effective in finding cases with early-stage diseases. Sensitivity, the conditional probability of getting a positive test result when one truly has a disease, represents one measure of accuracy for a screening test. Since the true disease status is unknown, it is not straightforward to estimate the sensitivity directly from observed data. Furthermore, the sensitivity is associated with other parameters related to the disease progression. This feature introduces additional numerical complexity and limitations, especially when the sensitivity depends on age. In this paper, we propose a new approach that, through combinatorial manipulation of probability statements, formulates the age-dependent sensitivity. This formulation has an exact and simple expression and can be estimated based on directly observable probabilities. This approach also helps evaluating other parameters associated with the natural history of disease more accurately. The proposed method was applied to estimate the mammography sensitivity for breast cancer using the data from the Health Insurance Plan trial.
Keywords:
Early Detection of Disease, Screening Test, Sensitivity

1. Introduction
Screening of asymptomatic individuals for chronic diseases is a rapidly growing public health initiative. Early detection programs are aimed at detecting the disease in the stage when a disease is present without symptoms. For example, in breast cancer, there had been eight randomized screening trials demonstrating that mammography screening is beneficial in finding breast cancer at an earlier stage and consequently leads to a decrease in mortality among women of 50 - 65 years of age ([1] -[7] ).
One key element of these programs is a screening test. An important measure for the effectiveness of a screening test is sensitivity (b), the conditional probability of getting a positive screening test result given that one has the disease. Ideally it should be evaluated in the setting of natural history of disease model ([8] -[11] ). Often parameters like the sojourn time distribution in early stage of disease (pre-clinical state), transition probability from no disease state to early-stage disease state are needed to estimate the sensitivity.
These parameters are not directly observable and add to the complexity of the problem formulation and numerical computation of the sensitivity. Furthermore, the sensitivity can be age-dependent. For example in breast cancer the mammogram sensitivity in younger women is lower than that in older women [12] . The formulation for estimating age-dependent sensitivity becomes complex and does not always guarantee a numerical solution.
In this paper, we derive a formula that expresses age-dependent sensitivity in terms of probabilities that are directly observable in screening trials/programs and discuss the characteristics and generalization of this formula. We apply the formula to breast cancer screening trial (Health Insurance Plan) data to estimate the mammography sensitivity [1] .
2. Method: An Exact Expression for Age-Dependent Sensitivity 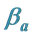
Consider the following health states in the natural history of disease progression:
· 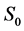 , the disease-free state, when the disease cannot be detected by any current early detection program;
, the disease-free state, when the disease cannot be detected by any current early detection program;
·  , the pre-clinical state, when the disease is detectable by an early detection program, but no symptoms are shown; and
, the pre-clinical state, when the disease is detectable by an early detection program, but no symptoms are shown; and
· 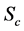 , the clinical state, when symptoms show.
, the clinical state, when symptoms show.
A progressive disease model assumes that the disease progresses in the direction  unless it is interrupted by a medical intervention. In the case of chronic progressive diseases, the goal of screening program in detecting the disease in
unless it is interrupted by a medical intervention. In the case of chronic progressive diseases, the goal of screening program in detecting the disease in . The age is denoted by a. Let
. The age is denoted by a. Let
·  be the sensitivity of the screening exam (i.e., the conditional probability that a disease is detected by the screening exam given disease is present) if the exam is taken at age a;
be the sensitivity of the screening exam (i.e., the conditional probability that a disease is detected by the screening exam given disease is present) if the exam is taken at age a;
· 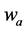 be the transition rate from
be the transition rate from 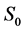 to
to 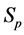 at age a;
at age a;
· 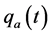 be the sojourn time distribution in
be the sojourn time distribution in 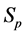 if the transition
if the transition  happens at age a; and
happens at age a; and
· 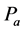 be the probability for case being in the pre-clinical state
be the probability for case being in the pre-clinical state 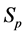 at age a, i.e. the proportion of people in
at age a, i.e. the proportion of people in 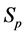 at age a in absence of screening examinations.
at age a in absence of screening examinations.
Note that


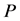
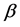
We now introduce two important probabilities that all the subsequent derivations are based upon. Suppose there are no screening examinations before age a, and a series of examinations are scheduled (but not necessarily taken) at times 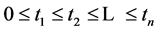


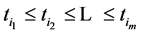
· 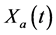
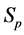
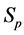

· 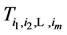
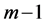

The importance of 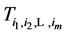


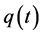
Note that it is implied in the definition of T and X that by the time of the last examination, one would either be in 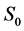

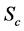
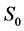
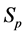
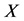
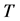
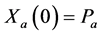
We derive a formula for 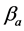
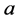
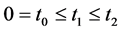
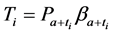
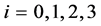
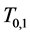
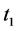
· before time 0 (or age a), go undetected at time 0, and stay in 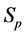

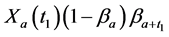
· between time 0 and
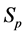
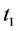
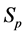
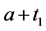
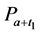
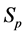
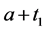
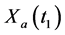
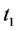
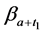
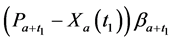
Therefore,
Or,
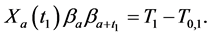
Similarly, for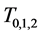
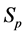
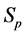
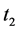
· before age a and go undetected at times 0 and
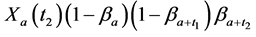
· between ages a and 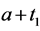
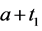

· between ages 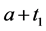

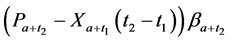
Therefore,
From (1), we have 
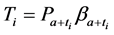
which gives

Observing (1) and (2), we arrive at our main result in this section:
Theorem 2.1.
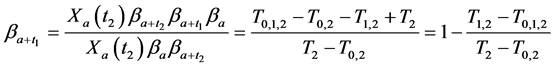
Therefore by writing out a few recursions, we are able to eliminate all 

Let 
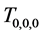

Corollary 2.2. When at least three repeated tests with the same sensitivity 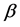
The result is achieved by simply taking limits 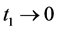

Theorem 2.1 is far from being intuitive, but corollary is easily verified, when we realize that when 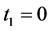
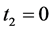



Advantage of Theorem 2.1. One main advantage of Theorem 2.1 is that it enables us to ignore the consideration for transition rate 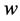

where 



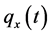
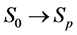
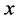
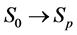



Thus in just this one term, all the

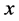



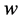
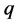
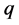



However Theorem 2.1 allows us to bypass 
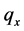
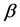
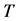
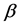
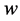
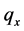

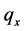

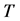
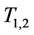
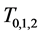
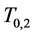
Another important advantage of Theorem 2.1 is that once (age-dependent) 
One limitation of the Theorem 2.1 is that it does not provide a way to apply the “interval cases”, or the cases that enter clinical stages between two scheduled screening exams. These cases, however, can be used later on to determine w and 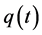

3. Symmetry between X and T
An interesting mathematical result involves certain symmetry between X and T. We use the same setup as in the last section: suppose there are no examinations before age a, and a series of exams are scheduled (but not necessarily taken) at times 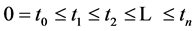
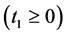
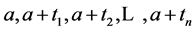

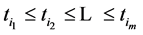
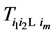


Under the same set up, we introduce the new notation:
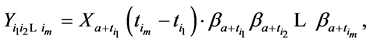
where 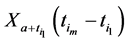

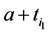
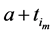

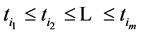
We also recall how we have defined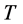
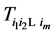
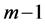
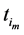
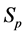
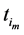
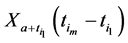
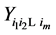
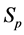
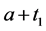
Recall we derived the following expressions in the last section (notice that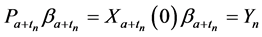
or, after some reorganizing of the terms, and recognizing that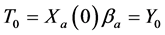
Therefore it is clear that there is a symmetric relationship between the T terms and the corresponding Y terms, in the case of 1, 2 and 3 examinations. The pattern of these expressions becomes more obvious in case of 4 examinations: (which will be proved along with the general case) to make it more obvious:
In the expression of 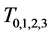

Theorem 3.1. For any
and
where S goes over all subsets of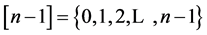

Proof. Because we will be applying the inclusion-exclusion principle later, to make the corresponding arguments, we revise the definition of the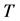

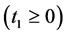



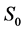
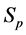
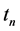
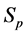

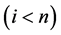
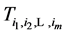

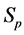


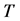
Let
· 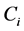

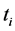
· 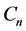
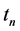
· 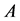
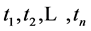
Therefore we have
and 

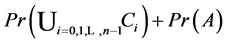
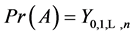
By inclusion-exclusion principle [14] ,
But 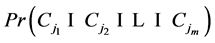
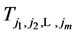
Or,
The second expression can be proved in a similar manner. With the same set up as the above, let
· 
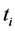
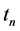
· 
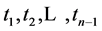
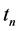
Recall that 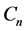
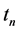
and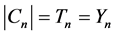
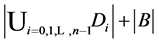
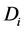

Again by inclusion-exclusion principle,
However 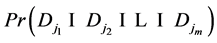

Or,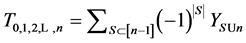
Corollary 3.2. There are infinitely many expressions of age-specificity in terms of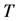
Proof. This is because each 
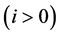
where 


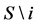

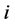
we saw in the last section that
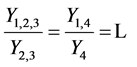
Each 

Given expressions like Theorem 3.1, the proof for Theorem 2.1 is not as straightforward. However the purpose of that proof was to relate some of the traditional considerations and reasoning’s to our new notions. This will be useful when evaluating important parameters such as age-dependent disease transition probabilities and sojourn time distribution.
4. An Example
We illustrate the proposed method using the data from the Health Insurance Plan Project, or HIP data [1] . HIP is a randomized screening trial of mammography screening vs. no screening for the women who did not have previous mammography. Even though HIP is a large-scale screening trial, because breast cancer incidence rate is relatively low, we do not have sufficient number of screen-detected and interval cases to readily estimate age-specific
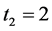
To calculate, saying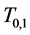
Note that this estimate is essentially identical to Shen and Zelen’s published estimate of 0.7 ([10] [11] ) based on the maximum likelihood method, but is computationally trivial.
Acknowledgements
This work was supported by grants 1RC CA 146496-01 and 1R01 CA16430 from the National Cancer Institute/National Institute of Health.
References
- Shapiro, S., Venet, W., Strax, P., et al. (1988) Periodic Screening for Breast Cancer: The Health Insurance Plan Project and Its Sequelae, 1963-1986. The Johns Hopkins University Press, Baltimore.
- Tabar, L., Gunnar, F., Duffy, S.W., et al. (1992) Update of the Swedish Two-County Program of Mammographic Screening for Breast Cancer. Radiologic Clinics of North America, 30, 187-210.
- Andersson, I., Aspegren, K., Janzon, L., et al. (1988) Mammographic Screening and Mortality from Breast Cancer: The Malmo, Mammographic Screening Trial. British Medical Journal, 297, 943-948. http://dx.doi.org/10.1136/bmj.297.6654.943
- Frisell, J., Glas, U., Hellstrom, L., et al. (1986) Randomized Mammographic Screening for Breast Cancer in Stockholm. Breast Cancer Research and Treatment, 8, 45-54. http://dx.doi.org/10.1007/BF01805924
- Bjurstam, N., Bjorneld, L., Duffy, S.W., et al. (1997) The Gothenburg Breast Screening Trial: First Results on Mortality, Incidence, and Mode of Detection for Women Ages 39 - 49 Years at Randomization. Cancer, 80, 2091-2099. http://dx.doi.org/10.1002/(SICI)1097-0142(19971201)80:11<2091::AID-CNCR8>3.0.CO;2-#
- Roberts, M.M., Alexander, F.E., Anderson, T.J., et al. (1990) Edinburgh Trial of Screening for Breast Cancer: Mortality at Seven Years. Lancet, 335, 241-246. http://dx.doi.org/10.1016/0140-6736(90)90066-E
- Miller, A.B., Baines, C.J., To, T., et al. (1992) Canadian National Breast Screening Study 1: Breast Cancer Detection and Death Rates among Women Aged 40 to 49 Years. Canadian Medical Association Journal, 147, 1459-1476.
- Duffy, S.W., Chen, H., Tabar, L. and Day, N. (1995) Estimation of Mean Sojourn Time in Breast Cancer Screening Using a Markov Chain Model of Both Entry to and Exit from the Preclinical Detectable Phase. Statistics in Medicine, 14, 1531-1553. http://dx.doi.org/10.1002/sim.4780141404
- Paci, E. and Duffy, S.W. (1991) Modeling the Analysis of Breast Cancer Screening Programmes: Sensitivity, Lead Time and Predictive Value in the Florence District Programmes (1975-1986). International Journal of Cancer, 20, 852-858.
- Shen, Y. and Zelen, M. (1999) Parametric Estimation Procedures for Screening Programmes: Stable and Non-Stable Disease Models for Multimodality Case Finding. Biometrika, 86, 503-515. http://dx.doi.org/10.1093/biomet/86.3.503
- Shen, Y. and Zelen, M. (2001) Screening Sensitivity and Sojourn Time from Breast Cancer Early Detection Trials: Mammograms and Physical Examinations. Journal of Clinical Oncology, 19, 3496-3499.
- Tabar, L., Fagerberg, G., Chen, H., et al. (1995) Efficacy of Breast Cancer Screening by Age. Cancer, 75, 2507-2517. http://dx.doi.org/10.1002/1097-0142(19950515)75:10<2507::AID-CNCR2820751017>3.0.CO;2-H
- Zelen, M. (1993) Optimal Scheduling of Examinations for the Early Detection of Disease. Biometrika, 80, 279-293. http://dx.doi.org/10.1093/biomet/80.2.279
- Stanley, R.P. (1999) Enumerative Combinatorics, Vol. 1. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511609589
NOTES
*Corresponding author.