Applied Mathematics
Vol. 4 No. 2 (2013) , Article ID: 28213 , 8 pages DOI:10.4236/am.2013.42054
Decomposition of Supercritical Linear-Fractional Branching Processes
1Mathematical Sciences, Chalmers University of Technology and University of Gothenburg, Gothenburg, Sweden
2Faculty of Mechanics and Mathematics, Al-Farabi Kazakh National University, Almaty, Kazakhstan
Email: serik@chalmers.se, altynay.kaznu@gmail.com
Received November 29, 2012; revised December 29, 2012; accepted January 6, 2013
Keywords: Harris-Sevastyanov Transformation; Dual Reproduction Law; Branching Process with Countably Many Types; Multivariate Linear-Fractional Distribution; Bienaymé-Galton-Watson Process; Conditioned Branching Process
ABSTRACT
It is well known that a supercritical single-type Bienaymé-Galton-Watson process can be viewed as a decomposable branching process formed by two subtypes of particles: those having infinite line of descent and those who have finite number of descendants. In this paper we analyze such a decomposition for the linear-fractional Bienaymé-GaltonWatson processes with countably many types. We find explicit expressions for the main characteristics of the reproduction laws for so-called skeleton and doomed particles.
1. Introduction
The Bienaymé-Galton-Watson (BGW-) process is a basic model for the stochastic dynamics of the size of a population formed by independently reproducing particles. It has a long history [1] with its origin dating back to 1837. This paper is devoted to the BGW-processes with countably many types. One of the founders of the theory of multi-type branching processes is B. A. Sevastyanov [2,3].
A single-type BGW-process is a Markov chain
 with countably many states
with countably many states  . The evolution of the process is described by a probability generating function
. The evolution of the process is described by a probability generating function
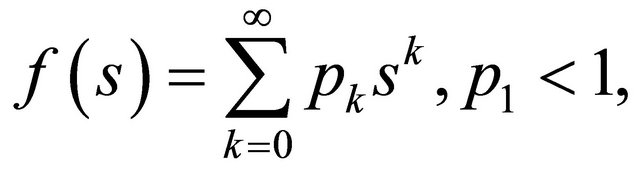 (1)
(1)
where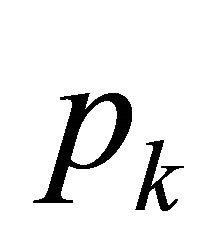 stands for the probability that a single particle produces exactly k offspring. If particles reproduce independently with the same reproduction law (1), then the chain
stands for the probability that a single particle produces exactly k offspring. If particles reproduce independently with the same reproduction law (1), then the chain 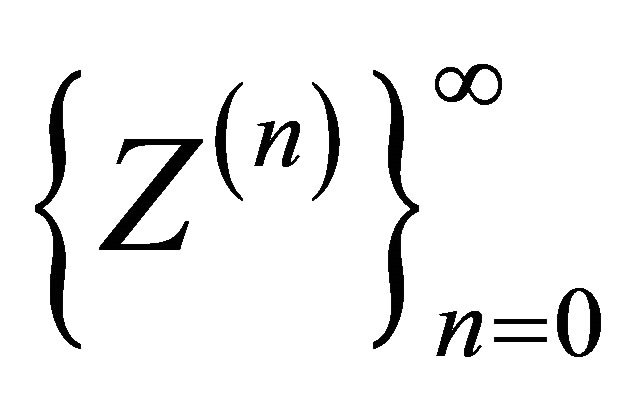 represents consecutive generation sizes. In this paper, if not specified otherwise, we assume that, the branching process stems from a single particle,
represents consecutive generation sizes. In this paper, if not specified otherwise, we assume that, the branching process stems from a single particle, . Due to the reproductive independence it follows that
. Due to the reproductive independence it follows that 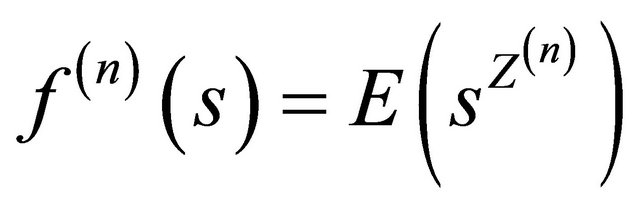 is the n-th iteration of
is the n-th iteration of
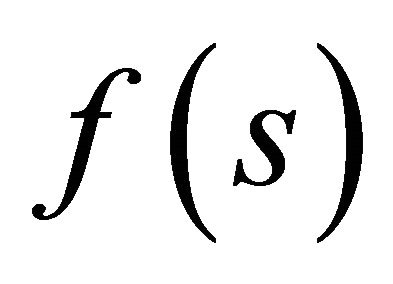 .
.
Since zero is an absorbing state of the BGW-process, 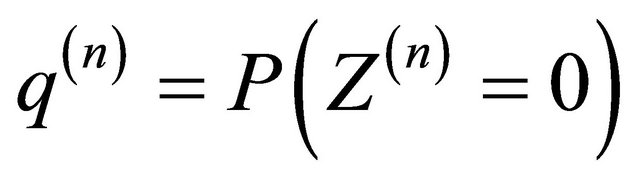 monotonely increases to a limit q called the extinction probability. The latter is implicitly determined as a minimal non-negative solution of the equation
monotonely increases to a limit q called the extinction probability. The latter is implicitly determined as a minimal non-negative solution of the equation
 (2)
(2)
A key characteristic of the BGW-process is the mean offspring number  In the subcritical
In the subcritical
 and critical
and critical  cases the process is bound to go extinct
cases the process is bound to go extinct 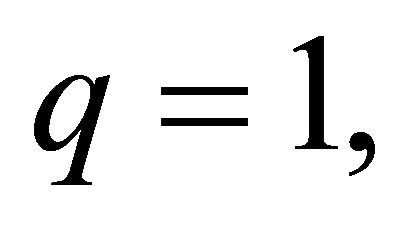 while in the supercritical case
while in the supercritical case  we have
we have 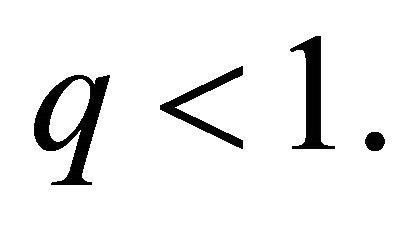 Clearly
Clearly 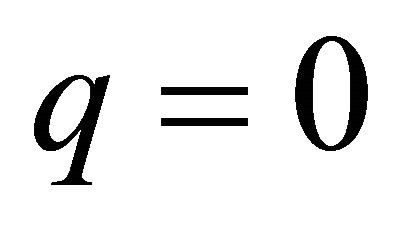 if and only if
if and only if 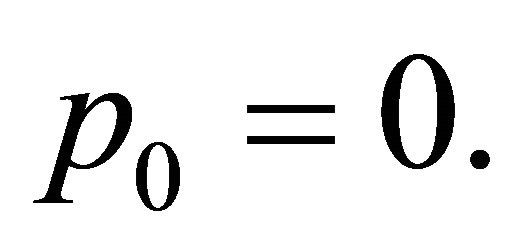
In the supercritical case the number of descendants of the progenitor particle is either finite with probability q or infinite with probability  Recognizing that the same is true for any particle appearing in the BGWprocess we can distinguish between skeleton particles having an infinite line of descent [4] and doomed particles having a finite line of descent. Graphically we get a picture of the genealogical tree similar to that given in Figure 1.
Recognizing that the same is true for any particle appearing in the BGWprocess we can distinguish between skeleton particles having an infinite line of descent [4] and doomed particles having a finite line of descent. Graphically we get a picture of the genealogical tree similar to that given in Figure 1.
If we disregard the doomed particles, the skeleton particles form a BGW-process with a transformed reproduction law excluding extinction
 (3)
(3)
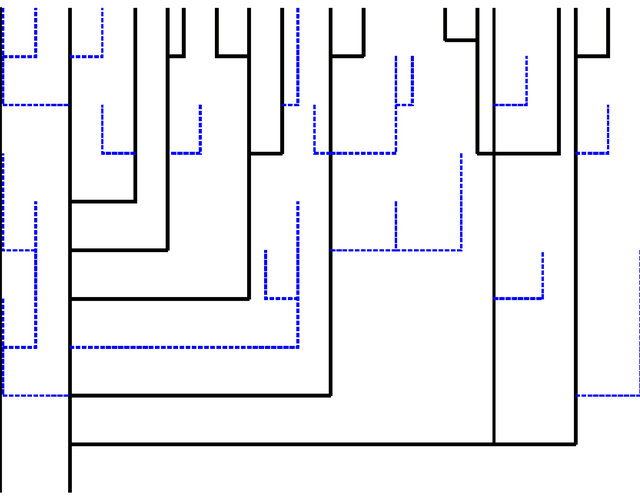
Figure 1. An example of a BGW-tree up to level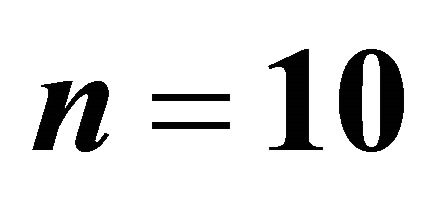 . Solid lines represent the infinite lines of descent and dotted lines represent the finite lines of descent.
. Solid lines represent the infinite lines of descent and dotted lines represent the finite lines of descent.
and having the same mean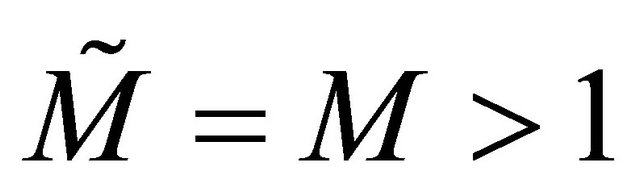 . Formula (3) is usually called the Harris-Sevastyanov transformation. On the other hand, the doomed particles form another branching process corresponding to the supercritical branching process conditioned on extinction. The doomed particles produce only doomed particles according to another transformation of the reproduction law
. Formula (3) is usually called the Harris-Sevastyanov transformation. On the other hand, the doomed particles form another branching process corresponding to the supercritical branching process conditioned on extinction. The doomed particles produce only doomed particles according to another transformation of the reproduction law
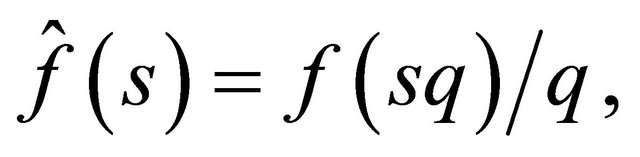
which is usually called the dual reproduction law and has mean  The supercritical BGW-process as a whole can be viewed as a decomposable branching process with two subtypes of particles [5]. Each skeleton particle must produce at least one new skeleton particle and also can give rise to a number of doomed particles. In Section 2 we describe in detail this decomposition for the single type supercritical BGW-processes.
The supercritical BGW-process as a whole can be viewed as a decomposable branching process with two subtypes of particles [5]. Each skeleton particle must produce at least one new skeleton particle and also can give rise to a number of doomed particles. In Section 2 we describe in detail this decomposition for the single type supercritical BGW-processes.
In the special case when the reproduction generating function (1) is linear-fractional many characteristics of the BGW-process can be computed in an explicit form [6]. In Section 3 we summarize explicit results concerning decomposition of a supercritical single-type BGWprocesses.
Section 4 presents the BGW-processes with countably many types. Our focus is on the linear-fractional case recently studied in [7]. The main results of this paper are collected in Section 5 and their derivation is given in Section 6. The remarkable fact that a supercritical branching process conditioned on extinction is again a branching process was recently established in [8] in a very general setting. In general, the transformed reproduction laws are characterized in an implicit way and are difficult to analyse. This paper presents a case where the properties of the skeleton and doomed particles are very transparent.
2. Decomposition of a Supercritical Single-Type BGW-Process
The BGW-process is a time homogeneous Markov chain with transition probabilities satisfying
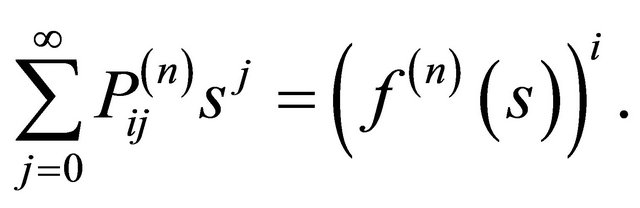
In the supercritical case with mean 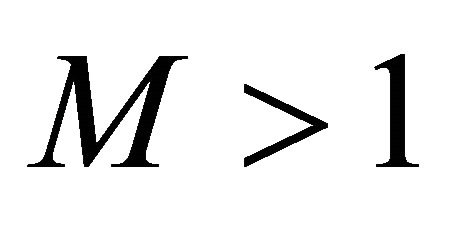 and extinction probability
and extinction probability 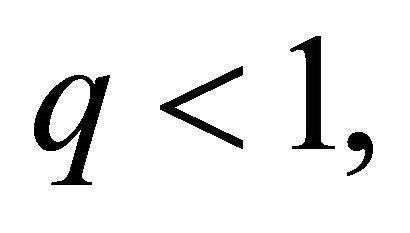 using the property
using the property

we can get another set of transition probabilities putting

The transformed transition probabilities also possess the branching property
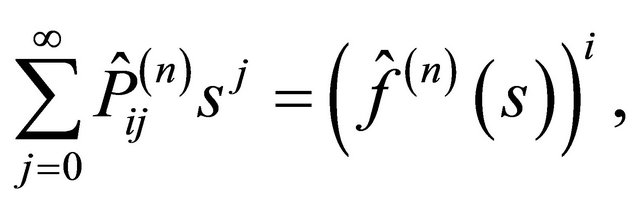
where 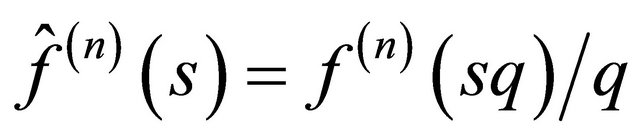 is the n-th iteration of the so-called dual generating function
is the n-th iteration of the so-called dual generating function

The corresponding dual BGW-process is a subcritical branching process with offspring mean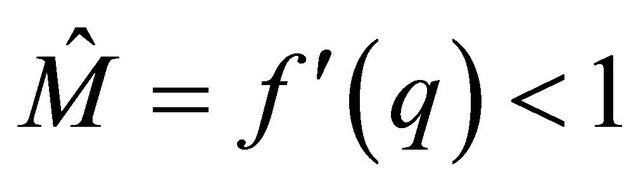 , see Figure 2. The dual BGW-process is distributed as the original supercritical BGW-process conditioned on extinction:
, see Figure 2. The dual BGW-process is distributed as the original supercritical BGW-process conditioned on extinction:
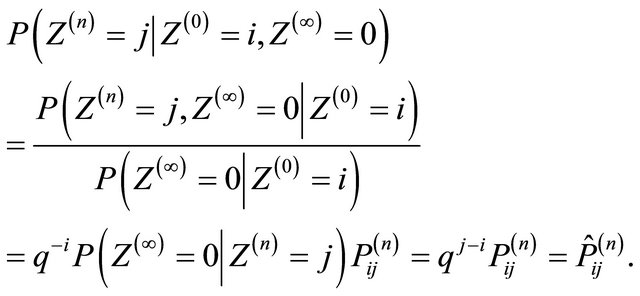
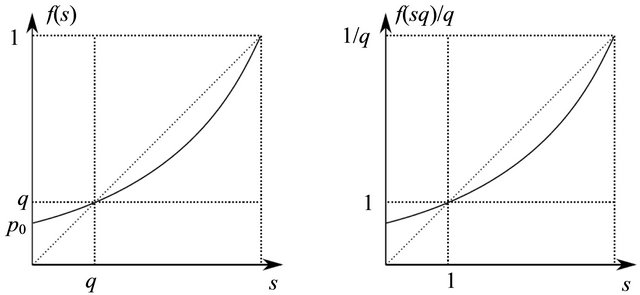
Figure 2. Duality between the subcritical and supercritical cases. Left: a supercritical generating function (1) with two positive roots  for the Equation (2). Right: the dual generating function drawn on a different scale.
for the Equation (2). Right: the dual generating function drawn on a different scale.
The two parts of the curve on the left panel of Figure 2 represent two transformations of the supercritical branching process. The lower-left part of the curve, replicated on the right panel of Figure 2 using a different scale, gives the generating function of the dual process. The upper-right of the curve on the left panel corresponds to the Harris-Sevastyanov transformation (3). The function (3) is the generating function for the probability distribution
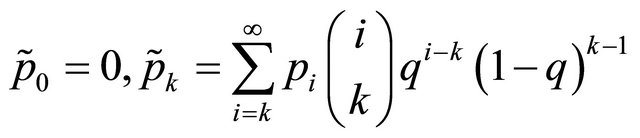
with the same mean  as the original offspring distribution. It is easy to see that the n-th iteration of
as the original offspring distribution. It is easy to see that the n-th iteration of  is given by
is given by

Looking into the future of the system of reproducing particles we can distinguish between two subtypes of particles:
• skeleton particles with infinite line of descent (building the skeleton of the genealogical tree);
• doomed particles having finite line of descent.
These two subtypes form a decomposable two-type BGW-process 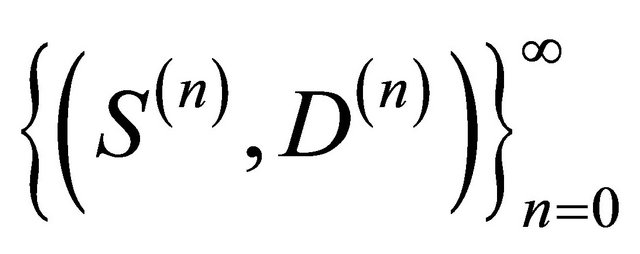 with
with
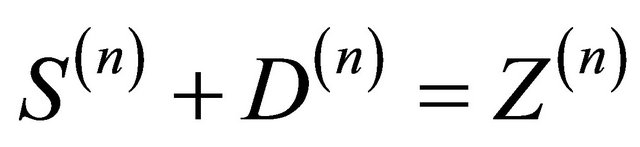
The joint reproduction law for the skeleton particles has the following generating function
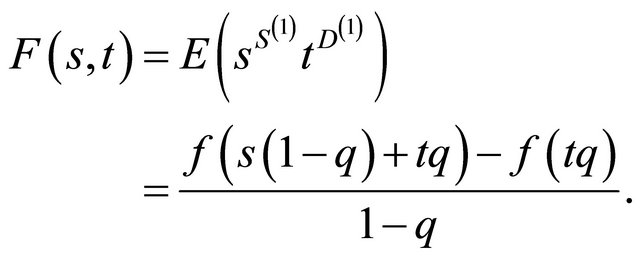
A check on the branching property for the decomposed process is given by
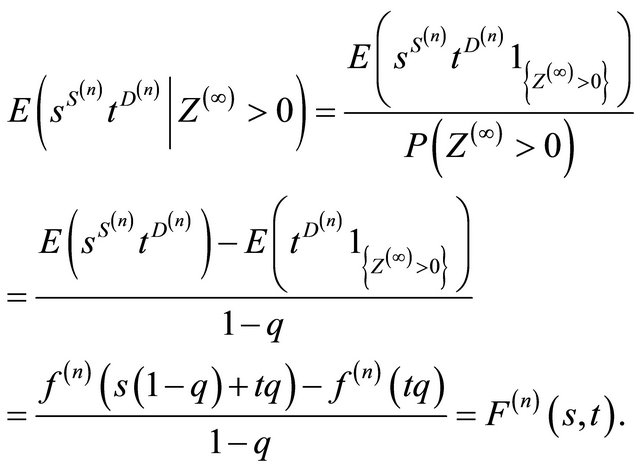
The original offspring distribution can be recovered as a mixture of the joint reproduction laws of the two subtypes

Observe also that the total number of offspring for a skeleton particle has a distribution given by
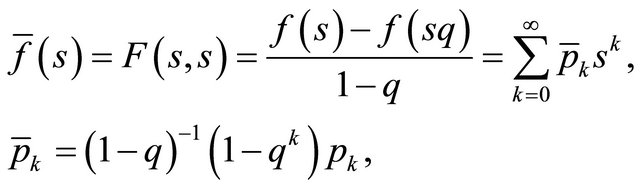
with mean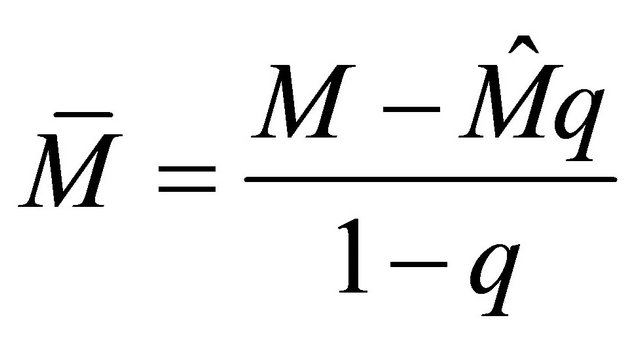 . It follows,
. It follows,
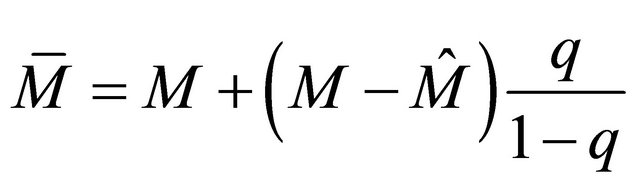
and we can summarize the relationship among different offspring means as
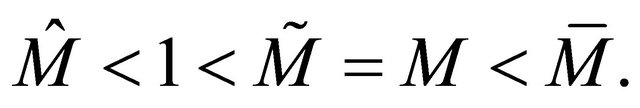
3. Linear-Fractional Single-Type BGW-Process
An important example of BGW-processes is the linearfractional branching process. Its reproduction law has a linear-fractional generating function
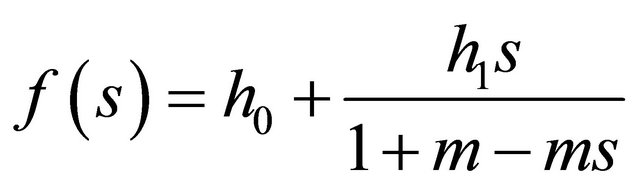 (4)
(4)
fully characterized by two parameters: the probability  of having no offspring, and the mean m of the geometric number of offspring beyond the first one. Here
of having no offspring, and the mean m of the geometric number of offspring beyond the first one. Here 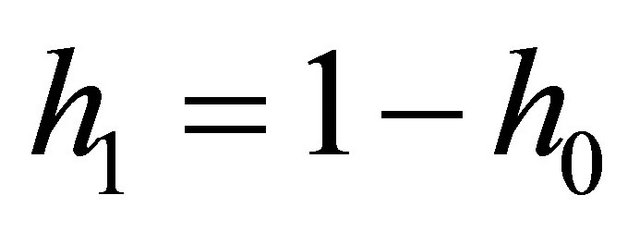 stands for the probability of having at least one offspring. Notice that with
stands for the probability of having at least one offspring. Notice that with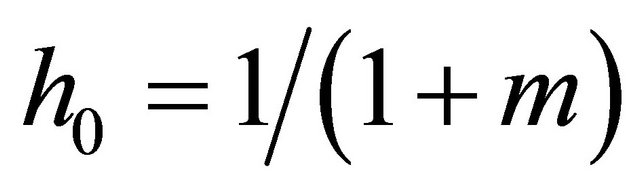 , the generating function (4) describes a Geometric
, the generating function (4) describes a Geometric 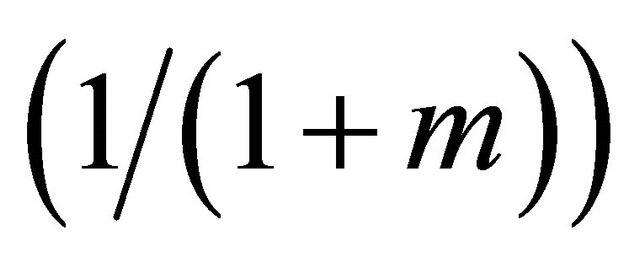
distribution with mean m. If  the generating function (4) gives a Shifted Geometric
the generating function (4) gives a Shifted Geometric 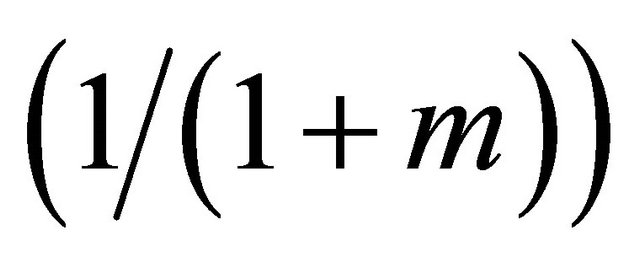 distribution with mean
distribution with mean 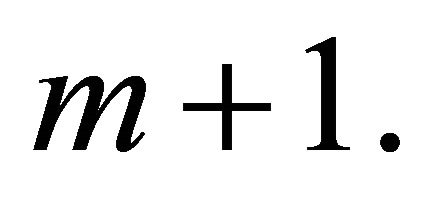 If
If 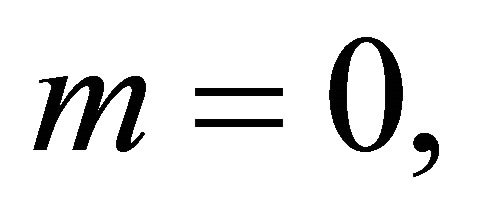 we arrive at a Bernoulli
we arrive at a Bernoulli 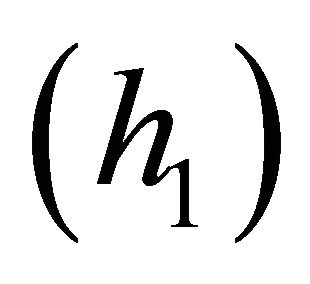 distribution.
distribution.
Since the iterations of the linear-fractional function are again linear-fractional, many key characteristics of the linear-fractional BGW-processes can be computed explicitly in terms of the parameters 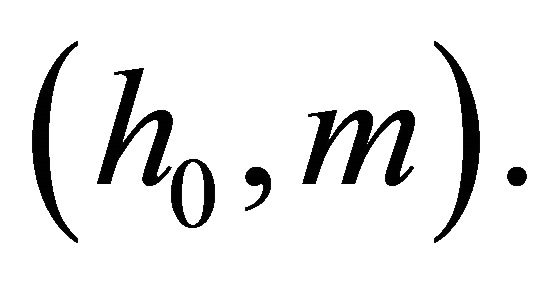 For example, we have
For example, we have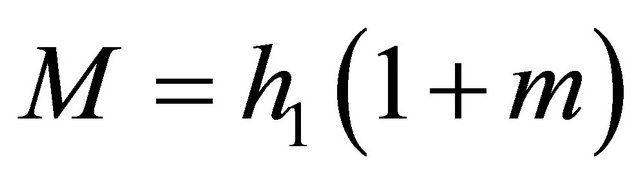 , and if
, and if , we get
, we get
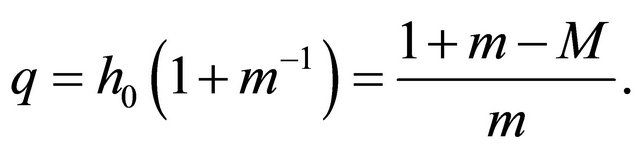
The dual reproduction law for (4) is again linearfractional
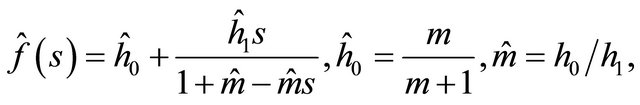
with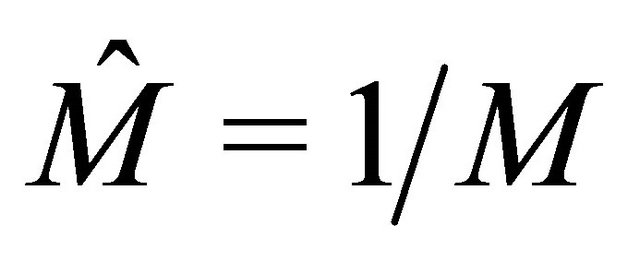 . The Harris-Sevastyanov transformation in the linear-fractional case corresponds to a shifted geometric distribution
. The Harris-Sevastyanov transformation in the linear-fractional case corresponds to a shifted geometric distribution
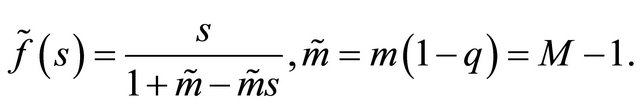
Interestingly, the joint reproduction law of skeleton particles
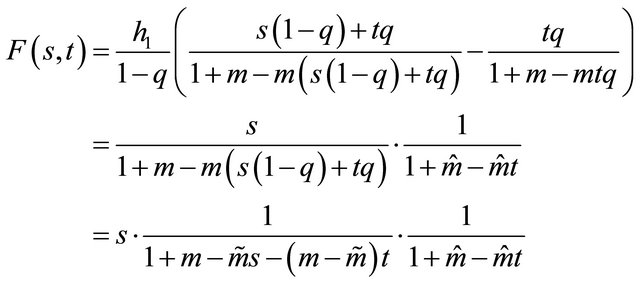
has three independent components:
• one particle of type 1 (the infinite lineage);
• a Geometric 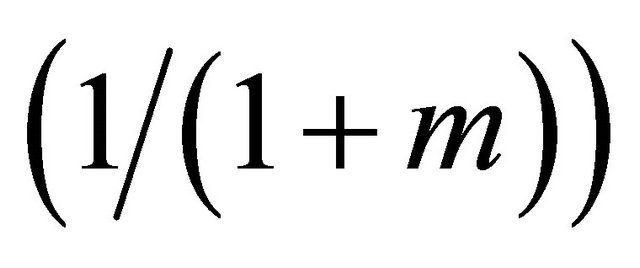 number of offspring each choosing independently between the skeleton and doomed subtypes with probabilities
number of offspring each choosing independently between the skeleton and doomed subtypes with probabilities 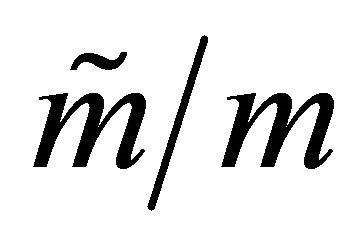 and
and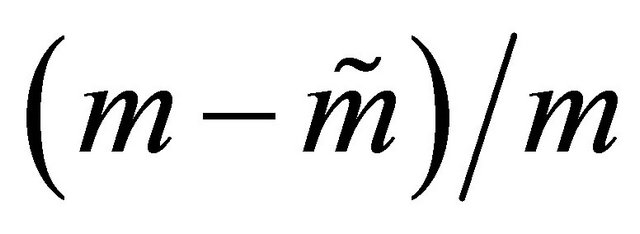 ;
;
• a Geometric 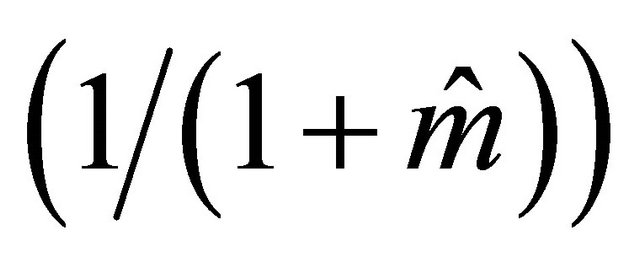 number of doomed offspring.
number of doomed offspring.
Observe that even though both marginal distributions 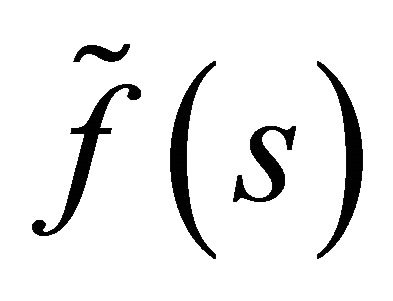 and
and 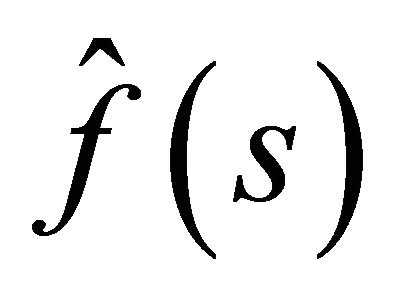 are linear-fractional, the decomposable BGW-process
are linear-fractional, the decomposable BGW-process 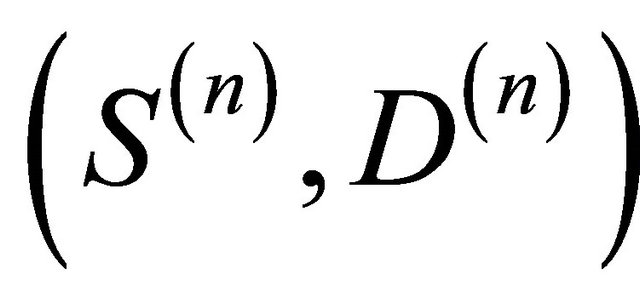 is not a two-type linearfractional BGW-process. The distribution of the total number of offspring for the skeleton particles is not linear-fractional
is not a two-type linearfractional BGW-process. The distribution of the total number of offspring for the skeleton particles is not linear-fractional
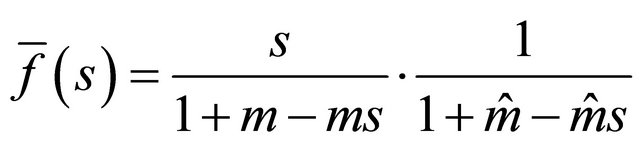
and has mean

4. BGW-Processes with Countably Many Types
A BGW-process with countably many types

describes demographic changes in a population of particles with different reproduction laws depending on the type of a particle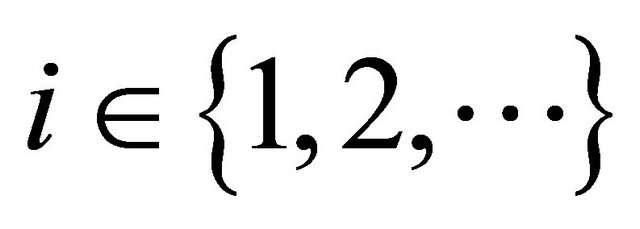 . Here
. Here 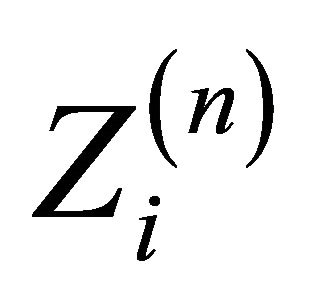 is the number of particles of type
is the number of particles of type  existing at generation n. In the multi-type setting we use the following vector notation:
existing at generation n. In the multi-type setting we use the following vector notation:
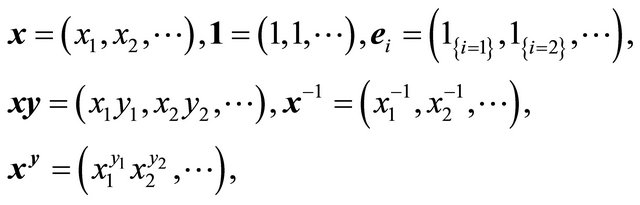
we write 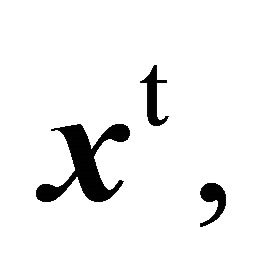 if we need a column version of a vector
if we need a column version of a vector![]() .
.
A particle of type i may produce random numbers of particles of different types so that the corresponding joint reproduction laws are given by the multivariate generating functions
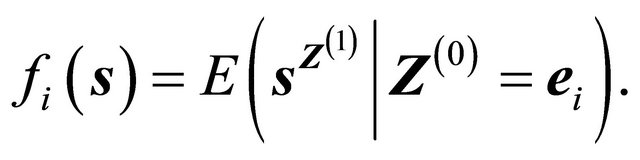 (5)
(5)
The offspring means
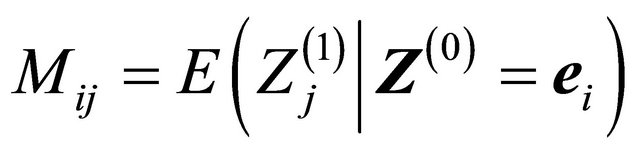
are convenient to summarize in a matrix form
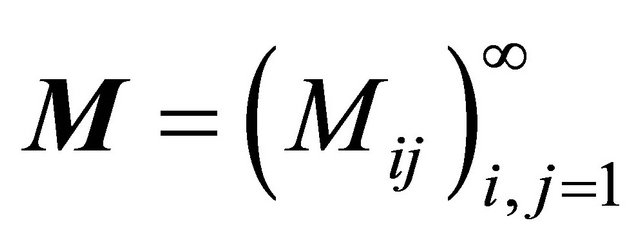 .
.
For the n-th generation the vector of generating functions  with components
with components
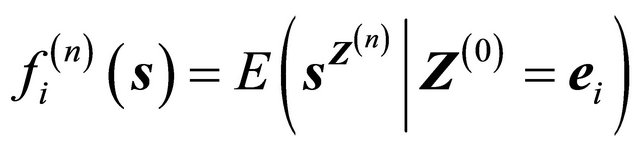
are obtained as iterations of 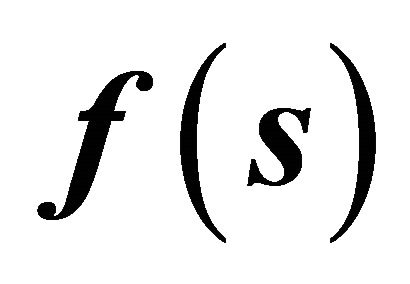 with components (5), and the matrix of means is given by
with components (5), and the matrix of means is given by  The vector of extinction probabilities
The vector of extinction probabilities 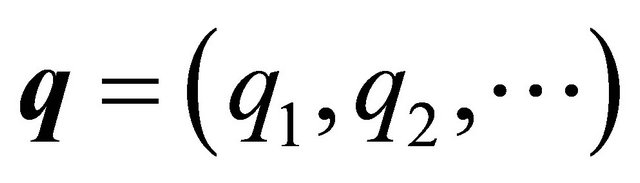 has its i-th component
has its i-th component 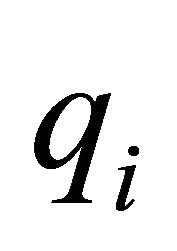 defined as the probability of extinction given that the BGW-process starts from a particle of type i. The vector
defined as the probability of extinction given that the BGW-process starts from a particle of type i. The vector  is found as the minimal solution with non-negative components of equation
is found as the minimal solution with non-negative components of equation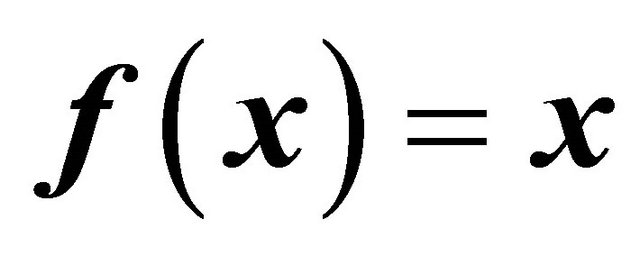 , which is a multidimensional version of (2).
, which is a multidimensional version of (2).
From now on we restrict our attention to the positive recurrent (with respect to the type space) case when there exists a Perron-Frobenius eigenvalue 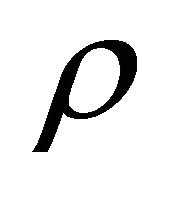 for
for 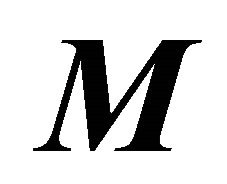 with positive eigenvectors
with positive eigenvectors ![]() and
and ![]() such that
such that
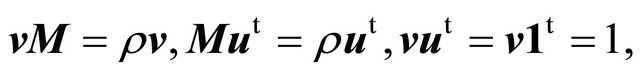
and
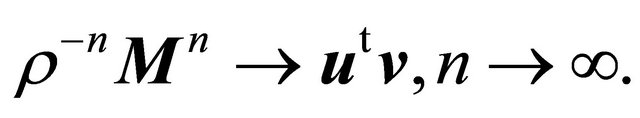
In the supercritical case, 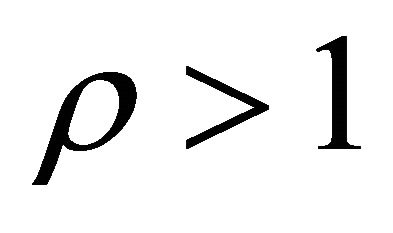 , all
, all 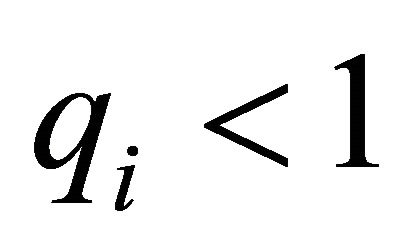 and we can speak about the decomposition of a supercritical BGW-process with countably many types:
and we can speak about the decomposition of a supercritical BGW-process with countably many types: . Now each type is decomposed in two subtypes: either with infinite or finite line of descent. The decomposed supercritical BGW-process is again a BGW-process with countably many types whose reproduction law is given by the expressions
. Now each type is decomposed in two subtypes: either with infinite or finite line of descent. The decomposed supercritical BGW-process is again a BGW-process with countably many types whose reproduction law is given by the expressions

Linear-fractional BGW-processes with countably many types were studied recently in [7]. In this case the joint probability generating functions (5) have a restricted linear-fractional form
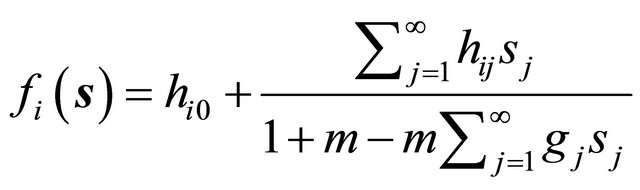 . (6)
. (6)
The defining parameters of this branching process form a triplet , where
, where  is a sub-stochastic matrix,
is a sub-stochastic matrix, 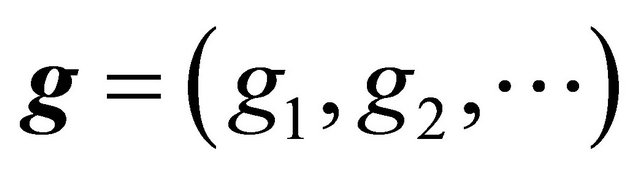 is a proper probability distribution, and m is a positive constant. The free term in (6) is defined as
is a proper probability distribution, and m is a positive constant. The free term in (6) is defined as
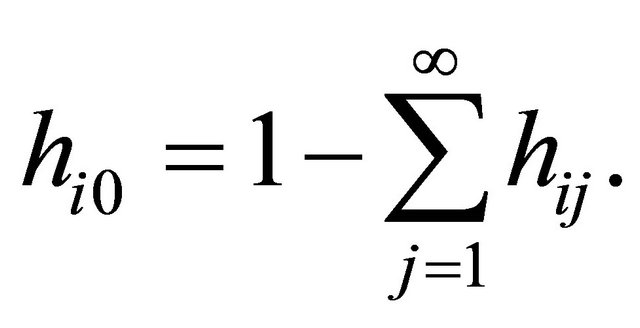
The denominators in (6) are necessarily independent of the mother type to ensure that the iterations are also linear-fractional. This is a major restriction of the multitype linear-fractional BGW-process excluding for example decomposable branching processes.
It is shown in [7] that in the linear-fractional case the Perron-Frobenius eigenvalue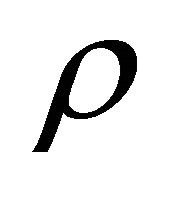 , if exists, is the unique positive solution of the equation
, if exists, is the unique positive solution of the equation
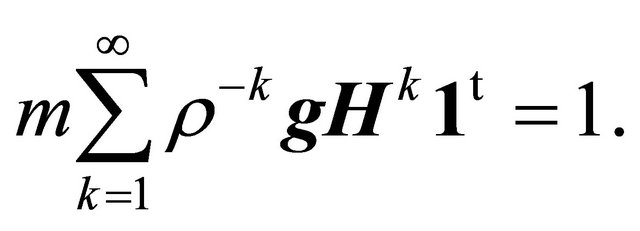 (7)
(7)
In the positive recurrent case, when the next sum is finite
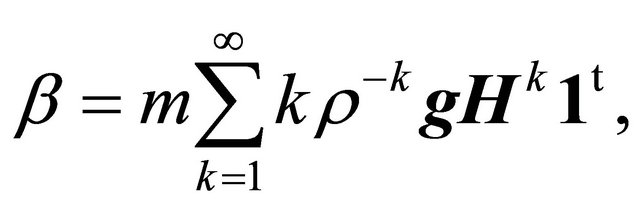 (8)
(8)
the Perron-Frobenius eigenvectors  can be normalized in such a way that
can be normalized in such a way that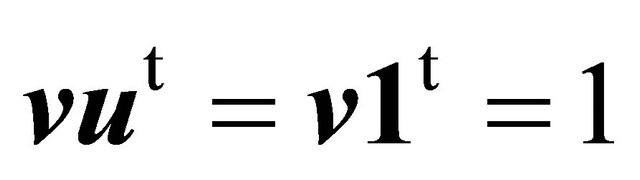 . They are computed as
. They are computed as
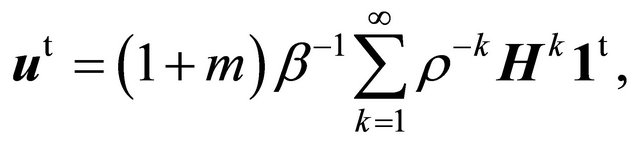 (9)
(9)
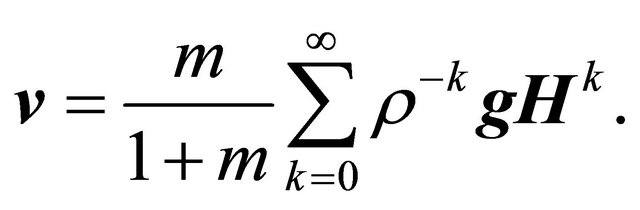 (10)
(10)
In the supercritical positive recurrent case with 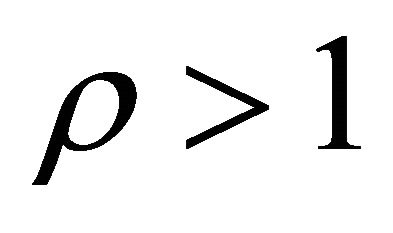 and
and  the extinction probabilities are given by
the extinction probabilities are given by
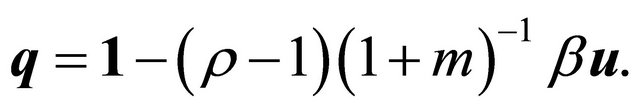 (11)
(11)
Observe that 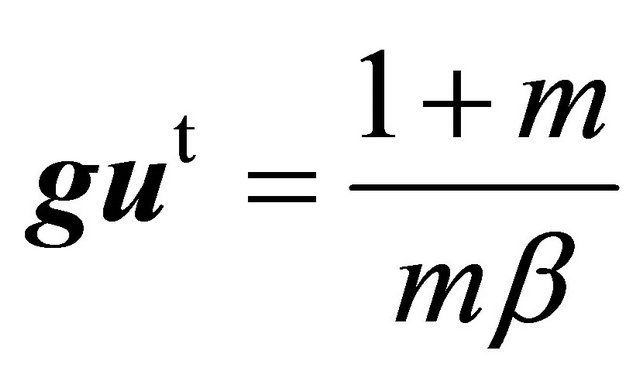 and
and
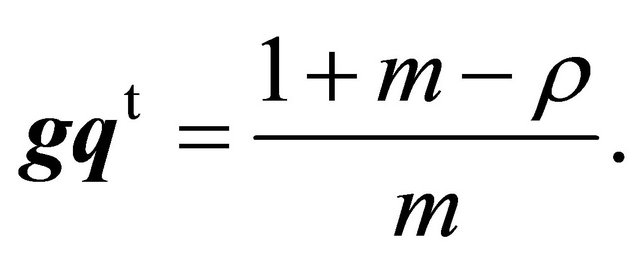 (12)
(12)
The total offspring number for a type i particle has mean
 (13)
(13)
5. Main Results
In this section, we summarize explicit formulae that we were able to obtain for the decomposition of the supercritical linear-fractional BGW-processes with countably many types. The derivation of these results is given in the next section.
Consider the positive recurrent supercritical case with  and
and . We demonstrate that the dual reproduction laws are again linear-fractional
. We demonstrate that the dual reproduction laws are again linear-fractional
 (14)
(14)
with
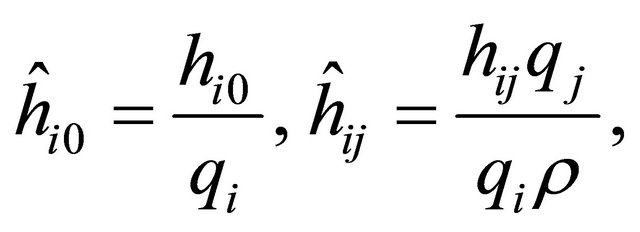 (15)
(15)
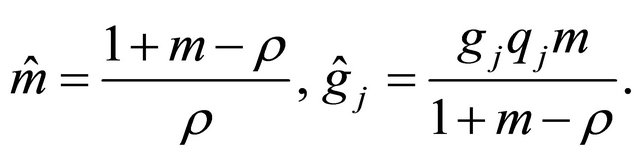 (16)
(16)
It turns out that the following remarkably simple formulae hold for the key characteristics of the dual branching process
 (17)
(17)
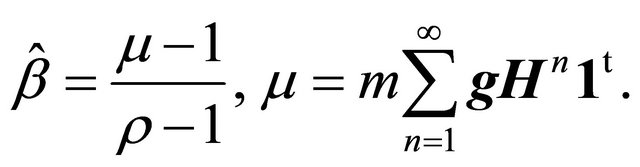 (18)
(18)
For the Perron-Frobenius eigenvectors we obtain the following expressions
![]() (19)
(19)
 (20)
(20)
We show that the Harris-Sevastyanov transformation results in multivariate shifted geometric distributions
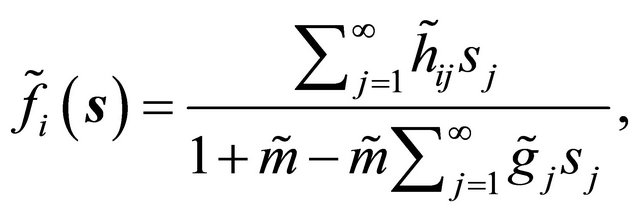 (21)
(21)
where
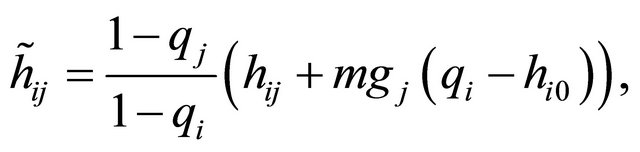 (22)
(22)
 (23)
(23)
Moreover, we demonstrate that
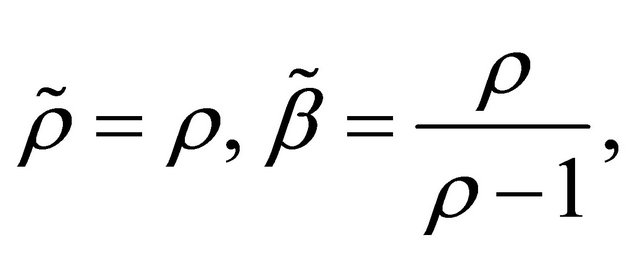 (24)
(24)
and 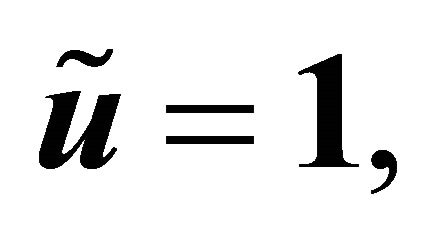
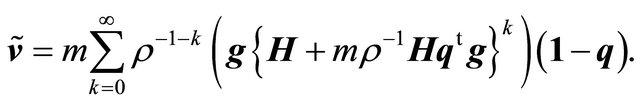 (25)
(25)
Theorem 5.1 Consider a linear-fractional BGW-process characterized by a triplet 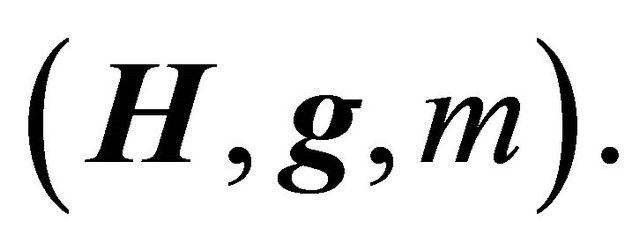 Assume it is supercritical and positively recurrent over the state space, that is
Assume it is supercritical and positively recurrent over the state space, that is 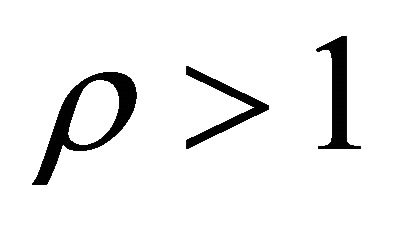 and
and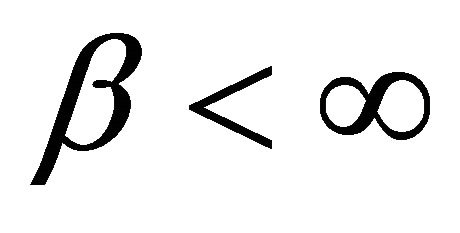 . Its dual BGW-process and its skeleton are also linear-fractional BGWprocesses with the transformed parameter triplets
. Its dual BGW-process and its skeleton are also linear-fractional BGWprocesses with the transformed parameter triplets 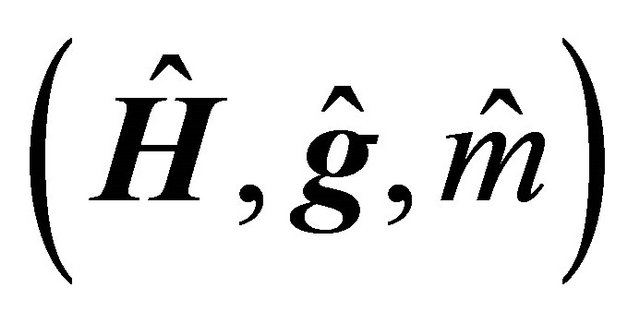 and
and 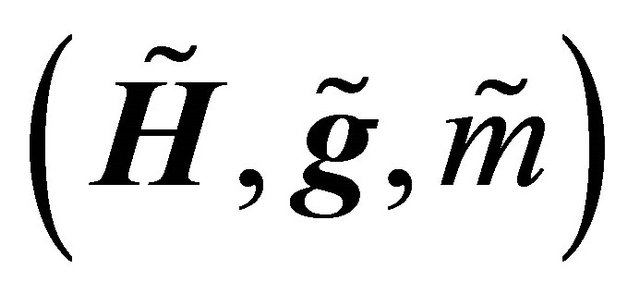 with components given by Equations (15), (16), (22) and (23).
with components given by Equations (15), (16), (22) and (23).
The joint offspring generating function for a skeleton particle of type  has the form
has the form
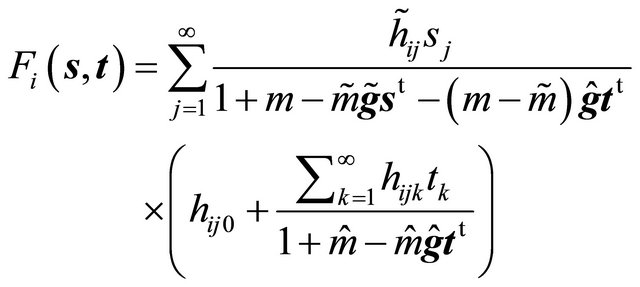 (26)
(26)
where
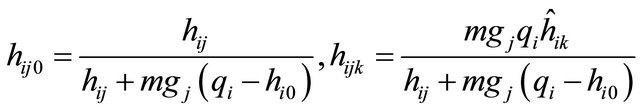 .
.
Similarly to the single-type case, we can distinguish in (26) three components but now with dependence:
• a “reborn” skeleton particle of type i may change its type to j with probability ;
;
• independent of i and j a multivariate geometric number of offspring of both subtypes;
• a linear-fractional number of doomed offspring with the fate of the first offspring being dependent on .
.
The total number of offspring of a skeleton particle of type i has generating function  of the next form
of the next form
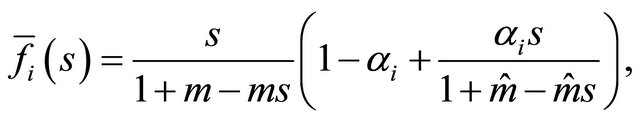
where 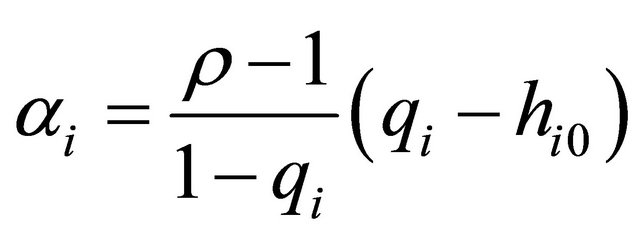 must belong to the interval
must belong to the interval
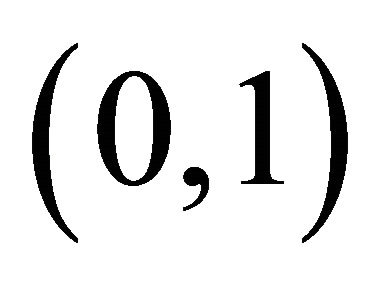 . The corresponding mean offspring number is larger than that given by (13):
. The corresponding mean offspring number is larger than that given by (13):
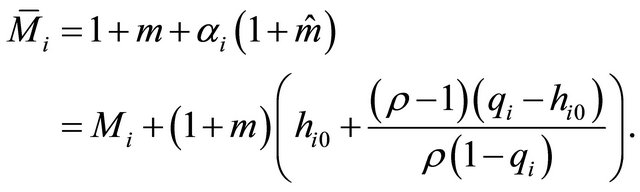
6. Proof of Theorem 5.1
In this section we derive the formulae stated in Section 5.
Proof of (14). From
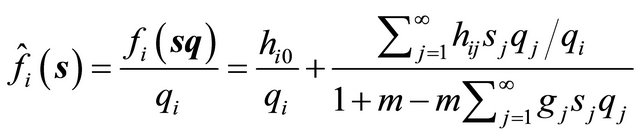
it is straightforward to obtain Equation (14) with Equations (15) and (16). We have to verify that 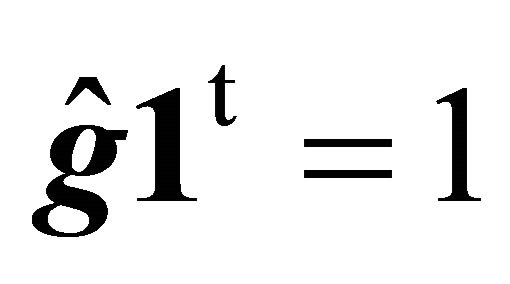 and
and
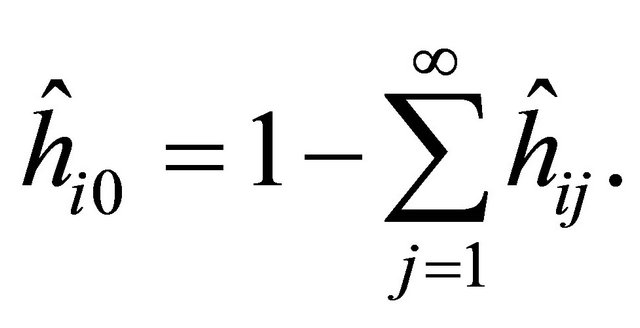
The first requirement follows from (12). The second is obtained from
 (27)
(27)
which is proved next. We have (relation (6) in [7])
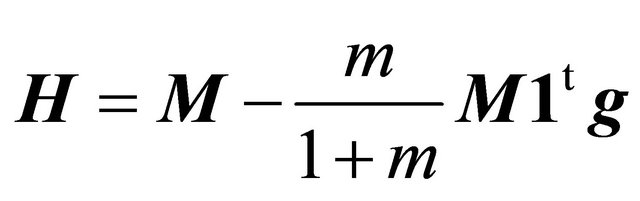
and therefore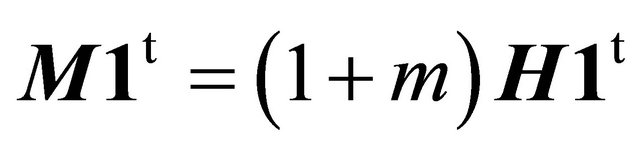 , which is (13). Using the last two equalities and (11) we find first
, which is (13). Using the last two equalities and (11) we find first
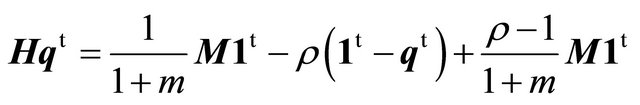
and then obtain (27).
Proof of (17). In view of Equation (7) determining the Perron-Frobenius eigenvalue for a linear-fractional BGWprocess, to show (17) it is enough to verify that
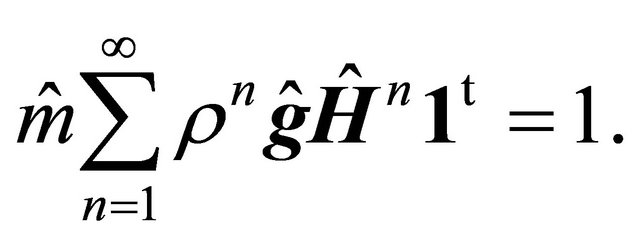
Observe that according to Equation (15)
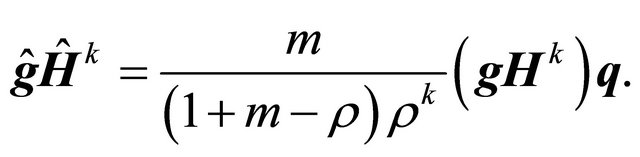 (28)
(28)
It follows,
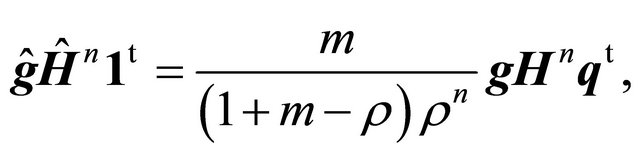 (29)
(29)
so that we have to check that
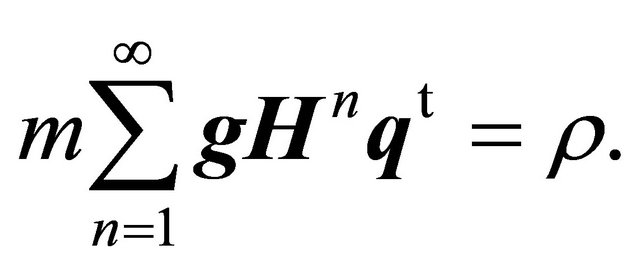 (30)
(30)
Turning to Equation (27) we find
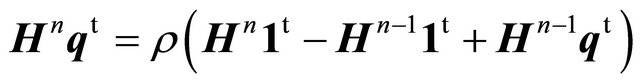 (31)
(31)
yielding
 (32)
(32)
This and Equation (12) entail Equation (30).
Proof of (18). Starting from a counterpart of Equation (8) we find using Equation (29)
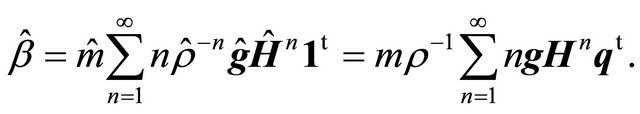
Rewrite Equation (31) as
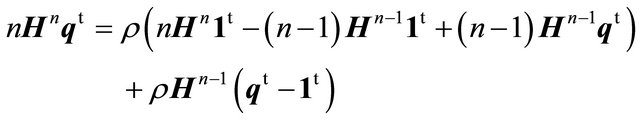
to obtain
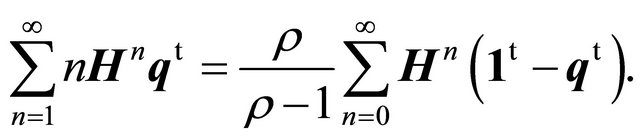
Thus

Proof of (19) and (20). From (15) we derive

This and a counterpart of (9)
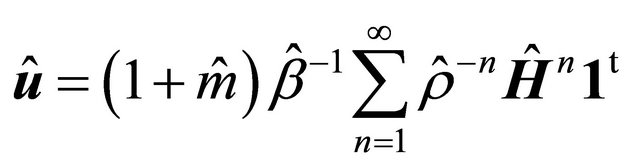
in view of (32) brings (19)
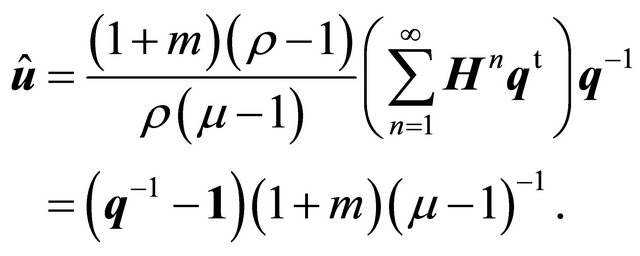
On the other hand, a counterpart of (10) together with (28) yields
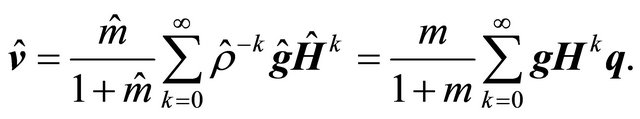
Proof of (26). We have
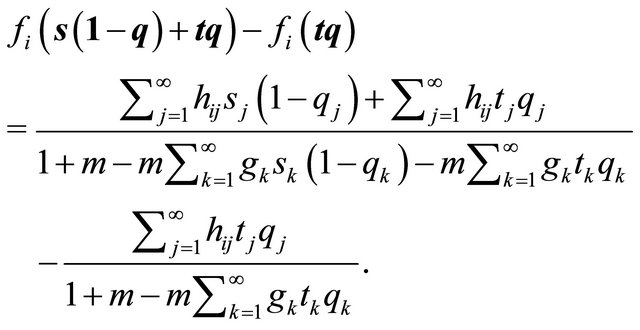
It follows,
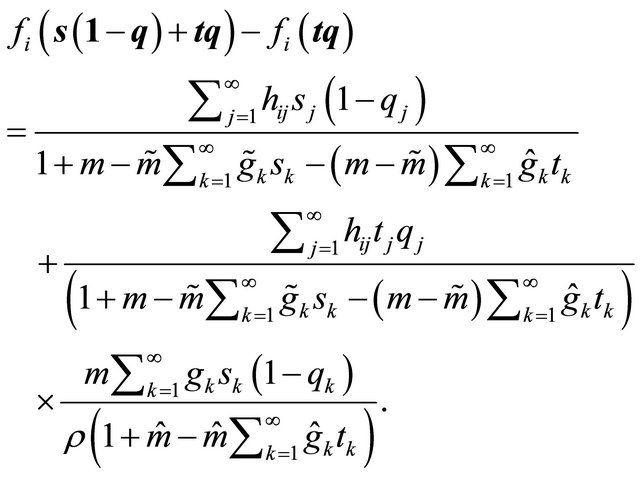
Replacing the last numerator by
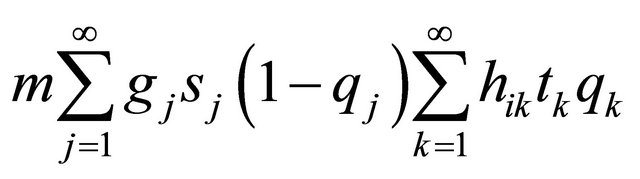
and dividing the whole expression by 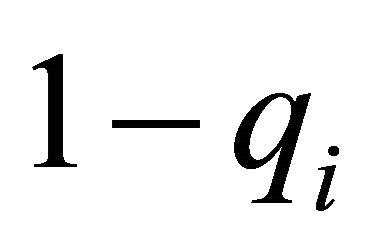 we get
we get

and the relation (26) follows.
Proof of (21) and (24). Putting 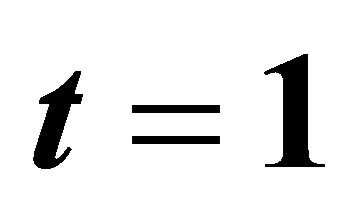 in (26) we arrive at (21). Notice that according to definition (22) and relations (12), (27) we have
in (26) we arrive at (21). Notice that according to definition (22) and relations (12), (27) we have
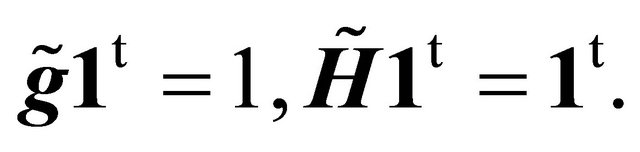
Since 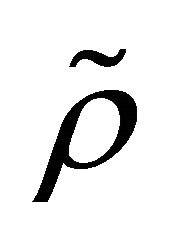 is the unique positive solution of
is the unique positive solution of
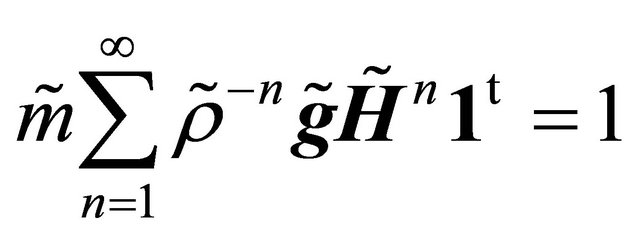
and 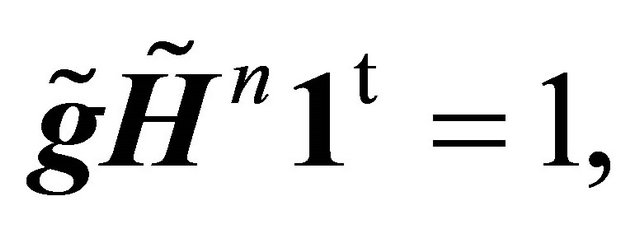 we derive
we derive

Thus 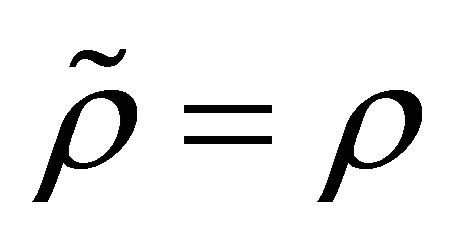 and
and
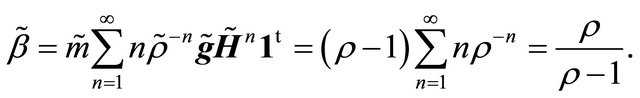
7. Acknowledgements
Serik Sagitov was supported by the Swedish Research Council grant 621-2010-5623. Altynay Shaimerdenova was supported by the Scientific Committee of Kazakhstan’s Ministry of Education and Science, grant 0732/ GF 2012-14.
REFERENCES
- C. C. Heyde and E. J. Seneta “Bienaymé: Statistical Theory Anticipated,” Springer, New York, 1977. doi:10.1007/978-1-4684-9469-3
- B. A. Sevastyanov, “The Theory of Branching Random Processes,” Uspehi Matematicheskih Nauk, Vol. 6, 1951, pp. 47-99.
- B. A. Sewastjanow, “Verzweigungsprozesse,” AkademieVerlag, Berlin, 1974.
- N. O’Connell, “Yule Process Approximation of the Skeleton of a Branching Process,” Journal of Applied Probability, Vol. 30, No. 3, 1993, pp. 725-729. doi:10.2307/3214778
- K. B. Athreya and P. E. Ney, “Branching Processes,” Dover, Mineola, 2004.
- F. Klebaner, U. Rosler and S. Sagitov, “Transformations of Galton-Watson Processes and Linear Fractional Reproduction,” Advances in Applied Probability, Vol. 39, No. 4, 2007, pp. 1036-1053. doi:10.1239/aap/1198177238
- S. Sagitov, “Linear-Fractional Branching Processes with Countably Many Types,” 2012, 24 p. http://arxiv.org/abs/1111.4689
- P. Jagers and A. N. Lagerås, “General Branching Processes Conditioned on Extinction Are Still Branching Processes,” Electronic Communications in Probability, Vol. 13, 2008, pp. 540-547. doi:10.1214/ECP.v13-1419

