Applied Mathematics
Vol.4 No.1A(2013), Article ID:27507,8 pages DOI:10.4236/am.2013.41A040
Spherical Harmonic Solution of the Robin Problem for the Helmholtz Equation in a Supershaped Shell*
1Microwave Sensing, Signals and Systems, Delft University of Technology, Delft, The Netherlands
2Department of Bioscience Engineering, University of Antwerp, Antwerp, Belgium
3Faculty of Exact and Natural Sciences, Tbilisi State University, Tbilisi, Georgia
4Faculty of Engineering, Campus Bio-Medico University, Rome, Italy
Email: d.caratelli@tudelft.nl
Received August 11, 2012; revised September 11, 2012; accepted September 19, 2012
Keywords: Robin Problem; Helmholtz Equation; Spherical Harmonic Expansion; Gielis Formula; Supershaped Shell
ABSTRACT
The Robin problem for the Helmholtz equation in normal-polar shells is addressed by using a suitable spherical harmonic expansion technique. Attention is in particular focused on the wide class of domains whose boundaries are defined by a generalized version of the so-called “superformula” introduced by Gielis. A dedicated numerical procedure based on the computer algebra system Mathematica© is developed in order to validate the proposed methodology. In this way, highly accurate approximations of the solution, featuring properties similar to the classical ones, are obtained.
1. Introduction
Many problems of mathematical physics and electromagnetics are related to the Laplacian differential operator. Among them, it is worth mentioning those relevant to the Laplace and Helmholtz equations. However, most of the mentioned differential problems can be solved in explicit way only in canonical domains with special symmetries, such as intervals, cylinders or spheres [1]. The solution in more general domains can be obtained by using the Riemann theorem on conformal mappings and the relevant invariance of the Laplacian [2]. However, it is clear that conformal mapping techniques can not be used in the three-dimensional case where approaches based on suitable spatial discretization procedures, such as such as finite-difference or finite-element methods, are usually adopted [3].
Different techniques have been proposed in order to solve the mentioned class of differential problems both from a theoretical and numerical point of view (e.g., representing the solution by means of boundary layer techniques [4], solving the corresponding boundary integral equation by iterative methods [5], approximating the relevant Green function by means of the least squares fitting technique [6], solving the linear system relevant to an elliptic partial differential equation by means of relaxation methods [7]). However, none of the contributions already available in the scientific literature deals with the classical Fourier projection method [8] which has been extended in recent papers [9-16] in order to address boundary-value problems (BVPs) in simply connected starlike domains whose boundaries may be regarded as an anisotropically stretched unit circle or sphere centered at the origin.
In this contribution, a suitable methodology, based on the theory of spherical harmonics [17], has been developed in order to compute the solution of the Robin problem for the Helmholtz equation in normal-polar shell-like domains. In particular, the boundaries of the considered domains are supposed to be defined by a generalized version of the so-called Gielis formula (also known as “superformula”) [18]. Regular functions are assumed to describe the boundary values, but the proposed approach can be easily generalized in case of weakened hypotheses.
In order to verify and validate the developed technique, a suitable numerical procedure based on the computer algebra system Mathematica© has been adopted. By using such procedure, a point-wise convergence of the spherical harmonic series representation of the solution has been observed in the regular points of the boundaries, with Gibbs-like phenomena potentially occurring in the quasi-cusped points. The obtained numerical results are in good agreement with theoretical findings by Carleson [19].
2. The Laplacian in Stretched Spherical Coordinates
Let us introduce in the real space the usual spherical coordinate system:
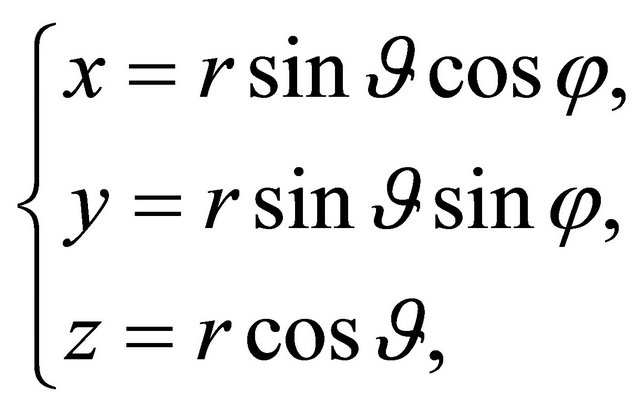 (1)
(1)
and the polar equations:
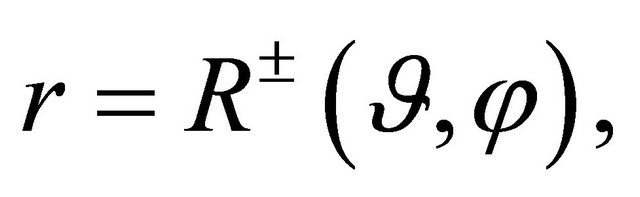 (2)
(2)
relevant to the boundaries of the supershaped shell  which is described by the following chain of inequalities:
which is described by the following chain of inequalities:
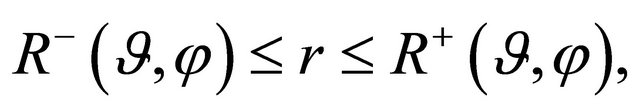 (3)
(3)
with 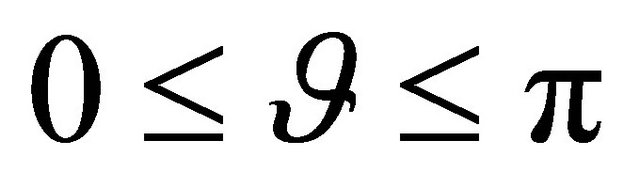 and
and . In (2),
. In (2), 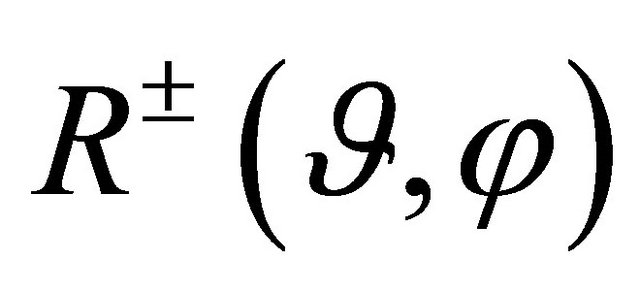 are assumed to be piece-wise
are assumed to be piece-wise  functions satisfying the condition:
functions satisfying the condition:
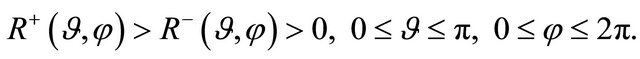 (4)
(4)
In this way, upon introducing the stretched radius  such that:
such that:
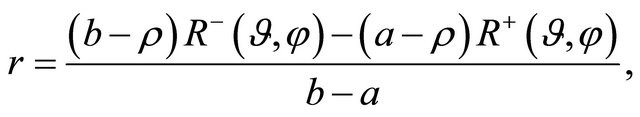 (5)
(5)
with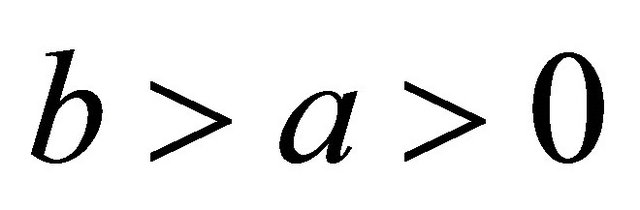 , the considered shell-like domain
, the considered shell-like domain  can be readily obtained by assuming
can be readily obtained by assuming ,
, 
 and
and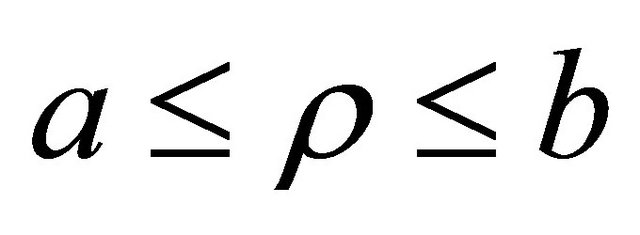 .
.
Remark: Note that, in the stretched coordinate system 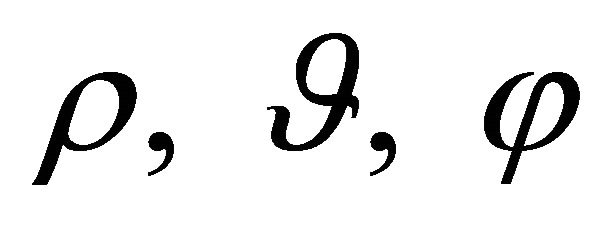 the original domain
the original domain  is transformed into the spherical shell of radii a and b, respectively. Hence, in this system one can use classical techniques to solve the Helmholtz equation, including the eigenfunction method [1].
is transformed into the spherical shell of radii a and b, respectively. Hence, in this system one can use classical techniques to solve the Helmholtz equation, including the eigenfunction method [1].
Let us consider a piece-wise  function ν (x, y, z)
function ν (x, y, z)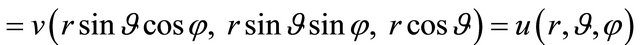 and the Laplace operator,
and the Laplace operator,  , in spherical coordinates:
, in spherical coordinates:
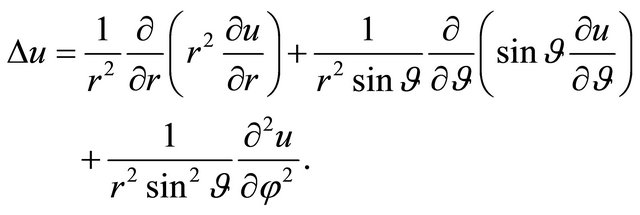 (6)
(6)
In the considered stretched coordinate system,  can be represented by setting:
can be represented by setting:
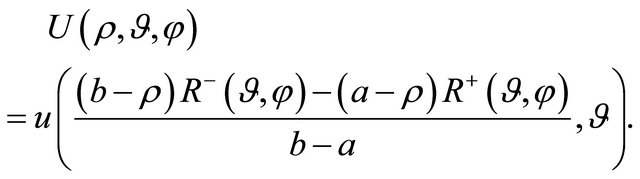 (7)
(7)
In this way, by denoting 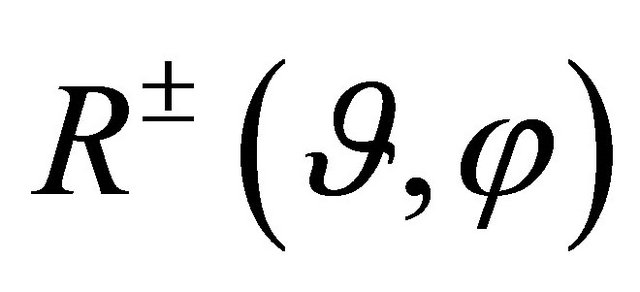 as
as  for the sake of shortness, one can readily find:
for the sake of shortness, one can readily find:
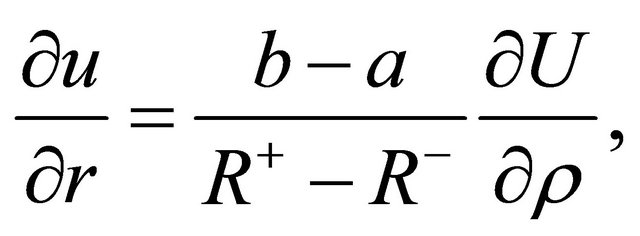 (8)
(8)
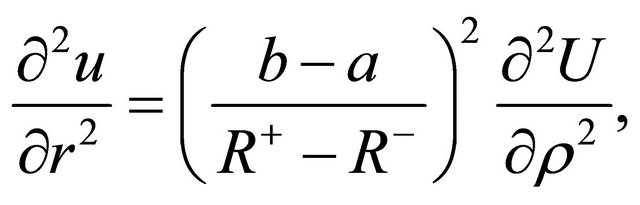 (9)
(9)
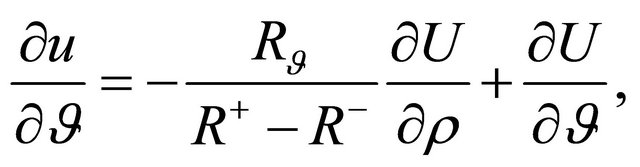 (10)
(10)
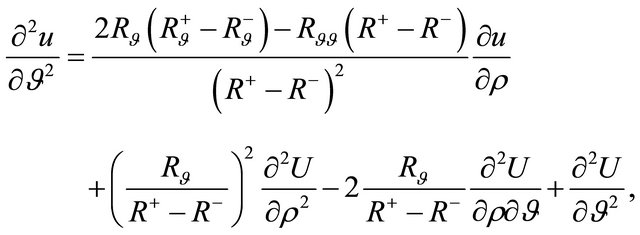 (11)
(11)
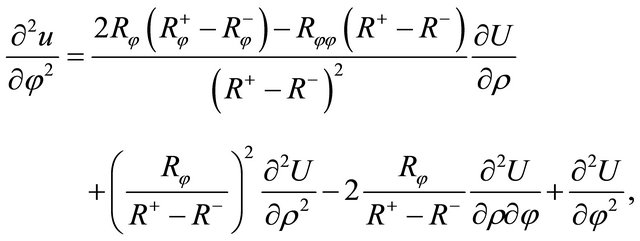 (12)
(12)
with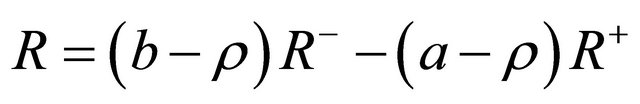 , and where the subscripts denote the partial differentiation with respect to the polar angles
, and where the subscripts denote the partial differentiation with respect to the polar angles 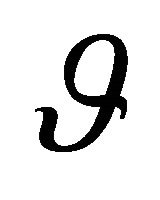 and
and . Substituting Equations (8)- (12) into Equation (6) finally yields Equation (13).
. Substituting Equations (8)- (12) into Equation (6) finally yields Equation (13).
 (13)
(13)
As it can be easily noticed, upon setting 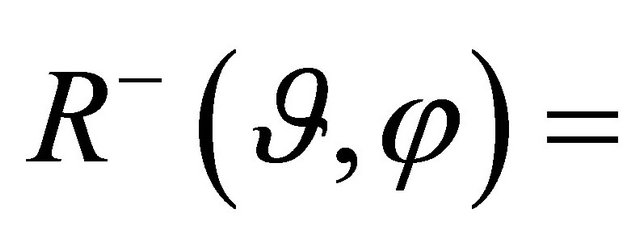
 and
and , the classical expression of the Laplacian in spherical coordinates is recovered.
, the classical expression of the Laplacian in spherical coordinates is recovered.
3. The Robin Problem for the Helmholtz Equation
Let us consider the interior Robin problem for the Helmholtz equation in a starlike shell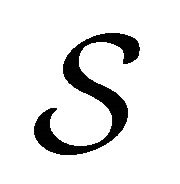 , whose boundaries
, whose boundaries  are described by the polar equations
are described by the polar equations 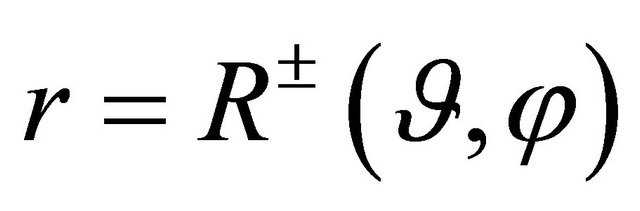 respectively:
respectively:
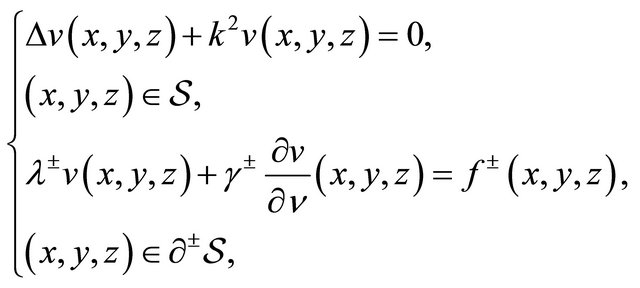 (14)
(14)
where 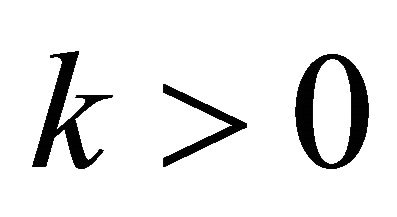 denotes the propagation constant,
denotes the propagation constant, 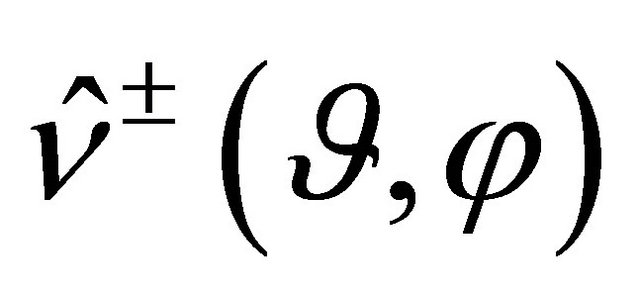
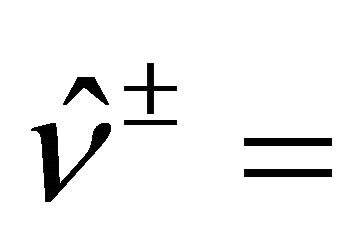 are the outward-pointing normal unit vectors to the domain boundaries
are the outward-pointing normal unit vectors to the domain boundaries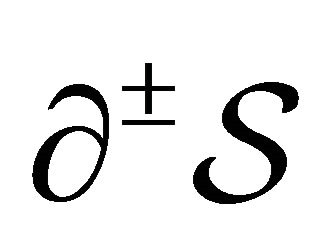 , respectively, and
, respectively, and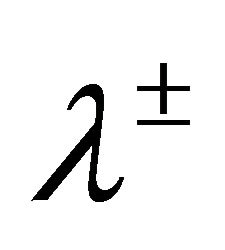 ,
,  are given regular weighting coefficients.
are given regular weighting coefficients.
Under the mentioned assumptions, one can prove the following theorem.
Theorem. Let:
 (15)
(15)
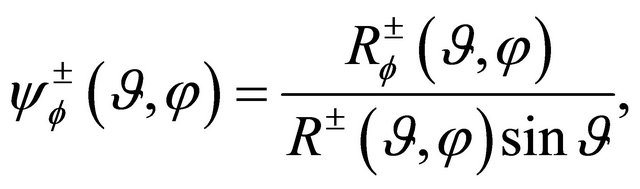 (16)
(16)
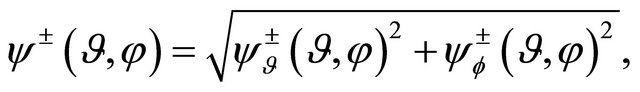 (17)
(17)
and
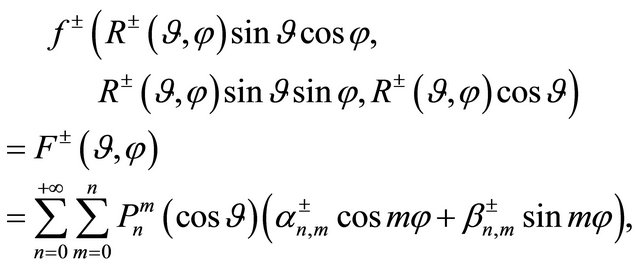 (18)
(18)
where:
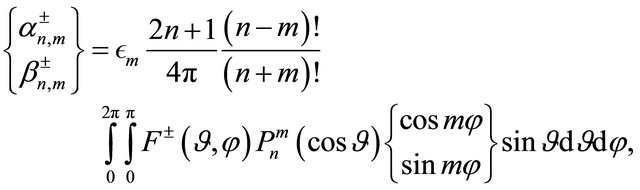 (19)
(19)
 being the usual Neumann’s symbol and
being the usual Neumann’s symbol and 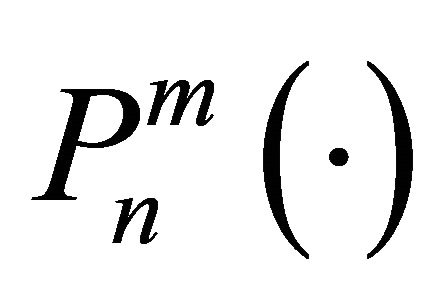 the associated Legendre function of the first kind and orders n, m. Then, the boundary-value problem (14) for the Helmholtz equation admits a classical solution
the associated Legendre function of the first kind and orders n, m. Then, the boundary-value problem (14) for the Helmholtz equation admits a classical solution 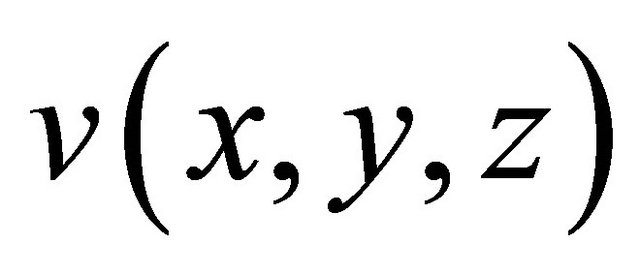
 such that the series expansion (20) holds true.
such that the series expansion (20) holds true.
In Equation (20) 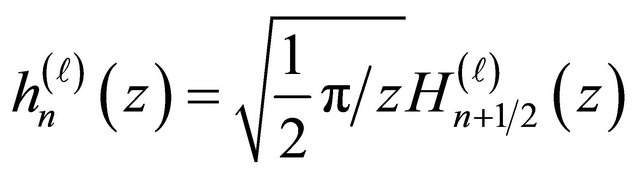 denotes the spherical Hankel function of kind
denotes the spherical Hankel function of kind 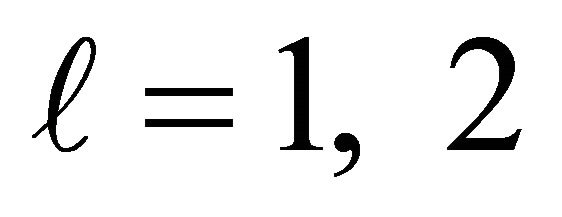 and order n. For each pair of indices
and order n. For each pair of indices 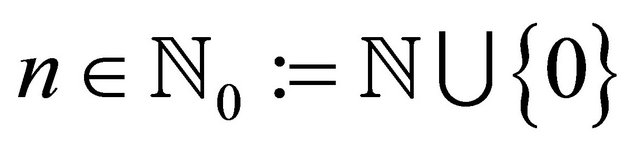 and
and 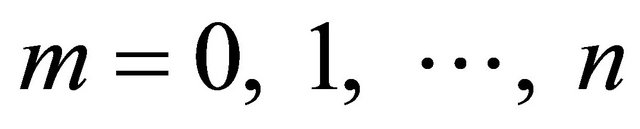 introduce the terms reported in Equation (21), where:
introduce the terms reported in Equation (21), where:
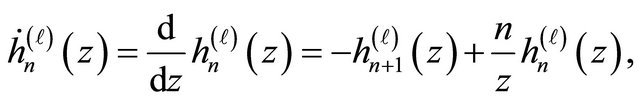 (22)
(22)
and
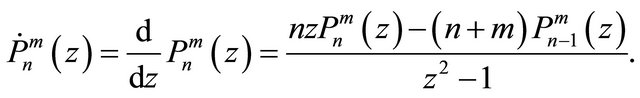 (23)
(23)
Therefore, the coefficients 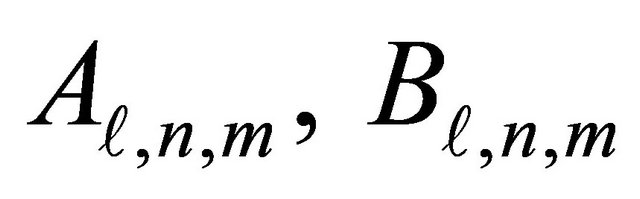 in (20) can be determined by solving the infinite linear system:
in (20) can be determined by solving the infinite linear system:
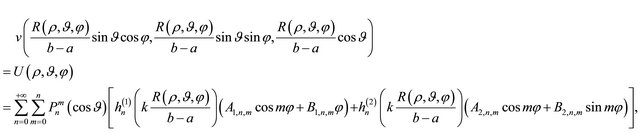 (20)
(20)
 (21)
(21)
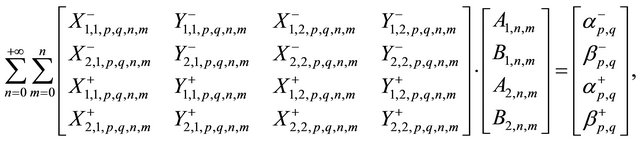 (24)
(24)
where:
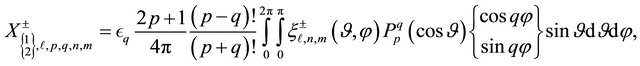 (25)
(25)
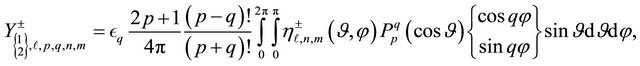 (26)
(26)
with 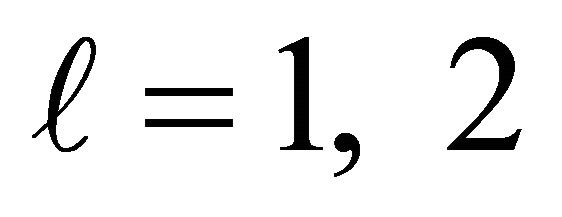 and
and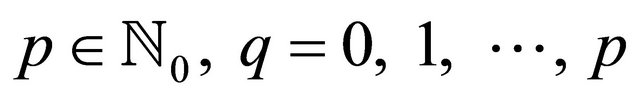 .
.
Proof: Upon noting that in the stretched coordinate system 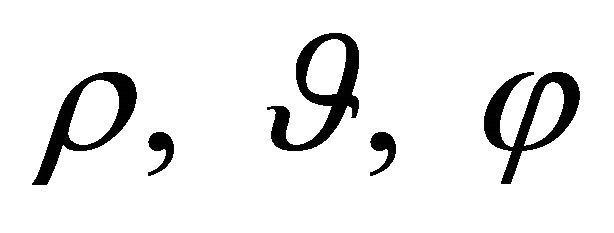 introduced in the
introduced in the 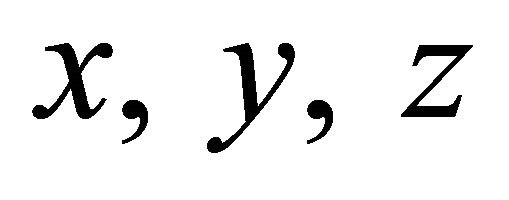 space, the considered domain
space, the considered domain  turns into the spherical shell of radii a and b, one can readily adopt the usual eigenfunction method [1] in combination with the separation of variables (with respect to
turns into the spherical shell of radii a and b, one can readily adopt the usual eigenfunction method [1] in combination with the separation of variables (with respect to 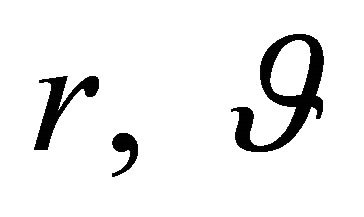 and
and ). As a consequence, elementary solutions of the problem can be searched in the form:
). As a consequence, elementary solutions of the problem can be searched in the form:
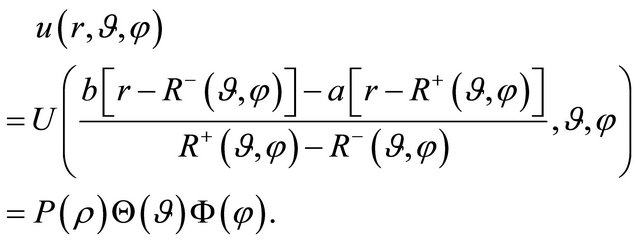 (27)
(27)
Substituting into the Helmholtz equation, one easily finds that the functions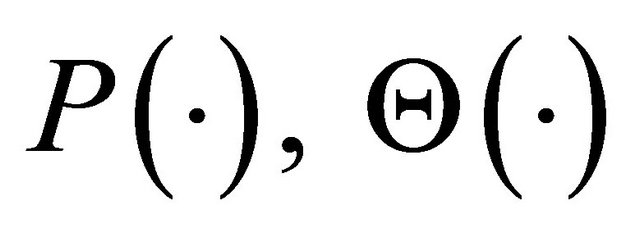 , and
, and 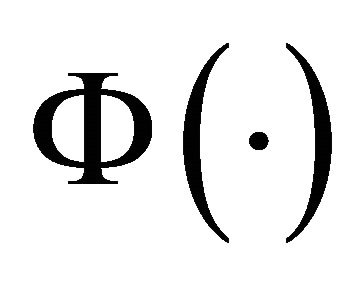 must satisfy the ordinary differential equations:
must satisfy the ordinary differential equations:
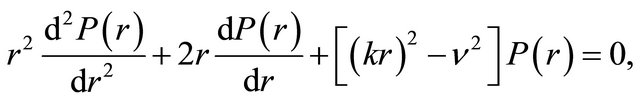 (28)
(28)
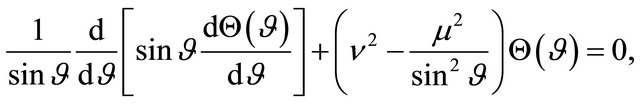 (29)
(29)
 (30)
(30)
respectively. The parameters 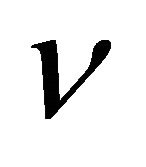 and
and  are separation constants, whose choice is governed by the physical requirement that at any fixed point in space the scalar field
are separation constants, whose choice is governed by the physical requirement that at any fixed point in space the scalar field 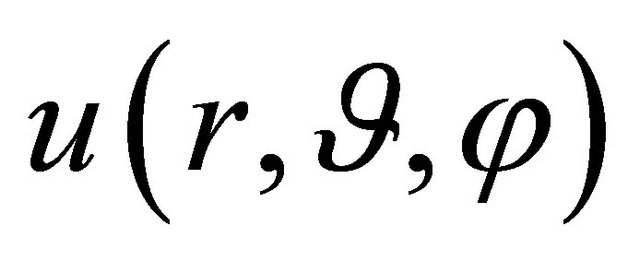 must be single-valued. So, by setting:
must be single-valued. So, by setting:
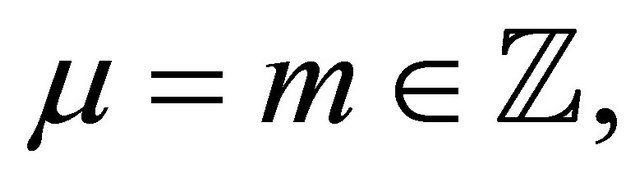 (31)
(31)
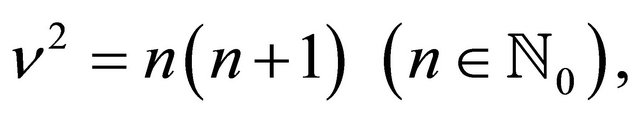 (32)
(32)
one can easily find:
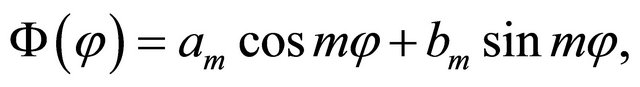 (33)
(33)
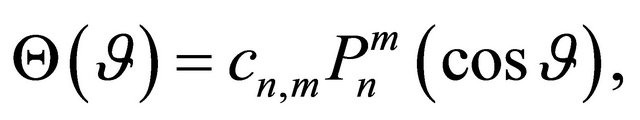 (34)
(34)
where 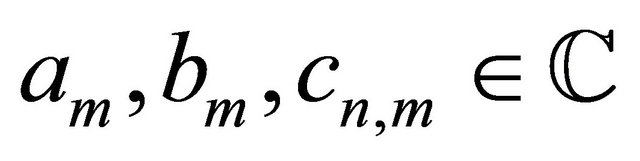 denote arbitrary constants. In order to identify the radial function
denote arbitrary constants. In order to identify the radial function  introduced in (27), it is convenient to set:
introduced in (27), it is convenient to set:
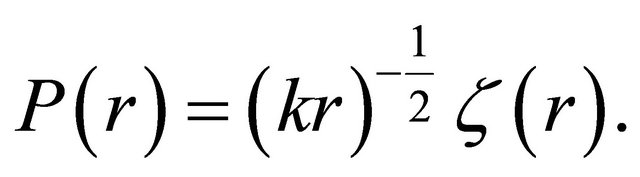 (35)
(35)
In this way, it is readily shown that 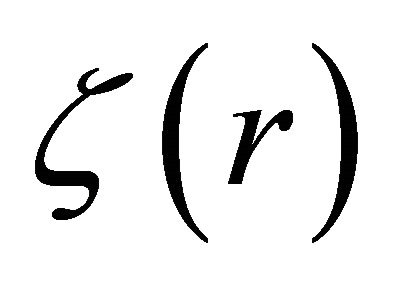 satisfies:
satisfies:
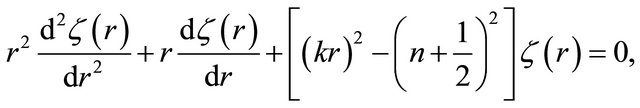 (36)
(36)
and, hence, is a cylinder function of half order that, without loss of generality, can be expressed as a linear combination of ordinary Hankel functions of first and second kind must, so that:
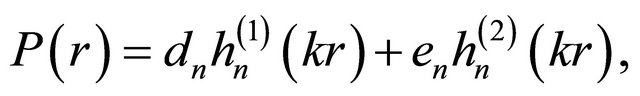 (37)
(37)
with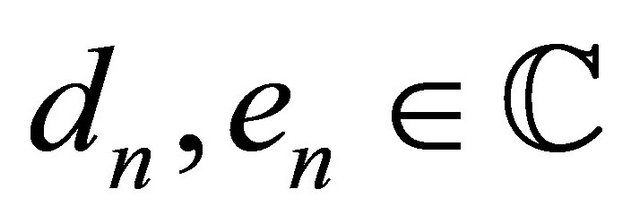 . Therefore, the general solution of the Robin problem (14) can be searched in the form:
. Therefore, the general solution of the Robin problem (14) can be searched in the form:
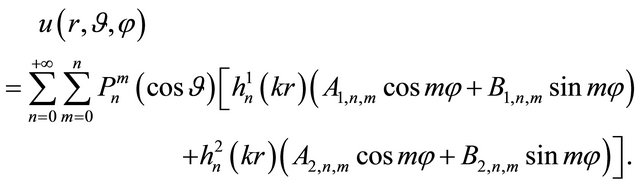 (38)
(38)
Enforcing the Robin boundary condition yields:
 (39)
(39)
where:
 (40)
(40)
and:
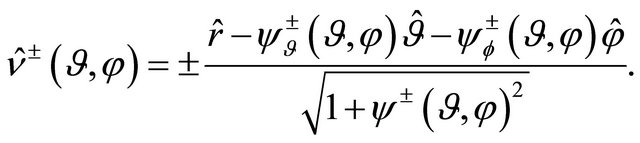 (41)
(41)
Hence, combining equations above and using a classical harmonic projection method, the Equations (21)-(26) follow after some algebraic manipulations.
It is worth noting that the derived expressions still hold under the assumption that 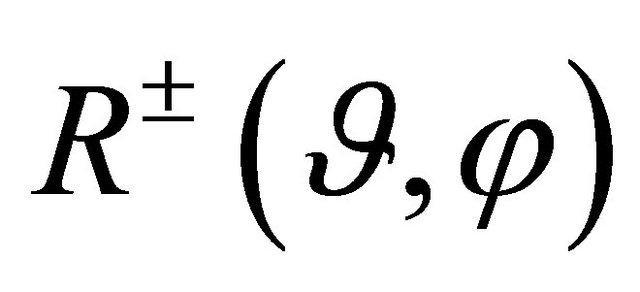 are piecewise continuous functions, and the boundary values are described by square integrable, not necessarily continuous, functions, so that the relevant spherical harmonic coefficients
are piecewise continuous functions, and the boundary values are described by square integrable, not necessarily continuous, functions, so that the relevant spherical harmonic coefficients 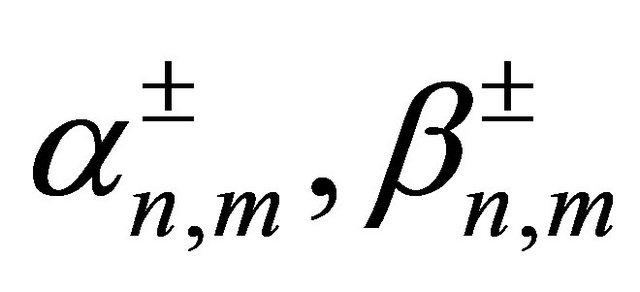 in Equation (19) are finite quantities.
in Equation (19) are finite quantities.
4. Numerical Procedure
In the following numerical examples, let us assume, for the boundaries 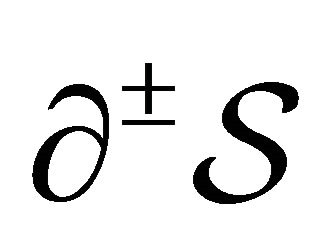 of the considered annulus, general polar equations of the type:
of the considered annulus, general polar equations of the type:
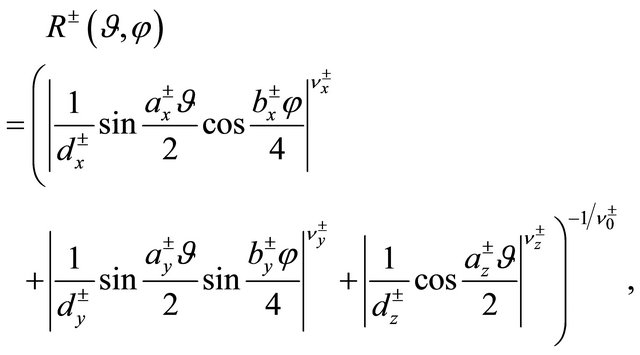 (42)
(42)
which provides an extension, to the three-dimensional case, of the “superformula” introduced by Gielis in [18] . Very different characteristic geometries, including ellipsoids, ovaloids, and Lamé-type domains (also called “superellipsoids”) can be obtained by assuming suitable values of the parameters 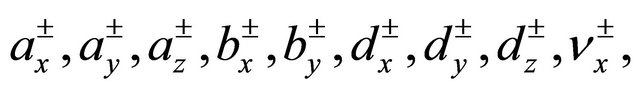
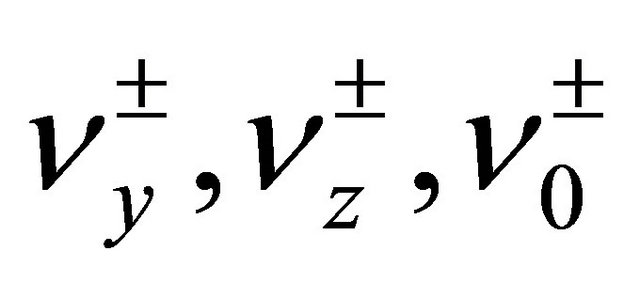 in (42). It is to emphasized that almost all three-dimensional normalpolar shell-like domains can be described, or closely approximated, by the considered formula.
in (42). It is to emphasized that almost all three-dimensional normalpolar shell-like domains can be described, or closely approximated, by the considered formula.
In order to assess the performance of the proposed methodology in terms of numerical accuracy and convergence rate, the relative boundary error has been evaluated according to Equation (43), where 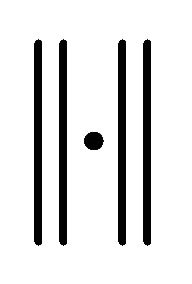 is the usual
is the usual 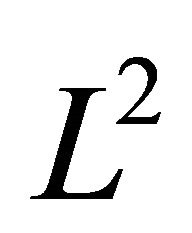 norm, and
norm, and 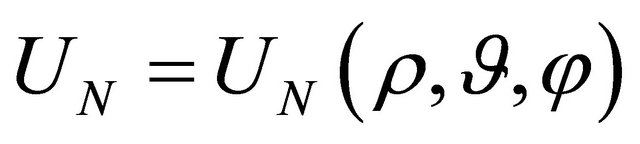 denotes the partial sum of order N relevant to the spherical harmonic expansion representing the solution of the boundary-value problem for the Helmholtz equation (see Equation (44)).
denotes the partial sum of order N relevant to the spherical harmonic expansion representing the solution of the boundary-value problem for the Helmholtz equation (see Equation (44)).
Remark: It is to be noted that, where the boundary values exhibit a rapidly oscillating behavior, the number N of terms in the spherical harmonic expansion approximating the solution of the problem should be increased accordingly in order to achieve the desired numerical accuracy.
Example
Upon assuming in (42) 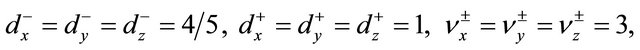
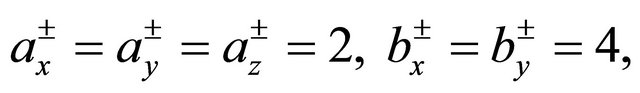
and , the shell
, the shell  turns to feature a cuboidal shape. Let
turns to feature a cuboidal shape. Let  and
and 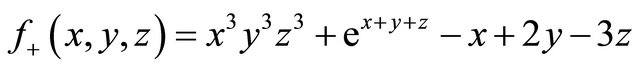 be the functions describing the boundary values. Provided that the propagation constant is
be the functions describing the boundary values. Provided that the propagation constant is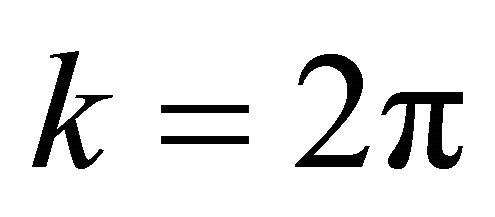 , and
, and 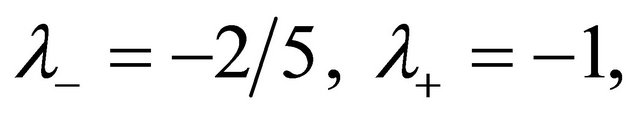
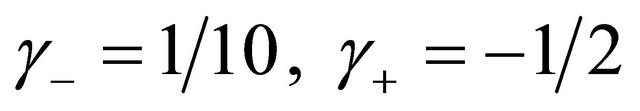 are the weighting coefficients in the Robin condition, the relative boundary error
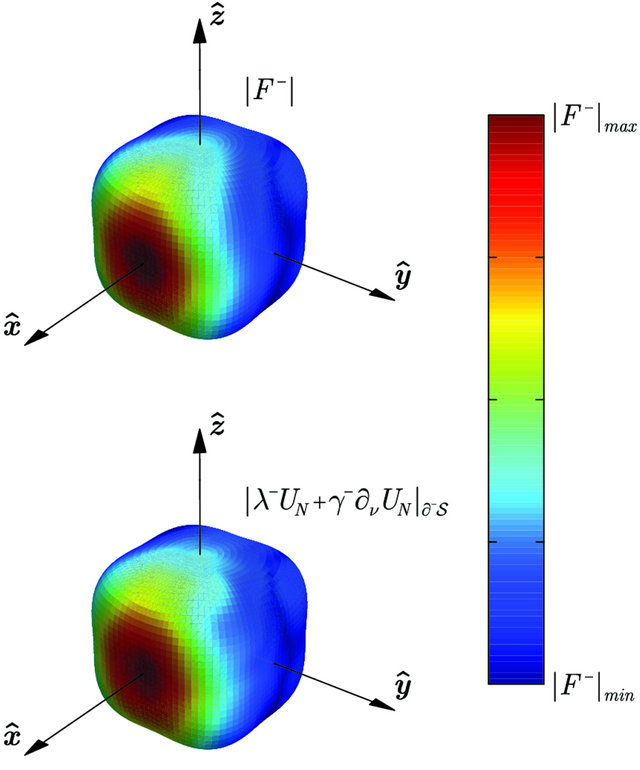
are the weighting coefficients in the Robin condition, the relative boundary error 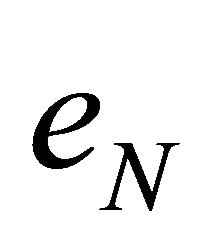 as function of the number N of terms in the truncated series expansion (44) exhibits the behavior shown in Figure 1. As it appears from Figure 2, the selection of the expansion order
as function of the number N of terms in the truncated series expansion (44) exhibits the behavior shown in Figure 1. As it appears from Figure 2, the selection of the expansion order  leads to a very accurate representation of the solution
leads to a very accurate representation of the solution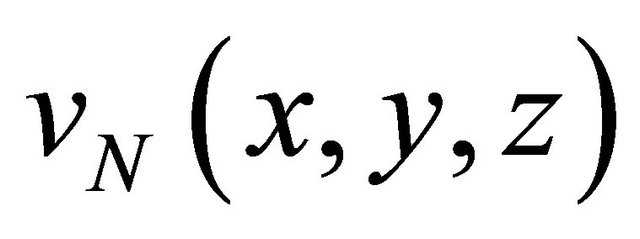 , whose spherical harmonic coefficients
, whose spherical harmonic coefficients  and
and 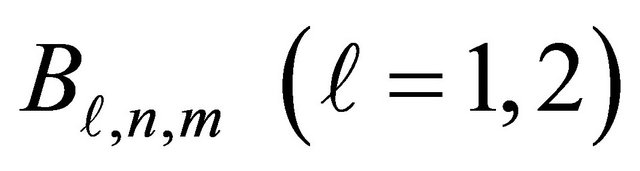 are plotted in Figure 3.
are plotted in Figure 3.
Remark: It has been observed that  norm of the difference between the exact solution and the relevant approximation is generally negligible. Point-wise convergence seems to be verified in the considered domains, with the only exception of a set of measure zero consisting of quasi-cusped points. In the neighbourhood of these points, oscillations of the truncated order solution, recalling the classical Gibbs phenomenon, usually take place.
norm of the difference between the exact solution and the relevant approximation is generally negligible. Point-wise convergence seems to be verified in the considered domains, with the only exception of a set of measure zero consisting of quasi-cusped points. In the neighbourhood of these points, oscillations of the truncated order solution, recalling the classical Gibbs phenomenon, usually take place.
 (43)
(43)
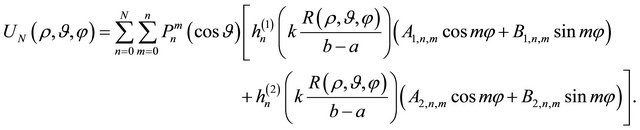 (44)
(44)

Figure 1. Relative boundary error eN as function of the order N of the truncated spherical harmonic expansion representing the solution of the considered Robin problem for the Helmholtz equation in the supershaped shell  described by the generalized Gielis formula with parameters
described by the generalized Gielis formula with parameters 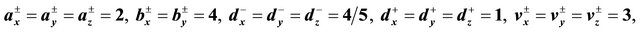
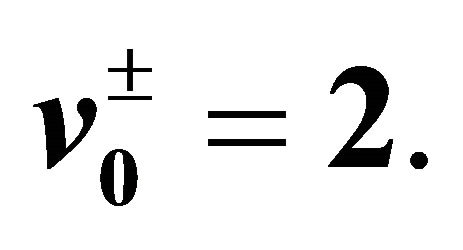
 (a)
(a)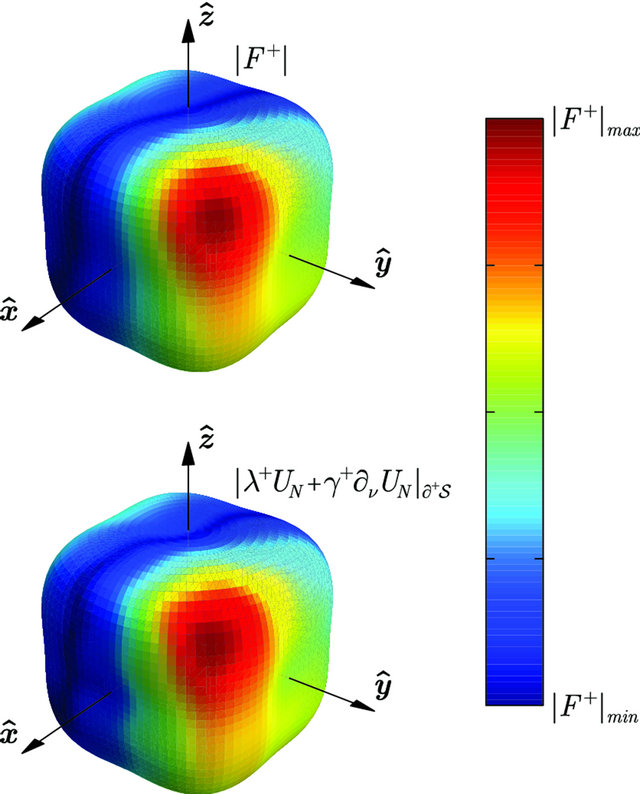 (b)
(b)
Figure 2. Boundary behavior along 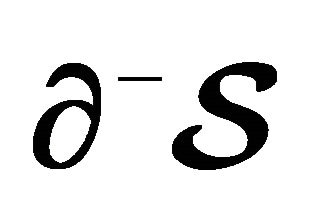 (a) and
(a) and 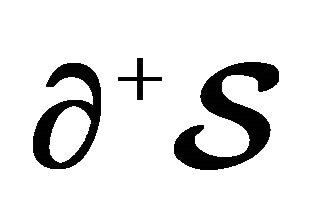 (b) of the partial sum
(b) of the partial sum 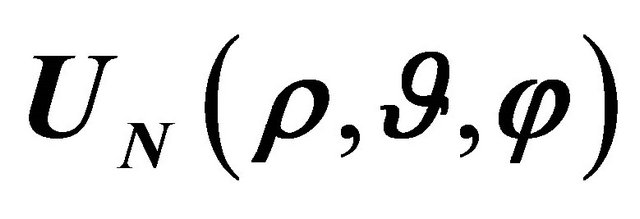 of order
of order  representing the solution of the considered Robin problem for the Helmholtz equation in the supershaped shell
representing the solution of the considered Robin problem for the Helmholtz equation in the supershaped shell .
.
5. Conclusion
A harmonic projection method, in combination with the adoption of a suitable stretched coordinate system, has been developed for solving the Robin problem for the Helmholtz equation in supershaped shell. In this way, analytically based expressions of the solution of the considered class of BVPs can be derived by using classical quadrature rules, so overcoming the need for cumbersome numerical techniques such as finite-difference or finite-element methods. The proposed approach has been successfully validated by means of a dedicated numerical procedure based on the computer-aided algebra tool Mathematica©. A point-wise convergence of the expansion series representing the solution seems to be verified
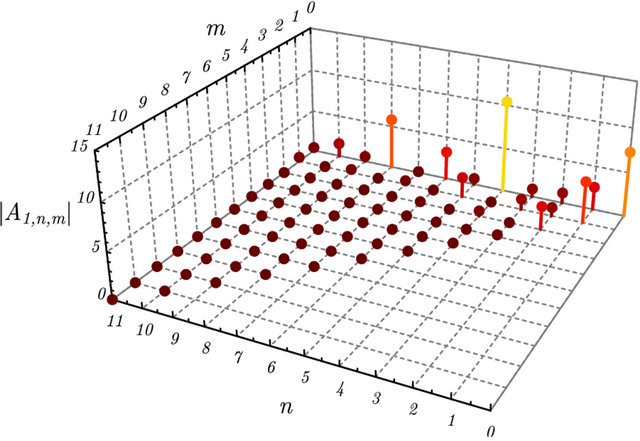 (a)
(a)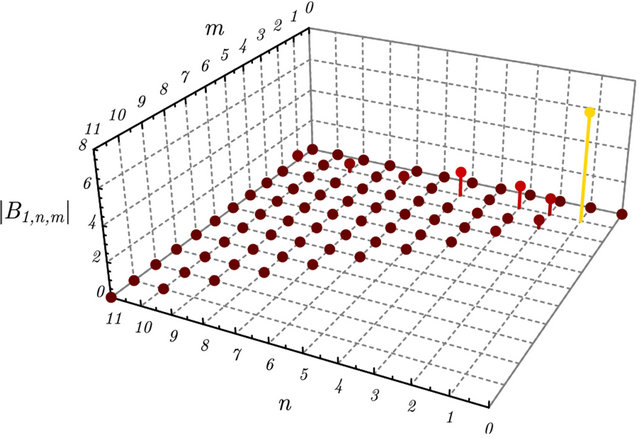 (b)
(b)
Figure 3. Magnitude of the coefficients 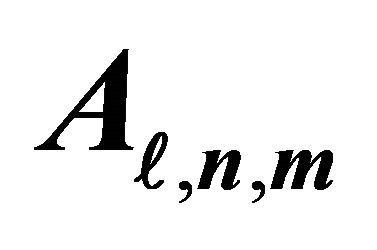 and
and 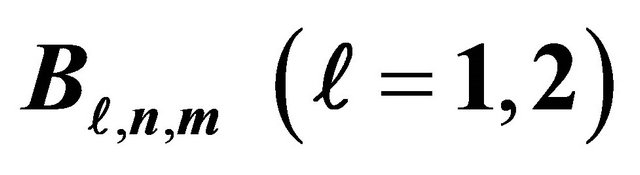 relevant to the spherical harmonic expansion
relevant to the spherical harmonic expansion 
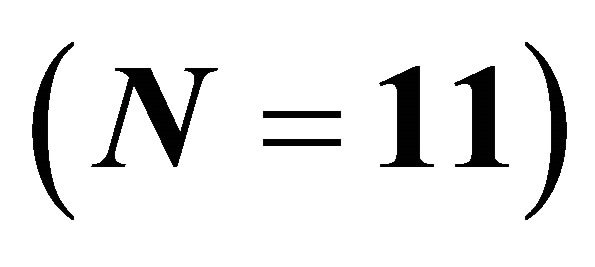 representing the solution of the considered Robin problem for the Helmholtz equation in the supershaped shell
representing the solution of the considered Robin problem for the Helmholtz equation in the supershaped shell .
.
with the only exception of a set of measure zero consisting of the quasi-cusped points along the boundary of the problem domain. In these points, Gibbs-like oscillations may occur. The computed results are found to be in good agreement with the theoretical findings on Fourier series.
REFERENCES
- N. N. Lebedev, “Special Functions and Their Applications,” Dover Inc., New York, 1972.
- G. Krall, “Meccanica Tecnica Delle Vibrazioni,” Vol. 2, Veschi, Roma, 1970.
- A. Bondeson, T. Rylander and P. Ingelstrom, “Computational Electromagnetics,” Springer Science, New York, 2005.
- D. Medková, “Solution of the Dirichlet Problem for the Laplace Equation,” Applications of Mathematics, Vol. 44, No. 2, 1999, pp. 143-168. doi:10.1023/A:1022209421576
- B. N. Khoromski, “Integro-Difference Method of Solution of the Dirichlet Problem for the Laplace Equation,” Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, Vol. 24, No. 1, 1984, pp. 53-64.
- A. P. Volkov, “An Effective Method for Solving the Dirichlet Problem for the Laplace Equation,” Differentsial’nye Uravneniya, Vol. 19, 1983, pp. 1000-1007.
- D. M. Young, “Iterative Methods for Solving Partial Difference Equations of Elliptic Type,” Transactions on American Mathematical Society, Vol. 76, 1954, pp. 92- 111. doi:10.1090/S0002-9947-1954-0059635-7
- G. P. Tolstov, “Fourier Series,” Dover Inc., New York, 1962.
- P. Natalini, R. Patrizi, and P. E. Ricci, “The Dirichlet Problem for the Laplace Equation in a Starlike Domain of a Riemann Surface,” Numerical Algorithms, Vol. 28, No. 1-4, 2001, pp. 215-227. doi:10.1023/A:1014059219005
- D. Caratelli and P. E. Ricci, “The Dirichlet Problem for the Laplace Equation in a Starlike Domain,” Proceedings of International Conference on Scientific Computing, Las Vegas, 14-17 July 2008, pp. 160-166.
- D. Caratelli, B. Germano, J. Gielis, M. X. He, P. Natalini and P. E. Ricci, “Fourier Solution of the Dirichlet Problem for the Laplace and Helmholtz Equations in Starlike Domains,” Lecture Notes of Tbilisi International Centre of Mathematics and Informatics, Tbilisi University Press, Tbilisi, 2010.
- D. Caratelli, P. Natalini, P. E. Ricci and A. Yarovoy, “The Neumann Problem for the Helmholtz Equation in a Starlike Planar Domain,” Applied Mathematics and Computation, Vol. 216, No. 2, 2010, pp. 556-564. doi:10.1016/j.amc.2010.01.077
- D. Caratelli, J. Gielis, P. Natalini, P. E. Ricci and I. Tavkelidze, “The Robin Problem for the Helmholtz Equation in a Starlike Planar Domain,” Georgian Mathematical Journal, Vol. 18, No. 3, 2011, pp. 465-480.
- D. Caratelli, J. Gielis and P. E. Ricci, “Fourier-Like Solution of the Dirichlet Problem for the Laplace Equation in k-Type Gielis Domains,” Journal of Pure and Applied Mathematics: Advances and Applications, Vol. 5, No. 2, 2011, pp. 99-111.
- D. Caratelli, P. E. Ricci and J. Gielis, “The Robin Problem for the Laplace Equation in a Three-Dimensional Starlike Domain,” Applied Mathematics and Computation, Vol. 218, No. 3, 2011, pp. 713-719.
- J. Gielis, D. Caratelli, Y. Fougerolle, P. E. Ricci and T. Gerats, “Universal Natural Shapes from Unifying Shape Description to Simple Methods for Shape Analysis and Boundary Value Problems,” PLoS One, Vol. 7, No. 9, 2012, Article ID: e29324. doi:10.1371/journal.pone.0029324
- G. Dattoli, B. Germano, M. R. Martinelli and P. E. Ricci, “A Novel Theory of Legendre Polynomials,” Mathematical and Computer Modelling, Vol. 54, No. 1-2, 2011, pp. 80-87. doi:10.1016/j.mcm.2011.01.037
- J. Gielis, “A Generic Geometric Transformation that Unifies a Wide Range of Natural and Abstract Shapes,” American Journal of Botany, Vol. 90, No. 3, 2003, pp. 333-338. doi:10.3732/ajb.90.3.333
- L. Carleson, “On Convergence and Growth of Partial Sums of Fourier Series,” Acta Mathematica, Vol. 116, No. 1, 1966, pp. 135-157. doi:10.1007/BF02392815
NOTES
*This research has been partly carried out under the grant PRIN/2006 Cap. 7320.

