Applied Mathematics
Vol.4 No.1(2013), Article ID:27199,5 pages DOI:10.4236/am.2013.41014
Optimal Redundancy Allocation in Hierarchical Series—Parallel Systems Using Mixed Integer Programming
Department of Industrial Engineering, University of Bojnord, Bojnord, Iran
Email: ziaee@iust.ac.ir
Received September 23, 2012; revised October 22, 2012; accepted October 30, 2012
Keywords: Hierarchical Series-Parallel System; Optimal Redundancy Allocation; Mixed Integer Programming Formulation; Reliability Optimization
ABSTRACT
Reliability optimization plays an important role in design, operation and management of the industrial systems. System reliability can be easily enhanced by improving the reliability of unreliable components and/or by using redundant configuration with subsystems/components in parallel. Redundancy Allocation Problem (RAP) was studied in this research. A mixed integer programming model was proposed to solve the problem, which considers simultaneously two objectives under several resource constraints. The model is only for the hierarchical series-parallel systems in which the elements of any subset of subsystems or components are connected in series or parallel and constitute a larger subsystem or total system. At the end of the study, the performance of the proposed approach was evaluated by a numerical example.
1. Introduction
The reliability optimization plays an important role in design, operation and management of the industrial systems. The reliability of a system can be easily enhanced by improving the reliability of unreliable components and/or by using redundant configuration with subsystems/components in parallel. Improving component reliability has been generally preferred over adding redundancy in industry, because the redundancy is difficult to add to the real systems due to the technical limitations such as weight, volume, and cost. However, recently developed advanced technologies such as semiconductor integrated circuits and nanotechnology, have revived the importance of the redundancy strategy [1].
A well-known and complex reliability optimization problem is the redundancy apportionment problem for the series-parallel systems which can be defined as the problem of the selection of the optimal combination of component type and redundancy level for each subsystem in order to meet various objectives under given constraints on the overall system [2]. This problem was studied in this research. The objectives considered were the maximization of the system reliability, and the minimization of the system cost. The study was looking for the number and the type of the redundant components which optimize the objective function under several different constraints such as the overall system weight and total number of the components used in all redundancies.
The literature abounds with numerous and very different techniques for solving the optimal redundancy allocation problem with various objectives and different resource constraints. Ha and Kuo [1] presented a branchand-bound approach to solve the redundancy allocation problem (RAP) formulated as a non-convex integer nonlinear programming model. Their computational experiments demonstrated that the method was superior to the other existing exact algorithms for RAP in terms of computation time. A combined approach was presented by Nourelfath and Dutuit [3] to solve the redundancy optimization problem for multi-state systems under repair policies. Azaron et al. [4] dealt with the reliability function of a class of time-dependent systems with stand by redundancy. You and Chen [5] proposed a heuristic algorithm based on a multi-start search procedure for solving a series-parallel RAP with separable linear constraints. An Ant Colony Optimization (ACO) algorithm was proposed by Liang and Smith [6] for the RAP. Shelokar et al. [7] applied an ACO algorithm for single and multi-objective reliability optimization problems. Nahas and Nourelfath [8] examined applying an ant system to reliability optimization of a series system with multiple-choice and budget constraints. An ACO algorithm with a multi-objective formulation was developed by Zhao et al. [2] in order to solve the redundancy apportionment problem of seriesparallel k-out-of-n G: subsystems (denoted by ACSRAP). Mahapatra and Roy [9] dealt with the reliability optimization problem with several mutually conflicting objectives, which were the minimization of the system cost and the maximization of the system reliability, and proposed a fuzzy multi-objective optimization method for the series and complex system reliability. Ouzineb et al. [10] presented a heuristic approach based on a combination of space partitioning, genetic algorithm and tabu search to solve the redundancy allocation problem for series—parallel binary-state systems. The design goal of the RAP was to select the optimal combination of elements and redundancy levels to maximize system reliability subject to the system budget and to the system weight. After dividing the search space into a set of disjoint subsets, this approach uses GA to select the subspaces, and applies TS to each selected subspace. A heterogeneous redundancy optimization model based on genetic algorithm was proposed by Li et al. [11] for multistate series—parallel systems subject to common cause failures, in order to provide a desired level of reliability with minimum cost. Recently, Sharma et al. [12] investigated the heterogeneous RAP in multi-state series parallel reliability structures with the objective of the minimization of the total cost of system design satisfying given reliability constraint and consumer load demand. The demand distribution was presented as a piecewise cumulative load curve and each subsystem was allowed to consist of parallel redundant components of not more than three types. They proposed an ACO algorithm to solve the problem. There are many other researches on this topic in the literature (see, for example [13-16]). This study dealt with the RAP for hierarchical series—parallel systems and a new approach for mathematically modeling the problem was presented.
2. Assumptions and Notations
The assumptions considered in this study were as follows:
1) The model was only for the hierarchical series—parallel systems. A reliability system is called a Hierarchical Series Parallel system (HSP) if the system can be viewed as a set of subsystems arranged in a series parallel; each subsystem has a similar configuration; subsystems of each subsystem have a similar configuration and so on.
2) It was assumed that in a parallel configuration, at least one active component is required for the function; and in a series configuration, all components have to be active for the function.
3) The constrained resources considered in this problem were the repair times (in man-months, for example) and total number of components used in all redundancies.
4) The overall system weight (including all redundancies) could not exceed its upper limit.
5) Although in many real-world optimization problems, the financial budget is the most important constrained resource, in the reliability optimization problems, it is usually of less importance than technical constraints such as lower limit of whole system reliability; and therefore, in the problem studied in this paper, it was not considered as a constraint of the model and inadequacy of the system reliability coming from the budget limitation would not occur. Instead, the cost minimization was taken into account as an objective.
6) The maximization of the overall system reliability was also considered as an objective; moreover, it was assumed that the overall system reliability can not be less than its lower limit.
7) For each subsystem (component or system), there were several choices of subsystems (components or systems) with different reliability and resource requirements which could be used as redundancies.
The following notations were used in the proposed method.
2.1. Indices
i: If the total system is decomposed into several series/ parallel subsystems again and again until indecomposable subsystems (i.e. components) are reached, then a subsystem is at level i if it is result of decomposing the total system to series/parallel subsystems (n − i) times (if the total system can be decomposed up to n levels). We have i = 0, ..., n; i = n for the total system, and i = 0 for the components at the last level).
j: denotes jth subsystem of a given decomposition level (say i), j = 1, 2, …, mi; i.e. at level i, there are mi subsystems. Note that a subsystem may be a component or a set of components configured as a series/parallel system.
k: denotes kth redundant subsystem for a given subsystem.
2.2. Parameters
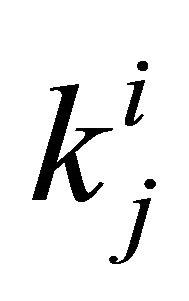 : Number of redundant subsystems for subsystem j at level i. These redundancies have different characteristics and performances, i.e. different reliabilities, procurement costs, repair costs, ..., and any arbitrary subset of them can be used as redundant subsystems for that subsystem; so k = 1, 2, ...,
: Number of redundant subsystems for subsystem j at level i. These redundancies have different characteristics and performances, i.e. different reliabilities, procurement costs, repair costs, ..., and any arbitrary subset of them can be used as redundant subsystems for that subsystem; so k = 1, 2, ...,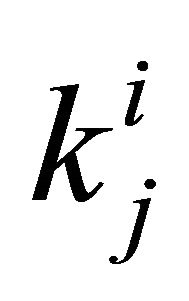 .
.
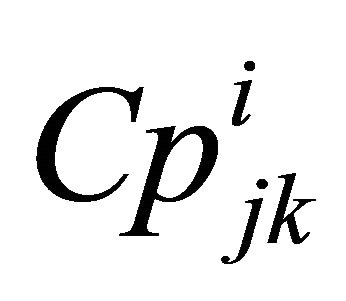 : Procurement cost of redundant subsystem k for subsystem j at level i.
: Procurement cost of redundant subsystem k for subsystem j at level i.
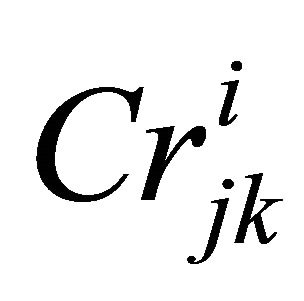 : Repair cost of redundant subsystem k for subsystem j at level i.
: Repair cost of redundant subsystem k for subsystem j at level i.
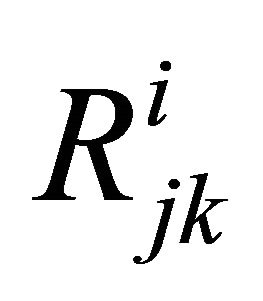 : Reliability of redundant subsystem k for subsystem j at level i.
: Reliability of redundant subsystem k for subsystem j at level i.
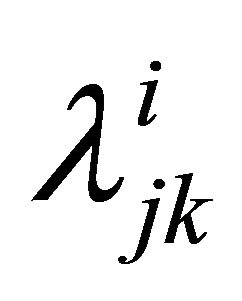 : Failure rate of redundant subsystem k for subsystem j at level i.
: Failure rate of redundant subsystem k for subsystem j at level i.
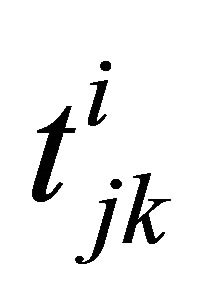 : Repair time of redundant subsystem k for subsystem j at level i.
: Repair time of redundant subsystem k for subsystem j at level i.
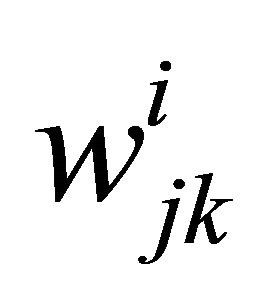 : Weight of redundant subsystem k for subsystem j at level i.
: Weight of redundant subsystem k for subsystem j at level i.
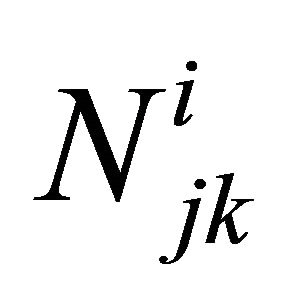 : Number of components used in redundant subsystem k for subsystem j at level i. Therefore, if the subsystem is a component, then its
: Number of components used in redundant subsystem k for subsystem j at level i. Therefore, if the subsystem is a component, then its 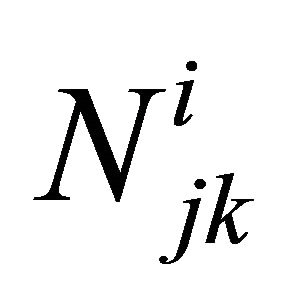 is equal to 1.
is equal to 1.
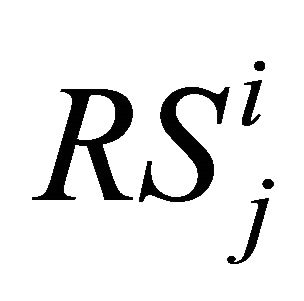 : Reliability of subsystem j at level i.
: Reliability of subsystem j at level i.
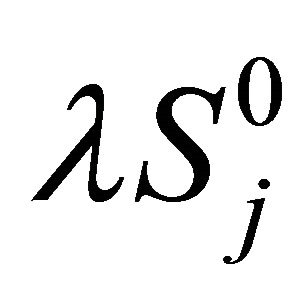 : Failure rate of subsystem j at level 0 (which is a component).
: Failure rate of subsystem j at level 0 (which is a component).
![]() : Repair time of subsystem j at level 0 (i.e. a component).
: Repair time of subsystem j at level 0 (i.e. a component).
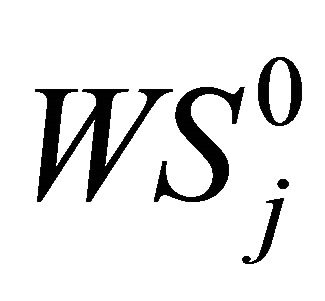 : Weight of subsystem j at level 0 (i.e. a component).
: Weight of subsystem j at level 0 (i.e. a component).
L: A scaling parameter.
T: Mission time.
Tr: Total available repair time (for example manmonths).
R: A lower limit on the overall system (including its redundant subsystems) reliability.
W: Maximum weight of the overall system (including its redundant subsystems).
A: An upper limit on the number of all redundant components used in the system.
2.3. Variables
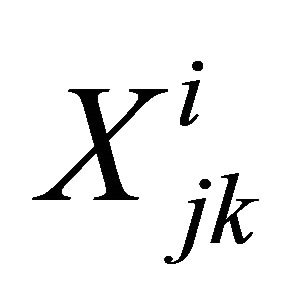 : Binary variable taking value 1 if redundant subsystem k for subsystem j at level i is used for improving the system reliability and 0 otherwise.
: Binary variable taking value 1 if redundant subsystem k for subsystem j at level i is used for improving the system reliability and 0 otherwise.
 (
( /
/ ): Total reliability of subsystem j at level i (including its redundant subsystems). The letter a (letter b) denotes that the subsystem is constituted of several subsystems connected in series (parallel).
): Total reliability of subsystem j at level i (including its redundant subsystems). The letter a (letter b) denotes that the subsystem is constituted of several subsystems connected in series (parallel).
3. Mixed Integer Programming Model
In this section, a mixed integer programming formulation is presented to solve the problem.
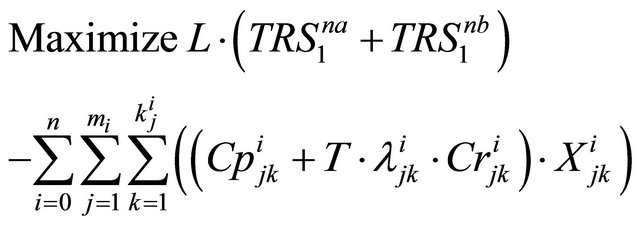
Subject to:
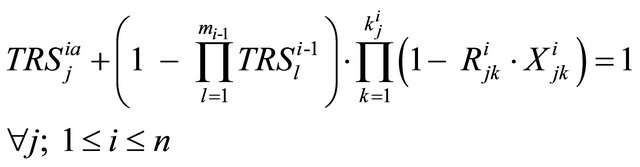 (1)
(1)
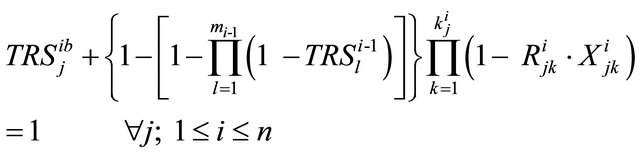 (2)
(2)
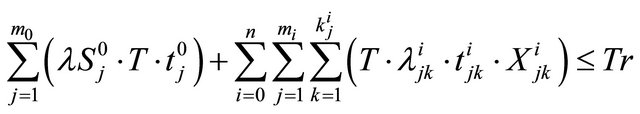 (3)
(3)
 (4)
(4)
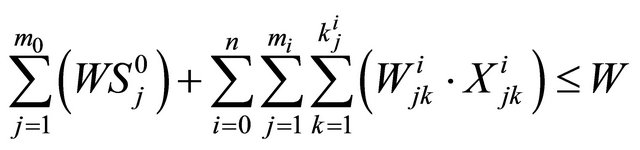 (5)
(5)
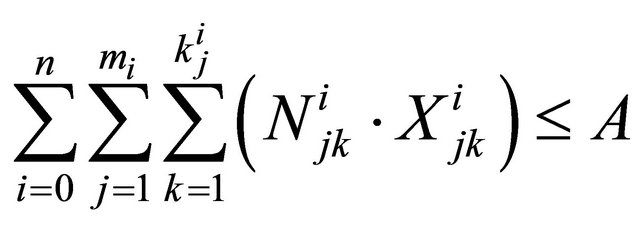 (6)
(6)
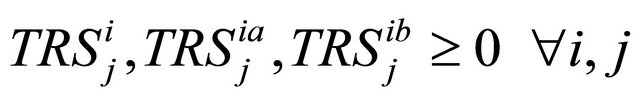
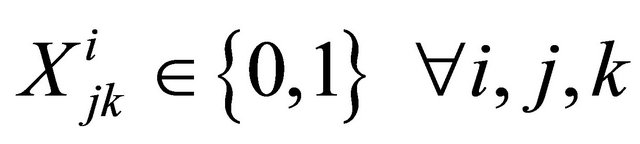
In the above model, 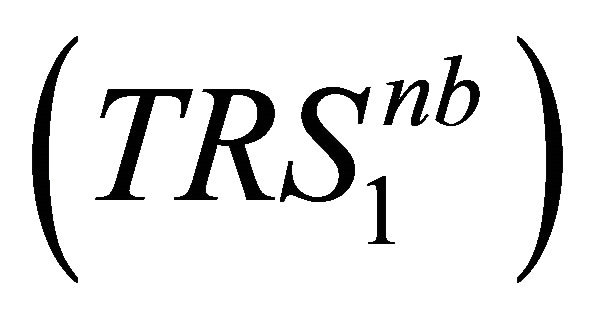
 is the reliability of the overall system if its subsystems are connected in series (parallel). Constraint sets (1) and (2) are recursive equations for calculating the reliability of any subsystem. Constraint (3) ensures that total required repair time does not exceed total available repair time. Constraint (4) guarantees that the overall system reliability is not less than its lower limit. Constraint sets (5) and (6) ensure that the overall system weight and the total number of components used in redundancies do not exceed their upper limits.
is the reliability of the overall system if its subsystems are connected in series (parallel). Constraint sets (1) and (2) are recursive equations for calculating the reliability of any subsystem. Constraint (3) ensures that total required repair time does not exceed total available repair time. Constraint (4) guarantees that the overall system reliability is not less than its lower limit. Constraint sets (5) and (6) ensure that the overall system weight and the total number of components used in redundancies do not exceed their upper limits.
4. Numerical Example
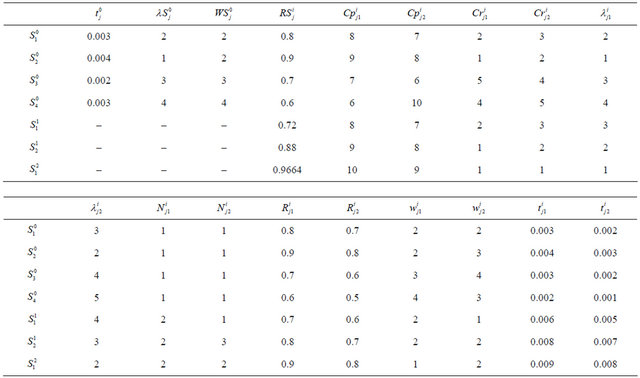
The proposed method was applied to solve a test problem. Figure 1 shows this problem of the hierarchical seriesparallel system configuration. The parameter values for the problem are listed in Table 1.
Other input data are L = 2, A = 10, T = 0.5, Tr = 0.98, R = 30, W = 8,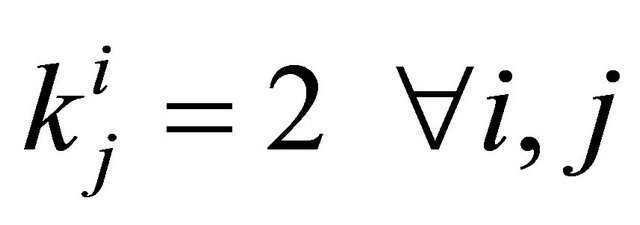 . The results obtained from solving the problem were as follows:
. The results obtained from solving the problem were as follows:
The objective function value was −590.0054,
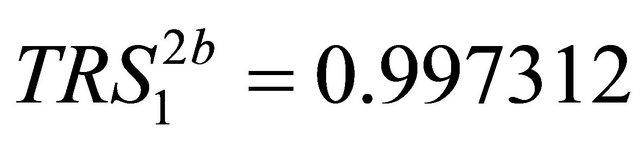 ,
, 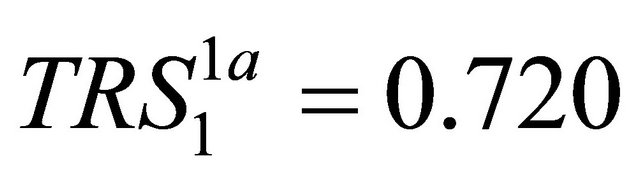 ,
,
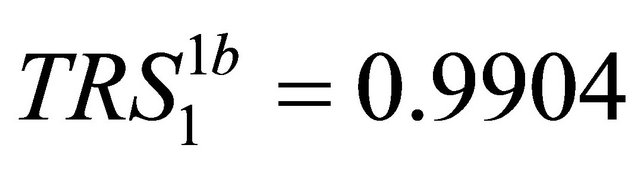 ,
, 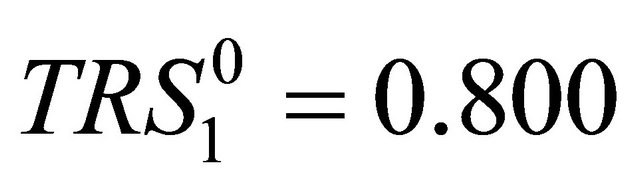 ,
,
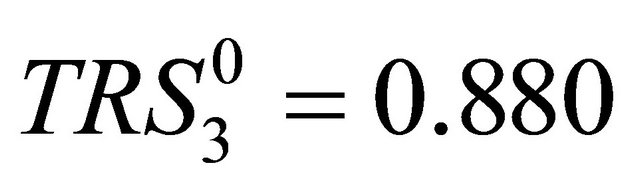 ,
, 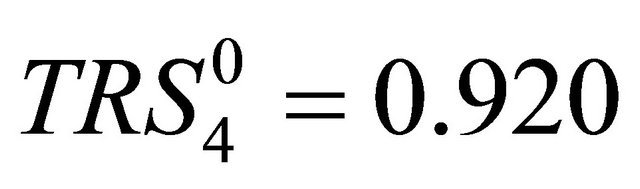 ,
,
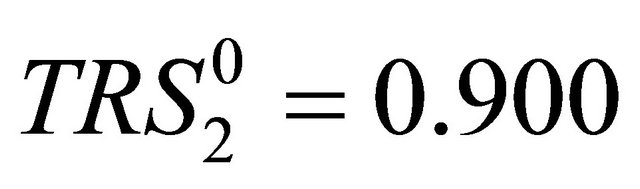 ,
,
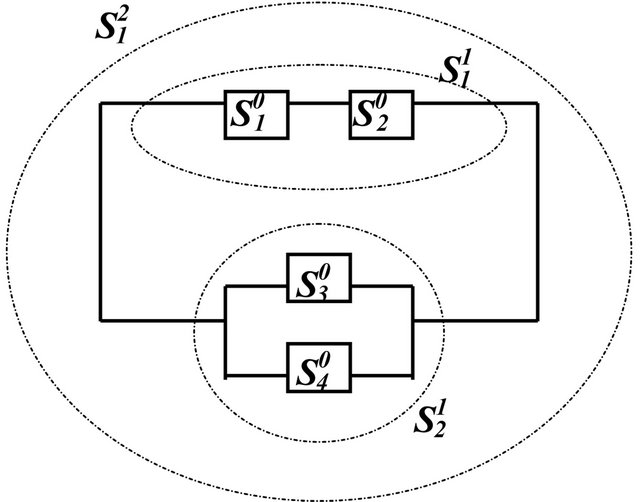
Figure 1. A hierarchical series-parallel system (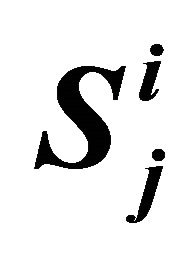 denotes subsystem j at level i).
denotes subsystem j at level i).
Table 1. Parameter values for the test problem.
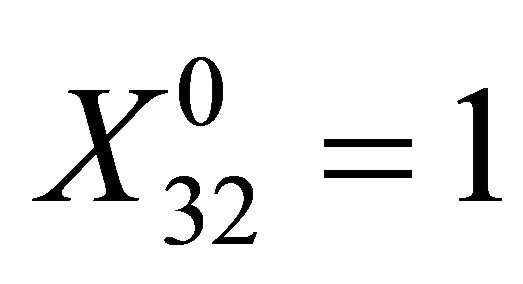 ,
, 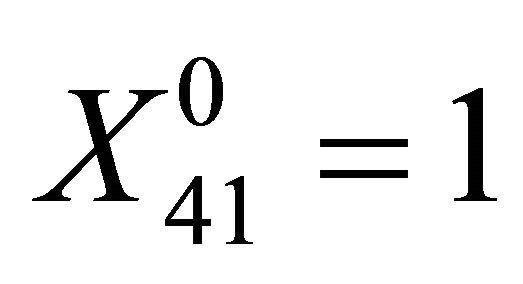 ,
, 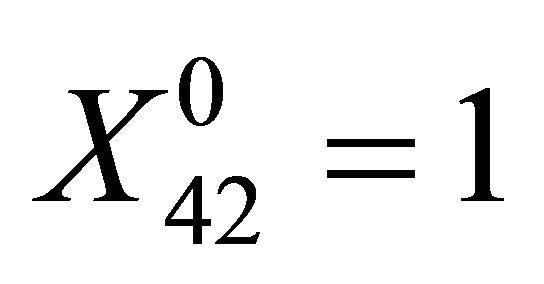 All other
All other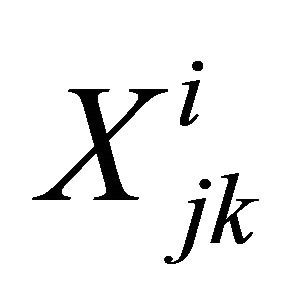 ’s were zero.
’s were zero.
5. Conclusion
In this paper, the RAP for a hierarchical series-parallel system under several resource constraints was studied. The following two objectives were considered: the maximization of the system reliability, and the minimization of the system cost. A new approach for mathematically modeling the problem was presented. The implementation of the proposed approach was illustrated by a sample application on a numerical example. Further work can be performed on to adapt the approach to other objectives and to extend it to more complex systems.
REFERENCES
- C. Ha and W. Kuo, “Reliability Redundancy Allocation: An Improved Realization for Nonconvex Nonlinear Programming Problems,” European Journal of Operational Research, Vol. 171, No. 1, 2006, pp. 24-38. doi:10.1016/j.ejor.2004.06.006
- J.-H. Zhao, Z. Liu and M.-T. Dao, “Reliability Optimization Using Multi-Objective Ant Colony System Approaches,” Reliability Engineering and System Safety, Vol. 92, No. 1, 2007, pp. 109-120. doi:10.1016/j.ress.2005.12.001
- M. Nourelfath and Y. Dutuit, “A Combined Approach to Solve the Redundancy Optimization Problem for MultiState Systems under Repair Policies,” Reliability Engineering and System Safety, Vol. 86, No. 3, 2004, pp. 205- 213. doi:10.1016/j.ress.2004.01.008
- A. Azaron, H. Katagiri, M. Sakawa and M. Modarres, “Reliability Function of a Class of Time-Dependent Systems with Standby Redundancy,” European Journal of Operational Research, Vol. 164, No. 2, 2005, pp. 378- 386. doi:10.1016/j.ejor.2003.10.044
- P.-S. You and T.-C. Chen, “An Efficient Heuristic for Series-Parallel Redundant Reliability Problems,” Computers & Operations Research, Vol. 32, No. 8, 2005, pp. 2117- 2127. doi:10.1016/j.cor.2004.02.003
- Y.-C. Liang and A. E. Smith, “An Ant Colony Optimization Algorithm for the Redundancy Allocation Problem (RAP),” IEEE Transactions on Reliability, Vol. 53, No. 3, 2004, pp. 417-423. doi:10.1109/TR.2004.832816
- P. S. Shelokar, V. K. Jayaraman and B. D. Kulkarni, “Ant Algorithm for Single and Multi-Objective Reliability Optimization Problems,” Quality and Reliability Engineering International, Vol. 18, No. 6, 2002, pp. 497-514. doi:10.1002/qre.499
- N. Nahas and M. Nourelfath, “Ant System for Reliability Optimization of a Series System with Multiple-Choice and Budget Constraints,” Reliability Engineering and System Safety, Vol. 87, No. 1, 2005, pp. 1-12. doi:10.1016/j.ress.2004.02.007
- G. S. Mahapatra and T. K. Roy, “Fuzzy Multi-Objective Mathematical Programming on Reliability Optimization Model,” Applied Mathematics and Computation, Vol. 174, No. 1, 2006, pp. 643-659. doi:10.1016/j.amc.2005.04.105
- M. Ouzineb, M. Nourelfath and M. Gendreau, “An Efficient Heuristic for Reliability Design Optimization Problems,” Computers & Operations Research, Vol. 37, No. 2, 2010, pp. 223-235. doi:10.1016/j.cor.2009.04.011
- C.-Y. Li , X. Chen, X.-S. Yi and J.-Y. Tao, “Heterogeneous Redundancy Optimization for Multi-State Series-Parallel Systems Subject to Common Cause Failures,” Reliability Engineering & System Safety, Vol. 95, No. 3, 2010, pp. 202-207. doi:10.1016/j.ress.2009.09.011
- V. K. Sharma, M. Agarwal and K. Sen, “Reliability Evaluation and Optimal Design in Heterogeneous Multi-State Series-Parallel Systems,” Information Sciences, Vol. 181, No. 2, 2011, pp. 362-378. doi:10.1016/j.ins.2010.09.015
- M. S. Chern, “On the Computational Complexity of Reliability Redundancy Allocation in a Series System,” Operations Research Letters, Vol. 11, No. 5, 1992, pp. 309- 315. doi:10.1016/0167-6377(92)90008-Q
- S. B. Graves, D. C. Murphy and J. L. Ringuest, “Acceptance Sampling and Reliability: The Tradeoff between Component Quality and Redundancy,” Computers & Industrial Engineering, Vol. 38, No. 1, 2000, pp. 79-91. doi:10.1016/S0360-8352(00)00030-9
- T. Nakagawa and K. Yasui, “Note on Optimal Redundant Policies for Reliability Models,” Journal of Quality in Maintenance Engineering, Vol. 11, No. 1, 2005, pp. 82- 96. doi:10.1108/13552510510589398
- K. Y. K. Ng and N. G. F. Sancho, “A Hybrid Dynamic Programming/Depth-First Search Algorithm with an Application to Redundancy Allocation,” IIE Transactions, Vol. 33, No. 12, 2001, pp. 1047-1058. doi:10.1080/07408170108936895

